许多问题需要将概率估算值作为输出。逻辑回归是一种非常高的概率计算机制。实际上,您可以通过以下两种方式之一使用返回的概率:
- 原样
- 已转换为二元类别。
我们来了解一下如何“按原样”使用概率。假设我们创建一个逻辑回归模型来预测狗在半夜发出叫声的概率。我们将这一概率称为:
\[p(bark | night)\]
如果逻辑回归模型预测到 \(p(bark | night) = 0.05\),那么一年内,狗狗的主人应该被惊醒约 18 次:
\[\begin{align} startled &= p(bark | night) \cdot nights \\ &= 0.05 \cdot 365 \\ &~= 18 \end{align} \]
在许多情况下,您需要将逻辑回归输出映射到二元分类问题,其中目标是正确预测两个可能的标签之一(例如,“垃圾邮件”或“不是垃圾邮件”)。后续模块会重点介绍这一点。
您可能想知道逻辑回归模型如何确保输出值始终介于 0 和 1 之间。巧合的是,S 型函数会产生如下具有相同特征的输出(定义如下):
S 型函数生成以下图表:
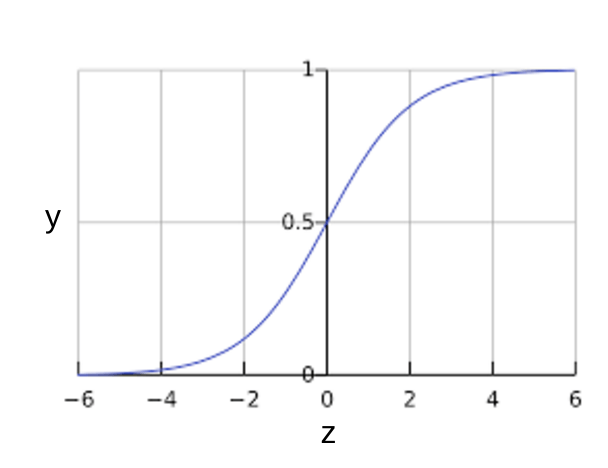
图 1:S 型函数。
如果 \(z\) 表示使用逻辑回归训练的模型的线性层的输出,则 \(sigmoid(z)\) 将生成一个介于 0 和 1 之间的值(概率)。用数学方式表示:
其中:
- \(y'\) 是特定示例的逻辑回归模型的输出。
- \(z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\)
- \(w\) 值是模型学习的权重, \(b\) 是偏差。
- \(x\) 值是特定样本的特征值。
请注意, \(z\) 也称为对数几率,因为 S 型函数的逆函数 \(z\) 可定义为 \(1\) 标签概率的对数(例如,“狗吠声”除以“ \(0\)”标签的概率(例如,&got;狗不会发出叫声):
以下是带有机器学习标签的 S 型函数:

图 2:逻辑回归输出。

