تحتوي هذه الصفحة على مصطلحات مسرد "غابات القرارات". للاطّلاع على جميع مصطلحات المسرد، يُرجى النقر هنا.
A
أخذ عيّنات من السمات
أسلوب لتدريب غابة القرارات، حيث لا تأخذ كل شجرة قرارات في الاعتبار سوى مجموعة فرعية عشوائية من الميزات المحتملة عند تعلُّم الشرط. بشكل عام، يتم أخذ عيّنة من مجموعة فرعية مختلفة من الميزات لكل عقدة. في المقابل، عند تدريب شجرة قرارات بدون أخذ عيّنات من السمات، يتم أخذ جميع الميزات المحتملة في الاعتبار لكل عقدة.
شرط محاذاة المحور
في شجرة القرارات، شرط
يتضمّن ميزة واحدة فقط. على سبيل المثال، إذا كانت area
سمة، يكون الشرط التالي متوافقًا مع المحور:
area > 200
قارِن ذلك بالشرط المائل.
B
التجميع
يشير ذلك المصطلح إلى طريقة تدريب مجموعة موحّدة يتم فيها تدريب كل نموذج مكوِّن على مجموعة فرعية عشوائية من أمثلة التدريب يتم جمعها مع الاستبدال. على سبيل المثال، الغابة العشوائية هي مجموعة من أشجار القرارات التي يتم تدريبها باستخدام أسلوب التجميع.
يشير مصطلح التجميع إلى تجميع عينات التمهيد.
يمكنك الاطّلاع على الغابات العشوائية في دورة "أشجار القرارات" للحصول على مزيد من المعلومات.
الشرط الثنائي
في شجرة القرار، الشرط الذي يتضمّن نتيجتَين محتمَلتَين فقط، عادةً نعم أو لا. على سبيل المثال، الشرط الثنائي التالي:
temperature >= 100
يختلف عن الحالة غير الثنائية.
اطّلِع على أنواع الشروط في دورة "أشجار القرار" للحصول على مزيد من المعلومات.
C
الشرط
في شجرة القرار، يشير ذلك المصطلح إلى أي عقدة تجري اختبارًا. على سبيل المثال، تحتوي شجرة القرارات التالية على شرطَين:

يُطلق على الشرط أيضًا اسم تقسيم أو اختبار.
حالة التباين مع ورقة الشجر
انظر أيضًا:
اطّلِع على أنواع الشروط في دورة "أشجار القرار" للحصول على مزيد من المعلومات.
D
غابة القرارات
نموذج تم إنشاؤه من عدة أشجار قرارات تُجري "غابة القرارات" عملية توقّع من خلال تجميع التوقّعات التي تقدّمها أشجار القرارات. تشمل الأنواع الشائعة من غابات القرارات الغابات العشوائية وأشجار التدرّج المعزّز.
يمكنك الاطّلاع على قسم أشجار القرارات العشوائية في دورة "أشجار القرارات" للحصول على مزيد من المعلومات.
شجرة القرارات
نموذج تعلُّم بإشراف يتألف من مجموعة من الشروط والعُقد الطرفية منظَّمة بشكل هرمي. على سبيل المثال، ما يلي هو شجرة قرارات:
E
الإنتروبيا
في نظرية المعلومات، القصور هو وصف لمدى عدم القدرة على التنبؤ بتوزيع الاحتمالات. ويمكن تعريف القصور أيضًا بأنه مقدار المعلومات التي يحتوي عليها كل مثال. يكون التوزيع ذا أعلى إنتروبيا ممكنة عندما تكون جميع قيم المتغيّر العشوائي متساوية الاحتمالية.
إنّ إنتروبيا مجموعة تتضمّن قيمتَين محتملتَين هما "0" و "1" (على سبيل المثال، التصنيفات في مسألة تصنيف ثنائي) تخضع للصيغة التالية:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
where:
- H هو القصور.
- p هي نسبة الأمثلة التي تكون فيها القيمة "1".
- q هي نسبة الأمثلة التي تكون فيها القيمة "0". يُرجى العِلم أنّ q = (1 - p)
- log هو بشكل عام log2. في هذه الحالة، وحدة الإنتروبيا هي بت.
على سبيل المثال، لنفترض ما يلي:
- تحتوي 100 عينة على القيمة "1"
- تحتوي 300 عينة على القيمة "0"
وبالتالي، تكون قيمة القصور كما يلي:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 0.81 بت لكل مثال
ستكون قيمة الإنتروبيا لمجموعة متوازنة تمامًا (على سبيل المثال، 200 من القيمة "0" و200 من القيمة "1") هي 1.0 بت لكل مثال. وكلما أصبحت المجموعة أكثر عدم توازن، اقترب القصور فيها من 0.0.
في أشجار القرارات، يساعد الانتروبيا في صياغة تحصيل المعلومات لمساعدة المقسّم في اختيار الشروط أثناء نمو شجرة قرارات التصنيف.
مقارنة الإنتروبيا بما يلي:
- مقياس جيني للتفاوت
- دالة الخسارة الإنتروبيا المتداخلة
يُطلق على القصور غالبًا اسم قصور شانون.
لمزيد من المعلومات، راجِع أداة التقسيم التام للتصنيف الثنائي باستخدام الميزات الرقمية في دورة "غابات القرارات".
F
أهمية الميزات
مرادف أهمية المتغيرات
G
gini impurity
مقياس مشابه لإنتروبيا تستخدم أدوات التقسيم قيمًا مشتقة من عدم المساواة في جيني أو الإنتروبيا لإنشاء شروط لتصنيف أشجار القرارات. يتم استنتاج تحصيل المعلومات من قصور المعلومات. لا يوجد مصطلح مكافئ مقبول عالميًا للمقياس المستمد من عدم نقاء جيني، ولكن هذا المقياس غير المسمى لا يقل أهمية عن اكتساب المعلومات.
يُطلق على عدم نقاء جيني أيضًا اسم مؤشر جيني أو ببساطة جيني.
أشجار القرارات المعزّزة بالتدرّج (GBT)
هو نوع من غابة القرارات حيث:
- تعتمد التدريبات على التعزيز الاشتقاقي.
- النموذج الضعيف هو شجرة قرارات.
يمكنك الاطّلاع على أشجار القرارات المعزّزة بالتدرّج في دورة "غابات القرارات" التدريبية للحصول على مزيد من المعلومات.
التعزيز الاشتقاقي
خوارزمية تدريب يتم فيها تدريب نماذج ضعيفة لتحسين جودة نموذج قوي بشكل متكرر (تقليل الخسارة). على سبيل المثال، قد يكون النموذج الضعيف نموذجًا خطيًا أو نموذج شجرة قرار صغيرًا. يصبح النموذج القوي مجموع كل النماذج الضعيفة التي تم تدريبها سابقًا.
في أبسط أشكال تعزيز التدرّج، يتم في كل تكرار تدريب نموذج منخفض الدقة لتوقُّع تدرّج الفقد في النموذج العالي الدقة. بعد ذلك، يتم تعديل ناتج النموذج القوي من خلال طرح التدرّج المتوقّع، على غرار خوارزمية انحدار التدرّج.
where:
- $F_{0}$ هو نموذج البدء القوي.
- $F_{i+1}$ هو النموذج القوي التالي.
- $F_{i}$ هو النموذج القوي الحالي.
- $\xi$ هي قيمة بين 0.0 و1.0 تُسمى التقلّص، وهي مشابهة لمعدّل التعلّم في خوارزمية انحدار التدرّج.
- $f_{i}$ هو النموذج الضعيف الذي تم تدريبه لتوقُّع تدرّج الخسارة في $F_{i}$.
تتضمّن الأنواع الحديثة من تعزيز التدرّج أيضًا المشتقة الثانية (Hessian) للدالة الخسارة في حساباتها.
تُستخدَم أشجار القرارات عادةً كنماذج ضعيفة في تعزيز التدرّج. اطّلِع على أشجار القرارات المعزّزة بالتدرّج.
I
مسار الاستدلال
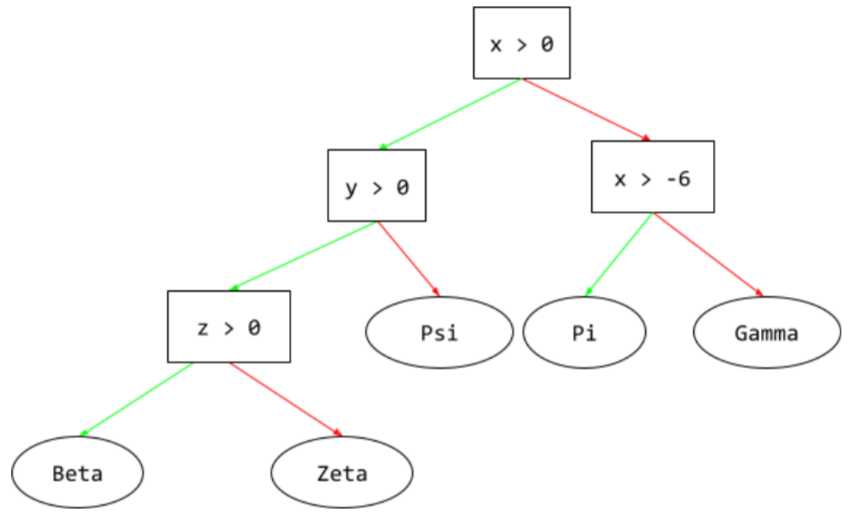
في شجرة القرارات، أثناء الاستدلال، يسلك مثال معيّن مسارًا من الجذر إلى شروط أخرى، وينتهي بـ ورقة. على سبيل المثال، في شجرة القرار التالية، توضّح الأسهم السميكة مسار الاستنتاج لمثال يتضمّن قيم الميزات التالية:
- x = 7
- y = 12
- z = -3
في الرسم التوضيحي التالي، يمر مسار الاستنتاج بثلاث حالات قبل الوصول إلى العقدة الطرفية (Zeta).

تشير الأسهم الثلاثة السميكة إلى مسار الاستدلال.
يمكنك الاطّلاع على أشجار القرارات في دورة "غابات القرارات" للحصول على مزيد من المعلومات.
تحصيل المعلومات
في غابات القرارات، يشير إلى الفرق بين القصور في أحد الأجزاء ومجموع القصور في الأجزاء الفرعية المرجّح (حسب عدد الأمثلة). القصور في أحد الأجزاء هو القصور في الأمثلة الواردة في هذا الجزء.
على سبيل المثال، إليك قيم الإنتروبيا التالية:
- إنتروبيا العقدة الرئيسية = 0.6
- القصور في جزء ثانوي واحد مع 16 مثالاً ذا صلة = 0.2
- مقياس القصور في جزء فرعي آخر يتضمّن 24 مثالاً ذا صلة = 0.1
وبالتالي، فإنّ% 40 من الأمثلة تقع في إحدى العُقد الفرعية و% 60 في العقدة الفرعية الأخرى. ولذلك:
- مجموع القصور المرجّح للعُقد الثانوية = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
إذًا، تحصيل المعلومات هو:
- تحصيل المعلومات = قصور الجزء الأصلي - مجموع القصور المرجّح للأجزاء الفرعية
- تحصيل المعلومات = 0.6 - 0.14 = 0.46
تسعى معظم أدوات التقسيم إلى إنشاء شروط تزيد من اكتساب المعلومات إلى أقصى حد.
الشرط داخل المجموعة
في شجرة القرارات، شرط يختبر وجود عنصر واحد في مجموعة من العناصر. على سبيل المثال، ما يلي هو شرط ضمن المجموعة:
house-style in [tudor, colonial, cape]
أثناء الاستنتاج، إذا كانت قيمة السمة الخاصة بنمط المنزل هي tudor أو colonial أو cape، سيتم تقييم هذا الشرط على أنّه "نعم". إذا كانت قيمة ميزة "أسلوب المنزل" شيئًا آخر (على سبيل المثال، ranch)، سيتم تقييم هذا الشرط إلى "لا".
تؤدي الشروط داخل المجموعة عادةً إلى أشجار قرارات أكثر فعالية من الشروط التي تختبر الميزات المشفّرة بترميز واحد.
L
ورقة شجر
أي نقطة نهاية في شجرة القرارات على عكس الشرط، لا تنفّذ الورقة اختبارًا. بل إنّ الورقة هي عبارة عن توقّع محتمل. العقدة الطرفية هي أيضًا العقدة النهائية في مسار الاستدلال.
على سبيل المثال، تحتوي شجرة القرارات التالية على ثلاث أوراق:
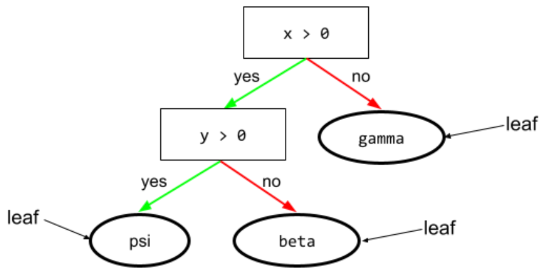
يمكنك الاطّلاع على أشجار القرارات في دورة "غابات القرارات" للحصول على مزيد من المعلومات.
لا
عقدة (شجرة القرار)
في شجرة القرار، يمثّل ذلك أي شرط أو ورقة.
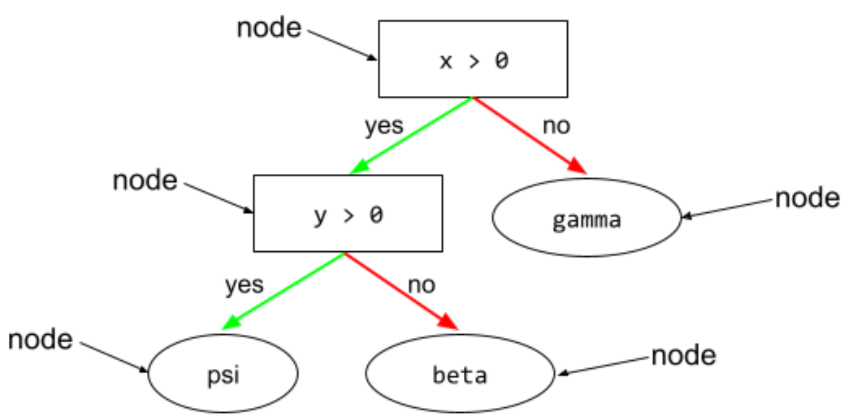
يمكنك الاطّلاع على أشجار القرارات في دورة "غابات القرارات" للحصول على مزيد من المعلومات.
حالة غير ثنائية
شرط يحتوي على أكثر من نتيجتَين محتملتَين. على سبيل المثال، يتضمّن الشرط غير الثنائي التالي ثلاث نتائج محتملة:
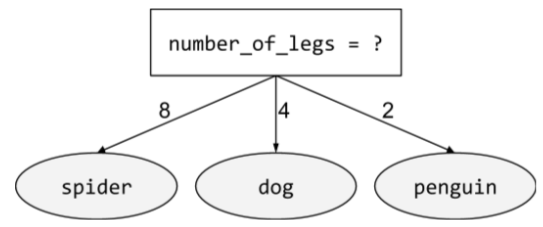
اطّلِع على أنواع الشروط في دورة "أشجار القرار" للحصول على مزيد من المعلومات.
O
الشرط المائل
في شجرة القرار، شرط يتضمّن أكثر من ميزة. على سبيل المثال، إذا كان الارتفاع والعرض كلاهما من السمات، يكون الشرط التالي شرطًا مائلاً:
height > width
يجب التمييز بينها وبين الشرط المحاذي للمحور.
اطّلِع على أنواع الشروط في دورة "أشجار القرار" للحصول على مزيد من المعلومات.
التقييم خارج المجموعة (OOB)
آلية لتقييم جودة غابة القرارات من خلال اختبار كل شجرة قرارات مقابل الأمثلة غير المستخدَمة أثناء التدريب على شجرة القرارات هذه. على سبيل المثال، في الرسم البياني التالي، لاحظ أنّ النظام يدرب كل شجرة قرار على حوالي ثلثَي الأمثلة، ثم يقيّمها باستخدام الثلث المتبقي من الأمثلة.
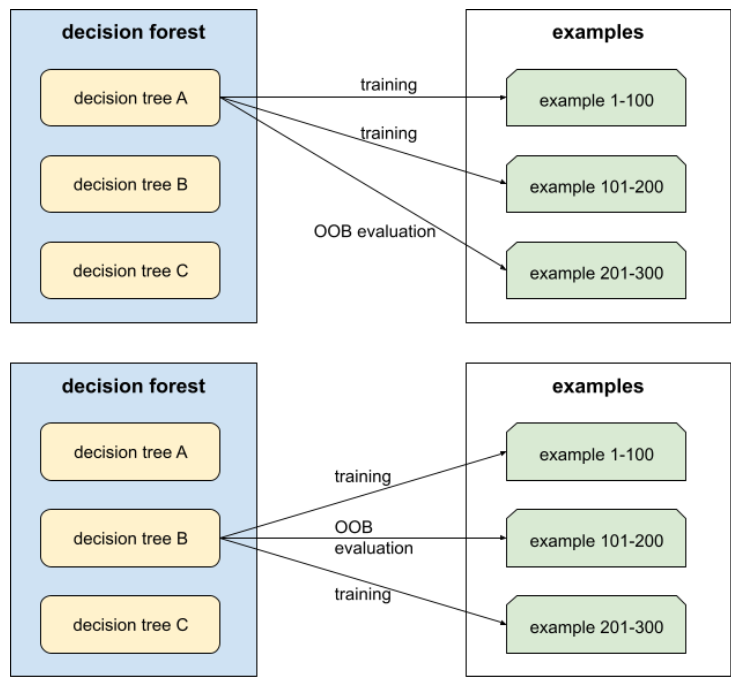
التقييم خارج المجموعة هو تقريب فعال من الناحية الحسابية ومحافظ لآلية التحقّق المتبادل. في التصديق المتقاطع، يتم تدريب نموذج واحد لكل جولة من جولات التصديق المتقاطع (على سبيل المثال، يتم تدريب 10 نماذج في عملية تصديق متقاطع من 10 أجزاء). باستخدام التقييم خارج النطاق، يتم تدريب نموذج واحد. بما أنّ عملية التجميع تحجب بعض البيانات عن كل شجرة أثناء التدريب، يمكن أن يستخدم تقييم OOB هذه البيانات لتقريب عملية التحقّق من الصحة المتبادل.
يمكنك الاطّلاع على التقييم خارج المجموعة في دورة "أشجار القرارات" للحصول على مزيد من المعلومات.
P
أهمية المتغيرات في التبديل
أحد أنواع أهمية المتغير الذي يقيّم الزيادة في خطأ التوقّع للنموذج بعد تبديل قيم الميزة. أهمية المتغيرات المستندة إلى التبديل هي مقياس مستقل عن النموذج.
R
الغابة العشوائية
مجموعة من أشجار القرارات يتم تدريب كل شجرة قرارات فيها باستخدام ضوضاء عشوائية محددة، مثل التجميع.
الغابات العشوائية هي نوع من غابات القرارات.
يمكنك الاطّلاع على الغابة العشوائية في دورة "أشجار القرارات" للحصول على مزيد من المعلومات.
الجذر
العقدة الأولية (الشرط الأول) في شجرة القرارات تضع المخططات عادةً الجذر في أعلى شجرة القرارات. على سبيل المثال:

S
جمع العيّنات مع الاستبدال
طريقة لاختيار عناصر من مجموعة من العناصر المرشّحة، حيث يمكن اختيار العنصر نفسه عدة مرات. تعني عبارة "مع الإحلال" أنّه بعد كل عملية اختيار، يتم إرجاع العنصر المحدّد إلى مجموعة العناصر المرشّحة. أما الطريقة العكسية، أي جمع العيّنات بدون استبدال، فتعني أنّه لا يمكن اختيار عنصر مرشّح إلا مرة واحدة.
على سبيل المثال، ضع في اعتبارك مجموعة الفاكهة التالية:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}لنفترض أنّ النظام يختار fig عشوائيًا كعنصر أول.
في حال استخدام أخذ العيّنات مع الاستبدال، يختار النظام العنصر الثاني من المجموعة التالية:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}نعم، هذه المجموعة هي نفسها المجموعة السابقة، لذا قد يختار النظام fig مرة أخرى.
في حال استخدام أخذ العيّنات بدون استبدال، لا يمكن اختيار عيّنة مرة أخرى بعد اختيارها. على سبيل المثال، إذا اختار النظام عشوائيًا fig كأول عيّنة، لا يمكن اختيار fig مرة أخرى. لذلك، يختار النظام العيّنة الثانية من المجموعة التالية (المخفَّضة):
fruit = {kiwi, apple, pear, cherry, lime, mango}الانكماش
المعلَمة الفائقة في تعزيز التدرّج التي تتحكّم في التطابق الزائد يشبه الانكماش في تعزيز التدرّج معدّل التعلّم في خوارزمية انحدار التدرّج. الانكماش هو قيمة عشرية تتراوح بين 0.0 و1.0. تؤدي قيمة الانكماش المنخفضة إلى تقليل التكيّف الزائد أكثر من قيمة الانكماش الكبيرة.
تقسيم
في شجرة القرار، هو اسم آخر للشرط.
المقسّم
أثناء تدريب شجرة القرارات، يتم استخدام الروتين (والخوارزمية) المسؤول عن العثور على أفضل شرط في كل عقدة.
T
اختبار
في شجرة القرار، هو اسم آخر للشرط.
الحدّ (لأشجار القرارات)
في الشرط المحاذي للمحور، تكون القيمة هي القيمة التي تتم مقارنة العنصر بها. على سبيل المثال، 75 هي قيمة الحد في الشرط التالي:
grade >= 75
يمكنك الاطّلاع على Exact splitter for binary classification with numerical features في دورة "أشجار القرار" التدريبية للحصول على مزيد من المعلومات.
V
أهمية المتغيرات
مجموعة من النتائج تشير إلى الأهمية النسبية لكل سمة في النموذج.
على سبيل المثال، لنفترض أنّ لديك شجرة قرارات تقدّر أسعار المنازل. لنفترض أنّ شجرة القرار هذه تستخدم ثلاث سمات: الحجم والعمر والأسلوب. إذا تم حساب مجموعة من أهمية المتغيرات للميزات الثلاث على النحو التالي: {size=5.8, age=2.5, style=4.7}، فإنّ الحجم أكثر أهمية لشجرة القرار من العمر أو النمط.
تتوفّر مقاييس مختلفة لأهمية المتغيرات، ويمكن أن تفيد خبراء تعلُّم الآلة بشأن جوانب مختلفة من النماذج.
واط
حكمة الجموع
تشير إلى فكرة أنّ احتساب متوسط آراء أو تقديرات مجموعة كبيرة من الأشخاص (أي "الجمهور") غالبًا ما يؤدي إلى نتائج جيدة بشكل مدهش. على سبيل المثال، لنفترض أنّ هناك لعبة يخمّن فيها المشاركون عدد حبّات الحلوى الهلامية المعبّأة في برطمان كبير. مع أنّ معظم التخمينات الفردية ستكون غير دقيقة، تبيّن تجريبيًا أنّ متوسط جميع التخمينات يكون قريبًا بشكل مدهش من العدد الفعلي لحبات الحلوى الهلامية في المرطبان.
المجموعات هي نظير برمجي لـ "حكمة الجموع". حتى إذا كانت النماذج الفردية تقدّم توقّعات غير دقيقة بشكل كبير، فإنّ حساب متوسط التوقّعات الناتجة عن العديد من النماذج يؤدي غالبًا إلى توقّعات جيدة بشكل مدهش. على سبيل المثال، على الرغم من أنّ شجرة القرار الفردية قد تقدّم تنبؤات غير دقيقة، إلا أنّ غابة القرار غالبًا ما تقدّم تنبؤات دقيقة جدًا.
