En esta página, se incluyen los términos del glosario de los bosques de decisión. Para consultar todos los términos del glosario, haz clic aquí.
A
muestreo de atributos
Es una táctica para entrenar un bosque de decisión en el que cada árbol de decisión considera solo un subconjunto aleatorio de posibles atributos cuando aprende la condición. En general, se muestrea un subconjunto diferente de atributos para cada nodo. En cambio, cuando se entrena un árbol de decisión sin muestreo de atributos, se consideran todos los atributos posibles para cada nodo.
condición alineada con el eje
En un árbol de decisión, una condición que involucra solo una característica. Por ejemplo, si area es una característica, la siguiente es una condición alineada con el eje:
area > 200
Compara esto con la condición oblicua.
B
Bagging
Es un método para entrenar un ensamble en el que cada modelo constituyente se entrena con un subconjunto aleatorio de ejemplos de entrenamiento muestreados con reemplazo. Por ejemplo, un bosque aleatorio es una colección de árboles de decisión entrenados con bagging.
El término bagging es la abreviatura de bootstrap aggregating.
Consulta Bosques aleatorios en el curso de Bosques de decisión para obtener más información.
condición binaria
En un árbol de decisión, una condición que tiene solo dos resultados posibles, por lo general, sí o no. Por ejemplo, la siguiente es una condición binaria:
temperature >= 100
Compara esto con la condición no binaria.
Consulta Tipos de condiciones en el curso de Bosques de decisión para obtener más información.
C
de transición
En un árbol de decisión, cualquier nodo que realice una prueba. Por ejemplo, el siguiente árbol de decisión contiene dos condiciones:

Una condición también se denomina división o prueba.
Condición de contraste con hoja.
Consulta lo siguiente:
Consulta Tipos de condiciones en el curso de Bosques de decisión para obtener más información.
D
bosque de decisión
Es un modelo creado a partir de varios árboles de decisión. Un bosque de decisión realiza una predicción agregando las predicciones de sus árboles de decisión. Los tipos populares de bosques de decisión incluyen los bosques aleatorios y los árboles potenciados con gradientes.
Consulta la sección Bosques de decisión del curso sobre bosques de decisión para obtener más información.
árbol de decisión
Es un modelo de aprendizaje supervisado compuesto por un conjunto de condiciones y hojas organizadas de forma jerárquica. Por ejemplo, el siguiente es un árbol de decisión:
E
entropía
En la teoría de la información, es una descripción de qué tan impredecible es una distribución de probabilidad. Como alternativa, la entropía también se define como la cantidad de información que contiene cada ejemplo. Una distribución tiene la entropía más alta posible cuando todos los valores de una variable aleatoria son igualmente probables.
La entropía de un conjunto con dos valores posibles "0" y "1" (por ejemplo, las etiquetas en un problema de clasificación binaria) tiene la siguiente fórmula:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
Donde:
- H es la entropía.
- p es la fracción de ejemplos de "1".
- q es la fracción de ejemplos "0". Ten en cuenta que q = (1 - p).
- log suele ser log2. En este caso, la unidad de entropía es un bit.
Por ejemplo, supongamos lo siguiente:
- 100 ejemplos contienen el valor "1".
- 300 ejemplos contienen el valor "0".
Por lo tanto, el valor de la entropía es el siguiente:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 0.81 bits por ejemplo
Un conjunto perfectamente equilibrado (por ejemplo, 200 "0" y 200 "1") tendría una entropía de 1.0 bits por ejemplo. A medida que un conjunto se vuelve más desequilibrado, su entropía se acerca a 0.0.
En los árboles de decisión, la entropía ayuda a formular la ganancia de información para ayudar al divisor a seleccionar las condiciones durante el crecimiento de un árbol de decisión de clasificación.
Compara la entropía con lo siguiente:
- impureza de Gini
- Función de pérdida de entropía cruzada
A menudo, la entropía se denomina entropía de Shannon.
Consulta Divisor exacto para la clasificación binaria con características numéricas en el curso de Bosques de decisión para obtener más información.
F
Importancia de los atributos
Sinónimo de importancia de las variables.
G
Impureza de Gini
Es una métrica similar a la entropía. Los divisores usan valores derivados de la impureza de Gini o la entropía para componer condiciones para los árboles de decisión de clasificación. La ganancia de información se deriva de la entropía. No existe un término equivalente aceptado universalmente para la métrica derivada de la impureza de Gini. Sin embargo, esta métrica sin nombre es tan importante como la ganancia de información.
La impureza de Gini también se denomina índice de Gini o, simplemente, Gini.
Árboles de decisión impulsados por gradientes (GBT)
Es un tipo de bosque de decisión en el que se cumplen las siguientes condiciones:
- Entrenamiento se basa en el potenciamiento del gradiente.
- El modelo débil es un árbol de decisión.
Para obtener más información, consulta Árboles de decisión potenciados por gradiente en el curso de Bosques de decisión.
potenciación del gradiente
Es un algoritmo de entrenamiento en el que se entrenan modelos débiles para mejorar de forma iterativa la calidad (reducir la pérdida) de un modelo sólido. Por ejemplo, un modelo débil podría ser un modelo lineal o un modelo de árbol de decisión pequeño. El modelo sólido se convierte en la suma de todos los modelos débiles entrenados anteriormente.
En la forma más simple del boosting de gradientes, en cada iteración, se entrena un modelo débil para predecir el gradiente de pérdida del modelo fuerte. Luego, el resultado del modelo sólido se actualiza restando el gradiente predicho, de manera similar al descenso del gradiente.
Donde:
- $F_{0}$ es el modelo inicial sólido.
- $F_{i+1}$ es el siguiente modelo sólido.
- $F_{i}$ es el modelo sólido actual.
- $\xi$ es un valor entre 0.0 y 1.0 llamado reducción, que es análogo a la tasa de aprendizaje en el descenso del gradiente.
- $f_{i}$ es el modelo débil entrenado para predecir el gradiente de pérdida de $F_{i}$.
Las variaciones modernas del aumento de gradiente también incluyen la segunda derivada (hessiana) de la pérdida en su cálculo.
Los árboles de decisión se suelen usar como modelos débiles en el boosting de gradiente. Consulta Árboles (de decisión) potenciados por gradientes.
I
ruta de inferencia
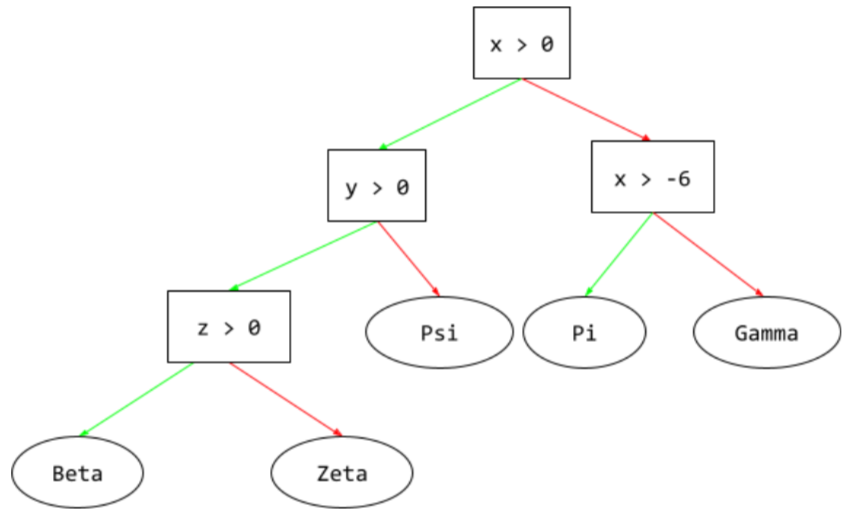
En un árbol de decisión, durante la inferencia, la ruta que toma un ejemplo particular desde la raíz hasta otras condiciones, que termina con una hoja. Por ejemplo, en el siguiente árbol de decisión, las flechas más gruesas muestran la ruta de inferencia para un ejemplo con los siguientes valores de atributos:
- x = 7
- y = 12
- z = -3
La ruta de inferencia en la siguiente ilustración pasa por tres condiciones antes de llegar a la hoja (Zeta).

Las tres flechas gruesas muestran la ruta de inferencia.
Consulta Árboles de decisión en el curso de Bosques de decisión para obtener más información.
Ganancia de información
En los bosques de decisión, es la diferencia entre la entropía de un nodo y la suma ponderada (según la cantidad de ejemplos) de la entropía de sus nodos secundarios. La entropía de un nodo es la entropía de los ejemplos en ese nodo.
Por ejemplo, considera los siguientes valores de entropía:
- entropía del nodo principal = 0.6
- entropía de un nodo secundario con 16 ejemplos relevantes = 0.2
- entropía de otro nodo secundario con 24 ejemplos relevantes = 0.1
Por lo tanto, el 40% de los ejemplos se encuentran en un nodo secundario y el 60% en el otro. Por lo tanto:
- Suma de entropía ponderada de los nodos secundarios = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
Por lo tanto, la ganancia de información es la siguiente:
- Ganancia de información = entropía del nodo principal - suma ponderada de la entropía de los nodos secundarios
- Ganancia de información = 0.6 - 0.14 = 0.46
La mayoría de los divisores buscan crear condiciones que maximicen la ganancia de información.
condición de conjunto
En un árbol de decisión, una condición que prueba la presencia de un elemento en un conjunto de elementos. Por ejemplo, la siguiente es una condición dentro del conjunto:
house-style in [tudor, colonial, cape]
Durante la inferencia, si el valor del atributo de estilo de la casa es tudor, colonial o cape, esta condición se evalúa como Sí. Si el valor del atributo de estilo de la casa es otro (por ejemplo, ranch), esta condición se evalúa como No.
Por lo general, las condiciones establecidas en el conjunto generan árboles de decisión más eficientes que las condiciones que prueban atributos codificados como one-hot.
L
hoja
Cualquier extremo en un árbol de decisión. A diferencia de una condición, una hoja no realiza una prueba. Más bien, una hoja es una predicción posible. Una hoja también es el nodo terminal de una ruta de inferencia.
Por ejemplo, el siguiente árbol de decisión contiene tres hojas:
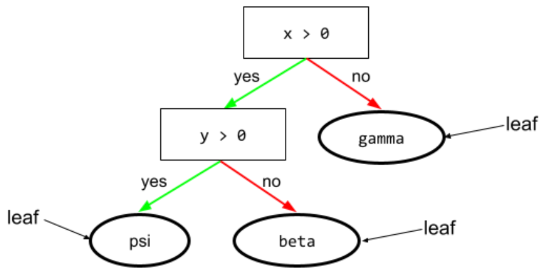
Consulta Árboles de decisión en el curso de Bosques de decisión para obtener más información.
N
nodo (árbol de decisión)
En un árbol de decisión, cualquier condición o hoja.
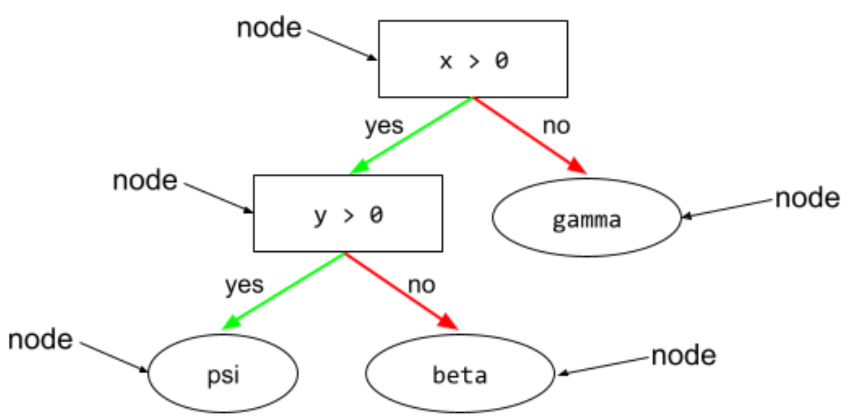
Consulta Árboles de decisión en el curso de Bosques de decisión para obtener más información.
condición no binaria
Una condición que contiene más de dos resultados posibles. Por ejemplo, la siguiente condición no binaria contiene tres resultados posibles:
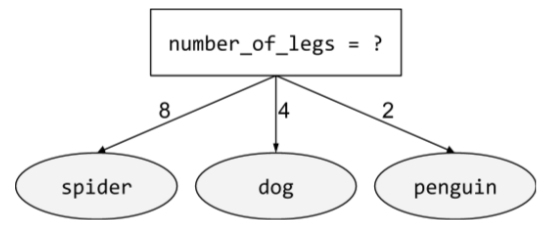
Consulta Tipos de condiciones en el curso de Bosques de decisión para obtener más información.
O
condición oblicua
En un árbol de decisión, una condición que involucra más de una característica. Por ejemplo, si la altura y el ancho son atributos, la siguiente es una condición oblicua:
height > width
Compara esto con la condición alineada con el eje.
Consulta Tipos de condiciones en el curso de Bosques de decisión para obtener más información.
Evaluación fuera de la bolsa (evaluación OOB)
Es un mecanismo para evaluar la calidad de un bosque de decisión probando cada árbol de decisión con los ejemplos que no se usaron durante el entrenamiento de ese árbol de decisión. Por ejemplo, en el siguiente diagrama, observa que el sistema entrena cada árbol de decisión con aproximadamente dos tercios de los ejemplos y, luego, realiza la evaluación con el tercio restante.
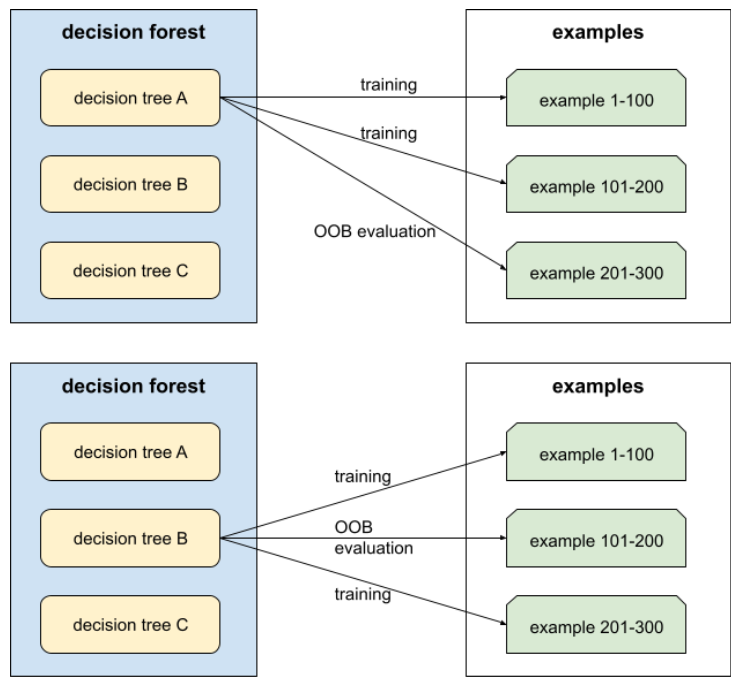
La evaluación fuera de la bolsa es una aproximación conservadora y eficiente en términos de procesamiento del mecanismo de validación cruzada. En la validación cruzada, se entrena un modelo para cada ronda de validación cruzada (por ejemplo, se entrenan 10 modelos en una validación cruzada de 10 segmentos). Con la evaluación fuera de la muestra, se entrena un solo modelo. Dado que el bagging retiene algunos datos de cada árbol durante el entrenamiento, la evaluación OOB puede usar esos datos para aproximar la validación cruzada.
Consulta Evaluación fuera de la bolsa en el curso de Bosques de decisión para obtener más información.
P
Importancia de las variables por permutación
Es un tipo de importancia de la variable que evalúa el aumento en el error de predicción de un modelo después de permutar los valores del atributo. La importancia de las variables de permutación es una métrica independiente del modelo.
R
bosque aleatorio
Es un ensamble de árboles de decisión en el que cada árbol de decisión se entrena con un ruido aleatorio específico, como el bagging.
Los bosques aleatorios son un tipo de bosque de decisión.
Consulta Bosque aleatorio en el curso de Bosques de decisión para obtener más información.
raíz
Es el nodo inicial (la primera condición) en un árbol de decisión. Por convención, los diagramas colocan la raíz en la parte superior del árbol de decisión. Por ejemplo:

S
Muestreo con reemplazo
Es un método para elegir elementos de un conjunto de elementos candidatos en el que se puede elegir el mismo elemento varias veces. La frase "con reemplazo" significa que, después de cada selección, el elemento seleccionado se devuelve al conjunto de elementos candidatos. El método inverso, muestreo sin reemplazo, significa que un elemento candidato solo se puede elegir una vez.
Por ejemplo, considera el siguiente conjunto de frutas:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Supongamos que el sistema elige de forma aleatoria fig como el primer elemento.
Si se usa el muestreo con reemplazo, el sistema elige el segundo elemento del siguiente conjunto:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Sí, es el mismo conjunto que antes, por lo que el sistema podría volver a elegir fig.
Si se usa el muestreo sin reemplazo, una vez que se selecciona una muestra, no se puede volver a seleccionar. Por ejemplo, si el sistema elige al azar fig como la primera muestra, no se puede volver a elegir fig. Por lo tanto, el sistema elige la segunda muestra del siguiente conjunto (reducido):
fruit = {kiwi, apple, pear, cherry, lime, mango}Contracción
Es un hiperparámetro en el aumento de gradiente que controla el sobreajuste. La reducción en el aumento del gradiente es análoga a la tasa de aprendizaje en el descenso de gradientes. La reducción es un valor decimal entre 0.0 y 1.0. Un valor de reducción más bajo reduce el sobreajuste más que un valor de reducción más alto.
split
En un árbol de decisión, otro nombre para una condición.
divisor
Durante el entrenamiento de un árbol de decisión, la rutina (y el algoritmo) se encargan de encontrar la mejor condición en cada nodo.
T
prueba
En un árbol de decisión, otro nombre para una condición.
Umbral (para árboles de decisión)
En una condición alineada con el eje, es el valor con el que se compara una característica. Por ejemplo, 75 es el valor del umbral en la siguiente condición:
grade >= 75
Consulta Divisor exacto para la clasificación binaria con atributos numéricos en el curso de Bosques de decisión para obtener más información.
V
Importancia de las variables
Es un conjunto de puntuaciones que indica la importancia relativa de cada atributo para el modelo.
Por ejemplo, considera un árbol de decisión que estima los precios de las casas. Supongamos que este árbol de decisión usa tres atributos: tamaño, edad y estilo. Si se calcula que un conjunto de importancias de variables para las tres características es {tamaño=5.8, edad=2.5, estilo=4.7}, entonces el tamaño es más importante para el árbol de decisión que la edad o el estilo.
Existen diferentes métricas de importancia de las variables que pueden informar a los expertos en AA sobre diferentes aspectos de los modelos.
W
Sabiduría de la multitud
La idea de que promediar las opiniones o estimaciones de un grupo grande de personas ("la multitud") suele producir resultados sorprendentemente buenos. Por ejemplo, considera un juego en el que las personas adivinan la cantidad de caramelos de goma que hay en un frasco grande. Si bien la mayoría de las conjeturas individuales serán imprecisas, se ha demostrado empíricamente que el promedio de todas las conjeturas es sorprendentemente cercano a la cantidad real de gomitas en el frasco.
Los modelos de conjunto son un análogo de software de la sabiduría de la multitud. Incluso si los modelos individuales hacen predicciones muy imprecisas, promediar las predicciones de muchos modelos suele generar predicciones sorprendentemente buenas. Por ejemplo, aunque un árbol de decisión individual puede generar predicciones deficientes, un bosque de decisión suele generar predicciones muy buenas.
