本页包含决策森林术语。如需查看所有术语,请点击此处。
A
属性抽样
一种用于训练决策森林的策略,其中每个决策树在学习条件时仅考虑随机选择的可能特征子集。一般来说,每个节点都会对不同的特征子集进行抽样。相比之下,在训练不进行属性抽样的决策树时,系统会考虑每个节点的所有可能特征。
轴对齐条件
在决策树中,仅涉及单个特征的条件。例如,如果 area 是一个特征,则以下是轴对齐条件:
area > 200
与斜条件相对。
B
装袋
一种用于训练集成的方法,其中每个组成模型都基于有放回抽样的随机训练示例子集进行训练。例如,随机森林是使用 Bagging 训练的决策树的集合。
术语“bagging”是“bootstrap aggregating”(自助抽样集成)的简称。
如需了解详情,请参阅“决策森林”课程中的随机森林。
二元条件
在决策树中,条件只有两种可能的结果,通常是是或否。例如,以下是一个二元条件:
temperature >= 100
与非二元条件相对。
如需了解详情,请参阅决策森林课程中的条件类型。
C
condition
在决策树中,执行测试的任何节点。例如,以下决策树包含两个条件:

条件也称为拆分或测试。
对比条件与叶。
另请参阅:
如需了解详情,请参阅决策森林课程中的条件类型。
D
决策森林
一种由多个决策树创建的模型。决策森林通过汇总其决策树的预测结果来进行预测。常见的决策森林类型包括随机森林和梯度提升树。
如需了解详情,请参阅决策森林课程中的决策森林部分。
决策树
一种监督式学习模型,由一组按层次结构组织的条件和叶组成。例如,以下是一个决策树:
E
熵
在 信息论中,用于描述概率分布的不可预测程度。或者,熵也可以定义为每个示例包含的信息量。当随机变量的所有值具有相同的可能性时,分布具有尽可能高的熵。
具有两个可能值“0”和“1”(例如,二元分类问题中的标签)的集合的熵具有以下公式:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
其中:
- H 是熵。
- p 是“1”示例的比例。
- q 是“0”示例的比例。请注意,q = (1 - p)
- 对数通常为以 2 为底的对数。在本例中,熵单位为比特。
例如,假设情况如下:
- 100 个示例包含值“1”
- 300 个示例包含值“0”
因此,熵值为:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 每个示例 0.81 位
完全平衡的集合(例如,200 个“0”和 200 个“1”)的每个示例的熵为 1.0 位。随着集合变得越来越不平衡,其熵会趋近于 0.0。
在决策树中,熵有助于制定信息增益,从而帮助分裂器在分类决策树的增长过程中选择条件。
将熵与以下对象进行比较:
熵通常称为香农熵。
如需了解详情,请参阅决策森林课程中的使用数值特征进行二元分类的精确分裂器。
F
特征重要性
与变量重要性的含义相同。
G
Gini 不纯度
与 entropy 类似的指标。拆分器使用从 Gini 不纯度或熵派生的值来为分类决策树组成条件。 信息增益源自熵。 对于从 Gini 不纯度派生的指标,目前还没有普遍接受的等效术语;不过,这个未命名的指标与信息增益同样重要。
Gini 不纯度也称为 Gini 指数,或简称为 Gini。
梯度提升(决策)树 (GBT)
一种决策森林,其中:
如需了解详情,请参阅决策森林课程中的梯度提升决策树。
梯度提升
一种训练算法,其中训练弱模型以迭代方式提高强模型的质量(减少损失)。例如,弱模型可以是线性模型或小型决策树模型。强模型成为之前训练的所有弱模型的总和。
在最简单的梯度提升形式中,每次迭代都会训练一个弱模型来预测强模型的损失梯度。然后,通过减去预测的梯度来更新强模型的输出,类似于梯度下降。
其中:
- $F_{0}$ 是初始强模型。
- $F_{i+1}$ 是下一个强模型。
- $F_{i}$ 是当前的强模型。
- $\xi$ 是一个介于 0.0 和 1.0 之间的值,称为收缩率,类似于梯度下降中的学习率。
- $f_{i}$ 是经过训练用于预测 $F_{i}$ 的损失梯度的弱模型。
梯度提升的现代变体还在计算中纳入了损失的二阶导数(Hessian)。
决策树通常用作梯度提升中的弱模型。请参阅梯度提升(决策)树。
I
推理路径
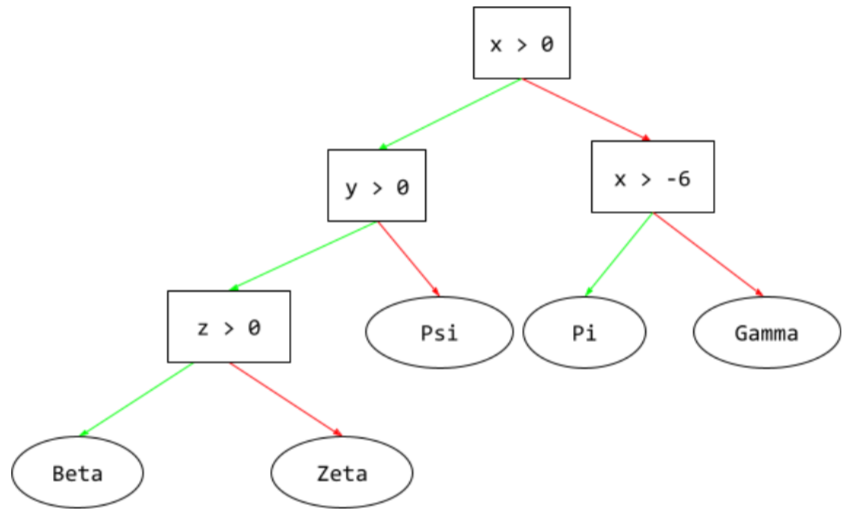
在决策树中,在推理过程中,特定示例从根到其他条件所采用的路线,最终以叶结束。例如,在以下决策树中,较粗的箭头显示了具有以下特征值的示例的推理路径:
- x = 7
- y = 12
- z = -3
下图中的推理路径在到达叶节点 (Zeta) 之前会经历三种情况。

三条粗箭头显示了推理路径。
如需了解详情,请参阅“决策森林”课程中的决策树。
信息增益
在决策森林中,节点熵与其子节点熵的加权(按示例数量)和之间的差。节点的熵是指该节点中示例的熵。
例如,请考虑以下熵值:
- 父节点的熵 = 0.6
- 一个子节点的熵(包含 16 个相关示例)= 0.2
- 另一个具有 24 个相关示例的子节点的熵 = 0.1
因此,40% 的示例位于一个子节点中,而 60% 的示例位于另一个子节点中。因此:
- 子节点的加权熵之和 = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
因此,信息增益为:
- 信息增益 = 父节点的熵 - 子节点的加权熵之和
- 信息增益 = 0.6 - 0.14 = 0.46
在集合条件中
在决策树中,一种用于测试一组项中是否存在某个项的条件。 例如,以下是一个集合内条件:
house-style in [tudor, colonial, cape]
在推理期间,如果房屋风格 特征的值为 tudor、colonial 或 cape,则此条件的评估结果为“是”。如果住宅风格特征的值为其他值(例如 ranch),则此条件的计算结果为“否”。
与测试独热编码特征的条件相比,集合内条件通常会生成更高效的决策树。
L
leaf
决策树中的任何端点。与条件不同,叶不执行测试。相反,叶节点是一种可能的预测。叶也是推理路径的终端节点。
例如,以下决策树包含三个叶节点:
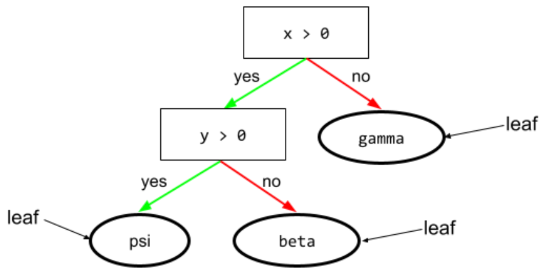
如需了解详情,请参阅“决策森林”课程中的决策树。
否
节点(决策树)
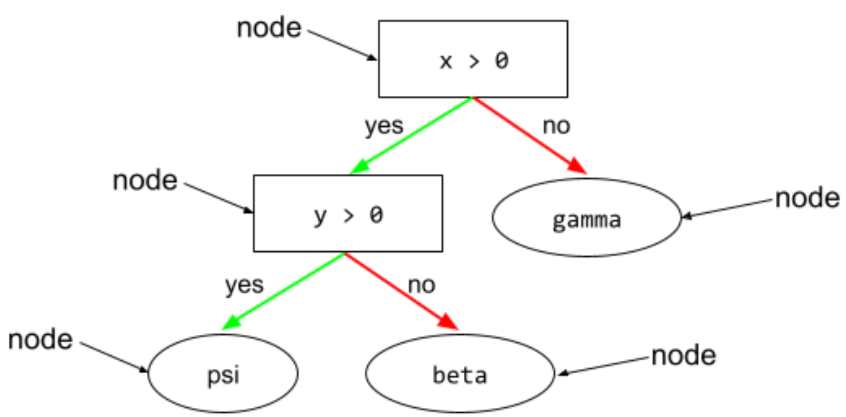
如需了解详情,请参阅决策森林课程中的决策树。
非二元性别条件
包含两种以上可能结果的条件。例如,以下非二元条件包含三种可能的结果:

如需了解详情,请参阅决策森林课程中的条件类型。
O
斜向条件
在决策树中,涉及多个特征的条件。例如,如果高度和宽度都是特征,则以下是倾斜条件:
height > width
与轴对齐条件相对。
如需了解详情,请参阅决策森林课程中的条件类型。
袋外评估(OOB 评估)
一种用于评估决策森林质量的机制,通过针对决策树的训练期间未使用的示例来测试每个决策树。例如,在下图中,请注意,系统会使用大约三分之二的示例来训练每个决策树,然后使用剩余的三分之一示例进行评估。
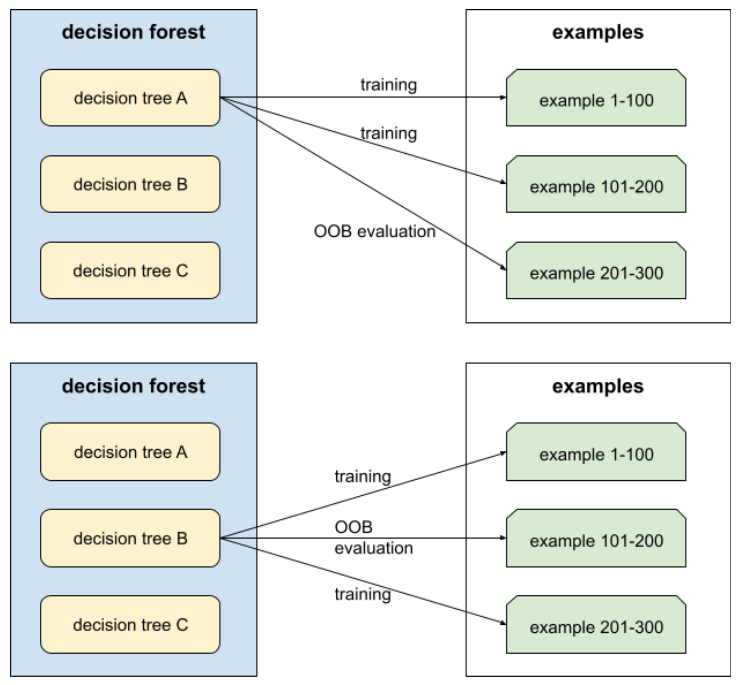
袋外评估是一种计算效率高且保守的交叉验证机制的近似方法。在交叉验证中,每个交叉验证轮次都会训练一个模型(例如,在 10 折交叉验证中会训练 10 个模型)。借助 OOB 评估,系统会训练单个模型。由于 bagging 在训练期间会从每棵树中留出一些数据,因此 OOB 评估可以使用这些数据来近似交叉验证。
如需了解详情,请参阅决策森林课程中的袋外评估。
P
排列变量重要性
一种变量重要性,用于评估在对特征值进行置换后模型预测误差的增加情况。排列变量重要性是一种与模型无关的指标。
R
随机森林
一种由决策树组成的集成,其中每棵决策树都使用特定的随机噪声进行训练,例如 bagging。
随机森林是一种决策森林。
如需了解详情,请参阅决策森林课程中的随机森林。
root
决策树中的起始节点(第一个条件)。按照惯例,图表会将根放在决策树的顶部。例如:

S
放回抽样
一种从一组候选商品中挑选商品的方法,其中同一商品可以多次被选中。“放回”是指每次选择后,所选项目都会返回到候选项目池中。相反的方法是不放回抽样,这意味着候选商品只能被选中一次。
例如,假设有以下水果集:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}假设系统随机选择 fig 作为第一个商品。如果采用放回抽样,系统会从以下集合中选择第二个项:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}是的,这与之前的集合相同,因此系统可能会再次选择 fig。
如果使用不放回抽样,一旦选中某个样本,就无法再次选中该样本。例如,如果系统随机选择 fig 作为第一个样本,则不能再次选择 fig。因此,系统会从以下(缩减的)集合中选择第二个样本:
fruit = {kiwi, apple, pear, cherry, lime, mango}收缩
梯度提升中的超参数,用于控制过拟合。梯度提升中的收缩率类似于梯度下降中的学习速率。收缩率是介于 0.0 到 1.0 之间的小数值。与较大的收缩值相比,较小的收缩值可更有效地减少过拟合。
拆分
分割器
在训练决策树时,负责在每个节点上找到最佳条件的例程(和算法)。
T
test
阈值(对于决策树)
在轴对齐条件中,特征要比较的值。例如,在以下条件中,75 是阈值:
grade >= 75
如需了解详情,请参阅决策森林课程中的使用数值特征进行二元分类的精确拆分器。
V
变量重要性
一组分数,用于指示每个特征对模型的相对重要性。
例如,假设有一个用于估算房价的决策树。假设此决策树使用三个特征:尺寸、年龄和款式。如果计算出的三个特征的一组变量重要性为 {size=5.8, age=2.5, style=4.7},则对于决策树而言,size 比 age 或 style 更重要。
存在不同的变量重要性指标,可让机器学习专家了解模型的不同方面。
W
群体的智慧
一种理论,认为对一大群人(“大众”)的意见或估计值求平均值通常会产生出人意料的好结果。例如,假设有一款游戏,玩家需要猜测一个大罐子里装了多少颗软糖。虽然大多数个人猜测都不准确,但经验表明,所有猜测的平均值与罐中实际的糖豆数量非常接近。
集成是“群体的智慧”的软件类比。 即使单个模型做出的预测非常不准确,但对多个模型的预测结果求平均值通常会生成出人意料的良好预测。例如,虽然单个决策树的预测效果可能不佳,但决策森林的预测效果通常非常好。
