בדף הזה מופיעים מונחים במילון המונחים של Decision Forests. כאן אפשר לראות את כל המונחים במילון המונחים.
A
דגימת מאפיינים
טקטיקה לאימון של יער החלטות שבה כל עץ החלטות מתבסס רק על קבוצת משנה אקראית של תכונות אפשריות כשהוא לומד את התנאי. באופן כללי, קבוצת משנה שונה של תכונות נדגמת עבור כל צומת. לעומת זאת, כשמאמנים עץ החלטה בלי דגימת מאפיינים, כל התכונות האפשריות נלקחות בחשבון לכל צומת.
תנאי שמתייחס לציר
בעץ החלטה, תנאי שכולל רק תכונה אחת. לדוגמה, אם area הוא מאפיין, אז התנאי הבא הוא תנאי שמתייחס לציר:
area > 200
השוואה למצב אלכסוני.
B
bagging
שיטה לאימון אנסמבל שבו כל מודל מרכיב מתאמן על קבוצת משנה אקראית של דוגמאות לאימון שנדגמו עם החזרה. לדוגמה, יער אקראי הוא אוסף של עצי החלטה שאומנו באמצעות שיטת ה-bagging.
המונח bagging הוא קיצור של bootstrap aggregating.
מידע נוסף זמין במאמר יערות אקראיים בקורס בנושא יערות החלטה.
תנאי בינארי
בעץ החלטה, תנאי שיש לו רק שתי תוצאות אפשריות, בדרך כלל כן או לא. לדוגמה, התנאי הבא הוא תנאי בינארי:
temperature >= 100
ההפך מתנאי לא בינארי.
מידע נוסף זמין במאמר סוגי תנאים בקורס בנושא יערות החלטה.
C
תנאי
בעץ החלטה, כל צומת שמבצע בדיקה. לדוגמה, עץ ההחלטות הבא מכיל שני תנאים:

תנאי נקרא גם פיצול או בדיקה.
תנאי ניגודיות עם עלה.
ראה גם:
מידע נוסף זמין במאמר סוגי תנאים בקורס בנושא יערות החלטה.
D
יער החלטות
מודל שנוצר מכמה עצי החלטות. כדי לבצע חיזוי, יער ההחלטות צובר את החיזויים של עצי ההחלטות שלו. סוגים פופולריים של יערות החלטה כוללים יערות אקראיים ועצים עם שיפור גרדיאנט.
מידע נוסף זמין בקטע יערות של החלטות בקורס בנושא יערות של החלטות.
עץ החלטה
מודל של למידה מונחית שמורכב מקבוצה של תנאים וענפים שמאורגנים בהיררכיה. לדוגמה, זהו עץ החלטות:
E
אנטרופיה
ב תורת המידע, אנטרופיה היא מדד למידת חוסר הצפיות של התפלגות הסתברויות. לחלופין, אנטרופיה מוגדרת גם ככמות המידע שכל דוגמה מכילה. הפיזור הוא בעל האנטרופיה הגבוהה ביותר האפשרית כשכל הערכים של משתנה אקראי הם בעלי הסתברות שווה.
הנוסחה לחישוב האנטרופיה של קבוצה עם שני ערכים אפשריים, 0 ו-1 (לדוגמה, התוויות בבעיית סיווג בינארי), היא:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
where:
- H היא האנטרופיה.
- p הוא השבר של הדוגמאות '1'.
- q הוא החלק של הדוגמאות עם הערך '0'. שימו לב: q = (1 - p)
- log הוא בדרך כלל log2. במקרה הזה, יחידת האנטרופיה היא ביט.
לדוגמה, נניח את הדברים הבאים:
- 100 דוגמאות מכילות את הערך '1'
- 300 דוגמאות מכילות את הערך '0'
לכן, ערך האנטרופיה הוא:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 0.81 bits per example
קבוצה מאוזנת לחלוטין (לדוגמה, 200 ערכים של '0' ו-200 ערכים של '1') תהיה בעלת אנטרופיה של 1.0 ביט לכל דוגמה. ככל שקבוצה הופכת לא מאוזנת יותר, האנטרופיה שלה מתקרבת ל-0.0.
בעצי החלטה, האנטרופיה עוזרת לגבש רווח מידע כדי לעזור למפצל לבחור את התנאים במהלך הצמיחה של עץ החלטה לסיווג.
השוואת האנטרופיה עם:
- מדד גיני לאי-טוהר
- פונקציית האובדן cross-entropy
אנטרופיה נקראת לעיתים קרובות אנטרופיה של שאנון.
מידע נוסף זמין במאמר Exact splitter for binary classification with numerical features בקורס Decision Forests.
F
חשיבות התכונות
מילה נרדפת למונח חשיבות משתנים.
G
gini impurity
מדד שדומה לאנטרופיה. מפצלים משתמשים בערכים שנגזרים מאי-טוהר גיני או מאנטרופיה כדי ליצור תנאים לסיווג עצי החלטה. הרווח במידע נגזר מאנטרופיה. אין מונח מקביל שמקובל באופן אוניברסלי למדד שנגזר מאי-טוהר של גיני. עם זאת, המדד הזה, שאין לו שם, חשוב בדיוק כמו מדד הרווח במידע.
המדד הזה נקרא גם מדד ג'יני או פשוט ג'יני.
עצי החלטה עם חיזוק גרדיאנט (GBT)
סוג של יער החלטות שבו:
- הדרכה מתבססת על חיזוק גרדיאנט.
- המודל החלש הוא עץ החלטה.
מידע נוסף זמין במאמר Gradient Boosted Decision Trees (עצים להחלטות עם שיפור גרדיאנט) בקורס בנושא Decision Forests (יערות החלטה).
חיזוק גרדיאנט
אלגוריתם אימון שבו מודלים חלשים מאומנים באופן איטרטיבי כדי לשפר את האיכות של מודל חזק (להפחית את האובדן). לדוגמה, מודל חלש יכול להיות מודל לינארי או מודל קטן של עץ החלטות. המודל החזק הופך לסכום של כל המודלים החלשים שאומנו קודם.
בצורה הפשוטה ביותר של שיטת Gradient Boosting, בכל איטרציה מאמנים מודל חלש כדי לחזות את שיפוע אובדן המידע של המודל החזק. לאחר מכן, הפלט של המודל החזק מתעדכן על ידי חיסור הגרדיאנט החזוי, בדומה לירידת גרדיאנט.
where:
- $F_{0}$ הוא המודל להתחלה חזקה.
- $F_{i+1}$ הוא המודל החזק הבא.
- $F_{i}$ הוא המודל החזק הנוכחי.
- $\xi$ הוא ערך בין 0.0 ל-1.0 שנקרא התכווצות, שדומה לקצב הלמידה בשיטת הגרדיאנט.
- $f_{i}$ הוא מודל חלש שאומן לחזות את שיפוע ההפסד של $F_{i}$.
וריאציות מודרניות של gradient boosting כוללות גם את הנגזרת השנייה (Hessian) של הפסד בחישוב שלהן.
עצי החלטה משמשים בדרך כלל כמודלים חלשים בשיטת הגרדיאנט בוסטינג. מידע נוסף על עצים עם שיפור גרדיאנט (החלטה)
I
נתיב הסקה
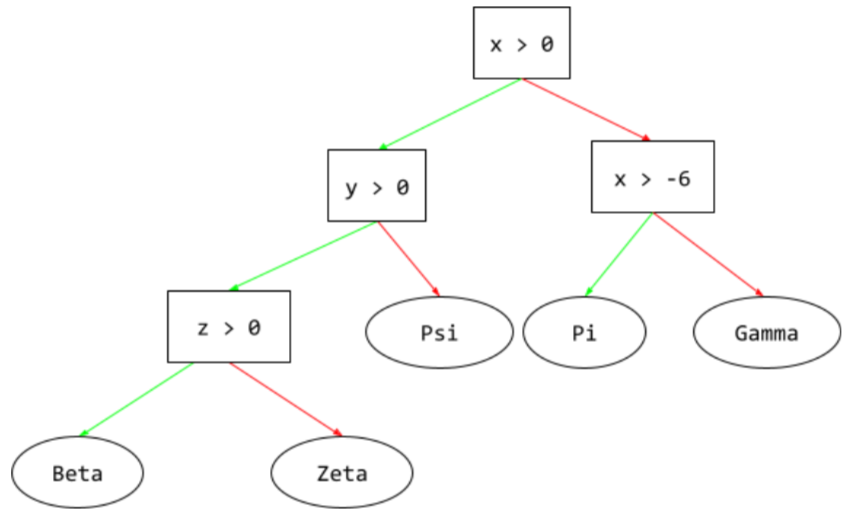
בעץ החלטה, במהלך הסקת מסקנות, המסלול שדוגמה ספציפית עוברת מהשורש לתנאים אחרים, ומסתיים בעלה. לדוגמה, בעץ ההחלטה הבא, החצים העבים יותר מראים את נתיב ההסקה לדוגמה עם ערכי התכונות הבאים:
- x = 7
- y = 12
- z = -3
נתיב ההסקה באיור הבא עובר דרך שלושה תנאים לפני שהוא מגיע לעלה (Zeta).

שלושת החיצים העבים מראים את נתיב ההסקה.
מידע נוסף זמין במאמר עצי החלטה בקורס בנושא יערות החלטה.
הרווח ממידע
ביערות החלטה, ההפרש בין האנטרופיה של צומת לבין הסכום המשוקלל (לפי מספר הדוגמאות) של האנטרופיה של צמתי הצאצאים שלה. האנטרופיה של צומת היא האנטרופיה של הדוגמאות בצומת הזה.
לדוגמה, נניח שיש לכם את ערכי האנטרופיה הבאים:
- האנטרופיה של צומת ההורה = 0.6
- האנטרופיה של צומת משני אחד עם 16 דוגמאות רלוונטיות = 0.2
- האנטרופיה של צומת צאצא אחר עם 24 דוגמאות רלוונטיות = 0.1
לכן, 40% מהדוגמאות נמצאות בצומת צאצא אחד ו-60% נמצאות בצומת הצאצא השני. לכן:
- סכום האנטרופיה המשוקללת של צומתי הצאצא = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
לכן, הרווח במידע הוא:
- הרווח במידע = האנטרופיה של צומת האב – סכום האנטרופיה המשוקלל של צמתי הבן
- הרווח במידע = 0.6 – 0.14 = 0.46
רוב המסַפְּקִים מנסים ליצור תנאים שממקסמים את הרווח במידע.
תנאי בתוך קבוצה
בעץ החלטות, תנאי שבודק אם פריט מסוים קיים בקבוצת פריטים. לדוגמה, התנאי הבא הוא תנאי בתוך קבוצה:
house-style in [tudor, colonial, cape]
במהלך ההסקה, אם הערך של feature בסגנון הבית הוא tudor או colonial או cape, התנאי הזה מקבל את הערך Yes. אם הערך של התכונה house-style הוא משהו אחר (לדוגמה, ranch), התנאי הזה מקבל את הערך No.
תנאים בתוך קבוצת תנאים בדרך כלל מובילים לעצי החלטה יעילים יותר מאשר תנאים שבודקים תכונות מקודדות בשיטת one-hot.
L
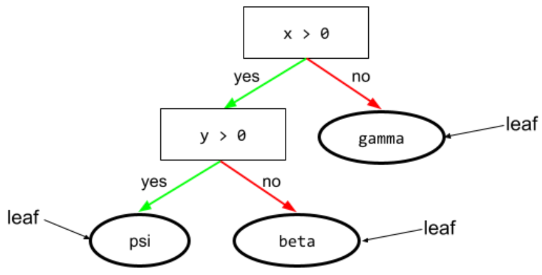
עלה
כל נקודת סיום בעץ החלטות. בניגוד לתנאי, צומת עלה לא מבצע בדיקה. במקום זאת, עלה הוא תחזית אפשרית. עלה הוא גם צומת סופית של נתיב הסקה.
לדוגמה, עץ ההחלטה הבא מכיל שלושה עלים:
מידע נוסף זמין במאמר עצי החלטה בקורס בנושא יערות החלטה.
לא
צומת (עץ החלטה)
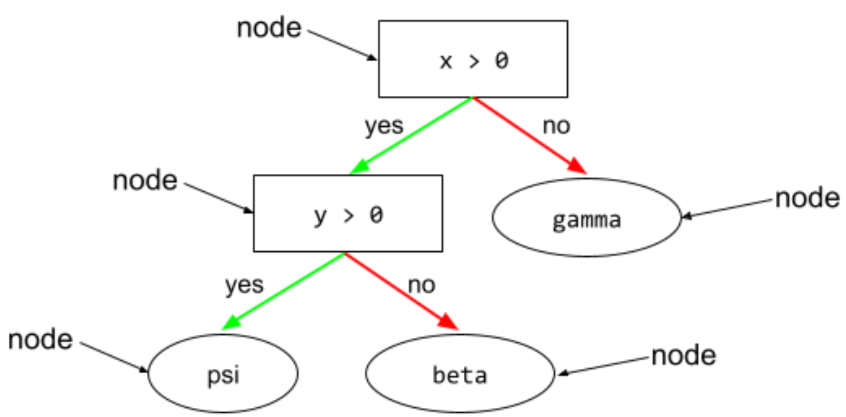
מידע נוסף זמין במאמר עצי החלטה בקורס בנושא יערות החלטה.
מצב לא בינארי
תנאי שמכיל יותר משני תוצאות אפשריות. לדוגמה, התנאי הלא בינארי הבא מכיל שלושה תוצאות אפשריות:
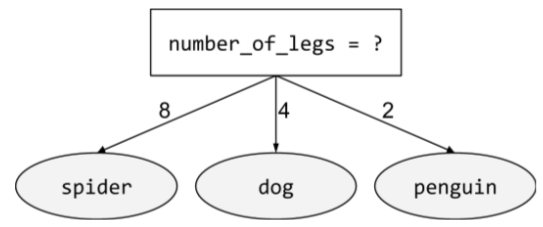
מידע נוסף זמין במאמר סוגי תנאים בקורס בנושא יערות החלטה.
O
תנאי עקיף
בעץ החלטה, תנאי שכולל יותר ממאפיין אחד. לדוגמה, אם הגובה והרוחב הם מאפיינים, אז התנאי הבא הוא תנאי אלכסוני:
height > width
ההגדרה הזו שונה מתנאי שמתיישר עם הציר.
מידע נוסף זמין במאמר סוגי תנאים בקורס בנושא יערות החלטה.
הערכה מחוץ לתיק (OOB)
מנגנון להערכת האיכות של יער החלטות על ידי בדיקה של כל עץ החלטות מול הדוגמאות שלא שימשו במהלך האימון של עץ ההחלטות הזה. לדוגמה, בתרשים הבא אפשר לראות שהמערכת מאמנת כל עץ החלטה על כשני שלישים מהדוגמאות, ואז בודקת אותו מול השליש הנותר של הדוגמאות.
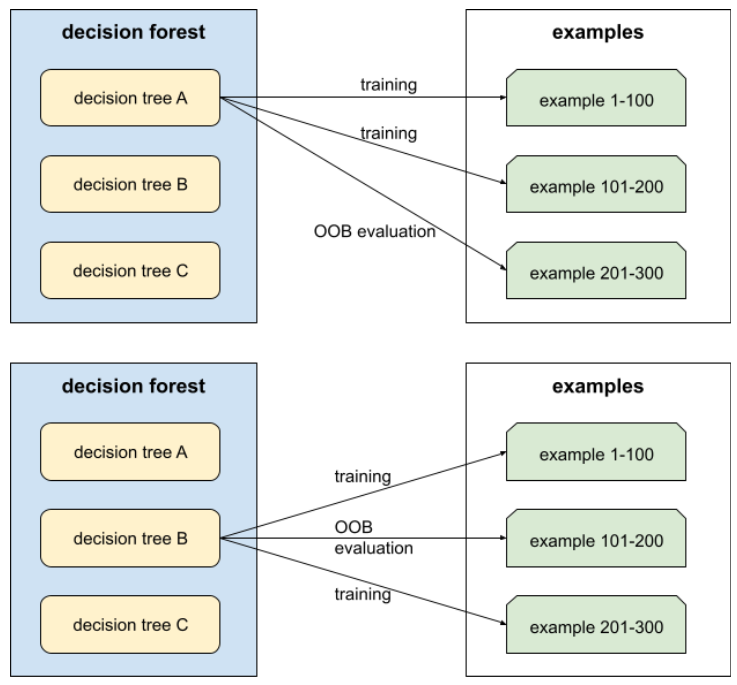
הערכה מחוץ לתיק היא קירוב יעיל מבחינה חישובית ושמרני של מנגנון האימות הצולב. באימות צולב, מאמנים מודל אחד לכל סבב של אימות צולב (לדוגמה, 10 מודלים מאומנים באימות צולב של 10 קפלים). בשיטת ההערכה OOB, מאמנים מודל יחיד. מכיוון שbagging מעכב חלק מהנתונים מכל עץ במהלך האימון, אפשר להשתמש בנתוני OOB כדי לבצע קירוב של אימות צולב.
מידע נוסף זמין במאמר הערכה מחוץ לתיק בקורס בנושא יערות החלטה.
P
חשיבות משתנים בתמורה
סוג של חשיבות משתנה שמעריך את העלייה בשגיאת החיזוי של מודל אחרי שינוי הערכים של התכונה. חשיבות המשתנה בפרמוטציה היא מדד שלא תלוי במודל.
R
יער אקראי
אנסמבל של עצי החלטה שבהם כל עץ החלטה מאומן עם רעש אקראי ספציפי, כמו bagging.
יערות אקראיים הם סוג של יער החלטות.
מידע נוסף זמין במאמר Random Forest (יער אקראי) בקורס בנושא Decision Forests (יערות החלטה).
הרמה הבסיסית (root)
הצומת ההתחלתי (התנאי הראשון) בעץ החלטה. לפי המוסכמה, שורש העץ מוצג בחלק העליון של תרשימי עץ ההחלטות. לדוגמה:

S
דגימה עם החזרה
שיטה לבחירת פריטים מתוך קבוצת פריטים אפשריים, שבה אפשר לבחור את אותו פריט כמה פעמים. הביטוי 'עם החזרה' מציין שאחרי כל בחירה, הפריט שנבחר מוחזר למאגר הפריטים שאפשר לבחור מהם. בשיטה ההפוכה, דגימה ללא החזרה, אפשר לבחור פריט מועמד רק פעם אחת.
לדוגמה, נניח שיש לכם את קבוצת הפירות הבאה:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}נניח שהמערכת בוחרת באופן אקראי את fig כפריט הראשון.
אם משתמשים בדגימה עם החזרה, המערכת בוחרת את הפריט השני מתוך הקבוצה הבאה:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}כן, זה אותו סט כמו קודם, כך שהמערכת יכולה לבחור שוב את fig.
אם משתמשים בדגימה ללא החזרה, אחרי שבוחרים דגימה אי אפשר לבחור אותה שוב. לדוגמה, אם המערכת בוחרת באופן אקראי את fig כמדגם הראשון, היא לא יכולה לבחור בו שוב.fig לכן, המערכת בוחרת את הדגימה השנייה מתוך הקבוצה הבאה (המצומצמת):
fruit = {kiwi, apple, pear, cherry, lime, mango}כיווץ
היפר-פרמטר בשיטת הגרדיאנט ששולט בהתאמת יתר. ההתכווצות בחיזוק גרדיאנט דומה לקצב הלמידה בירידת גרדיאנט. הערך של ההתכווצות הוא מספר עשרוני בין 0.0 ל-1.0. ערך כיווץ נמוך יותר מפחית את התאמת היתר יותר מערך כיווץ גבוה יותר.
פיצול
מפצל
במהלך אימון עץ החלטה, השגרה (והאלגוריתם) שאחראית למציאת התנאי הטוב ביותר בכל צומת.
T
בדיקה
סף (עבור עצי החלטה)
בתנאי שמוגדר לאורך ציר, הערך שמאפיין מושווה אליו. לדוגמה, 75 הוא ערך הסף בתנאי הבא:
grade >= 75
מידע נוסף זמין במאמר Exact splitter for binary classification with numerical features בקורס בנושא Decision Forests.
V
חשיבות המשתנים
קבוצת ציונים שמציינת את החשיבות היחסית של כל תכונה למודל.
לדוגמה, נניח שיש עץ החלטה שמבצע הערכה של מחירי בתים. נניח שעץ ההחלטה הזה משתמש בשלושה מאפיינים: מידה, גיל וסגנון. אם קבוצת חשיבות המשתנים של שלושת המאפיינים היא {size=5.8, age=2.5, style=4.7}, אז המאפיין size חשוב יותר לעץ ההחלטה מהמאפיינים age או style.
קיימים מדדים שונים לחשיבות משתנים, שיכולים לספק למומחי למידת מכונה מידע על היבטים שונים של מודלים.
W
חוכמת ההמונים
הרעיון שלפיו חישוב ממוצע של דעות או הערכות של קבוצה גדולה של אנשים ("הקהל") מניב לעיתים קרובות תוצאות טובות באופן מפתיע. לדוגמה, נניח שמשחקים משחק שבו אנשים מנחשים כמה סוכריות ג'לי יש בצנצנת גדולה. למרות שרוב הניחושים האישיים לא יהיו מדויקים, הוכח אמפירית שהממוצע של כל הניחושים קרוב באופן מפתיע למספר האמיתי של סוכריות הג'לי בצנצנת.
מודלים משולבים הם מקבילה בתוכנה לחוכמת ההמונים. גם אם מודלים בודדים יוצרים תחזיות לא מדויקות, ממוצע התחזיות של הרבה מודלים יוצר לעיתים קרובות תחזיות טובות באופן מפתיע. לדוגמה, למרות שעץ החלטה בודד עשוי לספק תחזיות לא טובות, יער החלטה לרוב מספק תחזיות טובות מאוד.