このページには、デシジョン フォレストの用語集が記載されています。用語集のすべての用語については、こちらをクリックしてください。
A
属性サンプリング
各ディシジョン ツリーが条件を学習するときに、可能な特徴のランダムなサブセットのみを考慮するディシジョン フォレストをトレーニングする戦術。通常、各ノードに対して異なる特徴量のサブセットがサンプリングされます。一方、属性サンプリングなしで決定木をトレーニングする場合、各ノードで可能なすべての特徴が考慮されます。
軸に沿った条件
ディシジョン ツリーで、単一の特徴のみを含む条件。たとえば、area が特徴量の場合、軸に沿った条件は次のようになります。
area > 200
斜め条件も参照してください。
B
バギング
各構成要素のモデルが、復元抽出でサンプリングされたトレーニング例のランダムなサブセットでトレーニングされるアンサンブルをトレーニングする方法。たとえば、ランダム フォレストは、バギングでトレーニングされたディシジョン ツリーのコレクションです。
バギングという用語は、ブートストラップ集計の略です。
詳細については、Decision Forests コースのランダム フォレストをご覧ください。
バイナリ条件
決定木では、通常は yes または no の 2 つの結果のみが可能な条件。たとえば、次の条件はバイナリ条件です。
temperature >= 100
非バイナリ条件も参照してください。
詳細については、Decision Forests コースの条件のタイプをご覧ください。
C
商品の状態(condition)
ディシジョン ツリーでは、テストを実行する任意のノード。たとえば、次のディシジョン ツリーには 2 つの条件が含まれています。

条件は、分割またはテストとも呼ばれます。
leaf と条件を対比します。
関連項目:
詳細については、Decision Forests コースの条件のタイプをご覧ください。
D
デシジョン フォレスト
複数のディシジョン ツリーから作成されたモデル。ディシジョン フォレストは、ディシジョン ツリーの予測を集計して予測を行います。一般的なディシジョン フォレストには、ランダム フォレストや勾配ブースト ツリーなどがあります。
詳細については、デシジョン フォレスト コースのデシジョン フォレストのセクションをご覧ください。
ディシジョン ツリー
階層的に編成された一連の条件とリーフで構成される教師あり学習モデル。たとえば、次の図は意思決定ツリーです。
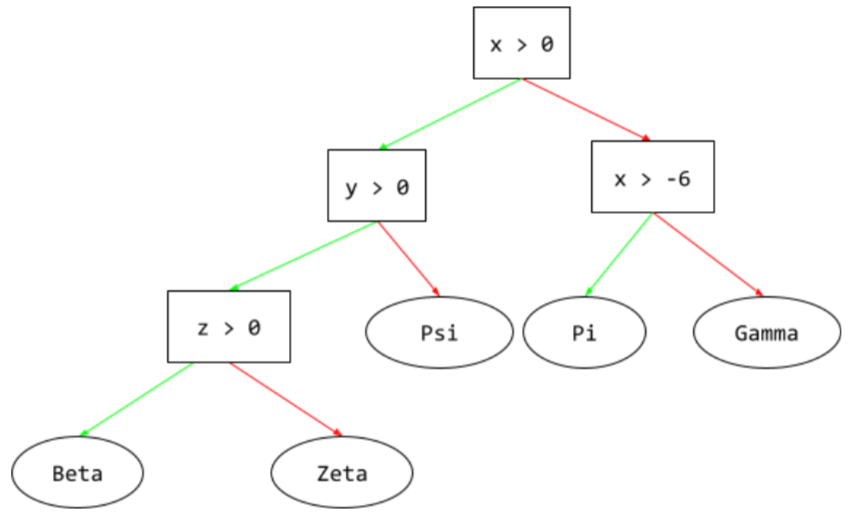
E
エントロピー
情報理論では、確率分布の予測不可能性を説明します。また、エントロピーは、各例に含まれる情報量としても定義されます。分布のエントロピーが最大になるのは、確率変数のすべての値が等しい確率で発生する場合です。
2 つの値「0」と「1」を持つセットのエントロピー(たとえば、バイナリ分類問題のラベル)は、次の式で表されます。
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
ここで
- H はエントロピーです。
- p は「1」の例の割合です。
- q は「0」の例の割合です。q = (1 - p) であることに注意してください。
- log は通常 log2 です。この場合、エントロピー単位はビットです。
たとえば、次のように仮定します。
- 100 個の例に値「1」が含まれている
- 300 個の例に値「0」が含まれている
したがって、エントロピー値は次のようになります。
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 1 例あたり 0.81 ビット
完全にバランスの取れたセット(たとえば、200 個の「0」と 200 個の「1」)のエントロピーは、例あたり 1.0 ビットになります。セットのバランスが崩れるほど、エントロピーは 0.0 に近づきます。
決定木では、エントロピーは情報ゲインの定式化に役立ち、スプリッタが分類決定木の成長中に条件を選択するのに役立ちます。
エントロピーを以下と比較します。
エントロピーは、シャノンのエントロピーと呼ばれることもあります。
詳細については、Decision Forests コースの数値特徴を使用したバイナリ分類の正確な分割ツールをご覧ください。
F
特徴の重要度
変数の重要度と同義。
G
ジニ不純度
エントロピーに似た指標。スプリッタは、ジニ不純度またはエントロピーから導出された値を使用して、分類の決定木の条件を構成します。情報ゲインはエントロピーから導出されます。ジニ不純度から導出された指標に、一般的に受け入れられている同等の用語はありません。ただし、この名前のない指標は情報ゲインと同じくらい重要です。
ジニ不純度は、ジニ係数または単にジニとも呼ばれます。
勾配ブースト(ディシジョン)ツリー(GBT)
次のようなデシジョン フォレストの一種。
- トレーニングは、グラデーション ブースティングに依存します。
- 弱いモデルはディシジョン ツリーです。
詳細については、意思決定フォレスト コースの勾配ブースティング決定木をご覧ください。
勾配ブースティング
弱いモデルをトレーニングして、強いモデルの品質を反復的に改善(損失を削減)するトレーニング アルゴリズム。たとえば、弱いモデルは線形モデルや小さなディシジョン ツリー モデルです。強いモデルは、以前にトレーニングされた弱いモデルの合計になります。
最も単純な形式のグラデーション ブースティングでは、各イテレーションで、強力なモデルの損失勾配を予測するように弱いモデルがトレーニングされます。次に、勾配降下法と同様に、予測された勾配を減算して、強いモデルの出力を更新します。
ここで
- $F_{0}$ は、開始時の強力なモデルです。
- $F_{i+1}$ は次の強力なモデルです。
- $F_{i}$ は現在の強力なモデルです。
- $\xi$ は 0.0 ~ 1.0 の値で、収縮と呼ばれます。これは、勾配降下法の学習率に類似しています。
- $f_{i}$ は、$F_{i}$ の損失勾配を予測するようにトレーニングされた弱いモデルです。
勾配ブースティングの最新のバリエーションでは、損失の 2 次導関数(ヘシアン)も計算に含まれます。
ディシジョン ツリーは、勾配ブースティングで弱いモデルとしてよく使用されます。勾配ブースト(ディシジョン)ツリーをご覧ください。
I
推論パス
決定木では、推論中に、特定の例がルートから他の条件をたどって、リーフで終了します。たとえば、次の決定木では、太い矢印は、次の特徴値を持つ例の推論パスを示しています。
- x = 7
- y = 12
- z = -3
次の図の推論パスは、リーフ(Zeta)に到達する前に 3 つの条件を通過します。

3 つの太い矢印は推論パスを示しています。
詳細については、デシジョン フォレスト コースのデシジョン ツリーをご覧ください。
情報利得
決定フォレストでは、ノードのエントロピーと、子ノードのエントロピーの重み付け(例の数による)された合計の差。ノードのエントロピーは、そのノード内の例のエントロピーです。
たとえば、次のエントロピー値を考えてみましょう。
- 親ノードのエントロピー = 0.6
- 16 個の関連する例を含む 1 つの子ノードのエントロピー = 0.2
- 関連する例が 24 個ある別の子ノードのエントロピー = 0.1
したがって、例の 40% は一方の子ノードにあり、60% はもう一方の子ノードにあります。そのため、次のようになります。
- 子ノードの重み付きエントロピーの合計 = (0.4 × 0.2) + (0.6 × 0.1) = 0.14
したがって、情報利得は次のようになります。
- 情報利得 = 親ノードのエントロピー - 子ノードの重み付きエントロピーの合計
- 情報利得 = 0.6 - 0.14 = 0.46
ほとんどの分割器は、情報ゲインを最大化する条件を作成しようとします。
インセット条件
ディシジョン ツリーで、アイテムのセット内の 1 つのアイテムの存在をテストする条件。たとえば、次の条件はセット内の条件です。
house-style in [tudor, colonial, cape]
推論時に、住宅スタイルの特徴の値が tudor、colonial、cape のいずれかの場合、この条件は Yes と評価されます。住宅スタイルの特徴の値がそれ以外の場合(ranch など)、この条件は No と評価されます。
通常、インセット条件は、ワンホット エンコードされた特徴をテストする条件よりも効率的なディシジョン ツリーにつながります。
L
leaf
ディシジョン ツリー内のエンドポイント。条件とは異なり、リーフはテストを実行しません。リーフは予測候補です。リーフは、推論パスの終端ノードでもあります。
たとえば、次のディシジョン ツリーには 3 つのリーフが含まれています。
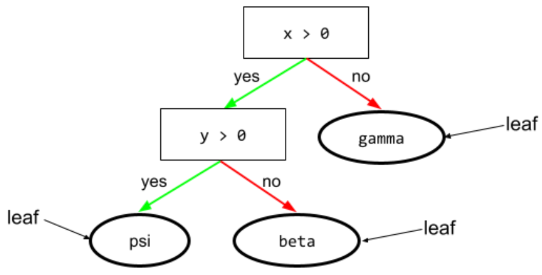
詳細については、デシジョン フォレスト コースのデシジョン ツリーをご覧ください。
N
ノード(ディシジョン ツリー)
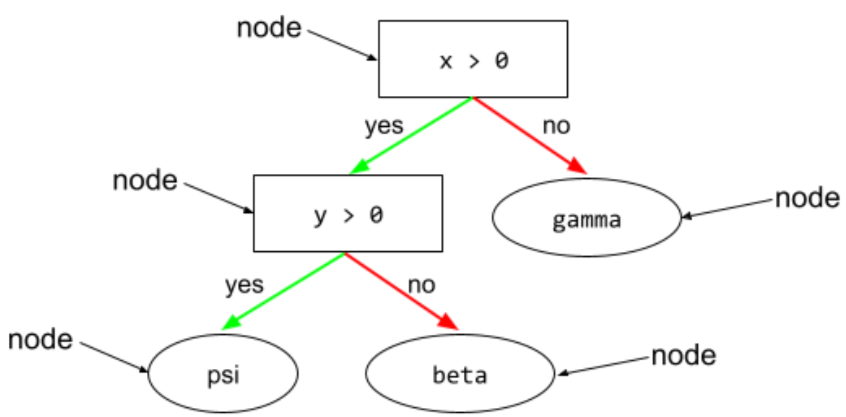
詳細については、デシジョン フォレスト コースのデシジョン ツリーをご覧ください。
非バイナリ条件
2 つ以上の結果が考えられる条件。たとえば、次の非バイナリ条件には 3 つの結果が含まれています。
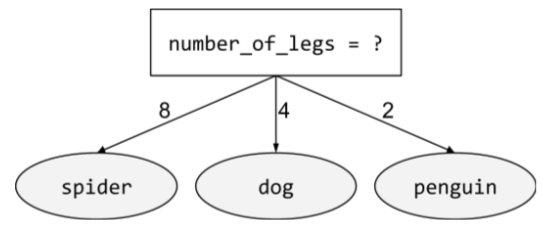
詳細については、Decision Forests コースの条件のタイプをご覧ください。
O
斜め条件
ディシジョン ツリーで、複数の特徴を含む条件。たとえば、高さと幅が両方とも特徴量の場合、次の条件は斜め条件です。
height > width
軸に沿った条件も参照してください。
詳細については、Decision Forests コースの条件のタイプをご覧ください。
アウトオブバッグ評価(OOB 評価)
各ディシジョン ツリーを、そのディシジョン ツリーのトレーニング中に使用されなかった例に対してテストすることで、ディシジョン フォレストの品質を評価するメカニズム。たとえば、次の図では、システムが各決定木を約 3 分の 2 の例でトレーニングし、残りの 3 分の 1 の例で評価していることがわかります。
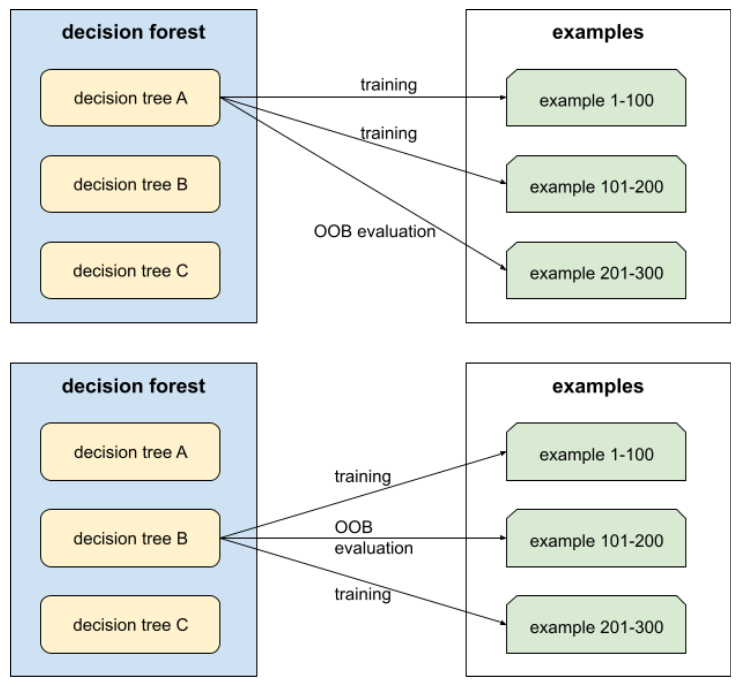
アウトオブバッグ評価は、交差検証メカニズムの計算効率が高く、保守的な近似です。交差検証では、交差検証ラウンドごとに 1 つのモデルがトレーニングされます(たとえば、10 分割交差検証では 10 個のモデルがトレーニングされます)。OOB 評価では、単一のモデルがトレーニングされます。バギングでは、トレーニング中に各ツリーから一部のデータが保持されるため、OOB 評価でそのデータを使用して交差検証を近似できます。
詳細については、デシジョン フォレスト コースのバッグ外評価をご覧ください。
P
permutation variable importances
特徴量の値を並べ替えた後のモデルの予測誤差の増加を評価する変数重要度の一種。順列変数重要度は、モデルに依存しない指標です。
R
ランダム フォレスト
各ディシジョン ツリーが特定のランダム ノイズでトレーニングされるディシジョン ツリーのアンサンブル(バギングなど)。
ランダム フォレストは、デシジョン フォレストの一種です。
詳細については、ディシジョン フォレスト コースのランダム フォレストをご覧ください。
root
決定木の開始ノード(最初の条件)。慣例により、図ではルートがディシジョン ツリーの上部に配置されます。次に例を示します。

S
復元抽出
候補アイテムのセットからアイテムを選択する方法。同じアイテムを複数回選択できます。「復元あり」とは、選択したアイテムが選択のたびに候補アイテムのプールに戻されることを意味します。逆の方法である非復元抽出では、候補アイテムは 1 回しか選択できません。
たとえば、次のような果物のセットについて考えてみましょう。
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}システムが最初のアイテムとして fig をランダムに選択したとします。復元抽出を使用する場合、システムは次のセットから 2 番目のアイテムを選択します。
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}はい。以前と同じセットなので、システムが fig を再び選択する可能性があります。
復元なしのサンプリングを使用する場合、一度選択したサンプルを再度選択することはできません。たとえば、システムが最初のサンプルとして fig をランダムに選択した場合、fig を再度選択することはできません。そのため、システムは次の(縮小された)セットから 2 番目のサンプルを選択します。
fruit = {kiwi, apple, pear, cherry, lime, mango}収縮
グラデーション ブースティングのハイパーパラメータ。過剰適合を制御します。勾配ブースティングの縮小は、勾配降下法の学習率に類似しています。シュリンケージは 0.0 ~ 1.0 の範囲の小数値です。収縮値が小さいほど、収縮値が大きい場合よりも過適合が軽減されます。
分割
スプリッター
決定木のトレーニング中に、各ノードで最適な条件を見つけるルーティン(およびアルゴリズム)。
T
test
しきい値(ディシジョン ツリーの場合)
軸に沿った条件では、特徴と比較される値。たとえば、次の条件では 75 がしきい値です。
grade >= 75
詳細については、デシジョン フォレスト コースの数値特徴量を使用したバイナリ分類の正確な分割ツールをご覧ください。
V
変数の重要度
各特徴のモデルに対する相対的な重要度を示すスコアのセット。
たとえば、住宅価格を推定する決定木について考えてみましょう。この決定木では、サイズ、年齢、スタイルの 3 つの特徴を使用するとします。3 つの特徴の変数重要度のセットが {size=5.8, age=2.5, style=4.7} と計算された場合、サイズは年齢やスタイルよりも決定木にとって重要です。
さまざまな変数重要度指標があり、ML の専門家はモデルのさまざまな側面について知ることができます。
W
群衆の知恵
大勢の人々(「群衆」)の意見や推定値を平均すると、驚くほど良い結果が得られることが多いという考え方。たとえば、大きな瓶に詰められたジェリービーンズの数を当てるゲームを考えてみましょう。個々の推測はほとんどが不正確ですが、すべての推測の平均は、瓶の中の実際のジェリービーンズの数に驚くほど近いことが経験的に示されています。
アンサンブルは、群衆の知恵のソフトウェア アナログです。個々のモデルの予測が大きく外れていても、多くのモデルの予測を平均すると、驚くほど正確な予測が得られることがよくあります。たとえば、個々のディシジョン ツリーの予測精度は低い可能性がありますが、ディシジョン フォレストの予測精度は非常に高いことがよくあります。