Glossário de machine learning: florestas de decisão

Esta página contém termos do glossário de florestas de decisão. Para conferir todos os termos do glossário, clique aqui.

A

amostragem de atributos

#df

Uma tática para treinar uma floresta de decisão em que cada árvore de decisão considera apenas um subconjunto aleatório de possíveis atributos ao aprender a condição. Em geral, um subconjunto diferente de recursos é amostrado para cada nó. Por outro lado, ao treinar uma árvore de decisão sem amostragem de atributos, todos os recursos possíveis são considerados para cada nó.

condição alinhada ao eixo

#df

Em uma árvore de decisão, uma condição que envolve apenas um único recurso. Por exemplo, se area for um recurso, a condição a seguir será alinhada ao eixo:

area > 200

Contraste com a condição oblíqua.

B

ensacamento

#df

Um método para treinar um conjunto em que cada modelo constituinte é treinado em um subconjunto aleatório de exemplos de treinamento amostrados com substituição. Por exemplo, uma floresta aleatória é um conjunto de árvores de decisão treinadas com bagging.

O termo bagging é uma abreviação de bootstrap aggregating.

Consulte Florestas aleatórias no curso "Florestas de decisão" para mais informações.

condição binária

#df

Em uma árvore de decisão, uma condição que tem apenas dois resultados possíveis, geralmente sim ou não. Por exemplo, esta é uma condição binária:

temperature >= 100

Contraste com a condição não binária.

Consulte Tipos de condições no curso "Florestas de decisão" para mais informações.

C

condição

#df
Em uma árvore de decisão, qualquer nó que realiza um teste. Por exemplo, a árvore de decisão a seguir contém duas condições:

Uma árvore de decisão com duas condições: (x > 0) e (y > 0).

Uma condição também é chamada de divisão ou teste.

Contraste a condição com o nó.

Consulte também:

Consulte Tipos de condições no curso "Florestas de decisão" para mais informações.

D

floresta de decisão

#df

Um modelo criado com várias árvores de decisão. Uma floresta de decisão faz uma previsão agregando as previsões das árvores de decisão. Os tipos mais usados de florestas de decisão incluem florestas aleatórias e árvores aprimoradas por gradiente.

Consulte a seção Florestas de decisão no curso sobre florestas de decisão para mais informações.

árvore de decisão

#df

Um modelo de aprendizado supervisionado composto por um conjunto de condições e folhas organizadas hierarquicamente. Por exemplo, esta é uma árvore de decisão:

Uma árvore de decisão com quatro condições organizadas hierarquicamente, que levam a cinco folhas.

E

entropia

#df
#Metric

Na teoria da informação, uma descrição de como uma distribuição de probabilidade é imprevisível. Outra definição de entropia é a quantidade de informações que cada exemplo contém. Uma distribuição tem a maior entropia possível quando todos os valores de uma variável aleatória têm a mesma probabilidade.

A entropia de um conjunto com dois valores possíveis "0" e "1" (por exemplo, os rótulos em um problema de classificação binária) tem a seguinte fórmula:

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

em que:

  • H é a entropia.
  • p é a fração de exemplos "1".
  • q é a fração de exemplos "0". q = (1 - p)
  • log geralmente é log2. Nesse caso, a unidade de entropia é um bit.

Por exemplo, suponha que:

  • 100 exemplos contêm o valor "1"
  • 300 exemplos contêm o valor "0"

Portanto, o valor de entropia é:

  • p = 0,25
  • q = 0,75
  • H = (-0,25)log2(0,25) - (0,75)log2(0,75) = 0,81 bits por exemplo

Um conjunto perfeitamente equilibrado (por exemplo, 200 "0"s e 200 "1"s) teria uma entropia de 1,0 bit por exemplo. À medida que um conjunto se torna mais desequilibrado, a entropia se aproxima de 0,0.

Nas árvores de decisão, a entropia ajuda a formular o ganho de informações para que o divisor selecione as condições durante o crescimento de uma árvore de decisão de classificação.

Compare a entropia com:

A entropia é geralmente chamada de entropia de Shannon.

Consulte Divisor exato para classificação binária com recursos numéricos no curso "Florestas de decisão" para mais informações.

F

importâncias de atributos

#df
#Metric

Sinônimo de importâncias de variáveis.

G

impureza de Gini

#df
#Metric

Uma métrica semelhante à entropia. Divisores usam valores derivados da impureza de Gini ou da entropia para compor condições para classificação árvores de decisão. O ganho de informação é derivado da entropia. Não existe um termo equivalente universalmente aceito para a métrica derivada da impureza de Gini. No entanto, essa métrica sem nome é tão importante quanto o ganho de informação.

A impureza de Gini também é chamada de índice de Gini ou simplesmente Gini.

árvores de decisão aprimoradas por gradiente (GBT)

#df

Um tipo de floresta de decisão em que:

Consulte Árvores de decisão com aumento de gradiente no curso sobre florestas de decisão para mais informações.

aumento de gradiente

#df

Um algoritmo de treinamento em que modelos fracos são treinados para melhorar iterativamente a qualidade (reduzir a perda) de um modelo forte. Por exemplo, um modelo fraco pode ser um modelo linear ou de árvore de decisão pequena. O modelo forte se torna a soma de todos os modelos fracos treinados anteriormente.

Na forma mais simples de otimização de gradiente, a cada iteração, um modelo fraco é treinado para prever o gradiente de perda do modelo forte. Em seguida, a saída do modelo forte é atualizada subtraindo o gradiente previsto, semelhante ao descida do gradiente.

$$F_{0} = 0$$ $$F_{i+1} = F_i - \xi f_i $$

em que:

  • $F_{0}$ é o modelo de início forte.
  • $F_{i+1}$ é o próximo modelo forte.
  • $F_{i}$ é o modelo forte atual.
  • $\xi$ é um valor entre 0,0 e 1,0 chamado de contração, que é análogo à taxa de aprendizado no gradiente descendente.
  • $f_{i}$ é o modelo fraco treinado para prever o gradiente de perda de $F_{i}$.

As variações modernas do gradient boosting também incluem a segunda derivada (Hessiana) da perda no cálculo.

As árvores de decisão são usadas com frequência como modelos fracos em gradient boosting. Consulte árvores de decisão aprimoradas por gradiente.

I

caminho de inferência

#df

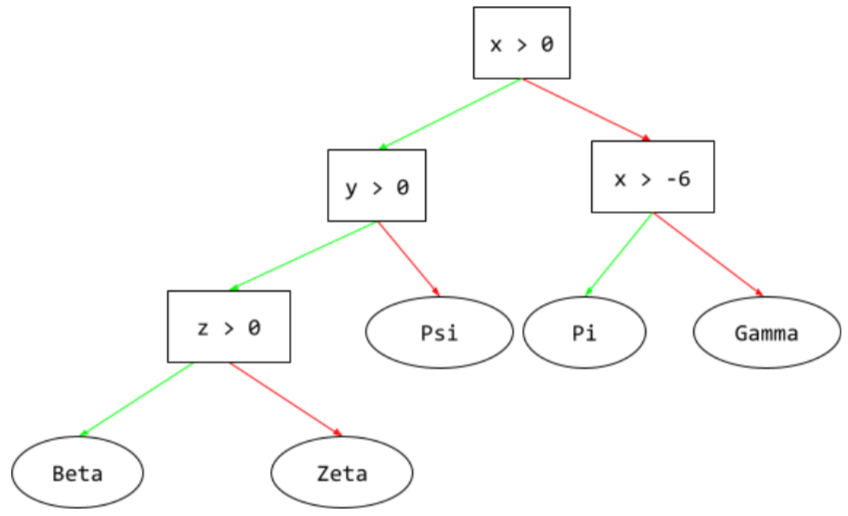
Em uma árvore de decisão, durante a inferência, o caminho que um exemplo específico percorre da raiz até outras condições, terminando com uma folha. Por exemplo, na árvore de decisões a seguir, as setas mais grossas mostram o caminho de inferência para um exemplo com os seguintes valores de recursos:

  • x = 7
  • y = 12
  • z = -3

O caminho de inferência na ilustração a seguir passa por três condições antes de chegar à folha (Zeta).

Uma árvore de decisão com quatro condições e cinco folhas. A condição raiz é (x > 0). Como a resposta é "Sim", o caminho de inferência vai da raiz até a próxima condição (y > 0). Como a resposta é "Sim", o caminho de inferência vai para a próxima condição (z > 0). Como a resposta é "Não", o caminho de inferência vai até o nó terminal, que é a folha (Zeta).

As três setas grossas mostram o caminho de inferência.

Consulte Árvores de decisão no curso "Florestas de decisão" para mais informações.

ganho de informação

#df
#Metric

Em florestas de decisão, a diferença entre a entropia de um nó e a soma ponderada (pelo número de exemplos) da entropia dos nós filhos. A entropia de um nó é a entropia dos exemplos nesse nó.

Por exemplo, considere os seguintes valores de entropia:

  • entropia do nó pai = 0,6
  • entropia de um nó filho com 16 exemplos relevantes = 0,2
  • entropia de outro nó filho com 24 exemplos relevantes = 0,1

Portanto, 40% dos exemplos estão em um nó filho e 60% estão no outro. Assim:

  • Soma ponderada da entropia dos nós filhos = (0,4 * 0,2) + (0,6 * 0,1) = 0,14

Portanto, o ganho de informação é:

  • ganho de informação = entropia do nó pai - soma ponderada da entropia dos nós filhos
  • ganho de informação = 0,6 - 0,14 = 0,46

A maioria dos divisores tenta criar condições que maximizam o ganho de informações.

condição no conjunto

#df

Em uma árvore de decisão, uma condição que testa a presença de um item em um conjunto de itens. Por exemplo, esta é uma condição de conjunto:

  house-style in [tudor, colonial, cape]

Durante a inferência, se o valor do recurso de estilo de casa for tudor, colonial ou cape, essa condição será avaliada como "Sim". Se o valor do recurso de estilo da casa for algo diferente (por exemplo, ranch), essa condição será avaliada como "Não".

As condições no conjunto geralmente levam a árvores de decisão mais eficientes do que as condições que testam recursos codificados com one-hot.

L

folha

#df

Qualquer endpoint em uma árvore de decisão. Ao contrário de uma condição, uma folha não realiza um teste. Em vez disso, uma folha é uma previsão possível. Uma folha também é o nó terminal de um caminho de inferência.

Por exemplo, a árvore de decisão a seguir contém três folhas:

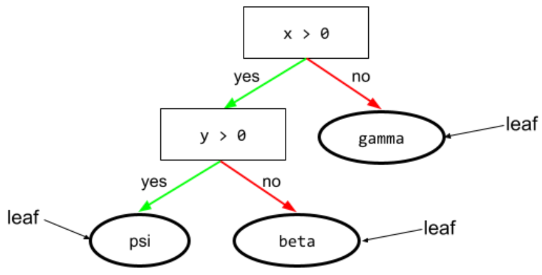
Uma árvore de decisão com duas condições que levam a três folhas.

Consulte Árvores de decisão no curso "Florestas de decisão" para mais informações.

N

nó (árvore de decisão)

#df

Em uma árvore de decisão, qualquer condição ou folha.

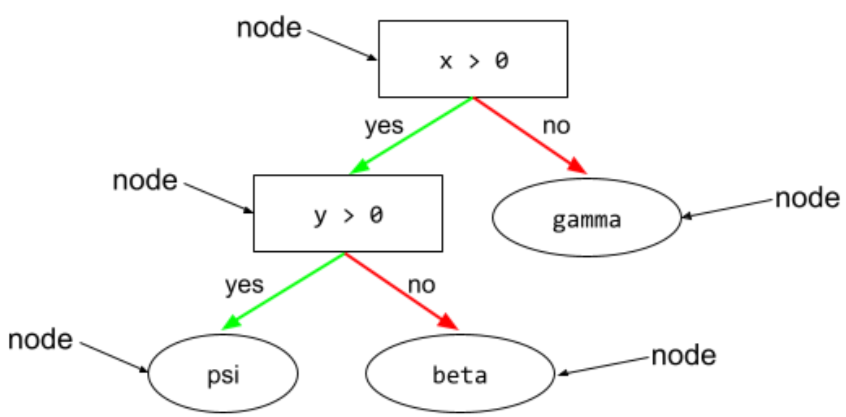
Uma árvore de decisão com duas condições e três folhas.

Consulte Árvores de decisão no curso "Florestas de decisão" para mais informações.

condição não binária

#df

Uma condição que contém mais de dois resultados possíveis. Por exemplo, a condição não binária a seguir tem três resultados possíveis:

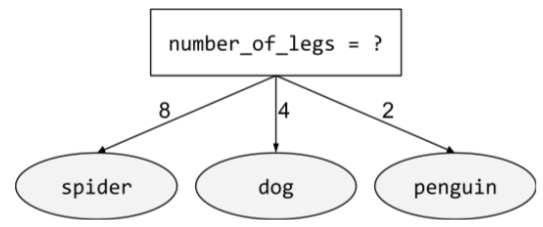
Uma condição (number_of_legs = ?) que leva a três resultados possíveis. Um resultado (number_of_legs = 8) leva a uma folha chamada spider. Um segundo resultado (number_of_legs = 4) leva a uma folha chamada "dog". Um terceiro resultado (number_of_legs = 2) leva a uma folha chamada "penguin".

Consulte Tipos de condições no curso "Florestas de decisão" para mais informações.

O

condição oblíqua

#df

Em uma árvore de decisão, uma condição que envolve mais de uma característica. Por exemplo, se altura e largura forem recursos, a condição a seguir será oblíqua:

  height > width

Contraste com a condição alinhada ao eixo.

Consulte Tipos de condições no curso "Florestas de decisão" para mais informações.

avaliação fora da amostra (OOB)

#df

Um mecanismo para avaliar a qualidade de uma floresta de decisão testando cada árvore de decisão em relação aos exemplos não usados durante o treinamento dessa árvore de decisão. Por exemplo, no diagrama a seguir, observe que o sistema treina cada árvore de decisão em cerca de dois terços dos exemplos e depois avalia o restante.

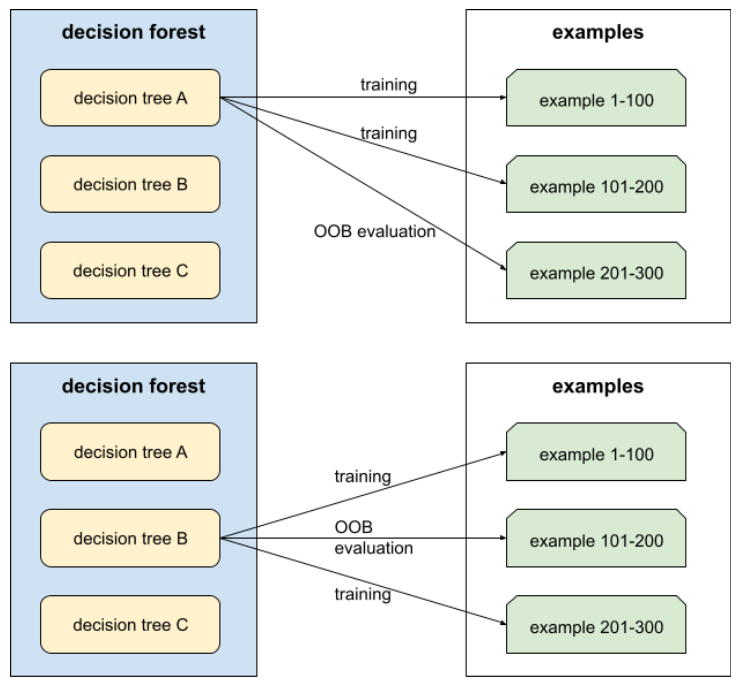
Uma floresta de decisão com três árvores de decisão. Uma árvore de decisão é treinada em dois terços dos exemplos e usa o restante para avaliação OOB. Uma segunda árvore de decisão é treinada em dois terços diferentes dos exemplos em comparação com a árvore anterior e usa um terço diferente para avaliação OOB.

A avaliação fora da amostra é uma aproximação computacionalmente eficiente e conservadora do mecanismo de validação cruzada. Na validação cruzada, um modelo é treinado para cada rodada de validação cruzada (por exemplo, 10 modelos são treinados em uma validação cruzada de 10 dobras). Com a avaliação OOB, um único modelo é treinado. Como o bagging retém alguns dados de cada árvore durante o treinamento, a avaliação OOB pode usar esses dados para aproximar a validação cruzada.

Consulte Avaliação fora da amostra no curso "Florestas de decisão" para mais informações.

P

Importâncias de variáveis de troca

#df
#Metric

Um tipo de importância da variável que avalia o aumento no erro de previsão de um modelo após a troca dos valores do atributo. A importância da variável de permutação é uma métrica independente do modelo.

R

floresta aleatória

#df

Um conjunto de árvores de decisão em que cada árvore é treinada com um ruído aleatório específico, como bagging.

As florestas aleatórias são um tipo de floresta de decisão.

Consulte Floresta aleatória no curso "Florestas de decisão" para mais informações.

root

#df

O nó inicial (a primeira condição) em uma árvore de decisão. Por convenção, os diagramas colocam a raiz na parte de cima da árvore de decisões. Exemplo:

Uma árvore de decisão com duas condições e três folhas. A condição inicial (x > 2) é a raiz.

S

amostragem com substituição

#df

Um método de escolha de itens de um conjunto de itens candidatos em que o mesmo item pode ser escolhido várias vezes. A frase "com substituição" significa que, após cada seleção, o item escolhido é retornado ao conjunto de itens candidatos. O método inverso, amostragem sem substituição, significa que um item candidato só pode ser escolhido uma vez.

Por exemplo, considere o seguinte conjunto de frutas:

fruit = {kiwi, apple, pear, fig, cherry, lime, mango}

Suponha que o sistema escolha aleatoriamente fig como o primeiro item. Se você estiver usando amostragem com substituição, o sistema vai escolher o segundo item do seguinte conjunto:

fruit = {kiwi, apple, pear, fig, cherry, lime, mango}

Sim, é o mesmo conjunto de antes. Portanto, o sistema pode escolher fig novamente.

Se você usar amostragem sem substituição, uma amostra escolhida não poderá ser selecionada novamente. Por exemplo, se o sistema escolher aleatoriamente fig como a primeira amostra, fig não poderá ser escolhido novamente. Portanto, o sistema escolhe a segunda amostra do seguinte conjunto (reduzido):

fruit = {kiwi, apple, pear, cherry, lime, mango}

encolhimento

#df

Um hiperparâmetro no gradient boosting que controla o overfitting. A redução em gradient boosting é análoga à taxa de aprendizado no gradiente descendente. A redução é um valor decimal entre 0,0 e 1,0. Um valor de redução menor reduz o overfitting mais do que um valor maior.

dividir

#df

Em uma árvore de decisão, outro nome para uma condição.

divisor

#df

Ao treinar uma árvore de decisão, a rotina (e o algoritmo) responsável por encontrar a melhor condição em cada node.

T

teste

#df

Em uma árvore de decisão, outro nome para uma condição.

limiar (para árvores de decisão)

#df

Em uma condição alinhada ao eixo, o valor com que um recurso está sendo comparado. Por exemplo, 75 é o valor de limite na seguinte condição:

grade >= 75

Consulte Divisor exato para classificação binária com recursos numéricos no curso "Florestas de decisão" para mais informações.

V

importâncias de variáveis

#df
#Metric

Um conjunto de pontuações que indica a importância relativa de cada atributo para o modelo.

Por exemplo, considere uma árvore de decisão que estima os preços das casas. Suponha que essa árvore de decisão use três recursos: tamanho, idade e estilo. Se um conjunto de importâncias de variáveis para os três recursos for calculado como {size=5.8, age=2.5, style=4.7}, o tamanho será mais importante para a árvore de decisão do que a idade ou o estilo.

Existem diferentes métricas de importância da variável, que podem informar aos especialistas em ML sobre diferentes aspectos dos modelos.

W

sabedoria da multidão

#df

A ideia de que a média das opiniões ou estimativas de um grande grupo de pessoas ("a multidão") geralmente produz resultados surpreendentemente bons. Por exemplo, considere um jogo em que as pessoas adivinham o número de jujubas em um pote grande. Embora a maioria dos palpites individuais seja imprecisa, a média de todos os palpites se mostrou empiricamente surpreendentemente próxima do número real de jujubas no pote.

Os ensembles são um análogo de software da sabedoria da multidão. Mesmo que modelos individuais façam previsões muito imprecisas, a média das previsões de muitos modelos geralmente gera previsões surpreendentemente boas. Por exemplo, embora uma árvore de decisão individual possa fazer previsões ruins, uma floresta de decisão geralmente faz previsões muito boas.