इस पेज का अनुवाद Cloud Translation API से किया गया है.

मशीन लर्निंग शब्दावली: फ़ैसले लेने के जंगल

इस पेज पर, डिसिज़न फ़ॉरेस्ट के शब्दकोश में शामिल शब्दों की जानकारी दी गई है. सभी शब्दावली के लिए, यहां क्लिक करें.

A

एट्रिब्यूट सैंपलिंग

#df

यह डिसिज़न फ़ॉरेस्ट को ट्रेन करने की एक रणनीति है. इसमें हर डिसिज़न ट्री, शर्त के बारे में सीखते समय, संभावित सुविधाओं के सिर्फ़ एक रैंडम सबसेट पर विचार करता है. आम तौर पर, हर नोड के लिए, सुविधाओं का अलग सबसेट सैंपल किया जाता है. इसके उलट, एट्रिब्यूट सैंपलिंग के बिना किसी फ़ैसले के ट्री को ट्रेन करते समय, हर नोड के लिए सभी संभावित सुविधाओं पर विचार किया जाता है.

ऐक्सिस के साथ अलाइन की गई शर्त

#df

डिसिज़न ट्री में, शर्त ऐसी होती है जिसमें सिर्फ़ एक फ़ीचर शामिल होता है. उदाहरण के लिए, अगर area एक सुविधा है, तो ऐक्सिस के साथ अलाइन की गई शर्त यह है:

area > 200

तिरछी स्थिति के साथ कंट्रास्ट.

B

बैगिंग

#df

यह एन्सेम्बल को ट्रेन करने का एक तरीका है. इसमें हर मॉडल, ट्रेनिंग के उदाहरणों के रैंडम सबसेट पर ट्रेन करता है. इन उदाहरणों को रिप्लेसमेंट के साथ सैंपल किया जाता है. उदाहरण के लिए, रैंडम फ़ॉरेस्ट, डिसिज़न ट्री का एक कलेक्शन है. इसे बैगिंग की मदद से ट्रेन किया जाता है.

बैगिंग शब्द, बूटस्ट्रैप ऐग्रीगेटिंग का छोटा रूप है.

ज़्यादा जानकारी के लिए, फ़ैसले लेने में मदद करने वाले फ़ॉरेस्ट कोर्स में रैंडम फ़ॉरेस्ट देखें.

बाइनरी शर्त

#df

डिसिज़न ट्री में, शर्त ऐसी होती है जिसके सिर्फ़ दो संभावित नतीजे होते हैं. आम तौर पर, हां या नहीं. उदाहरण के लिए, यहां दी गई शर्त बाइनरी शर्त है:

temperature >= 100

नॉन-बाइनरी स्थिति से अलग.

ज़्यादा जानकारी के लिए, Decision Forests कोर्स में शर्तों के टाइप देखें.

C

शर्त

#df

डिसिज़न ट्री में, ऐसा कोई भी नोड जो टेस्ट करता है. उदाहरण के लिए, इस फ़ैसले के ट्री में दो शर्तें शामिल हैं:

यह एक फ़ैसला लेने वाला ट्री है. इसमें दो शर्तें हैं: (x > 0) और (y > 0).

कंडीशन को स्प्लिट या टेस्ट भी कहा जाता है.

पत्ती के साथ कंट्रास्ट की स्थिति.

यह भी देखें:

बाइनरी शर्त
अन्य स्थिति.
axis-aligned-condition
oblique-condition

ज़्यादा जानकारी के लिए, Decision Forests कोर्स में शर्तों के टाइप देखें.

D

डिसीज़न फ़ॉरेस्ट

#df

यह मॉडल, कई डिसिज़न ट्री से बनाया जाता है. डिसिज़न फ़ॉरेस्ट, अपने डिसिज़न ट्री के अनुमानों को इकट्ठा करके अनुमान लगाता है. फ़ैसले लेने वाले फ़ॉरेस्ट के लोकप्रिय टाइप में, रैंडम फ़ॉरेस्ट और ग्रेडिएंट बूस्टेड ट्री शामिल हैं.

ज़्यादा जानकारी के लिए, Decision Forests कोर्स में Decision Forests सेक्शन देखें.

डिसीज़न ट्री

#df

यह एक सुपरवाइज़्ड लर्निंग मॉडल है. इसमें शर्तों और लीफ़ का एक सेट होता है, जिसे क्रम से व्यवस्थित किया जाता है. उदाहरण के लिए, यहां एक फ़ैसला लेने वाला ट्री दिया गया है:

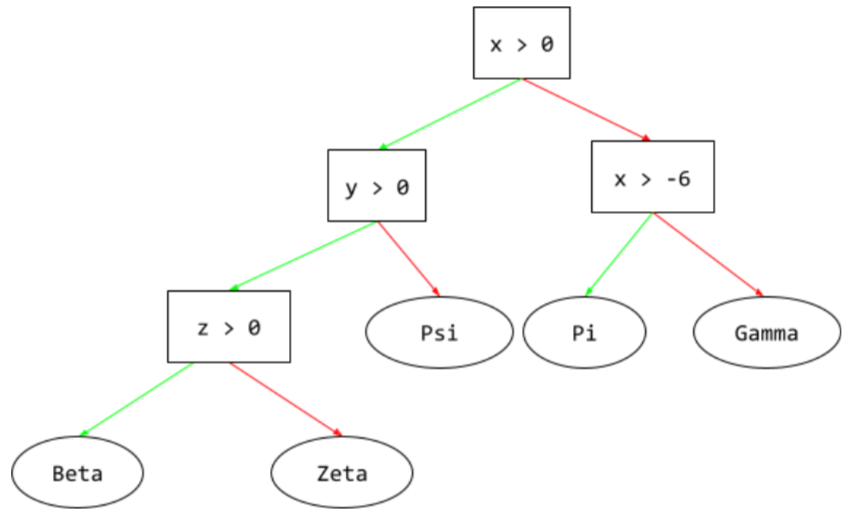
चार शर्तों वाला डिसिज़न ट्री, जिसे क्रम से लगाया गया है. इससे पांच पत्तियां मिलती हैं.

E

एन्ट्रॉपी

#df

#Metric

सूचना सिद्धांत में, यह बताया जाता है कि किसी संभावना वितरण का अनुमान लगाना कितना मुश्किल है. इसके अलावा, एन्ट्रापी को इस तरह भी परिभाषित किया जाता है कि हर उदाहरण में कितनी जानकारी शामिल है. किसी डिस्ट्रिब्यूशन की एंट्रॉपी सबसे ज़्यादा तब होती है, जब रैंडम वैरिएबल की सभी वैल्यू की संभावना बराबर होती है.

दो संभावित वैल्यू "0" और "1" वाले सेट की एंट्रॉपी (उदाहरण के लिए, बाइनरी क्लासिफ़िकेशन की समस्या में लेबल) का फ़ॉर्मूला यह है:

H = -p log p - q log q = -p log p - (1-p) * log (1-p)

कहां:

H एन्ट्रॉपी है.
p, "1" उदाहरणों का फ़्रैक्शन है.
q, "0" उदाहरणों का फ़्रैक्शन है. ध्यान दें कि q = (1 - p)
लॉग आम तौर पर log₂ होता है. इस मामले में, एंट्रॉपी यूनिट एक बिट है.

उदाहरण के लिए, मान लें कि:

100 उदाहरणों में "1" वैल्यू मौजूद है
300 उदाहरणों में वैल्यू "0" मौजूद है

इसलिए, एंट्रॉपी की वैल्यू यह होगी:

p = 0.25
q = 0.75
H = (-0.25)log₂(0.25) - (0.75)log₂(0.75) = 0.81 बिट प्रति उदाहरण

पूरी तरह से संतुलित सेट (उदाहरण के लिए, 200 "0" और 200 "1") में, हर उदाहरण के लिए एंट्रॉपी 1.0 बिट होगी. सेट के इंबैलेंस होने पर, उसकी एंट्रॉपी 0.0 की ओर बढ़ती है.

डिसिज़न ट्री में, एंट्रॉपी सूचना लाभ को फ़ॉर्म्युलेट करने में मदद करती है, ताकि स्प्लिटर, क्लासिफ़िकेशन डिसिज़न ट्री के बढ़ने के दौरान शर्तें चुन सके.

एंट्रॉपी की तुलना इससे करें:

गिनी अशुद्धता
क्रॉस-एंट्रॉपी लॉस फ़ंक्शन

एंट्रॉपी को अक्सर शैनन की एंट्रॉपी कहा जाता है.

ज़्यादा जानकारी के लिए, फ़ैसले लेने वाले फ़ॉरेस्ट कोर्स में संख्यात्मक सुविधाओं के साथ बाइनरी क्लासिफ़िकेशन के लिए सटीक स्प्लिटर देखें.

F

सुविधाओं की अहमियत

#df

#Metric

यह वैरिएबल के महत्व का समानार्थी शब्द है.

G

गिनी अशुद्धता

#df

#Metric

एंट्रॉपी से मिलती-जुलती मेट्रिक. स्प्लिटर, क्लासिफ़िकेशन डिसिज़न ट्री के लिए शर्तें बनाने के लिए, गिनी इंप्योरिटी या एंट्रॉपी से मिली वैल्यू का इस्तेमाल करते हैं. सूचना लाभ, एंट्रॉपी से मिलता है. गिनी अशुद्धता से निकाली गई मेट्रिक के लिए, कोई भी ऐसा शब्द नहीं है जिसे सभी लोग स्वीकार करते हों. हालांकि, बिना नाम वाली यह मेट्रिक, सूचना के फ़ायदे जितनी ही अहम होती है.

Gini अशुद्धता को Gini इंडेक्स या सिर्फ़ Gini भी कहा जाता है.

गिनी अशुद्धता के बारे में गणितीय जानकारी पाने के लिए, आइकॉन पर क्लिक करें.

गिनी अशुद्धता, एक ही डिस्ट्रिब्यूशन से लिए गए नए डेटा को गलत तरीके से क्लासिफ़ाई करने की संभावना होती है. दो संभावित वैल्यू "0" और "1" वाले सेट की गिनी अशुद्धता (उदाहरण के लिए, बाइनरी क्लासिफ़िकेशन की समस्या में लेबल) की गणना इस फ़ॉर्मूले से की जाती है:

I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

कहां:

I, गिनी अशुद्धता है.
p, "1" उदाहरणों का फ़्रैक्शन है.
q, "0" उदाहरणों का फ़्रैक्शन है. ध्यान दें कि q = 1-p

उदाहरण के लिए, इस डेटासेट पर ध्यान दें:

100 लेबल (डेटासेट का 0.25) में "1" वैल्यू मौजूद है
300 लेबल (डेटासेट का 0.75) में "0" वैल्यू शामिल है

इसलिए, गिनी अशुद्धता यह है:

p = 0.25
q = 0.75
I = 1 - (0.25² + 0.75²) = 0.375

इसलिए, उसी डेटासेट के किसी रैंडम लेबल के गलत तरीके से क्लासिफ़ाई होने की संभावना 37.5% होगी. वहीं, सही तरीके से क्लासिफ़ाई होने की संभावना 62.5% होगी.

पूरी तरह से बैलेंस किए गए लेबल (उदाहरण के लिए, 200 "0" और 200 "1") के लिए, गिनी अशुद्धता 0.5 होगी. बहुत ज़्यादा असंतुलित लेबल के लिए, गिनी अशुद्धता 0.0 के आस-पास होगी.

ग्रेडिएंट बूस्टेड (डिसिज़न) ट्री (GBT)

#df

यह डिसिज़न फ़ॉरेस्ट का एक टाइप है. इसमें:

ट्रेनिंग, ग्रेडिएंट बूस्टिंग पर निर्भर करती है.
कमज़ोर मॉडल एक डिसिज़न ट्री है.

ज़्यादा जानकारी के लिए, फ़ैसले लेने वाले फ़ॉरेस्ट कोर्स में ग्रेडिएंट बूस्टेड डिसिज़न ट्री देखें.

ग्रेडिएंट बूस्टिंग

#df

यह एक ट्रेनिंग एल्गोरिदम है. इसमें कमज़ोर मॉडल को बार-बार ट्रेन किया जाता है, ताकि वे किसी मज़बूत मॉडल की क्वालिटी को बेहतर बना सकें (नुकसान को कम कर सकें). उदाहरण के लिए, कमज़ोर मॉडल, लीनियर या छोटा डिसिज़न ट्री मॉडल हो सकता है. इस तरह, मज़बूत मॉडल, पहले से ट्रेन किए गए सभी कमज़ोर मॉडल का योग बन जाता है.

ग्रेडिएंट बूस्टिंग के सबसे आसान तरीके में, हर बार एक कमज़ोर मॉडल को ट्रेन किया जाता है, ताकि वह मज़बूत मॉडल के लॉस ग्रेडिएंट का अनुमान लगा सके. इसके बाद, अनुमानित ग्रेडिएंट को घटाकर, मॉडल के आउटपुट को अपडेट किया जाता है. यह ग्रेडिएंट डिसेंट की तरह होता है.

$$F_{0} = 0$$ $$F_{i+1} = F_i - \xi f_i $$

कहां:

$F_{0}$ शुरुआती मॉडल है.
$F_{i+1}$ अगला मज़बूत मॉडल है.
$F_{i}$ मौजूदा स्ट्रॉन्ग मॉडल है.
$\xi$ की वैल्यू 0.0 और 1.0 के बीच होती है. इसे श्रिंकेज कहा जाता है. यह ग्रेडिएंट डिसेंट में लर्निंग रेट के जैसा होता है.
$f_{i}$ एक ऐसा मॉडल है जिसे $F_{i}$ के लॉस ग्रेडिएंट का अनुमान लगाने के लिए ट्रेन किया गया है.

ग्रेडिएंट बूस्टिंग के आधुनिक वर्शन में, कंप्यूटेशन के दौरान नुकसान के दूसरे डेरिवेटिव (Hessian) को भी शामिल किया जाता है.

डिसिज़न ट्री का इस्तेमाल, आम तौर पर ग्रेडिएंट बूस्टिंग में कमज़ोर मॉडल के तौर पर किया जाता है. ग्रेडिएंट बूस्टेड (डिसिज़न) ट्री देखें.

I

अनुमान लगाने का पाथ

#df

डिसिज़न ट्री में, इनफ़रेंस के दौरान, कोई उदाहरण, रूट से लेकर अन्य शर्तों तक जाता है. इसके बाद, यह लीफ पर खत्म होता है. उदाहरण के लिए, यहां दिए गए फ़ैसले के ट्री में, मोटे ऐरो से ऐसे उदाहरण के लिए अनुमान लगाने का पाथ दिखाया गया है जिसमें ये फ़ीचर वैल्यू मौजूद हैं:

x = 7
y = 12
z = -3

नीचे दिए गए इलस्ट्रेशन में, अनुमान लगाने का पाथ तीन शर्तों से होकर गुज़रता है. इसके बाद, यह लीफ़ (Zeta) तक पहुंचता है.

चार शर्तों और पांच लीफ़ वाला डिसिज़न ट्री.
रूट की शर्त (x > 0) है. जवाब 'हां' होने की वजह से, अनुमान लगाने का पाथ रूट से अगली शर्त (y > 0) तक जाता है.
जवाब 'हां' होने की वजह से, अनुमान लगाने का पाथ अगली शर्त (z > 0) पर चला जाता है. जवाब 'नहीं' होने की वजह से, अनुमान लगाने का पाथ अपने टर्मिनल नोड पर जाता है, जो कि लीफ़ (ज़ेटा) है.

तीन मोटे ऐरो, अनुमान लगाने का पाथ दिखाते हैं.

ज़्यादा जानकारी के लिए, Decision Forests कोर्स में डिसीज़न ट्री देखें.

सूचना लाभ

#df

#Metric

डिसिज़न फ़ॉरेस्ट में, किसी नोड की एंट्रॉपी और उसके चाइल्ड नोड की एंट्रॉपी के वज़न (उदाहरणों की संख्या के हिसाब से) के योग के बीच का अंतर. किसी नोड की एंट्रॉपी, उस नोड में मौजूद उदाहरणों की एंट्रॉपी होती है.

उदाहरण के लिए, यहां दी गई एंट्रॉपी वैल्यू देखें:

पैरंट नोड की एन्ट्रॉपी = 0.6
काम के 16 उदाहरणों वाले एक चाइल्ड नोड की एंट्रॉपी = 0.2
24 काम के उदाहरणों वाले दूसरे चाइल्ड नोड की एंट्रॉपी = 0.1

इसलिए, 40% उदाहरण एक चाइल्ड नोड में हैं और 60% उदाहरण दूसरे चाइल्ड नोड में हैं. इसलिए:

चाइल्ड नोड की वेटेड एन्ट्रॉपी का योग = (0.4 * 0.2) + (0.6 * 0.1) = 0.14

इसलिए, जानकारी में हुई बढ़ोतरी यह है:

सूचना लाभ = पैरंट नोड की एन्ट्रॉपी - चाइल्ड नोड की वज़न के हिसाब से एन्ट्रॉपी का योग
सूचना लाभ = 0.6 - 0.14 = 0.46

ज़्यादातर स्प्लिटर, शर्तें बनाने की कोशिश करते हैं, ताकि ज़्यादा से ज़्यादा जानकारी मिल सके.

सेट में मौजूद होने की शर्त

#df

डिसिज़न ट्री में, शर्त यह जांच करती है कि आइटम के सेट में कोई आइटम मौजूद है या नहीं. उदाहरण के लिए, यहां दी गई शर्त, सेट में मौजूद होने की शर्त है:

  house-style in [tudor, colonial, cape]

अनुमान के दौरान, अगर हाउस-स्टाइल feature की वैल्यू tudor या colonial या cape है, तो यह शर्त 'हां' के तौर पर तय की जाती है. अगर हाउस-स्टाइल फ़ीचर की वैल्यू कुछ और है (उदाहरण के लिए, ranch), तो यह शर्त 'नहीं' के तौर पर तय होती है.

आम तौर पर, इन-सेट की गई शर्तों से, वन-हॉट एन्कोड की गई सुविधाओं की जांच करने वाली शर्तों की तुलना में, ज़्यादा असरदार फ़ैसले लेने वाले ट्री मिलते हैं.

L

पत्ती

#df

डिसिज़न ट्री में मौजूद कोई भी एंडपॉइंट. शर्त के उलट, लीफ़ कोई टेस्ट नहीं करती. हालांकि, पत्ता एक संभावित अनुमान है. कोई लीफ़, अनुमान के पाथ का टर्मिनल नोड भी होता है.

उदाहरण के लिए, इस फ़ैसले के ट्री में तीन पत्तियां हैं:

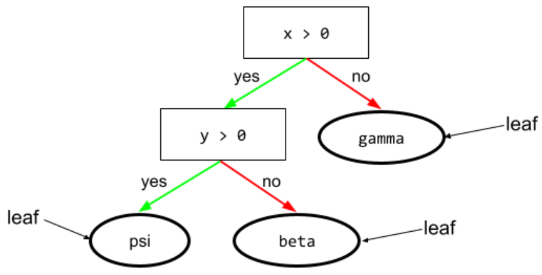
यह इमेज, दो शर्तों वाला फ़ैसला लेने वाला ट्री दिखाती है. इसमें तीन पत्तियां हैं.

ज़्यादा जानकारी के लिए, Decision Forests कोर्स में डिसीज़न ट्री देखें.

नहीं

नोड (डिसिज़न ट्री)

#df

डिसिज़न ट्री में, कोई भी शर्त या लीफ.

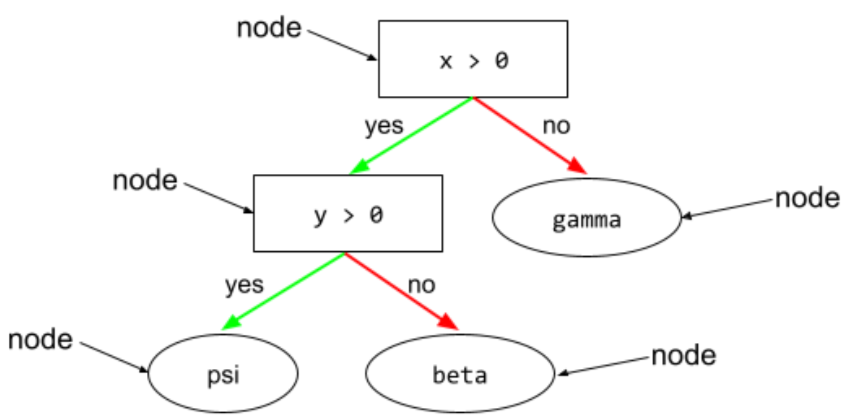
दो शर्तों और तीन लीफ़ वाला डिसिज़न ट्री.

ज़्यादा जानकारी के लिए, फ़ैसले लेने वाले फ़ॉरेस्ट कोर्स में डिसिज़न ट्री देखें.

अन्य शर्त

#df

ऐसी शर्त जिसमें दो से ज़्यादा संभावित नतीजे शामिल हों. उदाहरण के लिए, यहां दी गई नॉन-बाइनरी शर्त में तीन संभावित नतीजे शामिल हैं:

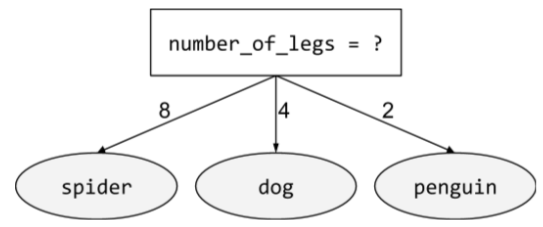
एक शर्त (number_of_legs = ?) जिससे तीन संभावित नतीजे मिलते हैं. एक नतीजे (number_of_legs = 8) से, स्पाइडर नाम की पत्ती मिलती है. दूसरे नतीजे (number_of_legs = 4) से, dog नाम का पत्ता मिलता है. तीसरा नतीजा (number_of_legs = 2) penguin नाम के
लीफ नोड पर ले जाता है.

ज़्यादा जानकारी के लिए, Decision Forests कोर्स में शर्तों के टाइप देखें.

O

तिरछी स्थिति

#df

डिसिज़न ट्री में, एक ऐसी शर्त जिसमें एक से ज़्यादा सुविधाएं शामिल हों. उदाहरण के लिए, अगर ऊंचाई और चौड़ाई, दोनों सुविधाएं हैं, तो यहां दी गई शर्त, अप्रत्यक्ष शर्त है:

  height > width

इसकी तुलना ऐक्सिस के साथ अलाइन की गई कंडिशन से करें.

ज़्यादा जानकारी के लिए, Decision Forests कोर्स में शर्तों के टाइप देखें.

आउट-ऑफ़-बैग इवैल्यूएशन (ओओबी इवैल्यूएशन)

#df

यह डिसिज़न फ़ॉरेस्ट की क्वालिटी का आकलन करने का एक तरीका है. इसमें हर डिसिज़न ट्री की जांच, उन उदाहरणों के आधार पर की जाती है जिनका इस्तेमाल, डिसिज़न ट्री की ट्रेनिंग के दौरान नहीं किया गया था. उदाहरण के लिए, इस डायग्राम में देखें कि सिस्टम, हर फ़ैसले के ट्री को करीब दो-तिहाई उदाहरणों के आधार पर ट्रेन करता है. इसके बाद, बाकी एक-तिहाई उदाहरणों के आधार पर उसका आकलन करता है.

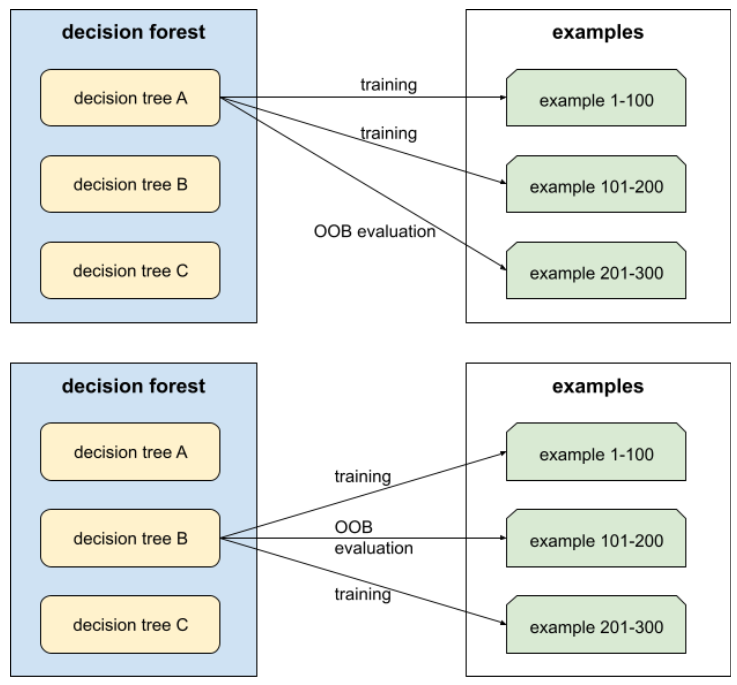
तीन डिसिज़न ट्री वाला डिसिज़न फ़ॉरेस्ट.
एक डिसीज़न ट्री, दो-तिहाई उदाहरणों पर ट्रेन करता है. इसके बाद, बचे हुए एक-तिहाई उदाहरणों का इस्तेमाल, ओओबी आकलन के लिए करता है.
दूसरा फ़ैसला लेने वाला ट्री, पिछले फ़ैसले लेने वाले ट्री के मुकाबले दो-तिहाई अलग उदाहरणों पर ट्रेन करता है. इसके बाद, ओओबी के आकलन के लिए, पिछले फ़ैसले लेने वाले ट्री के मुकाबले एक-तिहाई अलग उदाहरणों का इस्तेमाल करता है.

आउट-ऑफ़-बैग आकलन, क्रॉस-वैलिडेशन के तरीके का अनुमान लगाने का एक ऐसा तरीका है जो कम समय में सटीक नतीजे देता है. क्रॉस-वैलिडेशन में, हर क्रॉस-वैलिडेशन राउंड के लिए एक मॉडल को ट्रेन किया जाता है. उदाहरण के लिए, 10-फ़ोल्ड क्रॉस-वैलिडेशन में 10 मॉडल को ट्रेन किया जाता है. OOB आकलन में, सिर्फ़ एक मॉडल को ट्रेन किया जाता है. बैगिंग की वजह से, ट्रेनिंग के दौरान हर ट्री से कुछ डेटा अलग रखा जाता है. इसलिए, ओओबी आकलन इस डेटा का इस्तेमाल करके, क्रॉस-वैलिडेशन का अनुमान लगा सकता है.

ज़्यादा जानकारी के लिए, Decision Forests कोर्स में आउट-ऑफ़-बैग आकलन देखें.

P

पर्म्यूटेशन वैरिएबल के महत्व

#df

#Metric

यह वैरिएबल के महत्व का एक टाइप है. यह किसी मॉडल की अनुमान लगाने से जुड़ी गड़बड़ी में हुई बढ़ोतरी का आकलन करता है. ऐसा, फ़ीचर की वैल्यू को क्रम बदलने के बाद किया जाता है. परम्यूटेशन वैरिएबल इंपोर्टेंस, मॉडल से जुड़ी मेट्रिक नहीं है.

R

रैंडम फ़ॉरेस्ट

#df

यह डिसिज़न ट्री का ग्रुप होता है. इसमें हर डिसिज़न ट्री को खास रैंडम नॉइज़ के साथ ट्रेन किया जाता है. जैसे, बैगिंग.

रैंडम फ़ॉरेस्ट, डिसिज़न फ़ॉरेस्ट का एक टाइप है.

ज़्यादा जानकारी के लिए, फ़ैसले लेने वाले फ़ॉरेस्ट कोर्स में रैंडम फ़ॉरेस्ट देखें.

रूट

#df

डिसिज़न ट्री में, शुरुआती नोड (पहली शर्त). आम तौर पर, डायग्राम में रूट को डिसिज़न ट्री में सबसे ऊपर रखा जाता है. उदाहरण के लिए:

दो शर्तों और तीन लीफ़ वाला डिसिज़न ट्री. शुरुआती शर्त (x > 2) रूट है.

S

रिप्लेसमेंट के साथ सैंपलिंग

#df

यह, उम्मीदवार के तौर पर शामिल आइटम के सेट से आइटम चुनने का एक तरीका है. इसमें एक ही आइटम को कई बार चुना जा सकता है. "बदलाव के साथ" वाक्यांश का मतलब है कि हर बार चुनने के बाद, चुने गए आइटम को संभावित आइटम के पूल में वापस कर दिया जाता है. रिप्लेसमेंट के बिना सैंपलिंग, इसका मतलब है कि किसी आइटम को सिर्फ़ एक बार चुना जा सकता है.

उदाहरण के लिए, फलों का यह सेट देखें:

fruit = {kiwi, apple, pear, fig, cherry, lime, mango}

मान लें कि सिस्टम, fig को पहले आइटम के तौर पर रैंडम तरीके से चुनता है. अगर सैंपलिंग की सुविधा का इस्तेमाल किया जा रहा है, तो सिस्टम इस सेट से दूसरा आइटम चुनता है:

fruit = {kiwi, apple, pear, fig, cherry, lime, mango}

हां, यह पहले जैसा ही सेट है. इसलिए, सिस्टम fig को फिर से चुन सकता है.

रिप्लेसमेंट के बिना सैंपलिंग का इस्तेमाल करने पर, चुने गए सैंपल को दोबारा नहीं चुना जा सकता. उदाहरण के लिए, अगर सिस्टम ने पहले सैंपल के तौर पर fig को चुना है, तो fig को फिर से नहीं चुना जा सकता. इसलिए, सिस्टम नीचे दिए गए (कम किए गए) सेट से दूसरा सैंपल चुनता है:

fruit = {kiwi, apple, pear, cherry, lime, mango}

अन्य नोट के लिए, आइकॉन पर क्लिक करें.

रिप्लेसमेंट के साथ सैंपलिंग में रिप्लेसमेंट शब्द की वजह से, कई लोग भ्रमित हो जाते हैं. अंग्रेज़ी में, replacement का मतलब "substitution" होता है. हालांकि, रिप्लेसमेंट की मदद से सैंपलिंग में, रिप्लेसमेंट के लिए फ़्रेंच परिभाषा का इस्तेमाल किया जाता है. इसका मतलब है "किसी चीज़ को वापस रखना."

अंग्रेज़ी शब्द replacement का फ़्रेंच अनुवाद remplacement है.

श्रिंकेज

#df

यह ग्रैडिएंट बूस्टिंग में मौजूद एक हाइपरपैरामीटर है. यह ओवरफ़िटिंग को कंट्रोल करता है. ग्रेडिएंट बूस्टिंग में श्रिंकेज, ग्रेडिएंट डिसेंट में लर्निंग रेट के जैसा होता है. सिकुड़ने की दर, 0.0 और 1.0 के बीच की दशमलव वैल्यू होती है. श्रिंकेज वैल्यू कम होने पर, ओवरफ़िटिंग की समस्या कम होती है. वहीं, श्रिंकेज वैल्यू ज़्यादा होने पर, ओवरफ़िटिंग की समस्या ज़्यादा होती है.

बांटें

#df

डिसिज़न ट्री में, शर्त का दूसरा नाम.

स्प्लिटर

#df

डिसिज़न ट्री को ट्रेन करते समय, हर नोड पर सबसे अच्छी कंडीशन ढूंढने के लिए, रूटीन (और एल्गोरिदम) ज़िम्मेदार होता है.

T

जांच

#df

डिसिज़न ट्री में, शर्त का दूसरा नाम.

थ्रेशोल्ड (डिसिज़न ट्री के लिए)

#df

ऐक्सिस के साथ अलाइन की गई शर्त में, वह वैल्यू जिससे सुविधा की तुलना की जा रही है. उदाहरण के लिए, यहां दी गई शर्त में 75 थ्रेशोल्ड वैल्यू है:

grade >= 75

V

वैरिएबल के महत्व

#df

#Metric

स्कोर का एक ऐसा सेट जो मॉडल के लिए हर फ़ीचर की अहमियत दिखाता है.

उदाहरण के लिए, डिसिज़न ट्री पर आधारित एक मॉडल लें, जो घर की कीमतों का अनुमान लगाता है. मान लें कि यह फ़ैसला लेने वाला ट्री, तीन सुविधाओं का इस्तेमाल करता है: साइज़, उम्र, और स्टाइल. अगर तीन सुविधाओं के लिए, वैरिएबल के महत्व का सेट {size=5.8, age=2.5, style=4.7} के तौर पर कैलकुलेट किया जाता है, तो साइज़, उम्र या स्टाइल की तुलना में फ़ैसले के ट्री के लिए ज़्यादा अहम होता है.

वैरिएबल की अहमियत को मेज़र करने वाली अलग-अलग मेट्रिक मौजूद हैं. इनसे एमएल विशेषज्ञों को मॉडल के अलग-अलग पहलुओं के बारे में जानकारी मिल सकती है.

W

विज़डम ऑफ़ द क्राउड

#df

यह सिद्धांत बताता है कि लोगों के बड़े ग्रुप ("क्राउड") की राय या अनुमानों का औसत निकालने पर, अक्सर अच्छे नतीजे मिलते हैं. उदाहरण के लिए, एक ऐसे गेम के बारे में सोचें जिसमें लोग यह अनुमान लगाते हैं कि एक बड़े जार में कितनी जेली बीन्स भरी गई हैं. हालांकि, ज़्यादातर लोगों के अनुमान सही नहीं होंगे, लेकिन सभी अनुमानों का औसत, जार में मौजूद जेली बीन्स की असल संख्या के काफ़ी करीब होता है. यह बात अनुभव के आधार पर साबित हुई है.

Ensembles, सॉफ़्टवेयर के लिए 'क्राउड की समझ' के सिद्धांत पर काम करते हैं. भले ही, अलग-अलग मॉडल बहुत ज़्यादा गलत अनुमान लगाएं, लेकिन कई मॉडल के अनुमानों का औसत निकालने पर, अक्सर हैरान करने वाले सटीक अनुमान मिलते हैं. उदाहरण के लिए, भले ही कोई डिसिज़न ट्री सही अनुमान न लगा पाए, लेकिन डिसिज़न फ़ॉरेस्ट अक्सर बहुत अच्छे अनुमान लगाता है.