หน้านี้มีคำศัพท์ของ Decision Forests ดูคำศัพท์ทั้งหมดได้โดยคลิกที่นี่
A
การสุ่มตัวอย่างแอตทริบิวต์
กลยุทธ์สำหรับการฝึกDecision Forest ซึ่งแต่ละDecision Tree จะพิจารณาเฉพาะชุดย่อยแบบสุ่มของฟีเจอร์ที่เป็นไปได้เมื่อเรียนรู้เงื่อนไข โดยทั่วไป ระบบจะสุ่มตัวอย่างชุดฟีเจอร์ย่อยที่แตกต่างกันสำหรับแต่ละโหนด ในทางตรงกันข้าม เมื่อฝึกต้นไม้ตัดสินใจโดยไม่ใช้การสุ่มตัวอย่างแอตทริบิวต์ ระบบจะพิจารณาฟีเจอร์ที่เป็นไปได้ทั้งหมดสำหรับแต่ละโหนด
เงื่อนไขที่สอดคล้องกับแกน
ในแผนผังการตัดสินใจ เงื่อนไข
ที่มีฟีเจอร์เดียวเท่านั้น ตัวอย่างเช่น หาก area
เป็นฟีเจอร์ เงื่อนไขที่สอดคล้องกับแกนจะเป็นดังนี้
area > 200
เปรียบเทียบกับเงื่อนไขทางอ้อม
B
การใส่ถุง
วิธีการฝึกกลุ่ม โดยที่โมเดลแต่ละรายการจะฝึกในชุดย่อยแบบสุ่มของตัวอย่างการฝึกที่สุ่มโดยมีการแทนที่ ตัวอย่างเช่น Random Forest คือชุดของDecision Tree ที่ฝึกด้วยการ Bagging
คำว่า Bagging ย่อมาจาก Bootstrap Aggregating
ดูข้อมูลเพิ่มเติมได้ที่Random Forests ในหลักสูตร Decision Forests
เงื่อนไขไบนารี
ในแผนผังการตัดสินใจ เงื่อนไข ที่มีผลลัพธ์ที่เป็นไปได้เพียง 2 อย่าง โดยปกติคือใช่หรือไม่ใช่ ตัวอย่างเช่น เงื่อนไขต่อไปนี้เป็นเงื่อนไขแบบไบนารี
temperature >= 100
เปรียบเทียบกับเงื่อนไขนอนไบนารี
ดูข้อมูลเพิ่มเติมได้ที่ประเภทของเงื่อนไข ในหลักสูตร Decision Forests
C
เงื่อนไข
ในแผนผังการตัดสินใจ โหนดใดก็ตามที่ ทำการทดสอบ ตัวอย่างเช่น แผนผังการตัดสินใจต่อไปนี้มี เงื่อนไข 2 ข้อ

เงื่อนไขเรียกอีกอย่างว่าการแยกหรือการทดสอบ
สภาพคอนทราสต์ที่มีใบไม้
และดู:
ดูข้อมูลเพิ่มเติมได้ที่ประเภทของเงื่อนไข ในหลักสูตร Decision Forests
D
Decision Forest
โมเดลที่สร้างจากต้นไม้ตัดสินใจหลายต้น Decision Forest จะทำการคาดการณ์โดยการรวบรวมการคาดการณ์ของ Decision Tree ประเภทของป่าการตัดสินใจที่ได้รับความนิยม ได้แก่ Random Forest และ Gradient Boosted Tree
ดูข้อมูลเพิ่มเติมได้ที่ส่วนDecision Forests ในหลักสูตร Decision Forests
แผนผังการตัดสินใจ
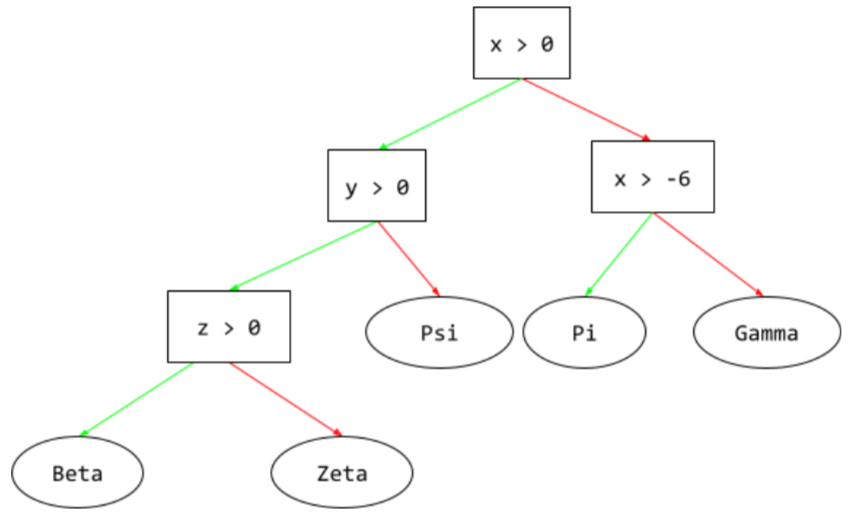
โมเดลการเรียนรู้ภายใต้การควบคุมดูแลซึ่งประกอบด้วยชุดเงื่อนไขและลีฟที่จัดระเบียบตามลำดับชั้น ตัวอย่างเช่น แผนผังการตัดสินใจมีลักษณะดังนี้
E
เอนโทรปี
ใน ทฤษฎีสารสนเทศ คำอธิบายว่าการกระจายความน่าจะเป็นคาดเดาไม่ได้เพียงใด หรืออาจกล่าวได้ว่าเอนโทรปีคือปริมาณข้อมูลที่ตัวอย่างแต่ละรายการมี การกระจายจะมี เอนโทรปีสูงสุดที่เป็นไปได้เมื่อค่าทั้งหมดของตัวแปรสุ่มมี โอกาสเท่ากัน
เอนโทรปีของชุดที่มีค่าที่เป็นไปได้ 2 ค่าคือ "0" และ "1" (เช่น ป้ายกำกับในปัญหาการแยกประเภทแบบไบนารี) มีสูตรดังนี้
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
ที่ไหน
- H คือเอนโทรปี
- p คือเศษส่วนของตัวอย่าง "1"
- q คือสัดส่วนของตัวอย่าง "0" โปรดทราบว่า q = (1 - p)
- log โดยทั่วไปคือ log2 ในกรณีนี้ หน่วยเอนโทรปี คือบิต
ตัวอย่างเช่น สมมติว่า
- ตัวอย่าง 100 รายการมีค่า "1"
- ตัวอย่าง 300 รายการมีค่า "0"
ดังนั้นค่าเอนโทรปีจึงเป็น
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 0.81 บิตต่อตัวอย่าง
ชุดข้อมูลที่สมดุลอย่างสมบูรณ์ (เช่น "0" 200 รายการและ "1" 200 รายการ) จะมีเอนโทรปี 1.0 บิตต่อตัวอย่าง เมื่อชุดข้อมูลไม่สมดุลมากขึ้น เอนโทรปีจะเข้าใกล้ 0.0
ในแผนผังการตัดสินใจ เอนโทรปีช่วยสร้างการได้ข้อมูลเพื่อช่วยให้ตัวแยกเลือกเงื่อนไข ในระหว่างการเติบโตของแผนผังการตัดสินใจในการจัดประเภท
เปรียบเทียบเอนโทรปีกับ
- ความไม่บริสุทธิ์ของ Gini
- ฟังก์ชันการสูญเสียเอนโทรปีครอส
โดยมักเรียกเอนโทรปีว่าเอนโทรปีของแชนนอน
ดูข้อมูลเพิ่มเติมได้ที่ตัวแยกที่แน่นอนสำหรับการแยกประเภทแบบไบนารีที่มีฟีเจอร์เชิงตัวเลข ในหลักสูตร Decision Forests
F
ความสำคัญของฟีเจอร์
คำพ้องความหมายของความสำคัญของตัวแปร
G
ความไม่บริสุทธิ์ของจีนี
เมตริกที่คล้ายกับเอนโทรปี ตัวแยก ใช้ค่าที่ได้จากความไม่บริสุทธิ์ของ Gini หรือเอนโทรปีเพื่อสร้าง เงื่อนไขสำหรับการจัดประเภท แผนผังการตัดสินใจ การได้ข้อมูลได้มาจากเอนโทรปี ไม่มีคำที่เทียบเท่าซึ่งเป็นที่ยอมรับกันโดยทั่วไปสำหรับเมตริกที่ได้จากความไม่บริสุทธิ์ของ Gini อย่างไรก็ตาม เมตริกที่ไม่มีชื่อนี้มีความสำคัญไม่แพ้การได้ข้อมูล
ความไม่บริสุทธิ์ของจีนียังเรียกว่าดัชนีจีนี หรือเรียกสั้นๆ ว่าจีนี
Gradient Boosted (Decision) Trees (GBT)
ป่าการตัดสินใจประเภทหนึ่งซึ่งมีลักษณะดังนี้
- การฝึกใช้ การเพิ่มประสิทธิภาพแบบไล่ระดับ
- โมเดลที่อ่อนแอคือแผนผังการตัดสินใจ
ดูข้อมูลเพิ่มเติมได้ที่ต้นไม้ตัดสินใจแบบ Gradient Boosting ในหลักสูตร Decision Forests
การเพิ่มประสิทธิภาพการไล่ระดับ
อัลกอริทึมการฝึกที่ฝึกโมเดลที่อ่อนแอเพื่อปรับปรุงคุณภาพ (ลดการสูญเสีย) ของโมเดลที่แข็งแกร่งอย่างต่อเนื่อง เช่น โมเดลที่อ่อนแออาจเป็นโมเดลเชิงเส้นหรือโมเดลต้นไม้ตัดสินขนาดเล็ก โมเดลที่แข็งแกร่งจะกลายเป็นผลรวมของโมเดลที่อ่อนแอทั้งหมดที่ได้รับการฝึกก่อนหน้านี้
ในรูปแบบที่ง่ายที่สุดของการเพิ่มประสิทธิภาพแบบไล่ระดับ ในแต่ละการทำซ้ำ โมเดลที่อ่อนแอจะได้รับการฝึกให้คาดการณ์การไล่ระดับการสูญเสียของโมเดลที่แข็งแกร่ง จากนั้น ระบบจะอัปเดตเอาต์พุตของโมเดล strong โดยการลบการไล่ระดับที่คาดการณ์ไว้ ซึ่งคล้ายกับการไล่ระดับ
ที่ไหน
- $F_{0}$ คือโมเดลเริ่มต้นอย่างมั่นคง
- $F_{i+1}$ คือโมเดลที่แข็งแกร่งถัดไป
- $F_{i}$ คือโมเดลที่แข็งแกร่งในปัจจุบัน
- $\xi$ คือค่าระหว่าง 0.0 ถึง 1.0 ที่เรียกว่าการหดตัว ซึ่งคล้ายกับ อัตราการเรียนรู้ใน การไล่ระดับการไล่ระดับ
- $f_{i}$ คือโมเดลแบบอ่อนที่ได้รับการฝึกให้คาดการณ์การไล่ระดับการสูญเสียของ $F_{i}$
การปรับปรุงการเพิ่มแบบไล่ระดับสมัยใหม่ยังรวมอนุพันธ์อันดับที่ 2 (เมทริกซ์เฮสเซียน) ของการสูญเสียในการคำนวณด้วย
แผนผังการตัดสินใจมักใช้เป็นโมเดลที่อ่อนแอใน Gradient Boosting ดูต้นไม้แบบไล่ระดับ (การตัดสินใจ)
I
เส้นทางการอนุมาน
ในแผนผังการตัดสินใจ ระหว่างการอนุมาน เส้นทางที่ตัวอย่างหนึ่งๆ ใช้จากรูทไปยังเงื่อนไขอื่นๆ ซึ่งสิ้นสุดด้วยลีฟ ตัวอย่างเช่น ในแผนผังการตัดสินใจต่อไปนี้ ลูกศรที่หนาขึ้นแสดงเส้นทางการอนุมานสำหรับตัวอย่างที่มีค่าฟีเจอร์ต่อไปนี้
- x = 7
- y = 12
- z = -3
เส้นทางการอนุมานในภาพประกอบต่อไปนี้จะผ่านเงื่อนไข 3 ข้อ
ก่อนที่จะไปถึงลีฟ (Zeta)

ลูกศรหนา 3 ดอกแสดงเส้นทางการอนุมาน
ดูข้อมูลเพิ่มเติมได้ที่แผนผังการตัดสินใจ ในหลักสูตร Decision Forests
การได้ข้อมูล
ในDecision Forest ความแตกต่างระหว่างเอนโทรปีของโหนดกับผลรวมของเอนโทรปีของโหนดลูกที่ถ่วงน้ำหนัก (ตามจำนวนตัวอย่าง) เอนโทรปีของโหนดคือเอนโทรปี ของตัวอย่างในโหนดนั้น
ตัวอย่างเช่น ลองพิจารณาค่าเอนโทรปีต่อไปนี้
- เอนโทรปีของโหนดหลัก = 0.6
- เอนโทรปีของโหนดลูกที่มีตัวอย่างที่เกี่ยวข้อง 16 รายการ = 0.2
- เอนโทรปีของโหนดย่อยอีกโหนดหนึ่งที่มีตัวอย่างที่เกี่ยวข้อง 24 รายการ = 0.1
ดังนั้น 40% ของตัวอย่างจึงอยู่ในโหนดย่อยหนึ่ง และ 60% อยู่ในโหนดย่อยอีกโหนดหนึ่ง ดังนั้น
- ผลรวมของเอนโทรปีแบบถ่วงน้ำหนักของโหนดย่อย = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
ดังนั้น การได้ข้อมูลจึงเป็นดังนี้
- การได้ข้อมูล = เอนโทรปีของโหนดแม่ - ผลรวมของเอนโทรปีแบบถ่วงน้ำหนักของโหนดลูก
- การได้ข้อมูล = 0.6 - 0.14 = 0.46
ตัวแยกส่วนใหญ่พยายามสร้างเงื่อนไข ที่เพิ่มการรับข้อมูลให้ได้มากที่สุด
เงื่อนไขในชุด
ในแผนผังการตัดสินใจ เงื่อนไข ที่ทดสอบการมีอยู่ของสินค้า 1 รายการในชุดสินค้า ตัวอย่างเช่น เงื่อนไขในชุดมีดังนี้
house-style in [tudor, colonial, cape]
ในระหว่างการอนุมาน หากค่าของฟีเจอร์
สไตล์บ้านเป็น tudor หรือ colonial หรือ cape เงื่อนไขนี้จะประเมินเป็น "ใช่" หากค่าของฟีเจอร์สไตล์บ้านเป็นอย่างอื่น (เช่น ranch)
เงื่อนไขนี้จะประเมินเป็น "ไม่"
โดยปกติแล้ว เงื่อนไขในชุดจะทำให้ได้แผนผังการตัดสินใจที่มีประสิทธิภาพมากกว่าเงื่อนไขที่ทดสอบฟีเจอร์ที่เข้ารหัสแบบ One-Hot
L
ใบไม้
แผนผังการตัดสินใจของปลายทาง เงื่อนไขต่างจากลีฟตรงที่ลีฟไม่ได้ทำการทดสอบ แต่ใบไม้คือการคาดการณ์ที่เป็นไปได้ ใบยังเป็นโหนดสุดท้ายของเส้นทางการอนุมานด้วย
ตัวอย่างเช่น แผนผังการตัดสินใจต่อไปนี้มี 3 ใบ
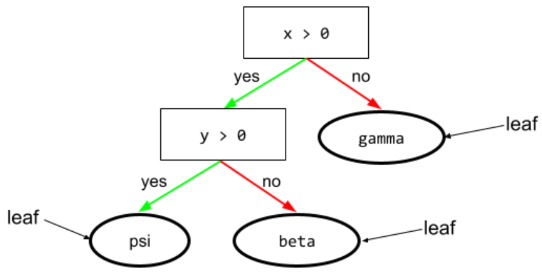
ดูข้อมูลเพิ่มเติมได้ที่แผนผังการตัดสินใจ ในหลักสูตร Decision Forests
N
โหนด (แผนผังการตัดสินใจ)
ในแผนผังการตัดสินใจ เงื่อนไขหรือโหนดปลายสุด
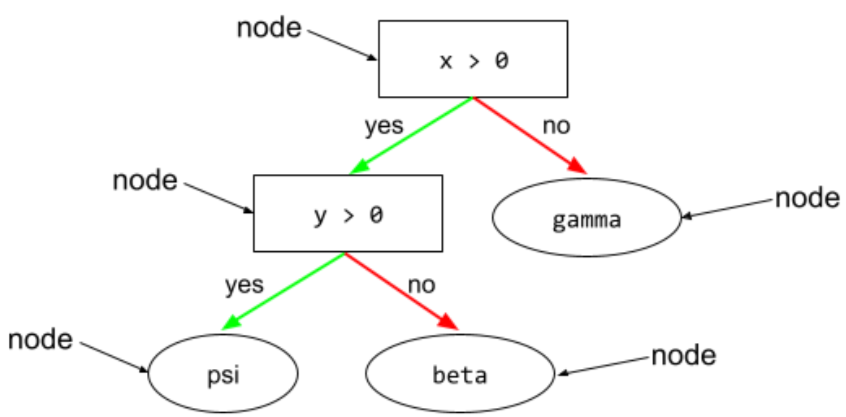
ดูข้อมูลเพิ่มเติมได้ที่แผนผังการตัดสินใจ ในหลักสูตร Decision Forests
เงื่อนไขนอนไบนารี
เงื่อนไขที่มีผลลัพธ์ที่เป็นไปได้มากกว่า 2 รายการ ตัวอย่างเช่น เงื่อนไขแบบไม่ใช่ไบนารีต่อไปนี้มีผลลัพธ์ที่เป็นไปได้ 3 อย่าง
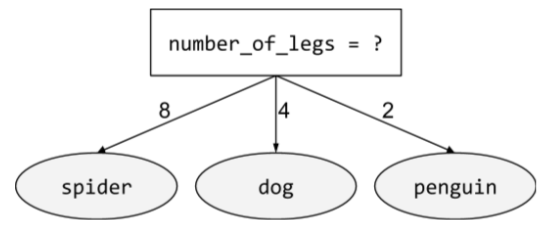
ดูข้อมูลเพิ่มเติมได้ที่ประเภทของเงื่อนไข ในหลักสูตร Decision Forests
O
เงื่อนไขเฉียง
ในแผนผังการตัดสินใจ เงื่อนไขที่เกี่ยวข้องกับฟีเจอร์มากกว่า 1 รายการ ตัวอย่างเช่น หากความสูงและความกว้างเป็นทั้งฟีเจอร์ เงื่อนไขที่อ้อมค้อมจะเป็นดังนี้
height > width
เปรียบเทียบกับเงื่อนไขที่สอดคล้องกับแกน
ดูข้อมูลเพิ่มเติมได้ที่ประเภทของเงื่อนไข ในหลักสูตร Decision Forests
การประเมินนอกกลุ่มตัวอย่าง (การประเมิน OOB)
กลไกในการประเมินคุณภาพของDecision Forest โดยการทดสอบDecision Tree แต่ละรายการกับตัวอย่างที่ไม่ได้ใช้ในระหว่างการฝึกของ Decision Tree นั้น ตัวอย่างเช่น ใน แผนภาพต่อไปนี้ คุณจะเห็นว่าระบบฝึกต้นไม้ตัดสินใจแต่ละต้น กับตัวอย่างประมาณ 2 ใน 3 แล้วประเมินกับ ตัวอย่างที่เหลืออีก 1 ใน 3
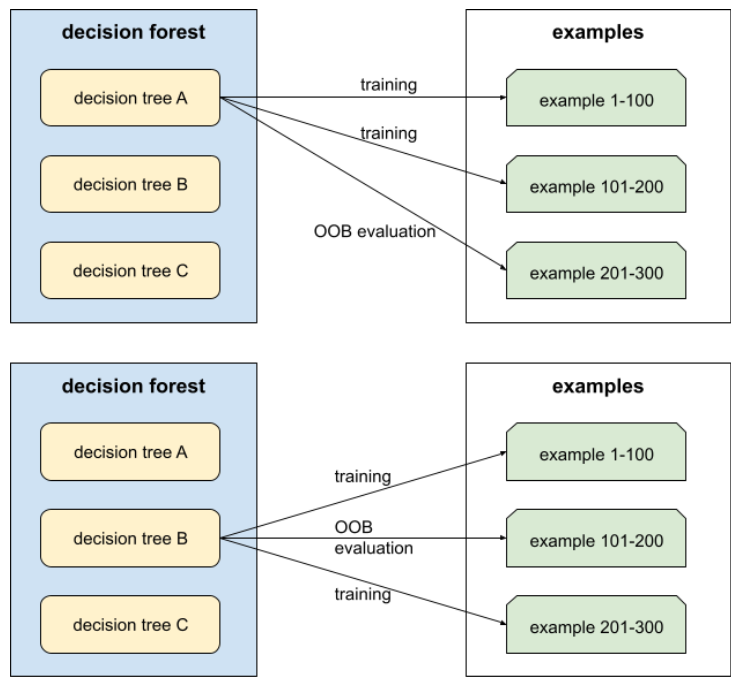
การประเมินนอกกลุ่มตัวอย่างเป็นการประมาณกลไกการตรวจสอบแบบไขว้ที่ประหยัดการคำนวณและรอบคอบ ในการตรวจสอบแบบไขว้ ระบบจะฝึกโมเดล 1 รายการสําหรับการตรวจสอบแบบไขว้แต่ละรอบ (เช่น ฝึกโมเดล 10 รายการในการตรวจสอบแบบไขว้ 10 โฟลด์) การประเมิน OOB จะฝึกโมเดลเดียว เนื่องจากการสุ่มตัวอย่างแบบแทนที่ จะละเว้นข้อมูลบางส่วนจากแต่ละทรีระหว่างการฝึก การประเมิน OOB จึงใช้ข้อมูลดังกล่าวเพื่อประมาณค่าการตรวจสอบแบบไขว้ได้
ดูข้อมูลเพิ่มเติมได้ที่การประเมินนอกกลุ่มตัวอย่าง ในหลักสูตร Decision Forests
P
ความสําคัญของตัวแปรการเรียงสับเปลี่ยน
ประเภทความสําคัญของตัวแปรที่ประเมิน การเพิ่มขึ้นของข้อผิดพลาดในการคาดการณ์ของโมเดลหลังจากสลับค่าของฟีเจอร์ ความสําคัญของตัวแปรการสับเปลี่ยนเป็นเมตริกที่ไม่ขึ้นอยู่กับโมเดล
R
ป่าสุ่ม
กลุ่มของแผนผังการตัดสินใจใน ซึ่งแผนผังการตัดสินใจแต่ละรายการได้รับการฝึกด้วยสัญญาณรบกวนแบบสุ่มที่เฉพาะเจาะจง เช่น Bagging
ป่าสุ่มเป็นป่าการตัดสินใจประเภทหนึ่ง
ดูข้อมูลเพิ่มเติมได้ที่Random Forest ในหลักสูตร Decision Forests
รูท
โหนดเริ่มต้น (เงื่อนไขแรก) ในแผนผังการตัดสินใจ ตามธรรมเนียมแล้ว แผนภาพจะวางรูทไว้ที่ด้านบนของแผนผังการตัดสินใจ เช่น

S
การสุ่มตัวอย่างแบบแทนที่
วิธีการเลือกรายการจากชุดรายการที่แนะนำซึ่งสามารถเลือกรายการเดียวกันได้หลายครั้ง วลี "โดยมีการแทนที่" หมายความว่า หลังจากเลือกแต่ละครั้ง ระบบจะส่งคืนรายการที่เลือกไปยังกลุ่ม ของรายการที่อาจเป็นไปได้ ส่วนวิธีผกผัน การสุ่มตัวอย่างแบบไม่แทนที่ หมายความว่าเลือกรายการที่ต้องการได้เพียงครั้งเดียว
ตัวอย่างเช่น ลองพิจารณาชุดผลไม้ต่อไปนี้
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}สมมติว่าระบบสุ่มเลือก fig เป็นรายการแรก
หากใช้การสุ่มตัวอย่างแบบแทนที่ ระบบจะเลือกรายการที่ 2 จากชุดต่อไปนี้
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}ใช่ ชุดคำถามนั้นเป็นชุดเดียวกับก่อนหน้านี้ ระบบจึงอาจfigอีกครั้ง
หากใช้การสุ่มตัวอย่างแบบไม่แทนที่ เมื่อเลือกแล้ว จะเลือกตัวอย่างนั้นอีกไม่ได้
ตัวอย่างเช่น หากระบบสุ่มเลือก fig เป็น
ตัวอย่างแรก ระบบจะเลือก fig อีกไม่ได้ ดังนั้น ระบบ
จะเลือกตัวอย่างที่ 2 จากชุด (ที่ลดลง) ต่อไปนี้
fruit = {kiwi, apple, pear, cherry, lime, mango}การหดตัว
ไฮเปอร์พารามิเตอร์ใน การเพิ่มประสิทธิภาพแบบไล่ระดับที่ควบคุม การปรับมากเกินไป การลดขนาดในการเพิ่มประสิทธิภาพแบบไล่ระดับ คล้ายกับอัตราการเรียนรู้ใน การไล่ระดับการลด การหดตัวคือค่าทศนิยม ระหว่าง 0.0 ถึง 1.0 ค่าการหดตัวที่ต่ำกว่าจะลดการปรับมากเกินไป ได้มากกว่าค่าการหดตัวที่สูงกว่า
แยก
ในแผนผังการตัดสินใจ ซึ่งเป็นอีกชื่อหนึ่งของ เงื่อนไข
ตัวแยก
ขณะฝึกต้นไม้ตัดสินใจ รูทีน (และอัลกอริทึม) มีหน้าที่ค้นหาเงื่อนไขที่ดีที่สุดในแต่ละโหนด
T
ทดสอบ
ในแผนผังการตัดสินใจ ซึ่งเป็นอีกชื่อหนึ่งของ เงื่อนไข
เกณฑ์ (สำหรับต้นไม้ตัดสินใจ)
ในเงื่อนไขที่สอดคล้องกับแกน ค่าที่ฟีเจอร์กำลังเปรียบเทียบด้วย ตัวอย่างเช่น 75 คือค่าเกณฑ์ในเงื่อนไขต่อไปนี้
grade >= 75
ดูข้อมูลเพิ่มเติมได้ที่ตัวแยกที่แน่นอนสำหรับการแยกประเภทแบบไบนารีที่มีฟีเจอร์เชิงตัวเลข ในหลักสูตร Decision Forests
V
ความสําคัญของตัวแปร
ชุดคะแนนที่บ่งบอกถึงความสำคัญที่สัมพันธ์กันของแต่ละฟีเจอร์ต่อโมเดล
ตัวอย่างเช่น ลองพิจารณาแผนผังการตัดสินใจที่ ประมาณราคาบ้าน สมมติว่าแผนผังการตัดสินใจนี้ใช้ฟีเจอร์ 3 อย่าง ได้แก่ ขนาด อายุ และสไตล์ หากระบบคำนวณชุดความสำคัญของตัวแปร สำหรับฟีเจอร์ทั้ง 3 รายการได้เป็น {size=5.8, age=2.5, style=4.7} แสดงว่าขนาดมีความสำคัญต่อ Decision Tree มากกว่าอายุหรือสไตล์
มีเมตริกความสําคัญของตัวแปรที่แตกต่างกัน ซึ่งจะช่วยให้ผู้เชี่ยวชาญด้าน ML ทราบถึงแง่มุมต่างๆ ของโมเดล
W
ภูมิปัญญาของมวลชน
แนวคิดที่ว่าการหาค่าเฉลี่ยของความคิดเห็นหรือการประมาณค่าจากกลุ่มคนจำนวนมาก ("ฝูงชน") มักจะให้ผลลัพธ์ที่ดีอย่างน่าประหลาดใจ ตัวอย่างเช่น ลองพิจารณาเกมที่ผู้คนทายจำนวน เยลลี่บีนที่บรรจุในโหลขนาดใหญ่ แม้ว่าการคาดเดาของแต่ละคนส่วนใหญ่จะไม่ถูกต้อง แต่ค่าเฉลี่ยของการคาดเดาทั้งหมดได้รับการพิสูจน์แล้วว่าใกล้เคียงกับจำนวนจริงของลูกอมในขวดอย่างน่าประหลาดใจ
กลุ่มเป็นซอฟต์แวร์ที่เทียบเท่ากับภูมิปัญญาของมวลชน แม้ว่าโมเดลแต่ละรายการจะคาดการณ์ได้อย่างไม่แม่นยำ แต่การหาค่าเฉลี่ยของการคาดการณ์ของโมเดลจำนวนมากมักจะสร้างการคาดการณ์ที่ดีอย่างน่าประหลาดใจ ตัวอย่างเช่น แม้ว่าแผนผังการตัดสินใจแต่ละรายการอาจให้การคาดการณ์ที่ไม่ดี แต่ป่าการตัดสินใจมักจะให้การคาดการณ์ที่ดีมาก