Glossaire du machine learning: forêts de décision

Cette page contient les termes du glossaire des forêts de décision. Pour consulter tous les termes du glossaire, cliquez ici.

A

échantillonnage d'attributs

#df

Tactique d'entraînement d'une forêt de décision dans laquelle chaque arbre de décision ne tient compte que d'un sous-ensemble aléatoire de caractéristiques lors de l'apprentissage de la condition. En général, un sous-ensemble différent de caractéristiques est échantillonné pour chaque nœud. En revanche, lorsque vous entraînez un arbre de décision sans échantillonnage d'attributs, toutes les caractéristiques possibles sont prises en compte pour chaque nœud.

condition alignée sur un axe

#df

Dans un arbre de décision, une condition qui n'implique qu'une seule caractéristique. Par exemple, si area est une caractéristique, la condition suivante est alignée sur un axe :

area > 200

À comparer à la condition oblique.

B

bagging

#df

Méthode d'entraînement d'un ensemble où chaque modèle constitutif s'entraîne sur un sous-ensemble aléatoire d'exemples d'entraînement échantillonnés avec remplacement. Par exemple, une forêt aléatoire est une collection d'arbres de décision entraînés avec le bagging.

Le terme bagging est l'abréviation de bootstrap aggregating.

Pour en savoir plus, consultez Forêts aléatoires dans le cours "Forêts de décision".

condition binaire

#df

Dans un arbre de décision, une condition qui n'a que deux résultats possibles, généralement oui ou non. Par exemple, la condition suivante est une condition binaire :

temperature >= 100

À comparer à la condition non binaire.

Pour en savoir plus, consultez Types de conditions dans le cours "Forêts de décision".

C

état

#df
Dans un arbre de décision, tout nœud effectuant un test. Par exemple, l'arbre de décision suivant contient deux conditions :

Arbre de décision composé de deux conditions : (x > 0) et (y > 0).

Une condition est également appelée "répartition" ou "test".

Condition de contraste avec leaf.

Voir également :

Pour en savoir plus, consultez Types de conditions dans le cours "Forêts de décision".

D

forêt de décision

#df

Modèle créé à partir de plusieurs arbres de décision. Une forêt de décision effectue une prédiction en agrégeant les prédictions de ses arbres de décision. Les forêts aléatoires et les arbres à boosting de gradient sont des types de forêts de décision populaires.

Pour en savoir plus, consultez la section Forêts de décision du cours sur les forêts de décision.

arbre de décision

#df

Modèle d'apprentissage supervisé composé d'un ensemble de conditions et de feuilles organisées de manière hiérarchique. Par exemple, voici un arbre de décision :

Arbre de décision composé de quatre conditions organisées de manière hiérarchique, qui mènent à cinq feuilles.

E

entropie

#df
#Metric

Dans la théorie de l'information, l'entropie est une description du degré d'imprévisibilité d'une distribution de probabilité. Elle est également définie comme la quantité d'informations contenues dans chaque exemple. Une distribution présente l'entropie la plus élevée possible lorsque toutes les valeurs d'une variable aléatoire sont équiprobables.

L'entropie d'un ensemble avec deux valeurs possibles "0" et "1" (par exemple, les libellés dans un problème de classification binaire) a la formule suivante :

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

où :

  • H est l'entropie.
  • p est la fraction d'exemples "1".
  • q correspond à la fraction d'exemples "0". Notez que q = (1 - p)
  • log est généralement log2. Dans ce cas, l'unité d'entropie est un bit.

Par exemple, supposons les éléments suivants :

  • 100 exemples contiennent la valeur "1"
  • 300 exemples contiennent la valeur "0"

La valeur d'entropie est donc la suivante :

  • p = 0,25
  • q = 0,75
  • H = (-0,25)log2(0,25) - (0,75)log2(0,75) = 0,81 bit par exemple

Un ensemble parfaitement équilibré (par exemple, 200 "0" et 200 "1") aurait une entropie de 1,0 bit par exemple. À mesure qu'un ensemble devient plus déséquilibré, son entropie tend vers 0.

Dans les arbres de décision, l'entropie permet de formuler le gain d'information pour aider le splitter à sélectionner les conditions lors de la croissance d'un arbre de décision de classification.

Comparer l'entropie avec :

L'entropie est souvent appelée entropie de Shannon.

Pour en savoir plus, consultez Splitter exact pour la classification binaire avec des caractéristiques numériques dans le cours sur les forêts de décision.

F

importance des caractéristiques.

#df
#Metric

Synonyme de importance des variables.

G

Impureté de Gini

#df
#Metric

Métrique semblable à l'entropie. Les splitters utilisent des valeurs dérivées de l'impureté de Gini ou de l'entropie pour composer des conditions pour les arbres de décision de classification. Le gain d'information est dérivé de l'entropie. Il n'existe pas de terme équivalent universellement accepté pour la métrique dérivée de l'impureté de Gini. Toutefois, cette métrique sans nom est tout aussi importante que le gain d'information.

L'impureté de Gini est également appelée indice de Gini ou simplement Gini.

arbres de décision à boosting de gradient (GBT, gradient boosted (decision) trees)

#df

Type de forêt de décision dans lequel :

Pour en savoir plus, consultez Arbres de décision à boosting de gradient dans le cours sur les forêts de décision.

gradient boosting

#df

Algorithme d'entraînement dans lequel des modèles faibles sont entraînés pour améliorer de manière itérative la qualité (réduire la perte) d'un modèle fort. Par exemple, un modèle faible peut être un modèle linéaire ou un petit modèle d'arbre de décision. Le modèle fort devient la somme de tous les modèles faibles précédemment entraînés.

Dans la forme la plus simple du boosting de gradient, à chaque itération, un modèle faible est entraîné pour prédire le gradient de perte du modèle fort. La sortie du modèle fort est ensuite mise à jour en soustrayant le gradient prédit, comme dans la descente de gradient.

$$F_{0} = 0$$ $$F_{i+1} = F_i - \xi f_i $$

où :

  • $F_{0}$ est le modèle fort de départ.
  • $F_{i+1}$ est le prochain modèle fort.
  • $F_{i}$ est le modèle fort actuel.
  • $\xi$ est une valeur comprise entre 0,0 et 1,0 appelée rétrécissement, qui est analogue au taux d'apprentissage dans la descente de gradient.
  • $f_{i}$ est le modèle faible entraîné pour prédire le gradient de perte de $F_{i}$.

Les variantes modernes du boosting de gradient incluent également la dérivée seconde (hessien) de la perte dans leur calcul.

Les arbres de décision sont souvent utilisés comme modèles faibles dans le boosting de gradient. Consultez Arbres de décision à boosting de gradient.

I

chemin d'inférence

#df

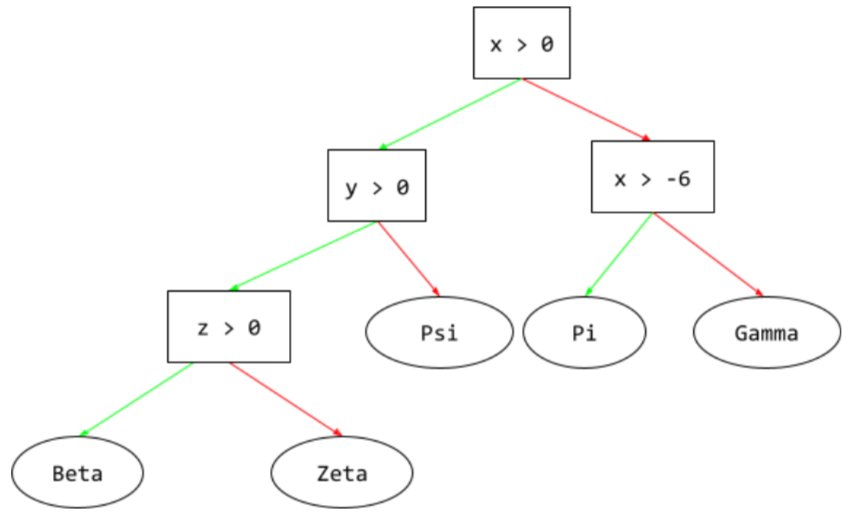
Dans un arbre de décision, lors de l'inférence, l'itinéraire qu'un exemple particulier emprunte de la racine à d'autres conditions, se terminant par une feuille. Par exemple, dans l'arbre de décision suivant, les flèches plus épaisses indiquent le chemin d'inférence pour un exemple avec les valeurs de caractéristiques suivantes :

  • x = 7
  • y = 12
  • z = -3

Le chemin d'inférence de l'illustration suivante passe par trois conditions avant d'atteindre la feuille (Zeta).

Arbre de décision composé de quatre conditions et de cinq feuilles. La condition racine est (x > 0). Comme la réponse est "Oui", le chemin d'inférence va de la racine à la condition suivante (y > 0). Comme la réponse est "Oui", le chemin d'inférence passe à la condition suivante (z > 0). Comme la réponse est "Non", le chemin d'inférence se termine au nœud feuille (Zêta).

Les trois flèches épaisses indiquent le chemin d'inférence.

Pour en savoir plus, consultez Arbres de décision dans le cours "Forêts de décision".

gain d'information

#df
#Metric

Dans les forêts de décision, il s'agit de la différence entre l'entropie d'un nœud et la somme pondérée (par nombre d'exemples) de l'entropie de ses nœuds enfants. L'entropie d'un nœud correspond à l'entropie des exemples de ce nœud.

Prenons par exemple les valeurs d'entropie suivantes :

  • Entropie du nœud parent = 0,6
  • L'entropie d'un nœud enfant avec 16 exemples pertinents est égale à 0,2.
  • Entropie d'un autre nœud enfant avec 24 exemples pertinents = 0,1

Ainsi, 40 % des exemples se trouvent dans un nœud enfant et 60 % dans l'autre. Par conséquent :

  • Somme pondérée de l'entropie des nœuds enfants = (0,4 * 0,2) + (0,6 * 0,1) = 0,14

Le gain d'information est donc le suivant :

  • Gain d'information = entropie du nœud parent - somme pondérée de l'entropie des nœuds enfants
  • gain d'information = 0,6 – 0,14 = 0,46

La plupart des splitters cherchent à créer des conditions qui maximisent le gain d'information.

condition dans l'ensemble

#df

Dans un arbre de décision, une condition qui teste la présence d'un élément dans un ensemble d'éléments. Par exemple, la condition suivante est une condition dans l'ensemble :

  house-style in [tudor, colonial, cape]

Lors de l'inférence, si la valeur de la caractéristique de style de maison est tudor, colonial ou cape, cette condition est évaluée sur "Oui". Si la valeur de la caractéristique "style de maison" est différente (par exemple, ranch), cette condition renvoie "Non".

Les conditions d'ensemble conduisent généralement à des arbres de décision plus efficaces que les conditions qui testent les caractéristiques encodées one-hot.

L

feuille

#df

Tout point de terminaison dans un arbre de décision. Contrairement à une condition, une feuille n'effectue pas de test. Une feuille est une prédiction possible. Une feuille est également le nœud terminal d'un chemin d'inférence.

Par exemple, l'arbre de décision suivant contient trois feuilles :

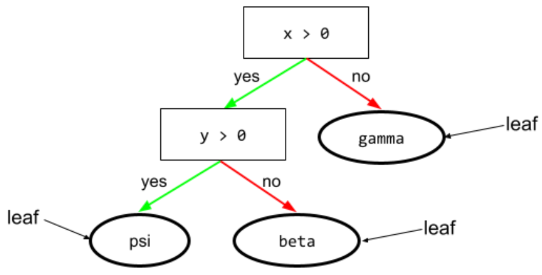
Arbre de décision avec deux conditions menant à trois feuilles.

Pour en savoir plus, consultez Arbres de décision dans le cours "Forêts de décision".

N

nœud (arbre de décision)

#df

Dans un arbre de décision, toute condition ou feuille.

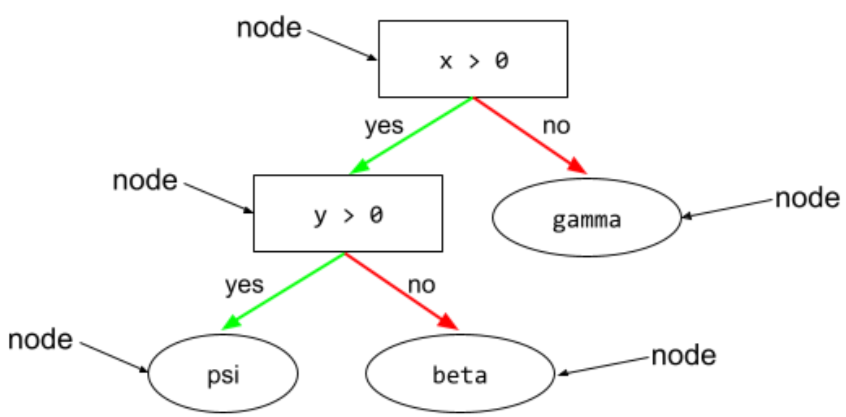
Arbre de décision avec deux conditions et trois feuilles.

Pour en savoir plus, consultez Arbres de décision dans le cours "Forêts de décision".

condition non binaire

#df

Une condition contenant plus de deux résultats possibles. Par exemple, la condition non binaire suivante contient trois résultats possibles :

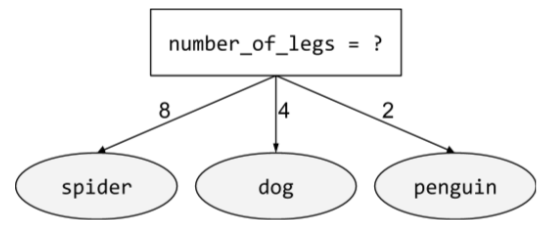
Une condition (number_of_legs = ?) qui conduit à trois résultats possibles. Un résultat (number_of_legs = 8) mène à une feuille nommée "spider". Un deuxième résultat (number_of_legs = 4) mène à une feuille nommée "dog". Un troisième résultat (number_of_legs = 2) mène à une feuille nommée "penguin".

Pour en savoir plus, consultez Types de conditions dans le cours "Forêts de décision".

O

condition oblique

#df

Dans un arbre de décision, une condition qui implique plusieurs caractéristiques. Par exemple, si la hauteur et la largeur sont toutes deux des caractéristiques, la condition suivante est oblique :

  height > width

À comparer à la condition alignée sur les axes.

Pour en savoir plus, consultez Types de conditions dans le cours "Forêts de décision".

Évaluation hors sac (OOB)

#df

Mécanisme permettant d'évaluer la qualité d'une forêt de décision en testant chaque arbre de décision par rapport aux exemples non utilisés lors de l'entraînement de cet arbre de décision. Par exemple, dans le schéma suivant, notez que le système entraîne chaque arbre de décision sur environ deux tiers des exemples, puis l'évalue par rapport au tiers restant.

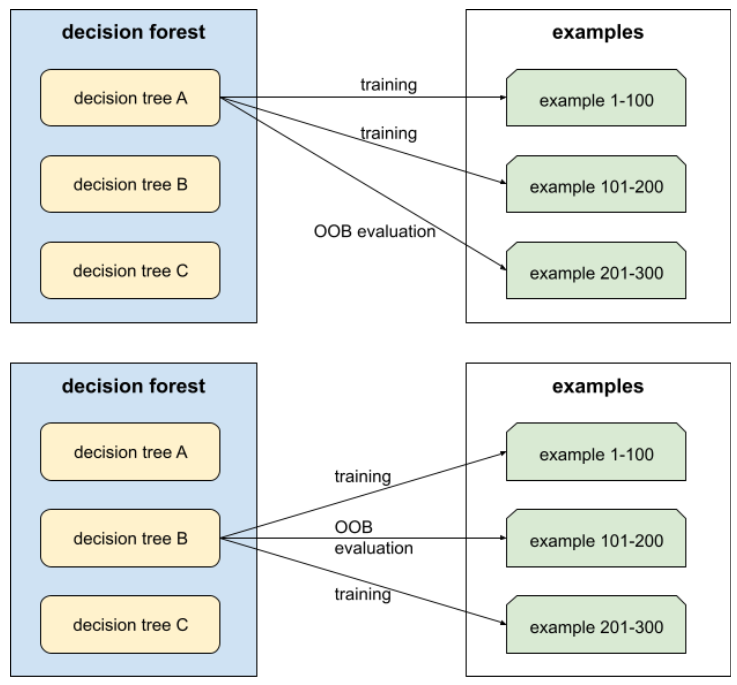
Forêt de décision composée de trois arbres de décision. Un arbre de décision s'entraîne sur les deux tiers des exemples, puis utilise le tiers restant pour l'évaluation OOB. Un deuxième arbre de décision s'entraîne sur les deux tiers des exemples différents de ceux de l'arbre de décision précédent, puis utilise un tiers différent pour l'évaluation OOB par rapport à l'arbre de décision précédent.

L'évaluation hors sac est une approximation conservative et efficace en termes de calcul du mécanisme de validation croisée. Dans la validation croisée, un modèle est entraîné pour chaque tour de validation croisée (par exemple, 10 modèles sont entraînés dans une validation croisée à 10 volets). Avec l'évaluation OOB, un seul modèle est entraîné. Étant donné que la bagging retient certaines données de chaque arbre pendant l'entraînement, l'évaluation OOB peut utiliser ces données pour approximer la validation croisée.

Pour en savoir plus, consultez la section Évaluation hors sac du cours sur les forêts de décision.

P

Importance des variables de permutation

#df
#Metric

Type d'importance des variables qui évalue l'augmentation de l'erreur de prédiction d'un modèle après permutation des valeurs de la caractéristique. L'importance des variables de permutation est une métrique indépendante du modèle.

R

forêt aléatoire

#df

Un ensemble d'arbres de décision dans lequel chaque arbre de décision est entraîné avec un bruit aléatoire spécifique, tel que l'agrégation bootstrap.

Les forêts d'arbres décisionnels sont un type de forêt de décision.

Pour en savoir plus, consultez Forêt aléatoire dans le cours "Forêts de décision".

racine

#df

Nœud de départ (première condition) d'un arbre de décision. Par convention, les diagrammes placent la racine en haut de l'arbre de décision. Exemple :

Arbre de décision avec deux conditions et trois feuilles. La condition de départ (x > 2) est la racine.

S

échantillonnage avec remplacement

#df

Méthode de sélection d'éléments à partir d'un ensemble d'éléments candidats dans laquelle le même élément peut être sélectionné plusieurs fois. L'expression "avec remise en place" signifie qu'après chaque sélection, l'élément sélectionné est remis dans le pool d'éléments candidats. La méthode inverse, l'échantillonnage sans remplacement, signifie qu'un élément candidat ne peut être sélectionné qu'une seule fois.

Prenons l'exemple de l'ensemble de fruits suivant :

fruit = {kiwi, apple, pear, fig, cherry, lime, mango}

Supposons que le système sélectionne aléatoirement fig comme premier élément. Si vous utilisez l'échantillonnage avec remplacement, le système sélectionne le deuxième élément de l'ensemble suivant :

fruit = {kiwi, apple, pear, fig, cherry, lime, mango}

Oui, il s'agit du même ensemble qu'avant. Le système pourrait donc potentiellement choisir à nouveau fig.

Si vous utilisez l'échantillonnage sans remplacement, une fois qu'un échantillon a été sélectionné, il ne peut plus l'être. Par exemple, si le système sélectionne aléatoirement fig comme premier échantillon, fig ne peut plus être sélectionné. Le système sélectionne donc le deuxième échantillon de l'ensemble (réduit) suivant :

fruit = {kiwi, apple, pear, cherry, lime, mango}

rétrécissement

#df

Un hyperparamètre dans le boosting de gradient qui contrôle le surapprentissage. La réduction dans le boosting de gradient est analogue au taux d'apprentissage dans la descente de gradient. La réduction est une valeur décimale comprise entre 0,0 et 1,0. Une valeur de réduction plus faible réduit davantage le surapprentissage qu'une valeur de réduction plus élevée.

split

#df

Dans un arbre de décision, il s'agit d'un autre nom pour une condition.

séparateur

#df

Lors de l'entraînement d'un arbre de décision, la routine (et l'algorithme) est chargée de trouver la meilleure condition à chaque nœud.

T

test

#df

Dans un arbre de décision, il s'agit d'un autre nom pour une condition.

Seuil (pour les arbres de décision)

#df

Dans une condition alignée sur un axe, il s'agit de la valeur à laquelle une caractéristique est comparée. Par exemple, 75 est la valeur seuil dans la condition suivante :

grade >= 75

Pour en savoir plus, consultez Splitter exact pour la classification binaire avec des caractéristiques numériques dans le cours sur les forêts de décision.

V

importance des variables

#df
#Metric

Ensemble de scores indiquant l'importance relative de chaque caractéristique pour le modèle.

Prenons l'exemple d'un arbre de décision qui estime le prix des maisons. Supposons que cet arbre de décision utilise trois caractéristiques : la taille, l'âge et le style. Si un ensemble d'importances de variables pour les trois caractéristiques est calculé comme suit : {size=5.8, age=2.5, style=4.7}, alors la taille est plus importante pour l'arbre de décision que l'âge ou le style.

Il existe différentes métriques d'importance des variables, qui peuvent informer les experts en ML sur différents aspects des modèles.

W

sagesse de la foule

#df

L'idée selon laquelle la moyenne des opinions ou des estimations d'un grand groupe de personnes ("la foule") produit souvent des résultats étonnamment bons. Prenons l'exemple d'un jeu dans lequel les participants doivent deviner le nombre de bonbons contenus dans un grand bocal. Bien que la plupart des estimations individuelles soient inexactes, la moyenne de toutes les estimations s'est avérée étonnamment proche du nombre réel de bonbons dans le bocal.

Les ensembles sont l'équivalent logiciel de la sagesse de la foule. Même si les modèles individuels font des prédictions très inexactes, la moyenne des prédictions de nombreux modèles génère souvent des prédictions étonnamment bonnes. Par exemple, même si un arbre de décision individuel peut générer de mauvaises prédictions, une forêt de décision en génère souvent de très bonnes.