Глоссарий машинного обучения: леса решений

Эта страница содержит термины глоссария «Леса решений». Все термины глоссария можно найти здесь .

А

выборка атрибутов

#дф

Тактика обучения леса решений, при которой каждое дерево решений учитывает только случайное подмножество возможных признаков при изучении условия . Как правило, для каждого узла выбирается свой подмножество признаков. Напротив, при обучении дерева решений без выборки атрибутов для каждого узла рассматриваются все возможные признаки.

состояние выравнивания по оси

#дф

В дереве решений условие , которое включает только один объект . Например, если объектом является area , то следующее условие является условием, выровненным по осям:

area > 200

Сравните с косым состоянием .

Б

упаковка в мешки

#дф

Метод обучения ансамбля , в котором каждая составляющая модель обучается на случайном подмножестве обучающих примеров , выбранных с заменой . Например, случайный лес — это набор деревьев решений, обученных с помощью бэггинга.

Термин «бэггинг» является сокращением от « bootstrap agg regating» .

Более подробную информацию см. в разделе Случайные леса в курсе Леса решений.

бинарное условие

#дф

В дереве решений условие , имеющее только два возможных результата, обычно «да» или «нет» . Например, следующее условие является бинарным:

temperature >= 100

Сравните с небинарным состоянием .

Более подробную информацию см. в разделе «Типы условий» курса «Леса решений».

С

состояние

#дф
В дереве решений — любой узел , выполняющий проверку. Например, следующее дерево решений содержит два условия:

Дерево решений, состоящее из двух условий: (x > 0) и (y > 0).

Условие также называется разделением или тестом.

Сравните состояние с листом .

Смотрите также:

Более подробную информацию см. в разделе «Типы условий» курса «Леса решений».

Д

лес решений

#дф

Модель, созданная на основе нескольких деревьев решений . Лес решений формирует прогноз, суммируя прогнозы своих деревьев решений. К распространённым типам лесов решений относятся случайные леса и деревья с градиентным бустингом .

Более подробную информацию см. в разделе «Леса решений» курса «Леса решений».

дерево решений

#дф

Модель контролируемого обучения, состоящая из набора условий и листьев, организованных иерархически. Например, ниже представлено дерево решений:

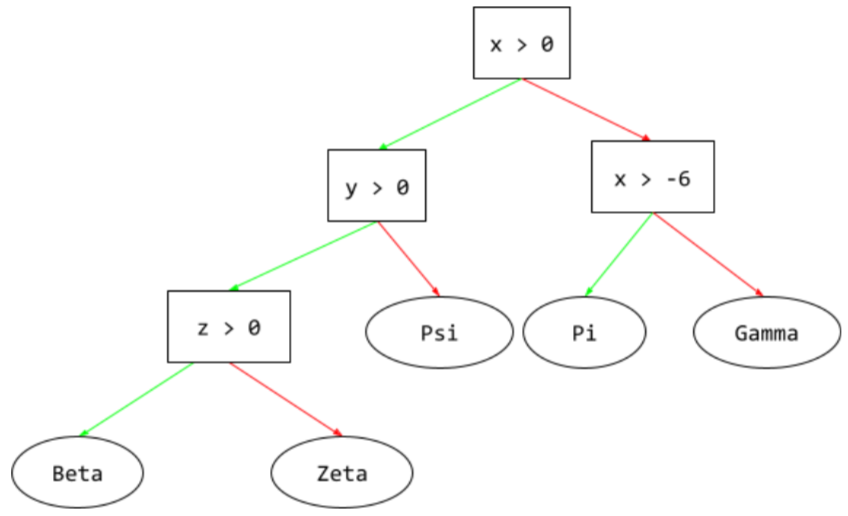
Дерево решений, состоящее из четырёх условий, расположенных иерархически, которые приводят к пяти листьям.

Э

энтропия

#дф
#Метрика

В теории информации — описание непредсказуемости распределения вероятностей. В качестве альтернативы, энтропия также определяется как количество информации, содержащейся в каждом примере . Распределение имеет максимально возможную энтропию, когда все значения случайной величины равновероятны.

Энтропия набора с двумя возможными значениями «0» и «1» (например, метки в задаче бинарной классификации ) имеет следующую формулу:

H = -p log p - q log q = -p log p - (1-p) * log (1-p)

где:

  • H — энтропия.
  • p — доля примеров «1».
  • q — доля примеров, равных нулю. Обратите внимание, что q = (1 - p).
  • Логарифм обычно равен логарифму 2. В данном случае единицей измерения энтропии является бит.

Например, предположим следующее:

  • 100 примеров содержат значение «1»
  • 300 примеров содержат значение «0»

Следовательно, значение энтропии равно:

  • р = 0,25
  • q = 0,75
  • H = (-0,25)log 2 (0,25) - (0,75)log 2 (0,75) = 0,81 бита на пример

Идеально сбалансированный набор (например, 200 нулей и 200 единиц) будет иметь энтропию 1,0 бит на экземпляр. По мере того, как набор становится более несбалансированным , его энтропия стремится к 0,0.

В деревьях решений энтропия помогает сформулировать прирост информации , чтобы помочь разделителю выбрать условия в процессе роста дерева решений классификации.

Сравните энтропию с:

Энтропию часто называют энтропией Шеннона .

Дополнительную информацию см. в разделе Точный разделитель для бинарной классификации с числовыми признаками в курсе «Леса решений».

Ф

важность функций

#дф
#Метрика

Синоним переменных важностей .

Г

примесь джини

#дф
#Метрика

Метрика, аналогичная энтропии . Разделители используют значения, полученные либо из коэффициента Джини, либо из энтропии, для составления условий для деревьев решений классификации. Прирост информации определяется энтропией. Общепринятого эквивалентного термина для метрики, полученной из коэффициента Джини, не существует; однако эта безымянная метрика так же важна, как и прирост информации.

Примесь Джини также называется индексом Джини или просто Джини .

деревья решений с градиентным усилением (GBT)

#дф

Тип леса решений, в котором:

Дополнительную информацию см. в разделе «Градиентно-усиленные деревья решений» курса «Леса решений».

усиление градиента

#дф

Алгоритм обучения, в котором слабые модели обучаются для итеративного улучшения качества (уменьшения потерь) сильной модели. Например, слабая модель может представлять собой линейную модель или модель с небольшим деревом решений. Сильная модель становится суммой всех ранее обученных слабых моделей.

В простейшей форме градиентного бустинга на каждой итерации слабая модель обучается предсказывать градиент потерь сильной модели. Затем выходные данные сильной модели обновляются путём вычитания предсказанного градиента, аналогично градиентному спуску .

$$F_{0} = 0$$$$F_{i+1} = F_i - \xi f_i $$

где:

  • $F_{0}$ — начальная сильная модель.
  • $F_{i+1}$ — следующая сильная модель.
  • $F_{i}$ — текущая сильная модель.
  • $\xi$ — это значение между 0,0 и 1,0, называемое усадкой , что аналогично скорости обучения в градиентном спуске.
  • $f_{i}$ — слабая модель, обученная прогнозировать градиент потерь $F_{i}$.

Современные варианты градиентного бустинга также включают в свои вычисления вторую производную (гессиан) потерь.

Деревья решений обычно используются в качестве слабых моделей в градиентном бустинге. См. градиентный бустинг (деревья решений) .

я

путь вывода

#дф

В дереве решений , во время вывода , маршрут, который проходит конкретный пример от корня к другим условиям , завершаясь листом . Например, в следующем дереве решений более толстые стрелки показывают путь вывода для примера со следующими значениями признаков:

  • х = 7
  • у = 12
  • z = -3

Путь вывода на следующей иллюстрации проходит через три условия, прежде чем достичь листа ( Zeta ).

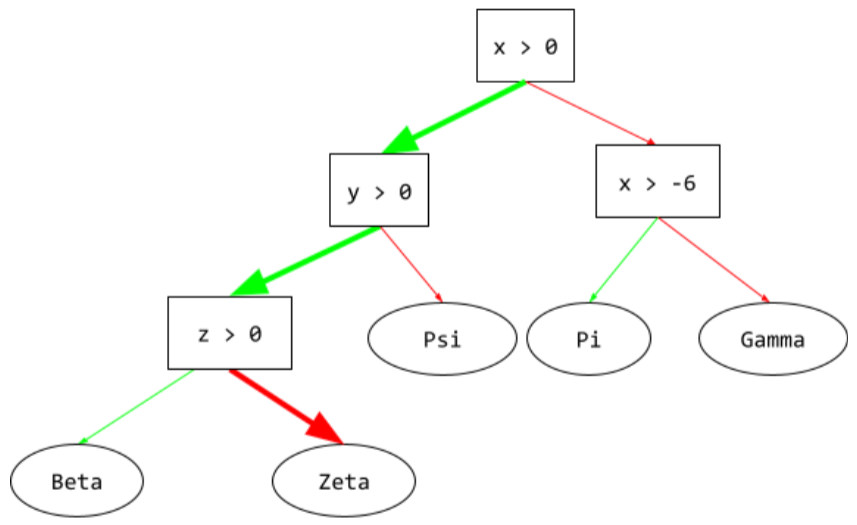
Дерево решений, состоящее из четырёх условий и пяти листьев. Корневое условие: (x > 0). Поскольку ответ «Да», путь вывода идёт от корня к следующему условию (y > 0). Поскольку ответ «Да», путь вывода идёт к следующему условию (z > 0). Поскольку ответ «Нет», путь вывода идёт к своему конечному узлу, который является листом (дзета).

Три толстые стрелки показывают путь вывода.

Более подробную информацию см. в разделе «Деревья решений» курса «Леса решений».

получение информации

#дф
#Метрика

В лесах решений — разность между энтропией узла и взвешенной (по числу примеров) суммой энтропии его дочерних узлов. Энтропия узла — это энтропия примеров в этом узле.

Например, рассмотрим следующие значения энтропии:

  • Энтропия родительского узла = 0,6
  • Энтропия одного дочернего узла с 16 соответствующими примерами = 0,2
  • Энтропия другого дочернего узла с 24 соответствующими примерами = 0,1

Таким образом, 40% примеров находятся в одном дочернем узле, а 60% — в другом дочернем узле. Следовательно:

  • Сумма взвешенной энтропии дочерних узлов = (0,4 * 0,2) + (0,6 * 0,1) = 0,14

Итак, прирост информации составляет:

  • прирост информации = энтропия родительского узла - взвешенная сумма энтропии дочерних узлов
  • прирост информации = 0,6 - 0,14 = 0,46

Большинство разделителей стремятся создать условия , которые максимизируют получение информации.

в установленном состоянии

#дф

В дереве решений — условие , проверяющее наличие одного элемента в наборе элементов. Например, следующее условие является условием вхождения:

  house-style in [tudor, colonial, cape]

В процессе вывода, если значение признака стиля дома — tudor , colonial или cape , то это условие оценивается как «Да». Если значение признака стиля дома — что-то другое (например, ranch ), то это условие оценивается как «Нет».

Встроенные условия обычно приводят к более эффективным деревьям решений, чем условия, которые проверяют признаки , закодированные методом прямого кодирования .

Л

лист

#дф

Любая конечная точка в дереве решений . В отличие от условия , лист не выполняет проверку. Вместо этого лист представляет собой возможное предсказание. Лист также является конечным узлом пути вывода .

Например, следующее дерево решений содержит три листа:

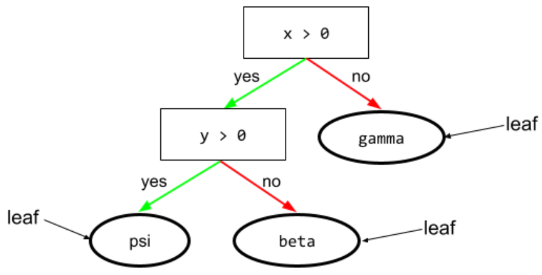
Дерево решений с двумя условиями, ведущими к трем листьям.

Более подробную информацию см. в разделе «Деревья решений» курса «Леса решений».

Н

узел (дерево решений)

#дф

В дереве решений — любое условие или лист .

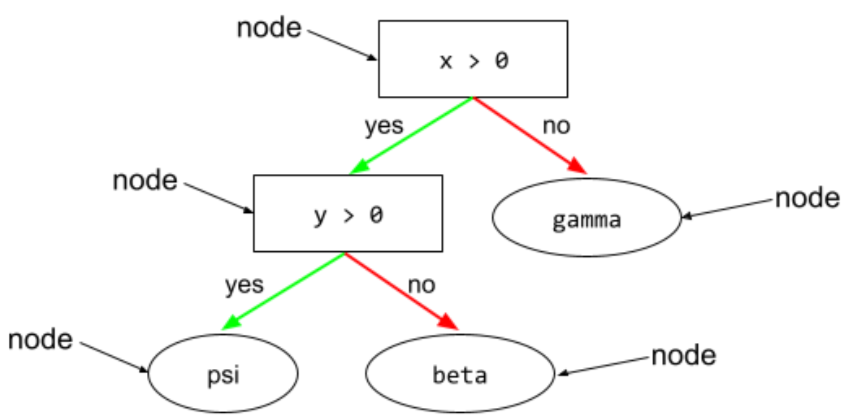
Дерево решений с двумя условиями и тремя листьями.

Более подробную информацию см. в разделе «Деревья решений» курса «Леса решений».

небинарное состояние

#дф

Условие , содержащее более двух возможных исходов. Например, следующее небинарное условие содержит три возможных исхода:

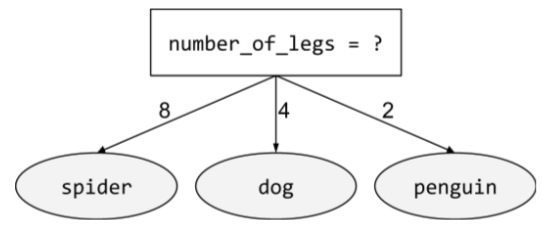
Условие (число_ног = ?) приводит к трём возможным результатам. Один результат (число_ног = 8) приводит к листу с названием «паук». Второй результат (число_ног = 4) приводит к листу с названием «собака». Третий результат (число_ног = 2) приводит к листу с названием «пингвин».

Более подробную информацию см. в разделе «Типы условий» курса «Леса решений».

О

косое состояние

#дф

В дереве решений условие , включающее более одного признака . Например, если высота и ширина являются признаками, то следующее условие является косвенным:

  height > width

Сравните с условием выравнивания по оси .

Более подробную информацию см. в разделе «Типы условий» курса «Леса решений».

оценка вне сумки (оценка OOB)

#дф

Механизм оценки качества леса решений путем тестирования каждого дерева решений на примерах , не использованных при его обучении . Например, на следующей диаграмме обратите внимание, что система обучает каждое дерево решений примерно на двух третях примеров, а затем оценивает его на оставшейся трети.

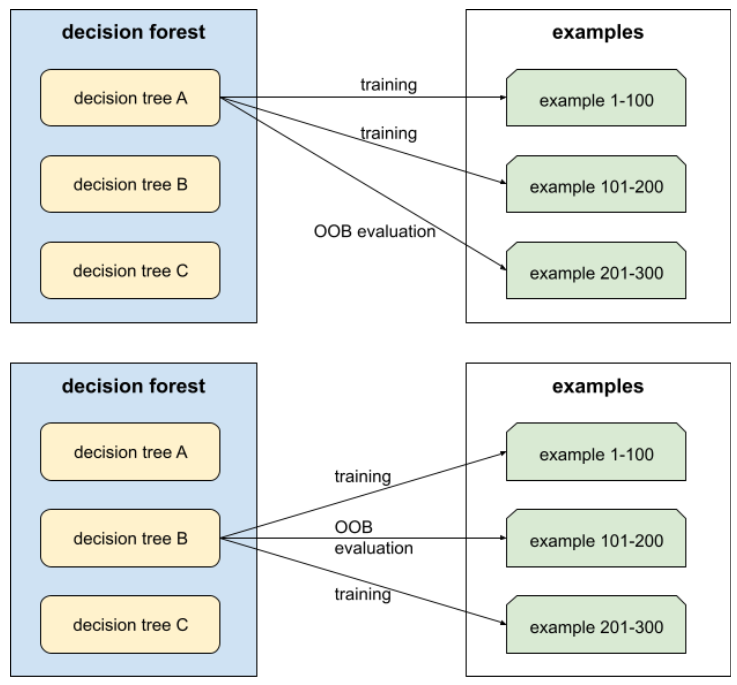
Лес решений, состоящий из трёх деревьев решений. Одно дерево решений обучается на двух третях примеров, а затем использует оставшуюся треть для оценки OOB. Второе дерево решений обучается на двух третях примеров, отличных от предыдущего дерева решений, а затем использует другую треть для оценки OOB, отличную от предыдущего дерева решений.

Оценка вне мешка (Out-of-bag) — это вычислительно эффективное и консервативное приближение к механизму перекрёстной проверки . При перекрёстной проверке обучается одна модель для каждого раунда (например, при 10-кратной перекрёстной проверке обучаются 10 моделей). При оценке вне мешка (OOB) обучается одна модель. Поскольку бэггинг скрывает часть данных из каждого дерева во время обучения, оценка вне мешка может использовать эти данные для аппроксимации перекрёстной проверки.

Более подробную информацию см. в разделе «Оценка по запросу» курса «Леса решений».

П

Значения переменных перестановки

#дф
#Метрика

Тип важности переменной , который оценивает увеличение ошибки прогноза модели после перестановки значений признака. Важность переменной перестановки — это независимая от модели метрика.

Р

случайный лес

#дф

Ансамбль деревьев решений , в котором каждое дерево решений обучается с использованием определенного случайного шума, например, бэггинга .

Случайные леса являются разновидностью леса решений .

Более подробную информацию см. в разделе «Случайный лес» курса «Леса решений».

корень

#дф

Начальный узел (первое условие ) в дереве решений . Корень обычно размещается на диаграммах в верхней части дерева решений. Например:

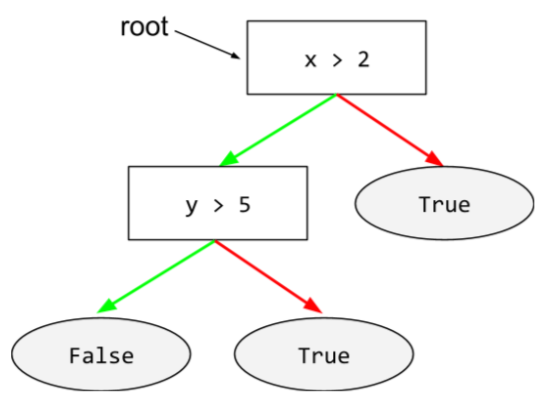
Дерево решений с двумя условиями и тремя листьями. Начальное условие (x > 2) является корнем.

С

выборка с заменой

#дф

Метод выбора элементов из набора элементов-кандидатов, при котором один и тот же элемент может быть выбран несколько раз. Фраза «с заменой» означает, что после каждого выбора выбранный элемент возвращается в набор элементов-кандидатов. Обратный метод, выборка без замены , означает, что элемент-кандидат может быть выбран только один раз.

Например, рассмотрим следующий набор фруктов:

fruit = {kiwi, apple, pear, fig, cherry, lime, mango}

Предположим, что система случайным образом выбирает fig в качестве первого элемента. При использовании выборки с возвращением система выбирает второй элемент из следующего набора:

fruit = {kiwi, apple, pear, fig, cherry, lime, mango}

Да, это тот же набор, что и раньше, так что система потенциально может снова выбрать fig .

При использовании выборки без повторного выбора, однажды выбранный образец не может быть выбран повторно. Например, если система случайным образом выбирает fig в качестве первого образца, то fig не может быть выбран повторно. Поэтому система выбирает второй образец из следующего (сокращенного) набора:

fruit = {kiwi, apple, pear, cherry, lime, mango}

усадка

#дф

Гиперпараметр в градиентном бустинге , контролирующий переобучение . Сжатие в градиентном бустинге аналогично скорости обучения в градиентном спуске . Сжатие — это десятичное значение от 0,0 до 1,0. Меньшее значение сжатия снижает переобучение сильнее, чем большее.

расколоть

#дф

В дереве решений — другое название условия .

разветвитель

#дф

При обучении дерева решений процедура (и алгоритм) отвечает за поиск наилучшего условия в каждом узле .

Т

тест

#дф

В дереве решений — другое название условия .

порог (для деревьев решений)

#дф

В условиях выравнивания по осям — значение, с которым сравнивается объект . Например, 75 — это пороговое значение в следующем состоянии: 

grade >= 75

Дополнительную информацию см. в разделе Точный разделитель для бинарной классификации с числовыми признаками в курсе «Леса решений».

В

переменные значения

#дф
#Метрика

Набор оценок, указывающих относительную важность каждой характеристики для модели.

Например, рассмотрим дерево решений , оценивающее цены на жильё. Предположим, что это дерево решений использует три характеристики: размер, возраст и стиль. Если набор значений важности этих трёх характеристик равен {размер=5,8, возраст=2,5, стиль=4,7}, то размер важнее для дерева решений, чем возраст или стиль.

Существуют различные метрики важности переменных, которые могут информировать экспертов по машинному обучению о различных аспектах моделей.

В

мудрость толпы

#дф

Идея о том, что усреднение мнений или оценок большой группы людей («толпы») часто даёт удивительно хорошие результаты. Например, представьте себе игру, в которой люди пытаются угадать количество желейных конфет в большой банке. Хотя большинство индивидуальных догадок будут неточными, эмпирически доказано, что среднее значение всех догадок удивительно близко к фактическому количеству желейных конфет в банке.

Ансамбли — это программный аналог коллективного разума. Даже если отдельные модели дают крайне неточные прогнозы, усреднение прогнозов многих моделей часто даёт удивительно хорошие результаты. Например, хотя отдельное дерево решений может давать плохие прогнозы, лес решений часто даёт очень хорошие.