Auf dieser Seite finden Sie Glossarbegriffe für Decision Forests. Hier finden Sie alle Glossarbegriffe.
A
Attribut-Sampling
Eine Taktik zum Trainieren eines Entscheidungsbaums, bei dem jeder Entscheidungsbaum beim Lernen der Bedingung nur eine zufällige Teilmenge der möglichen Features berücksichtigt. Im Allgemeinen wird für jeden Knoten eine andere Teilmenge von Features ausgewählt. Beim Trainieren eines Entscheidungsbaums ohne Attribut-Sampling werden dagegen alle möglichen Features für jeden Knoten berücksichtigt.
Achsenparallele Bedingung
In einem Entscheidungsbaum ist eine Bedingung, die nur ein einzelnes Attribut umfasst. Wenn area beispielsweise ein Merkmal ist, ist Folgendes eine achsenorientierte Bedingung:
area > 200
Kontrast zur schrägen Bedingung.
B
Bagging
Eine Methode zum Trainieren eines Ensembles, bei dem jedes Modell auf einer zufälligen Teilmenge von Trainingsbeispielen mit Zurücklegen trainiert wird. Ein Random Forest ist beispielsweise eine Sammlung von Entscheidungsbäumen, die mit Bagging trainiert wurden.
Der Begriff Bagging ist eine Abkürzung für Bootstrap Aggregating.
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Random Forests.
Binärbedingung
In einem Entscheidungsbaum ist eine Bedingung, die nur zwei mögliche Ergebnisse hat, in der Regel Ja oder Nein. Beispiel:
temperature >= 100
Im Gegensatz dazu steht die nicht binäre Bedingung.
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Arten von Bedingungen.
C
Bedingung
In einem Entscheidungsbaum ist jeder Knoten, in dem ein Test durchgeführt wird. Der folgende Entscheidungsbaum enthält beispielsweise zwei Bedingungen:

Eine Bedingung wird auch als Aufteilung oder Test bezeichnet.
Kontrastbedingung mit leaf.
Siehe auch:
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Arten von Bedingungen.
D
Entscheidungsbaumgruppe
Ein Modell, das aus mehreren Entscheidungsbäumen erstellt wurde. Bei einem Entscheidungsbaum wird eine Vorhersage getroffen, indem die Vorhersagen der einzelnen Entscheidungsbäume zusammengefasst werden. Beliebte Arten von Entscheidungsbäumen sind Random Forests und Gradient Boosted Trees.
Weitere Informationen finden Sie im Kurs „Decision Forests“ im Abschnitt Decision Forests.
Entscheidungsbaum
Ein Modell für überwachtes Lernen, das aus einer Reihe von hierarchisch organisierten Bedingungen und Blättern besteht. Hier ist ein Beispiel für einen Entscheidungsbaum:

E
Entropie
In der Informationstheorie wird die Unvorhersehbarkeit einer Wahrscheinlichkeitsverteilung beschrieben. Alternativ wird die Entropie auch als die Menge an Informationen definiert, die jedes Beispiel enthält. Eine Verteilung hat die höchstmögliche Entropie, wenn alle Werte einer Zufallsvariablen gleich wahrscheinlich sind.
Die Entropie einer Menge mit zwei möglichen Werten „0“ und „1“ (z. B. die Labels in einem binären Klassifizierungsproblem) wird mit der folgenden Formel berechnet:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
Dabei gilt:
- H ist die Entropie.
- p ist der Anteil der Beispiele mit dem Wert „1“.
- q ist der Anteil der Beispiele mit dem Wert „0“. Hinweis: q = (1 – p)
- log ist im Allgemeinen log2. In diesem Fall ist die Entropieeinheit ein Bit.
Nehmen wir beispielsweise Folgendes an:
- 100 Beispiele enthalten den Wert „1“.
- 300 Beispiele enthalten den Wert „0“
Der Entropiewert ist also:
- p = 0,25
- q = 0,75
- H = (-0,25)log2(0,25) – (0,75)log2(0,75) = 0,81 Bit pro Beispiel
Ein perfekt ausgeglichener Satz (z. B. 200 „0“ und 200 „1“) hätte eine Entropie von 1, 0 Bit pro Beispiel. Je unausgewogener ein Set ist, desto mehr nähert sich seine Entropie dem Wert 0,0 an.
In Entscheidungsbäumen wird mit Entropie der Informationsgewinn formuliert, damit der Splitter beim Erstellen eines Klassifizierungsentscheidungsbaums die Bedingungen auswählen kann.
Entropie vergleichen mit:
- Gini-Unreinheit
- Kreuzentropie-Verlustfunktion
Entropie wird oft als Shannon-Entropie bezeichnet.
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Exact splitter for binary classification with numerical features (Genaue Aufteilung für die binäre Klassifizierung mit numerischen Features).
F
Featurewichtigkeiten
Synonym für Variablenwichtigkeit.
G
Gini-Unreinheit
Ein Messwert ähnlich der Entropie. Splitter verwenden Werte, die entweder aus der Gini-Unreinheit oder der Entropie abgeleitet werden, um Bedingungen für die Klassifizierung Entscheidungsbäume zu erstellen. Information Gain wird aus der Entropie abgeleitet. Es gibt keinen allgemein akzeptierten Begriff für den Messwert, der aus der Gini-Unreinheit abgeleitet wird. Dieser unbenannte Messwert ist jedoch genauso wichtig wie der Informationsgewinn.
Die Gini-Unreinheit wird auch als Gini-Index oder einfach als Gini bezeichnet.
Gradient Boosted Trees (GBT)
Eine Art von Entscheidungsbaum, bei der:
- Training basiert auf Gradient Boosting.
- Das schwache Modell ist ein Entscheidungsbaum.
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Gradient Boosted Decision Trees.
Gradient Boosting
Ein Trainingsalgorithmus, bei dem schwache Modelle iterativ trainiert werden, um die Qualität (Verlust) eines starken Modells zu verbessern. Ein schwaches Modell kann beispielsweise ein lineares Modell oder ein kleines Entscheidungsbaummodell sein. Das starke Modell ist die Summe aller zuvor trainierten schwachen Modelle.
In der einfachsten Form von Gradient Boosting wird in jeder Iteration ein schwaches Modell trainiert, um den Verlustgradienten des starken Modells vorherzusagen. Die Ausgabe des starken Modells wird dann aktualisiert, indem der vorhergesagte Gradient subtrahiert wird, ähnlich wie beim Gradientenabstieg.
Dabei gilt:
- $F_{0}$ ist das Ausgangsmodell.
- $F_{i+1}$ ist das nächste starke Modell.
- $F_{i}$ ist das aktuelle starke Modell.
- $\xi$ ist ein Wert zwischen 0,0 und 1,0, der als Shrinkage bezeichnet wird und analog zur Lernrate beim Gradientenabstieg ist.
- $f_{i}$ ist das schwache Modell, das darauf trainiert wird, den Verlustgradienten von $F_{i}$ vorherzusagen.
Moderne Varianten von Gradient Boosting berücksichtigen auch die zweite Ableitung (Hessian) des Verlusts in ihren Berechnungen.
Entscheidungsbäume werden häufig als schwache Modelle beim Gradient Boosting verwendet. Weitere Informationen finden Sie unter Gradient Boosted-Entscheidungsbäume.
I
Inferenzpfad
In einem Entscheidungsbaum wird während der Inferenz der Pfad eines bestimmten Beispiels vom Stamm zu anderen Bedingungen verfolgt, bis er in einem Blatt endet. Im folgenden Entscheidungsbaum zeigen die dickeren Pfeile beispielsweise den Inferenzpfad für ein Beispiel mit den folgenden Feature-Werten:
- x = 7
- y = 12
- z = -3
Der Inferenzpfad in der folgenden Abbildung durchläuft drei Bedingungen, bevor er das Blatt (Zeta) erreicht.

Die drei dicken Pfeile zeigen den Inferenzpfad.
Weitere Informationen finden Sie im Kurs „Decision Forests“ unter Entscheidungsbäume.
Informationsgewinn
In Entscheidungsbäumen ist das die Differenz zwischen der Entropie eines Knotens und der gewichteten (nach Anzahl der Beispiele) Summe der Entropie seiner untergeordneten Knoten. Die Entropie eines Knotens ist die Entropie der Beispiele in diesem Knoten.
Sehen wir uns zum Beispiel die folgenden Entropiewerte an:
- Entropie des übergeordneten Knotens = 0,6
- Entropie eines untergeordneten Knotens mit 16 relevanten Beispielen = 0,2
- Entropie eines anderen untergeordneten Knotens mit 24 relevanten Beispielen = 0,1
40% der Beispiele befinden sich also in einem untergeordneten Knoten und 60% im anderen. Beispiele:
- Gewichtete Entropiesumme der untergeordneten Knoten = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Der Informationsgewinn ist also:
- Informationsgewinn = Entropie des übergeordneten Knotens – gewichtete Entropiesumme der untergeordneten Knoten
- Information Gain = 0,6 – 0,14 = 0,46
Die meisten Splitter versuchen, Bedingungen zu erstellen, die den Informationsgewinn maximieren.
Bedingung für die Gruppe
In einem Entscheidungsbaum ist eine Bedingung, mit der geprüft wird, ob ein Element in einer Gruppe von Elementen vorhanden ist. Das Folgende ist beispielsweise eine Bedingung für die Anzeige in der Suchergebnisseite:
house-style in [tudor, colonial, cape]
Wenn der Wert des Features „house-style“ während der Inferenz tudor, colonial oder cape ist, wird diese Bedingung als „Ja“ ausgewertet. Wenn der Wert des Features „Hausstil“ etwas anderes ist (z. B. ranch), wird diese Bedingung als „Nein“ ausgewertet.
In-Set-Bedingungen führen in der Regel zu effizienteren Entscheidungsbäumen als Bedingungen, mit denen One-Hot-codierte Merkmale getestet werden.
L
Blatt
Jeder Endpunkt in einem Entscheidungsbaum. Im Gegensatz zu einer Bedingung wird bei einem Blatt kein Test durchgeführt. Vielmehr ist ein Blatt eine mögliche Vorhersage. Ein Blatt ist auch der Endknoten eines Inferenzpfads.
Der folgende Entscheidungsbaum enthält beispielsweise drei Blätter:
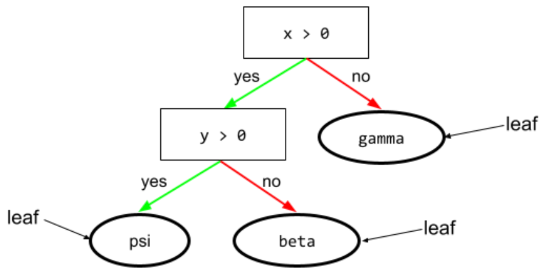
Weitere Informationen finden Sie im Kurs „Decision Forests“ unter Entscheidungsbäume.
N
Knoten (Entscheidungsbaum)
In einem Entscheidungsbaum kann jede Bedingung oder jedes Blatt sein.
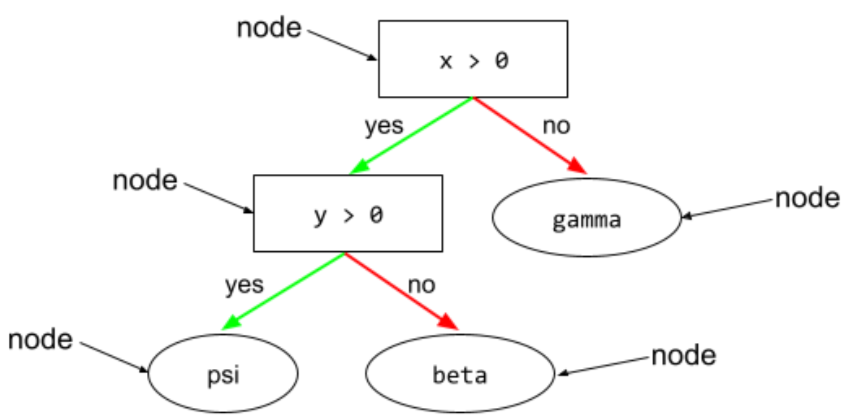
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Entscheidungsbäume.
nicht binäre Bedingung
Eine Bedingung mit mehr als zwei möglichen Ergebnissen. Die folgende nicht binäre Bedingung enthält beispielsweise drei mögliche Ergebnisse:
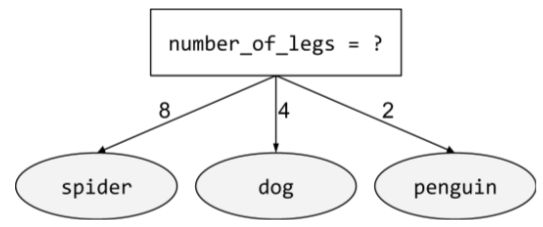
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Arten von Bedingungen.
O
schräge Bedingung
In einem Entscheidungsbaum ist eine Bedingung, die mehr als ein Merkmal umfasst. Wenn Höhe und Breite beispielsweise beides Features sind, ist Folgendes eine schräge Bedingung:
height > width
Im Gegensatz zur achsenorientierten Bedingung.
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Arten von Bedingungen.
Out-of-Bag-Bewertung (OOB-Bewertung)
Ein Mechanismus zur Bewertung der Qualität eines Entscheidungsbaums, indem jeder Entscheidungsbaum anhand der Beispiele getestet wird, die nicht während des Trainings dieses Entscheidungsbaums verwendet wurden. Im folgenden Diagramm sehen Sie beispielsweise, dass das System jeden Entscheidungsbaum mit etwa zwei Dritteln der Beispiele trainiert und dann mit dem verbleibenden Drittel der Beispiele bewertet.
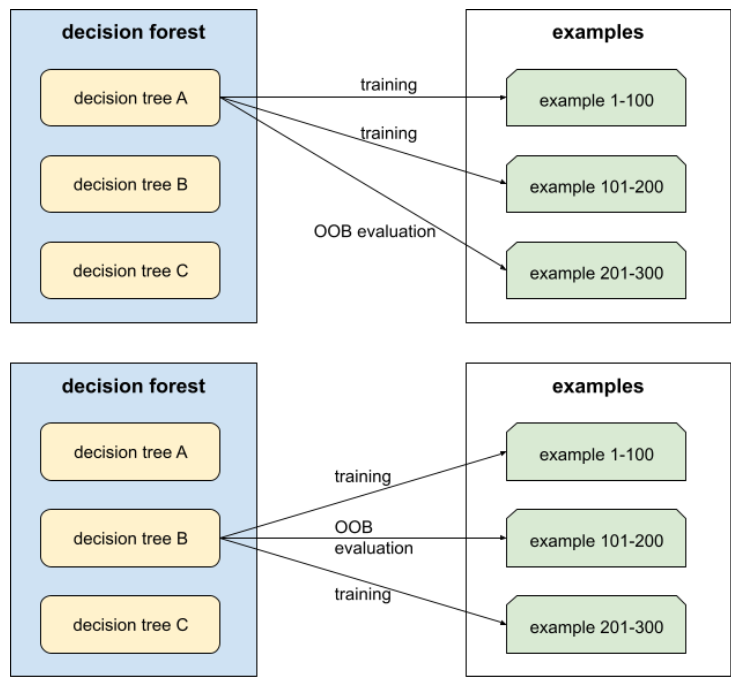
Die Out-of-Bag-Bewertung ist eine recheneffiziente und konservative Annäherung des Kreuzvalidierungsmechanismus. Bei der Kreuzvalidierung wird für jede Kreuzvalidierungsrunde ein Modell trainiert (z. B. 10 Modelle bei einer 10‑fachen Kreuzvalidierung). Bei der OOB-Bewertung wird ein einzelnes Modell trainiert. Da beim Bagging während des Trainings einige Daten für jeden Baum zurückgehalten werden, kann bei der OOB-Bewertung mit diesen Daten eine Kreuzvalidierung angenähert werden.
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Out-of-bag evaluation.
P
Bewertung von Variablen durch Permutation
Eine Art von Variablenwichtigkeit, die die Zunahme des Vorhersagefehlers eines Modells nach Permutation der Werte des Features bewertet. Die Permutationsvariablenwichtigkeit ist ein modellunabhängiger Messwert.
R
Random Forest
Ein Ensemble von Entscheidungsbäumen, in dem jeder Entscheidungsbaum mit einem bestimmten zufälligen Rauschen trainiert wird, z. B. Bagging.
Random Forests sind eine Art von Entscheidungsbäumen.
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Random Forest.
Stamm
Der Startknoten (die erste Bedingung) in einem Entscheidungsbaum. Üblicherweise wird die Wurzel oben im Entscheidungsbaum platziert. Beispiel:

S
Stichprobennahme mit Zurücklegen
Eine Methode zum Auswählen von Elementen aus einer Menge von Kandidatenelementen, bei der dasselbe Element mehrmals ausgewählt werden kann. Der Begriff „mit Zurücklegen“ bedeutet, dass das ausgewählte Element nach jeder Auswahl in den Pool der infrage kommenden Elemente zurückgelegt wird. Bei der umgekehrten Methode, dem Sampling ohne Zurücklegen, kann ein Kandidatenelement nur einmal ausgewählt werden.
Betrachten Sie beispielsweise die folgende Menge an Früchten:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Angenommen, das System wählt fig als erstes Element zufällig aus.
Wenn Sie Stichproben mit Zurücklegen verwenden, wählt das System das zweite Element aus der folgenden Menge aus:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Ja, das ist dasselbe Set wie zuvor. Das System könnte also wieder fig auswählen.
Wenn Sie Stichproben ohne Zurücklegen verwenden, kann eine ausgewählte Stichprobe nicht noch einmal ausgewählt werden. Wenn das System beispielsweise fig als erste Stichprobe zufällig auswählt, kann fig nicht noch einmal ausgewählt werden. Daher wählt das System das zweite Beispiel aus der folgenden (reduzierten) Menge aus:
fruit = {kiwi, apple, pear, cherry, lime, mango}Einlaufen
Ein Hyperparameter in Gradient Boosting, der Overfitting steuert. Die Schrumpfung beim Gradient Boosting entspricht der Lernrate beim Gradientenabstieg. Der Schrumpfungswert ist eine Dezimalzahl zwischen 0,0 und 1,0. Ein niedrigerer Schrumpfungswert reduziert die Überanpassung stärker als ein höherer Schrumpfungswert.
aufteilen
In einem Entscheidungsbaum ist das ein anderer Name für eine Bedingung.
Splitter
Beim Trainieren eines Entscheidungsbaums wird die Routine (und der Algorithmus) verwendet, um die beste Bedingung für jeden Knoten zu finden.
T
Test
In einem Entscheidungsbaum ist das ein anderer Name für eine Bedingung.
Grenzwert (für Entscheidungsbäume)
In einer achsenorientierten Bedingung der Wert, mit dem ein Attribut verglichen wird. Beispiel: 75 ist der Grenzwert in der folgenden Bedingung:
grade >= 75
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Exact splitter for binary classification with numerical features.
V
Variablenwichtigkeiten
Eine Reihe von Werten, die die relative Wichtigkeit der einzelnen Features für das Modell angibt.
Betrachten Sie beispielsweise einen Entscheidungsbaum, der Hauspreise schätzt. Angenommen, in diesem Entscheidungsbaum werden drei Attribute verwendet: Größe, Alter und Stil. Wenn die Wichtigkeit der drei Variablen {size=5.8, age=2.5, style=4.7} ist, ist die Größe für den Entscheidungsbaum wichtiger als das Alter oder der Stil.
Es gibt verschiedene Messwerte für die Wichtigkeit von Variablen, die ML-Experten über unterschiedliche Aspekte von Modellen informieren können.
W
Schwarmintelligenz
Die Idee, dass das Mitteln der Meinungen oder Schätzungen einer großen Gruppe von Menschen („der Menge“) oft überraschend gute Ergebnisse liefert. Stellen Sie sich beispielsweise ein Spiel vor, bei dem die Teilnehmer die Anzahl der Gummibärchen in einem großen Glas schätzen. Die meisten einzelnen Schätzungen sind zwar ungenau, aber der Durchschnitt aller Schätzungen liegt erfahrungsgemäß überraschend nahe an der tatsächlichen Anzahl der Jelly Beans im Glas.
Ensembles sind das Software-Analogon der Weisheit der Menge. Auch wenn einzelne Modelle sehr ungenaue Vorhersagen treffen, werden durch die Mittelung der Vorhersagen vieler Modelle oft überraschend gute Vorhersagen generiert. Ein einzelner Entscheidungsbaum kann beispielsweise schlechte Vorhersagen treffen, ein Entscheidungsbaum hingegen oft sehr gute.