このページには、ML の基礎用語集が記載されています。用語集のすべての用語については、こちらをクリックしてください。
A
accuracy
分類予測の正解の数を予測の総数で割った数。具体的には、次のことが求められます。
たとえば、40 個の正しい予測と 10 個の誤った予測を行ったモデルの精度は次のようになります。
バイナリ分類では、正しい予測と誤った予測のさまざまなカテゴリに固有の名前が付けられます。したがって、二項分類の精度の式は次のようになります。
ここで
詳細については、ML 集中講座の分類: 正確度、再現率、適合率、関連指標をご覧ください。
活性化関数
ニューラル ネットワークが特徴とラベルの間の非線形(複雑な)関係を学習できるようにする関数。
よく使用される活性化関数には、次のようなものがあります。
活性化関数のプロットは、単一の直線になることはありません。たとえば、ReLU 活性化関数のプロットは 2 つの直線で構成されます。

シグモイド活性化関数のプロットは次のようになります。

詳細については、ML 集中講座のニューラル ネットワーク: 活性化関数をご覧ください。
AI
複雑なタスクを解決できる人間以外のプログラムまたはモデル。たとえば、テキストを翻訳するプログラムやモデル、放射線画像から病気を特定するプログラムやモデルは、どちらも人工知能を示しています。
正式には、ML は AI の一分野です。しかし、近年では、人工知能と機械学習という用語を同じ意味で使用する組織も出てきています。
AUC(ROC 曲線の下の面積)
陽性クラスと陰性クラスを分離するバイナリ分類モデルの能力を表す 0.0 ~ 1.0 の数値。AUC が 1.0 に近いほど、クラスを互いに分離するモデルの能力が優れています。
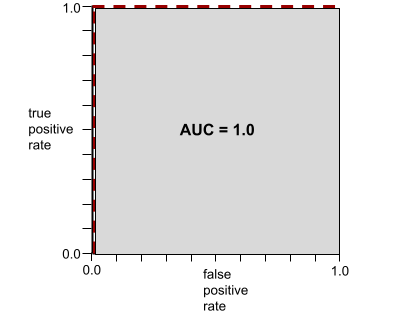
たとえば、次の図は、陽性クラス(緑色の楕円)と陰性クラス(紫色の長方形)を完全に分離する分類モデルを示しています。この非現実的な完全なモデルの AUC は 1.0 です。

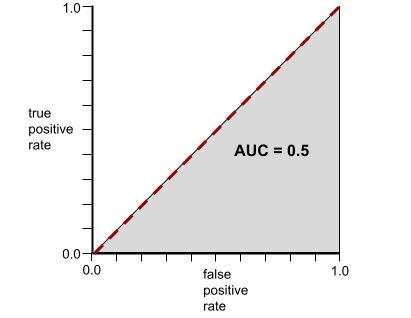
一方、次の図は、ランダムな結果を生成した分類モデルの結果を示しています。このモデルの AUC は 0.5 です。

はい。上記のモデルの AUC は 0.0 ではなく 0.5 です。
ほとんどのモデルは、この 2 つの極端なモデルの中間に位置します。たとえば、次のモデルは陽性と陰性をある程度分離しているため、AUC は 0.5 ~ 1.0 の範囲になります。

AUC は、分類しきい値に設定した値を無視します。AUC は、可能なすべての分類しきい値を考慮します。
詳細については、ML 集中講座の分類: ROC と AUC をご覧ください。
B
バックプロパゲーション
ニューラル ネットワークで勾配降下法を実装するアルゴリズム。
ニューラル ネットワークのトレーニングには、次の 2 パス サイクルの多くの反復が含まれます。
- フォワード パスでは、システムは バッチの例を処理して、予測を生成します。システムは、各予測を各ラベル値と比較します。予測値とラベル値の差は、その例の損失です。システムは、すべての例の損失を集計して、現在のバッチの合計損失を計算します。
- バックワード パス(バックプロパゲーション)では、すべての隠れ層のすべてのニューロンの重みを調整することで、損失を減らします。
ニューラル ネットワークには、多くの隠れ層に多くのニューロンが含まれていることがよくあります。これらのニューロンはそれぞれ異なる方法で全体的な損失に貢献します。バックプロパゲーションは、特定のニューロンに適用される重みを増減するかどうかを決定します。
学習率は、各バックワード パスで各重みを増減させる程度を制御する乗数です。学習率が大きいほど、各重みの増減が大きくなります。
微積分の用語で言うと、バックプロパゲーションは微積分の連鎖律を実装します。つまり、バックプロパゲーションは、各パラメータに関するエラーの偏導関数を計算します。
数年前までは、ML 実務家は逆伝播を実装するためにコードを記述する必要がありました。Keras などの最新の ML API では、バックプロパゲーションが実装されています。さて、
詳細については、ML 集中講座のニューラル ネットワークをご覧ください。
Batch
1 回のトレーニングイテレーションで使用されるサンプルのセット。バッチサイズは、バッチ内のサンプル数を決定します。
バッチとエポックの関係については、エポックをご覧ください。
詳細については、ML 集中講座の線形回帰: ハイパーパラメータをご覧ください。
バッチサイズ
バッチ内のサンプルの数。たとえば、バッチサイズが 100 の場合、モデルは 1 回のイテレーションごとに 100 個の例を処理します。
一般的なバッチサイズ戦略は次のとおりです。
- バッチサイズが 1 の確率的勾配降下法(SGD)。
- フルバッチ。バッチサイズは、トレーニング セット全体のサンプル数です。たとえば、トレーニング セットに 100 万個のサンプルが含まれている場合、バッチサイズは 100 万個のサンプルになります。通常、フルバッチは非効率的な戦略です。
- バッチサイズが通常 10 ~ 1,000 の ミニバッチ。通常、ミニバッチが最も効率的な戦略です。
詳しくは以下をご覧ください。
- 機械学習集中講座の本番環境 ML システム: 静的推論と動的推論。
- ディープ ラーニング チューニング ハンドブック。
バイアス(倫理/公平性)
1. 特定のこと、人、グループに対する固定観念、偏見、またはえこひいき。こうしたバイアスは、データの収集と解釈、システムの設計、ユーザーがシステムを操作する方法に影響する可能性があります。このタイプのバイアスの形式には、次のようなものがあります。
2. サンプリングや報告の手順で体系的に生じたエラー。このタイプのバイアスの形式には、次のようなものがあります。
機械学習モデルのバイアス項や予測バイアスと混同しないでください。
詳細については、ML 集中講座の公平性: 偏りの種類をご覧ください。
バイアス(数学)またはバイアス項
原点からの切片またはオフセット。バイアスは、機械学習モデルのパラメータです。次のいずれかで表されます。
- b
- w0
たとえば、次の数式では、バイアスは b です。
単純な 2 次元線では、バイアスは単に「y 切片」を意味します。たとえば、次の図の線のバイアスは 2 です。
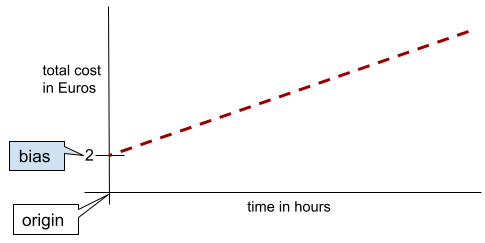
バイアスが存在するのは、すべてのモデルが原点(0,0)から始まるわけではないためです。たとえば、遊園地の入場料が 2 ユーロで、滞在 1 時間ごとに 0.5 ユーロの追加料金が発生するとします。したがって、総費用をマッピングするモデルのバイアスは 2 になります。これは、最低費用が 2 ユーロであるためです。
バイアスは、倫理と公平性のバイアスや予測バイアスと混同しないでください。
詳細については、ML 集中講座の線形回帰をご覧ください。
バイナリ分類
2 つの相互に排他的なクラスのいずれかを予測する分類タスクの一種。
たとえば、次の 2 つの機械学習モデルはそれぞれバイナリ分類を実行します。
- メール メッセージが迷惑メール(ポジティブ クラス)か迷惑メールではない(ネガティブ クラス)かを判断するモデル。
- 病状を評価して、特定の病気がある(陽性クラス)か、その病気がない(陰性クラス)かを判断するモデル。
マルチクラス分類と比較してください。
詳細については、機械学習集中講座の分類をご覧ください。
バケット化、
通常は値の範囲に基づいて、1 つの特徴をバケットまたはビンと呼ばれる複数のバイナリ特徴に変換します。通常、切り捨てられた特徴量は連続特徴量です。
たとえば、温度を 1 つの連続する浮動小数点型の特徴量として表すのではなく、温度の範囲を次のような離散的なバケットに分割できます。
- 摂氏 10 度以下は「コールド」バケットになります。
- 11 ~ 24 度の場合は「温帯」バケットになります。
- 摂氏 25 度以上は「暖かい」バケットになります。
モデルは、同じバケット内のすべての値を同じように扱います。たとえば、値 13 と 22 はどちらも中温バケットにあるため、モデルは 2 つの値を同じように扱います。
詳細については、機械学習集中講座の数値データ: ビン分割をご覧ください。
C
カテゴリデータ
特徴。取り得る値の特定のセットがあります。たとえば、traffic-light-state という名前のカテゴリ特徴について考えてみます。この特徴は、次の 3 つの値のいずれか 1 つのみを持つことができます。
redyellowgreen
traffic-light-state をカテゴリ特徴量として表現することで、モデルは red、green、yellow が運転者の行動に与える影響の違いを学習できます。
数値データと対照的です。
詳細については、ML 集中講座のカテゴリデータの操作をご覧ください。
クラス
ラベルが属することができるカテゴリ。次に例を示します。
分類モデルは、クラスを予測します。一方、回帰モデルはクラスではなく数値を予測します。
詳細については、機械学習集中講座の分類をご覧ください。
分類モデル
予測がクラスであるモデル。たとえば、次のモデルはすべて分類モデルです。
- 入力文の言語を予測するモデル(フランス語か、スペイン語ですか?イタリア語か、など)。
- 樹木の種類を予測するモデル(メープルか、オークか、バオバブか、など)。
- 特定の病状について、陽性クラスか陰性クラスかを予測するモデル。
一方、回帰モデルはクラスではなく数値を予測します。
一般的な分類モデルには次の 2 つがあります。
分類しきい値
バイナリ分類では、ロジスティック回帰モデルの未加工の出力を陽性クラスまたは陰性クラスのいずれかの予測に変換する 0 ~ 1 の数値。分類しきい値は、モデルのトレーニングによって選択される値ではなく、人間が選択する値です。
ロジスティック回帰モデルは、0 ~ 1 の範囲の生の値を出力します。以下の手順を行います。
- この生の値が分類しきい値より大きい場合、正のクラスが予測されます。
- この生の値が分類しきい値より小さい場合、負のクラスが予測されます。
たとえば、分類しきい値が 0.8 であるとします。生の値が 0.9 の場合、モデルは陽性クラスを予測します。生の値が 0.7 の場合、モデルは負のクラスを予測します。
分類しきい値の選択は、偽陽性と偽陰性の数に大きく影響します。
詳細については、ML 集中講座のしきい値と混同行列をご覧ください。
分類器
分類モデルのカジュアルな用語。
クラスの不均衡なデータセット
各クラスのラベルの総数が大幅に異なる分類のデータセット。たとえば、2 つのラベルが次のように分割されているバイナリ分類データセットについて考えてみましょう。
- 1,000,000 個の負のラベル
- 10 個の正のラベル
ネガティブ ラベルとポジティブ ラベルの比率は 100,000 対 1 であるため、これはクラス不均衡データセットです。
一方、次のデータセットは、ネガティブ ラベルとポジティブ ラベルの比率が 1 に比較的近いため、クラス バランスが取れています。
- 517 個の負のラベル
- 483 個の正のラベル
マルチクラス データセットは、クラスの不均衡が生じている場合もあります。たとえば、次のマルチクラス分類データセットもクラス不均衡です。これは、1 つのラベルの例が他の 2 つのラベルよりもはるかに多いためです。
- クラス「green」のラベルが 1,000,000 個
- クラス「purple」のラベルが 200 個
- クラス「orange」のラベルが 350 個
クラスの不均衡なデータセットのトレーニングには、特別な課題があります。詳細については、ML 集中講座の不均衡なデータセットをご覧ください。
クリッピング
次のいずれかまたは両方を行うことで、外れ値を処理する手法。
- 最大しきい値を超える特徴の値を最大しきい値まで減らします。
- 最小しきい値を下回る特徴量の値を、その最小しきい値まで引き上げます。
たとえば、特定の特徴の値の 0.5% 未満が 40 ~ 60 の範囲外にあるとします。この場合は、次の操作を行います。
- 60(最大しきい値)を超えるすべての値を 60 にクリップします。
- 40(最小しきい値)未満のすべての値を 40 にクリップします。
外れ値はモデルを損傷し、トレーニング中に重みがオーバーフローすることがあります。一部の外れ値は、精度などの指標を大幅に損なう可能性があります。クリッピングは、損傷を制限する一般的な手法です。
勾配クリッピングは、トレーニング中に指定された範囲内の勾配値を強制します。
詳細については、ML 集中講座の数値データ: 正規化をご覧ください。
混同行列
分類モデルが行った正しい予測と誤った予測の数をまとめた NxN の表。たとえば、バイナリ分類モデルの次の混同行列について考えてみましょう。
| 腫瘍(予測) | 腫瘍なし(予測) | |
|---|---|---|
| 腫瘍(グラウンド トゥルース) | 18(TP) | 1(FN) |
| 腫瘍なし(グラウンド トゥルース) | 6(FP) | 452(TN) |
上の混同行列は、次のことを示しています。
- グラウンド トゥルースが「腫瘍」である 19 個の予測のうち、モデルは 18 個を正しく分類し、1 個を誤って分類しました。
- グラウンド トゥルースが「Non-Tumor」である 458 件の予測のうち、モデルは 452 件を正しく分類し、6 件を誤って分類しました。
マルチクラス分類問題の混同行列は、間違いのパターンを特定するのに役立ちます。たとえば、3 つの異なるアヤメの種類(Virginica、Versicolor、Setosa)を分類する 3 クラスのマルチクラス分類モデルの次の混同行列について考えてみましょう。正解が Virginica の場合、混同行列は、モデルが Setosa よりも Versicolor を誤って予測する可能性がはるかに高いことを示しています。
| Setosa(予測) | Versicolor(予測) | Virginica(予測) | |
|---|---|---|---|
| Setosa(グラウンド トゥルース) | 88 | 12 | 0 |
| Versicolor(グラウンド トゥルース) | 6 | 141 | 7 |
| Virginica(グラウンド トゥルース) | 2 | 27 | 109 |
別の例として、手書きの数字を認識するようにトレーニングされたモデルが、4 ではなく 9 を誤って予測したり、7 ではなく 1 を誤って予測したりする傾向があることが、混同行列で明らかになることがあります。
混同行列には、適合率や再現率など、さまざまなパフォーマンス指標を計算するのに十分な情報が含まれています。
連続特徴
温度や重さなど、可能な値の範囲が無限の浮動小数点特徴。
離散特徴と比較してください。
収束
反復処理ごとに 損失値がほとんど変化しないか、まったく変化しない状態。たとえば、次の損失曲線は、約 700 回の反復で収束することを示しています。
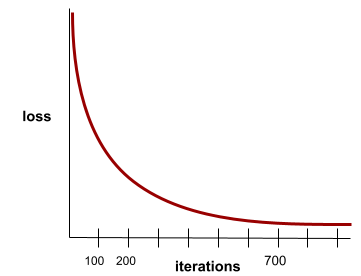
モデルが収束するのは、追加のトレーニングを行ってもモデルが改善されない場合です。
ディープ ラーニングでは、損失値が最終的に減少するまで、多くのイテレーションで一定またはほぼ一定になることがあります。損失値が一定の期間続くと、一時的に収束したように見えることがあります。
早期停止もご覧ください。
詳細については、ML 集中講座のモデルの収束と損失曲線をご覧ください。
D
DataFrame
メモリ内のデータセットを表す一般的な pandas データ型。
DataFrame は、テーブルやスプレッドシートに似ています。DataFrame の各列には名前(ヘッダー)があり、各行は一意の数値で識別されます。
DataFrame の各列は 2 次元配列のように構造化されていますが、各列に独自のデータ型を割り当てられる点が特徴です。
公式の pandas.DataFrame リファレンス ページもご覧ください。
データセット
通常は(ただし限定されない)次のいずれかの形式で整理された、未加工データのコレクションです。
- スプレッドシート
- CSV(カンマ区切り値)形式のファイル
ディープモデル
複数の隠れ層を含むニューラル ネットワーク。
ディープモデルは、ディープ ニューラル ネットワークとも呼ばれます。
ワイドモデルと比較してください。
密な特徴
ほとんどまたはすべての値がゼロ以外の特徴。通常は浮動小数点値の Tensor。たとえば、次の 10 要素の Tensor は、9 つの値がゼロ以外であるため、密です。
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
スパースな特徴と比較してください。
深さ
ニューラル ネットワーク内の次の合計:
- 隠れ層の数
- 出力レイヤの数(通常は 1)
- エンベディング レイヤの数
たとえば、隠れ層が 5 つ、出力層が 1 つのニューラル ネットワークの深さは 6 です。
入力レイヤは depth に影響しないことに注意してください。
離散特徴
取り得る値の有限集合を持つ特徴。たとえば、値が animal、vegetable、mineral のいずれかである特徴は、離散(またはカテゴリカル)特徴です。
連続特徴と対照的です。
動的
頻繁にまたは継続的に行われること。機械学習では、動的とオンラインという用語は同義語です。機械学習における dynamic と online の一般的な使用例は次のとおりです。
- 動的モデル(またはオンライン モデル)は、頻繁にまたは継続的に再トレーニングされるモデルです。
- 動的トレーニング(またはオンライン トレーニング)は、頻繁にまたは継続的にトレーニングを行うプロセスです。
- 動的推論(またはオンライン推論)は、オンデマンドで予測を生成するプロセスです。
動的モデル
頻繁に(継続的に)再トレーニングされるモデル。動的モデルは、進化するデータに常に適応する「生涯学習者」です。動的モデルは、オンライン モデルとも呼ばれます。
静的モデルも参照してください。
E
早期停止
トレーニングの損失が減少を終える前にトレーニングを終了する正則化の手法。早期停止では、検証データセットの損失が上昇し始めたとき、つまり汎化性能が低下したときに、モデルのトレーニングを意図的に停止します。
早期終了との違い。
エンベディング レイヤ
高次元のカテゴリカル特徴でトレーニングし、低次元の埋め込みベクトルを徐々に学習する特別な隠れ層。埋め込みレイヤを使用すると、高次元のカテゴリ特徴のみでトレーニングする場合よりも、ニューラル ネットワークのトレーニング効率が大幅に向上します。
たとえば、Earth は現在約 73,000 種の樹木をサポートしています。モデルの特徴が樹種であるとします。この場合、モデルの入力レイヤには 73,000 個の要素を含むワンホット ベクトルが含まれます。たとえば、baobab は次のように表されます。

73,000 個の要素を含む配列は非常に長くなります。モデルにエンベディング レイヤを追加しないと、72,999 個のゼロを乗算するため、トレーニングに非常に時間がかかります。たとえば、エンベディング レイヤを 12 個のディメンションで構成するとします。その結果、エンベディング レイヤは各樹種の新しいエンベディング ベクトルを徐々に学習します。
状況によっては、ハッシュ化がエンベディング レイヤーの妥当な代替手段となることがあります。
詳細については、ML 集中講座のエンベディングをご覧ください。
エポック
各サンプルが 1 回処理されるように、トレーニング セット全体に対するトレーニング パス全体。
エポックは N/バッチサイズ 回のトレーニング イテレーションを表します。ここで、N は例の総数です。
たとえば、次のように仮定します。
- データセットは 1,000 個の例で構成されています。
- バッチサイズは 50 個のサンプルです。
したがって、1 つのエポックには 20 回の反復が必要です。
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
詳細については、ML 集中講座の線形回帰: ハイパーパラメータをご覧ください。
例
特徴の 1 行の値と、場合によってはラベル。教師あり学習の例は、次の 2 つの一般的なカテゴリに分類されます。
- ラベル付きの例は、1 つ以上の特徴とラベルで構成されます。トレーニング中にラベル付きの例が使用されます。
- ラベルなしの例は、1 つ以上の特徴で構成されますが、ラベルはありません。ラベルなしの例は推論時に使用されます。
たとえば、天気予報が学生のテストの点数に与える影響を判断するモデルをトレーニングするとします。ラベル付きの例を 3 つ示します。
| 機能 | ラベル | ||
|---|---|---|---|
| 温度 | 湿度 | 気圧 | テストスコア |
| 15 | 47 | 998 | 良い |
| 19 | 34 | 1020 | 非常に良い |
| 18 | 92 | 1012 | 悪い |
ラベルなしの例を 3 つ示します。
| 温度 | 湿度 | 気圧 | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
通常、データセットの行は、例の未加工のソースです。つまり、通常、例はデータセット内の列のサブセットで構成されます。また、例の特徴には、特徴交差などの合成特徴を含めることもできます。
詳細については、機械学習入門コースの教師あり学習をご覧ください。
F
偽陰性(FN)
モデルが陰性クラスを誤って予測した例。たとえば、特定のメール メッセージがスパムではない(負のクラス)と予測されたが、そのメール メッセージが実際にはスパムである場合などです。
偽陽性(FP)
モデルが陽性クラスを誤って予測した例。たとえば、特定のメール メッセージがスパム(ポジティブ クラス)であるとモデルが予測したが、そのメール メッセージは実際にはスパムではない場合などです。
詳細については、ML 集中講座のしきい値と混同行列をご覧ください。
偽陽性率(FPR)
モデルが陽性クラスを誤って予測した実際の陰性例の割合。次の式は、偽陽性率を計算します。
偽陽性率は、ROC 曲線の X 軸です。
詳細については、ML 集中講座の分類: ROC と AUC をご覧ください。
機能
ML モデルへの入力変数。例は 1 つ以上の特徴で構成されます。たとえば、天気予報が学生のテストの点数に与える影響を判断するモデルをトレーニングするとします。次の表に、3 つの特徴と 1 つのラベルを含む 3 つの例を示します。
| 機能 | ラベル | ||
|---|---|---|---|
| 温度 | 湿度 | 気圧 | テストスコア |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
ラベルとのコントラスト。
詳細については、機械学習入門コースの教師あり学習をご覧ください。
特徴クロス
カテゴリ特徴量またはバケット化された特徴量を「クロス」することで形成される合成特徴量。
たとえば、温度を次の 4 つのバケットのいずれかで表す「気分予測」モデルについて考えてみましょう。
freezingchillytemperatewarm
風速を次の 3 つのバケットのいずれかで表します。
stilllightwindy
特徴量クロスがない場合、線形モデルは上記の 7 つのバケットそれぞれで個別にトレーニングされます。そのため、モデルはたとえば windy のトレーニングとは独立して freezing でトレーニングされます。
または、気温と風速の特徴クロスを作成することもできます。この合成特徴には、次の 12 個の可能な値があります。
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
特徴クロスにより、モデルは freezing-windy の日と freezing-still の日の気分を学習できます。
それぞれに多数のバケットがある 2 つの特徴から合成特徴を作成すると、結果として得られる特徴クロスには膨大な数の組み合わせが存在することになります。たとえば、ある特徴に 1,000 個のバケットがあり、別の特徴に 2,000 個のバケットがある場合、結果の特徴の交差には 2,000,000 個のバケットがあります。
形式的には、クロスはデカルト積です。
特徴の交差は主に線形モデルで使用され、ニューラル ネットワークで使用されることはほとんどありません。
詳細については、ML 集中講座のカテゴリデータ: 特徴の交差をご覧ください。
2つのステップが含まれます
次の手順を含むプロセス。
- モデルのトレーニングに役立つ可能性のある特徴を特定する。
- データセットの元データを、それらの特徴の効率的なバージョンに変換します。
たとえば、temperature が便利な機能であると判断できます。次に、バケット化を試して、モデルがさまざまな temperature 範囲から学習できる内容を最適化します。
特徴量エンジニアリングは、特徴量抽出または特徴量化と呼ばれることもあります。
詳細については、ML 集中講座の数値データ: モデルが特徴ベクトルを使用してデータを読み込む方法をご覧ください。
機能セット
機械学習モデルがトレーニングに使用する特徴のグループ。たとえば、住宅価格を予測するモデルの単純な特徴セットは、郵便番号、物件の広さ、物件の状態で構成される場合があります。
特徴ベクトル
例を構成する特徴値の配列。特徴ベクトルは、トレーニング時と推論時に入力されます。たとえば、2 つの離散特徴を持つモデルの特徴ベクトルは次のようになります。
[0.92, 0.56]
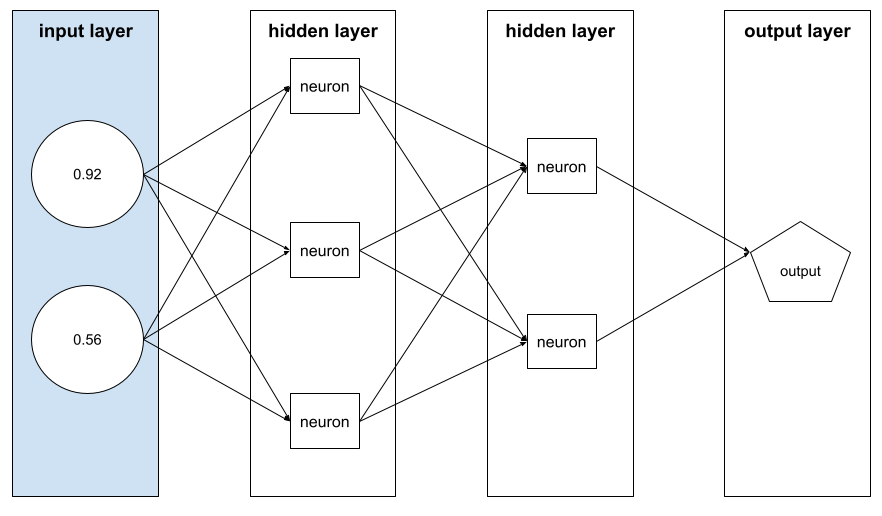
各サンプルは特徴ベクトルに異なる値を指定するため、次のサンプルの特徴ベクトルは次のようになります。
[0.73, 0.49]
特徴量エンジニアリングでは、特徴ベクトルで特徴をどのように表現するかを決定します。たとえば、5 つの可能な値を持つバイナリ カテゴリ特徴は、ワンホット エンコーディングで表すことができます。この場合、特定の例のフィーチャー ベクトルの部分は、次のように 4 つのゼロと 3 番目の位置の 1 つの 1.0 で構成されます。
[0.0, 0.0, 1.0, 0.0, 0.0]
別の例として、モデルが次の 3 つの特徴で構成されているとします。
- ワンホット エンコーディングで表される 5 つの可能な値を持つバイナリ カテゴリ特徴。例:
[0.0, 1.0, 0.0, 0.0, 0.0] - ワンホット エンコーディングで表される 3 つの可能な値を持つ別のバイナリ カテゴリ特徴。例:
[0.0, 0.0, 1.0] - 浮動小数点特徴。例:
8.3。
この場合、各サンプルの特徴ベクトルは 9 つの値で表されます。上記のリストの例の値が指定されている場合、特徴ベクトルは次のようになります。
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
詳細については、ML 集中講座の数値データ: モデルが特徴ベクトルを使用してデータを読み込む方法をご覧ください。
フィードバック ループ
ML において、モデルの予測が同じモデルまたは別のモデルのトレーニング データに影響を与える状況。たとえば、映画をおすすめするモデルは、ユーザーが視聴する映画に影響を与え、その結果、後続の映画おすすめモデルに影響を与えます。
詳細については、ML 集中講座の本番環境の ML システム: 質問をご覧ください。
G
一般化
新しい未知のデータに対して正しい予測を行えるモデルの能力。汎化性能が高いモデルは、過学習しているモデルとは正反対の状態です。
詳細については、ML 集中講座の汎化をご覧ください。
汎化曲線
トレーニング損失と検証損失の両方を反復回数の関数としてプロットします。
汎化曲線は、過適合の可能性を検出するのに役立ちます。たとえば、次の汎化曲線は、検証損失が最終的にトレーニング損失よりも大幅に高くなるため、過学習を示しています。
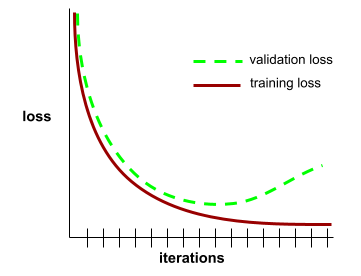
詳細については、ML 集中講座の汎化をご覧ください。
勾配降下法
損失を最小限に抑えるための数学的手法。勾配降下法では、重みとバイアスを繰り返し調整し、損失を最小限に抑える最適な組み合わせを徐々に見つけます。
勾配降下法は、機械学習よりもはるかに古いものです。
詳細については、機械学習集中講座の線形回帰: 勾配降下法をご覧ください。
グラウンド トゥルース
現実。
実際に起こったこと。
たとえば、大学 1 年生の学生が 6 年以内に卒業するかどうかを予測するバイナリ分類モデルを考えてみましょう。このモデルのグラウンド トゥルースは、その生徒が 6 年以内に実際に卒業したかどうかです。
H
隠れ層
入力層(特徴)と出力層(予測)の間にあるニューラル ネットワークの層。各隠れ層は 1 つ以上のニューロンで構成されます。たとえば、次のニューラル ネットワークには 2 つの隠れ層が含まれています。1 つ目は 3 つのニューロン、2 つ目は 2 つのニューロンです。
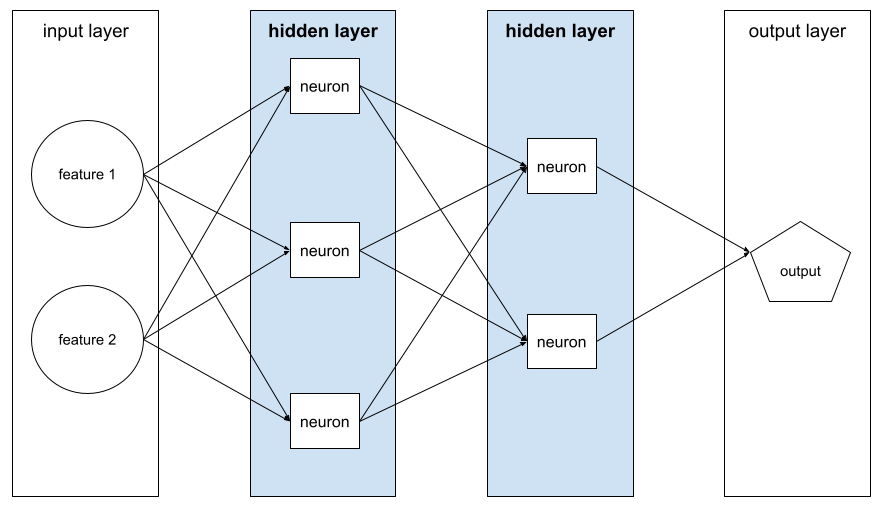
ディープ ニューラル ネットワークには複数の隠れ層が含まれています。たとえば、上の図は、モデルに 2 つの隠れ層が含まれているため、ディープ ニューラル ネットワークです。
詳細については、ML 集中講座のニューラル ネットワーク: ノードと隠れ層をご覧ください。
ハイパーパラメータ
モデルのトレーニングを連続して実行する際に、ユーザーまたはハイパーパラメータ チューニング サービス(Vizier など)が調整する変数。たとえば、学習率はハイパーパラメータです。1 回のトレーニング セッションの前に学習率を 0.01 に設定できます。0.01 が高すぎると判断した場合は、次のトレーニング セッションの学習率を 0.003 に設定します。
一方、パラメータは、モデルがトレーニング中に学習するさまざまな重みとバイアスです。
詳細については、ML 集中講座の線形回帰: ハイパーパラメータをご覧ください。
I
独立同分布(i.i.d)
変化しない分布から抽出されたデータ。抽出された各値は、以前に抽出された値に依存しません。i.i.d. は機械学習の理想気体です。有用な数学的構成ですが、現実世界で正確に見つかることはほとんどありません。たとえば、ウェブページへの訪問者の分布は、短い期間にわたって i.i.d. である可能性があります。つまり、その短い期間中は分布が変化せず、あるユーザーの訪問は一般的に別のユーザーの訪問とは独立しています。ただし、期間を拡大すると、ウェブページの訪問者の季節的な違いが表示されることがあります。
非定常性もご覧ください。
推論
従来の ML では、トレーニング済みのモデルをラベルなしの例に適用して予測を行うプロセス。詳細については、ML の概要コースの教師あり学習をご覧ください。
大規模言語モデルでは、推論は、トレーニング済みのモデルを使用して、入力プロンプトに対するレスポンスを生成するプロセスです。
推論は、統計ではやや異なる意味を持ちます。詳しくは、 統計的推論に関する Wikipedia の記事をご覧ください。
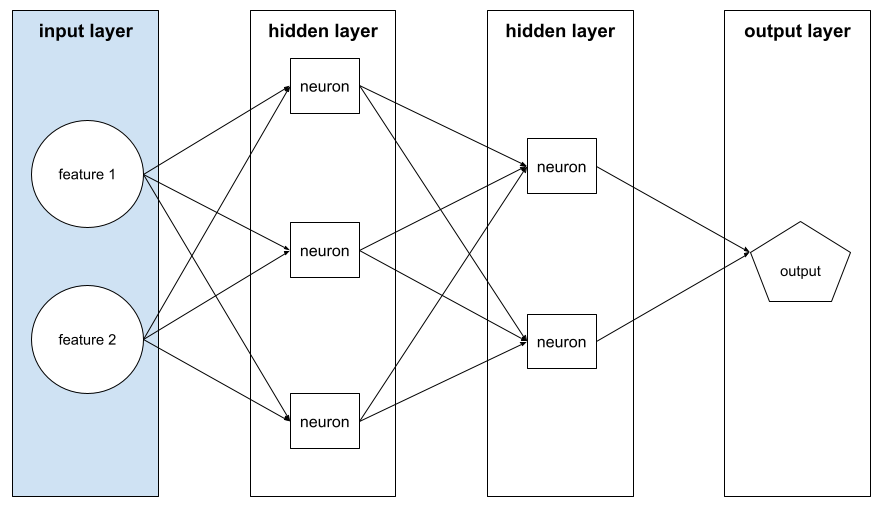
入力レイヤ
特徴ベクトルを保持するニューラル ネットワークのレイヤ。つまり、入力レイヤはトレーニングまたは推論用の例を提供します。たとえば、次のニューラル ネットワークの入力レイヤは 2 つの特徴で構成されています。
解釈可能性
ML モデルの推論を人間にわかりやすい言葉で説明または提示する能力。
たとえば、ほとんどの線形回帰モデルは解釈可能性が高いです。(各特徴量のトレーニング済み重みを確認するだけで済みます)。デシジョン フォレストは解釈可能性も高いです。ただし、一部のモデルでは、解釈可能にするために高度な可視化が必要になります。
Learning Interpretability Tool(LIT)を使用して、ML モデルを解釈できます。
繰り返し
トレーニング中に、モデルのパラメータ(モデルの重みとバイアス)を 1 回更新すること。バッチサイズは、モデルが 1 回のイテレーションで処理するサンプル数を決定します。たとえば、バッチサイズが 20 の場合、モデルはパラメータを調整する前に 20 個の例を処理します。
ニューラル ネットワークのトレーニングでは、1 回の反復で次の 2 つのパスが実行されます。
- 単一バッチの損失を評価するフォワード パス。
- 損失と学習率に基づいてモデルのパラメータを調整するバックワード パス(バックプロパゲーション)。
詳細については、機械学習集中講座の勾配降下法をご覧ください。
L
L0 正規化
モデル内のゼロ以外の重みの合計数にペナルティを課す正則化の一種。たとえば、ゼロ以外の重みが 11 個あるモデルは、ゼロ以外の重みが 10 個ある同様のモデルよりもペナルティが大きくなります。
L0 正則化は、L0 ノルム正則化と呼ばれることもあります。
L1 損失
実際のラベル値とモデルが予測する値の差の絶対値を計算する損失関数。たとえば、5 つの例のバッチの L1 損失の計算は次のようになります。
| 例の実際の値 | モデルの予測値 | デルタの絶対値 |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1 損失 | ||
L1 損失は、L2 損失よりも外れ値の影響を受けにくいです。
詳細については、ML 集中講座の線形回帰: 損失をご覧ください。
L1 正則化
正則化の一種で、重みの絶対値の合計に比例して重みにペナルティを課します。L1 正則化は、無関係な特徴やほとんど関係のない特徴の重みを正確に 0 にするのに役立ちます。重みが 0 の特徴量は、モデルから事実上削除されます。
L2 正則化と比較してください。
L2 損失
実際のラベル値とモデルが予測する値の差の二乗を計算する損失関数。たとえば、5 つの例のバッチの L2 損失の計算は次のようになります。
| 例の実際の値 | モデルの予測値 | デルタの二乗 |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 損失 | ||
2 乗するため、L2 損失は外れ値の影響を増幅します。つまり、L2 損失は、L1 損失よりも悪い予測に強く反応します。たとえば、前のバッチの L1 損失は 16 ではなく 8 になります。16 個のうち 9 個が 1 つの外れ値で占められていることに注目してください。
回帰モデルでは、通常、損失関数として L2 損失が使用されます。
平均二乗誤差は、例ごとの L2 損失の平均です。二乗損失は、L2 損失の別名です。
詳細については、ML 集中講座のロジスティック回帰: 損失と正則化をご覧ください。
L2 正則化
重みの平方の合計に比例して重みにペナルティを課す正則化の一種。L2 正則化は、外れ値の重み(正の値が大きいか負の値が小さいもの)を 0 に近づけますが、完全に 0 にはなりません。値が 0 に非常に近い特徴はモデルに残りますが、モデルの予測に大きな影響を与えません。
L2 正則化は、線形モデルの一般化を常に改善します。
L1 正則化と比較してください。
詳細については、機械学習集中講座の過学習: L2 正則化をご覧ください。
ラベル
各ラベル付きの例は、1 つ以上の特徴とラベルで構成されます。たとえば、迷惑メール検出データセットでは、ラベルは「迷惑メール」または「迷惑メールではない」のいずれかになります。降雨量データセットでは、ラベルは特定の期間に降った雨の量になることがあります。
詳細については、ML の概要の教師あり学習をご覧ください。
ラベル付きの例
1 つ以上の特徴とラベルを含む例。たとえば、次の表は、住宅評価モデルのラベル付きサンプルを 3 つ示しています。各サンプルには 3 つの特徴と 1 つのラベルがあります。
| 寝室の数 | 浴室の数 | 築年数 | 住宅価格(ラベル) |
|---|---|---|---|
| 3 | 2 | 15 | $345,000 |
| 2 | 1 | 72 | $179,000 |
| 4 | 2 | 34 | $392,000 |
教師あり ML では、モデルはラベル付きの例でトレーニングされ、ラベルなしの例で予測を行います。
ラベル付きの例とラベルなしの例を比較します。
詳細については、ML の概要の教師あり学習をご覧ください。
lambda
正則化率と同義。
Lambda はオーバーロードされた用語です。ここでは、正則化における用語の定義に焦点を当てます。
レイヤ
ニューラル ネットワーク内のニューロンのセット。一般的なレイヤには次の 3 種類があります。
たとえば、次の図は、入力層が 1 つ、隠れ層が 2 つ、出力層が 1 つのニューラル ネットワークを示しています。
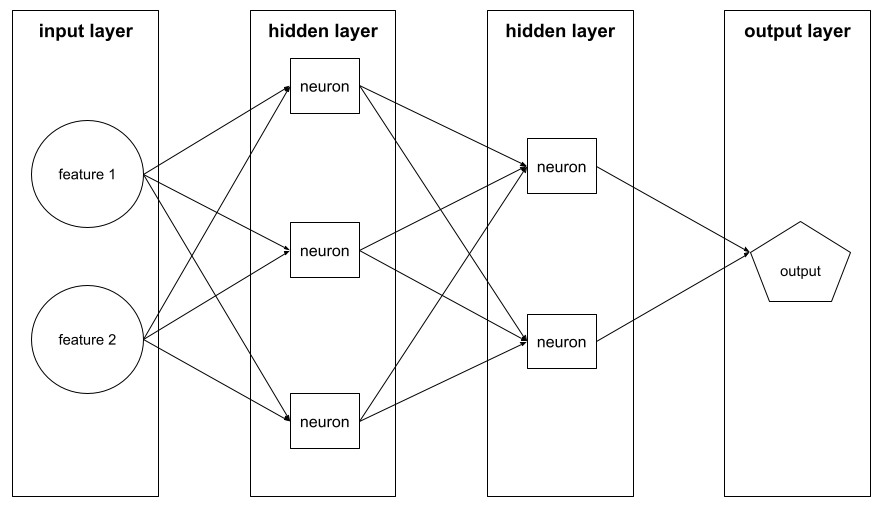
TensorFlow では、レイヤも Python 関数であり、テンソルと構成オプションを入力として受け取り、他のテンソルを出力として生成します。
学習率
各イテレーションで重みとバイアスを調整する強さを勾配降下法アルゴリズムに伝える浮動小数点数。たとえば、学習率が 0.3 の場合、学習率が 0.1 の場合よりも 3 倍強力に重みとバイアスが調整されます。
学習率は重要なハイパーパラメータです。学習率を低く設定しすぎると、トレーニングに時間がかかりすぎます。学習率が高すぎると、勾配降下法で収束に到達するのが難しくなることがよくあります。
詳細については、ML 集中講座の線形回帰: ハイパーパラメータをご覧ください。
線形
加算と乗算のみで表すことができる 2 つ以上の変数間の関係。
線形関係のプロットは直線になります。
非線形と比較してください。
線形モデル
特徴量ごとに 1 つの重みを割り当てて予測を行うモデル。(線形モデルにはバイアスも組み込まれています)。一方、ディープモデルでは、特徴と予測の関係は一般的に非線形です。
一般的に、線形モデルはディープ モデルよりもトレーニングが容易で、解釈しやすいです。ただし、ディープモデルは特徴間の複雑な関係を学習できます。
線形回帰
次の両方が当てはまる ML モデルのタイプ。
線形回帰とロジスティック回帰を比較します。また、回帰と分類を比較します。
詳細については、ML 集中講座の線形回帰をご覧ください。
ロジスティック回帰
確率を予測する回帰モデルの一種。ロジスティック回帰モデルには次の特徴があります。
- ラベルはカテゴリカルです。ロジスティック回帰という用語は通常、バイナリ ロジスティック回帰、つまり、2 つの値を取り得るラベルの確率を計算するモデルを指します。あまり一般的ではないバリアントである多項ロジスティック回帰は、2 つ以上の候補値を持つラベルの確率を計算します。
- トレーニング中の損失関数は 対数損失です。(2 つ以上の可能な値を持つラベルに対して、複数の Log Loss ユニットを並列に配置できます)。
- モデルはディープ ニューラル ネットワークではなく、線形アーキテクチャです。ただし、この定義の残りの部分は、カテゴリラベルの確率を予測するディープモデルにも適用されます。
たとえば、入力メールが迷惑メールであるかそうでないかの確率を計算するロジスティック回帰モデルについて考えてみましょう。推論時に、モデルが 0.72 を予測したとします。したがって、モデルは次のように推定します。
- メールが迷惑メールである可能性が 72% である。
- メールがスパムではない確率は 28% です。
ロジスティック回帰モデルは、次の 2 段階のアーキテクチャを使用します。
- モデルは、入力特徴の線形関数を適用して、未加工の予測(y')を生成します。
- モデルは、その未加工の予測を シグモイド関数への入力として使用します。この関数は、未加工の予測を 0 から 1 の間の値(0 と 1 は含まない)に変換します。
他の回帰モデルと同様に、ロジスティック回帰モデルは数値を予測します。ただし、通常、この数値は次のようにバイナリ分類モデルの一部になります。
- 予測された数値が分類しきい値より大きい場合、バイナリ分類モデルは陽性クラスを予測します。
- 予測された数が分類しきい値より小さい場合、バイナリ分類モデルは負のクラスを予測します。
詳細については、ML 集中講座のロジスティック回帰をご覧ください。
ログ損失
詳細については、ML 集中講座のロジスティック回帰: 損失と正則化をご覧ください。
対数オッズ
あるイベントのオッズの対数。
損失
教師ありモデルのトレーニングで、モデルの予測がラベルからどのくらい離れているかを表す指標。
損失関数は損失を計算します。
詳細については、ML 集中講座の線形回帰: 損失をご覧ください。
損失曲線
トレーニングのイテレーションの数に対する損失のプロット。次のプロットは、一般的な損失曲線を示しています。
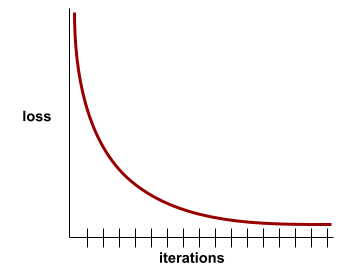
損失曲線は、モデルが収束しているか、過学習しているかを判断するのに役立ちます。
損失曲線では、次のすべての種類の損失をプロットできます。
汎化曲線もご覧ください。
詳細については、ML 集中講座の過剰適合: 損失曲線の解釈をご覧ください。
損失関数
トレーニングまたはテスト中に、例のバッチの損失を計算する数学関数。損失関数は、予測が悪いモデルよりも予測がよいモデルに対して、より低い損失を返します。
通常、トレーニングの目標は、損失関数が返す損失を最小限に抑えることです。
損失関数にはさまざまな種類があります。構築するモデルの種類に適した損失関数を選択します。次に例を示します。
M
機械学習
入力データからモデルをトレーニングするプログラムまたはシステム。トレーニングされたモデルは、モデルのトレーニングに使用された分布と同じ分布から抽出された新しい(初めて見る)データから有用な予測を行うことができます。
機械学習は、これらのプログラムやシステムに関わる研究分野を指すこともあります。
詳細については、機械学習の概要コースをご覧ください。
多数派クラス
クラス不均衡データセットでより一般的なラベル。たとえば、99% の負のラベルと 1% の正のラベルを含むデータセットの場合、負のラベルが多数派クラスになります。
少数派クラスと比較してください。
詳細については、ML 集中講座のデータセット: 不均衡なデータセットをご覧ください。
ミニバッチ
1 回のイテレーションで処理されるバッチのランダムに選択された小さなサブセット。ミニバッチのバッチサイズは、通常 10 ~ 1,000 サンプルです。
たとえば、トレーニング セット全体(フルバッチ)が 1,000 個の例で構成されているとします。さらに、各ミニバッチのバッチサイズを 20 に設定したとします。したがって、各イテレーションでは、1,000 個の例のうち 20 個をランダムに選択して損失を特定し、それに応じて重みとバイアスを調整します。
ミニバッチの損失を計算する方が、フルバッチのすべての例の損失を計算するよりもはるかに効率的です。
詳細については、ML 集中講座の線形回帰: ハイパーパラメータをご覧ください。
少数派クラス
クラス不均衡データセットで、頻度の低いラベル。たとえば、99% のネガティブ ラベルと 1% のポジティブ ラベルを含むデータセットの場合、ポジティブ ラベルは少数クラスです。
多数派クラスと比較してください。
詳細については、ML 集中講座のデータセット: 不均衡なデータセットをご覧ください。
モデル
一般に、入力データを処理して出力を返す数学的構造を指します。別の言い方をすれば、モデルとは、システムが予測を行うために必要なパラメータと構造のセットです。教師あり機械学習では、モデルは例を入力として受け取り、予測を出力として推論します。教師あり機械学習では、モデルは多少異なります。次に例を示します。
- 線形回帰モデルは、一連の重みとバイアスで構成されます。
- ニューラル ネットワーク モデルは、次の要素で構成されます。
- ディシジョン ツリー モデルは、次の要素で構成されます。
- ツリーの形状。つまり、条件とリーフが接続されるパターン。
- 条件とリーフ。
モデルの保存、復元、コピーを作成できます。
教師なし ML もモデルを生成します。通常、入力例を最も適切なクラスタにマッピングできる関数です。
マルチクラス分類
教師あり学習では、データセットに 2 つ以上のラベルのクラスが含まれている分類問題。たとえば、Iris データセットのラベルは、次の 3 つのクラスのいずれかである必要があります。
- Iris setosa
- Iris virginica
- Iris versicolor
新しい例でアヤメの種類を予測するアヤメ データセットでトレーニングされたモデルは、マルチクラス分類を実行しています。
これに対し、2 つのクラスを区別する分類問題は、バイナリ分類モデルです。たとえば、スパムまたはスパムではないのいずれかを予測するメールモデルは、バイナリ分類モデルです。
クラスタリング問題では、マルチクラス分類は 3 つ以上のクラスタを指します。
詳細については、ML 集中講座のニューラル ネットワーク: 多クラス分類をご覧ください。
N
陰性クラス
バイナリ分類では、一方のクラスを「陽性」、もう一方のクラスを「陰性」と呼びます。陽性クラスはモデルがテストしているものまたはイベントであり、陰性クラスはそれ以外の可能性です。次に例を示します。
- 医学検査の陰性クラスは「腫瘍なし」などになります。
- メールの分類モデルの負のクラスは「迷惑メールではない」です。
ポジティブ クラスと対照的です。
ニューラル ネットワークの
隠れ層を 1 つ以上含むモデル。ディープ ニューラル ネットワークは、複数の隠れ層を含むニューラル ネットワークの一種です。たとえば、次の図は 2 つの隠れ層を含むディープ ニューラル ネットワークを示しています。
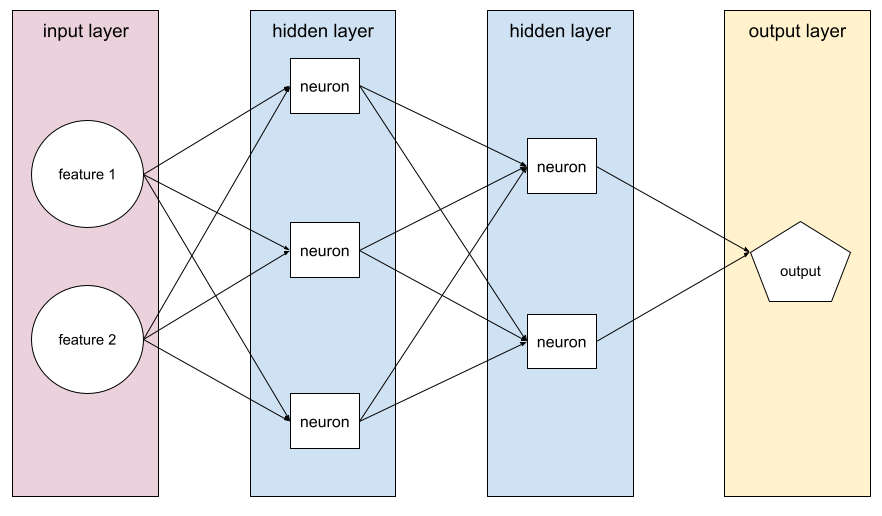
ニューラル ネットワークの各ニューロンは、次のレイヤのすべてのノードに接続します。たとえば、上の図では、最初の隠れ層にある 3 つのニューロンが、2 番目の隠れ層にある 2 つのニューロンにそれぞれ個別に接続されています。
コンピュータに実装されたニューラル ネットワークは、脳や他の神経系にあるニューラル ネットワークと区別するために、人工ニューラル ネットワークと呼ばれることがあります。
一部のニューラル ネットワークは、さまざまな特徴とラベルの間の非常に複雑な非線形関係を模倣できます。
畳み込みニューラル ネットワークと再帰型ニューラル ネットワークもご覧ください。
詳細については、ML 集中講座のニューラル ネットワークをご覧ください。
ニューロン
機械学習では、ニューラル ネットワークの隠れ層内の個別のユニット。各ニューロンは、次の 2 段階のアクションを実行します。
最初の隠れ層のニューロンは、入力層の特徴値から入力を受け取ります。最初の隠れ層より後の隠れ層のニューロンは、前の隠れ層のニューロンから入力を受け取ります。たとえば、2 番目の隠れ層のニューロンは、最初の隠れ層のニューロンから入力を受け取ります。
次の図は、2 つのニューロンとその入力を示しています。
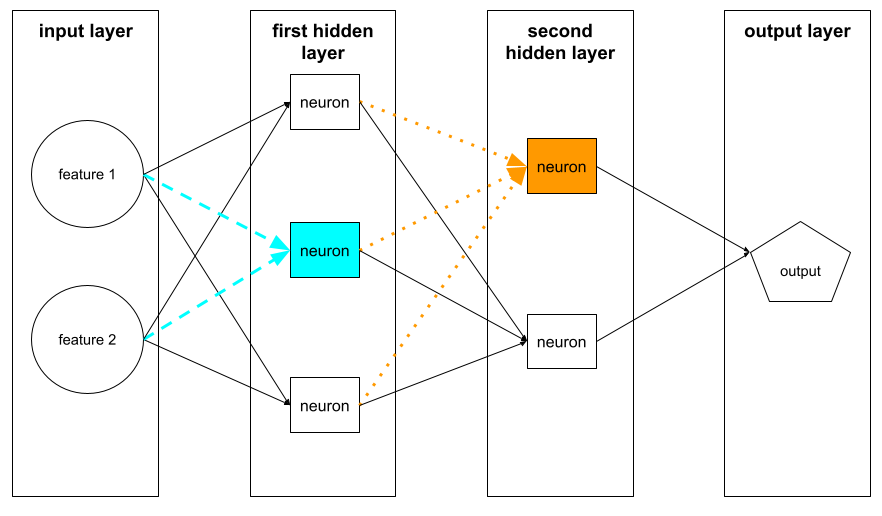
ニューラル ネットワークのニューロンは、脳や神経系の他の部分のニューロンの動作を模倣します。
ノード(ニューラル ネットワーク)
詳細については、ML 集中講座のニューラル ネットワークをご覧ください。
非線形
加算と乗算のみでは表現できない、2 つ以上の変数間の関係。線形関係は線として表すことができますが、非線形関係は線として表すことができません。たとえば、それぞれが 1 つの特徴を 1 つのラベルに関連付ける 2 つのモデルについて考えてみましょう。左のモデルは線形、右のモデルは非線形です。

さまざまな種類の非線形関数を試すには、ML 集中講座のニューラル ネットワーク: ノードと隠れ層をご覧ください。
非定常性
1 つ以上のディメンション(通常は時間)にわたって値が変化する特徴。たとえば、次のような非定常性の例を考えてみましょう。
- 特定の店舗で販売される水着の数は季節によって異なります。
- 特定の地域で収穫される特定の果物の量は、1 年のほとんどがゼロですが、短い期間だけ大量になります。
- 気候変動により、年間の平均気温が変化しています。
定常性との違い。
正規化
大まかに言うと、変数の実際の値の範囲を標準の値の範囲に変換するプロセスです。たとえば、次のような場合です。
- -1 ~+1
- 0 to 1
- Z スコア(おおよそ -3 ~+3)
たとえば、特定の特徴の値の実際の範囲が 800 ~ 2,400 であるとします。特徴エンジニアリングの一環として、実際の値を -1 ~+1 などの標準範囲に正規化できます。
正規化は、特徴エンジニアリングの一般的なタスクです。通常、特徴ベクトル内のすべての数値特徴の範囲がほぼ同じである場合、モデルのトレーニングは高速になり(予測の精度も向上します)。
Z スコアの正規化もご覧ください。
詳細については、ML 集中講座の数値データ: 正規化をご覧ください。
数値データ
整数または実数値で表される特徴。たとえば、住宅評価モデルでは、住宅の広さ(平方フィートまたは平方メートル)が数値データとして表される可能性があります。特徴を数値データとして表すことは、特徴の値がラベルと数学的な関係にあることを示します。つまり、家の広さ(平方メートル)と家の価値の間には、数学的な関係があると考えられます。
すべての整数データを数値データとして表す必要はありません。たとえば、世界のいくつかの地域では郵便番号は整数ですが、整数の郵便番号はモデルで数値データとして表すべきではありません。これは、郵便番号 20000 の効果が郵便番号 10000 の 2 倍(または半分)ではないためです。また、郵便番号が異なれば不動産価格も異なることは確かですが、郵便番号 20000 の不動産価格が郵便番号 10000 の不動産価格の 2 倍になるとは限りません。郵便番号は、カテゴリデータとして表す必要があります。
詳細については、ML 集中講座の数値データの操作をご覧ください。
O
オフライン
static と同義。
オフライン推論
モデルが 予測のバッチを生成し、その予測をキャッシュに保存するプロセス。これにより、アプリはモデルを再実行するのではなく、キャッシュから推論された予測にアクセスできます。
たとえば、4 時間ごとに地域の天気予報(予測)を生成するモデルについて考えてみましょう。モデルを実行するたびに、システムはすべての地域の天気予報をキャッシュに保存します。天気アプリはキャッシュから予報を取得します。
オフライン推論は静的推論とも呼ばれます。
オンライン推論と比較してください。詳細については、ML 集中講座の本番環境の ML システム: 静的推論と動的推論をご覧ください。
ワンホット エンコード
カテゴリデータをベクトルとして表します。
- 1 つの要素が 1 に設定されています。
- 他のすべての要素は 0 に設定されます。
ワンホット エンコードは、利用できる値が有限である文字列や識別子を表すためによく使用されます。たとえば、Scandinavia という名前のカテゴリ特徴に 5 つの可能な値があるとします。
- "デンマーク"
- "Sweden"
- "Norway"
- "フィンランド"
- 「アイスランド」
ワンホット エンコードでは、5 つの値を次のように表すことができます。
| 国 | ベクトル | ||||
|---|---|---|---|---|---|
| "デンマーク" | 1 | 0 | 0 | 0 | 0 |
| "Sweden" | 0 | 1 | 0 | 0 | 0 |
| "Norway" | 0 | 0 | 1 | 0 | 0 |
| "フィンランド" | 0 | 0 | 0 | 1 | 0 |
| 「アイスランド」 | 0 | 0 | 0 | 0 | 1 |
ワンホット エンコードにより、モデルは 5 つの国それぞれに基づいて異なる接続を学習できます。
特徴を数値データとして表現することは、ワンホット エンコードの代替手段です。残念ながら、スカンジナビア諸国を数値で表すのは適切ではありません。たとえば、次の数値表現について考えてみましょう。
- 「デンマーク」は 0
- 「スウェーデン」は 1
- 「Norway」は 2
- 「フィンランド」は 3
- 「アイスランド」は 4
数値エンコードを使用すると、モデルは生数値を数学的に解釈し、それらの数値でトレーニングしようとします。しかし、アイスランドは実際にはノルウェーの 2 倍(または半分)ではないため、モデルは奇妙な結論に達します。
詳細については、ML 集中講座のカテゴリデータ: 語彙とワンホット エンコードをご覧ください。
1 対すべて
N 個のクラスがある分類問題の場合、N 個の個別のバイナリ分類モデルで構成されるソリューション(考えられる結果ごとに 1 つのバイナリ分類モデル)。たとえば、例を動物、野菜、鉱物に分類するモデルの場合、一対多のソリューションは次の 3 つの個別のバイナリ分類モデルを提供します。
- 動物か動物でないか
- 野菜か野菜以外か
- ミネラルかミネラル以外か
オンライン
dynamic と同義。
オンライン推論
オンデマンドで予測を生成する。たとえば、アプリがモデルに入力を渡し、予測のリクエストを発行するとします。オンライン推論を使用するシステムは、モデルを実行してリクエストに応答します(予測をアプリに返します)。
オフライン推論と比較してください。
詳細については、ML 集中講座の本番環境の ML システム: 静的推論と動的推論をご覧ください。
出力レイヤ
ニューラル ネットワークの「最終」レイヤ。出力レイヤには予測が含まれます。
次の図は、入力レイヤ、2 つの隠れレイヤ、出力レイヤを含む小さなディープ ニューラル ネットワークを示しています。
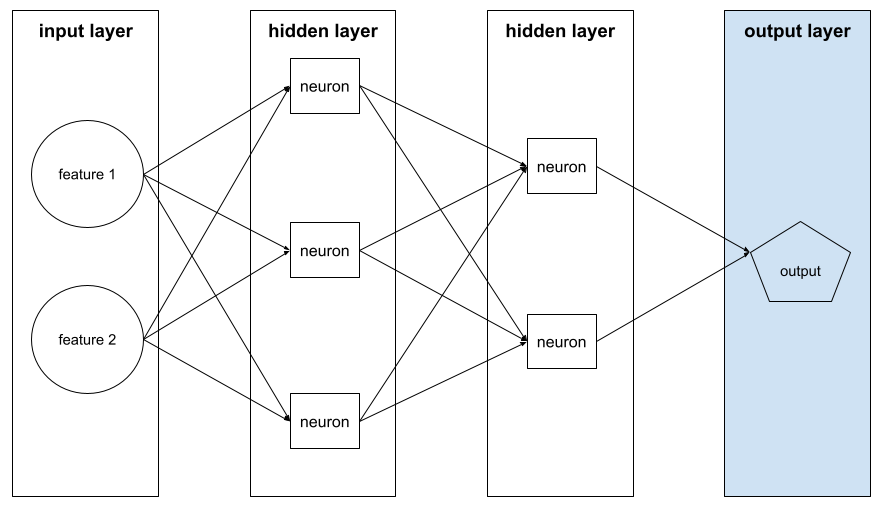
過学習
トレーニング データにあまりにも一致しすぎて、新しいデータに対して正しい予測を行えないモデルを作成する。
正則化により、過剰適合を減らすことができます。大規模で多様なトレーニング セットでトレーニングを行うと、過学習を減らすこともできます。
詳細については、機械学習集中講座の過剰適合をご覧ください。
P
pandas
numpy 上に構築された列指向のデータ分析 API。TensorFlow を含む多くの ML フレームワークは、入力として pandas データ構造をサポートしています。詳しくは、pandas のドキュメントをご覧ください。
パラメータ
モデルがトレーニング中に学習する重みとバイアス。たとえば、線形回帰モデルでは、パラメータは次の式でバイアス(b)とすべての重み(w1、w2 など)で構成されます。
一方、ハイパーパラメータは、ユーザー(またはハイパーパラメータ チューニング サービス)がモデルに提供する値です。たとえば、学習率はハイパーパラメータです。
陽性クラス
テスト対象のクラス。
たとえば、がんモデルのポジティブ クラスは「腫瘍」になります。メールの分類モデルのポジティブ クラスは「迷惑メール」になる可能性があります。
陰性クラスと比較してください。
後処理
モデルの実行後にモデルの出力を調整する。後処理を使用すると、モデル自体を変更せずに公平性制約を適用できます。
たとえば、バイナリ分類モデルに後処理を適用して、分類しきい値を設定し、真陽性率がその属性のすべての値で同じであることを確認することで、一部の属性の機会の平等を維持できます。
precision
「全陽性のラベルの中でモデルが正しく識別したラベルの数は?」という質問に回答する分類モデルの指標。
モデルが陽性クラスを予測したとき、予測が正しかった割合はどのくらいですか?
式は次のとおりです。
ここで
- 真陽性とは、モデルが陽性のクラスを正しく予測したことを意味します。
- 偽陽性とは、モデルが陽性クラスを誤って予測したことを意味します。
たとえば、モデルが 200 件のポジティブ予測を行ったとします。この 200 件の正の予測のうち:
- 150 件が真陽性でした。
- 50 件は誤検知でした。
この例の場合は、次のようになります。
詳細については、ML 集中講座の分類: 正確度、再現率、適合率、関連指標をご覧ください。
予測
モデルの出力。次に例を示します。
- バイナリ分類モデルの予測は、陽性クラスまたは陰性クラスのいずれかです。
- マルチクラス分類モデルの予測は 1 つのクラスです。
- 線形回帰モデルの予測は数値です。
プロキシラベル
データセットで直接利用できないラベルを近似するために使用されるデータ。
たとえば、従業員のストレス レベルを予測するモデルをトレーニングする必要があるとします。データセットには予測特徴が多数含まれていますが、ストレス レベルというラベルは含まれていません。そこで、ストレス レベルのプロキシラベルとして「職場での事故」を選択します。ストレスの高い従業員は、ストレスの低い従業員よりも事故を起こす可能性が高くなります。それとも、そうなのでしょうか?労働災害は、実際にはさまざまな理由で増減しているのかもしれません。
2 つ目の例として、データセットのブール値ラベルとして「雨が降っているか?」を使用したいが、データセットに雨のデータが含まれていないとします。写真が利用可能な場合は、傘をさしている人の写真を「雨が降っているか?」のプロキシラベルとして設定できます。これは適切なプロキシラベルですか?そうかもしれませんが、文化によっては、雨ではなく日差しから身を守るために傘をさす人が多いかもしれません。
プロキシ ラベルは完全ではないことがよくあります。可能な場合は、プロキシ ラベルではなく実際のラベルを選択します。ただし、実際のラベルがない場合は、最も悪い候補ではないプロキシラベルを慎重に選択してください。
詳細については、ML 集中講座のデータセット: ラベルをご覧ください。
R
RAG
検索拡張生成の略語。
rater
例にラベルを付ける人。「アノテーター」は、評価者の別の名前です。
詳細については、ML 集中講座のカテゴリデータ: 一般的な問題をご覧ください。
recall
「全陽性のラベルの中でモデルが正しく識別したラベルの数は?」という質問に回答する分類モデルの指標。
グラウンド トゥルースが陽性クラスだった場合、モデルが陽性クラスとして正しく識別した予測の割合はどのくらいですか?
式は次のとおりです。
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
ここで
- 真陽性とは、モデルが陽性のクラスを正しく予測したことを意味します。
- 偽陰性とは、モデルが陰性クラスを誤って予測したことを意味します。
たとえば、モデルがグラウンド トゥルースが陽性クラスである例について 200 件の予測を行ったとします。これらの 200 個の予測のうち:
- 180 件が真陽性でした。
- 20 件は偽陰性でした。
この例の場合は、次のようになります。
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
詳細については、分類: 精度、再現率、適合率、関連指標をご覧ください。
正規化線形ユニット(ReLU)
次の動作を行うアクティベーション関数:
- 入力が負の値またはゼロの場合、出力は 0 になります。
- 入力が正の場合、出力は入力と同じになります。
次に例を示します。
- 入力が -3 の場合、出力は 0 になります。
- 入力が +3 の場合、出力は 3.0 になります。
ReLU のプロットを次に示します。
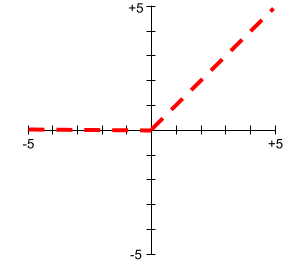
ReLU は非常に一般的な活性化関数です。ReLU は単純な動作ですが、ニューラル ネットワークが特徴量とラベルの間の非線形の関係を学習できるようにします。
回帰モデル
数値予測を生成するモデル。(これに対し、分類モデルはクラス予測を生成します)。たとえば、次のすべてが回帰モデルです。
- 特定の住宅の価値をユーロで予測するモデル(423,000 など)。
- 特定の樹木の寿命を年単位で予測するモデル(23.2 など)。
- 特定の都市で今後 6 時間に降る雨の量をインチ単位で予測するモデル(0.18 など)。
一般的な回帰モデルには次の 2 つがあります。
数値予測を出力するモデルがすべて回帰モデルであるとは限りません。場合によっては、数値予測は数値クラス名を持つ分類モデルにすぎません。たとえば、数値の郵便番号を予測するモデルは、回帰モデルではなく分類モデルです。
正則化
過適合を軽減するメカニズム。正則化の一般的なタイプは次のとおりです。
- L1 正則化
- L2 正則化
- ドロップアウト正則化
- 早期停止(正式な正則化手法ではありませんが、過適合を効果的に制限できます)
正則化は、モデルの複雑さに対するペナルティとして定義することもできます。
詳細については、ML 集中講座の過剰適合: モデルの複雑さをご覧ください。
正則化率
トレーニング中の正則化の相対的な重要度を指定する数値。正則化率を上げると、過剰適合が軽減されますが、モデルの予測能力が低下する可能性があります。逆に、正則化率を減らすか省略すると、過適合が増加します。
詳細については、機械学習集中講座の過学習: L2 正則化をご覧ください。
ReLU
正規化線形ユニットの略。
検索拡張生成(RAG)
モデルのトレーニング後に取得されたナレッジソースを使用してグラウンディングすることで、大規模言語モデル(LLM)の出力の品質を向上させる手法。RAG は、信頼できるナレッジベースやドキュメントから取得した情報へのアクセスをトレーニング済みの LLM に提供することで、LLM の回答の精度を向上させます。
検索拡張生成を使用する一般的な動機は次のとおりです。
- モデルの生成された回答の事実の正確性を高める。
- モデルにトレーニングされていない知識へのアクセス権を付与する。
- モデルが使用する知識を変更する。
- モデルがソースを引用できるようにする。
たとえば、化学アプリが PaLM API を使用して、ユーザーのクエリに関連する要約を生成するとします。アプリのバックエンドがクエリを受信すると、バックエンドは次の処理を行います。
- ユーザーのクエリに関連するデータを検索(取得)します。
- 関連する化学データをユーザーのクエリに追加(「拡張」)します。
- 追加されたデータに基づいて要約を作成するように LLM に指示します。
ROC(受信者操作特性)曲線
バイナリ分類におけるさまざまな分類しきい値に対する真陽性率と偽陽性率のグラフ。
ROC 曲線の形状は、陽性クラスと陰性クラスを分離するバイナリ分類モデルの能力を示します。たとえば、バイナリ分類モデルがすべての陰性クラスとすべての陽性クラスを完全に分離するとします。
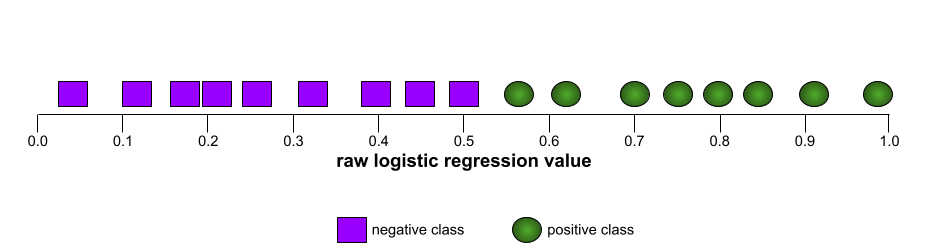
上記のモデルの ROC 曲線は次のようになります。
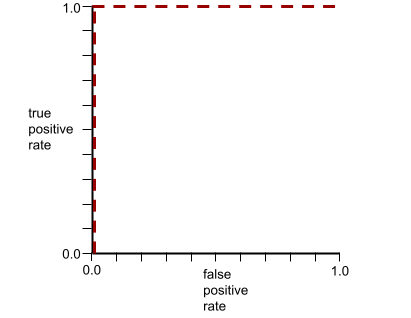
一方、次の図は、負のクラスと正のクラスをまったく分離できないひどいモデルのロジスティック回帰の生値をグラフ化したものです。
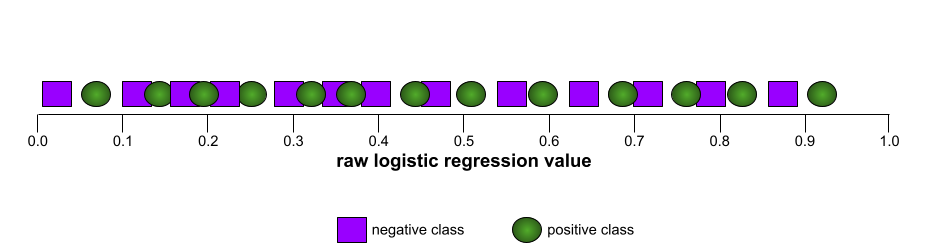
このモデルの ROC 曲線は次のようになります。
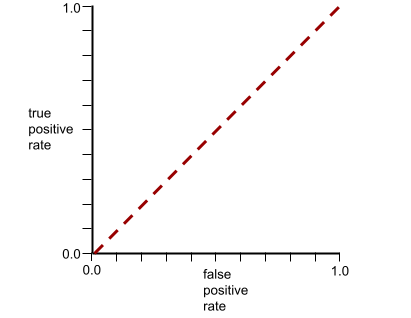
一方、現実の世界では、ほとんどのバイナリ分類モデルは陽性クラスと陰性クラスをある程度分離しますが、完全に分離することは通常ありません。したがって、一般的な ROC 曲線は、次の 2 つの極端なケースの中間に位置します。
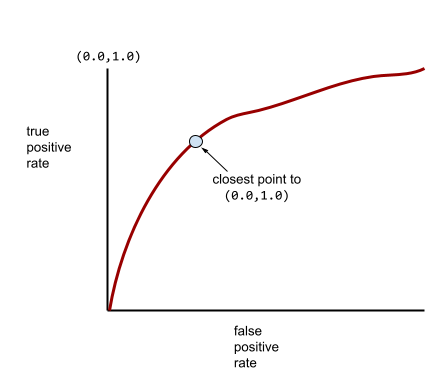
ROC 曲線上の点のうち、(0.0,1.0) に最も近い点が、理論上は理想的な分類しきい値を特定します。ただし、理想的な分類しきい値の選択には、他のいくつかの現実世界の問題が影響します。たとえば、偽陰性の方が偽陽性よりもはるかに大きな問題を引き起こす可能性があります。
AUC という数値指標は、ROC 曲線を単一の浮動小数点値に要約します。
二乗平均平方根誤差(RMSE)
平均二乗誤差の平方根。
S
シグモイド関数
入力値を制約された範囲(通常は 0 ~ 1 または -1 ~+1)に「圧縮」する数学関数。つまり、シグモイドには任意の数(2、100 万、マイナス 10 億など)を渡すことができ、出力は制約された範囲内に収まります。シグモイド活性化関数のプロットは次のようになります。

シグモイド関数は、機械学習で次のような用途に使用されます。
Softmax
マルチクラス分類モデルで、考えられる各クラスの確率を決定する関数。確率の合計は 1.0 になります。たとえば、次の表は、ソフトマックスがさまざまな確率をどのように分布させるかを示しています。
| 画像は... | 確率 |
|---|---|
| 犬 | .85 |
| 猫 | .13 |
| 馬 | .02 |
ソフトマックスは、フル ソフトマックスとも呼ばれます。
候補サンプリングと比較してください。
詳細については、ML 集中講座のニューラル ネットワーク: 多クラス分類をご覧ください。
スパース特徴
値の大部分がゼロまたは空の特徴。たとえば、1 つの 1 の値と 100 万個の 0 の値を含む特徴はスパースです。一方、密な特徴は、ゼロまたは空ではない値が大部分を占めています。
ML では、驚くほど多くの特徴量がスパース特徴量です。カテゴリ特徴は通常、スパース特徴です。たとえば、森に 300 種類の樹木が生息している場合、1 つの例で カエデの木だけを特定する場合があります。また、動画ライブラリ内の数百万もの動画の中から、1 つの例として「カサブランカ」だけが識別されることもあります。
通常、モデルではスパース特徴をワンホット エンコーディングで表します。ワンホット エンコードが大きい場合は、効率を高めるために、ワンホット エンコードの上にエンベディング レイヤーを配置することがあります。
スパース表現
スパース特徴でゼロ以外の要素の位置のみを保存します。
たとえば、species という名前のカテゴリ特徴が、特定の森林に生息する 36 種類の樹木を識別するとします。また、各例は 1 つの種のみを識別するとします。
ワンホット ベクトルを使用して、各例の樹種を表すことができます。ワンホット ベクトルには、1 つの 1(その例の特定の樹種を表す)と 35 個の 0(その例にない 35 個の樹種を表す)が含まれます。したがって、maple のワンホット表現は次のようになります。

一方、スパース表現では、特定の種の場所を特定するだけです。maple が位置 24 にある場合、maple のスパース表現は次のようになります。
24
スパース表現は、ワンホット表現よりもはるかにコンパクトです。
詳細については、ML 集中講座のカテゴリデータの操作をご覧ください。
スパース ベクトル
値のほとんどがゼロのベクトル。スパース特徴とスパース性もご覧ください。
二乗損失
L2 損失と同義。
static
継続的ではなく、一度だけ実行されるもの。静的とオフラインという用語は同義語です。以下に、マシンラーニングにおける static と offline の一般的な使用例を示します。
- 静的モデル(またはオフライン モデル)は、一度トレーニングされてからしばらく使用されるモデルです。
- 静的トレーニング(またはオフライン トレーニング)は、静的モデルをトレーニングするプロセスです。
- 静的推論(またはオフライン推論)は、モデルが一度にバッチ予測を生成するプロセスです。
動的とのコントラスト。
静的推論
オフライン推論と同義。
定常性
1 つ以上のディメンション(通常は時間)で値が変化しない特徴。たとえば、2021 年と 2023 年で値がほぼ同じ特徴は定常性を示します。
現実の世界では、定常性を示す特徴はほとんどありません。安定性の代名詞とも言える海面水位でさえ、時間とともに変化します。
非定常性と比較してください。
確率的勾配降下法(SGD)
バッチサイズが 1 の勾配降下法アルゴリズム。つまり、SGD はトレーニング セットから一様にランダムに選択された単一の例でトレーニングします。
詳細については、ML 集中講座の線形回帰: ハイパーパラメータをご覧ください。
教師あり機械学習
特徴とその対応するラベルからモデルをトレーニングします。教師あり ML は、一連の質問とその対応する回答を学習して科目を学習することに似ています。質問と回答のマッピングを習得すると、生徒は同じトピックに関する新しい(これまで見たことのない)質問に回答できるようになります。
教師なし機械学習と比較します。
詳細については、ML の概要コースの教師あり学習をご覧ください。
合成特徴
入力特徴には存在しないが、入力特徴の 1 つ以上から組み立てられた特徴。合成特徴を作成する方法は次のとおりです。
- 連続する特徴を範囲ビンにバケット化します。
- 特徴クロスを作成する。
- 1 つの特徴量の値を他の特徴量の値またはそれ自体で乗算(または除算)します。たとえば、
aとbが入力特徴の場合、合成特徴の例は次のようになります。- ab
- a2
- 特徴値に超越関数を適用する。たとえば、
cが入力特徴の場合、合成特徴の例は次のようになります。- sin(c)
- ln(c)
正規化またはスケーリングのみで作成された特徴量は、合成特徴量とは見なされません。
T
テスト損失
テストセットに対するモデルの損失を表す指標。モデルを構築する場合、通常はテスト損失を最小限に抑えようとします。これは、テスト損失が小さいほど、トレーニング損失や検証損失が小さい場合よりも品質シグナルが強くなるためです。
テスト損失とトレーニング損失または検証損失の間に大きな差がある場合は、正則化率を上げる必要があることを示している場合があります。
トレーニング
モデルを構成する最適なパラメータ(重みとバイアス)を決定するプロセス。トレーニング中、システムは例を読み込み、パラメータを徐々に調整します。トレーニングでは、各例が数回から数十億回使用されます。
詳細については、ML の概要コースの教師あり学習をご覧ください。
トレーニングの損失
特定のトレーニング反復処理中のモデルの損失を表す指標。たとえば、損失関数が平均二乗誤差であるとします。たとえば、10 回目の反復のトレーニング損失(平均二乗誤差)が 2.2 で、100 回目の反復のトレーニング損失が 1.9 であるとします。
損失曲線は、トレーニングの損失と反復回数をプロットしたものです。損失曲線は、トレーニングについて次のヒントを提供します。
- 右下がりの傾斜は、モデルが改善されていることを意味します。
- 上向きの傾斜は、モデルが悪化していることを意味します。
- 傾斜が平らな場合は、モデルが収束に達したことを意味します。
たとえば、次のやや理想化された損失曲線は、次のようになります。
- 初期の反復で急激な下降勾配が見られる。これは、モデルが急速に改善していることを意味します。
- トレーニングの終了近くまで徐々に平坦になる(ただし、まだ下降している)傾斜。これは、最初の反復処理よりもやや遅いペースでモデルの改善が継続していることを意味します。
- トレーニングの終わりに近づくにつれて傾斜が平らになり、収束を示しています。
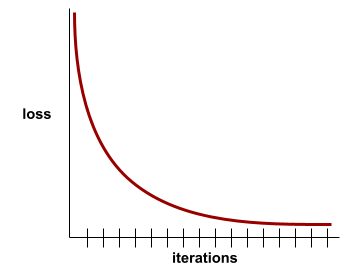
トレーニング損失は重要ですが、汎化もご覧ください。
トレーニング サービング スキュー
トレーニング時のモデルのパフォーマンスと、同じモデルのサービング時のパフォーマンスの差。
トレーニング セット
従来、データセット内の例は次の 3 つの異なるサブセットに分割されます。
理想的には、データセット内の各例は上記のサブセットのいずれか 1 つにのみ属している必要があります。たとえば、1 つの例がトレーニング セットと検証セットの両方に属することはできません。
詳細については、ML 集中講座のデータセット: 元のデータセットを分割するをご覧ください。
真陰性(TN)
モデルが陰性クラスを正しく予測した例。たとえば、特定のメール メッセージが迷惑メールではないとモデルが推論し、そのメール メッセージが実際に迷惑メールではない場合です。
真陽性(TP)
モデルが陽性クラスを正しく予測した例。たとえば、特定のメール メッセージがスパムであるとモデルが推論し、そのメール メッセージが実際にスパムである場合です。
真陽性率(TPR)
再現率と同義。具体的には、次のことが求められます。
真陽性率は、ROC 曲線の Y 軸です。
U
アンダーフィット
モデルがトレーニング データの複雑さを十分に把握していないため、予測能力の低いモデルが生成される。過小適合を引き起こす問題は多数あります。たとえば、次のようなものがあります。
詳細については、機械学習集中講座の過剰適合をご覧ください。
ラベルのない例
特徴は含まれているが、ラベルは含まれていない例。たとえば、次の表は、住宅評価モデルのラベルなしの 3 つの例を示しています。各例には 3 つの特徴がありますが、住宅の価値はありません。
| 寝室の数 | 浴室の数 | 築年数 |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
教師あり ML では、モデルはラベル付きの例でトレーニングされ、ラベルなしの例で予測を行います。
半教師あり学習と教師なし学習では、トレーニング中にラベルなしの例が使用されます。
ラベルなしの例とラベル付きの例を比較します。
教師なし機械学習
データセット(通常はラベルなしデータセット)内のパターンを見つけるようにモデルをトレーニングします。
教師なし ML の最も一般的な用途は、類似した例のグループにデータをクラスタリングすることです。たとえば、教師なし ML アルゴリズムは、音楽のさまざまなプロパティに基づいて曲をクラスタリングできます。クラスタリングの結果は、他の ML アルゴリズム(音楽レコメンデーション サービスなど)の入力として使用できます。クラスタリングは、有用なラベルが少ない場合や存在しない場合に役立ちます。たとえば、不正使用や不正行為などのドメインでは、クラスタリングによって人間がデータをより深く理解できます。
教師あり機械学習と比較してください。
詳細については、ML 入門コースの機械学習とはをご覧ください。
V
検証
モデルの品質の初期評価。検証では、検証セットと比較してモデルの予測の品質を検査します。
検証セットはトレーニング セットとは異なるため、検証は過学習を防ぐのに役立ちます。
検証セットに対するモデルの評価を最初のテストラウンド、テストセットに対するモデルの評価を 2 回目のテストラウンドと考えることができます。
検証損失
トレーニングの特定の反復中に、検証セットでのモデルの損失を表す指標。
汎化曲線もご覧ください。
検証セット
トレーニング済みのモデルに対して初期評価を行うデータセットのサブセット。通常、トレーニング済みモデルは、テストセットに対して評価する前に、検証セットに対して数回評価します。
通常、データセット内の例は次の 3 つの異なるサブセットに分割します。
- トレーニング セット
- 検証セット
- テストセット
理想的には、データセット内の各例は上記のサブセットのいずれか 1 つにのみ属している必要があります。たとえば、1 つの例がトレーニング セットと検証セットの両方に属することはできません。
詳細については、ML 集中講座のデータセット: 元のデータセットを分割するをご覧ください。
W
weight
モデルが別の値に乗算する値。トレーニングは、モデルの理想的な重みを決定するプロセスです。推論は、学習した重みを使用して予測を行うプロセスです。
詳細については、ML 集中講座の線形回帰をご覧ください。
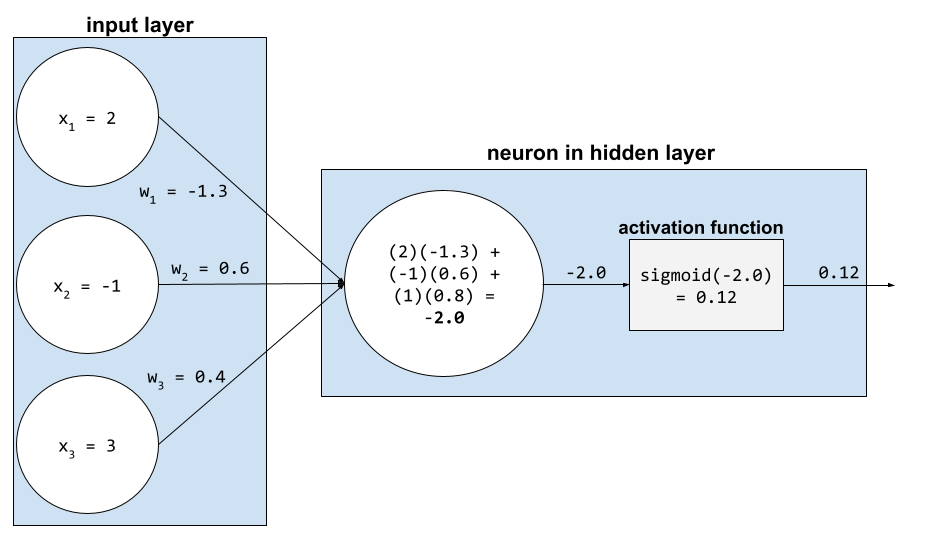
加重合計
関連するすべての入力値に、対応する重みを掛けて合計した値。たとえば、関連する入力が次の要素で構成されているとします。
| 入力値 | 入力の重み |
| 2 | -1.3 |
| -1 | 0.6 |
| 3 | 0.4 |
したがって、加重和は次のようになります。
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
加重合計は、活性化関数の入力引数です。
Z
Z スコアの正規化
生の特徴値を、その特徴の平均からの標準偏差の数を表す浮動小数点値に置き換えるスケーリング手法。たとえば、平均が 800 で標準偏差が 100 の特徴について考えてみましょう。次の表に、Z スコア正規化によって生の値が Z スコアにどのようにマッピングされるかを示します。
| Raw 値 | Z スコア |
|---|---|
| 800 | 0 |
| 950 | +1.5 |
| 575 | -2.25 |
その後、機械学習モデルは、生の値ではなく、その特徴の Z スコアに基づいてトレーニングを行います。
詳細については、ML 集中講座の数値データ: 正規化をご覧ください。