이 페이지에는 ML 기본사항 용어가 포함되어 있습니다. 모든 용어집 용어는 여기를 클릭하세요.
A
정확성
올바른 분류 예측 수를 총 예측 수로 나눈 값입니다. 이는 다음과 같은 의미입니다.
예를 들어 올바른 예측을 40번 하고 잘못된 예측을 10번 한 모델의 정확도는 다음과 같습니다.
이진 분류는 올바른 예측과 잘못된 예측의 다양한 카테고리에 대한 구체적인 이름을 제공합니다. 따라서 이진 분류의 정확도 공식은 다음과 같습니다.
각 항목의 의미는 다음과 같습니다.
자세한 내용은 머신러닝 단기집중과정의 분류: 정확도, 재현율, 정밀도 및 관련 측정항목을 참고하세요.
활성화 함수
신경망이 특성과 라벨 간의 비선형 (복잡한) 관계를 학습할 수 있도록 지원하는 함수입니다.
인기 있는 활성화 함수는 다음과 같습니다.
활성화 함수의 플롯은 단일 직선이 아닙니다. 예를 들어 ReLU 활성화 함수의 플롯은 두 개의 직선으로 구성됩니다.

시그모이드 활성화 함수의 플롯은 다음과 같습니다.

자세한 내용은 머신러닝 단기집중과정의 신경망: 활성화 함수를 참고하세요.
인공지능
정교한 작업을 해결할 수 있는 인간이 아닌 프로그램 또는 모델 예를 들어 텍스트를 번역하는 프로그램이나 모델, 방사선 이미지에서 질병을 식별하는 프로그램이나 모델은 모두 인공지능을 나타냅니다.
공식적으로 머신러닝은 인공지능의 하위 분야입니다. 하지만 최근 몇 년간 일부 조직에서는 인공지능과 머신러닝이라는 용어를 혼용하기 시작했습니다.
AUC (ROC 곡선 아래 영역)
긍정 클래스와 부정 클래스를 구분하는 이진 분류 모델의 능력을 나타내는 0.0~1.0 사이의 숫자입니다. AUC가 1.0에 가까울수록 모델이 클래스를 서로 분리하는 능력이 우수합니다.
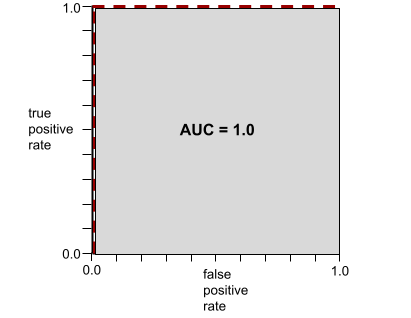
예를 들어 다음 그림은 포지티브 클래스 (녹색 타원)를 네거티브 클래스 (보라색 직사각형)와 완벽하게 구분하는 분류 모델을 보여줍니다. 이 비현실적으로 완벽한 모델의 AUC는 1.0입니다.

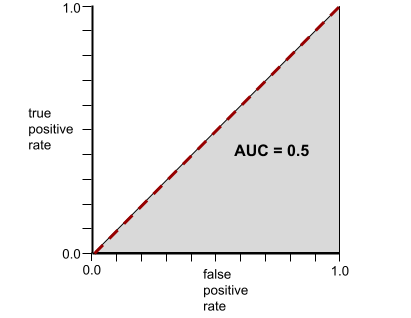
반대로 다음 그림은 무작위 결과를 생성한 분류 모델의 결과를 보여줍니다. 이 모델의 AUC는 0.5입니다.

예, 앞의 모델의 AUC는 0.0이 아닌 0.5입니다.
대부분의 모델은 두 극단 사이에 있습니다. 예를 들어 다음 모델은 긍정적인 것과 부정적인 것을 어느 정도 구분하므로 AUC가 0.5와 1.0 사이에 있습니다.

AUC는 분류 기준점에 설정된 값을 무시합니다. AUC는 가능한 모든 분류 임곗값을 고려합니다.
자세한 내용은 머신러닝 단기집중과정의 분류: ROC 및 AUC를 참고하세요.
B
역전파
신경망 학습에는 다음 2패스 주기의 여러 반복이 포함됩니다.
- 정방향 패스 중에 시스템은 예의 배치를 처리하여 예측을 생성합니다. 시스템은 각 예측을 각 라벨 값과 비교합니다. 예측값과 라벨 값의 차이가 해당 예의 손실입니다. 시스템은 모든 예의 손실을 집계하여 현재 배치에 대한 총 손실을 계산합니다.
- 역방향 패스(역전파) 중에 시스템은 모든 숨겨진 레이어에 있는 모든 뉴런의 가중치를 조정하여 손실을 줄입니다.
신경망에는 여러 히든 레이어에 걸쳐 많은 뉴런이 포함되는 경우가 많습니다. 이러한 각 뉴런은 다양한 방식으로 전체 손실에 기여합니다. 역전파는 특정 뉴런에 적용되는 가중치를 늘릴지 줄일지 결정합니다.
학습률은 각 역방향 패스가 각 가중치를 늘리거나 줄이는 정도를 제어하는 승수입니다. 학습률이 크면 학습률이 작은 경우보다 각 가중치가 더 많이 증가하거나 감소합니다.
미적분학 용어로 역전파는 미적분학의 연쇄 법칙을 구현합니다. 즉, 역전파는 각 매개변수에 대한 오류의 편미분을 계산합니다.
몇 년 전에는 ML 실무자가 역전파를 구현하기 위해 코드를 작성해야 했습니다. 이제 Keras와 같은 최신 ML API가 역전파를 구현합니다. 다양한 혜택이 마음에 드셨나요?
자세한 내용은 머신러닝 단기집중과정의 신경망을 참고하세요.
일괄
한 번의 학습 반복에 사용되는 예의 집합입니다. 배치 크기에 따라 배치에 포함되는 예시 수가 결정됩니다.
배치가 에포크와 어떤 관련이 있는지는 에포크를 참고하세요.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 하이퍼파라미터를 참고하세요.
배치 크기
배치의 예 수입니다. 예를 들어 배치 크기가 100이면 모델은 반복당 100개의 예시를 처리합니다.
다음은 인기 있는 배치 크기 전략입니다.
- 확률적 경사하강법 (SGD): 배치 크기가 1입니다.
- 전체 배치: 배치 크기가 전체 학습 세트의 예시 수입니다. 예를 들어 학습 세트에 백만 개의 예가 포함되어 있으면 배치 크기는 백만 개의 예가 됩니다. 전체 배치 전략은 일반적으로 비효율적입니다.
- 미니 배치: 배치 크기는 일반적으로 10~1,000입니다. 일반적으로 미니 배치가 가장 효율적인 전략입니다.
자세한 내용은 다음을 참조하세요.
- 머신러닝 단기집중과정의 프로덕션 ML 시스템: 정적 추론과 동적 추론 비교
- 딥 러닝 조정 플레이북
편향(bias)(윤리학/공정성)
1. 특정 사물, 인물 또는 그룹에 대한 정형화, 편견 또는 편애를 말합니다. 이러한 편향은 데이터의 수집과 해석 가능성, 시스템 설계, 사용자가 시스템과 상호작용하는 방식 등에 영향을 줍니다. 이러한 유형의 편향에는 다음이 포함됩니다.
2. 샘플링 또는 보고 절차로 인해 발생하는 체계적인 오류입니다. 이러한 유형의 편향에는 다음이 포함됩니다.
머신러닝 모델의 바이어스 항 또는 예측 편향과 혼동하지 마시기 바랍니다.
자세한 내용은 머신러닝 단기집중과정의 공정성: 편향 유형을 참고하세요.
편향(bias)(수학) 또는 편향 항
원점을 기준으로 한 절편 또는 오프셋입니다. 편향은 머신러닝 모델의 매개변수이며 다음 중 하나로 표시됩니다.
- b
- w0
예를 들어 다음 수식에서 편향은 b입니다.
단순한 2차원 선에서 편향은 'y 절편'을 의미합니다. 예를 들어 다음 그림의 선의 편향은 2입니다.
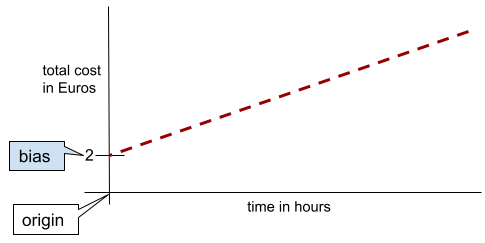
모든 모델이 원점 (0,0)에서 시작하지 않기 때문에 편향이 존재합니다. 예를 들어 놀이공원 입장료가 2유로이고 고객이 머무는 시간당 0.5유로가 추가로 부과된다고 가정해 보겠습니다. 따라서 총비용을 매핑하는 모델에는 가장 낮은 비용이 2유로이므로 2의 편향이 있습니다.
편향은 윤리학 및 공정성의 편향 또는 예측 편향과 혼동하지 마시기 바랍니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀를 참고하세요.
이진 분류
상호 배타적인 두 클래스 중 하나를 예측하는 분류 작업의 유형입니다.
예를 들어 다음 두 머신러닝 모델은 각각 이진 분류를 실행합니다.
- 이메일 메시지가 스팸 (포지티브 클래스)인지 스팸 아님 (네거티브 클래스)인지 판단하는 모델입니다.
- 의학적 증상을 평가하여 사람이 특정 질병 (양성 클래스)에 걸렸는지 또는 걸리지 않았는지 (음성 클래스)를 판단하는 모델입니다.
다중 클래스 분류와 대비되는 개념입니다.
자세한 내용은 머신러닝 단기집중과정의 분류를 참고하세요.
버킷팅,
하나의 특성을 버킷 또는 빈이라고 하는 다중 이진 특성으로 변환하는 작업으로서, 일반적으로 값 범위를 기준으로 합니다. 잘린 특성은 일반적으로 연속 특성입니다.
예를 들어 온도를 단일 연속 부동 소수점 특성으로 표현하는 대신 온도 범위를 다음과 같은 불연속 버킷으로 나눌 수 있습니다.
- 섭씨 10도 이하가 '차가운' 버킷입니다.
- 11~24도는 '온대' 버킷에 해당합니다.
- 섭씨 25도 이상은 '따뜻함' 버킷이 됩니다.
모델은 동일한 버킷의 모든 값을 동일하게 취급합니다. 예를 들어 13와 22 값은 모두 온대 버킷에 있으므로 모델은 두 값을 동일하게 취급합니다.
자세한 내용은 머신러닝 단기집중과정의 숫자 데이터: 구간화를 참고하세요.
C
범주형 데이터
가능한 값의 특정 집합을 갖는 특성입니다. 예를 들어 다음 세 가지 값 중 하나만 가질 수 있는 traffic-light-state이라는 범주형 특성을 생각해 보겠습니다.
redyellowgreen
traffic-light-state를 범주형 특성으로 표현하면 모델이 운전자 행동에 대한 red, green, yellow의 서로 다른 영향을 학습할 수 있습니다.
범주형 특성을 불연속 특성이라고도 합니다.
수치 데이터와 대비되는 개념입니다.
자세한 내용은 머신러닝 단기집중과정의 범주형 데이터 작업을 참고하세요.
클래스
라벨이 속할 수 있는 카테고리입니다. 예를 들면 다음과 같습니다.
분류 모델은 클래스를 예측합니다. 반면 회귀 모델은 클래스가 아닌 숫자를 예측합니다.
자세한 내용은 머신러닝 단기집중과정의 분류를 참고하세요.
분류 모델
예측이 클래스인 모델입니다. 예를 들어 다음은 모두 분류 모델입니다.
- 입력 문장의 언어 (프랑스어? 스페인어? 이탈리아어?)
- 나무 종(단풍나무? 오크? 바오밥?).
- 특정 질병의 양성 또는 음성 클래스를 예측하는 모델입니다.
반면 회귀 모델은 클래스가 아닌 숫자를 예측합니다.
일반적인 분류 모델에는 다음 두 가지 유형이 있습니다.
분류 기준점
이진 분류에서 로지스틱 회귀 모델의 원시 출력을 양성 클래스 또는 음성 클래스 예측으로 변환하는 0과 1 사이의 숫자입니다. 분류 기준은 모델 학습에서 선택한 값이 아니라 사람이 선택한 값입니다.
로지스틱 회귀 모델은 0과 1 사이의 원시 값을 출력합니다. 그런 다음 아래를 실행합니다.
- 이 원시 값이 분류 기준보다 크면 포지티브 클래스가 예측됩니다.
- 이 원시 값이 분류 임계값보다 작으면 부정 클래스가 예측됩니다.
예를 들어 분류 기준이 0.8이라고 가정해 보겠습니다. 원시 값이 0.9이면 모델이 포지티브 클래스를 예측합니다. 원시 값이 0.7이면 모델이 네거티브 클래스를 예측합니다.
분류 기준점 선택은 거짓양성 및 거짓음성 수에 큰 영향을 미칩니다.
자세한 내용은 머신러닝 단기집중과정의 기준점 및 혼동 행렬을 참고하세요.
분류기
분류 모델의 비공식 용어입니다.
클래스 불균형 데이터 세트
각 클래스의 총 라벨 수가 크게 다른 분류의 데이터 세트 예를 들어 두 라벨이 다음과 같이 나뉘는 이진 분류 데이터 세트를 생각해 보겠습니다.
- 1,000,000개의 음수 값 표시 라벨
- 10개의 긍정적 라벨
부정적 라벨과 긍정적 라벨의 비율이 100,000:1이므로 클래스 불균형 데이터 세트입니다.
반면 다음 데이터 세트는 음성 라벨과 양성 라벨의 비율이 1에 비교적 가까우므로 클래스 균형을 이룹니다.
- 517개의 부정적 라벨
- 483개의 긍정적 라벨
다중 클래스 데이터 세트도 클래스 불균형일 수 있습니다. 예를 들어 다음 다중 클래스 분류 데이터 세트는 한 라벨에 다른 두 라벨보다 훨씬 많은 예가 있으므로 클래스 불균형이기도 합니다.
- 클래스가 'green'인 라벨 1,000,000개
- 클래스가 'purple'인 라벨 200개
- 'orange' 클래스가 있는 라벨 350개
클래스 불균형 데이터 세트를 학습하는 데는 특별한 문제가 있을 수 있습니다. 자세한 내용은 머신러닝 단기집중과정의 불균형 데이터 세트를 참고하세요.
클리핑
다음 중 하나 또는 둘 다를 실행하여 이상치를 처리하는 기술입니다.
- 최대 기준점보다 큰 특성 값을 해당 최대 기준점으로 줄입니다.
- 최소 기준점보다 작은 특성 값을 해당 최소 기준점까지 늘립니다.
예를 들어 특정 특성의 값 중 0.5% 미만이 40~60 범위를 벗어난다고 가정합니다. 이 경우 다음과 같이 할 수 있습니다.
- 60 (최대 기준점)을 초과하는 모든 값을 정확히 60으로 자릅니다.
- 40 (최소 기준점) 미만인 모든 값을 정확히 40으로 자릅니다.
이상치는 모델을 손상시켜 학습 중에 가중치가 오버플로되는 경우가 있습니다. 일부 이상치는 정확도와 같은 측정항목을 크게 망칠 수도 있습니다. 클리핑은 손상을 제한하는 일반적인 기법입니다.
경사 제한은 학습 중에 지정된 범위 이내의 경사 값을 강제 적용합니다.
자세한 내용은 머신러닝 단기집중과정의 숫자 데이터: 정규화를 참고하세요.
혼동 행렬
분류 모델이 수행한 올바른 예측과 잘못된 예측의 수를 요약한 NxN 표입니다. 예를 들어 이진 분류 모델의 다음 혼동 행렬을 고려해 보세요.
| 종양 (예측) | 종양 아님 (예측) | |
|---|---|---|
| 종양 (정답) | 18 (TP) | 1 (FN) |
| 종양이 아님 (정답) | 6 (FP) | 452 (TN) |
위의 혼동 행렬은 다음을 보여줍니다.
- 그라운드 트루스가 종양인 19개의 예측 중 모델이 18개를 올바르게 분류하고 1개를 잘못 분류했습니다.
- 그라운드 트루스가 Non-Tumor인 458개의 예측 중 모델이 452개를 올바르게 분류하고 6개를 잘못 분류했습니다.
다중 클래스 분류 문제의 혼동 행렬은 실수 패턴을 파악하는 데 도움이 될 수 있습니다. 예를 들어 세 가지 다른 붓꽃 유형(버지니카, 버시컬러, 세토사)을 분류하는 3개 클래스 다중 클래스 분류 모델의 다음 혼동 행렬을 고려해 보세요. 실측값이 Virginica인 경우 혼동 행렬을 보면 모델이 Setosa보다 Versicolor를 잘못 예측할 가능성이 훨씬 더 높습니다.
| Setosa (예측) | Versicolor (예측) | Virginica (예측) | |
|---|---|---|---|
| Setosa (정답) | 88 | 12 | 0 |
| Versicolor (정답) | 6 | 141 | 7 |
| Virginica (정답) | 2 | 27 | 109 |
또 다른 예로, 혼동 행렬은 필기 숫자를 인식하도록 학습된 모델이 4를 9로, 아니면 7을 1로 잘못 예측하는 경향이 있음을 드러낼 수 있습니다.
혼동 행렬에는 정밀도 및 재현율을 비롯한 다양한 성능 측정항목을 계산하기에 충분한 정보가 포함되어 있습니다.
연속 특성
온도나 무게와 같이 가능한 값의 범위가 무한한 부동 소수점 특성입니다.
불연속 특성과 대비되는 개념입니다.
수렴
반복마다 손실 값이 거의 또는 전혀 변화하지 않는 상태입니다. 예를 들어 다음 손실 곡선은 약 700회 반복에서 수렴을 보여줍니다.
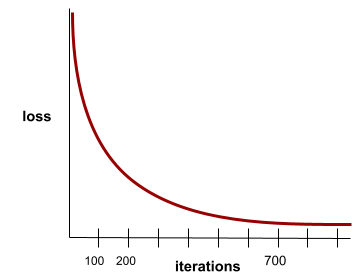
추가 학습으로 모델이 개선되지 않으면 모델이 수렴됩니다.
딥 러닝에서는 손실 값이 최종적으로 감소하기 전에 여러 반복 동안 일정하게 유지되거나 거의 일정하게 유지되는 경우가 있습니다. 손실 값이 일정하게 유지되는 기간이 길어지면 일시적으로 수렴이 이루어진 것처럼 느껴질 수 있습니다.
조기 중단도 참고하세요.
자세한 내용은 머신러닝 단기집중과정의 모델 수렴 및 손실 곡선을 참고하세요.
D
DataFrame
메모리에서 데이터 세트를 표현하는 데 널리 사용되는 pandas 데이터 유형입니다.
DataFrame은 테이블이나 스프레드시트와 비슷합니다. DataFrame의 각 열에는 이름 (헤더)이 있으며 각 행은 고유한 숫자로 식별됩니다.
DataFrame의 각 열은 2D 배열처럼 구성되지만 각 열에 고유한 데이터 유형을 할당할 수 있다는 점이 다릅니다.
공식 pandas.DataFrame 참조 페이지도 참고하세요.
데이터 세트(data set 또는 dataset)
일반적으로 다음 형식 중 하나로 구성되지만 이에 국한되지는 않는 원시 데이터 모음입니다.
- 스프레드시트
- CSV (쉼표로 구분된 값) 형식의 파일
심층 모델
심층 모델을 심층신경망이라고도 합니다.
와이드 모델과 대비되는 개념입니다.
밀집 특성
대부분 또는 모든 값이 0이 아닌 특성으로, 일반적으로 부동 소수점 값의 텐서입니다. 예를 들어 다음 10요소 텐서는 값이 0이 아닌 요소가 9개이므로 밀집되어 있습니다.
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
희소 특성과 대비되는 개념입니다.
깊이
신경망에서 다음을 합산한 값입니다.
예를 들어 히든 레이어 5개와 출력 레이어 1개가 있는 신경망의 깊이는 6입니다.
입력 레이어는 깊이에 영향을 미치지 않습니다.
불연속 특성
가능한 값의 유한 집합을 갖는 특성입니다. 예를 들어 값이 animal, vegetable 또는 mineral만 될 수 있는 특성은 이산 (또는 범주형) 특성입니다.
연속 특성과 대비되는 개념입니다.
동적
자주 또는 지속적으로 수행되는 작업 머신러닝에서 동적과 온라인은 동의어입니다. 다음은 머신러닝에서 동적 및 온라인이 일반적으로 사용되는 경우입니다.
- 동적 모델 (또는 온라인 모델)은 자주 또는 지속적으로 재학습되는 모델입니다.
- 동적 학습 (또는 온라인 학습)은 자주 또는 지속적으로 학습하는 프로세스입니다.
- 동적 추론 (또는 온라인 추론)은 요청 시 예측을 생성하는 프로세스입니다.
동적 모델
모델이 자주 (심지어 지속적으로) 재학습됩니다. 동적 모델은 진화하는 데이터에 지속적으로 적응하는 '평생 학습자'입니다. 동적 모델은 온라인 모델이라고도 합니다.
정적 모델과 대비되는 개념입니다.
E
조기 중단
학습 손실이 감소하기 전에 학습을 종료하는 정규화 방법입니다. 조기 중단에서는 검증 데이터 세트의 손실이 증가하기 시작하면(즉, 일반화 성능이 저하되면) 의도적으로 모델 학습을 중단합니다.
조기 종료와 대비되는 개념입니다.
임베딩 레이어
고차원 카테고리 특성을 학습하여 점진적으로 하위 차원 임베딩 벡터를 학습하는 특수 숨겨진 레이어 임베딩 레이어를 사용하면 신경망이 고차원 카테고리 특성으로만 학습하는 것보다 훨씬 효율적으로 학습할 수 있습니다.
예를 들어 지구에는 현재 약 73,000가지의 수종이 생식하고 있습니다. 나무 종이 모델의 특성이라고 가정해 보겠습니다. 그러면 모델의 입력 레이어에는 길이가 73,000인 원-핫 벡터가 포함됩니다.
예를 들어 baobab는 다음과 같이 표현될 수 있습니다.

73,000개 요소 배열은 매우 깁니다. 모델에 삽입 레이어를 추가하지 않으면 72,999개의 0을 곱해야 하므로 학습에 시간이 매우 오래 걸립니다. 임베딩 레이어가 12개의 차원으로 구성되도록 선택할 수 있습니다. 따라서 임베딩 레이어는 각 나무 종에 대한 새로운 임베딩 벡터를 점진적으로 학습합니다.
경우에 따라 해싱이 삽입 레이어의 합리적인 대안이 될 수 있습니다.
자세한 내용은 머신러닝 단기집중과정의 임베딩을 참고하세요.
에포크
각 예가 한 번 처리되도록 전체 학습 세트에 대한 전체 학습 패스입니다.
에포크는 N/배치 크기 학습 반복을 나타내며, 여기서 N은 총 예시 수입니다.
예를 들어 다음과 같이 가정해 보겠습니다.
- 데이터 세트는 1,000개의 예시로 구성됩니다.
- 배치 크기는 50개 예시입니다.
따라서 단일 에포크에는 20번의 반복이 필요합니다.
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 하이퍼파라미터를 참고하세요.
예시
특성의 한 행 값과 라벨 값(있는 경우) 지도 학습의 예는 다음 두 가지 일반 카테고리로 나뉩니다.
- 라벨이 지정된 예는 하나 이상의 특성과 하나의 라벨로 구성됩니다. 라벨이 지정된 예가 학습에 사용됩니다.
- 라벨이 없는 예는 하나 이상의 특성으로 구성되지만 라벨은 없습니다. 라벨이 없는 예는 추론 중에 사용됩니다.
예를 들어 날씨 조건이 학생 시험 점수에 미치는 영향을 파악하도록 모델을 학습시킨다고 가정해 보겠습니다. 다음은 라벨이 지정된 세 가지 예입니다.
| 기능 | 라벨 | ||
|---|---|---|---|
| 온도 | 습도 | 압력 | 테스트 점수 |
| 15 | 47 | 998 | 좋음 |
| 19 | 34 | 1020 | 매우 좋음 |
| 18 | 92 | 1012 | 나쁨 |
다음은 라벨이 지정되지 않은 세 가지 예입니다.
| 온도 | 습도 | 압력 | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
데이터 세트의 행은 일반적으로 예시의 원시 소스입니다. 즉, 예시는 일반적으로 데이터 세트의 열 하위 집합으로 구성됩니다. 또한 예의 특성에는 특성 교차와 같은 합성 특성도 포함될 수 있습니다.
자세한 내용은 머신러닝 소개 과정의 감독 학습을 참고하세요.
F
거짓음성 (FN)
모델에서 네거티브 클래스로 잘못 예측한 예입니다. 예를 들어 모델에서 특정 이메일 메시지가 스팸이 아닌 것으로(네거티브 클래스) 예측했지만 해당 이메일 메시지가 실제로 스팸인 경우가 여기에 해당합니다.
거짓양성 (FP)
모델에서 포지티브 클래스로 잘못 예측한 예입니다. 예를 들어 모델에서 특정 이메일 메시지가 스팸 (포지티브 클래스)인 것으로 예측했지만 실제로는 스팸이 아닌 경우가 여기에 해당합니다.
자세한 내용은 머신러닝 단기집중과정의 기준점 및 혼동 행렬을 참고하세요.
거짓양성률 (FPR)
모델이 포지티브 클래스로 잘못 예측한 실제 네거티브 예의 비율입니다. 다음 공식은 거짓양성률을 계산합니다.
거짓양성률은 ROC 곡선의 x축입니다.
자세한 내용은 머신러닝 단기집중과정의 분류: ROC 및 AUC를 참고하세요.
특징
머신러닝 모델의 입력 변수입니다. example은 하나 이상의 특성으로 구성됩니다. 예를 들어 날씨 조건이 학생 시험 점수에 미치는 영향을 파악하기 위해 모델을 학습한다고 가정해 보겠습니다. 다음 표에는 각각 3개의 특징과 하나의 라벨이 포함된 세 가지 예가 나와 있습니다.
| 기능 | 라벨 | ||
|---|---|---|---|
| 온도 | 습도 | 압력 | 테스트 점수 |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
라벨과 대비되는 개념입니다.
자세한 내용은 머신러닝 소개 과정의 감독 학습을 참고하세요.
특성 교차
범주형 또는 버케팅된 특성을 '교차'하여 형성된 합성 특성입니다.
예를 들어 다음 네 가지 버킷 중 하나로 온도를 나타내는 '기분 예측' 모델을 생각해 보겠습니다.
freezingchillytemperatewarm
다음 세 버킷 중 하나로 풍속을 나타냅니다.
stilllightwindy
특성 교차가 없으면 선형 모델은 앞의 7가지 다양한 버킷 각각에 대해 독립적으로 학습됩니다. 따라서 모델은 예를 들어 windy 학습과 독립적으로 freezing 학습을 진행합니다.
또는 온도와 풍속의 특성 교차를 만들 수도 있습니다. 이 합성 기능에는 다음과 같은 12가지 가능한 값이 있습니다.
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
특성 교차 덕분에 모델은 freezing-windy일과 freezing-still일 간의 분위기 차이를 학습할 수 있습니다.
각각 다양한 버킷이 많은 두 가지 특징에서 합성 특징을 만들면 결과 특징 교차에 가능한 조합이 엄청나게 많아집니다. 예를 들어 한 특성에 1,000개의 버킷이 있고 다른 특성에 2,000개의 버킷이 있는 경우 결과 특성 교차에는 2,000,000개의 버킷이 있습니다.
공식적으로 크로스는 카티전 프로덕트입니다.
특성 교차는 주로 선형 모델과 함께 사용되며 신경망에서는 거의 사용되지 않습니다.
자세한 내용은 머신러닝 단기집중과정의 범주형 데이터: 특성 교차를 참고하세요.
특성 추출 단계를 포함합니다
다음 단계를 포함하는 프로세스:
- 모델을 학습시키는 데 유용할 특성이 무엇인지 판단합니다.
- 데이터 세트의 원시 데이터를 이러한 특성의 효율적인 버전으로 변환합니다.
예를 들어 temperature이 유용한 기능일 수 있다고 판단할 수 있습니다. 그런 다음 버킷팅을 실험하여 모델이 다양한 temperature 범위에서 학습할 수 있는 내용을 최적화할 수 있습니다.
특성 추출을 특징 추출 또는 특성 생성이라고도 합니다.
자세한 내용은 머신러닝 단기집중과정의 숫자 데이터: 모델이 특징 벡터를 사용하여 데이터를 수집하는 방법을 참고하세요.
기능 세트
머신러닝 모델에서 학습에 사용하는 특성 그룹입니다. 예를 들어 주택 가격을 예측하는 모델의 간단한 특성 집합은 우편번호, 부동산 크기, 부동산 상태로 구성될 수 있습니다.
특성 벡터
예을 구성하는 특성 값의 배열입니다. 특성 벡터는 학습 및 추론 중에 입력됩니다. 예를 들어 이산 특성이 두 개인 모델의 특성 벡터는 다음과 같을 수 있습니다.
[0.92, 0.56]
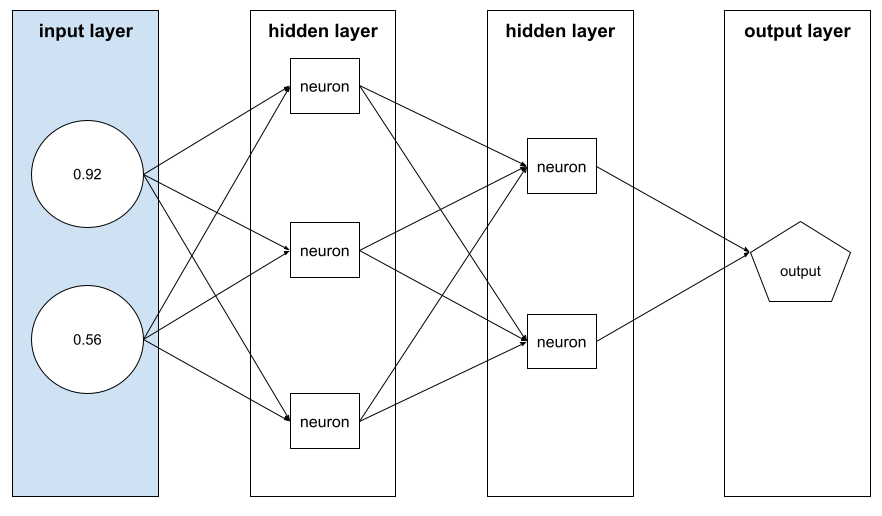
각 예시에서는 특성 벡터에 다른 값을 제공하므로 다음 예시의 특성 벡터는 다음과 같을 수 있습니다.
[0.73, 0.49]
특성 추출은 특성 벡터에서 특성을 표현하는 방법을 결정합니다. 예를 들어 가능한 값이 5개인 이진 범주형 특성은 원-핫 인코딩으로 표현할 수 있습니다. 이 경우 특정 예의 특징 벡터 부분은 다음과 같이 0이 4개이고 세 번째 위치에 1.0이 하나로 구성됩니다.
[0.0, 0.0, 1.0, 0.0, 0.0]
또 다른 예로 모델이 다음 세 가지 특성으로 구성되어 있다고 가정해 보겠습니다.
- 원-핫 인코딩으로 표현된 가능한 값이 5개인 이진 범주형 특성(예:
[0.0, 1.0, 0.0, 0.0, 0.0]) - 원-핫 인코딩으로 표현된 가능한 값이 3개인 또 다른 이진 범주형 특성(예:
[0.0, 0.0, 1.0]) - 부동 소수점 특징입니다(예:
8.3).
이 경우 각 예시의 특징 벡터는 9개 값으로 표현됩니다. 위 목록의 예시 값을 고려할 때 특징 벡터는 다음과 같습니다.
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
자세한 내용은 머신러닝 단기집중과정의 숫자 데이터: 모델이 특징 벡터를 사용하여 데이터를 수집하는 방법을 참고하세요.
피드백 루프
머신러닝에서 모델의 예측이 동일한 모델 또는 다른 모델의 학습 데이터에 영향을 미치는 상황입니다. 예를 들어 영화를 추천하는 모델은 사람들이 보는 영화에 영향을 미치고, 이는 후속 영화 추천 모델에 영향을 미칩니다.
자세한 내용은 머신러닝 단기집중과정의 프로덕션 ML 시스템: 질문하기를 참고하세요.
G
일반화
모델이 이전에 접하지 못한 새로운 데이터에 대해 올바른 예측을 수행하는 능력입니다. 일반화할 수 있는 모델은 과적합된 모델과는 반대입니다.
자세한 내용은 머신러닝 단기집중과정의 일반화를 참고하세요.
일반화 곡선
반복 수의 함수로 학습 손실과 검증 손실을 모두 표시한 그래프
일반화 곡선을 사용하면 가능한 과적합을 감지하는 데 도움이 됩니다. 예를 들어 다음 일반화 곡선은 검증 손실이 학습 손실보다 훨씬 높아지므로 과적합을 암시합니다.
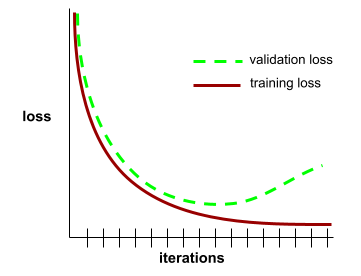
자세한 내용은 머신러닝 단기집중과정의 일반화를 참고하세요.
경사하강법
손실을 최소화하는 수학적 기법입니다. 경사하강법은 가중치와 편향을 반복적으로 조정하면서 손실을 최소화하는 최적의 조합을 점진적으로 찾습니다.
경사 하강법은 머신러닝보다 훨씬 오래되었습니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 경사 하강법을 참고하세요.
정답
현실
실제로 발생한 일
예를 들어 대학 1학년 학생이 6년 이내에 졸업할지 여부를 예측하는 이진 분류 모델을 생각해 보세요. 이 모델의 그라운드 트루스는 해당 학생이 실제로 6년 이내에 졸업했는지 여부입니다.
H
히든 레이어
신경망에서 입력 레이어 (특성)와 출력 레이어 (예측) 사이에 있는 레이어입니다. 각 숨겨진 레이어는 하나 이상의 뉴런으로 구성됩니다. 예를 들어 다음 신경망에는 히든 레이어가 두 개 있습니다. 첫 번째 레이어에는 뉴런이 3개 있고 두 번째 레이어에는 뉴런이 2개 있습니다.
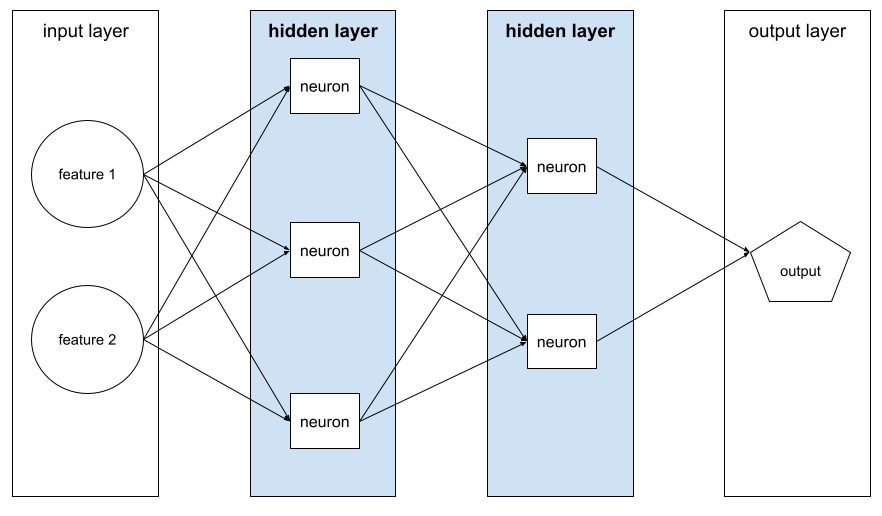
심층신경망에는 여러 히든 레이어가 포함되어 있습니다. 예를 들어 위의 그림은 모델에 숨겨진 레이어가 두 개 포함되어 있으므로 심층 신경망입니다.
자세한 내용은 머신러닝 단기집중과정의 신경망: 노드 및 숨겨진 레이어를 참고하세요.
하이퍼파라미터
모델 학습을 연속으로 실행하는 동안 사용자가 또는 초매개변수 조정 서비스(예: Vizier)가 조정하는 변수입니다.예를 들어 학습률은 초매개변수 중 하나입니다. 한 학습 세션 전에 학습률을 0.01로 설정할 수 있습니다. 0.01이 너무 높다고 판단되면 다음 학습 세션의 학습률을 0.003으로 설정할 수 있습니다.
반면 파라미터는 모델이 학습 중에 학습하는 다양한 가중치와 편향입니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 하이퍼파라미터를 참고하세요.
I
독립적이고 동일한 분포 (i.i.d, independently and identically distributed)
변경되지 않는 분포에서 추출된 데이터로, 추출된 각 값은 이전에 추출된 값에 종속되지 않습니다. i.i.d.는 머신러닝의 이상기체로, 유용한 수학적 구조이지만 현실에서는 거의 찾아볼 수 없습니다. 예를 들어 웹페이지의 방문자 분포는 짧은 기간에는 i.i.d.일 수 있습니다. 즉, 짧은 기간에는 분포가 변하지 않으며 각 사용자의 방문은 일반적으로 서로 독립적입니다. 하지만 기간을 늘리면 웹페이지 방문자의 계절별 차이가 나타날 수 있습니다.
비정상성도 참고하세요.
추론
기존 머신러닝에서 학습된 모델을 라벨이 없는 예에 적용하여 예측을 수행하는 과정입니다. 자세한 내용은 ML 소개 과정의 지도 학습을 참고하세요.
대규모 언어 모델에서 추론은 학습된 모델을 사용하여 입력 프롬프트에 대한 응답을 생성하는 프로세스입니다.
통계에서는 추론의 의미가 약간 다릅니다. 자세한 내용은 통계적 추론에 대한 위키백과 문서를 참고하세요.
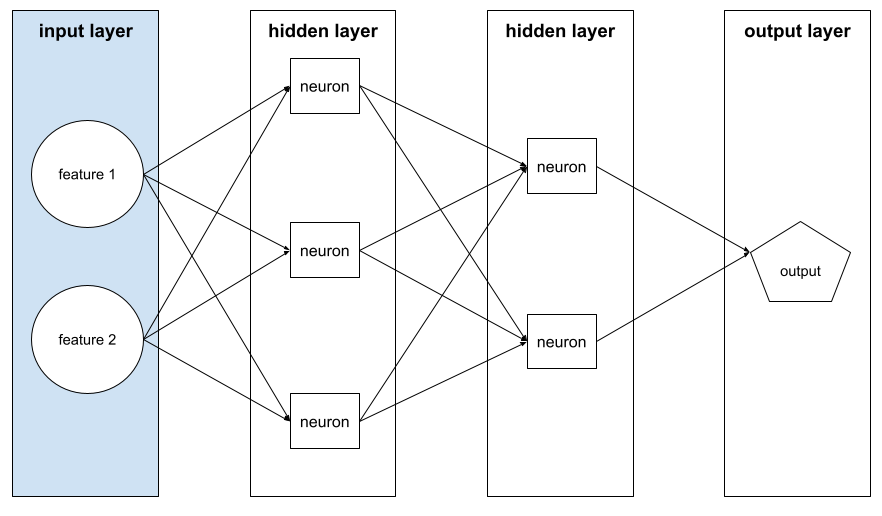
입력 레이어
특성 벡터를 보유하는 신경망의 레이어입니다. 즉, 입력 레이어는 학습 또는 추론을 위한 예를 제공합니다. 예를 들어 다음 신경망의 입력 레이어는 두 가지 기능으로 구성됩니다.
해석 가능성
사람이 이해할 수 있는 용어로 ML 모델의 추론을 설명하거나 제시할 수 있는 능력입니다.
예를 들어 대부분의 선형 회귀 모델은 해석 가능성이 높습니다. (각 기능의 학습된 가중치만 보면 됩니다.) 결정 포레스트는 해석 가능성도 높습니다. 하지만 일부 모델은 정교한 시각화가 있어야만 해석 가능합니다.
Learning Interpretability Tool (LIT)을 사용하여 ML 모델을 해석할 수 있습니다.
iteration
학습 중에 모델's 파라미터(모델의 가중치 및 편향)를 한 번 업데이트합니다. 배치 크기는 모델이 단일 반복에서 처리하는 예시 수를 결정합니다. 예를 들어 배치 크기가 20이면 모델은 매개변수를 조정하기 전에 20개의 예시를 처리합니다.
신경망을 학습시킬 때 단일 반복에는 다음 두 패스가 포함됩니다.
- 단일 배치에서 손실을 평가하는 정방향 패스입니다.
- 손실과 학습률을 기반으로 모델의 매개변수를 조정하는 역방향 패스 (역전파)
자세한 내용은 머신러닝 단기집중과정의 경사 하강법을 참고하세요.
L
L0 정규화
모델에서 0이 아닌 가중치의 총 개수에 페널티를 주는 정규화 유형입니다. 예를 들어 0이 아닌 가중치가 11개인 모델은 0이 아닌 가중치가 10개인 유사한 모델보다 더 많은 페널티를 받습니다.
L0 정규화를 L0-norm 정규화라고도 합니다.
L1 손실
실제 라벨 값과 모델이 예측한 값 간의 차이의 절대값을 계산하는 손실 함수입니다. 예를 들어 예 5개의 배치에 대한 L1 손실 계산은 다음과 같습니다.
| 예의 실제 값 | 모델의 예측값 | 델타의 절댓값 |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1 손실 | ||
평균 절대 오차는 예시당 평균 L1 손실입니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 손실을 참고하세요.
L1 정규화
가중치의 절대값 합에 비례하여 가중치에 페널티를 주는 정규화 유형입니다. L1 정규화는 관련성이 없거나 매우 낮은 특성의 가중치를 정확히 0으로 유도하는 데 도움이 됩니다. 가중치가 0인 기능은 모델에서 효과적으로 삭제됩니다.
L2 정규화와 대비되는 개념입니다.
L2 손실
실제 라벨 값과 모델이 예측한 값 간의 차이 제곱을 계산하는 손실 함수입니다. 예를 들어 예 5개의 배치에 대한 L2 손실 계산은 다음과 같습니다.
| 예의 실제 값 | 모델의 예측값 | 델타의 제곱 |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 손실 | ||
제곱으로 인해 L2 손실은 이상치의 영향을 증폭합니다. 즉, L2 손실은 L1 손실보다 잘못된 예측에 더 강하게 반응합니다. 예를 들어 이전 배치에 대한 L1 손실은 16이 아닌 8이 됩니다. 단일 이상치가 16개 중 9개를 차지합니다.
회귀 모델은 일반적으로 L2 손실을 손실 함수로 사용합니다.
평균 제곱 오차는 예시당 평균 L2 손실입니다. 제곱 손실은 L2 손실의 또 다른 이름입니다.
자세한 내용은 머신러닝 단기집중과정의 로지스틱 회귀: 손실 및 정규화를 참고하세요.
L2 정규화
가중치의 제곱 합에 비례하여 가중치에 페널티를 주는 정규화 유형입니다. L2 정규화는 이상치 가중치 (높은 양수 값 또는 낮은 음수 값을 갖는 가중치)를 0에 가깝게 유도하지만 0은 아닙니다. 값이 0에 매우 가까운 특성은 모델에 남아 있지만 모델의 예측에 큰 영향을 미치지 않습니다.
L2 정규화는 항상 선형 모델의 일반화를 개선합니다.
L1 정규화와 대비되는 개념입니다.
자세한 내용은 머신러닝 단기집중과정의 과적합: L2 정규화를 참고하세요.
라벨
지도 머신러닝에서 예의 '답' 또는 '결과' 부분을 의미합니다.
각 라벨이 지정된 예는 하나 이상의 특성과 라벨로 구성됩니다. 예를 들어 스팸 감지 데이터 세트의 경우 라벨은 '스팸' 또는 '스팸 아님'일 가능성이 높습니다. 강우량 데이터 세트에서 라벨은 특정 기간 동안 내린 비의 양일 수 있습니다.
자세한 내용은 머신러닝 소개의 지도 학습을 참고하세요.
라벨이 지정된 예
하나 이상의 특성과 라벨이 포함된 예입니다. 예를 들어 다음 표에는 주택 평가 모델의 라벨이 지정된 세 가지 예가 나와 있습니다. 각 예에는 세 가지 특성과 하나의 라벨이 있습니다.
| 침실 수 | 욕실 수 | 주택 연령 | 주택 가격 (라벨) |
|---|---|---|---|
| 3 | 2 | 15 | $345,000 |
| 2 | 1 | 72 | $179,000 |
| 4 | 2 | 34 | $392,000 |
지도 머신러닝에서 모델은 라벨이 지정된 예로 학습하고 라벨이 지정되지 않은 예에 대한 예측을 수행합니다.
라벨이 지정된 예와 라벨이 지정되지 않은 예를 비교합니다.
자세한 내용은 머신러닝 소개의 지도 학습을 참고하세요.
람다
정규화율의 동의어입니다.
람다는 과부하된 용어입니다. 여기에서는 정규화 맥락의 용어 정의에 집중합니다.
레이어
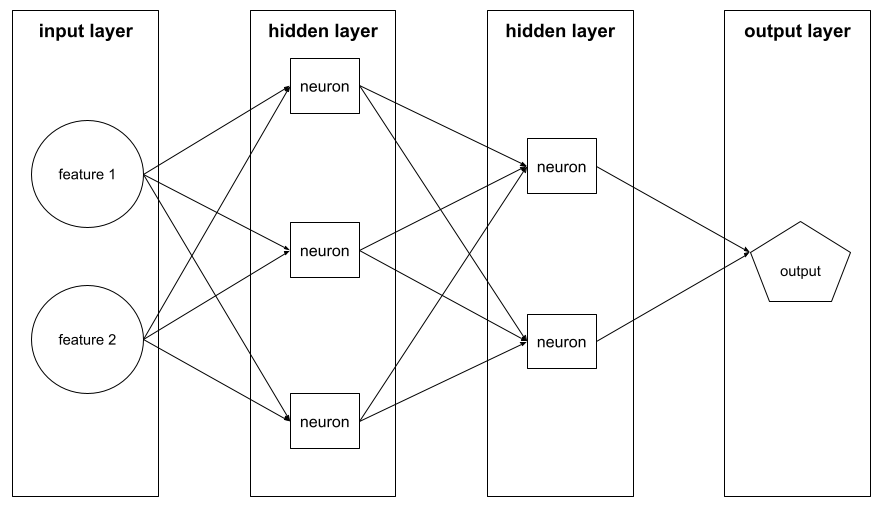
신경망의 뉴런 집합입니다. 일반적인 세 가지 유형의 레이어는 다음과 같습니다.
예를 들어 다음 그림은 입력 레이어 1개, 히든 레이어 2개, 출력 레이어 1개가 있는 신경망을 보여줍니다.
TensorFlow에서 레이어는 텐서 및 구성 옵션을 입력으로 취하고 다른 텐서를 출력하는 Python 함수이기도 합니다.
학습률
경사하강법 알고리즘에 각 반복에서 가중치와 편향을 조정하는 정도를 알려주는 부동 소수점 숫자입니다. 예를 들어 학습률이 0.3이면 학습률이 0.1일 때보다 가중치와 편향이 3배 더 강력하게 조정됩니다.
학습률은 핵심적인 초매개변수입니다. 학습률을 너무 낮게 설정하면 학습에 시간이 너무 오래 걸립니다. 학습률을 너무 높게 설정하면 경사하강법이 수렴에 도달하는 데 문제가 있는 경우가 많습니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 하이퍼파라미터를 참고하세요.
선형
덧셈과 곱셈만으로 나타낼 수 있는 두 개 이상의 변수 간의 관계입니다.
선형 관계의 플롯은 선입니다.
비선형과 대비되는 개념입니다.
선형 모델
특성당 하나의 가중치를 할당하여 예측을 수행하는 모델 (선형 모델에는 편향도 포함됩니다.) 반면 심층 모델에서 특성과 예측 간의 관계는 일반적으로 비선형입니다.
선형 모델은 일반적으로 심층 모델보다 학습하기 쉽고 해석 가능성이 높습니다. 하지만 딥 모델은 특성 간의 복잡한 관계를 학습할 수 있습니다.
선형 회귀와 로지스틱 회귀는 두 가지 유형의 선형 모델입니다.
선형 회귀
다음 두 가지가 모두 참인 머신러닝 모델의 유형입니다.
선형 회귀와 로지스틱 회귀를 비교합니다. 또한 회귀와 분류를 비교해 보세요.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀를 참고하세요.
로지스틱 회귀
확률을 예측하는 회귀 모델의 한 유형입니다. 로지스틱 회귀 모델에는 다음과 같은 특징이 있습니다.
- 라벨은 범주형입니다. 로지스틱 회귀라는 용어는 일반적으로 이진 로지스틱 회귀, 즉 가능한 값이 두 개인 라벨의 확률을 계산하는 모델을 의미합니다. 덜 일반적인 변형인 다항 로지스틱 회귀는 가능한 값이 2개를 초과하는 라벨의 확률을 계산합니다.
- 학습 중 손실 함수는 로그 손실입니다. (가능한 값이 3개 이상인 라벨의 경우 여러 로그 손실 단위를 병렬로 배치할 수 있습니다.)
- 모델은 심층 신경망이 아닌 선형 아키텍처를 사용합니다. 하지만 이 정의의 나머지 부분은 범주형 라벨의 확률을 예측하는 심층 모델에도 적용됩니다.
예를 들어 입력 이메일이 스팸인지 스팸이 아닌지 확률을 계산하는 로지스틱 회귀 모델을 생각해 보겠습니다. 추론 중에 모델이 0.72를 예측한다고 가정해 보겠습니다. 따라서 모델은 다음을 추정합니다.
- 이메일이 스팸일 가능성이 72% 입니다.
- 이메일이 스팸이 아닐 가능성이 28% 입니다.
로지스틱 회귀 모델은 다음 2단계 아키텍처를 사용합니다.
- 모델은 입력 기능의 선형 함수를 적용하여 원시 예측 (y')을 생성합니다.
- 모델은 이 원시 예측을 시그모이드 함수의 입력으로 사용합니다. 이 함수는 원시 예측을 0과 1 사이의 값(0과 1은 제외)으로 변환합니다.
모든 회귀 모델과 마찬가지로 로지스틱 회귀 모델은 숫자를 예측합니다. 하지만 이 숫자는 일반적으로 다음과 같이 이진 분류 모델의 일부가 됩니다.
- 예측된 숫자가 분류 임곗값보다 큰 경우 이진 분류 모델은 포지티브 클래스를 예측합니다.
- 예측된 수가 분류 기준점보다 작으면 이진 분류 모델은 네거티브 클래스를 예측합니다.
자세한 내용은 머신러닝 단기집중과정의 로지스틱 회귀를 참고하세요.
로그 손실
자세한 내용은 머신러닝 단기집중과정의 로지스틱 회귀: 손실 및 정규화를 참고하세요.
로그 오즈
일부 이벤트의 오즈의 로그입니다.
손실
지도 모델의 학습 중에 모델의 예측이 라벨에서 얼마나 벗어났는지 나타내는 척도입니다.
손실 함수는 손실을 계산합니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 손실을 참고하세요.
손실 곡선
학습 반복 수의 함수로 표시된 손실의 그래프 다음 플롯은 일반적인 손실 곡선을 보여줍니다.
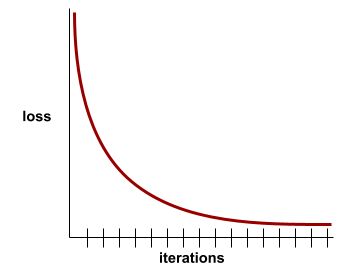
손실 곡선을 사용하면 모델이 수렴하는지 과적합되는지 확인할 수 있습니다.
손실 곡선은 다음 유형의 손실을 모두 표시할 수 있습니다.
일반화 곡선도 참고하세요.
자세한 내용은 머신러닝 단기집중과정의 과적합: 손실 곡선 해석을 참고하세요.
손실 함수
학습 또는 테스트 중에 예시 배치의 손실을 계산하는 수학 함수입니다. 손실 함수는 부정확한 예측을 하는 모델보다 정확한 예측을 하는 모델에 더 낮은 손실을 반환합니다.
학습의 목표는 일반적으로 손실 함수가 반환하는 손실을 최소화하는 것입니다.
다양한 종류의 손실 함수가 있습니다. 빌드 중인 모델의 종류에 적합한 손실 함수를 선택합니다. 예를 들면 다음과 같습니다.
M
머신러닝
입력 데이터로 모델을 학습시키는 프로그램 또는 시스템입니다. 학습된 모델은 모델 학습에 사용된 것과 동일한 분포에서 가져온 새로운 (이전에 본 적 없는) 데이터로부터 유용한 예측을 할 수 있습니다.
머신러닝은 이러한 프로그램 또는 시스템과 관련된 학문 분야를 가리키는 용어이기도 합니다.
자세한 내용은 머신러닝 소개 과정을 참고하세요.
다수 클래스
클래스 불균형 데이터 세트에서 더 일반적으로 사용되는 라벨입니다. 예를 들어 부정 라벨 99% 와 긍정 라벨 1% 가 포함되어 있는 데이터 세트의 경우 부정 라벨이 다수 범주입니다.
소수 클래스와 대비되는 개념입니다.
자세한 내용은 머신러닝 단기집중과정의 데이터 세트: 불균형 데이터 세트를 참고하세요.
미니 배치
하나의 반복에서 처리되는 배치의 무작위로 선택된 소규모 부분집합입니다. 미니 배치의 배치 크기는 일반적으로 10~1,000개입니다.
예를 들어 전체 학습 세트 (전체 배치)가 1,000개의 예시로 구성되어 있다고 가정해 보겠습니다. 각 미니 배치의 배치 크기를 20으로 설정한다고 가정해 보겠습니다. 따라서 각 반복에서는 1,000개의 예 중 무작위로 선택된 20개의 예에 대한 손실을 확인한 다음 이에 따라 가중치와 편향을 조정합니다.
전체 배치에 있는 모든 예의 손실보다 미니배치의 손실을 계산하는 것이 훨씬 효율적입니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 하이퍼파라미터를 참고하세요.
소수 범주
클래스 불균형 데이터 세트의 덜 일반적인 라벨입니다. 예를 들어 부정 라벨 99% 와 긍정 라벨 1% 가 포함되어 있는 데이터 세트의 경우 긍정 라벨이 소수 범주입니다.
다수 클래스와 대비되는 개념입니다.
자세한 내용은 머신러닝 단기집중과정의 데이터 세트: 불균형 데이터 세트를 참고하세요.
모델
일반적으로 입력 데이터를 처리하고 출력을 반환하는 모든 수학적 구성입니다. 달리 말해 모델은 시스템이 예측을 수행하는 데 필요한 파라미터 및 구조의 집합입니다. 지도 머신러닝에서 모델은 예를 입력으로 사용하고 예측을 출력으로 추론합니다. 지도 학습 머신러닝 내에서 모델은 약간 다릅니다. 예를 들면 다음과 같습니다.
- 선형 회귀 모델은 가중치 집합과 편향으로 구성됩니다.
- 신경망 모델은 다음으로 구성됩니다.
- 결정 트리 모델은 다음으로 구성됩니다.
- 트리의 모양입니다. 즉, 조건과 리프가 연결되는 패턴입니다.
- 조건과 리브입니다.
모델을 저장, 복원 또는 복사할 수 있습니다.
비지도 머신러닝은 모델(일반적으로 입력 예시를 가장 적절한 클러스터에 매핑할 수 있는 함수)도 생성합니다.
다중 클래스 분류
지도 학습에서 데이터 세트에 라벨의 두 개 이상 클래스가 포함된 분류 문제입니다. 예를 들어 Iris 데이터 세트의 라벨은 다음 세 가지 클래스 중 하나여야 합니다.
- Iris setosa
- Iris virginica
- Iris versicolor
새로운 예시에서 아이리스 유형을 예측하는 아이리스 데이터 세트에서 학습된 모델은 다중 클래스 분류를 실행합니다.
반면 정확히 두 클래스를 구분하는 분류 문제는 이진 분류 모델입니다. 예를 들어 스팸 또는 스팸 아님을 예측하는 이메일 모델은 이진 분류 모델입니다.
클러스터링 문제에서 다중 클래스 분류는 두 개 이상의 클러스터를 의미합니다.
자세한 내용은 머신러닝 단기집중과정의 신경망: 다중 클래스 분류를 참고하세요.
N
음성 클래스
이진 분류에서는 클래스 중 하나는 포지티브로, 다른 하나는 네거티브로 규정됩니다. 포지티브 클래스는 모델에서 테스트하는 대상 또는 이벤트이고, 네거티브 클래스는 그와 다른 가능성입니다. 예를 들면 다음과 같습니다.
- 의료 검사의 네거티브 클래스는 '종양 아님'일 수 있습니다.
- 이메일 분류 모델의 네거티브 클래스는 '스팸 아님'일 수 있습니다.
포지티브 클래스와 대비되는 개념입니다.
출력은
숨겨진 레이어가 하나 이상 포함된 모델 심층신경망은 여러 히든 레이어가 포함된 신경망의 한 유형입니다. 예를 들어 다음 다이어그램은 두 개의 숨겨진 레이어가 포함된 심층 신경망을 보여줍니다.
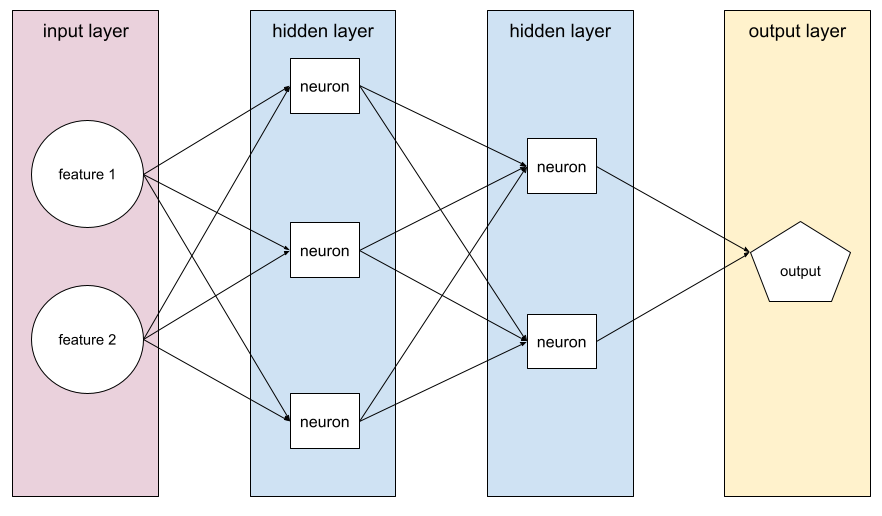
신경망의 각 뉴런은 다음 레이어의 모든 노드에 연결됩니다. 예를 들어 위의 다이어그램에서 첫 번째 히든 레이어의 세 뉴런 각각이 두 번째 히든 레이어의 두 뉴런 모두에 별도로 연결되어 있습니다.
컴퓨터에 구현된 신경망은 뇌 및 기타 신경계에서 발견되는 신경망과 구분하기 위해 인공 신경망이라고도 합니다.
일부 신경망은 다양한 특성과 라벨 간의 매우 복잡한 비선형 관계를 모방할 수 있습니다.
자세한 내용은 머신러닝 단기집중과정의 신경망을 참고하세요.
뉴런
머신러닝에서 신경망의 히든 레이어 내에 있는 개별 단위입니다. 각 뉴런은 다음 두 단계 작업을 실행합니다.
첫 번째 숨겨진 레이어의 뉴런은 입력 레이어의 특성 값에서 입력을 수락합니다. 첫 번째 히든 레이어를 넘어선 히든 레이어의 뉴런은 이전 히든 레이어의 뉴런으로부터 입력을 받습니다. 예를 들어 두 번째 히든 레이어의 뉴런은 첫 번째 히든 레이어의 뉴런에서 입력을 받습니다.
다음 그림은 두 뉴런과 그 입력을 강조 표시합니다.
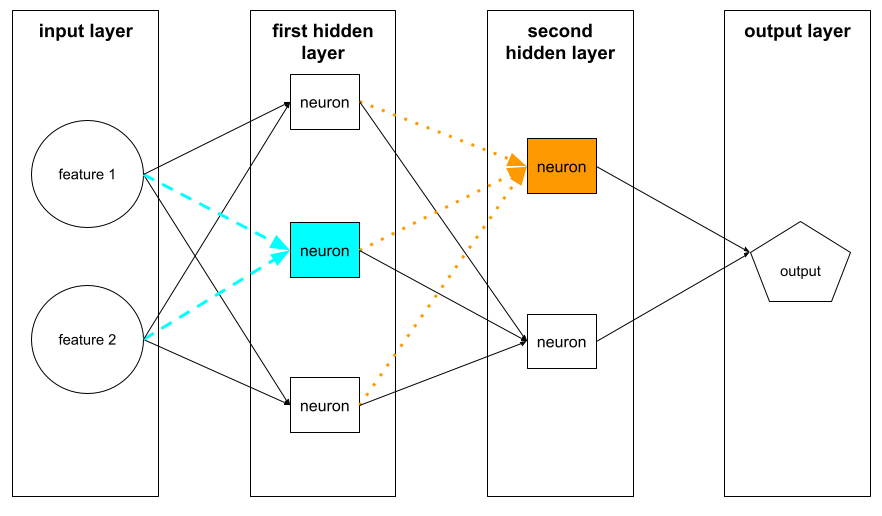
신경망의 뉴런은 뇌와 신경계의 다른 부분에 있는 뉴런의 동작을 모방합니다.
노드 (신경망)
자세한 내용은 머신러닝 단기집중과정의 신경망을 참고하세요.
비선형
덧셈과 곱셈만으로는 나타낼 수 없는 두 개 이상의 변수 간의 관계입니다. 선형 관계는 선으로 나타낼 수 있지만 비선형 관계는 선으로 나타낼 수 없습니다. 예를 들어 단일 특성을 단일 라벨과 각각 연결하는 두 모델을 생각해 보세요. 왼쪽 모델은 선형이고 오른쪽 모델은 비선형입니다.

머신러닝 단기집중과정의 신경망: 노드 및 숨겨진 레이어에서 다양한 종류의 비선형 함수를 실험해 보세요.
비정상성
하나 이상의 측정기준(일반적으로 시간)에 따라 값이 변경되는 특성입니다. 예를 들어 다음과 같은 비정상성 사례를 생각해 보세요.
- 특정 매장에서 판매되는 수영복의 수는 계절에 따라 다릅니다.
- 특정 지역에서 수확되는 특정 과일의 양은 연중 대부분 0이지만 짧은 기간 동안은 많습니다.
- 기후 변화로 인해 연간 평균 기온이 변화하고 있습니다.
정상성과 대비되는 개념입니다.
정규화
변수의 실제 값 범위를 다음과 같은 표준 값 범위로 변환하는 프로세스를 광범위하게 설명합니다.
- -1~+1
- 0~1
- Z 점수 (대략 -3~+3)
예를 들어 특정 특성의 실제 값 범위가 800~2,400이라고 가정해 보겠습니다. 특성 엔지니어링의 일환으로 실제 값을 -1~+1과 같은 표준 범위로 정규화할 수 있습니다.
정규화는 특성 엔지니어링에서 일반적인 작업입니다. 특성 벡터의 모든 숫자 특성의 범위가 대략 동일하면 모델이 더 빠르게 학습되고 더 나은 예측을 생성합니다.
Z 점수 정규화도 참고하세요.
자세한 내용은 머신러닝 단기집중과정의 숫자 데이터: 정규화를 참고하세요.
수치 데이터
정수 또는 실수로 나타낸 특성입니다. 예를 들어 주택 평가 모델은 주택의 크기 (제곱피트 또는 제곱미터)를 숫자 데이터로 나타낼 것입니다. 특성을 숫자 데이터로 나타내는 것은 특성의 값이 라벨과 수학적 관계가 있음을 나타냅니다. 즉, 주택의 평방미터 수는 주택의 가치와 수학적 관계가 있을 수 있습니다.
모든 정수 데이터가 숫자 데이터로 표현되는 것은 아닙니다. 예를 들어 일부 지역의 우편번호는 정수입니다. 하지만 정수 우편번호는 모델에서 숫자 데이터로 표현하면 안 됩니다. 20000 우편번호가 10000 우편번호보다 두 배 (또는 절반) 더 강력하지 않기 때문입니다. 또한 우편번호가 다르면 부동산 가치가 다를 수 있지만 우편번호 20000의 부동산 가치가 우편번호 10000의 부동산 가치의 두 배라고 가정할 수는 없습니다.
따라서 우편번호는 범주형 데이터로 표현되어야 합니다.
수치 특성을 연속 특성이라고도 합니다.
자세한 내용은 머신러닝 단기집중과정의 숫자 데이터 작업을 참고하세요.
O
오프라인
static의 동의어입니다.
오프라인 추론
모델이 예측을 일괄적으로 생성한 다음 이러한 예측을 캐싱 (저장)하는 프로세스입니다. 그러면 앱이 모델을 다시 실행하는 대신 캐시에서 추론된 예측에 액세스할 수 있습니다.
예를 들어 4시간마다 지역 날씨 예보(예측)를 생성하는 모델을 생각해 보세요. 각 모델 실행 후 시스템은 모든 지역 날씨 예보를 캐시합니다. 날씨 앱은 캐시에서 일기예보를 가져옵니다.
오프라인 추론을 정적 추론이라고도 합니다.
온라인 추론과 대비되는 개념입니다. 자세한 내용은 머신러닝 단기집중과정의 프로덕션 ML 시스템: 정적 추론과 동적 추론 비교을 참고하세요.
원-핫 인코딩
다음과 같은 벡터로 범주형 데이터를 표현합니다.
- 한 요소가 1로 설정됩니다.
- 다른 모든 요소는 0으로 설정됩니다.
원-핫 인코딩은 가능한 값의 유한 집합을 갖는 문자열 또는 식별자를 표현하는 데 널리 사용됩니다.
예를 들어 Scandinavia라는 특정 범주형 특성에 다음과 같은 5가지 가능한 값이 있다고 가정해 보겠습니다.
- '덴마크'
- '스웨덴'
- '노르웨이'
- '핀란드'
- '아이슬란드'
원-핫 인코딩은 5개의 값을 다음과 같이 나타낼 수 있습니다.
| 국가 | 벡터 | ||||
|---|---|---|---|---|---|
| '덴마크' | 1 | 0 | 0 | 0 | 0 |
| '스웨덴' | 0 | 1 | 0 | 0 | 0 |
| '노르웨이' | 0 | 0 | 1 | 0 | 0 |
| '핀란드' | 0 | 0 | 0 | 1 | 0 |
| '아이슬란드' | 0 | 0 | 0 | 0 | 1 |
원-핫 인코딩 덕분에 모델은 5개 국가 각각에 따라 다른 연결을 학습할 수 있습니다.
특성을 숫자 데이터로 표현하는 것은 원-핫 인코딩의 대안입니다. 안타깝게도 스칸디나비아 국가를 숫자로 표현하는 것은 적절하지 않습니다. 예를 들어 다음 숫자 표현을 살펴보세요.
- '덴마크'는 0입니다.
- '스웨덴'은 1
- '노르웨이'는 2
- '핀란드'는 3
- '아이슬란드'는 4
숫자 인코딩을 사용하면 모델이 원시 숫자를 수학적으로 해석하고 이러한 숫자를 기반으로 학습하려고 합니다. 하지만 아이슬란드는 실제로 노르웨이의 두 배 (또는 절반)가 아니므로 모델이 이상한 결론을 내릴 수 있습니다.
자세한 내용은 머신러닝 단기집중과정의 범주형 데이터: 어휘 및 원-핫 인코딩을 참고하세요.
일대다
클래스가 N개인 분류 문제에서, 가능한 각 결과에 하나씩 서로 다른 N개의 이진 분류 모델로 구성된 솔루션입니다. 예를 들어 예시를 동물, 식물 또는 광물로 분류하는 모델이 있다고 가정해 보겠습니다. 일대다 솔루션은 다음 세 가지 별도의 이진 분류 모델을 제공합니다.
- 동물 대 동물 아님
- 채소와 비채소
- 무기물과 유기물의 차이
online
동적의 동의어입니다.
온라인 추론
요청에 따라 예측을 생성합니다. 예를 들어 앱이 모델에 입력을 전달하고 예측을 요청한다고 가정해 보겠습니다. 온라인 추론을 사용하는 시스템은 모델을 실행하여 요청에 응답합니다 (예측을 앱에 반환).
오프라인 추론과 대비되는 개념입니다.
자세한 내용은 머신러닝 단기집중과정의 프로덕션 ML 시스템: 정적 추론과 동적 추론 비교을 참고하세요.
출력 레이어
신경망의 '최종' 레이어입니다. 출력 레이어에는 예측이 포함됩니다.
다음 그림은 입력 레이어, 히든 레이어 2개, 출력 레이어가 있는 작은 심층 신경망을 보여줍니다.
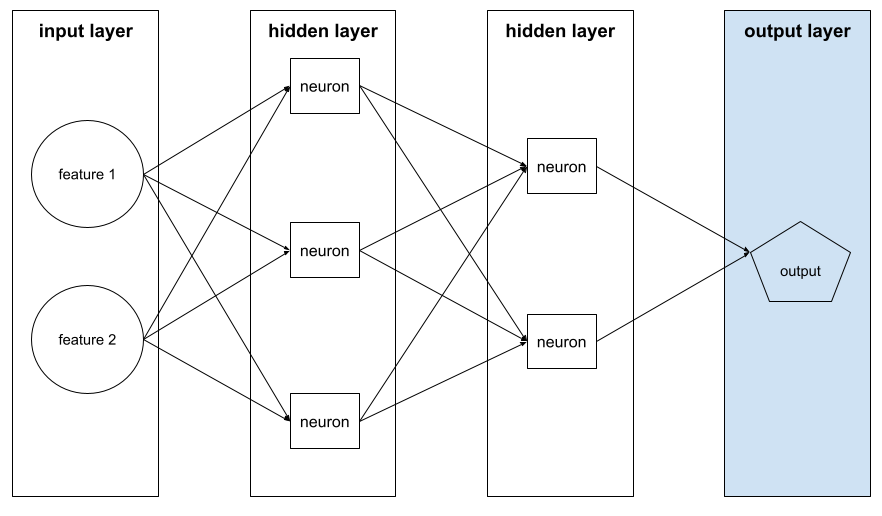
과적합
생성된 모델이 학습 데이터와 지나치게 일치하여 새 데이터를 올바르게 예측하지 못하는 경우입니다.
정규화는 과적합을 줄일 수 있습니다. 크고 다양한 학습 세트로 학습하면 과적합을 줄일 수도 있습니다.
자세한 내용은 머신러닝 단기집중과정의 과적합을 참고하세요.
P
pandas
numpy를 기반으로 빌드된 열 지향 데이터 분석 API입니다. TensorFlow를 비롯한 다양한 머신러닝 프레임워크에서 pandas 데이터 구조를 입력으로 지원합니다. 자세한 내용은 Pandas 문서를 참고하세요.
파라미터
모델이 학습 중에 학습하는 가중치와 편향입니다. 예를 들어 선형 회귀 모델에서 매개변수는 다음 수식의 편향 (b)과 모든 가중치 (w1, w2 등)로 구성됩니다.
반면 초매개변수는 사용자 (또는 초매개변수 조정 서비스)가 모델에 제공하는 값입니다. 예를 들어 학습률은 초매개변수 중 하나입니다.
양성 클래스
테스트할 클래스입니다.
예를 들어 암 모델의 포지티브 클래스는 '종양'일 수 있습니다. 이메일 분류 모델의 포지티브 클래스는 '스팸'일 수 있습니다.
네거티브 클래스와 대비되는 개념입니다.
후처리
모델이 실행된 후에 모델의 출력을 조정합니다. 후처리를 사용하면 모델 자체를 수정하지 않고도 공정성 제약 조건을 적용할 수 있습니다.
예를 들어 진양성률이 해당 속성의 모든 값에 대해 동일한지 확인하여 일부 속성에 대해 기회의 평등이 유지되도록 분류 기준을 설정하여 이진 분류 모델에 후처리를 적용할 수 있습니다.
precision
분류 모델과 관련해 다음과 같은 의문에 답하는 측정항목입니다.
모델이 포지티브 클래스를 예측한 경우 예측의 몇 퍼센트가 올바른가요?
공식은 다음과 같습니다.
각 항목의 의미는 다음과 같습니다.
- 참양성은 모델이 포지티브 클래스를 정확하게 예측했음을 의미합니다.
- 거짓양성은 모델이 포지티브 클래스를 잘못 예측했음을 의미합니다.
예를 들어 모델에서 200개의 포지티브 예측을 했다고 가정해 보겠습니다. 이 200개의 긍정적 예측 중
- 150개가 참양성이었습니다.
- 50건은 거짓양성이었습니다.
이 경우에는 다음과 같습니다.
자세한 내용은 머신러닝 단기집중과정의 분류: 정확도, 재현율, 정밀도 및 관련 측정항목을 참고하세요.
예측
모델의 출력입니다. 예를 들면 다음과 같습니다.
- 이진 분류 모델의 예측은 포지티브 클래스 또는 네거티브 클래스입니다.
- 다중 클래스 분류 모델의 예측은 하나의 클래스입니다.
- 선형 회귀 모델의 예측은 숫자입니다.
프록시 라벨
데이터 세트에서 직접 사용할 수 없는 라벨을 대략적으로 지정하는 데 사용되는 데이터입니다.
예를 들어 직원 스트레스 수준을 예측하는 모델을 학습시켜야 한다고 가정해 보겠습니다. 데이터 세트에 예측 기능이 많이 포함되어 있지만 스트레스 수준이라는 라벨은 포함되어 있지 않습니다. 굴하지 않고 스트레스 수준의 프록시 라벨로 '직장 내 사고'를 선택합니다. 결국 스트레스를 많이 받는 직원은 침착한 직원보다 사고를 더 많이 냅니다. 아니면 그럴까요? 직장 내 사고는 여러 가지 이유로 실제로 증가했다가 감소할 수 있습니다.
두 번째 예로, 비가 오나요?를 데이터 세트의 불리언 라벨로 지정하려고 하지만 데이터 세트에 비 데이터가 없다고 가정합니다. 사진을 사용할 수 있는 경우 우산을 들고 있는 사람의 사진을 is it raining?에 대한 유추 라벨로 지정할 수 있습니다. 이것이 좋은 프록시 라벨인가요? 그럴 수도 있지만 일부 문화권에서는 비보다 햇빛을 가리기 위해 우산을 들고 다니는 것이 더 일반적일 수 있습니다.
프록시 라벨은 완전하지 않은 경우가 많습니다. 가능한 경우 프록시 라벨보다 실제 라벨을 선택하세요. 하지만 실제 라벨이 없는 경우 가장 끔찍하지 않은 프록시 라벨 후보를 선택하여 프록시 라벨을 매우 신중하게 선택하세요.
자세한 내용은 머신러닝 단기집중과정의 데이터 세트: 라벨을 참고하세요.
R
RAG
검색 증강 생성의 약어입니다.
평가자
예시에 라벨을 제공하는 사람입니다. '주석 작성자'는 평가자의 또 다른 이름입니다.
자세한 내용은 머신러닝 단기집중과정의 범주형 데이터: 일반적인 문제를 참고하세요.
recall
분류 모델과 관련해 다음과 같은 의문에 답하는 측정항목입니다.
그라운드 트루스가 포지티브 클래스인 경우 모델이 포지티브 클래스로 올바르게 식별한 예측의 비율은 얼마인가요?
공식은 다음과 같습니다.
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
각 항목의 의미는 다음과 같습니다.
- 참양성은 모델이 포지티브 클래스를 정확하게 예측했음을 의미합니다.
- 거짓음성은 모델이 네거티브 클래스를 잘못 예측했음을 의미합니다.
예를 들어 모델이 정답이 포지티브 클래스인 예시에 대해 200개의 예측을 했다고 가정해 보겠습니다. 이 200개의 예측 중
- 180개가 참양성이었습니다.
- 20건은 거짓음성이었습니다.
이 경우에는 다음과 같습니다.
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
자세한 내용은 분류: 정확도, 재현율, 정밀도 및 관련 측정항목을 참고하세요.
정류 선형 유닛 (ReLU)
다음 동작을 따르는 활성화 함수입니다.
- 입력이 음수 또는 0이면 출력은 0입니다.
- 입력이 양수이면 출력은 입력과 같습니다.
예를 들면 다음과 같습니다.
- 입력이 -3이면 출력은 0입니다.
- 입력이 +3이면 출력은 3.0입니다.
다음은 ReLU의 그래프입니다.
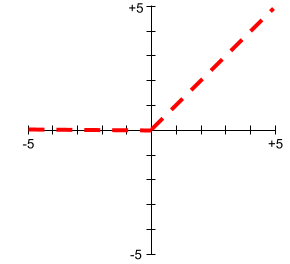
ReLU는 매우 인기 있는 활성화 함수입니다. ReLU는 동작이 단순하지만 신경망이 특성과 라벨 간의 비선형 관계를 학습할 수 있도록 지원합니다.
회귀 모델
비공식적으로 숫자 예측을 생성하는 모델입니다. (반대로 분류 모델은 클래스 예측을 생성합니다.) 예를 들어 다음은 모두 회귀 모델입니다.
- 특정 주택의 가치를 유로로 예측하는 모델(예: 423,000)
- 특정 나무의 기대 수명을 연 단위로 예측하는 모델입니다(예: 23.2).
- 다음 6시간 동안 특정 도시에 내릴 비의 양을 인치로 예측하는 모델입니다(예: 0.18).
일반적인 두 가지 유형의 회귀 모델은 다음과 같습니다.
숫자 예측을 출력하는 모든 모델이 회귀 모델은 아닙니다. 숫자 예측이 숫자 클래스 이름을 갖는 분류 모델인 경우도 있습니다. 예를 들어 숫자 우편번호를 예측하는 모델은 회귀 모델이 아닌 분류 모델입니다.
정규화
과적합을 줄이는 메커니즘 일반적인 정규화 유형은 다음과 같습니다.
정규화는 모델의 복잡성에 대한 페널티로 정의할 수도 있습니다.
자세한 내용은 머신러닝 단기집중과정의 과적합: 모델 복잡성을 참고하세요.
정규화율
학습 중 정규화의 상대적 중요도를 지정하는 숫자입니다. 정규화 비율을 높이면 과적합이 줄어들지만 모델의 예측력이 감소할 수 있습니다. 반대로 정규화 비율을 줄이거나 생략하면 과적합이 증가합니다.
자세한 내용은 머신러닝 단기집중과정의 과적합: L2 정규화를 참고하세요.
ReLU
Rectified Linear Unit의 약어입니다.
검색 증강 생성(RAG)
모델이 학습된 후에 검색된 지식 소스로 그라운딩하여 대규모 언어 모델 (LLM) 출력의 품질을 개선하는 기법입니다. RAG는 학습된 LLM에 신뢰할 수 있는 기술 자료나 문서에서 검색된 정보에 대한 액세스 권한을 제공하여 LLM 대답의 정확성을 개선합니다.
검색 증강 생성을 사용하는 일반적인 동기는 다음과 같습니다.
- 모델이 생성한 대답의 사실 정확성을 높입니다.
- 모델이 학습되지 않은 지식에 액세스하도록 허용
- 모델이 사용하는 지식 변경
- 모델이 출처를 인용할 수 있도록 지원합니다.
예를 들어 화학 앱이 PaLM API를 사용하여 사용자 질문과 관련된 요약을 생성한다고 가정해 보겠습니다. 앱의 백엔드가 쿼리를 수신하면 백엔드는 다음을 실행합니다.
- 사용자의 질문과 관련된 데이터를 검색합니다.
- 사용자의 질문에 관련 화학 데이터를 추가합니다 ('보강').
- 추가된 데이터를 기반으로 요약을 만들도록 LLM에 지시합니다.
수신자 조작 특성 곡선 (ROC curve, Receiver Operating Characteristic curve)
이진 분류에서 다양한 분류 임곗값에 대한 참양성률 대 거짓양성률 그래프입니다.
ROC 곡선의 모양은 이진 분류 모델이 포지티브 클래스와 네거티브 클래스를 구분하는 능력을 나타냅니다. 예를 들어 이진 분류 모델이 모든 음성 클래스를 모든 양성 클래스와 완벽하게 구분한다고 가정해 보겠습니다.
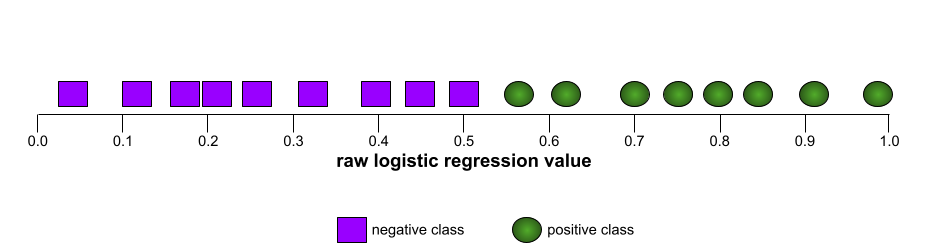
위 모델의 ROC 곡선은 다음과 같습니다.
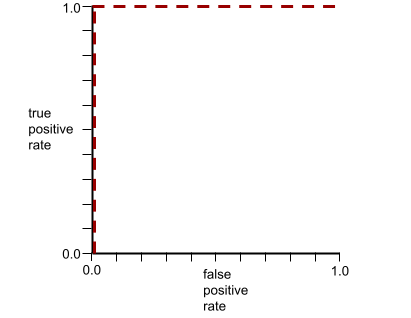
반면 다음 그림은 부정 클래스를 긍정 클래스와 전혀 구분할 수 없는 형편없는 모델의 원시 로지스틱 회귀 값을 그래프로 나타냅니다.
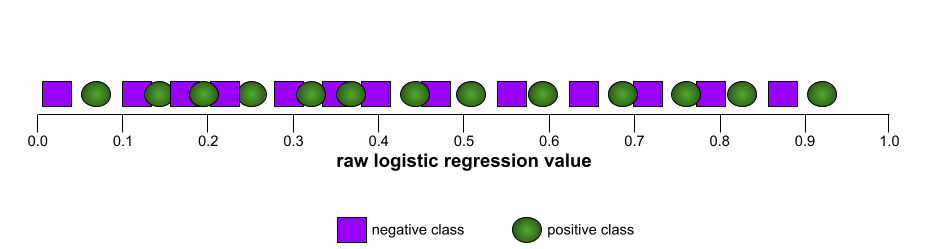
이 모델의 ROC 곡선은 다음과 같습니다.
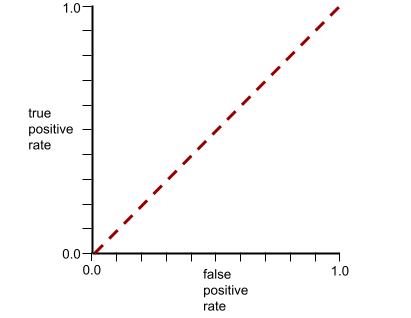
한편 실제 세계에서는 대부분의 이진 분류 모델이 포지티브 클래스와 네거티브 클래스를 어느 정도 구분하지만 완벽하지는 않습니다. 따라서 일반적인 ROC 곡선은 다음 두 극단 사이에 있습니다.
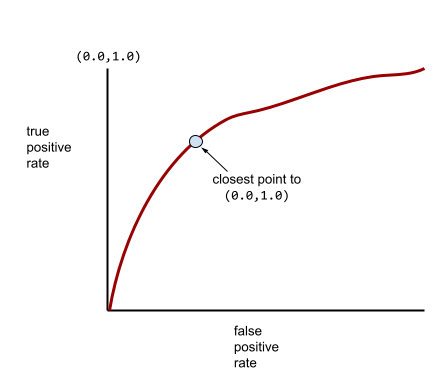
이론적으로 ROC 곡선에서 (0.0,1.0)에 가장 가까운 점은 이상적인 분류 임곗값을 나타냅니다. 하지만 이상적인 분류 기준점을 선택하는 데 영향을 미치는 다른 실제 문제가 몇 가지 있습니다. 예를 들어 거짓음성이 거짓양성보다 훨씬 더 큰 고통을 유발할 수 있습니다.
AUC라는 수치 측정항목은 ROC 곡선을 단일 부동 소수점 값으로 요약합니다.
평균 제곱근 오차(RMSE)
평균 제곱 오차의 제곱근입니다.
S
시그모이드 함수
입력 값을 제한된 범위(일반적으로 0~1 또는 -1~+1)로 '압축'하는 수학 함수입니다. 즉, 시그모이드에 어떤 숫자 (2, 100만, -10억 등)를 전달하더라도 출력은 제한된 범위 내에 있습니다. 시그모이드 활성화 함수의 플롯은 다음과 같습니다.

시그모이드 함수는 머신러닝에서 다음과 같은 여러 용도로 사용됩니다.
소프트맥스
다중 클래스 분류 모델에서 가능한 각 클래스의 확률을 결정하는 함수입니다. 확률의 합은 정확히 1.0입니다. 예를 들어 다음 표에서는 소프트맥스가 다양한 확률을 분배하는 방법을 보여줍니다.
| 이미지가... | 확률 |
|---|---|
| 개 | .85 |
| 고양이 | .13 |
| 말 | .02 |
소프트맥스를 전체 소프트맥스라고도 합니다.
후보 샘플링과 대비되는 개념입니다.
자세한 내용은 머신러닝 단기집중과정의 신경망: 다중 클래스 분류를 참고하세요.
희소 특성
값이 대부분 0이거나 비어 있는 특징입니다. 예를 들어 1 값이 하나 있고 0 값이 백만 개 있는 특성은 희소합니다. 반면 밀도 높은 특징은 대부분의 값이 0이거나 비어 있지 않습니다.
머신러닝에서 놀라울 정도로 많은 특성이 희소 특성입니다. 범주형 특성은 일반적으로 희소 특성입니다. 예를 들어 숲에 있을 수 있는 300가지 수종 중 하나의 예에서는 단풍나무만 식별할 수 있습니다. 또는 동영상 라이브러리에 있을 수 있는 수백만 개의 동영상 중에서 단일 예시가 '카사블랑카'만 식별할 수 있습니다.
모델에서 일반적으로 원-핫 인코딩을 사용하여 희소 특성을 나타냅니다. 원-핫 인코딩이 큰 경우 효율성을 높이기 위해 원-핫 인코딩 위에 임베딩 레이어를 배치할 수 있습니다.
희소 표현
희소 기능에서 0이 아닌 요소의 위치만 저장합니다.
예를 들어 species이라는 범주형 특성이 특정 숲에 있는 36가지 수종을 식별한다고 가정해 보겠습니다. 또한 각 예는 단일 종만 식별한다고 가정합니다.
원-핫 벡터를 사용하여 각 예의 수종을 나타낼 수 있습니다.
원-핫 벡터에는 1 하나 (해당 예의 특정 나무 종을 나타냄)와 0 35개 (해당 예에 없는 나무 종 35개를 나타냄)가 포함됩니다. 따라서 maple의 원-핫 표현은 다음과 같을 수 있습니다.

또는 희소 표현은 특정 종의 위치만 식별합니다. maple이 24번째 위치에 있다면 maple의 희소 표현은 다음과 같습니다.
24
희소 표현이 원-핫 표현보다 훨씬 더 간결합니다.
자세한 내용은 머신러닝 단기집중과정의 범주형 데이터 작업을 참고하세요.
희소 벡터
값이 대부분 0인 벡터입니다. 희소 특성 및 희소성도 참고하세요.
제곱 손실
L2 손실의 동의어입니다.
정적
지속적으로 수행하는 것이 아니라 한 번 수행하는 작업입니다. 정적과 오프라인은 동의어입니다. 다음은 머신러닝에서 정적 및 오프라인을 사용하는 일반적인 경우입니다.
- 정적 모델 (또는 오프라인 모델)은 한 번 학습된 후 일정 기간 사용되는 모델입니다.
- 정적 학습 (또는 오프라인 학습)은 정적 모델을 학습하는 프로세스입니다.
- 정적 추론 (또는 오프라인 추론)은 모델이 한 번에 일괄 예측을 생성하는 프로세스입니다.
동적과 대비되는 개념입니다.
정적 추론
오프라인 추론의 동의어입니다.
정상성
하나 이상의 측정기준(일반적으로 시간)에서 값이 변경되지 않는 특성입니다. 예를 들어 2021년과 2023년에 값이 거의 동일한 특성은 정상성을 나타냅니다.
실제로는 정상성을 나타내는 특징이 거의 없습니다. 안정성과 동의어인 기능 (예: 해수면)도 시간이 지남에 따라 변합니다.
비정상성과 대비되는 개념입니다.
확률적 경사하강법 (SGD, stochastic gradient descent)
배치 크기가 1인 경사하강법 알고리즘입니다. 즉, SGD는 학습 세트에서 무작위로 균일하게 선택한 하나의 예로 학습합니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀: 하이퍼파라미터를 참고하세요.
지도 머신러닝
특성과 해당 라벨에서 모델을 학습시킵니다. 지도 머신러닝은 일련의 질문과 그에 상응하는 답변을 공부하여 주제를 학습하는 것과 유사합니다. 질문과 답변 간의 매핑을 숙달한 후 학생은 동일한 주제에 관한 새로운 (이전에 본 적 없는) 질문에 답변할 수 있습니다.
비지도 머신러닝과 비교되는 개념입니다.
자세한 내용은 머신러닝 소개 과정의 감독 학습을 참고하세요.
합성 특성
입력 특성 중에는 없지만 하나 이상의 입력 특성으로부터 조립되는 특성입니다. 합성 특성을 만드는 방법은 다음과 같습니다.
- 연속 특성을 범위 빈으로 버케팅합니다.
- 특성 교차를 생성합니다.
- 하나의 특성 값에 다른 특성 값이나
자체 특성 값을 곱하거나 나눕니다. 예를 들어
a와b이 입력 특성인 경우 합성 특성의 예는 다음과 같습니다.- ab
- a2
- 초월 함수를 특성 값에 적용합니다. 예를 들어
c이 입력 특성인 경우 합성 특성의 예는 다음과 같습니다.- sin(c)
- ln(c)
정규화 또는 조정만으로 생성한 특성은 합성 특성에 해당하지 않습니다.
T
테스트 손실
테스트 세트에 대한 모델의 손실을 나타내는 측정항목입니다. 모델을 빌드할 때는 일반적으로 테스트 손실을 최소화하려고 합니다. 테스트 손실이 낮을수록 낮은 학습 손실 또는 낮은 검증 손실보다 강력한 품질 신호이기 때문입니다.
테스트 손실과 학습 손실 또는 검증 손실 간의 큰 격차는 정규화 비율을 늘려야 함을 나타낼 수 있습니다.
학습
모델을 구성하는 이상적인 매개변수 (가중치 및 편향)를 결정하는 과정입니다. 학습 중에 시스템은 예를 읽어 들이고 매개변수를 점진적으로 조정합니다. 학습에서는 각 예시를 몇 번에서 수십억 번까지 사용합니다.
자세한 내용은 머신러닝 소개 과정의 감독 학습을 참고하세요.
학습 손실
특정 학습 반복 중에 모델의 손실을 나타내는 측정항목입니다. 예를 들어 손실 함수가 평균 제곱 오차라고 가정해 보겠습니다. 예를 들어 10번째 반복의 학습 손실 (평균 제곱 오차)이 2.2이고 100번째 반복의 학습 손실이 1.9일 수 있습니다.
손실 곡선은 학습 손실과 반복 횟수를 비교하여 표시합니다. 손실 곡선은 학습에 관한 다음과 같은 힌트를 제공합니다.
- 경사가 아래로 향하면 모델이 개선되고 있음을 의미합니다.
- 위쪽으로 기울어지면 모델이 악화되고 있음을 의미합니다.
- 경사가 평평하다는 것은 모델이 수렴에 도달했음을 의미합니다.
예를 들어 다음은 다소 이상적인 손실 곡선을 보여줍니다.
- 초기 반복 중에 급격한 하향 경사: 모델이 빠르게 개선됨을 의미합니다.
- 학습이 끝날 때까지 점차 평탄해지지만 여전히 하향하는 기울기. 이는 초기 반복보다 약간 느린 속도로 모델이 계속 개선됨을 의미합니다.
- 학습이 끝날 때 평평한 기울기(수렴을 나타냄)
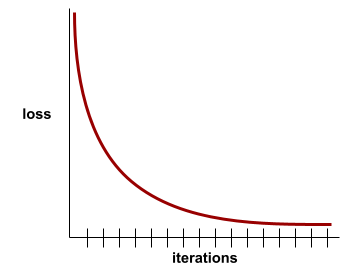
학습 손실도 중요하지만 일반화도 참고하세요.
학습-제공 편향
학습 중 모델의 성능과 서빙 중 동일한 모델의 성능 간의 차이입니다.
학습 세트
모델을 학습시키는 데 사용되는 데이터 세트의 하위 집합입니다.
일반적으로 데이터 세트의 예는 다음과 같은 세 가지 개별 하위 집합으로 나뉩니다.
데이터 세트의 각 예시는 앞의 하위 집합 중 하나에만 속해야 합니다. 예를 들어 단일 예시가 학습 세트와 검증 세트에 모두 속해서는 안 됩니다.
자세한 내용은 머신러닝 단기집중과정의 데이터 세트: 원본 데이터 세트 나누기를 참고하세요.
참음성 (TN, true negative)
모델에서 네거티브 클래스를 올바르게 예측한 예입니다. 예를 들어 모델에서 특정 이메일 메시지가 스팸이 아닌 것으로 추론했으며 실제로도 스팸이 아닌 경우가 여기에 해당합니다.
참양성 (TP)
모델에서 포지티브 클래스로 올바르게 예측한 예입니다. 예를 들어 모델에서 특정 이메일 메시지가 스팸인 것으로 추론했으며 실제로도 스팸이었던 경우가 여기에 해당합니다.
참양성률 (TPR)
재현율의 동의어입니다. 이는 다음과 같은 의미입니다.
참양성률은 ROC 곡선의 y축입니다.
U
과소적합
모델에서 학습 데이터의 복잡성을 완전히 포착하지 않았기 때문에 열악한 예측 기능으로 모델을 생성하는 경우입니다. 다음과 같은 여러 문제로 인해 과소적합이 발생할 수 있습니다.
자세한 내용은 머신러닝 단기집중과정의 과적합을 참고하세요.
라벨이 없는 예
특성은 포함하지만 라벨은 포함하지 않는 예 예를 들어 다음 표에는 주택 가치 평가 모델의 라벨이 지정되지 않은 세 가지 예가 표시되어 있습니다. 각 예에는 세 가지 특징이 있지만 주택 가치는 없습니다.
| 침실 수 | 욕실 수 | 주택 연령 |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
지도 머신러닝에서 모델은 라벨이 지정된 예로 학습하고 라벨이 지정되지 않은 예에 대한 예측을 수행합니다.
준지도 및 비지도 학습에서는 라벨이 없는 예가 학습에 사용됩니다.
라벨이 없는 예와 라벨이 있는 예를 비교합니다.
비지도 머신러닝
일반적으로 라벨이 없는 데이터 세트에서 패턴을 찾도록 모델을 학습시킵니다.
비지도 머신러닝의 가장 일반적인 용도는 데이터를 서로 비슷한 예의 그룹으로 클러스터링하는 것입니다. 예를 들어 비지도 머신러닝 알고리즘은 음악의 다양한 속성을 기반으로 노래를 클러스터링할 수 있습니다. 결과 클러스터는 다른 머신러닝 알고리즘 (예: 음악 추천 서비스)의 입력이 될 수 있습니다. 클러스터링은 유용한 라벨이 부족하거나 없는 경우에 도움이 될 수 있습니다. 예를 들어 악용 및 사기 행위 방지와 같은 분야에서 클러스터는 사람이 데이터를 이해하는 데 도움을 줄 수 있습니다.
지도 머신러닝과 대비되는 개념입니다.
자세한 내용은 ML 소개 과정의 머신러닝이란 무엇인가요?를 참고하세요.
V
validation
모델 품질의 초기 평가입니다. 검증은 검증 세트에 대해 모델의 예측 품질을 확인합니다.
검증 세트는 학습 세트와 다르므로 검증을 통해 과적합을 방지할 수 있습니다.
검증 세트를 기준으로 모델을 평가하는 것을 첫 번째 테스트 라운드로 생각하고 테스트 세트를 기준으로 모델을 평가하는 것을 두 번째 테스트 라운드로 생각할 수 있습니다.
검증 손실
학습의 특정 반복 중에 검증 세트에서 모델의 손실을 나타내는 측정항목입니다.
일반화 곡선도 참고하세요.
검증 세트
학습된 모델에 대해 초기 평가를 실행하는 데이터 세트의 하위 집합입니다. 일반적으로 테스트 세트에 대해 모델을 평가하기 전에 검증 세트에 대해 학습된 모델을 여러 번 평가합니다.
일반적으로 데이터 세트의 예는 다음과 같은 세 가지 개별 하위 집합으로 나뉩니다.
데이터 세트의 각 예시는 앞의 하위 집합 중 하나에만 속해야 합니다. 예를 들어 단일 예시가 학습 세트와 검증 세트에 모두 속해서는 안 됩니다.
자세한 내용은 머신러닝 단기집중과정의 데이터 세트: 원본 데이터 세트 나누기를 참고하세요.
W
무게
모델이 다른 값에 곱하는 값입니다. 학습은 모델의 이상적인 가중치를 결정하는 프로세스이고, 추론은 학습된 가중치를 사용하여 예측을 수행하는 프로세스입니다.
자세한 내용은 머신러닝 단기집중과정의 선형 회귀를 참고하세요.
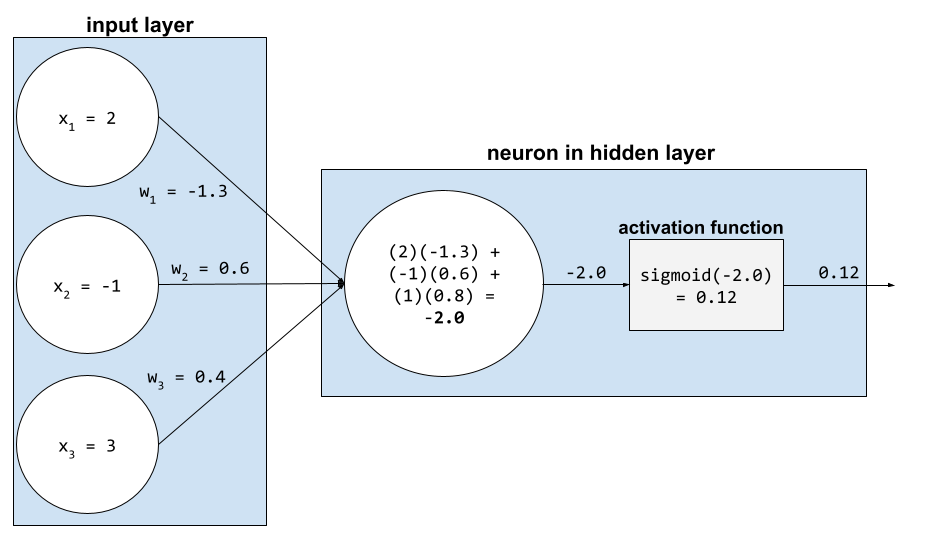
가중치가 적용된 합계
모든 관련 입력 값에 해당 가중치를 곱한 값의 합계입니다. 예를 들어 관련 입력이 다음과 같다고 가정해 보겠습니다.
| 입력 값 | 입력 가중치 |
| 2 | -1.3 |
| -1 | 0.6 |
| 3 | 0.4 |
따라서 가중치 합계는 다음과 같습니다.
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
가중치가 적용된 합계는 활성화 함수의 입력 인수입니다.
Z
Z-점수 정규화
원시 특성 값을 해당 특성의 평균에서 표준 편차 수를 나타내는 부동 소수점 값으로 대체하는 스케일링 기법입니다. 예를 들어 평균이 800이고 표준편차가 100인 특성을 생각해 보겠습니다. 다음 표는 Z 점수 정규화가 원시 값을 Z 점수에 매핑하는 방법을 보여줍니다.
| 원본 값 | Z-점수 |
|---|---|
| 800 | 0 |
| 950 | +1.5 |
| 575 | -2.25 |
그러면 머신러닝 모델이 원시 값이 아닌 해당 특성의 Z 점수를 기반으로 학습합니다.
자세한 내용은 머신러닝 단기집중과정의 숫자 데이터: 정규화를 참고하세요.