หน้านี้มีคำศัพท์ในคำศัพท์พื้นฐานของ ML ดูคำศัพท์ทั้งหมดได้โดยคลิกที่นี่
A
ความแม่นยำ
จำนวนการคาดการณ์การจัดประเภทที่ถูกต้องหารด้วยจำนวนการคาดการณ์ทั้งหมด โดยการ
เช่น โมเดลที่คาดการณ์ถูกต้อง 40 รายการและคาดการณ์ไม่ถูกต้อง 10 รายการ จะมีความแม่นยำดังนี้
การจัดประเภทแบบไบนารีจะระบุชื่อที่เฉพาะเจาะจง สำหรับหมวดหมู่ต่างๆ ของการคาดการณ์ที่ถูกต้องและ การคาดการณ์ที่ไม่ถูกต้อง ดังนั้น สูตรความแม่นยำสำหรับการจัดประเภทแบบไบนารี จึงเป็นดังนี้
ที่ไหน
- TP คือจำนวนผลบวกจริง (การคาดการณ์ที่ถูกต้อง)
- TN คือจำนวนผลลบจริง (การคาดการณ์ที่ถูกต้อง)
- FP คือจำนวนผลบวกลวง (การคาดการณ์ที่ไม่ถูกต้อง)
- FN คือจำนวนผลลบลวง (การคาดการณ์ที่ไม่ถูกต้อง)
เปรียบเทียบความแม่นยำกับความเที่ยงตรงและความอ่อนไหว
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ความแม่นยำ การเรียกคืน ความเที่ยงตรง และเมตริกที่เกี่ยวข้อง ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ฟังก์ชันการเปิดใช้งาน
ฟังก์ชันที่ช่วยให้โครงข่ายประสาทเทียมเรียนรู้ความสัมพันธ์ที่ไม่ใช่เชิงเส้น (ซับซ้อน) ระหว่างฟีเจอร์ กับป้ายกำกับ
ฟังก์ชันการเปิดใช้งานที่ได้รับความนิยมมีดังนี้
กราฟของฟังก์ชันการเปิดใช้งานจะไม่ใช่เส้นตรงเส้นเดียว ตัวอย่างเช่น พล็อตของฟังก์ชันกระตุ้น ReLU ประกอบด้วยเส้นตรง 2 เส้น ดังนี้

กราฟของฟังก์ชันการกระตุ้นแบบซิคมอยด์มีลักษณะดังนี้

ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม: ฟังก์ชันการเปิดใช้งาน ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ปัญญาประดิษฐ์ (AI)
โปรแกรมหรือโมเดลที่ไม่ใช่มนุษย์ซึ่งสามารถแก้โจทย์ที่ซับซ้อนได้ ตัวอย่างเช่น โปรแกรมหรือโมเดลที่แปลข้อความ หรือโปรแกรมหรือโมเดลที่ระบุโรคจากภาพรังสีวิทยาล้วนแสดงให้เห็นถึงปัญญาประดิษฐ์
ในทางเทคนิคแล้ว แมชชีนเลิร์นนิงเป็นสาขาย่อยของปัญญาประดิษฐ์ (AI) อย่างไรก็ตาม ในช่วงไม่กี่ปีที่ผ่านมา องค์กรบางแห่งเริ่มใช้คำว่าปัญญาประดิษฐ์และแมชชีนเลิร์นนิงสลับกัน
AUC (พื้นที่ใต้กราฟ ROC)
ตัวเลขระหว่าง 0.0 ถึง 1.0 ซึ่งแสดงถึงความสามารถของโมเดลการจัดประเภทแบบไบนารี ในการแยกคลาสที่เป็นบวกออกจากคลาสที่เป็นลบ ยิ่ง AUC ใกล้ 1.0 มากเท่าใด ความสามารถของโมเดลในการแยก คลาสออกจากกันก็จะยิ่งดีขึ้นเท่านั้น
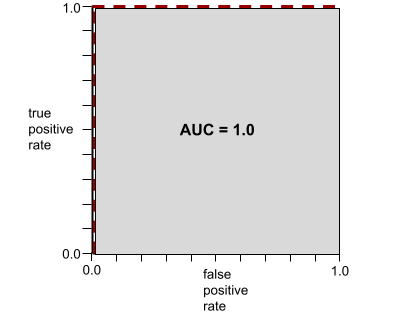
ตัวอย่างเช่น ภาพต่อไปนี้แสดงโมเดลการจัดประเภทที่แยกคลาสเชิงบวก (วงรีสีเขียว) ออกจากคลาสเชิงลบ (สี่เหลี่ยมผืนผ้าสีม่วง) ได้อย่างสมบูรณ์ โมเดลที่สมบูรณ์แบบอย่างไม่สมจริงนี้มี AUC เท่ากับ 1.0

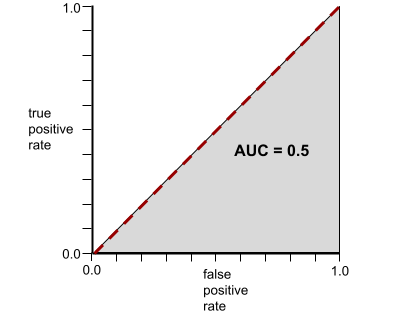
ในทางกลับกัน ภาพต่อไปนี้แสดงผลลัพธ์ของโมเดลการจัดประเภทที่สร้างผลลัพธ์แบบสุ่ม โมเดลนี้มี AUC เท่ากับ 0.5

ใช่ โมเดลก่อนหน้ามี AUC เท่ากับ 0.5 ไม่ใช่ 0.0
โมเดลส่วนใหญ่อยู่ระหว่าง 2 สุดขั้วนี้ ตัวอย่างเช่น โมเดลต่อไปนี้จะแยกผลลัพธ์เชิงบวกออกจากเชิงลบได้ในระดับหนึ่ง ดังนั้นจึงมี AUC อยู่ระหว่าง 0.5 ถึง 1.0

AUC จะไม่สนใจค่าที่คุณตั้งไว้สำหรับเกณฑ์การจัดประเภท แต่ AUC จะพิจารณาเกณฑ์การแยกประเภทที่เป็นไปได้ทั้งหมด
ดูข้อมูลเพิ่มเติมได้ที่การแยกประเภท: ROC และ AUC ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
B
การแพร่ย้อนกลับ
อัลกอริทึมที่ใช้ การไล่ระดับความชันใน โครงข่ายประสาทเทียม
การฝึกโครงข่ายประสาทเทียมต้องทำการทำซ้ำหลายครั้ง ในวงจร 2 รอบต่อไปนี้
- ในระหว่างการส่งต่อ ระบบจะประมวลผลกลุ่มของ ตัวอย่างเพื่อให้ได้การคาดการณ์ ระบบจะเปรียบเทียบค่าการคาดการณ์แต่ละค่ากับค่าป้ายกำกับแต่ละค่า ความแตกต่างระหว่างค่าการคาดการณ์และค่าป้ายกำกับคือการสูญเสียสำหรับตัวอย่างนั้น ระบบจะรวมการสูญเสียสำหรับตัวอย่างทั้งหมดเพื่อคำนวณการสูญเสียทั้งหมดสำหรับกลุ่มปัจจุบัน
- ในการส่งผ่านย้อนกลับ (การแพร่ย้อนกลับ) ระบบจะลดการสูญเสียโดยการ ปรับน้ำหนักของนิวรอนทั้งหมดในเลเยอร์ที่ซ่อนอยู่ทั้งหมด
โดยมักจะมีนิวรอนจำนวนมากในเลเยอร์ที่ซ่อนอยู่หลายเลเยอร์ นิวรอนแต่ละตัวมีส่วนทำให้เกิดการสูญเสียโดยรวมในรูปแบบต่างๆ การแพร่ย้อนกลับจะพิจารณาว่าจะเพิ่มหรือลดน้ำหนัก ที่ใช้กับนิวรอนเฉพาะหรือไม่
อัตราการเรียนรู้คือตัวคูณที่ควบคุม ระดับที่แต่ละการส่งผ่านย้อนกลับจะเพิ่มหรือลดน้ำหนักแต่ละรายการ อัตราการเรียนรู้ที่สูงจะเพิ่มหรือลดน้ำหนักแต่ละรายการมากกว่าอัตราการเรียนรู้ที่ต่ำ
ในแง่ของแคลคูลัส การแพร่ย้อนกลับจะใช้กฎลูกโซ่ จากแคลคูลัส กล่าวคือ การแพร่ย้อนกลับจะคำนวณอนุพันธ์ย่อยของข้อผิดพลาดที่ เกี่ยวข้องกับแต่ละพารามิเตอร์
เมื่อหลายปีก่อน ผู้ปฏิบัติงานด้าน ML ต้องเขียนโค้ดเพื่อใช้การแพร่ย้อนกลับ API ของ ML รุ่นใหม่ เช่น Keras จะใช้การแพร่ย้อนกลับให้คุณ ในที่สุด
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
กลุ่ม
ชุดตัวอย่างที่ใช้ในการฝึกซ้ำ 1 ครั้ง ขนาดกลุ่มจะกำหนดจำนวนตัวอย่างในกลุ่ม
ดูคำอธิบายว่ากลุ่มข้อมูลเกี่ยวข้องกับ Epoch อย่างไรได้ที่Epoch
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ขนาดกลุ่ม
จำนวนตัวอย่างในกลุ่ม เช่น หากขนาดกลุ่มคือ 100 โมเดลจะประมวลผลตัวอย่าง 100 รายการต่อการทำซ้ำ
กลยุทธ์ขนาดกลุ่มยอดนิยมมีดังนี้
- การไล่ระดับสีแบบสุ่ม (SGD) ซึ่งมีขนาดกลุ่มเท่ากับ 1
- การประมวลผลแบบกลุ่มเต็ม ซึ่งขนาดกลุ่มคือจํานวนตัวอย่างในชุดการฝึกทั้งหมด เช่น หากชุดการฝึกมีตัวอย่าง 1 ล้านรายการ ขนาดกลุ่มจะเท่ากับตัวอย่าง 1 ล้านรายการ โดยปกติแล้ว การประมวลผลแบบกลุ่มทั้งหมดมักเป็นกลยุทธ์ที่ไม่มีประสิทธิภาพ
- มินิแบตช์ ซึ่งโดยปกติแล้วขนาดแบตช์จะอยู่ระหว่าง 10 ถึง 1,000 โดยปกติแล้ว มินิแบทช์เป็นกลยุทธ์ที่มีประสิทธิภาพมากที่สุด
โปรดดูข้อมูลเพิ่มเติมที่ด้านล่าง
- ระบบ ML ที่ใช้งานจริง: การอนุมานแบบคงที่เทียบกับการอนุมานแบบไดนามิก ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
- Playbook การปรับแต่ง Deep Learning
อคติ (จริยธรรม/ความเป็นธรรม)
1. การเหมารวม อคติ หรือการเข้าข้างสิ่งต่างๆ บุคคล หรือกลุ่มบางกลุ่มมากกว่ากลุ่มอื่นๆ อคติเหล่านี้อาจส่งผลต่อการเก็บรวบรวมและการตีความข้อมูล การออกแบบระบบ และวิธีที่ผู้ใช้โต้ตอบกับระบบ รูปแบบของอคติประเภทนี้ ได้แก่
- อคติในการทำงานอัตโนมัติ
- อคติยืนยันความคิดตัวเอง
- อคติของผู้ทดลอง
- อคติในการระบุแหล่งที่มาของกลุ่ม
- อคติโดยไม่รู้ตัว
- อคติในกลุ่ม
- อคติเกี่ยวกับความเหมือนกันของกลุ่มนอก
2. ข้อผิดพลาดของระบบที่เกิดจากขั้นตอนการสุ่มตัวอย่างหรือการรายงาน รูปแบบของอคติประเภทนี้ ได้แก่
- อคติในการครอบคลุม
- ความลำเอียงเนื่องจากไม่ได้ตอบ
- อคติในการเข้าร่วม
- อคติในการรายงาน
- อคติในการสุ่มตัวอย่าง
- อคติในการเลือก
อย่าสับสนกับคำอคติในโมเดลแมชชีนเลิร์นนิง หรืออคติในการคาดการณ์
ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ประเภทของอคติใน หลักสูตรเร่งรัดแมชชีนเลิร์นนิง
อคติ (คณิตศาสตร์) หรือเทอมอคติ
จุดตัดหรือออฟเซ็ตจากต้นทาง อคติเป็นพารามิเตอร์ในโมเดลแมชชีนเลิร์นนิง ซึ่งแสดงด้วยสัญลักษณ์ต่อไปนี้
- b
- w0
ตัวอย่างเช่น อคติคือ b ในสูตรต่อไปนี้
ในเส้น 2 มิติแบบง่ายๆ อคติหมายถึง "จุดตัดแกน y" ตัวอย่างเช่น อคติของเส้นในภาพต่อไปนี้คือ 2
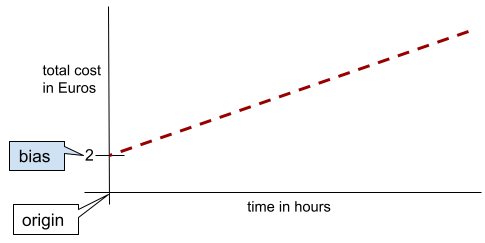
ความเอนเอียงเกิดขึ้นเนื่องจากไม่ใช่ทุกโมเดลที่เริ่มต้นจากจุดกำเนิด (0,0) ตัวอย่างเช่น สมมติว่าค่าเข้าสวนสนุกคือ 20 บาท และมีค่าใช้จ่ายเพิ่มเติม 5 บาทต่อชั่วโมงที่ลูกค้าอยู่ในสวนสนุก ดังนั้น โมเดลที่แมปต้นทุนทั้งหมดจึงมีอคติเป็น 2 เนื่องจากต้นทุนต่ำสุดคือ 2 ยูโร
อย่าสับสนระหว่างอคติกับอคติในด้านจริยธรรมและความเป็นธรรม หรืออคติในการคาดการณ์
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การจัดประเภทแบบไบนารี
งานการจัดประเภทประเภทหนึ่งที่ คาดการณ์คลาสใดคลาสหนึ่งใน 2 คลาสที่แยกกันโดยสิ้นเชิง
ตัวอย่างเช่น โมเดลแมชชีนเลิร์นนิง 2 โมเดลต่อไปนี้แต่ละโมเดลทําการ การจัดประเภทแบบไบนารี
- โมเดลที่พิจารณาว่าข้อความอีเมลเป็นจดหมายขยะ (คลาสเชิงบวก) หรือไม่ใช่จดหมายขยะ (คลาสเชิงลบ)
- โมเดลที่ประเมินอาการทางการแพทย์เพื่อพิจารณาว่าบุคคล เป็นโรคใดโรคหนึ่ง (คลาสบวก) หรือไม่เป็นโรคดังกล่าว (คลาสลบ)
เปรียบเทียบกับการจัดประเภทแบบหลายคลาส
ดูเพิ่มเติมที่การถดถอยโลจิสติกและ เกณฑ์การจัดประเภท
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การจัดกลุ่ม
การแปลงฟีเจอร์เดียวเป็นฟีเจอร์ไบนารีหลายรายการ ที่เรียกว่ากลุ่มหรือถัง โดยปกติจะอิงตามช่วงค่า โดยปกติแล้วฟีเจอร์ที่ถูกตัดออกจะเป็นฟีเจอร์ต่อเนื่อง
เช่น แทนที่จะแสดงอุณหภูมิเป็นฟีเจอร์ทศนิยมต่อเนื่องเดียว คุณสามารถแบ่งช่วงอุณหภูมิออกเป็นกลุ่มที่ไม่ต่อเนื่อง เช่น
- <= 10 องศาเซลเซียสจะเป็นกลุ่ม "เย็น"
- 11-24 องศาเซลเซียสจะอยู่ในกลุ่ม "อบอุ่น"
- >= 25 องศาเซลเซียสจะเป็นกลุ่ม "อุ่น"
โมเดลจะถือว่าค่าทุกค่าในกลุ่มเดียวกันเหมือนกัน ตัวอย่างเช่น ค่า 13 และ 22 อยู่ในกลุ่มอุณหภูมิปานกลางทั้งคู่ โมเดลจึงถือว่าค่าทั้ง 2 ค่าเหมือนกัน
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงตัวเลข: การจัดกลุ่ม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
C
ข้อมูลเชิงหมวดหมู่
ฟีเจอร์ที่มีชุดค่าที่เป็นไปได้ที่เฉพาะเจาะจง ตัวอย่างเช่น
พิจารณาฟีเจอร์เชิงหมวดหมู่ชื่อ traffic-light-state ซึ่งมีค่าได้เพียงค่าใดค่าหนึ่งจาก 3 ค่าต่อไปนี้
redyellowgreen
การแสดง traffic-light-state เป็นฟีเจอร์เชิงหมวดหมู่
จะช่วยให้โมเดลเรียนรู้
ผลกระทบที่แตกต่างกันของ red, green และ yellow ต่อพฤติกรรมของผู้ขับขี่ได้
บางครั้งฟีเจอร์เชิงหมวดหมู่เรียกว่าฟีเจอร์ที่ไม่ต่อเนื่อง
แตกต่างจากข้อมูลเชิงตัวเลข
ดูข้อมูลเพิ่มเติมได้ที่การทำงานกับข้อมูลเชิงหมวดหมู่ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
คลาส
หมวดหมู่ที่ป้ายกำกับสามารถเป็นของได้ เช่น
- ในโมเดลการจัดประเภทแบบไบนารีที่ตรวจหาสแปม คลาสทั้ง 2 อาจเป็นสแปมและไม่ใช่สแปม
- ในโมเดลการจัดประเภทแบบหลายคลาส ที่ระบุสายพันธุ์สุนัข คลาสอาจเป็นพุดเดิล บีเกิล ปั๊ก และอื่นๆ
โมเดลการจัดประเภทจะคาดการณ์คลาส ในทางตรงกันข้าม โมเดลการถดถอยจะคาดการณ์ตัวเลข แทนที่จะเป็นคลาส
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
โมเดลการแยกประเภท
โมเดลที่มีการคาดการณ์เป็นคลาส ตัวอย่างเช่น โมเดลต่อไปนี้เป็นโมเดลการแยกประเภททั้งหมด
- โมเดลที่คาดการณ์ภาษาของประโยคอินพุต (ฝรั่งเศสใช่ไหม สเปน อิตาลี)
- โมเดลที่คาดการณ์สายพันธุ์ของต้นไม้ (เมเปิล Oak บาวบับ)
- โมเดลที่คาดการณ์คลาสที่เป็นบวกหรือลบสำหรับ ภาวะทางการแพทย์ที่เฉพาะเจาะจง
ในทางตรงกันข้าม โมเดลการเกิดปัญหาซ้ำจะคาดการณ์ตัวเลข แทนที่จะเป็นคลาส
โมเดลการจัดประเภทที่ใช้กันทั่วไปมี 2 ประเภท ได้แก่
เกณฑ์การจัดประเภท
ในการจัดประเภทแบบไบนารี ค่า ระหว่าง 0 ถึง 1 ที่แปลงเอาต์พุตดิบของโมเดลการถดถอยโลจิสติก เป็นการคาดการณ์คลาสที่เป็นบวก หรือคลาสที่เป็นลบ โปรดทราบว่าเกณฑ์การแยกประเภทคือค่าที่มนุษย์เลือก ไม่ใช่ค่าที่ได้จากการฝึกโมเดล
โมเดลการถดถอยโลจิสติกจะแสดงผลค่าดิบระหว่าง 0 ถึง 1 จากนั้นให้ทำดังนี้
- หากค่าดิบนี้มากกว่าเกณฑ์การจัดประเภท ระบบจะคาดการณ์ คลาสที่เป็นบวก
- หากค่าดิบนี้น้อยกว่าเกณฑ์การจัดประเภท ระบบจะคาดการณ์คลาสเชิงลบ
เช่น สมมติว่าเกณฑ์การแยกประเภทคือ 0.8 หากค่าดิบ เป็น 0.9 โมเดลจะคาดการณ์คลาสเชิงบวก หากค่าดิบเป็น 0.7 โมเดลจะคาดการณ์คลาสเชิงลบ
การเลือกเกณฑ์การแยกประเภทส่งผลอย่างมากต่อจำนวนผลบวกลวงและผลลบลวง
ดูข้อมูลเพิ่มเติมได้ที่เกณฑ์และเมทริกซ์ความสับสน ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ตัวแยกประเภท
คำที่ใช้กันทั่วไปสำหรับโมเดลการจัดประเภท
ชุดข้อมูลที่มีความไม่สมดุลของคลาส
ชุดข้อมูลสำหรับการแยกประเภท ซึ่งมีจำนวนป้ายกำกับทั้งหมดของคลาสแต่ละคลาส แตกต่างกันอย่างมาก ตัวอย่างเช่น พิจารณาชุดข้อมูลการจัดประเภทแบบไบนารีที่มีป้ายกำกับ 2 รายการ ซึ่งแบ่งออกเป็นดังนี้
- ป้ายกำกับเชิงลบ 1,000,000 รายการ
- ป้ายกำกับเชิงบวก 10 รายการ
อัตราส่วนของป้ายกำกับเชิงลบต่อป้ายกำกับเชิงบวกคือ 100,000 ต่อ 1 ดังนั้นชุดข้อมูลนี้จึงเป็นชุดข้อมูลที่มีความไม่สมดุลของคลาส
ในทางตรงกันข้าม ชุดข้อมูลต่อไปนี้เป็นคลาสที่สมดุลเนื่องจากอัตราส่วนของป้ายกำกับเชิงลบต่อป้ายกำกับเชิงบวกค่อนข้างใกล้เคียงกับ 1
- ป้ายกำกับเชิงลบ 517 รายการ
- ป้ายกำกับค่าบวก 483 รายการ
ชุดข้อมูลแบบหลายคลาสอาจเป็นแบบคลาสไม่สมดุลได้เช่นกัน ตัวอย่างเช่น ชุดข้อมูลการจัดประเภทแบบหลายคลาสต่อไปนี้ยังเป็นชุดข้อมูลที่มีความไม่สมดุลของคลาสด้วย เนื่องจากป้ายกำกับหนึ่งมีตัวอย่างมากกว่าอีก 2 ป้ายกำกับมาก
- ป้ายกำกับ 1,000,000 รายการที่มีคลาส "สีเขียว"
- ป้ายกำกับ 200 รายการที่มีคลาส "สีม่วง"
- ป้ายกำกับ 350 รายการที่มีคลาส "ส้ม"
การฝึกโมเดลด้วยชุดข้อมูลที่มีความไม่สมดุลของคลาสอาจเป็นเรื่องท้าทาย ดูรายละเอียดได้ที่ ชุดข้อมูลที่ไม่สมดุล ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ดูเอนโทรปี คลาสส่วนใหญ่ และคลาสส่วนน้อยด้วย
การตัด
เทคนิคในการจัดการค่าผิดปกติโดยทำอย่างใดอย่างหนึ่งหรือทั้ง 2 อย่างต่อไปนี้
- การลดค่าฟีเจอร์ที่มากกว่าเกณฑ์สูงสุด ลงมาที่เกณฑ์สูงสุดนั้น
- การเพิ่มค่าฟีเจอร์ที่ต่ำกว่าเกณฑ์ขั้นต่ำให้เป็นเกณฑ์ขั้นต่ำ
ตัวอย่างเช่น สมมติว่าค่าสำหรับฟีเจอร์หนึ่งๆ น้อยกว่า 0.5% อยู่ นอกช่วง 40–60 ในกรณีนี้ คุณสามารถทำสิ่งต่อไปนี้
- ตัดค่าทั้งหมดที่มากกว่า 60 (เกณฑ์สูงสุด) ให้เป็น 60
- คลิปค่าทั้งหมดที่ต่ำกว่า 40 (เกณฑ์ขั้นต่ำ) ให้เป็น 40
ค่าผิดปกติอาจทำให้โมเดลเสียหาย และในบางครั้งอาจทำให้น้ำหนัก ล้นระหว่างการฝึก ค่าผิดปกติบางค่าอาจทำให้เมตริกต่างๆ เช่น ความแม่นยำ เสียหายอย่างมาก การตัดเสียงเป็นเทคนิคที่ใช้กันทั่วไปเพื่อจำกัด ความเสียหาย
การจำกัดค่าความชันจะบังคับให้ค่าความชันอยู่ในช่วงที่กำหนดระหว่างการฝึก
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลตัวเลข: การปรับค่า ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
เมตริกความสับสน
ตาราง NxN ที่สรุปจำนวนการคาดการณ์ที่ถูกต้องและไม่ถูกต้อง ที่โมเดลการจัดประเภทสร้างขึ้น ตัวอย่างเช่น ลองดูเมทริกซ์ความสับสนต่อไปนี้สําหรับโมเดลการจัดประเภทแบบไบนารี
| เนื้องอก (คาดการณ์) | ไม่ใช่เนื้องอก (คาดการณ์) | |
|---|---|---|
| เนื้องอก (ข้อมูลจากการสังเกตการณ์โดยตรง) | 18 (TP) | 1 (FN) |
| ไม่ใช่เนื้องอก (ข้อมูลจากการสังเกตการณ์โดยตรง) | 6 (FP) | 452 (TN) |
เมตริกความสับสนก่อนหน้าแสดงข้อมูลต่อไปนี้
- จากการคาดการณ์ 19 รายการที่ข้อมูลที่ระบุว่าถูกต้องโดยเจ้าหน้าที่เป็นเนื้องอก โมเดลจัดประเภทได้อย่างถูกต้อง 18 รายการและจัดประเภทไม่ถูกต้อง 1 รายการ
- จากการคาดการณ์ 458 รายการซึ่งมีข้อมูลที่ระบุว่าถูกต้องโดยเจ้าหน้าที่เป็น "ไม่ใช่เนื้องอก" โมเดล จัดประเภทได้อย่างถูกต้อง 452 รายการและจัดประเภทไม่ถูกต้อง 6 รายการ
เมทริกซ์ความสับสนสำหรับปัญหาการจัดประเภทแบบหลายคลาส ช่วยให้คุณระบุรูปแบบของข้อผิดพลาดได้ ตัวอย่างเช่น ลองพิจารณาเมทริกซ์ความสับสนต่อไปนี้สําหรับโมเดลการจัดประเภทแบบหลายคลาส 3 คลาส ที่จัดหมวดหมู่ไอริส 3 ประเภทที่แตกต่างกัน (เวอร์จินิกา เวอร์ซิคอลอร์ และเซโตซา) เมื่อข้อมูลที่ระบุว่าถูกต้องโดยเจ้าหน้าที่คือ Virginica เมทริกซ์ความสับสนจะแสดงให้เห็นว่าโมเดลมีแนวโน้มที่จะคาดการณ์ Versicolor มากกว่า Setosa อย่างมาก
| Setosa (คาดการณ์) | Versicolor (คาดการณ์) | เวอร์จิเนีย (คาดการณ์) | |
|---|---|---|---|
| Setosa (ข้อมูลจากการสังเกตการณ์โดยตรง) | 88 | 12 | 0 |
| Versicolor (ข้อมูลจากการสังเกตการณ์โดยตรง) | 6 | 141 | 7 |
| เวอร์จินิกา (ข้อมูลจากการสังเกตการณ์โดยตรง) | 2 | 27 | 109 |
อีกตัวอย่างหนึ่งคือเมทริกซ์ความสับสนอาจเผยให้เห็นว่าโมเดลที่ฝึกมา เพื่อจดจำตัวเลขที่เขียนด้วยลายมือมักจะทำนายผิดเป็น 9 แทนที่จะเป็น 4 หรือทำนายผิดเป็น 1 แทนที่จะเป็น 7
เมทริกซ์ความสับสนมีข้อมูลเพียงพอที่จะคํานวณเมตริกประสิทธิภาพที่หลากหลาย รวมถึงความแม่นยำ และการเรียกคืน
ฟีเจอร์ต่อเนื่อง
ฟีเจอร์ทศนิยมที่มีค่าที่เป็นไปได้ไม่สิ้นสุด เช่น อุณหภูมิหรือน้ำหนัก
เปรียบเทียบกับฟีเจอร์ที่ไม่ต่อเนื่อง
การบรรจบกัน
สถานะที่เกิดขึ้นเมื่อค่าloss เปลี่ยนแปลงน้อยมากหรือ ไม่เปลี่ยนแปลงเลยในแต่ละการวนซ้ำ ตัวอย่างเช่น เส้นโค้งการสูญเสียต่อไปนี้แสดงให้เห็นว่าการบรรจบกันเกิดขึ้นที่การวนซ้ำประมาณ 700 ครั้ง
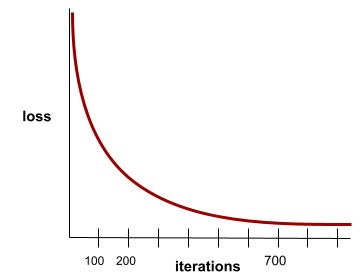
โมเดลจะบรรจบกันเมื่อการฝึกเพิ่มเติมไม่ ปรับปรุงโมเดล
ในดีปเลิร์นนิง บางครั้งค่าการสูญเสียจะคงที่หรือ เกือบคงที่สำหรับการวนซ้ำหลายครั้งก่อนที่จะลดลงในที่สุด ในช่วงระยะเวลานาน ที่ค่าการสูญเสียคงที่ คุณอาจรู้สึกว่ามีการบรรจบกันอย่างไม่ถูกต้องชั่วคราว
ดูการหยุดก่อนกำหนดด้วย
ดูข้อมูลเพิ่มเติมได้ที่เส้นโค้งการบรรจบกันของโมเดลและการสูญเสีย ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
D
DataFrame
ประเภทข้อมูล pandas ยอดนิยมสำหรับแสดงชุดข้อมูลในหน่วยความจำ
DataFrame มีลักษณะคล้ายกับตารางหรือสเปรดชีต แต่ละคอลัมน์ของ DataFrame มีชื่อ (ส่วนหัว) และแต่ละแถวจะระบุด้วยหมายเลขที่ไม่ซ้ำกัน
แต่ละคอลัมน์ใน DataFrame มีโครงสร้างเหมือนอาร์เรย์ 2 มิติ ยกเว้นว่า แต่ละคอลัมน์สามารถกำหนดประเภทข้อมูลของตัวเองได้
นอกจากนี้ โปรดดูหน้าข้อมูลอ้างอิง pandas.DataFrameอย่างเป็นทางการด้วย
ชุดข้อมูล
ชุดข้อมูลดิบที่มักจะ (แต่ไม่เสมอไป) จัดระเบียบในรูปแบบใดรูปแบบหนึ่งต่อไปนี้
- สเปรดชีต
- ไฟล์ในรูปแบบ CSV (ค่าที่คั่นด้วยคอมมา)
โมเดลเชิงลึก
โครงข่ายประสาทเทียมที่มีเลเยอร์ที่ซ่อนอยู่มากกว่า 1 เลเยอร์
โมเดลแบบลึกเรียกอีกอย่างว่าโครงข่ายประสาทแบบลึก
เปรียบเทียบกับโมเดลแบบกว้าง
ฟีเจอร์หนาแน่น
ฟีเจอร์ที่ค่าส่วนใหญ่หรือทั้งหมดไม่ใช่ศูนย์ โดยปกติจะเป็นเทนเซอร์ของค่าทศนิยม ตัวอย่างเช่น เทนเซอร์ 10 องค์ประกอบต่อไปนี้เป็นแบบหนาแน่นเนื่องจากค่า 9 ค่าเป็นค่าที่ไม่ใช่ 0
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
แตกต่างจากฟีเจอร์แบบกระจัดกระจาย
ความลึก
ผลรวมของรายการต่อไปนี้ในโครงข่ายประสาทเทียม
- จำนวนเลเยอร์ที่ซ่อนอยู่
- จำนวนเลเยอร์เอาต์พุต ซึ่งโดยปกติคือ 1
- จำนวนเลเยอร์การฝัง
เช่น โครงข่ายประสาทที่มีเลเยอร์ที่ซ่อนอยู่ 5 เลเยอร์และเลเยอร์เอาต์พุต 1 เลเยอร์ มีความลึกเท่ากับ 6
โปรดสังเกตว่าเลเยอร์อินพุตไม่มีผลต่อความลึก
ฟีเจอร์ที่ไม่ต่อเนื่อง
ฟีเจอร์ที่มีชุดค่าที่เป็นไปได้แบบจำกัด ตัวอย่างเช่น ฟีเจอร์ที่มีค่าเป็นได้เพียง animal, vegetable หรือ mineral คือฟีเจอร์ ไม่ต่อเนื่อง (หรือเชิงหมวดหมู่)
เปรียบเทียบกับฟีเจอร์ต่อเนื่อง
ไดนามิก
สิ่งที่ทำบ่อยๆ หรืออย่างต่อเนื่อง คำว่าไดนามิกและออนไลน์มีความหมายเหมือนกันในแมชชีนเลิร์นนิง การใช้งาน dynamic และ online ที่พบบ่อยในแมชชีนเลิร์นนิงมีดังนี้
- โมเดลแบบไดนามิก (หรือโมเดลออนไลน์) คือโมเดล ที่ได้รับการฝึกซ้ำบ่อยครั้งหรืออย่างต่อเนื่อง
- การฝึกแบบไดนามิก (หรือการฝึกออนไลน์) คือกระบวนการฝึก อย่างต่อเนื่องหรือสม่ำเสมอ
- การอนุมานแบบไดนามิก (หรือการอนุมานออนไลน์) คือกระบวนการ สร้างการคาดการณ์ตามต้องการ
โมเดลแบบไดนามิก
โมเดลที่ได้รับการฝึกใหม่บ่อยครั้ง (อาจจะอย่างต่อเนื่องด้วย) โมเดลแบบไดนามิกคือ "ผู้เรียนรู้ตลอดชีวิต" ที่ ปรับตัวให้เข้ากับข้อมูลที่เปลี่ยนแปลงอยู่เสมอ โมเดลแบบไดนามิกเรียกอีกอย่างว่าโมเดลออนไลน์
แตกต่างจากโมเดลคงที่
E
การหยุดก่อนกำหนด
วิธีการสำหรับการทำให้เป็นปกติที่เกี่ยวข้องกับการสิ้นสุดการฝึก ก่อนที่การลดลงของการฝึกจะสิ้นสุด การหยุดก่อนเวลาคือการหยุดฝึกโมเดลโดยตั้งใจ เมื่อการสูญเสียในชุดข้อมูลการตรวจสอบเริ่ม เพิ่มขึ้น นั่นคือเมื่อ การสรุปทั่วไปมีประสิทธิภาพแย่ลง
แตกต่างจากการออกก่อนเวลา
เลเยอร์การฝัง
เลเยอร์ที่ซ่อนอยู่พิเศษที่ฝึกในฟีเจอร์เชิงหมวดหมู่ที่มีมิติสูงเพื่อค่อยๆ เรียนรู้เวกเตอร์การฝังที่มีมิติต่ำกว่า เลเยอร์การฝังช่วยให้โครงข่ายประสาทเทียมฝึกได้อย่างมีประสิทธิภาพมากกว่าการฝึกเฉพาะฟีเจอร์เชิงหมวดหมู่ที่มีมิติสูง
ตัวอย่างเช่น ปัจจุบัน Earth รองรับต้นไม้ประมาณ 73,000 สายพันธุ์ สมมติว่า
สายพันธุ์ต้นไม้เป็นฟีเจอร์ในโมเดลของคุณ ดังนั้นเลเยอร์
อินพุตของโมเดลจึงมีเวกเตอร์แบบ One-Hot ที่มีความยาว 73,000
องค์ประกอบ
ตัวอย่างเช่น baobab อาจแสดงเป็น

อาร์เรย์ที่มีองค์ประกอบ 73,000 รายการถือว่ายาวมาก หากคุณไม่เพิ่มเลเยอร์การฝัง ลงในโมเดล การฝึกจะใช้เวลานานมากเนื่องจาก การคูณด้วย 0 จำนวน 72,999 ตัว คุณอาจเลือกเลเยอร์การฝังให้ประกอบด้วยมิติข้อมูล 12 มิติ ดังนั้น เลเยอร์การฝังจะค่อยๆ เรียนรู้ เวกเตอร์การฝังใหม่สำหรับต้นไม้แต่ละสายพันธุ์
ในบางสถานการณ์ การแฮชเป็นทางเลือกที่สมเหตุสมผล แทนเลเยอร์การฝัง
ดูข้อมูลเพิ่มเติมได้ที่การฝัง ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
Epoch
การส่งผ่านการฝึกแบบเต็มทั้งชุดการฝึก เพื่อให้ระบบประมวลผลตัวอย่างแต่ละรายการ 1 ครั้ง
Epoch แสดงถึงN/ขนาดกลุ่ม
การวนซ้ำในการฝึก โดย N คือ
จํานวนตัวอย่างทั้งหมด
เช่น สมมติว่ามีข้อมูลต่อไปนี้
- ชุดข้อมูลประกอบด้วยตัวอย่าง 1,000 รายการ
- ขนาดกลุ่มคือ 50 ตัวอย่าง
ดังนั้น 1 Epoch จึงต้องมีการวนซ้ำ 20 ครั้ง
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ตัวอย่าง
ค่าของแถวหนึ่งของ features และอาจมี label ตัวอย่างในการเรียนรู้แบบมีผู้ดูแลแบ่งออกเป็น 2 หมวดหมู่ ทั่วไป ดังนี้
- ตัวอย่างที่มีป้ายกำกับประกอบด้วยฟีเจอร์อย่างน้อย 1 รายการ และป้ายกำกับ ระบบจะใช้ตัวอย่างที่มีป้ายกำกับในระหว่างการฝึก
- ตัวอย่างที่ไม่มีป้ายกำกับประกอบด้วยฟีเจอร์อย่างน้อย 1 รายการแต่ไม่มีป้ายกำกับ ระบบจะใช้ตัวอย่างที่ไม่มีป้ายกำกับในระหว่างการอนุมาน
เช่น สมมติว่าคุณกำลังฝึกโมเดลเพื่อพิจารณาอิทธิพล ของสภาพอากาศต่อคะแนนสอบของนักเรียน ตัวอย่างที่มีป้ายกำกับ 3 รายการมีดังนี้
| ฟีเจอร์ | ป้ายกำกับ | ||
|---|---|---|---|
| อุณหภูมิ | ความชื้น | ความกดอากาศ | คะแนนสอบ |
| 15 | 47 | 998 | ดี |
| 19 | 34 | 1020 | ดีมาก |
| 18 | 92 | 1012 | แย่ |
ตัวอย่างที่ไม่มีป้ายกำกับ 3 รายการมีดังนี้
| อุณหภูมิ | ความชื้น | ความกดอากาศ | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
โดยปกติแล้ว แถวของชุดข้อมูลจะเป็นแหล่งที่มาดิบสำหรับตัวอย่าง กล่าวคือ โดยปกติแล้ว ตัวอย่างจะประกอบด้วยชุดย่อยของคอลัมน์ในชุดข้อมูล นอกจากนี้ ฟีเจอร์ในตัวอย่างยังอาจรวมถึงฟีเจอร์สังเคราะห์ เช่น การรวมฟีเจอร์
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแลใน หลักสูตรข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
F
ผลลบลวง (FN)
ตัวอย่างที่โมเดลคาดการณ์คลาสเชิงลบผิดพลาด เช่น โมเดล คาดการณ์ว่าข้อความอีเมลหนึ่งไม่ใช่จดหมายขยะ (คลาสเชิงลบ) แต่ข้อความอีเมลนั้นเป็นจดหมายขยะจริง
ผลบวกลวง (FP)
ตัวอย่างที่โมเดลคาดการณ์คลาสเชิงบวกอย่างไม่ถูกต้อง เช่น โมเดลคาดการณ์ว่าข้อความอีเมลหนึ่งๆ เป็นจดหมายขยะ (คลาสบวก) แต่ข้อความอีเมลนั้นไม่ใช่จดหมายขยะ
ดูข้อมูลเพิ่มเติมได้ที่เกณฑ์และเมทริกซ์ความสับสน ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
อัตราผลบวกลวง (FPR)
สัดส่วนของตัวอย่างเชิงลบจริงที่โมเดลคาดการณ์คลาสเชิงบวกผิดพลาด สูตรต่อไปนี้ใช้ในการคำนวณอัตราผลบวกลวง
อัตราผลบวกลวงคือแกน x ในกราฟ ROC
ดูข้อมูลเพิ่มเติมได้ที่การแยกประเภท: ROC และ AUC ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ฟีเจอร์
ตัวแปรอินพุตของโมเดลแมชชีนเลิร์นนิง ตัวอย่าง ประกอบด้วยฟีเจอร์อย่างน้อย 1 รายการ ตัวอย่างเช่น สมมติว่าคุณกำลังฝึกโมเดลเพื่อพิจารณาอิทธิพลของสภาพอากาศต่อคะแนนสอบของนักเรียน ตารางต่อไปนี้แสดงตัวอย่าง 3 รายการ ซึ่งแต่ละรายการมีฟีเจอร์ 3 รายการและป้ายกำกับ 1 รายการ
| ฟีเจอร์ | ป้ายกำกับ | ||
|---|---|---|---|
| อุณหภูมิ | ความชื้น | ความกดอากาศ | คะแนนสอบ |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
คอนทราสต์กับป้ายกำกับ
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้สอน ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
ฟีเจอร์ข้าม
ฟีเจอร์สังเคราะห์ที่เกิดจากการ "ครอส" ฟีเจอร์เชิงหมวดหมู่หรือแบบจัดกลุ่ม
ตัวอย่างเช่น ลองพิจารณารูปแบบ "การพยากรณ์อารมณ์" ที่แสดง อุณหภูมิในกลุ่มใดกลุ่มหนึ่งต่อไปนี้
freezingchillytemperatewarm
และแสดงความเร็วลมในกลุ่มใดกลุ่มหนึ่งต่อไปนี้
stilllightwindy
หากไม่มีฟีเจอร์ครอส โมเดลเชิงเส้นจะฝึกแยกกันในแต่ละกลุ่มต่างๆ 7 กลุ่มก่อนหน้า
ดังนั้น โมเดลจะฝึกใน เช่น
freezing โดยไม่ขึ้นอยู่กับการฝึกใน เช่น
windy
หรือจะสร้างฟีเจอร์ครอสของอุณหภูมิและ ความเร็วลมก็ได้ ฟีเจอร์สังเคราะห์นี้จะมีค่าที่เป็นไปได้ 12 ค่าดังนี้
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
การรวมฟีเจอร์ช่วยให้โมเดลเรียนรู้ความแตกต่างของอารมณ์
ระหว่างfreezing-windyวันที่มีฝนตกfreezing-stillกับวันที่ไม่มีฝนตกได้
หากคุณสร้างฟีเจอร์สังเคราะห์จาก 2 ฟีเจอร์ที่มีกลุ่มต่างๆ จำนวนมาก การครอสฟีเจอร์ที่ได้จะมีชุดค่าผสมที่เป็นไปได้จำนวนมาก เช่น หากฟีเจอร์หนึ่งมี 1,000 กลุ่ม และอีกฟีเจอร์หนึ่งมี 2,000 กลุ่ม ฟีเจอร์ครอสที่ได้จะมี 2,000,000 กลุ่ม
ในทางคณิตศาสตร์ ครอสคือผลคูณคาร์ทีเซียน
โดยส่วนใหญ่แล้ว Feature Cross จะใช้กับโมเดลเชิงเส้นและไม่ค่อยได้ใช้กับ โครงข่ายประสาทเทียม
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: การรวมฟีเจอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
Feature Engineering
กระบวนการที่มีขั้นตอนต่อไปนี้
- การพิจารณาว่าฟีเจอร์ใดบ้างที่อาจมีประโยชน์ ในการฝึกโมเดล
- การแปลงข้อมูลดิบจากชุดข้อมูลเป็นฟีเจอร์เวอร์ชันที่มีประสิทธิภาพ
เช่น คุณอาจพิจารณาว่า temperature อาจเป็นฟีเจอร์ที่มีประโยชน์
จากนั้นคุณอาจทดลองใช้การจัดกลุ่ม
เพื่อเพิ่มประสิทธิภาพสิ่งที่โมเดลสามารถเรียนรู้จากtemperatureช่วงต่างๆ ได้
บางครั้งเราเรียกการปรับแต่งฟีเจอร์ว่า การดึงฟีเจอร์หรือ การสร้างฟีเจอร์
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงตัวเลข: วิธีที่โมเดลรับข้อมูลโดยใช้เวกเตอร์ฟีเจอร์ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ชุดฟีเจอร์
กลุ่มฟีเจอร์ที่โมเดลแมชชีนเลิร์นนิงของคุณใช้ฝึก ตัวอย่างเช่น ชุดฟีเจอร์ที่เรียบง่ายสำหรับโมเดลที่คาดการณ์ราคาที่อยู่อาศัย อาจประกอบด้วยรหัสไปรษณีย์ ขนาดของที่พัก และสภาพของที่พัก
เวกเตอร์ฟีเจอร์
อาร์เรย์ของค่า feature ที่ประกอบกันเป็น example เวกเตอร์ฟีเจอร์เป็นอินพุตระหว่างการฝึกและระหว่างการอนุมาน เช่น เวกเตอร์ฟีเจอร์สําหรับโมเดลที่มีฟีเจอร์แยกกัน 2 รายการ อาจเป็นดังนี้
[0.92, 0.56]
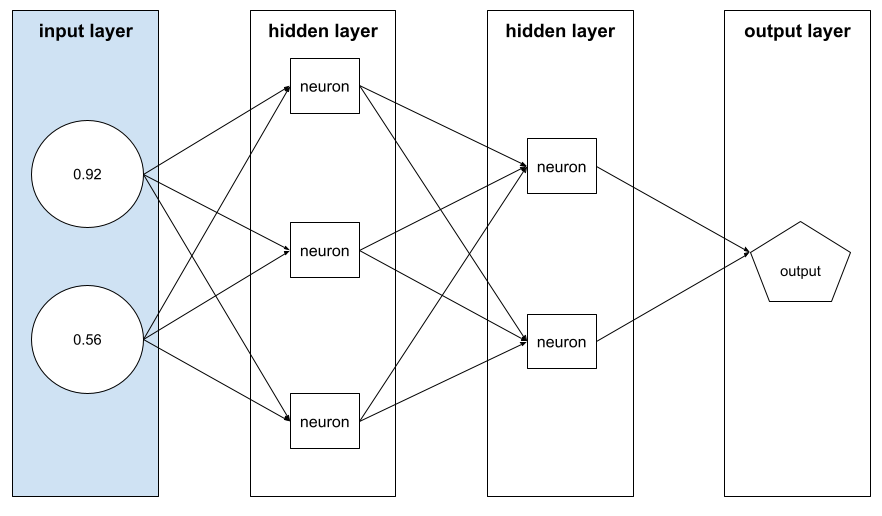
ตัวอย่างแต่ละรายการจะให้ค่าที่แตกต่างกันสำหรับเวกเตอร์ฟีเจอร์ ดังนั้น เวกเตอร์ฟีเจอร์สำหรับตัวอย่างถัดไปอาจมีลักษณะดังนี้
[0.73, 0.49]
การออกแบบฟีเจอร์จะกำหนดวิธีแสดงฟีเจอร์ในเวกเตอร์ฟีเจอร์ เช่น ฟีเจอร์เชิงหมวดหมู่แบบไบนารีที่มีค่าที่เป็นไปได้ 5 ค่าอาจแสดงด้วยการเข้ารหัสแบบ One-Hot ในกรณีนี้ ส่วนของเวกเตอร์ฟีเจอร์สำหรับตัวอย่างหนึ่งๆ จะประกอบด้วยเลข 0 จำนวน 4 ตัวและเลข 1.0 ตัวเดียวในตำแหน่งที่ 3 ดังนี้
[0.0, 0.0, 1.0, 0.0, 0.0]
อีกตัวอย่างหนึ่ง สมมติว่าโมเดลของคุณประกอบด้วยฟีเจอร์ 3 อย่าง
- ฟีเจอร์เชิงหมวดหมู่แบบไบนารีที่มีค่าที่เป็นไปได้ 5 ค่าซึ่งแสดงด้วย
การเข้ารหัสแบบ One-Hot เช่น
[0.0, 1.0, 0.0, 0.0, 0.0] - ฟีเจอร์เชิงหมวดหมู่แบบไบนารีอีกรายการที่มีค่าที่เป็นไปได้3 ค่า ซึ่งแสดงด้วยการเข้ารหัสแบบ One-hot เช่น
[0.0, 0.0, 1.0] - ฟีเจอร์จุดลอยตัว เช่น
8.3
ในกรณีนี้ เวกเตอร์ฟีเจอร์สำหรับแต่ละตัวอย่างจะแสดงด้วยค่า9 ค่า จากค่าตัวอย่างในรายการก่อนหน้า เวกเตอร์ฟีเจอร์จะเป็นดังนี้
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงตัวเลข: วิธีที่โมเดลรับข้อมูลโดยใช้เวกเตอร์ฟีเจอร์ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
วงจรความคิดเห็น
ในแมชชีนเลิร์นนิง สถานการณ์ที่การคาดการณ์ของโมเดลมีอิทธิพลต่อ ข้อมูลการฝึกของโมเดลเดียวกันหรือโมเดลอื่น ตัวอย่างเช่น โมเดลที่ แนะนำภาพยนตร์จะส่งผลต่อภาพยนตร์ที่ผู้คนเห็น ซึ่งจะ ส่งผลต่อโมเดลการแนะนำภาพยนตร์ในภายหลัง
ดูข้อมูลเพิ่มเติมได้ที่ระบบ ML ในเวอร์ชันที่ใช้งานจริง: คำถามที่ต้องถาม ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
G
การสรุป
ความสามารถของโมเดลในการคาดการณ์ข้อมูลใหม่ที่ไม่เคยเห็นมาก่อนได้อย่างถูกต้อง โมเดลที่สามารถสรุปได้จะตรงกันข้ามกับโมเดลที่โอเวอร์ฟิต
ดูข้อมูลเพิ่มเติมได้ที่การสรุปทั่วไป ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เส้นโค้งการสรุป
พล็อตของทั้งการสูญเสียการฝึกและ การสูญเสียการตรวจสอบเป็นฟังก์ชันของจำนวนการทำซ้ำ
เส้นโค้งการสรุปทั่วไปช่วยให้คุณตรวจพบการปรับมากเกินไปที่อาจเกิดขึ้นได้ ตัวอย่างเช่น เส้นโค้งการสรุปทั่วไปต่อไปนี้ แสดงให้เห็นว่าเกิดการปรับมากเกินไปเนื่องจากความสูญเสียในการตรวจสอบ ในท้ายที่สุดจะสูงกว่าความสูญเสียในการฝึกอย่างมาก
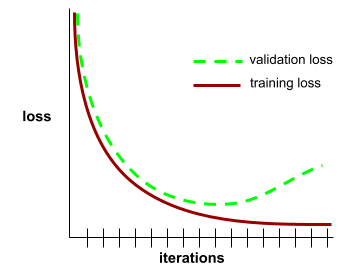
ดูข้อมูลเพิ่มเติมได้ที่การสรุปทั่วไป ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การไล่ระดับความชัน
เทคนิคทางคณิตศาสตร์เพื่อลดการสูญเสีย การไล่ระดับความชันจะปรับน้ำหนักและอคติซ้ำๆ เพื่อค่อยๆ ค้นหาการผสมผสานที่ดีที่สุดเพื่อลดการสูญเสีย
การไล่ระดับความชันมีมานานกว่าแมชชีนเลิร์นนิงมาก
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: การไล่ระดับสี ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ข้อมูลจากการสังเกตการณ์โดยตรง
เรียลลิตี้
สิ่งที่เกิดขึ้นจริง
ตัวอย่างเช่น ลองพิจารณาการแยกประเภทแบบไบนารี ที่คาดการณ์ว่านักศึกษาปี 1 จะสำเร็จการศึกษาภายใน 6 ปีหรือไม่ ข้อมูลจากการสังเกตการณ์โดยตรงสำหรับโมเดลนี้คือการที่นักเรียน คนนั้นจบการศึกษาภายใน 6 ปีหรือไม่
H
เลเยอร์ที่ซ่อนอยู่
เลเยอร์ในโครงข่ายประสาทเทียมระหว่างเลเยอร์อินพุต (ฟีเจอร์) กับเลเยอร์เอาต์พุต (การคาดการณ์) เลเยอร์ที่ซ่อนแต่ละเลเยอร์ประกอบด้วยนิวรอนอย่างน้อย 1 ตัว ตัวอย่างเช่น เครือข่ายประสาทต่อไปนี้มีเลเยอร์ที่ซ่อนไว้ 2 เลเยอร์ เลเยอร์แรกมี 3 นิวรอน และเลเยอร์ที่ 2 มี 2 นิวรอน
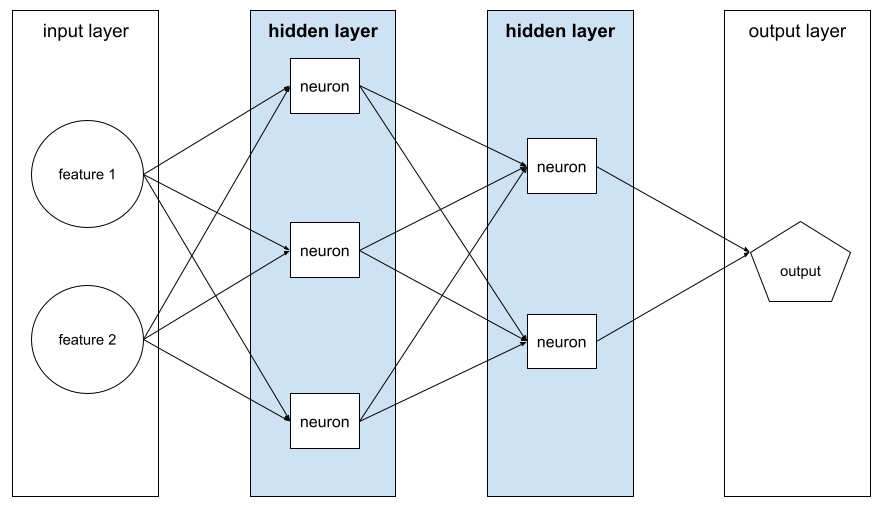
โครงข่ายประสาทแบบลึกมีเลเยอร์ที่ซ่อนอยู่มากกว่า 1 เลเยอร์ ตัวอย่างเช่น ภาพประกอบก่อนหน้าเป็นเครือข่ายประสาทเทียมแบบลึกเนื่องจากโมเดลมีเลเยอร์ที่ซ่อนอยู่ 2 เลเยอร์
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาท: โหนดและเลเยอร์ที่ซ่อนอยู่ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ไฮเปอร์พารามิเตอร์
ตัวแปรที่คุณหรือบริการปรับไฮเปอร์พารามิเตอร์ ปรับในระหว่างการเรียกใช้การฝึกโมเดลที่ต่อเนื่อง ตัวอย่างเช่น อัตราการเรียนรู้เป็นไฮเปอร์พารามิเตอร์ คุณอาจ ตั้งค่าอัตราการเรียนรู้เป็น 0.01 ก่อนเซสชันการฝึก 1 ครั้ง หากพิจารณาแล้วว่า 0.01 สูงเกินไป คุณอาจตั้งค่าอัตราการเรียนรู้เป็น 0.003 สำหรับเซสชันการฝึกครั้งถัดไป
ในทางตรงกันข้าม พารามิเตอร์คือน้ำหนักและอคติต่างๆ ที่โมเดลเรียนรู้ระหว่างการฝึก
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
I
มีการแจกแจงแบบอิสระและเหมือนกัน (i.i.d)
ข้อมูลที่ดึงมาจากการกระจายที่ไม่เปลี่ยนแปลง และค่าแต่ละค่า ที่ดึงมาจะไม่ขึ้นอยู่กับค่าที่ดึงมาก่อนหน้านี้ ข้อมูล i.i.d. คือก๊าซในอุดมคติ ของแมชชีนเลิร์นนิง ซึ่งเป็นโครงสร้างทางคณิตศาสตร์ที่มีประโยชน์ แต่แทบจะไม่พบในโลกแห่งความเป็นจริง ตัวอย่างเช่น การกระจายของผู้เข้าชมหน้าเว็บ อาจเป็นแบบ i.i.d. ในช่วงเวลาสั้นๆ นั่นคือ การกระจายจะไม่ เปลี่ยนแปลงในช่วงเวลาสั้นๆ นั้น และโดยทั่วไปแล้วการเข้าชมของบุคคลหนึ่งจะ ไม่ขึ้นอยู่กับการเข้าชมของอีกบุคคลหนึ่ง อย่างไรก็ตาม หากคุณขยายกรอบเวลาดังกล่าว ความแตกต่างตามฤดูกาลของผู้เข้าชมหน้าเว็บอาจปรากฏขึ้น
ดูความไม่คงที่ด้วย
การอนุมาน
ในแมชชีนเลิร์นนิงแบบเดิม กระบวนการคาดการณ์จะทำโดย การใช้โมเดลที่ฝึกแล้วกับตัวอย่างที่ไม่ได้ติดป้ายกำกับ ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแลในหลักสูตร Intro to ML
ในโมเดลภาษาขนาดใหญ่ การอนุมานคือ กระบวนการใช้โมเดลที่ฝึกแล้วเพื่อสร้างคำตอบ สำหรับพรอมต์ที่ป้อน
การอนุมานมีความหมายที่แตกต่างออกไปเล็กน้อยในสถิติ ดูรายละเอียดได้ใน บทความเกี่ยวกับอนุมานทางสถิติใน Wikipedia
เลเยอร์อินพุต
เลเยอร์ของโครงข่ายระบบประสาทเทียมที่ เก็บเวกเตอร์ฟีเจอร์ กล่าวคือ เลเยอร์อินพุต มีตัวอย่างสำหรับการฝึกหรือ การอนุมาน ตัวอย่างเช่น เลเยอร์อินพุตใน โครงข่ายประสาทเทียมต่อไปนี้ประกอบด้วยฟีเจอร์ 2 รายการ
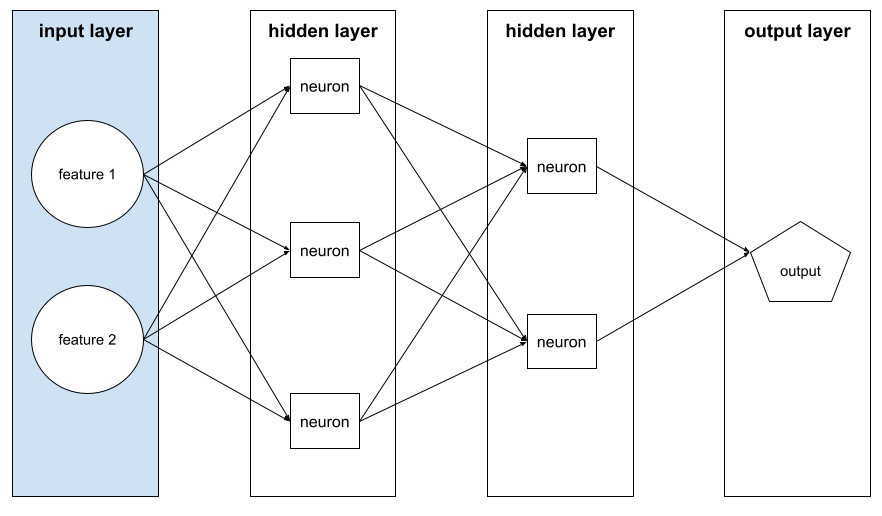
ความสามารถในการตีความ
ความสามารถในการอธิบายหรือนำเสนอการให้เหตุผลของโมเดล ML ใน รูปแบบที่มนุษย์เข้าใจได้
เช่น โมเดลการถดถอยเชิงเส้นส่วนใหญ่สามารถตีความได้สูง (คุณเพียงแค่ต้องดูน้ำหนักที่ฝึกแล้วสำหรับแต่ละฟีเจอร์) นอกจากนี้ ฟอเรสต์การตัดสินใจยังตีความได้สูงอีกด้วย อย่างไรก็ตาม โมเดลบางอย่าง ต้องใช้การแสดงภาพที่ซับซ้อนจึงจะตีความได้
คุณสามารถใช้ เครื่องมือการตีความการเรียนรู้ (LIT) เพื่อตีความโมเดล ML
การทำซ้ำ
การอัปเดตพารามิเตอร์ของโมเดลเพียงครั้งเดียว ซึ่งก็คือน้ำหนักและอคติของโมเดลระหว่างการฝึก ขนาดกลุ่มจะกำหนด จำนวนตัวอย่างที่โมเดลประมวลผลในการทำซ้ำครั้งเดียว เช่น หากขนาดกลุ่มคือ 20 โมเดลจะประมวลผลตัวอย่าง 20 รายการก่อน ปรับพารามิเตอร์
เมื่อฝึกโครงข่ายระบบประสาทเทียม การทำซ้ำครั้งเดียว จะเกี่ยวข้องกับการส่งผ่าน 2 ครั้งต่อไปนี้
- การส่งต่อเพื่อประเมินการสูญเสียในกลุ่มเดียว
- การส่งผ่านย้อนกลับ (การแพร่กระจายย้อนกลับ) เพื่อปรับ พารามิเตอร์ของโมเดลตามการสูญเสียและอัตราการเรียนรู้
ดูข้อมูลเพิ่มเติมได้ที่การไล่ระดับสี ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
L
Regularization แบบ L0
การทำให้เป็นปกติประเภทหนึ่งที่ ลงโทษจำนวนทั้งหมดของน้ำหนักที่ไม่ใช่ศูนย์ ในโมเดล เช่น โมเดลที่มีน้ำหนักที่ไม่ใช่ 0 จำนวน 11 รายการ จะถูกลงโทษมากกว่าโมเดลที่คล้ายกันซึ่งมีน้ำหนักที่ไม่ใช่ 0 จำนวน 10 รายการ
บางครั้งเราเรียก Regularization แบบ L0 ว่า Regularization แบบ L0-norm
แพ้ 1 นัด
ฟังก์ชันการสูญเสียที่คำนวณค่าสัมบูรณ์ของความแตกต่างระหว่างค่าป้ายกำกับจริงกับค่าที่โมเดลคาดการณ์ ตัวอย่างเช่น ต่อไปนี้คือการคำนวณการสูญเสีย L1 สำหรับกลุ่มของตัวอย่าง 5 รายการ
| มูลค่าที่แท้จริงของตัวอย่าง | ค่าที่โมเดลคาดการณ์ | ค่าสัมบูรณ์ของเดลต้า |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = การสูญเสีย L1 | ||
การสูญเสีย L1 มีความไวต่อค่าผิดปกติน้อยกว่าการสูญเสีย L2
ค่าเฉลี่ยความผิดพลาดสัมบูรณ์คือการสูญเสีย L1 โดยเฉลี่ยต่อตัวอย่าง
ดูข้อมูลเพิ่มเติมได้ที่ การถดถอยเชิงเส้น: การสูญเสีย ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
Regularization แบบ L1
การทำให้เป็นปกติประเภทหนึ่งที่ลงโทษน้ำหนักตามสัดส่วนของผลรวมค่าสัมบูรณ์ของน้ำหนัก การปรับค่า L1 ช่วยให้ค่าถ่วงน้ำหนักของฟีเจอร์ที่ไม่เกี่ยวข้อง หรือแทบไม่เกี่ยวข้องกลายเป็น 0 อย่างแน่นอน ฟีเจอร์ที่มีน้ำหนักเป็น 0 จะถูกนำออกจากโมเดล
เปรียบเทียบกับ L2 Regularization
การสูญเสีย L2
ฟังก์ชันการสูญเสียที่คำนวณกำลังสอง ของความแตกต่างระหว่างค่าป้ายกำกับจริงกับค่าที่โมเดลคาดการณ์ ตัวอย่างเช่น ต่อไปนี้คือการคำนวณการสูญเสีย L2 สำหรับกลุ่มของตัวอย่าง 5 รายการ
| มูลค่าที่แท้จริงของตัวอย่าง | ค่าที่โมเดลคาดการณ์ | สี่เหลี่ยมของเดลต้า |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 loss | ||
เนื่องจากการยกกำลังสอง การสูญเสีย L2 จึงขยายอิทธิพลของค่าผิดปกติ กล่าวคือ การสูญเสีย L2 จะตอบสนองต่อการคาดการณ์ที่ไม่ดีมากกว่าการสูญเสีย L1 เช่น การสูญเสีย L1 สำหรับกลุ่มก่อนหน้าจะเป็น 8 แทนที่จะเป็น 16 โปรดสังเกตว่าบัญชีที่ผิดปกติเพียงบัญชีเดียวคิดเป็น 9 จาก 16 รายการ
โมเดลการถดถอยมักใช้ Loss L2 เป็น Loss Function
ความคลาดเคลื่อนเฉลี่ยกำลังสองคือค่าเฉลี่ยของ การสูญเสีย L2 ต่อตัวอย่าง ความสูญเสียกำลังสองเป็นอีกชื่อหนึ่งของความสูญเสีย L2
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยโลจิสติก: การสูญเสียและ การทำให้เป็นปกติ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การทำ Regularization แบบ L2
การทำให้เป็นมาตรฐานประเภทหนึ่งที่ลงโทษน้ำหนักตามสัดส่วนของผลรวมของกำลังสองของน้ำหนัก การปรับค่า L2 ช่วยให้ค่าน้ำหนักค่าผิดปกติ (ค่าที่มีค่าบวกสูงหรือค่าลบต่ำ) เข้าใกล้ 0 มากขึ้น แต่ไม่ถึง 0 ฟีเจอร์ที่มีค่าใกล้ 0 มากจะยังคงอยู่ในโมเดล แต่จะไม่ส่งผลต่อการคาดการณ์ของโมเดลมากนัก
การทำให้เป็นมาตรฐาน L2 จะปรับปรุงการสรุปในโมเดลเชิงเส้นเสมอ
เปรียบเทียบกับ L1 Regularization
ดูข้อมูลเพิ่มเติมได้ที่การปรับมากเกินไป: การปรับ L2 ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ป้ายกำกับ
ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล ส่วน "คำตอบ" หรือ "ผลลัพธ์" ของตัวอย่าง
ตัวอย่างที่ติดป้ายกำกับแต่ละรายการประกอบด้วยฟีเจอร์อย่างน้อย 1 รายการและป้ายกำกับ ตัวอย่างเช่น ในชุดข้อมูลการตรวจหาสแปม ป้ายกำกับน่าจะเป็น "สแปม" หรือ "ไม่ใช่สแปม" ในชุดข้อมูลปริมาณน้ำฝน ป้ายกำกับอาจเป็นปริมาณ น้ำฝนที่ตกลงมาในช่วงระยะเวลาหนึ่ง
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแล ในข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
ตัวอย่างที่มีป้ายกำกับ
ตัวอย่างที่มีฟีเจอร์อย่างน้อย 1 รายการและป้ายกำกับ ตัวอย่างเช่น ตารางต่อไปนี้แสดงตัวอย่างที่ติดป้ายกำกับ 3 รายการจากโมเดลการประเมินบ้าน โดยแต่ละรายการมีฟีเจอร์ 3 รายการและป้ายกำกับ 1 รายการ
| จำนวนห้องนอน | จำนวนห้องน้ำ | อายุบ้าน | ราคาบ้าน (ป้ายกำกับ) |
|---|---|---|---|
| 3 | 2 | 15 | $345,000 |
| 2 | 1 | 72 | $179,000 |
| 4 | 2 | 34 | $392,000 |
ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โมเดลจะฝึกกับตัวอย่างที่ติดป้ายกำกับและทำการคาดการณ์กับ ตัวอย่างที่ไม่มีป้ายกำกับ
เปรียบเทียบตัวอย่างที่มีป้ายกำกับกับตัวอย่างที่ไม่มีป้ายกำกับ
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแล ในข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
lambda
คำพ้องความหมายของอัตราการปรับ
Lambda เป็นคำที่มีการใช้งานมากเกินไป ในที่นี้เราจะมุ่งเน้นที่คำจำกัดความของคำว่า การทำให้เป็นปกติ
เลเยอร์
ชุดนิวรอนในโครงข่ายระบบประสาทเทียม เลเยอร์ 3 ประเภทที่ใช้กันทั่วไป มีดังนี้
- เลเยอร์อินพุต ซึ่งให้ค่าสำหรับฟีเจอร์ทั้งหมด
- เลเยอร์ที่ซ่อนอย่างน้อย 1 เลเยอร์ ซึ่งจะค้นหา ความสัมพันธ์แบบไม่เชิงเส้นระหว่างฟีเจอร์กับป้ายกำกับ
- เลเยอร์เอาต์พุตซึ่งให้การคาดการณ์
ตัวอย่างเช่น ภาพต่อไปนี้แสดงโครงข่ายประสาทเทียมที่มีเลเยอร์อินพุต 1 เลเยอร์ เลเยอร์ที่ซ่อน 2 เลเยอร์ และเลเยอร์เอาต์พุต 1 เลเยอร์
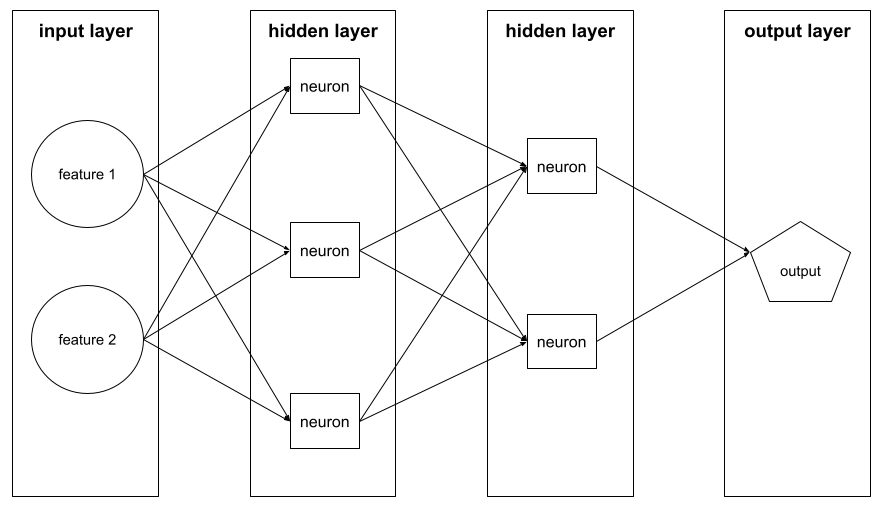
ใน TensorFlow เลเยอร์ยังเป็นฟังก์ชัน Python ที่รับTensor และตัวเลือกการกำหนดค่าเป็นอินพุต และสร้าง Tensor อื่นๆ เป็นเอาต์พุต
อัตราการเรียนรู้
จำนวนลอยตัวที่บอกอัลกอริทึมการไล่ระดับสี ว่าควรปรับน้ำหนักและอคติในแต่ละการทำซ้ำมากน้อยเพียงใด ตัวอย่างเช่น อัตราการเรียนรู้ที่ 0.3 จะปรับน้ำหนักและอคติได้แรงกว่าอัตราการเรียนรู้ที่ 0.1 ถึง 3 เท่า
อัตราการเรียนรู้เป็นไฮเปอร์พารามิเตอร์ที่สำคัญ หากตั้งค่า อัตราการเรียนรู้ต่ำเกินไป การฝึกจะใช้เวลานานเกินไป หาก คุณตั้งค่าอัตราการเรียนรู้สูงเกินไป การไล่ระดับการไล่ระดับมักมีปัญหาในการ เข้าถึงการบรรจบกัน
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เชิงเส้น
ความสัมพันธ์ระหว่างตัวแปรตั้งแต่ 2 ตัวขึ้นไปซึ่งแสดงได้โดยการบวกและการคูณเท่านั้น
พล็อตของความสัมพันธ์เชิงเส้นคือเส้นตรง
แตกต่างจากไม่ปรากฏร่วมกับเนื้อหา
รูปแบบเชิงเส้น
โมเดลที่กำหนดน้ำหนัก 1 รายการต่อฟีเจอร์เพื่อทำการคาดการณ์ (รูปแบบเชิงเส้นยังรวมอคติด้วย) ในทางตรงกันข้าม ความสัมพันธ์ของฟีเจอร์กับการคาดการณ์ในโมเดลแบบลึก โดยทั่วไปแล้วจะเป็นแบบไม่เชิงเส้น
โดยปกติแล้ว โมเดลเชิงเส้นจะฝึกได้ง่ายกว่าและตีความได้มากกว่าโมเดลเชิงลึก อย่างไรก็ตาม โมเดลเชิงลึกสามารถเรียนรู้ความสัมพันธ์ที่ซับซ้อนระหว่างฟีเจอร์ต่างๆ ได้
การถดถอยเชิงเส้นและ การถดถอยโลจิสติกเป็นโมเดลเชิงเส้น 2 ประเภท
การถดถอยเชิงเส้น
โมเดลแมชชีนเลิร์นนิงประเภทหนึ่งซึ่งมีลักษณะดังต่อไปนี้
- โมเดลนี้เป็นโมเดลเชิงเส้น
- การคาดการณ์เป็นค่าทศนิยม (นี่คือส่วนการถดถอยของการถดถอยเชิงเส้น)
เปรียบเทียบการถดถอยเชิงเส้นกับการถดถอยแบบโลจิสติก นอกจากนี้ ให้เปรียบเทียบการถดถอยกับการจัดประเภทด้วย
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การถดถอยแบบโลจิสติก
โมเดลการถดถอยประเภทหนึ่งที่คาดการณ์ความน่าจะเป็น โมเดลการถดถอยลอจิสติกมีลักษณะดังนี้
- ป้ายกำกับเป็นเชิงหมวดหมู่ โดยปกติแล้วคำว่าการถดถอยโลจิสติกจะหมายถึงการถดถอยโลจิสติกแบบไบนารี ซึ่งก็คือ โมเดลที่คำนวณความน่าจะเป็นสำหรับป้ายกำกับที่มีค่าที่เป็นไปได้ 2 ค่า การถดถอยโลจิสติกแบบมัลติโนเมียล ซึ่งเป็นรูปแบบที่พบได้น้อยกว่า จะคำนวณ ความน่าจะเป็นสำหรับป้ายกำกับที่มีค่าที่เป็นไปได้มากกว่า 2 ค่า
- ฟังก์ชันการสูญเสียระหว่างการฝึกคือLog Loss (วางหน่วย Log Loss หลายหน่วยแบบขนานกันสําหรับป้ายกํากับที่มีค่าที่เป็นไปได้มากกว่า 2 ค่าได้)
- โมเดลนี้มีสถาปัตยกรรมเชิงเส้น ไม่ใช่โครงข่ายประสาทเทียมแบบลึก อย่างไรก็ตาม คําจํากัดความที่เหลือนี้ยังใช้กับโมเดลเชิงลึกที่คาดการณ์ความน่าจะเป็น สําหรับป้ายกํากับเชิงหมวดหมู่ด้วย
ตัวอย่างเช่น พิจารณาโมเดลการถดถอยโลจิสติกส์ที่คำนวณ ความน่าจะเป็นของอีเมลขาเข้าที่อาจเป็นสแปมหรือไม่ใช่สแปม สมมติว่าในระหว่างการอนุมาน โมเดลคาดการณ์ได้ 0.72 ดังนั้น โมเดลจึงประมาณค่าต่อไปนี้
- มีโอกาส 72% ที่อีเมลจะเป็นจดหมายขยะ
- มีโอกาส 28% ที่อีเมลจะไม่ใช่จดหมายขยะ
โมเดลการถดถอยโลจิสติกใช้สถาปัตยกรรม 2 ขั้นตอนต่อไปนี้
- โมเดลสร้างการคาดการณ์ดิบ (y') โดยใช้ฟังก์ชันเชิงเส้น ของฟีเจอร์อินพุต
- โมเดลใช้การคาดการณ์ดิบดังกล่าวเป็นอินพุตสำหรับฟังก์ชันซิกมอยด์ ซึ่งจะแปลงการคาดการณ์ดิบเป็นค่าระหว่าง 0 ถึง 1 โดยไม่รวม 0 และ 1
โมเดลการถดถอยแบบโลจิสติกคาดการณ์ตัวเลขเช่นเดียวกับโมเดลการถดถอยอื่นๆ อย่างไรก็ตาม โดยปกติแล้วตัวเลขนี้จะกลายเป็นส่วนหนึ่งของโมเดลการจัดประเภทแบบไบนารี ดังนี้
- หากตัวเลขที่คาดการณ์มากกว่า เกณฑ์การจัดประเภท โมเดลการจัดประเภทแบบไบนารีจะคาดการณ์คลาสที่เป็นบวก
- หากตัวเลขที่คาดการณ์น้อยกว่าเกณฑ์การจัดประเภท โมเดลการจัดประเภทแบบไบนารีจะคาดการณ์คลาสเชิงลบ
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยโลจิสติก ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การสูญเสียของบันทึก
Loss Function ที่ใช้ในการถดถอยโลจิสติกแบบไบนารี
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยโลจิสติก: การสูญเสียและการทำให้เป็นปกติ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ล็อกออดส์
ลอการิทึมของอัตราต่อรองของเหตุการณ์
แพ้
ในระหว่างการฝึกโมเดลภายใต้การควบคุม จะมีการวัดว่าการคาดการณ์ของโมเดลอยู่ห่างจากป้ายกำกับมากน้อยเพียงใด
ฟังก์ชันการสูญเสียจะคำนวณการสูญเสีย
ดูข้อมูลเพิ่มเติมได้ที่ Linear regression: Loss ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
เส้นโค้งการสูญเสีย
พล็อตของการสูญเสียเป็นฟังก์ชันของจำนวนการทำซ้ำในการฝึก พล็อตต่อไปนี้แสดงเส้นโค้งการสูญเสียทั่วไป
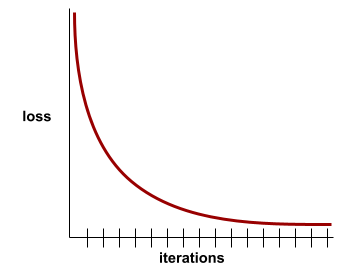
เส้นโค้งการสูญเสียช่วยให้คุณพิจารณาได้ว่าโมเดลบรรจบกันหรือฟิตมากเกินไปเมื่อใด
เส้นโค้งการสูญเสียสามารถพล็อตการสูญเสียประเภทต่อไปนี้ทั้งหมด
ดูเส้นโค้งการสรุปด้วย
ดูข้อมูลเพิ่มเติมได้ที่การปรับมากเกินไป: การตีความเส้นโค้งการสูญเสีย ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ฟังก์ชันการสูญเสีย
ในระหว่างการฝึกหรือการทดสอบ ฟังก์ชันทางคณิตศาสตร์ที่คำนวณ การสูญเสียในกลุ่มตัวอย่าง ฟังก์ชันการสูญเสียจะส่งคืนการสูญเสียที่ต่ำกว่า สำหรับโมเดลที่ทำการคาดการณ์ได้ดีกว่าโมเดลที่ทำการคาดการณ์ ได้ไม่ดี
โดยปกติแล้วเป้าหมายของการฝึกคือการลดการสูญเสียที่ฟังก์ชันการสูญเสีย ส่งคืน
ฟังก์ชันการสูญเสียมีอยู่หลายประเภท เลือกฟังก์ชันการสูญเสียที่เหมาะสม สำหรับโมเดลประเภทที่คุณกำลังสร้าง เช่น
- การสูญเสีย L2 (หรือข้อผิดพลาดกำลังสองเฉลี่ย) คือฟังก์ชันการสูญเสียสำหรับการถดถอยเชิงเส้น
- Log Loss คือฟังก์ชันการสูญเสียสำหรับ การถดถอยโลจิสติก
M
แมชชีนเลิร์นนิง
โปรแกรมหรือระบบที่ฝึก โมเดลจากข้อมูลที่ป้อน โมเดลที่ฝึกแล้วจะ ทําการคาดการณ์ที่เป็นประโยชน์จากข้อมูลใหม่ (ไม่เคยเห็นมาก่อน) ซึ่งดึงมาจาก การกระจายเดียวกันกับที่ใช้ฝึกโมเดล
แมชชีนเลิร์นนิงยังหมายถึงสาขาวิชาที่เกี่ยวข้องกับโปรแกรมหรือระบบเหล่านี้ด้วย
ดูข้อมูลเพิ่มเติมได้ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับแมชชีนเลิร์นนิง
คลาสส่วนใหญ่
ป้ายกำกับที่พบบ่อยกว่าในชุดข้อมูลที่มีความไม่สมดุลของคลาส ตัวอย่างเช่น หากชุดข้อมูลมีป้ายกำกับเชิงลบ 99% และป้ายกำกับเชิงบวก 1% ป้ายกำกับเชิงลบจะเป็นคลาสส่วนใหญ่
เปรียบเทียบกับคลาสส่วนน้อย
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: ชุดข้อมูลที่ไม่สมดุล ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
มินิแบทช์
กลุ่มเล็กๆ ที่สุ่มเลือกมาซึ่งประมวลผลในการทำซ้ำครั้งเดียว โดยปกติแล้ว ขนาดกลุ่มของมินิแบตช์จะอยู่ ระหว่าง 10 ถึง 1,000 ตัวอย่าง
ตัวอย่างเช่น สมมติว่าชุดการฝึกทั้งหมด (กลุ่มทั้งหมด) ประกอบด้วยตัวอย่าง 1,000 รายการ สมมติว่าคุณตั้งค่าขนาดกลุ่มของมินิแบตช์แต่ละรายการเป็น 20 ดังนั้น การวนซ้ำแต่ละครั้งจะกำหนดการสูญเสียในตัวอย่างแบบสุ่ม 20 รายการจาก 1,000 รายการ แล้วปรับน้ำหนักและอคติตามนั้น
การคำนวณการสูญเสียในมินิแบตช์มีประสิทธิภาพมากกว่าการคำนวณการสูญเสียในตัวอย่างทั้งหมดในฟูลแบตช์มาก
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
คลาสกลุ่มน้อย
ป้ายกำกับที่พบน้อยกว่าในชุดข้อมูลที่มีความไม่สมดุลของคลาส เช่น หากชุดข้อมูลมีป้ายกำกับเชิงลบ 99% และป้ายกำกับเชิงบวก 1% ป้ายกำกับเชิงบวกจะเป็นคลาสส่วนน้อย
เปรียบเทียบกับชั้นเรียนส่วนใหญ่
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: ชุดข้อมูลที่ไม่สมดุล ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
รุ่น
โดยทั่วไปแล้ว โครงสร้างทางคณิตศาสตร์ใดๆ ที่ประมวลผลข้อมูลอินพุตและส่งคืน เอาต์พุต กล่าวอีกนัยหนึ่งคือ โมเดลคือชุดพารามิเตอร์และโครงสร้าง ที่ระบบต้องใช้ในการคาดการณ์ ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โมเดลจะใช้ตัวอย่างเป็นข้อมูลป้อนเข้าและอนุมานการคาดการณ์เป็นข้อมูลผลลัพธ์ ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โมเดลจะแตกต่างกันเล็กน้อย เช่น
- โมเดลการถดถอยเชิงเส้นประกอบด้วยชุดน้ำหนัก และอคติ
- โมเดลโครงข่ายประสาทเทียมประกอบด้วยองค์ประกอบต่อไปนี้
- ชุดเลเยอร์ที่ซ่อน ซึ่งแต่ละเลเยอร์มีนิวรอนอย่างน้อย 1 ตัว
- น้ำหนักและความเอนเอียงที่เชื่อมโยงกับแต่ละนิวรอน
- โมเดลแผนผังการตัดสินใจประกอบด้วยองค์ประกอบต่อไปนี้
- รูปร่างของต้นไม้ ซึ่งก็คือรูปแบบที่เชื่อมต่อเงื่อนไข และใบไม้
- เงื่อนไขและใบไม้
คุณสามารถบันทึก กู้คืน หรือทำสำเนารูปแบบได้
แมชชีนเลิร์นนิงแบบไม่มีการกำกับดูแลยังสร้างโมเดลด้วย โดยปกติจะเป็นฟังก์ชันที่สามารถเชื่อมโยงตัวอย่างอินพุตกับคลัสเตอร์ที่เหมาะสมที่สุด
การจัดประเภทแบบหลายคลาส
ใน Supervised Learning ปัญหาการจัดประเภท ซึ่งชุดข้อมูลมีป้ายกำกับมากกว่า 2 คลาส ตัวอย่างเช่น ป้ายกำกับในชุดข้อมูล Iris ต้องเป็นหนึ่งใน 3 คลาสต่อไปนี้
- Iris setosa
- Iris virginica
- Iris versicolor
โมเดลที่ฝึกในชุดข้อมูล Iris ซึ่งคาดการณ์ประเภท Iris ในตัวอย่างใหม่ จะทำการจัดประเภทแบบหลายคลาส
ในทางตรงกันข้าม ปัญหาการจัดประเภทที่แยกความแตกต่างระหว่าง 2 คลาสอย่างชัดเจนคือโมเดลการจัดประเภทแบบไบนารี เช่น โมเดลอีเมลที่คาดการณ์ว่าจะเป็นสแปมหรือไม่ใช่สแปม คือโมเดลการจัดประเภทแบบไบนารี
ในปัญหาการจัดกลุ่ม การจัดประเภทแบบหลายคลาสหมายถึงคลัสเตอร์มากกว่า 2 คลัสเตอร์
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม: การจัดประเภทแบบหลายคลาส ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
N
คลาสที่เป็นลบ
ในการจัดประเภทแบบไบนารี คลาสหนึ่งเรียกว่าบวกและอีกคลาสหนึ่งเรียกว่าลบ คลาสที่เป็นบวกคือ สิ่งหรือเหตุการณ์ที่โมเดลกำลังทดสอบ และคลาสที่เป็นลบคือ ความเป็นไปได้อื่นๆ เช่น
- คลาสเชิงลบในการตรวจทางการแพทย์อาจเป็น "ไม่ใช่มะเร็ง"
- คลาสเชิงลบในโมเดลการจัดประเภทอีเมลอาจเป็น "ไม่ใช่จดหมายขยะ"
เปรียบเทียบกับคลาสที่เป็นบวก
โครงข่ายระบบประสาทเทียม
โมเดลที่มีเลเยอร์ที่ซ่อนอยู่อย่างน้อย 1 รายการ โครงข่ายประสาทแบบลึกเป็นโครงข่ายประสาทประเภทหนึ่ง ที่มีเลเยอร์ที่ซ่อนอยู่มากกว่า 1 เลเยอร์ ตัวอย่างเช่น ไดอะแกรมต่อไปนี้ แสดงโครงข่ายประสาทเทียมแบบลึกที่มีเลเยอร์ซ่อน 2 เลเยอร์
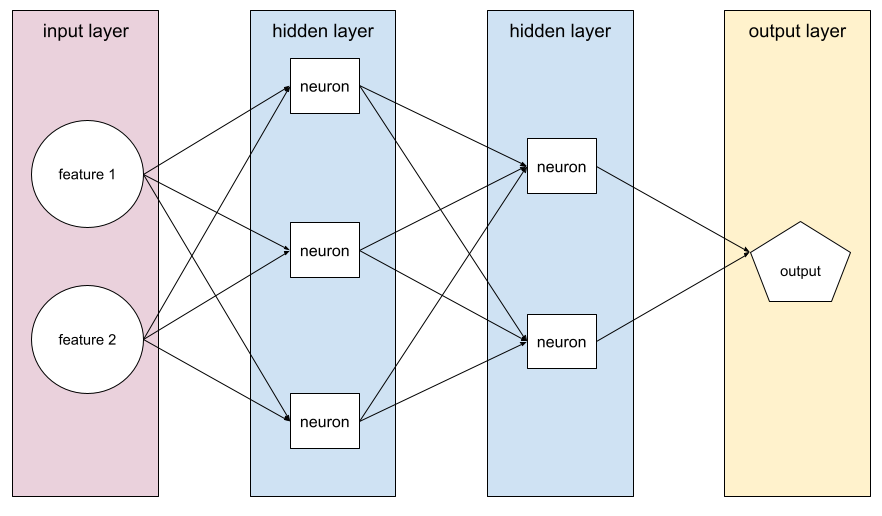
นิวรอนแต่ละตัวในโครงข่ายประสาทจะเชื่อมต่อกับโหนดทั้งหมดในเลเยอร์ถัดไป ตัวอย่างเช่น ในแผนภาพก่อนหน้า คุณจะเห็นว่านิวรอนทั้ง 3 ตัว ในเลเยอร์ที่ซ่อนอยู่แรกเชื่อมต่อกับนิวรอนทั้ง 2 ตัวใน เลเยอร์ที่ซ่อนอยู่ชั้นที่ 2 แยกกัน
บางครั้งเราเรียกโครงข่ายประสาทเทียมที่ใช้ในคอมพิวเตอร์ว่าโครงข่ายประสาทเทียมเพื่อแยกความแตกต่างจากโครงข่ายประสาทที่พบในสมองและระบบประสาทอื่นๆ
โครงข่ายประสาทเทียมบางอย่างสามารถเลียนแบบความสัมพันธ์แบบไม่เชิงเส้นที่ซับซ้อนอย่างยิ่ง ระหว่างฟีเจอร์ต่างๆ กับป้ายกำกับ
ดูโครงข่ายประสาทเทียมแบบคอนโวลูชันและ โครงข่ายประสาทเทียมแบบเกิดซ้ำด้วย
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เซลล์ประสาท
ในแมชชีนเลิร์นนิง หน่วยที่แตกต่างกันภายในเลเยอร์ที่ซ่อนอยู่ ของโครงข่ายประสาทเทียม นิวรอนแต่ละตัวจะดำเนินการ 2 ขั้นตอนต่อไปนี้
- คำนวณผลรวมแบบถ่วงน้ำหนักของค่าอินพุตที่คูณ ด้วยน้ำหนักที่เกี่ยวข้อง
- ส่งผลรวมแบบถ่วงน้ำหนักเป็นอินพุตไปยังฟังก์ชันการเปิดใช้งาน
นิวรอนในเลเยอร์ซ่อนชั้นแรกจะรับอินพุตจากค่าฟีเจอร์ ในเลเยอร์อินพุต นิวรอนในเลเยอร์ที่ซ่อนใดๆ ที่อยู่นอกเหนือจากเลเยอร์แรกจะรับอินพุตจากนิวรอนในเลเยอร์ที่ซ่อนก่อนหน้า ตัวอย่างเช่น นิวรอนในเลเยอร์ที่ซ่อนที่ 2 จะยอมรับอินพุตจากนิวรอนในเลเยอร์ที่ซ่อนที่ 1
ภาพต่อไปนี้ไฮไลต์นิวรอน 2 ตัวและอินพุตของนิวรอนเหล่านั้น
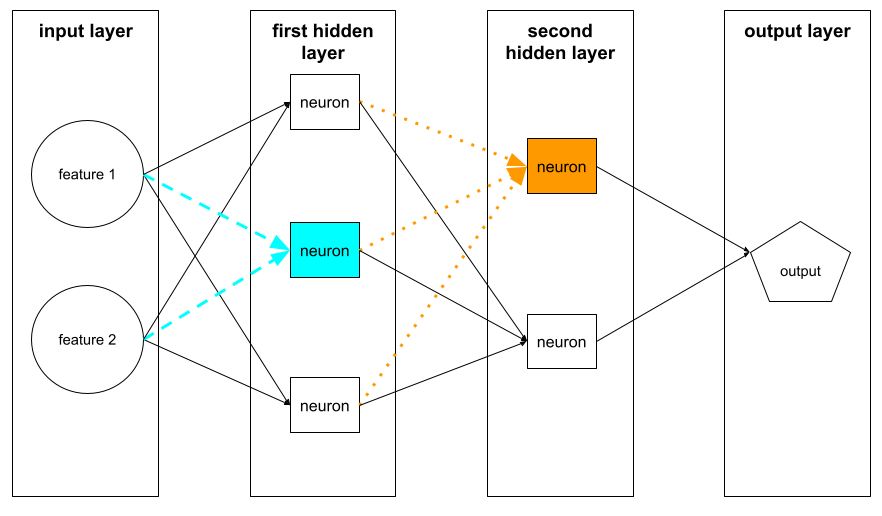
นิวรอนในโครงข่ายประสาทเทียมจะเลียนแบบพฤติกรรมของนิวรอนในสมองและ ส่วนอื่นๆ ของระบบประสาท
โหนด (โครงข่ายประสาทเทียม)
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ไม่ใช่แบบดั้งเดิม
ความสัมพันธ์ระหว่างตัวแปรตั้งแต่ 2 ตัวขึ้นไปซึ่งไม่สามารถแสดงได้ด้วยการบวกและการคูณเพียงอย่างเดียว ความสัมพันธ์เชิงเส้นแสดงเป็นเส้นได้ แต่ความสัมพันธ์ที่ไม่ใช่เชิงเส้นแสดงเป็นเส้นไม่ได้ ตัวอย่างเช่น ลองพิจารณารูปแบบ 2 รูปแบบที่แต่ละรูปแบบเชื่อมโยง ฟีเจอร์เดียวกับป้ายกำกับเดียว โมเดลทางด้านซ้ายเป็นแบบเชิงเส้น และโมเดลทางด้านขวาเป็นแบบไม่เชิงเส้น

ดูโครงข่ายประสาทเทียม: โหนดและเลเยอร์ที่ซ่อนอยู่ ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิงเพื่อทดลองใช้ฟังก์ชัน ที่ไม่ใช่เชิงเส้นประเภทต่างๆ
ความไม่คงที่
ฟีเจอร์ที่มีค่าเปลี่ยนแปลงในมิติข้อมูลอย่างน้อย 1 รายการ ซึ่งมักจะเป็นเวลา ตัวอย่างเช่น ลองพิจารณาตัวอย่างต่อไปนี้ของความไม่คงที่
- จำนวนชุดว่ายน้ำที่ขายในร้านค้าหนึ่งๆ จะแตกต่างกันไปตามฤดูกาล
- ปริมาณผลไม้ชนิดหนึ่งที่เก็บเกี่ยวในภูมิภาคหนึ่งๆ เป็น 0 ในช่วงเวลาส่วนใหญ่ของปี แต่มีปริมาณมากในช่วงเวลาสั้นๆ
- การเปลี่ยนแปลงสภาพภูมิอากาศทำให้อุณหภูมิเฉลี่ยรายปีเปลี่ยนแปลงไป
คอนทราสต์กับความคงที่
การแปลงเป็นรูปแบบมาตรฐาน
โดยทั่วไป กระบวนการแปลงช่วงค่าจริงของตัวแปร เป็นช่วงค่ามาตรฐาน เช่น
- -1 ถึง +1
- 0 ถึง 1
- คะแนนมาตรฐาน (Z-Score) (ประมาณ -3 ถึง +3)
ตัวอย่างเช่น สมมติว่าช่วงค่าจริงของฟีเจอร์หนึ่งคือ 800 ถึง 2,400 ในส่วนของการออกแบบฟีเจอร์ คุณสามารถปรับค่าจริงให้เป็นช่วงมาตรฐาน เช่น -1 ถึง +1
การปรับให้เป็นมาตรฐานเป็นงานที่พบบ่อยในการออกแบบฟีเจอร์ โดยปกติแล้ว โมเดลจะฝึกได้เร็วขึ้น (และให้การคาดการณ์ได้ดีขึ้น) เมื่อฟีเจอร์ที่เป็นตัวเลขทุกรายการในเวกเตอร์ฟีเจอร์มีช่วงที่ใกล้เคียงกัน
ดูการปรับค่าให้เป็นมาตรฐานแบบ Z-score ด้วย
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลตัวเลข: การปรับให้เป็นมาตรฐาน ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ข้อมูลเชิงตัวเลข
ฟีเจอร์แสดงเป็นจำนวนเต็มหรือจำนวนจริง เช่น โมเดลการประเมินบ้านอาจแสดงขนาด ของบ้าน (เป็นตารางฟุตหรือตารางเมตร) เป็นข้อมูลตัวเลข การแสดงฟีเจอร์เป็นข้อมูลตัวเลขบ่งชี้ว่าค่าของฟีเจอร์มีความสัมพันธ์ทางคณิตศาสตร์กับป้ายกำกับ กล่าวคือ จำนวนตารางเมตรในบ้านอาจมีความสัมพันธ์ทางคณิตศาสตร์กับมูลค่าของบ้าน
ข้อมูลจำนวนเต็มบางรายการไม่ควรแสดงเป็นข้อมูลตัวเลข ตัวอย่างเช่น
รหัสไปรษณีย์ในบางส่วนของโลกเป็นจำนวนเต็ม แต่ไม่ควรแสดงรหัสไปรษณีย์ที่เป็นจำนวนเต็ม
เป็นข้อมูลตัวเลขในโมเดล เนื่องจากรหัสไปรษณีย์ 20000 ไม่ได้มีประสิทธิภาพเป็น 2 เท่า (หรือครึ่งหนึ่ง) ของรหัสไปรษณีย์ 10000
นอกจากนี้ แม้ว่ารหัสไปรษณีย์ที่แตกต่างกันจะสัมพันธ์กับมูลค่าอสังหาริมทรัพย์ที่แตกต่างกัน แต่เราก็ไม่สามารถสรุปได้ว่ามูลค่าอสังหาริมทรัพย์ที่รหัสไปรษณีย์ 20000 มีมูลค่าเป็น 2 เท่าของมูลค่าอสังหาริมทรัพย์ที่รหัสไปรษณีย์ 10000
ควรแสดงรหัสไปรษณีย์เป็นข้อมูลเชิงหมวดหมู่แทน
บางครั้งฟีเจอร์ที่เป็นตัวเลขจะเรียกว่า ฟีเจอร์ต่อเนื่อง
ดูข้อมูลเพิ่มเติมได้ที่การทำงานกับข้อมูลตัวเลข ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
O
ออฟไลน์
คำพ้องความหมายของ static
การอนุมานแบบออฟไลน์
กระบวนการที่โมเดลสร้างการคาดการณ์ เป็นชุด แล้วแคช (บันทึก) การคาดการณ์เหล่านั้น จากนั้นแอปจะเข้าถึงการคาดคะเนที่อนุมานได้จากแคชแทนที่จะเรียกใช้โมเดลอีกครั้ง
ตัวอย่างเช่น ลองพิจารณาโมเดลที่สร้างพยากรณ์อากาศในพื้นที่ (การคาดการณ์) ทุกๆ 4 ชั่วโมง หลังจากเรียกใช้โมเดลแต่ละครั้ง ระบบจะ แคชพยากรณ์อากาศในพื้นที่ทั้งหมด แอปสภาพอากาศจะดึงข้อมูลพยากรณ์อากาศ จากแคช
การอนุมานแบบออฟไลน์เรียกอีกอย่างว่าการอนุมานแบบคงที่
เปรียบเทียบกับการอนุมานออนไลน์ ดูข้อมูลเพิ่มเติมได้ที่ระบบ ML ที่ใช้งานจริง: การอนุมานแบบคงที่เทียบกับการอนุมานแบบไดนามิก ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
การเข้ารหัสแบบ One-hot
การแสดงข้อมูลเชิงหมวดหมู่เป็นเวกเตอร์ซึ่งมีลักษณะดังนี้
- องค์ประกอบหนึ่งตั้งค่าเป็น 1
- และตั้งค่าองค์ประกอบอื่นๆ ทั้งหมดเป็น 0
โดยทั่วไปแล้ว การเข้ารหัสแบบ One-Hot จะใช้เพื่อแสดงสตริงหรือตัวระบุที่มีชุดค่าที่เป็นไปได้แบบจำกัด
ตัวอย่างเช่น สมมติว่าฟีเจอร์เชิงหมวดหมู่หนึ่งชื่อ
Scandinavia มีค่าที่เป็นไปได้ 5 ค่าดังนี้
- "เดนมาร์ก"
- "สวีเดน"
- "นอร์เวย์"
- "ฟินแลนด์"
- "ไอซ์แลนด์"
การเข้ารหัสแบบ One-Hot สามารถแสดงค่าทั้ง 5 ค่าได้ดังนี้
| ประเทศ | เวกเตอร์ | ||||
|---|---|---|---|---|---|
| "เดนมาร์ก" | 1 | 0 | 0 | 0 | 0 |
| "สวีเดน" | 0 | 1 | 0 | 0 | 0 |
| "นอร์เวย์" | 0 | 0 | 1 | 0 | 0 |
| "ฟินแลนด์" | 0 | 0 | 0 | 1 | 0 |
| "ไอซ์แลนด์" | 0 | 0 | 0 | 0 | 1 |
การเข้ารหัสแบบ One-Hot ช่วยให้โมเดลเรียนรู้การเชื่อมต่อต่างๆ ตามประเทศทั้ง 5 ประเทศได้
การแสดงฟีเจอร์เป็นข้อมูลตัวเลขเป็นอีกทางเลือกหนึ่งแทนการเข้ารหัสแบบ One-hot ขออภัย การแสดงประเทศในแถบสแกนดิเนเวียเป็นตัวเลขไม่ใช่ตัวเลือกที่ดี ตัวอย่างเช่น ลองพิจารณาการแสดงตัวเลขต่อไปนี้
- "เดนมาร์ก" คือ 0
- "สวีเดน" คือ 1
- "นอร์เวย์" คือ 2
- "ฟินแลนด์" คือ 3
- "ไอซ์แลนด์" คือ 4
เมื่อใช้การเข้ารหัสตัวเลข โมเดลจะตีความตัวเลขดิบในเชิงคณิตศาสตร์และจะพยายามฝึกกับตัวเลขเหล่านั้น อย่างไรก็ตาม ในความเป็นจริงแล้ว ไอซ์แลนด์ไม่ได้มีประชากรมากกว่า (หรือน้อยกว่า) นอร์เวย์ 2 เท่า โมเดลจึงอาจสรุปผลที่แปลกประหลาดได้
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: คำศัพท์และการเข้ารหัสแบบ One-Hot ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
หนึ่งเทียบกับทั้งหมด
เมื่อพิจารณาปัญหาการจัดประเภทที่มี N คลาส โซลูชันที่ประกอบด้วยโมเดลการจัดประเภทแบบไบนารีแยกกัน N โมเดล ซึ่งเป็นโมเดลการจัดประเภทแบบไบนารี 1 โมเดลสำหรับผลลัพธ์ที่เป็นไปได้แต่ละรายการ ตัวอย่างเช่น เมื่อพิจารณาโมเดล ที่จัดประเภทตัวอย่างเป็นสัตว์ พืช หรือแร่ธาตุ โซลูชันแบบหนึ่งเทียบกับทั้งหมด จะให้โมเดลการจัดประเภทแบบไบนารี 3 โมเดลแยกกันดังนี้
- สัตว์กับไม่ใช่สัตว์
- ผักกับไม่ใช่ผัก
- แร่ธาตุเทียบกับไม่ใช่แร่ธาตุ
ออนไลน์
คำพ้องความหมายของไดนามิก
การอนุมานออนไลน์
สร้างการคาดการณ์ตามต้องการ ตัวอย่างเช่น สมมติว่าแอปส่งอินพุตไปยังโมเดลและส่งคำขอสำหรับ การคาดการณ์ ระบบที่ใช้การอนุมานออนไลน์จะตอบสนองต่อคำขอโดยการเรียกใช้โมเดล (และส่งคืนการคาดการณ์ไปยังแอป)
เทียบกับการอนุมานแบบออฟไลน์
ดูข้อมูลเพิ่มเติมได้ที่ระบบ ML ที่ใช้งานจริง: การอนุมานแบบคงที่เทียบกับการอนุมานแบบไดนามิก ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เลเยอร์เอาต์พุต
เลเยอร์ "สุดท้าย" ของโครงข่ายประสาทเทียม เลเยอร์เอาต์พุตมีการคาดการณ์
ภาพต่อไปนี้แสดงโครงข่ายประสาทแบบลึกขนาดเล็กที่มีเลเยอร์อินพุต เลเยอร์ที่ซ่อน 2 เลเยอร์ และเลเยอร์เอาต์พุต
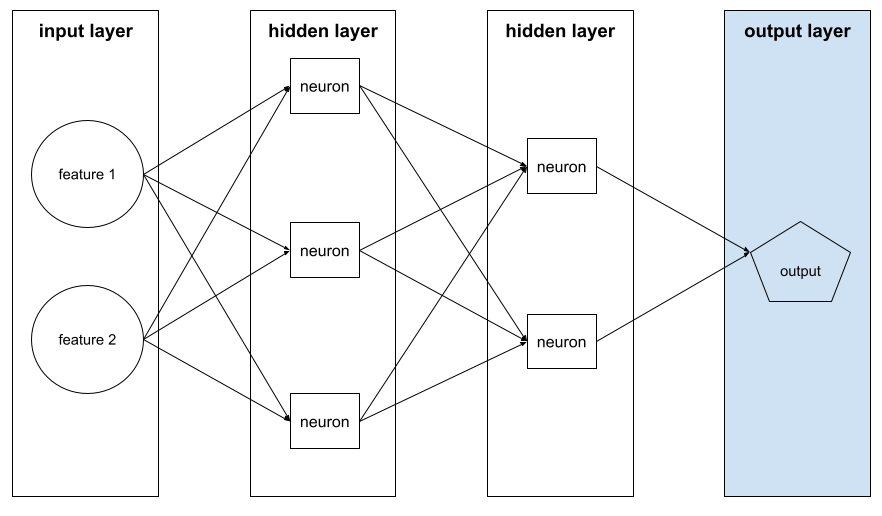
Overfitting
การสร้างโมเดลที่ตรงกับข้อมูลการฝึกอย่างใกล้ชิดมากจนโมเดลไม่สามารถคาดการณ์ข้อมูลใหม่ได้อย่างถูกต้อง
การทำให้เป็นปกติจะช่วยลดการเกิด Overfitting ได้ การฝึกในชุดการฝึกขนาดใหญ่และหลากหลายยังช่วยลดการเกิด Overfitting ได้ด้วย
ดูข้อมูลเพิ่มเติมได้ที่การเกิด Overfitting ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
P
แพนด้า
API การวิเคราะห์ข้อมูลแบบคอลัมน์ที่สร้างขึ้นบน numpy เฟรมเวิร์กแมชชีนเลิร์นนิงหลายรายการ รวมถึง TensorFlow รองรับโครงสร้างข้อมูล pandas เป็นอินพุต ดูรายละเอียดได้ที่ เอกสารประกอบของ Pandas
พารามิเตอร์
น้ำหนักและอคติที่โมเดลเรียนรู้ระหว่างการฝึก ตัวอย่างเช่น ในโมเดลการถดถอยเชิงเส้น พารามิเตอร์ประกอบด้วย อคติ (b) และน้ำหนักทั้งหมด (w1, w2, และอื่นๆ) ในสูตรต่อไปนี้
ในทางตรงกันข้าม ไฮเปอร์พารามิเตอร์คือค่าที่คุณ (หรือบริการปรับไฮเปอร์พารามิเตอร์) จัดหาให้แก่โมเดล เช่น อัตราการเรียนรู้เป็นไฮเปอร์พารามิเตอร์
คลาสที่เป็นบวก
ชั้นเรียนที่คุณกำลังทดสอบ
เช่น คลาสที่เป็นบวกในโมเดลมะเร็งอาจเป็น "เนื้องอก" คลาสที่เป็นบวกในโมเดลการจัดประเภทอีเมล อาจเป็น "จดหมายขยะ"
เปรียบเทียบกับคลาสที่เป็นลบ
หลังการประมวลผล
การปรับเอาต์พุตของโมเดลหลังจากเรียกใช้โมเดลแล้ว การประมวลผลภายหลังสามารถใช้เพื่อบังคับใช้ข้อจํากัดด้านความเป็นธรรมโดยไม่ต้อง แก้ไขโมเดลด้วยตนเอง
ตัวอย่างเช่น อาจใช้การประมวลผลภายหลังกับโมเดลการจัดประเภทแบบไบนารีโดยการตั้งค่าเกณฑ์การจัดประเภทเพื่อให้ความเท่าเทียมกันของโอกาสยังคงอยู่ สําหรับแอตทริบิวต์บางอย่างโดยตรวจสอบว่าอัตราผลบวกจริง มีค่าเท่ากันสําหรับค่าทั้งหมดของแอตทริบิวต์นั้น
ความแม่นยำ
เมตริกสําหรับโมเดลการจัดประเภทที่ตอบคําถามต่อไปนี้
เมื่อโมเดลคาดการณ์คลาสเชิงบวก การคาดการณ์กี่เปอร์เซ็นต์ที่ถูกต้อง
สูตรมีดังนี้
ที่ไหน
- ผลบวกจริงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกได้อย่างถูกต้อง
- ผลบวกลวงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกอย่างไม่ถูกต้อง
เช่น สมมติว่าโมเดลทำการคาดการณ์เชิงบวก 200 รายการ จากการคาดการณ์ที่เป็นบวก 200 รายการ
- 150 รายการเป็นผลบวกจริง
- 50 รายการเป็นการตรวจจับที่ผิดพลาด
ในกรณีนี้
เปรียบเทียบกับความแม่นยำและความอ่อนไหว
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ความแม่นยำ การเรียกคืน ความเที่ยงตรง และเมตริกที่เกี่ยวข้อง ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การคาดการณ์
เอาต์พุตของโมเดล เช่น
- การคาดการณ์ของโมเดลการจัดประเภทแบบไบนารีคือคลาสที่เป็นบวกหรือคลาสที่เป็นลบ
- การคาดการณ์ของโมเดลการจัดประเภทแบบหลายคลาสคือ 1 คลาส
- การคาดการณ์ของโมเดลการถดถอยเชิงเส้นคือตัวเลข
ป้ายกำกับพร็อกซี
ข้อมูลที่ใช้ในการประมาณป้ายกำกับซึ่งไม่มีในชุดข้อมูลโดยตรง
ตัวอย่างเช่น สมมติว่าคุณต้องฝึกโมเดลเพื่อคาดการณ์ระดับความเครียดของพนักงาน ชุดข้อมูลของคุณมีฟีเจอร์การคาดการณ์จำนวนมาก แต่ไม่มีป้ายกำกับที่ชื่อระดับความเครียด คุณจึงเลือก "อุบัติเหตุในที่ทำงาน" เป็นป้ายกำกับพร็อกซีสำหรับ ระดับความเครียด เพราะพนักงานที่อยู่ภายใต้ความเครียดสูงมีแนวโน้มที่จะเกิดอุบัติเหตุมากกว่าพนักงานที่ใจเย็น หรือว่าไม่ อุบัติเหตุในที่ทำงานอาจเพิ่มขึ้นและลดลงด้วยเหตุผลหลายประการ
ตัวอย่างที่ 2 สมมติว่าคุณต้องการให้ is it raining? เป็นป้ายกํากับบูลีน สําหรับชุดข้อมูล แต่ชุดข้อมูลไม่มีข้อมูลฝน หากมีรูปภาพ คุณอาจสร้างรูปภาพของผู้คน ที่ถือร่มเป็นป้ายกำกับพร็อกซีสำหรับฝนตกไหม ป้ายกำกับพร็อกซีที่ดี คืออะไร อาจเป็นไปได้ แต่ผู้คนในบางวัฒนธรรมอาจมีแนวโน้มที่จะพกร่มเพื่อป้องกันแสงแดดมากกว่าฝน
ป้ายกำกับพร็อกซีมักจะไม่สมบูรณ์ หากเป็นไปได้ ให้เลือกป้ายกำกับจริงแทน ป้ายกำกับพร็อกซี อย่างไรก็ตาม หากไม่มีป้ายกำกับจริง ให้เลือกป้ายกำกับพร็อกซีอย่างระมัดระวัง โดยเลือกป้ายกำกับพร็อกซีที่มีความเหมาะสมน้อยที่สุด
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: ป้ายกำกับ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
R
RAG
คำย่อของ การสร้างที่เพิ่มการดึงข้อมูล
ผู้ให้คะแนน
บุคคลที่ให้ป้ายกำกับสำหรับตัวอย่าง "ผู้ใส่คำอธิบายประกอบ" เป็นอีกชื่อหนึ่งของผู้จัดประเภท
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: ปัญหาที่พบบ่อย ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
การเรียกคืน
เมตริกสําหรับโมเดลการจัดประเภทที่ตอบคําถามต่อไปนี้
เมื่อความจริงพื้นฐานคือคลาสที่เป็นบวก โมเดลระบุการคาดการณ์เป็นคลาสที่เป็นบวกได้อย่างถูกต้องกี่เปอร์เซ็นต์
สูตรมีดังนี้
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
ที่ไหน
- ผลบวกจริงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกได้อย่างถูกต้อง
- ผลลบลวงหมายความว่าโมเดลคาดการณ์ผิดพลาดว่า คลาสเชิงลบ
เช่น สมมติว่าโมเดลของคุณทำการคาดการณ์ 200 รายการในตัวอย่างที่ความจริงพื้นฐานเป็นคลาสเชิงบวก โดยในการคาดการณ์ 200 รายการนี้
- 180 รายการเป็นผลบวกจริง
- 20 รายการเป็นผลลบลวง
ในกรณีนี้
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ความแม่นยำ การเรียกคืน ความแม่นยำ และเมตริกที่เกี่ยวข้อง
หน่วยเชิงเส้นที่มีการแก้ไข (ReLU)
ฟังก์ชันการเปิดใช้งานที่มีลักษณะการทำงานดังนี้
- หากอินพุตเป็นค่าลบหรือ 0 เอาต์พุตจะเป็น 0
- หากอินพุตเป็นค่าบวก เอาต์พุตจะเท่ากับอินพุต
เช่น
- หากอินพุตคือ -3 เอาต์พุตจะเป็น 0
- หากอินพุตคือ +3 เอาต์พุตจะเป็น 3.0
กราฟของ ReLU มีดังนี้
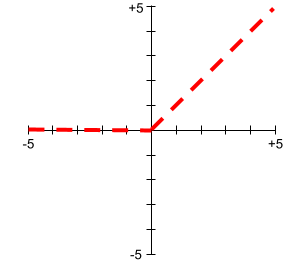
ReLU เป็นฟังก์ชันการเปิดใช้งานที่ได้รับความนิยมอย่างมาก แม้จะมีลักษณะการทำงานที่เรียบง่าย แต่ ReLU ก็ยังช่วยให้โครงข่ายประสาทเทียมเรียนรู้ความสัมพันธ์แบบไม่เชิงเส้นระหว่างฟีเจอร์กับป้ายกำกับได้
โมเดลการเกิดปัญหาซ้ำ
โดยทั่วไปแล้ว โมเดลที่สร้างการคาดการณ์เชิงตัวเลข (ในทางตรงกันข้าม โมเดลการแยกประเภทจะสร้างการคาดการณ์คลาส) ตัวอย่างเช่น โมเดลต่อไปนี้เป็นโมเดลการถดถอยทั้งหมด
- โมเดลที่คาดการณ์มูลค่าของบ้านหลังหนึ่งในสกุลเงินยูโร เช่น 423,000
- โมเดลที่คาดการณ์อายุคาดเฉลี่ยของต้นไม้หนึ่งๆ เป็นปี เช่น 23.2
- โมเดลที่คาดการณ์ปริมาณฝนเป็นนิ้วที่จะตกในเมืองหนึ่งๆ ในอีก 6 ชั่วโมงข้างหน้า เช่น 0.18
โมเดลการถดถอยที่ใช้กันทั่วไปมี 2 ประเภท ได้แก่
- การถดถอยเชิงเส้น ซึ่งจะค้นหาเส้นที่เหมาะสมที่สุด กับค่าป้ายกำกับสำหรับฟีเจอร์
- การถดถอยแบบโลจิสติก ซึ่งสร้างความน่าจะเป็นระหว่าง 0.0 ถึง 1.0 ที่โดยปกติแล้วระบบจะแมปกับการคาดการณ์คลาส
ไม่ใช่ทุกโมเดลที่แสดงผลการคาดการณ์เชิงตัวเลขจะเป็นโมเดลการถดถอย ในบางกรณี การคาดการณ์ที่เป็นตัวเลขก็เป็นเพียงโมเดลการจัดประเภท ที่มีชื่อคลาสเป็นตัวเลข ตัวอย่างเช่น โมเดลที่คาดการณ์รหัสไปรษณีย์ที่เป็นตัวเลขคือโมเดลการจัดประเภท ไม่ใช่โมเดลการถดถอย
Regularization
กลไกที่ช่วยลดการปรับมากเกินไป การทำให้เป็นปกติประเภทที่ได้รับความนิยมมีดังนี้
- การทำให้เป็นค่าปกติ L1
- การทำให้เป็นค่าปกติ L2
- การทำให้เป็นค่าปกติของ Dropout
- การหยุดก่อนเวลา (นี่ไม่ใช่ วิธีการปรับค่าปกติอย่างเป็นทางการ แต่สามารถจำกัดการปรับมากเกินไปได้อย่างมีประสิทธิภาพ)
นอกจากนี้ การปรับค่าปกติยังอาจกำหนดเป็นค่าปรับสำหรับความซับซ้อนของโมเดลได้ด้วย
ดูข้อมูลเพิ่มเติมได้ที่การปรับมากเกินไป: ความซับซ้อนของโมเดล ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
อัตราการปรับค่าปกติ
ตัวเลขที่ระบุความสําคัญสัมพัทธ์ของการทําให้เป็นปกติระหว่างการฝึก การเพิ่ม อัตราการทำให้เป็นปกติจะช่วยลดการปรับมากเกินไป แต่ก็อาจ ลดความสามารถในการคาดการณ์ของโมเดล ในทางกลับกัน การลดหรือละเว้น อัตราการทำให้เป็นปกติจะเพิ่มการปรับมากเกินไป
ดูข้อมูลเพิ่มเติมได้ที่การปรับมากเกินไป: การปรับ L2 ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ReLU
ตัวย่อของ Rectified Linear Unit
การสร้างเสริมด้วยการดึงข้อมูล (RAG)
เทคนิคในการปรับปรุงคุณภาพของเอาต์พุตโมเดลภาษาขนาดใหญ่ (LLM) โดยการอิงตามแหล่งความรู้ที่ดึงมาหลังจากฝึกโมเดลแล้ว RAG ช่วยปรับปรุงความแม่นยําของคําตอบของ LLM โดยให้ LLM ที่ผ่านการฝึกเข้าถึงข้อมูลที่ดึงมาจากฐานความรู้หรือเอกสารที่เชื่อถือได้
แรงจูงใจที่พบบ่อยในการใช้การสร้างที่เพิ่มการดึงข้อมูล ได้แก่
- เพิ่มความแม่นยำของข้อเท็จจริงในคำตอบที่โมเดลสร้างขึ้น
- การให้สิทธิ์โมเดลเข้าถึงความรู้ที่ไม่ได้ฝึก
- การเปลี่ยนความรู้ที่โมเดลใช้
- การเปิดใช้โมเดลเพื่ออ้างอิงแหล่งที่มา
ตัวอย่างเช่น สมมติว่าแอปเคมีใช้ PaLM API เพื่อสร้างข้อมูลสรุป ที่เกี่ยวข้องกับคำค้นหาของผู้ใช้ เมื่อแบ็กเอนด์ของแอปได้รับการค้นหา แบ็กเอนด์จะดำเนินการต่อไปนี้
- ค้นหา ("ดึง") ข้อมูลที่เกี่ยวข้องกับคําค้นหาของผู้ใช้
- ผนวก ("เพิ่ม") ข้อมูลเคมีที่เกี่ยวข้องกับคำค้นหาของผู้ใช้
- สั่งให้ LLM สร้างข้อมูลสรุปตามข้อมูลที่ต่อท้าย
เส้นโค้ง ROC (Receiver Operating Characteristic)
กราฟของอัตราผลบวกจริงเทียบกับ อัตราผลบวกลวงสำหรับเกณฑ์การจัดประเภทต่างๆ ในการจัดประเภทแบบไบนารี
รูปร่างของเส้นโค้ง ROC แสดงให้เห็นความสามารถของโมเดลการจัดประเภทแบบไบนารี ในการแยกคลาสที่เป็นบวกออกจากคลาสที่เป็นลบ สมมติว่าโมเดลการจัดประเภทแบบไบนารีแยกคลาสเชิงลบทั้งหมดออกจากคลาสเชิงบวกทั้งหมดได้อย่างสมบูรณ์ ดังนี้
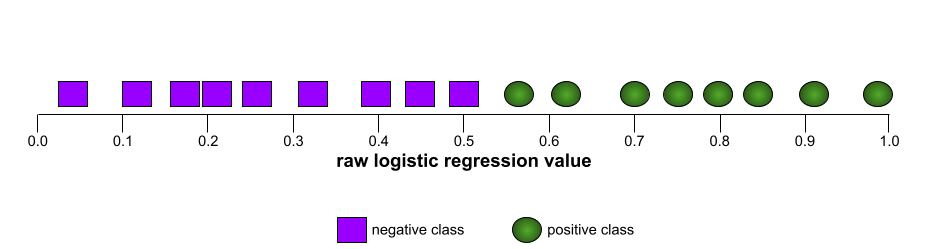
เส้นโค้ง ROC สำหรับโมเดลก่อนหน้ามีลักษณะดังนี้
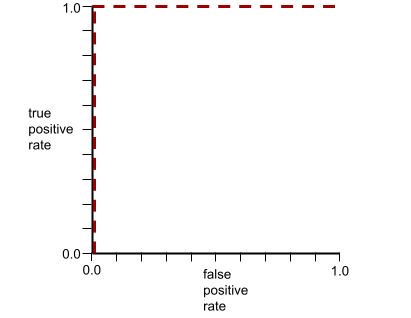
ในทางตรงกันข้าม ภาพประกอบต่อไปนี้แสดงกราฟค่าการถดถอยลอจิสติกแบบดิบ สำหรับโมเดลที่แย่ซึ่งแยกคลาสเชิงลบออกจาก คลาสเชิงบวกไม่ได้เลย
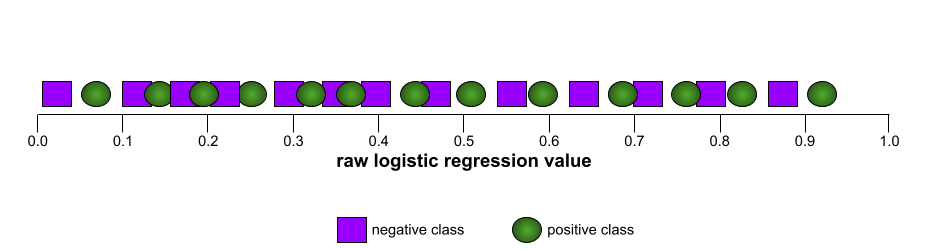
เส้นโค้ง ROC สำหรับโมเดลนี้มีลักษณะดังนี้
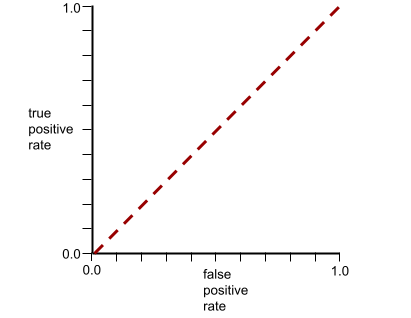
ในขณะเดียวกัน ในโลกแห่งความเป็นจริง โมเดลการจัดประเภทแบบไบนารีส่วนใหญ่จะแยก คลาสที่เป็นบวกและลบในระดับหนึ่ง แต่โดยปกติแล้วจะไม่สมบูรณ์แบบ ดังนั้น กราฟ ROC ทั่วไปจะอยู่ระหว่าง 2 สุดขั้วนี้
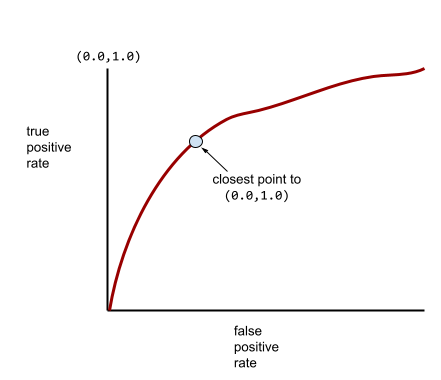
จุดบนเส้นโค้ง ROC ที่ใกล้กับ (0.0,1.0) มากที่สุดจะระบุเกณฑ์การแยกประเภทที่เหมาะสมในทางทฤษฎี อย่างไรก็ตาม ปัญหาอื่นๆ ในโลกแห่งความเป็นจริง มีผลต่อการเลือกเกณฑ์การแยกประเภทที่เหมาะสม ตัวอย่างเช่น ผลลบเท็จอาจสร้างความเจ็บปวดมากกว่าผลบวกเท็จ
เมตริกเชิงตัวเลขที่เรียกว่า AUC จะสรุปเส้นโค้ง ROC เป็นค่าทศนิยมค่าเดียว
ค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง (RMSE)
รากที่ 2 ของความคลาดเคลื่อนเฉลี่ยกำลังสอง
S
ฟังก์ชันซิกมอยด์
ฟังก์ชันทางคณิตศาสตร์ที่ "บีบ" ค่าอินพุตให้อยู่ในช่วงที่จำกัด โดยปกติคือ 0 ถึง 1 หรือ -1 ถึง +1 กล่าวคือ คุณสามารถส่งตัวเลขใดก็ได้ (2, 1 ล้าน, -1 พันล้าน หรืออะไรก็ตาม) ไปยังฟังก์ชัน Sigmoid และเอาต์พุตจะยังคงอยู่ในช่วงที่จำกัด กราฟของฟังก์ชันการกระตุ้นแบบซิคมอยด์มีลักษณะดังนี้

ฟังก์ชันซิกมอยด์มีการใช้งานหลายอย่างในแมชชีนเลิร์นนิง ซึ่งรวมถึง
- การแปลงเอาต์พุตดิบของโมเดลการถดถอยแบบโลจิสติก หรือโมเดลการถดถอยแบบมัลติโนเมียลเป็นความน่าจะเป็น
- ทำหน้าที่เป็นฟังก์ชันการเปิดใช้งานใน โครงข่ายประสาทเทียมบางส่วน
softmax
ฟังก์ชันที่กำหนดความน่าจะเป็นสำหรับแต่ละคลาสที่เป็นไปได้ในโมเดลการจัดประเภทแบบหลายคลาส ความน่าจะเป็นรวมกัน เป็น 1.0 พอดี ตัวอย่างเช่น ตารางต่อไปนี้แสดงวิธีที่ Softmax กระจาย ความน่าจะเป็นต่างๆ
| รูปภาพเป็น... | Probability |
|---|---|
| สุนัข | .85 |
| แมว | .13 |
| ม้า | .02 |
Softmax เรียกอีกอย่างว่า full softmax
แตกต่างจากการสุ่มตัวอย่างผู้สมัคร
ดูข้อมูลเพิ่มเติมได้ที่โครงข่ายประสาทเทียม: การจัดประเภทแบบหลายคลาส ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง
ฟีเจอร์ Sparse
ฟีเจอร์ที่มีค่าเป็น 0 หรือว่างเปล่าเป็นส่วนใหญ่ เช่น ฟีเจอร์ที่มีค่า 1 เพียงค่าเดียวและค่า 0 จำนวน 1 ล้านค่าถือเป็นฟีเจอร์ แบบกระจัดกระจาย ในทางตรงกันข้าม ฟีเจอร์แบบหนาแน่นจะมีค่าที่ส่วนใหญ่ไม่ใช่ 0 หรือว่าง
ในแมชชีนเลิร์นนิง คุณลักษณะจำนวนมากอย่างน่าประหลาดใจคือคุณลักษณะแบบเบาบาง ฟีเจอร์เชิงหมวดหมู่มักเป็นฟีเจอร์แบบกระจัดกระจาย ตัวอย่างเช่น จากต้นไม้ 300 สายพันธุ์ที่เป็นไปได้ในป่า ตัวอย่างเดียวอาจระบุได้แค่ต้นเมเปิล หรือจากวิดีโอหลายล้านรายการในคลังวิดีโอ ตัวอย่างเดียวอาจระบุได้เพียง "คาซาบลังกา"
ในโมเดล โดยปกติแล้วคุณจะแสดงฟีเจอร์แบบกระจัดกระจายด้วยการเข้ารหัสแบบ One-hot หากการเข้ารหัสแบบ One-hot มีขนาดใหญ่ คุณอาจวางเลเยอร์การฝังไว้เหนือ การเข้ารหัสแบบ One-hot เพื่อเพิ่มประสิทธิภาพ
การแสดงแบบกระจัดกระจาย
จัดเก็บเฉพาะตำแหน่งขององค์ประกอบที่ไม่ใช่ศูนย์ในฟีเจอร์แบบกระจัดกระจาย
ตัวอย่างเช่น สมมติว่าฟีเจอร์เชิงหมวดหมู่ชื่อ species ระบุพันธุ์ไม้ 36
ชนิดในป่าแห่งหนึ่ง สมมติว่าตัวอย่างแต่ละรายการระบุเพียงชนิดเดียว
คุณสามารถใช้เวกเตอร์แบบ One-Hot เพื่อแสดงสายพันธุ์ของต้นไม้ในแต่ละตัวอย่าง
เวกเตอร์แบบ One-Hot จะมี 1 เดียว (เพื่อแสดงถึง
สายพันธุ์ต้นไม้ที่เฉพาะเจาะจงในตัวอย่างนั้น) และ 0 35 รายการ (เพื่อแสดงถึง
สายพันธุ์ต้นไม้ 35 สายพันธุ์ที่ไม่ได้อยู่ในตัวอย่างนั้น) ดังนั้น การแสดงแบบ One-Hot ของ maple อาจมีลักษณะดังนี้

หรือการแสดงแบบกระจัดกระจายจะระบุตำแหน่งของ
สายพันธุ์ที่เฉพาะเจาะจง หาก maple อยู่ที่ตำแหน่ง 24 การแสดงแบบกระจัดกระจาย
ของ maple จะเป็นดังนี้
24
โปรดสังเกตว่าการแสดงแบบกระจัดกระจายนั้นกะทัดรัดกว่าการแสดงแบบ One-Hot มาก
ดูข้อมูลเพิ่มเติมได้ที่การทำงานกับข้อมูลเชิงหมวดหมู่ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
เวกเตอร์แบบกระจัดกระจาย
เวกเตอร์ที่มีค่าเป็น 0 เป็นส่วนใหญ่ ดูฟีเจอร์แบบกระจัดกระจาย และความกระจัดกระจายด้วย
การสูญเสียกำลังสอง
คำพ้องความหมายของL2 loss
คงที่
สิ่งที่ทำครั้งเดียวแทนที่จะทำอย่างต่อเนื่อง คำว่าคงที่และออฟไลน์มีความหมายเหมือนกัน ต่อไปนี้คือการใช้งาน static และ offline ทั่วไปในแมชชีนเลิร์นนิง
- โมเดลแบบคงที่ (หรือโมเดลออฟไลน์) คือโมเดลที่ได้รับการฝึกเพียงครั้งเดียวและ นำไปใช้เป็นระยะเวลาหนึ่ง
- การฝึกแบบคงที่ (หรือการฝึกแบบออฟไลน์) คือกระบวนการฝึก โมเดลแบบคงที่
- การอนุมานแบบคงที่ (หรือการอนุมานแบบออฟไลน์) คือกระบวนการที่โมเดลสร้างการคาดการณ์แบบกลุ่มครั้งละ 1 กลุ่ม
คอนทราสต์กับไดนามิก
การอนุมานแบบคงที่
คำพ้องความหมายของการอนุมานแบบออฟไลน์
ความคงที่
ฟีเจอร์ที่มีค่าไม่เปลี่ยนแปลงในมิติข้อมูลอย่างน้อย 1 รายการ ซึ่งมักจะเป็นเวลา ตัวอย่างเช่น ฟีเจอร์ที่มีค่าที่ดูเหมือนกันในปี 2021 และ 2023 จะแสดงความคงที่
ในโลกแห่งความเป็นจริง มีฟีเจอร์เพียงไม่กี่อย่างที่แสดงความคงที่ แม้แต่ฟีเจอร์ที่ มีความหมายเหมือนกันกับความเสถียร (เช่น ระดับน้ำทะเล) ก็เปลี่ยนแปลงไปตามกาลเวลา
แตกต่างจากความไม่คงที่
การไล่ระดับสีแบบสุ่ม (SGD)
อัลกอริทึมการไล่ระดับสีซึ่งมีขนาดกลุ่มเป็น 1 กล่าวอีกนัยหนึ่งคือ SGD ฝึกกับ ตัวอย่างเดียวที่เลือกแบบสุ่ม อย่างสม่ำเสมอจากชุดการฝึก
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น: ไฮเปอร์พารามิเตอร์ ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
แมชชีนเลิร์นนิงที่มีการควบคุมดูแล
การฝึกโมเดลจากฟีเจอร์และป้ายกำกับที่เกี่ยวข้อง แมชชีนเลิร์นนิงที่มีการควบคุมดูแลเปรียบเสมือน การเรียนรู้เรื่องหนึ่งๆ โดยการศึกษาชุดคำถามและคำตอบที่ เกี่ยวข้อง หลังจากเข้าใจความสัมพันธ์ระหว่างคำถามและคำตอบแล้ว นักเรียนจะสามารถตอบคำถามใหม่ (ที่ไม่เคยเห็นมาก่อน) ในหัวข้อเดียวกันได้
เปรียบเทียบกับแมชชีนเลิร์นนิงที่ไม่มีการควบคุมดูแล
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแล ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับ ML
ฟีเจอร์สังเคราะห์
ฟีเจอร์ที่ไม่มีในฟีเจอร์อินพุต แต่ ประกอบขึ้นจากฟีเจอร์อินพุตอย่างน้อย 1 รายการ วิธีการสร้างฟีเจอร์สังเคราะห์ มีดังนี้
- การจัดกลุ่มฟีเจอร์ต่อเนื่องเป็นกลุ่มช่วง
- การสร้างครอสฟีเจอร์
- การคูณ (หรือหาร) ค่าฟีเจอร์หนึ่งด้วยค่าฟีเจอร์อื่นๆ
หรือด้วยค่าของฟีเจอร์นั้นเอง เช่น หาก
aและbเป็นฟีเจอร์อินพุต ตัวอย่างฟีเจอร์สังเคราะห์มีดังนี้- ab
- a2
- การใช้ฟังก์ชันอดิศัยกับค่าฟีเจอร์ ตัวอย่างเช่น หาก
cเป็นฟีเจอร์อินพุต ตัวอย่างฟีเจอร์สังเคราะห์มีดังนี้- sin(c)
- ln(c)
ฟีเจอร์ที่สร้างขึ้นโดยการปรับให้เป็นมาตรฐานหรือปรับขนาด เพียงอย่างเดียวไม่ถือเป็นฟีเจอร์สังเคราะห์
T
การสูญเสียการทดสอบ
เมตริกที่แสดงถึงการสูญเสียของโมเดลเทียบกับ ชุดทดสอบ เมื่อสร้างโมเดล คุณ มักจะพยายามลดการสูญเสียในการทดสอบ เนื่องจากค่าการสูญเสียในการทดสอบที่ต่ำเป็นสัญญาณคุณภาพที่แข็งแกร่งกว่าการสูญเสียในการฝึกหรือการสูญเสียในการตรวจสอบที่ต่ำ
ช่องว่างขนาดใหญ่ระหว่างการสูญเสียในการทดสอบกับการสูญเสียในการฝึกหรือการสูญเสียในการตรวจสอบบางครั้ง บ่งชี้ว่าคุณต้องเพิ่มอัตราการทำให้เป็นปกติ
การฝึกอบรม
กระบวนการในการกำหนดพารามิเตอร์ (น้ำหนักและความเอนเอียง) ที่เหมาะสม ซึ่งประกอบกันเป็นโมเดล ในระหว่างการฝึก ระบบจะอ่านตัวอย่างและค่อยๆ ปรับพารามิเตอร์ การฝึกจะใช้ตัวอย่างแต่ละรายการตั้งแต่ไม่กี่ครั้งไปจนถึงหลายพันล้านครั้ง
ดูข้อมูลเพิ่มเติมได้ที่การเรียนรู้แบบมีผู้ดูแล ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับ ML
การลดลงของการฝึก
เมตริกที่แสดงการสูญเสียของโมเดลระหว่างการฝึก ในรอบการฝึกที่เฉพาะเจาะจง เช่น สมมติว่าฟังก์ชันการสูญเสีย คือความคลาดเคลื่อนกำลังสองเฉลี่ย เช่น การสูญเสียการฝึก (ข้อผิดพลาดกำลังสองเฉลี่ย) สำหรับการทำซ้ำครั้งที่ 10 คือ 2.2 และการสูญเสียการฝึกสำหรับการทำซ้ำครั้งที่ 100 คือ 1.9
เส้นโค้งการสูญเสียจะพล็อตการสูญเสียการฝึกเทียบกับจำนวน การทำซ้ำ เส้นโค้งการสูญเสียจะให้คำแนะนำต่อไปนี้เกี่ยวกับการฝึก
- เส้นโค้งที่ลาดลงหมายความว่าโมเดลกำลังปรับปรุง
- ความชันที่เพิ่มขึ้นหมายความว่าโมเดลแย่ลง
- ความชันที่แบนราบแสดงให้เห็นว่าโมเดลถึงการบรรจบกันแล้ว
ตัวอย่างเช่น เส้นโค้งการสูญเสีย ต่อไปนี้แสดงให้เห็นว่า
- ความชันที่ลดลงอย่างรวดเร็วในระหว่างการทำซ้ำครั้งแรก ซึ่งหมายถึงการปรับปรุงโมเดลอย่างรวดเร็ว
- ความชันที่ค่อยๆ แบนราบ (แต่ยังคงลดลง) จนกระทั่งใกล้สิ้นสุด การฝึก ซึ่งหมายถึงการปรับปรุงโมเดลอย่างต่อเนื่องในอัตราที่ช้าลงเล็กน้อย กว่าในช่วงการทำซ้ำครั้งแรก
- ความชันที่ราบเรียบในช่วงท้ายของการฝึก ซึ่งบ่งบอกถึงการบรรจบกัน
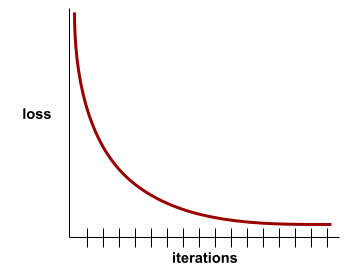
แม้ว่าการสูญเสียจากการฝึกจะมีความสําคัญ แต่โปรดดูการวางนัยทั่วไปด้วย
ความคลาดเคลื่อนระหว่างการฝึกและการให้บริการ
ความแตกต่างระหว่างประสิทธิภาพของโมเดลในระหว่างการฝึกกับประสิทธิภาพของโมเดลเดียวกันในระหว่างการแสดง
ชุดฝึก
ชุดย่อยของชุดข้อมูลที่ใช้ฝึกโมเดล
โดยปกติแล้ว ตัวอย่างในชุดข้อมูลจะแบ่งออกเป็น 3 กลุ่มย่อยที่แตกต่างกันดังนี้
ในอุดมคติ ตัวอย่างแต่ละรายการในชุดข้อมูลควรอยู่ในชุดย่อยที่กล่าวถึงก่อนหน้าเพียงชุดเดียว เช่น ตัวอย่างเดียวไม่ควรอยู่ในทั้งชุดข้อมูลการฝึกและชุดข้อมูลการตรวจสอบ
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: การแบ่งชุดข้อมูลเดิม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ผลลบจริง (TN)
ตัวอย่างที่โมเดลคาดการณ์อย่างถูกต้อง คลาสเชิงลบ ตัวอย่างเช่น โมเดลอนุมานว่า ข้อความอีเมลหนึ่งไม่ใช่จดหมายขยะ และข้อความอีเมลนั้นไม่ใช่จดหมายขยะจริงๆ
ผลบวกจริง (TP)
ตัวอย่างที่โมเดลคาดการณ์อย่างถูกต้องว่า คลาสที่เป็นบวก เช่น โมเดลอนุมานว่า ข้อความอีเมลหนึ่งๆ เป็นจดหมายขยะ และข้อความอีเมลนั้นเป็นจดหมายขยะจริงๆ
อัตราผลบวกจริง (TPR)
คำพ้องความหมายของการเรียกคืน โดยการ
อัตราผลบวกจริงคือแกน y ในกราฟ ROC
U
Underfitting
การสร้างโมเดลที่มีความสามารถในการคาดการณ์ต่ำเนื่องจากโมเดล ยังไม่ได้รับความซับซ้อนของข้อมูลการฝึกอย่างเต็มที่ ปัญหาหลายอย่าง อาจทำให้เกิดการปรับแบบน้อยเกินไป ได้แก่
- การฝึกกับชุดฟีเจอร์ที่ไม่ถูกต้อง
- การฝึกEpoch น้อยเกินไปหรือมีอัตราการเรียนรู้ต่ำเกินไป
- การฝึกที่มีอัตราการทำให้เป็นปกติสูงเกินไป
- การระบุเลเยอร์ที่ซ่อนน้อยเกินไปใน โครงข่ายประสาทเทียมแบบลึก
ดูข้อมูลเพิ่มเติมได้ที่การเกิด Overfitting ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
ตัวอย่างที่ไม่มีป้ายกำกับ
ตัวอย่างที่มีฟีเจอร์แต่ไม่มีป้ายกำกับ ตัวอย่างเช่น ตารางต่อไปนี้แสดงตัวอย่างที่ไม่ได้ติดป้ายกำกับ 3 รายการจากโมเดลการประเมินบ้าน โดยแต่ละรายการมีฟีเจอร์ 3 รายการแต่ไม่มีมูลค่าบ้าน
| จำนวนห้องนอน | จำนวนห้องน้ำ | อายุบ้าน |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
ในแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โมเดลจะฝึกกับตัวอย่างที่ติดป้ายกำกับและทำการคาดการณ์กับ ตัวอย่างที่ไม่มีป้ายกำกับ
ในการเรียนรู้แบบกึ่งควบคุมดูแลและ ไม่มีการควบคุมดูแล จะใช้ตัวอย่างที่ไม่มีป้ายกำกับในระหว่างการฝึก
เปรียบเทียบตัวอย่างที่ไม่มีป้ายกำกับกับตัวอย่างที่มีป้ายกำกับ
แมชชีนเลิร์นนิงที่ไม่มีการควบคุมดูแล
การฝึกโมเดลเพื่อค้นหารูปแบบในชุดข้อมูล ซึ่งโดยปกติจะเป็นชุดข้อมูลที่ไม่มีป้ายกำกับ
การใช้งานแมชชีนเลิร์นนิงแบบไม่มีการกำกับดูแลที่พบบ่อยที่สุดคือการจัดกลุ่มข้อมูล เป็นกลุ่มของตัวอย่างที่คล้ายกัน ตัวอย่างเช่น อัลกอริทึมแมชชีนเลิร์นนิงแบบไม่มีการกำกับดูแล สามารถจัดกลุ่มเพลงตามคุณสมบัติต่างๆ ของเพลงได้ คลัสเตอร์ที่ได้สามารถกลายเป็นอินพุตสำหรับอัลกอริทึมแมชชีนเลิร์นนิงอื่นๆ (เช่น สำหรับบริการแนะนำเพลง) การจัดกลุ่มช่วยได้ในกรณีที่ป้ายกำกับที่มีประโยชน์หายากหรือไม่มีเลย ตัวอย่างเช่น ในโดเมนต่างๆ เช่น การต่อต้านการละเมิดและการฉ้อโกง คลัสเตอร์จะช่วยให้ มนุษย์เข้าใจข้อมูลได้ดีขึ้น
เปรียบเทียบกับแมชชีนเลิร์นนิงที่มีการควบคุมดูแล
ดูข้อมูลเพิ่มเติมได้ที่แมชชีนเลิร์นนิงคืออะไร ในหลักสูตรข้อมูลเบื้องต้นเกี่ยวกับ ML
V
การตรวจสอบความถูกต้อง
การประเมินคุณภาพของโมเดลในขั้นต้น การตรวจสอบจะตรวจสอบคุณภาพของการคาดการณ์ของโมเดลเทียบกับชุดข้อมูลการตรวจสอบ
เนื่องจากชุดข้อมูลการตรวจสอบแตกต่างจากชุดข้อมูลการฝึก การตรวจสอบจึงช่วยป้องกันการปรับมากเกินไป
คุณอาจคิดว่าการประเมินโมเดลกับชุดการตรวจสอบเป็นการทดสอบรอบแรก และการประเมินโมเดลกับชุดการทดสอบเป็นการทดสอบรอบที่ 2
การสูญเสียการตรวจสอบ
เมตริกที่แสดงการสูญเสียของโมเดลในชุดข้อมูลการตรวจสอบระหว่างการวนซ้ำของการฝึก
ดูเส้นโค้งการสรุปด้วย
ชุดข้อมูลสำหรับตรวจสอบความถูกต้อง
ชุดย่อยของชุดข้อมูลที่ทำการประเมินเบื้องต้นกับโมเดลที่ฝึกแล้ว โดยปกติแล้ว คุณจะประเมิน โมเดลที่ฝึกแล้วกับชุดข้อมูลการตรวจสอบหลายครั้ง ก่อนที่จะประเมินโมเดลกับชุดข้อมูลทดสอบ
โดยปกติแล้ว คุณจะแบ่งตัวอย่างในชุดข้อมูลออกเป็น 3 ชุดย่อยที่แตกต่างกันดังนี้
ในอุดมคติ ตัวอย่างแต่ละรายการในชุดข้อมูลควรอยู่ในชุดย่อยที่กล่าวถึงก่อนหน้าเพียงชุดเดียว เช่น ตัวอย่างเดียวไม่ควรอยู่ในทั้งชุดข้อมูลการฝึกและชุดข้อมูลการตรวจสอบ
ดูข้อมูลเพิ่มเติมได้ที่ชุดข้อมูล: การแบ่งชุดข้อมูลเดิม ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
W
น้ำหนัก
ค่าที่โมเดลคูณด้วยค่าอื่น การฝึกคือกระบวนการกำหนดน้ำหนักที่เหมาะสมของโมเดล การอนุมานคือกระบวนการใช้น้ำหนักที่เรียนรู้เหล่านั้นเพื่อ ทำการคาดการณ์
ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้น ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
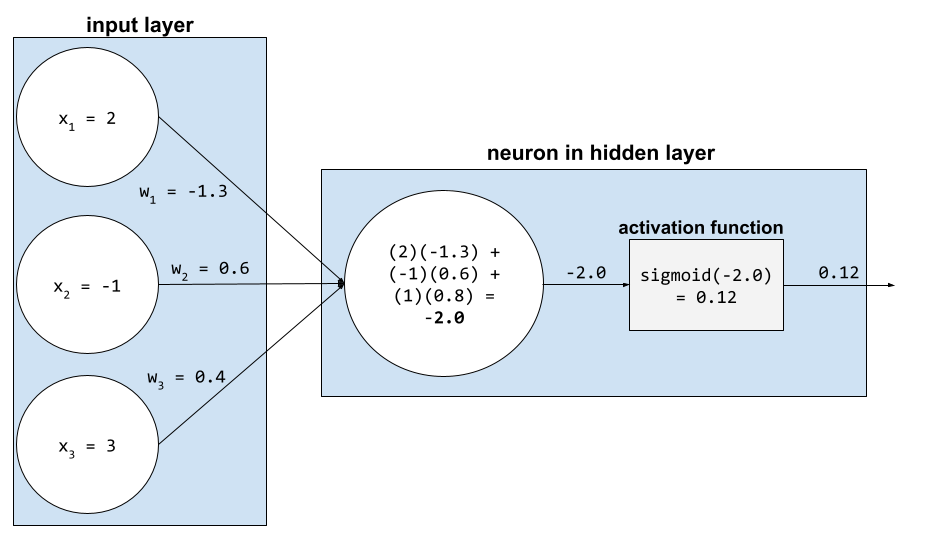
ผลรวมแบบถ่วงน้ำหนัก
ผลรวมของค่าอินพุตที่เกี่ยวข้องทั้งหมดคูณด้วย ค่าถ่วงน้ำหนักที่สอดคล้องกัน ตัวอย่างเช่น สมมติว่าอินพุตที่เกี่ยวข้องประกอบด้วยข้อมูลต่อไปนี้
| ค่าอินพุต | น้ำหนักอินพุต |
| 2 | -1.3 |
| -1 | 0.6 |
| 3 | 0.4 |
ดังนั้น ผลรวมแบบถ่วงน้ำหนักจึงเป็นดังนี้
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
ผลรวมแบบถ่วงน้ำหนักคืออาร์กิวเมนต์อินพุตของฟังก์ชันกระตุ้น
Z
การแปลงข้อมูลเป็นรูปแบบมาตรฐาน Z-Score
เทคนิคการปรับขนาดที่แทนที่ค่าฟีเจอร์ดิบด้วยค่าทศนิยมที่แสดงถึงจำนวนค่าเบี่ยงเบนมาตรฐานจากค่าเฉลี่ยของฟีเจอร์นั้น ตัวอย่างเช่น ลองพิจารณาฟีเจอร์ที่มีค่าเฉลี่ย 800 และค่าเบี่ยงเบนมาตรฐาน 100 ตารางต่อไปนี้แสดงวิธีที่การปรับค่าให้เป็นมาตรฐาน Z-score จะจับคู่ค่าดิบกับ Z-score
| ค่าดิบ | คะแนนมาตรฐาน (Z-Score) |
|---|---|
| 800 | 0 |
| 950 | +1.5 |
| 575 | -2.25 |
จากนั้นโมเดลแมชชีนเลิร์นนิงจะฝึกกับคะแนน Z สำหรับฟีเจอร์นั้นแทนที่จะฝึกกับค่าดิบ
ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลตัวเลข: การปรับให้เป็นมาตรฐาน ในหลักสูตรเร่งรัดแมชชีนเลิร์นนิง