Auf dieser Seite finden Sie Glossarbegriffe zu den ML-Grundlagen. Hier finden Sie alle Glossarbegriffe.
A
Genauigkeit
Die Anzahl der richtigen Klassifizierungsvorhersagen, dividiert durch die Gesamtzahl der Vorhersagen. Das bedeutet:
Ein Modell, das beispielsweise 40 korrekte und 10 falsche Vorhersagen getroffen hat, hätte eine Genauigkeit von:
Bei der binären Klassifizierung werden bestimmte Namen für die verschiedenen Kategorien von richtigen Vorhersagen und falschen Vorhersagen verwendet. Die Formel für die Genauigkeit bei der binären Klassifizierung lautet also:
Dabei gilt:
- TP ist die Anzahl der richtig positiven Ergebnisse (richtige Vorhersagen).
- TN ist die Anzahl der richtig negativen Ergebnisse (richtige Vorhersagen).
- FP ist die Anzahl der falsch positiven Ergebnisse (falsche Vorhersagen).
- FN ist die Anzahl der falsch negativen Ergebnisse (falsche Vorhersagen).
Vergleichen Sie die Genauigkeit mit Trefferquote und Erinnerung.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Klassifizierung: Genauigkeit, Trefferquote, Präzision und zugehörige Messwerte.
Aktivierungsfunktion
Eine Funktion, mit der neuronale Netze nicht lineare (komplexe) Beziehungen zwischen Features und dem Label erlernen können.
Beliebte Aktivierungsfunktionen sind:
Die Diagramme von Aktivierungsfunktionen sind nie einzelne gerade Linien. Das Diagramm der ReLU-Aktivierungsfunktion besteht beispielsweise aus zwei geraden Linien:

Ein Diagramm der Sigmoid-Aktivierungsfunktion sieht so aus:

Weitere Informationen finden Sie im Machine Learning Crash Course unter Neuronale Netze: Aktivierungsfunktionen.
künstliche Intelligenz
Ein nicht menschliches Programm oder Modell, das anspruchsvolle Aufgaben lösen kann. Ein Programm oder Modell, das Text übersetzt, oder ein Programm oder Modell, das Krankheiten anhand von radiologischen Bildern erkennt, sind Beispiele für künstliche Intelligenz.
Maschinelles Lernen ist ein Teilbereich der künstlichen Intelligenz. In den letzten Jahren haben einige Organisationen jedoch begonnen, die Begriffe künstliche Intelligenz und maschinelles Lernen synonym zu verwenden.
AUC (Area Under the ROC Curve, Bereich unter der ROC-Kurve)
Eine Zahl zwischen 0,0 und 1,0, die angibt, wie gut ein binäres Klassifizierungsmodell positive Klassen von negativen Klassen trennen kann. Je näher die AUC an 1,0 liegt, desto besser kann das Modell Klassen voneinander trennen.
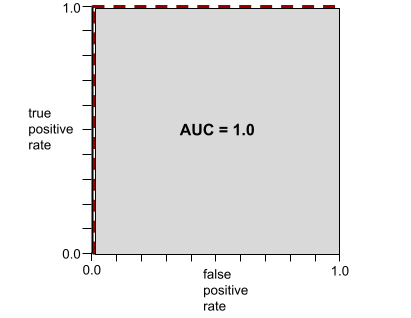
Die folgende Abbildung zeigt beispielsweise ein Klassifikationsmodell, das positive Klassen (grüne Ovale) perfekt von negativen Klassen (lila Rechtecke) trennt. Dieses unrealistisch perfekte Modell hat einen AUC-Wert von 1,0:

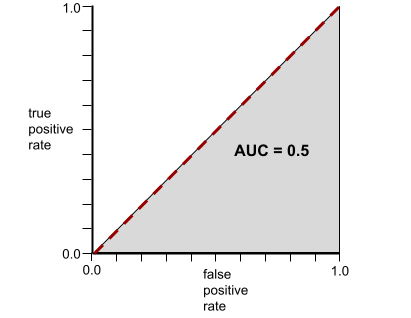
Die folgende Abbildung zeigt dagegen die Ergebnisse für ein Klassifizierungsmodell, das zufällige Ergebnisse generiert hat. Dieses Modell hat einen AUC-Wert von 0,5:

Ja, das vorherige Modell hat einen AUC-Wert von 0,5, nicht 0,0.
Die meisten Modelle liegen irgendwo zwischen den beiden Extremen. Im folgenden Modell werden beispielsweise positive und negative Ergebnisse etwas getrennt. Daher liegt die AUC zwischen 0, 5 und 1, 0:

Bei der AUC wird jeder Wert ignoriert, den Sie für Klassifizierungsschwellenwert festlegen. Stattdessen werden bei der AUC alle möglichen Klassifizierungsschwellenwerte berücksichtigt.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Klassifizierung: ROC und AUC.
B
Rückpropagation
Der Algorithmus, der den Gradientenabstieg in neuronalen Netzwerken implementiert.
Das Trainieren eines neuronalen Netzwerks umfasst viele Wiederholungen des folgenden Zwei-Pass-Zyklus:
- Während des Forward Pass verarbeitet das System einen Batch von Beispielen, um Vorhersagen zu treffen. Das System vergleicht jede Vorhersage mit jedem Label-Wert. Die Differenz zwischen der Vorhersage und dem Labelwert ist der Verlust für dieses Beispiel. Das System fasst die Verluste für alle Beispiele zusammen, um den Gesamtverlust für den aktuellen Batch zu berechnen.
- Während des Rückwärtsdurchlaufs (Backpropagation) wird der Verlust reduziert, indem die Gewichte aller Neuronen in allen verborgenen Schichten angepasst werden.
Neuronale Netze enthalten oft viele Neuronen in vielen verborgenen Schichten. Jedes dieser Neuronen trägt auf unterschiedliche Weise zum Gesamtverlust bei. Bei der Backpropagation wird ermittelt, ob die Gewichte, die auf bestimmte Neuronen angewendet werden, erhöht oder verringert werden müssen.
Die Lernrate ist ein Multiplikator, der steuert, in welchem Maße jeder Backward-Pass jedes Gewicht erhöht oder verringert. Bei einer großen Lernrate wird jedes Gewicht stärker erhöht oder verringert als bei einer kleinen Lernrate.
In der Analysis wird mit der Backpropagation die Kettenregel> implementiert. Bei der Backpropagation wird die partielle Ableitung des Fehlers in Bezug auf jeden Parameter berechnet.
Vor einigen Jahren mussten ML-Experten Code schreiben, um die Backpropagation zu implementieren. Moderne ML-APIs wie Keras implementieren die Backpropagation für Sie. Geschafft!
Weitere Informationen finden Sie im Machine Learning Crash Course unter Neuronale Netze.
Batch
Die Menge der Beispiele, die in einer Trainings-Iteration verwendet werden. Die Batchgröße bestimmt die Anzahl der Beispiele in einem Batch.
Eine Erläuterung, wie sich ein Batch auf eine Epoche bezieht, finden Sie unter Epoche.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Hyperparameter.
Batchgröße
Die Anzahl der Beispiele in einem Batch. Wenn die Batchgröße beispielsweise 100 ist, verarbeitet das Modell 100 Beispiele pro Iteration.
Im Folgenden finden Sie einige beliebte Strategien für die Batchgröße:
- Stochastic Gradient Descent (SGD), bei der die Batchgröße 1 ist.
- Vollständiger Batch, bei dem die Batchgröße der Anzahl der Beispiele im gesamten Trainingsset entspricht. Wenn der Trainingssatz beispielsweise eine Million Beispiele enthält, beträgt die Batchgröße eine Million Beispiele. Die vollständige Batch-Verarbeitung ist in der Regel eine ineffiziente Strategie.
- Minibatch, bei dem die Batch-Größe in der Regel zwischen 10 und 1.000 liegt. Die Mini-Batch-Strategie ist in der Regel die effizienteste.
Weitere Informationen finden Sie hier:
- ML-Produktionssysteme: Statische und dynamische Inferenz im Crashkurs zum maschinellen Lernen.
- Playbook zum Optimieren von Deep Learning
Bias (Ethik/Fairness)
1. Stereotypisierung, Vorurteile oder Bevorzugung bestimmter Dinge, Personen oder Gruppen gegenüber anderen. Diese Verzerrungen können sich auf die Erhebung und Interpretation von Daten, das Design eines Systems und die Interaktion von Nutzern mit einem System auswirken. Beispiele für diese Art von Bias:
- Automation Bias
- Bestätigungsfehler
- Experimentatorverzerrung
- Gruppenattributionsbias
- Implizites Bias
- Gruppenintern
- Homogenitätsbias außerhalb der Gruppe
2. Systematischer Fehler, der durch ein Sampling- oder Reportingverfahren eingeführt wird. Beispiele für diese Art von Bias:
- Coverage Bias
- Schweigeverzerrung
- Bias durch Teilnahme
- Reporting Bias
- Stichproben-Bias
- Stichproben-Bias
Nicht zu verwechseln mit dem Bias-Term in Modellen für maschinelles Lernen oder dem Vorhersage-Bias.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Fairness: Types of bias.
Bias (Mathematik) oder Bias-Term
Ein Achsenabschnitt oder ein Offset von einem Ursprung. Bias ist ein Parameter in Modellen für maschinelles Lernen, der durch einen der folgenden Werte symbolisiert wird:
- b
- w0
Bias ist beispielsweise das b in der folgenden Formel:
In einer einfachen zweidimensionalen Linie bedeutet Bias einfach „y-Achsenabschnitt“. In der folgenden Abbildung ist der Bias der Linie beispielsweise 2.
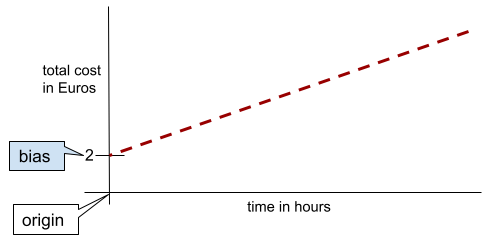
Bias ist vorhanden, da nicht alle Modelle vom Ursprung (0,0) ausgehen. Ein Beispiel: Der Eintritt in einen Vergnügungspark kostet 2 € und für jede Stunde, die ein Kunde dort verbringt, werden zusätzlich 0,50 € berechnet. Ein Modell, das die Gesamtkosten abbildet, hat daher einen Bias von 2, da die niedrigsten Kosten 2 € betragen.
Bias ist nicht mit Bias in Bezug auf Ethik und Fairness oder Vorhersage-Bias zu verwechseln.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression.
Binärklassifizierung
Eine Art von Klassifizierungsaufgabe, bei der eine von zwei sich gegenseitig ausschließenden Klassen vorhergesagt wird:
- die positive Klasse
- die negative Klasse
Die folgenden beiden Modelle für maschinelles Lernen führen beispielsweise jeweils eine binäre Klassifizierung durch:
- Ein Modell, das bestimmt, ob E‑Mail-Nachrichten Spam (die positive Klasse) oder kein Spam (die negative Klasse) sind.
- Ein Modell, das medizinische Symptome bewertet, um festzustellen, ob eine Person eine bestimmte Krankheit (die positive Klasse) hat oder nicht (die negative Klasse).
Im Gegensatz zur Klassifizierung mit mehreren Klassen.
Weitere Informationen finden Sie unter Logistische Regression und Klassifizierungsschwellenwert.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Classification.
Bucketing
Umwandlung eines einzelnen Features in mehrere binäre Features, die in der Regel auf einem Wertebereich basieren und als Buckets oder Klassen bezeichnet werden. Das gechoppte Feature ist in der Regel ein kontinuierliches Feature.
Anstatt die Temperatur als einzelnes kontinuierliches Gleitkomma-Feature darzustellen, können Sie beispielsweise Temperaturbereiche in diskrete Gruppen unterteilen, z. B.:
- <= 10 °C wäre der „kalte“ Bucket.
- 11–24 °C fallen in die Kategorie „gemäßigt“.
- >= 25 °C wäre die Kategorie „warm“.
Im Modell werden alle Werte im selben Bucket identisch behandelt. Die Werte 13 und 22 befinden sich beispielsweise beide im Bucket „gemäßigt“, sodass das Modell die beiden Werte identisch behandelt.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Numerical Data: Binning.
C
kategoriale Daten
Merkmale mit einer bestimmten Menge möglicher Werte. Nehmen wir als Beispiel ein kategoriales Feature mit dem Namen traffic-light-state an, das nur einen der folgenden drei möglichen Werte haben kann:
redyellowgreen
Wenn traffic-light-state als kategoriales Feature dargestellt wird, kann ein Modell die unterschiedlichen Auswirkungen von red, green und yellow auf das Fahrverhalten lernen.
Kategoriale Features werden manchmal auch als diskrete Features bezeichnet.
Im Gegensatz zu numerischen Daten.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Mit kategorischen Daten arbeiten.
Klasse
Eine Kategorie, zu der ein Label gehören kann. Beispiel:
- In einem binären Klassifizierungsmodell, das Spam erkennt, könnten die beiden Klassen Spam und Kein Spam sein.
- In einem Klassifizierungsmodell mit mehreren Klassen, das Hunderassen identifiziert, könnten die Klassen Pudel, Beagle, Mops usw. sein.
Ein Klassifizierungsmodell sagt eine Klasse vorher. Im Gegensatz dazu sagt ein Regressionsmodell eine Zahl und keine Klasse vorher.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Classification.
Klassifikationsmodell
Ein Modell, dessen Vorhersage eine Klasse ist. Beispiele für Klassifizierungsmodelle:
- Ein Modell, das die Sprache eines Eingabesatzes vorhersagt (Französisch? Spanisch? Italienisch?).
- Ein Modell, das Baumarten vorhersagt (Ahorn? Eiche? Baobab?).
- Ein Modell, das die positive oder negative Klasse für einen bestimmten medizinischen Zustand vorhersagt.
Regressionsmodelle sagen im Gegensatz dazu Zahlen und nicht Klassen vorher.
Zwei gängige Arten von Klassifizierungsmodellen sind:
Klassifizierungsschwellenwert
Bei der binären Klassifizierung wird die Rohausgabe eines logistischen Regressionsmodells in eine Vorhersage für die positive Klasse oder die negative Klasse umgewandelt. Der Klassifizierungsschwellenwert wird von einem Menschen ausgewählt, nicht durch das Modelltraining.
Ein Modell für die logistische Regression gibt einen Rohwert zwischen 0 und 1 aus. Dann:
- Wenn dieser Rohwert größer als der Klassifizierungsschwellenwert ist, wird die positive Klasse vorhergesagt.
- Wenn dieser Rohwert kleiner als der Klassifizierungsschwellenwert ist, wird die negative Klasse vorhergesagt.
Angenommen, der Klassifizierungsschwellenwert ist 0,8. Wenn der Rohwert 0,9 ist, sagt das Modell die positive Klasse vorher. Wenn der Rohwert 0,7 ist, sagt das Modell die negative Klasse vorher.
Die Wahl des Klassifizierungsschwellenwerts hat einen großen Einfluss auf die Anzahl der falsch positiven und falsch negativen Ergebnisse.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Schwellenwerte und die Konfusionsmatrix.
Klassifikator
Umgangssprachlicher Begriff für ein Klassifizierungsmodell.
Dataset mit Klassenungleichgewicht
Ein Dataset für eine Klassifizierung, in dem sich die Gesamtzahl der Labels jeder Klasse deutlich unterscheidet. Betrachten Sie beispielsweise ein Dataset für die binäre Klassifizierung, dessen zwei Labels so aufgeteilt sind:
- 1.000.000 Labels für negative Balken
- 10 positive Labels
Das Verhältnis von negativen zu positiven Labels beträgt 100.000 zu 1. Es handelt sich also um einen Datensatz mit unausgewogenen Klassen.
Im Gegensatz dazu ist das folgende Dataset klassenbalanciert, da das Verhältnis von negativen zu positiven Labels relativ nahe bei 1 liegt:
- 517 Labels für negative Balken
- 483 positive Labels
Datasets mit mehreren Klassen können auch ein Klassenungleichgewicht aufweisen. Das folgende Dataset für die Multiklassenklassifizierung ist beispielsweise auch klassenungleichgewichtig, da ein Label viel mehr Beispiele als die anderen beiden enthält:
- 1.000.000 Labels mit der Klasse „green“ (grün)
- 200 Labels mit der Klasse „Lila“
- 350 Labels mit der Klasse „orange“
Das Trainieren von Datasets mit ungleichmäßiger Klassenverteilung kann besondere Herausforderungen mit sich bringen. Weitere Informationen finden Sie im Machine Learning Crash Course unter Imbalanced datasets.
Siehe auch Entropie, Mehrheitsklasse und Minderheitsklasse.
Clipping
Eine Methode zum Verarbeiten von Ausreißern, indem Sie eine oder beide der folgenden Aktionen ausführen:
- Funktionswerte, die über einem maximalen Schwellenwert liegen, werden auf diesen maximalen Schwellenwert reduziert.
- Erhöhen von Feature-Werten, die unter einem Mindestschwellenwert liegen, bis zu diesem Mindestschwellenwert.
Angenommen, weniger als 0,5% der Werte für ein bestimmtes Merkmal liegen außerhalb des Bereichs 40–60. In diesem Fall haben Sie folgende Möglichkeiten:
- Alle Werte über 60 (dem maximalen Schwellenwert) werden auf genau 60 gekürzt.
- Alle Werte unter 40 (dem Mindestschwellenwert) werden auf genau 40 gekürzt.
Ausreißer können Modelle beschädigen und manchmal dazu führen, dass Gewichtungen während des Trainings überlaufen. Einige Ausreißer können auch Messwerte wie die Genauigkeit erheblich beeinträchtigen. Clipping ist eine gängige Methode, um Schäden zu begrenzen.
Gradient Clipping erzwingt Gradient-Werte innerhalb eines bestimmten Bereichs während des Trainings.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Numerische Daten: Normalisierung.
Wahrheitsmatrix
Eine NxN-Tabelle, in der die Anzahl der richtigen und falschen Vorhersagen eines Klassifizierungsmodells zusammengefasst wird. Betrachten Sie beispielsweise die folgende Konfusionsmatrix für ein binäres Klassifikationsmodell:
| Tumor (prognostiziert) | Kein Tumor (prognostiziert) | |
|---|---|---|
| Tumor (Ground Truth) | 18 (TP) | 1 (FN) |
| Kein Tumor (Ground Truth) | 6 (FP) | 452 (TN) |
Die obige Wahrheitsmatrix zeigt Folgendes:
- Von den 19 Vorhersagen, bei denen die Grundwahrheit „Tumor“ war, hat das Modell 18 richtig und 1 falsch klassifiziert.
- Von den 458 Vorhersagen, bei denen die Grundwahrheit „Kein Tumor“ war, hat das Modell 452 richtig und 6 falsch klassifiziert.
Die Wahrheitsmatrix für ein Klassifizierungsproblem mit mehreren Klassen kann Ihnen helfen, Fehlermuster zu erkennen. Betrachten Sie beispielsweise die folgende Konfusionsmatrix für ein Multiklassen-Klassifikationsmodell mit drei Klassen, das drei verschiedene Schwertlilienarten (Virginica, Versicolor und Setosa) kategorisiert. Wenn die Ground Truth „Virginica“ war, zeigt die Wahrheitsmatrix, dass das Modell viel wahrscheinlicher fälschlicherweise „Versicolor“ als „Setosa“ vorhergesagt hat:
| Setosa (prognostiziert) | Versicolor (prognostiziert) | Virginica (prognostiziert) | |
|---|---|---|---|
| Setosa (Ground Truth) | 88 | 12 | 0 |
| Versicolor (Ground Truth) | 6 | 141 | 7 |
| Virginica (Ground Truth) | 2 | 27 | 109 |
Ein weiteres Beispiel: Eine Konfusionsmatrix könnte zeigen, dass ein Modell, das zum Erkennen handschriftlicher Ziffern trainiert wurde, dazu neigt, fälschlicherweise 9 anstelle von 4 oder 1 anstelle von 7 vorherzusagen.
Konfusionsmatrizen enthalten genügend Informationen, um eine Vielzahl von Leistungsmesswerten zu berechnen, darunter Genauigkeit und Trefferquote.
stetiges Feature
Ein Gleitkomma-Feature mit einem unendlichen Bereich möglicher Werte, z. B. Temperatur oder Gewicht.
Im Gegensatz zu einem diskreten Feature
Konvergenz
Ein Zustand, der erreicht wird, wenn sich die Werte für Verlust mit jeder Iteration nur sehr wenig oder gar nicht ändern. Die folgende Verlustkurve deutet beispielsweise auf eine Konvergenz bei etwa 700 Iterationen hin:
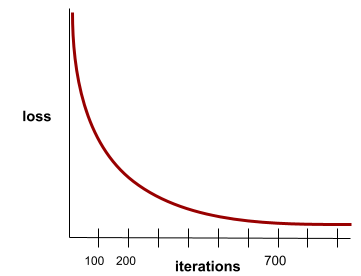
Ein Modell konvergiert, wenn zusätzliches Training das Modell nicht verbessert.
Beim Deep Learning bleiben die Verlustwerte manchmal über viele Iterationen hinweg konstant oder nahezu konstant, bevor sie schließlich sinken. Bei einem langen Zeitraum mit konstanten Verlustwerten kann es vorübergehend zu einem falschen Gefühl der Konvergenz kommen.
Weitere Informationen finden Sie unter Vorzeitiges Beenden.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Model convergence and loss curves.
D
DataFrame
Ein beliebter pandas-Datentyp zur Darstellung von Datasets im Arbeitsspeicher.
Ein DataFrame ist analog zu einer Tabelle oder einer Tabellenkalkulation. Jede Spalte eines DataFrames hat einen Namen (einen Header) und jede Zeile wird durch eine eindeutige Nummer identifiziert.
Jede Spalte in einem DataFrame ist wie ein zweidimensionales Array strukturiert, mit der Ausnahme, dass jeder Spalte ein eigener Datentyp zugewiesen werden kann.
Weitere Informationen finden Sie auf der offiziellen Referenzseite zu pandas.DataFrame.
Dataset oder Dataset
Eine Sammlung von Rohdaten, die in der Regel (aber nicht ausschließlich) in einem der folgenden Formate organisiert sind:
- eine Tabelle
- eine Datei im CSV-Format (Comma Separated Values, kommagetrennte Werte)
Deep-Modell
Ein neuronales Netzwerk mit mehr als einer ausgeblendeten Ebene.
Ein Deep-Learning-Modell wird auch als neuronales Deep-Learning-Netzwerk bezeichnet.
Kontrast zum Wide-Modell.
vollbesetztes Feature
Eine Funktion, bei der die meisten oder alle Werte ungleich null sind, in der Regel ein Tensor mit Gleitkommawerten. Der folgende Tensor mit 10 Elementen ist beispielsweise dicht, da 9 seiner Werte ungleich null sind:
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
Im Gegensatz dazu steht das dünnbesetzte Feature.
Tiefe
Die Summe der folgenden Elemente in einem neuronalen Netzwerk:
- die Anzahl der ausgeblendeten Ebenen
- die Anzahl der Ausgabeschichten, die in der Regel 1 ist
- die Anzahl der Einbettungsebenen
Ein neuronales Netzwerk mit fünf verborgenen Schichten und einer Ausgabeschicht hat beispielsweise eine Tiefe von 6.
Die Eingabeebene hat keinen Einfluss auf die Tiefe.
diskretes Feature
Ein Feature mit einer endlichen Menge möglicher Werte. Ein Feature, dessen Werte nur Tier, Gemüse oder Mineral sein können, ist beispielsweise ein diskretes (oder kategorisches) Feature.
Im Gegensatz dazu steht das stetige Feature.
dynamic
Etwas, das häufig oder kontinuierlich getan wird. Die Begriffe dynamisch und online sind im Bereich des maschinellen Lernens Synonyme. Im Folgenden finden Sie gängige Anwendungsfälle für dynamisch und online im Bereich des maschinellen Lernens:
- Ein dynamisches Modell (oder Onlinemodell) ist ein Modell, das häufig oder kontinuierlich neu trainiert wird.
- Dynamisches Training (oder Onlinetraining) ist der Prozess des häufigen oder kontinuierlichen Trainings.
- Dynamische Inferenzen (oder Onlineinferenzen) sind der Prozess der bedarfsgesteuerten Generierung von Vorhersagen.
dynamisches Modell
Ein Modell, das häufig (vielleicht sogar kontinuierlich) neu trainiert wird. Ein dynamisches Modell ist ein „lebenslanger Lernender“, der sich ständig an sich ändernde Daten anpasst. Ein dynamisches Modell wird auch als Onlinemodell bezeichnet.
Kontrast zum statischen Modell.
E
Vorzeitiges Beenden
Eine Methode zur Regularisierung, bei der das Training beendet wird, bevor der Trainingsverlust nicht mehr sinkt. Beim vorzeitigen Beenden wird das Training des Modells absichtlich beendet, wenn der Verlust in einem Validierungs-Dataset zu steigen beginnt, d. h., wenn sich die Generalisierungsleistung verschlechtert.
Einbettungsebene
Eine spezielle verdeckte Ebene, die auf einem hochdimensionalen kategorialen Merkmal trainiert wird, um nach und nach einen Einbettungsvektor mit niedrigerer Dimension zu lernen. Eine Einbettungsebene ermöglicht es einem neuronalen Netzwerk, viel effizienter zu trainieren, als wenn nur das hochdimensionale kategorische Merkmal verwendet wird.
Google Earth unterstützt derzeit beispielsweise etwa 73.000 Baumarten. Angenommen, die Baumart ist ein Feature in Ihrem Modell. Die Eingabeschicht Ihres Modells enthält also einen One-Hot-Vektor mit 73.000 Elementen.
baobab könnte beispielsweise so dargestellt werden:

Ein Array mit 73.000 Elementen ist sehr lang. Wenn Sie dem Modell keine Einbettungsebene hinzufügen, wird das Training sehr zeitaufwendig,da 72.999 Nullen multipliziert werden. Vielleicht wählen Sie die Einbettungsebene mit 12 Dimensionen aus. Folglich lernt die Einbettungsebene nach und nach einen neuen Einbettungsvektor für jede Baumart.
In bestimmten Situationen ist Hashing eine sinnvolle Alternative zu einer Einbettungsebene.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Embeddings.
Epoche
Ein vollständiger Trainingsdurchlauf über den gesamten Trainingsdatensatz, bei dem jedes Beispiel einmal verarbeitet wurde.
Eine Epoche entspricht N/Batchgröße Trainings-Iterationen, wobei N die Gesamtzahl der Beispiele ist.
Nehmen wir beispielsweise Folgendes an:
- Das Dataset besteht aus 1.000 Beispielen.
- Die Batchgröße beträgt 50 Beispiele.
Daher sind für eine Epoche 20 Iterationen erforderlich:
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Hyperparameter.
Beispiel
Die Werte einer Zeile von features und möglicherweise ein label. Beispiele für überwachtes Lernen lassen sich in zwei allgemeine Kategorien einteilen:
- Ein beispielhaftes Datenelement mit Label besteht aus einem oder mehreren Merkmalen und einem Label. Während des Trainings werden gelabelte Beispiele verwendet.
- Ein Beispiel ohne Label besteht aus einem oder mehreren Merkmalen, aber keinem Label. Beispiele ohne Label werden während der Inferenz verwendet.
Angenommen, Sie trainieren ein Modell, um den Einfluss von Wetterbedingungen auf die Prüfungsergebnisse von Schülern zu ermitteln. Hier sind drei Beispiele mit Labels:
| Funktionen | Label | ||
|---|---|---|---|
| Temperatur | Luftfeuchtigkeit | Luftdruck | Testergebnis |
| 15 | 47 | 998 | Gut |
| 19 | 34 | 1020 | Sehr gut |
| 18 | 92 | 1012 | Schlecht |
Hier sind drei Beispiele ohne Label:
| Temperatur | Luftfeuchtigkeit | Luftdruck | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
Die Zeile eines Datasets ist in der Regel die Rohquelle für ein Beispiel. Ein Beispiel besteht in der Regel aus einer Teilmenge der Spalten im Dataset. Außerdem können die Features in einem Beispiel auch synthetische Features wie Feature-Kombinationen enthalten.
Weitere Informationen finden Sie im Kurs „Einführung in maschinelles Lernen“ unter Supervised Learning.
F
falsch negativ (FN)
Ein Beispiel, in dem das Modell fälschlicherweise die negative Klasse vorhersagt. Das Modell sagt beispielsweise voraus, dass eine bestimmte E‑Mail-Nachricht kein Spam (die negative Klasse) ist, aber diese E‑Mail-Nachricht ist tatsächlich Spam.
Falsch positiv (FP)
Ein Beispiel, in dem das Modell fälschlicherweise die positive Klasse vorhersagt. Das Modell sagt beispielsweise voraus, dass eine bestimmte E‑Mail-Nachricht Spam (die positive Klasse) ist, aber diese E‑Mail-Nachricht ist tatsächlich kein Spam.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Schwellenwerte und die Konfusionsmatrix.
Rate falsch positiver Ergebnisse (False Positive Rate, FPR)
Der Anteil der tatsächlich negativen Beispiele, für die das Modell fälschlicherweise die positive Klasse vorhergesagt hat. Die Falsch-Positiv-Rate wird mit der folgenden Formel berechnet:
Die Rate falsch positiver Ergebnisse ist die X-Achse in einer ROC-Kurve.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Klassifizierung: ROC und AUC.
Feature
Eine Eingabevariable für ein Modell für maschinelles Lernen. Ein Beispiel besteht aus einem oder mehreren Merkmalen. Angenommen, Sie trainieren ein Modell, um den Einfluss von Wetterbedingungen auf die Prüfungsergebnisse von Schülern zu ermitteln. Die folgende Tabelle enthält drei Beispiele mit jeweils drei Features und einem Label:
| Funktionen | Label | ||
|---|---|---|---|
| Temperatur | Luftfeuchtigkeit | Luftdruck | Testergebnis |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
Kontrast mit dem Label.
Weitere Informationen finden Sie im Kurs „Einführung in maschinelles Lernen“ unter Supervised Learning.
Featureverknüpfung
Ein synthetisches Feature, das durch „Crossing“ von kategorialen oder in Buckets aufgeteilten Features gebildet wird.
Betrachten Sie beispielsweise ein Modell zur „Stimmungsprognose“, das die Temperatur in einem der folgenden vier Bereiche darstellt:
freezingchillytemperatewarm
und steht für die Windgeschwindigkeit in einem der folgenden drei Buckets:
stilllightwindy
Ohne Feature-Kombinationen wird das lineare Modell unabhängig für jede der sieben vorherigen verschiedenen Gruppen trainiert. Das Modell wird also beispielsweise anhand von freezing unabhängig vom Training anhand von windy trainiert.
Alternativ können Sie auch eine Kreuzung von Temperatur und Windgeschwindigkeit erstellen. Dieses synthetische Feature hätte die folgenden 12 möglichen Werte:
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
Dank der Feature-Kombinationen kann das Modell Stimmungsunterschiede zwischen einem freezing-windy- und einem freezing-still-Tag erkennen.
Wenn Sie ein synthetisches Feature aus zwei Features erstellen, die jeweils viele verschiedene Klassen haben, hat die resultierende Feature-Kombination eine große Anzahl möglicher Kombinationen. Wenn beispielsweise ein Merkmal 1.000 Buckets und das andere Merkmal 2.000 Buckets hat, enthält das resultierende Feature-Cross 2.000.000 Buckets.
Formal ist ein Cross ein kartesisches Produkt.
Feature-Kombinationen werden hauptsächlich mit linearen Modellen verwendet und nur selten mit neuronalen Netzen.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Kategorische Daten: Feature-Kombinationen.
Feature Engineering
Ein Prozess, der die folgenden Schritte umfasst:
- Ermitteln, welche Features für das Training eines Modells nützlich sein könnten.
- Rohdaten aus dem Dataset in effiziente Versionen dieser Features umwandeln.
Sie stellen beispielsweise fest, dass temperature eine nützliche Funktion sein könnte. Anschließend können Sie mit Klassierung experimentieren, um zu optimieren, was das Modell aus verschiedenen temperature-Bereichen lernen kann.
Feature Engineering wird manchmal auch als Feature-Extraktion oder Featurisierung bezeichnet.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Numerische Daten: Wie ein Modell Daten mithilfe von Feature-Vektoren aufnimmt.
Feature-Set
Die Gruppe von Features, mit denen Ihr Modell für maschinelles Lernen trainiert wird. Ein einfaches Feature-Set für ein Modell, das Immobilienpreise vorhersagt, könnte beispielsweise aus Postleitzahl, Grundstücksgröße und Zustand des Grundstücks bestehen.
Featurevektor
Das Array von feature-Werten, aus denen ein example besteht. Der Featurevektor wird während des Trainings und der Inferenz eingegeben. Der Merkmalsvektor für ein Modell mit zwei diskreten Merkmalen könnte beispielsweise so aussehen:
[0.92, 0.56]
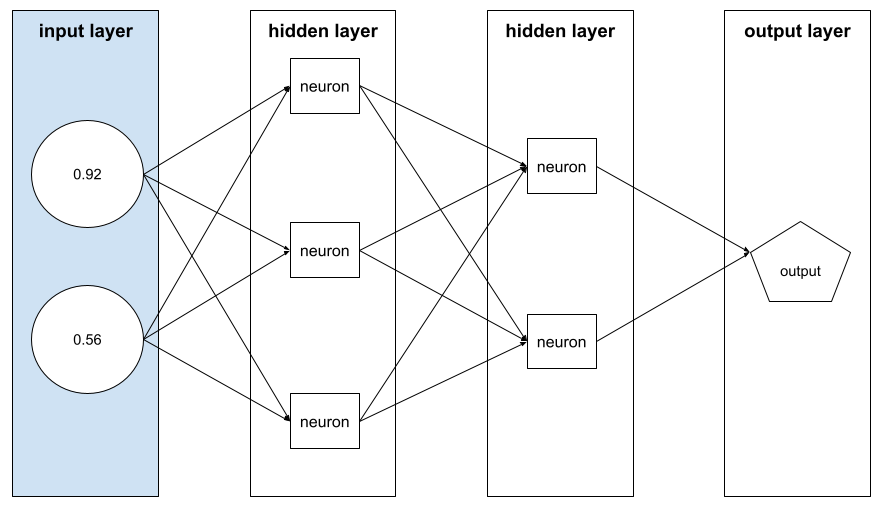
In jedem Beispiel werden unterschiedliche Werte für den Featurevektor angegeben. Der Featurevektor für das nächste Beispiel könnte so aussehen:
[0.73, 0.49]
Beim Feature Engineering wird festgelegt, wie Features im Featurevektor dargestellt werden. Ein binäres kategorisches Feature mit fünf möglichen Werten kann beispielsweise mit One-Hot-Codierung dargestellt werden. In diesem Fall würde der Teil des Feature-Vektors für ein bestimmtes Beispiel aus vier Nullen und einer einzelnen 1,0 an der dritten Position bestehen:
[0.0, 0.0, 1.0, 0.0, 0.0]
Angenommen, Ihr Modell besteht aus drei Features:
- ein binäres kategorisches Merkmal mit fünf möglichen Werten, die mit One-Hot-Codierung dargestellt werden, z. B.
[0.0, 1.0, 0.0, 0.0, 0.0] - ein weiteres binäres kategorisches Merkmal mit drei möglichen Werten, die mit One-Hot-Codierung dargestellt werden, z. B.
[0.0, 0.0, 1.0] - ein Gleitkomma-Feature, z. B.
8.3.
In diesem Fall würde der Featurevektor für jedes Beispiel durch neun Werte dargestellt. Bei den Beispielwerten in der vorherigen Liste wäre der Featurevektor:
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
Weitere Informationen finden Sie im Machine Learning Crash Course unter Numerische Daten: Wie ein Modell Daten mithilfe von Feature-Vektoren aufnimmt.
Feedbackschleife
Im maschinellen Lernen eine Situation, in der die Vorhersagen eines Modells die Trainingsdaten für dasselbe oder ein anderes Modell beeinflussen. Ein Modell, das Filme empfiehlt, beeinflusst beispielsweise die Filme, die Nutzer sehen, was wiederum nachfolgende Modelle für Filmempfehlungen beeinflusst.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Production ML systems: Questions to ask.
G
Generalisierung
Die Fähigkeit eines Modells, korrekte Vorhersagen für neue, bisher unbekannte Daten zu treffen. Ein Modell, das generalisieren kann, ist das Gegenteil eines Modells, das überangepasst ist.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Generalization.
Verallgemeinerungskurve
Ein Diagramm mit dem Trainingsverlust und dem Validierungsverlust als Funktion der Anzahl der Iteration.
Mithilfe einer Generalisierungskurve können Sie Overfitting erkennen. Die folgende Generalisierungskurve deutet beispielsweise auf eine Überanpassung hin, da der Validierungsverlust letztendlich deutlich höher als der Trainingsverlust ist.
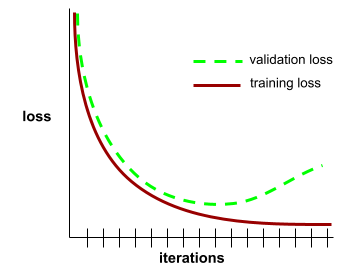
Weitere Informationen finden Sie im Machine Learning Crash Course unter Generalization.
Gradientenabstieg
Eine mathematische Methode zur Minimierung des Verlusts. Beim Gradientenabstieg werden Gewichte und Biasse iterativ angepasst, um nach und nach die beste Kombination zur Minimierung des Verlusts zu finden.
Der Gradientenabstieg ist viel älter als das maschinelle Lernen.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Gradientenabstieg.
Ground Truth
Realität.
Was ist stattdessen passiert?
Nehmen wir als Beispiel ein binäres Klassifizierungsmodell, das vorhersagt, ob ein Student im ersten Studienjahr innerhalb von sechs Jahren seinen Abschluss machen wird. Die Grundwahrheit für dieses Modell ist, ob der Schüler oder Student tatsächlich innerhalb von sechs Jahren seinen Abschluss gemacht hat.
H
versteckte Ebene
Eine Schicht in einem neuronalen Netzwerk zwischen der Eingabeschicht (den Features) und der Ausgabeschicht (der Vorhersage). Jede verborgene Ebene besteht aus einem oder mehreren Neuronen. Das folgende neuronale Netzwerk enthält beispielsweise zwei verborgene Schichten, die erste mit drei Neuronen und die zweite mit zwei Neuronen:
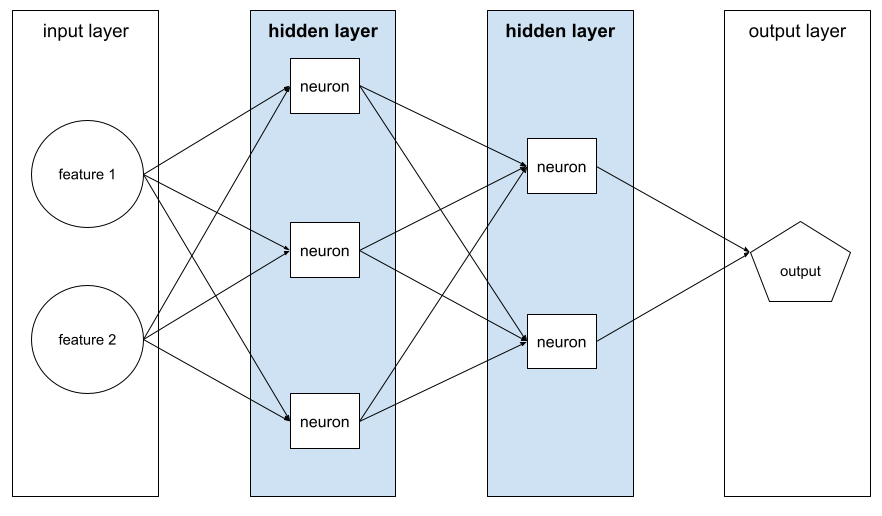
Ein neuronales Deep-Learning-Netzwerk enthält mehr als eine verborgene Ebene. Die Abbildung oben zeigt beispielsweise ein tiefes neuronales Netzwerk, da das Modell zwei verborgene Schichten enthält.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Neuronale Netze: Knoten und verborgene Ebenen.
Hyperparameter
Die Variablen, die Sie oder ein Hyperparameter-Abstimmungsdienst >bei aufeinanderfolgenden Durchläufen des Modelltrainings anpassen. Ein Beispiel ist die Lernrate. Sie könnten die Lernrate vor einer Trainingssitzung auf 0,01 festlegen. Wenn Sie feststellen, dass 0,01 zu hoch ist, können Sie die Lernrate für die nächste Trainingssitzung auf 0,003 festlegen.
Im Gegensatz dazu sind Parameter die verschiedenen Gewichtungen und Bias, die das Modell während des Trainings lernt.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Hyperparameter.
I
unabhängig und identisch verteilt (i.i.d.)
Daten, die aus einer unveränderlichen Verteilung stammen und bei denen jeder gezogene Wert nicht von zuvor gezogenen Werten abhängt. Eine i.i.d. ist das ideale Gas des maschinellen Lernens – ein nützliches mathematisches Konstrukt, das in der realen Welt jedoch fast nie genau zu finden ist. So kann die Verteilung der Besucher einer Webseite beispielsweise über einen kurzen Zeitraum hinweg unabhängig und identisch verteilt sein. Das bedeutet, dass sich die Verteilung in diesem kurzen Zeitraum nicht ändert und der Besuch einer Person im Allgemeinen unabhängig vom Besuch einer anderen Person ist. Wenn Sie diesen Zeitraum jedoch erweitern, können saisonale Unterschiede bei den Besuchern der Webseite auftreten.
Siehe auch Nichtstationarität.
Inferenz
Beim herkömmlichen maschinellen Lernen wird ein trainiertes Modell auf Beispiele ohne Label angewendet, um Vorhersagen zu treffen. Weitere Informationen finden Sie im Kurs „Einführung in ML“ unter Supervised Learning.
Bei Large Language Models ist die Inferenz der Prozess, bei dem ein trainiertes Modell verwendet wird, um eine Antwort auf einen Prompt zu generieren.
In der Statistik hat der Begriff „Inferenz“ eine etwas andere Bedeutung. Weitere Informationen finden Sie im Wikipedia-Artikel zur statistischen Inferenz.
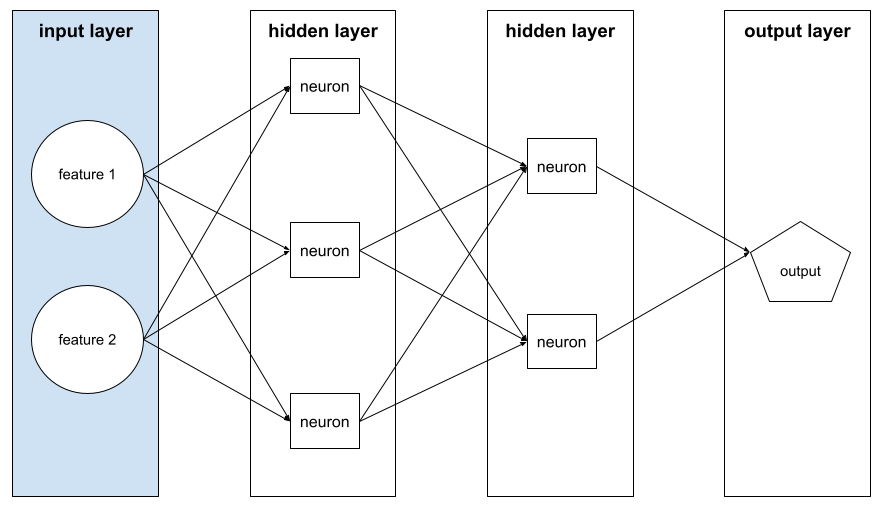
Eingabelayer
Die Ebene eines neuronalen Netzwerks, die den Merkmalsvektor enthält. Die Eingabeschicht stellt also Beispiele für das Training oder die Inferenz bereit. Die Eingabeschicht im folgenden neuronalen Netzwerk besteht beispielsweise aus zwei Features:
Interpretierbarkeit
Die Fähigkeit, die Argumentation eines ML-Modells in für Menschen verständlicher Form zu erläutern oder zu präsentieren.
Die meisten linearen Regressionsmodelle sind beispielsweise sehr gut interpretierbar. Sie müssen sich lediglich die trainierten Gewichte für jedes Feature ansehen. Entscheidungsbäume sind außerdem sehr gut interpretierbar. Bei einigen Modellen ist jedoch eine komplexe Visualisierung erforderlich, um interpretierbar zu werden.
Mit dem Learning Interpretability Tool (LIT) können Sie ML-Modelle interpretieren.
Iteration
Eine einzelne Aktualisierung der Parameter eines Modells – der Gewichtungen und Biases des Modells – während des Trainings. Die Batchgröße bestimmt, wie viele Beispiele das Modell in einer einzelnen Iteration verarbeitet. Wenn die Batchgröße beispielsweise 20 ist, verarbeitet das Modell 20 Beispiele, bevor die Parameter angepasst werden.
Beim Trainieren eines neuronalen Netzwerks umfasst eine einzelne Iteration die folgenden beiden Durchläufe:
- Ein Forward-Pass zur Berechnung des Verlusts für einen einzelnen Batch.
- Ein Backward-Pass (Backpropagation), um die Parameter des Modells basierend auf dem Verlust und der Lernrate anzupassen.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Gradient Descent.
L
L0-Regularisierung
Eine Art der Regularisierung, bei der die Gesamtzahl der Gewichtungen in einem Modell, die nicht null sind, bestraft wird. Ein Modell mit 11 Gewichten ungleich null wird beispielsweise stärker bestraft als ein ähnliches Modell mit 10 Gewichten ungleich null.
Die L0-Regularisierung wird manchmal auch als L0-Norm-Regularisierung bezeichnet.
L1-Verlust
Eine Verlustfunktion, die den absoluten Wert der Differenz zwischen den tatsächlichen Label-Werten und den Werten berechnet, die ein Modell vorhersagt. Hier ist beispielsweise die Berechnung des L1-Verlusts für einen Batch mit fünf Beispielen:
| Tatsächlicher Wert des Beispiels | Vom Modell prognostizierter Wert | Absoluter Wert des Deltas |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1-Verlust | ||
Der L1-Verlust reagiert weniger empfindlich auf Ausreißer als der L2-Verlust.
Der mittlere absolute Fehler ist der durchschnittliche L1-Verlust pro Beispiel.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Verlust.
L1-Regularisierung
Eine Art der Regularisierung, bei der Gewichtungen proportional zur Summe der absoluten Werte der Gewichtungen bestraft werden. Die L1-Regularisierung trägt dazu bei, die Gewichte irrelevanter oder kaum relevanter Features auf genau 0 zu setzen. Eine Funktion mit einem Gewicht von 0 wird effektiv aus dem Modell entfernt.
Kontrast zur L2-Regularisierung.
L2-Verlust
Eine Verlustfunktion, die das Quadrat der Differenz zwischen den tatsächlichen Label-Werten und den Werten berechnet, die ein Modell vorhersagt. Hier ist beispielsweise die Berechnung des L2-Verlusts für einen Batch mit fünf Beispielen:
| Tatsächlicher Wert des Beispiels | Vom Modell prognostizierter Wert | Quadrat von Delta |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2-Verlust | ||
Durch die Quadrierung verstärkt der L2-Verlust den Einfluss von Ausreißern. Das bedeutet, dass der L2-Verlust stärker auf schlechte Vorhersagen reagiert als der L1-Verlust. Der L1-Verlust für den vorherigen Batch wäre beispielsweise 8 statt 16. Ein einzelner Ausreißer macht 9 der 16 aus.
In Regressionsmodellen wird in der Regel der L2-Verlust als Verlustfunktion verwendet.
Der mittlere quadratische Fehler ist der durchschnittliche L2-Verlust pro Beispiel. Squared Loss ist ein anderer Name für den L2-Verlust.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Logistische Regression: Verlust und Regularisierung.
L2-Regularisierung
Eine Art der Regularisierung, bei der Gewichtungen proportional zur Summe der Quadrate der Gewichtungen bestraft werden. Die L2-Regularisierung trägt dazu bei, Ausreißergewichte (mit hohen positiven oder niedrigen negativen Werten) näher an 0 heranzuführen, aber nicht ganz auf 0 zu setzen. Features mit Werten, die sehr nahe an 0 liegen, bleiben im Modell, haben aber nur einen geringen Einfluss auf die Vorhersage des Modells.
Die L2-Regularisierung verbessert immer die Generalisierung in linearen Modellen.
Kontrast zur L1-Regularisierung.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Overfitting: L2 regularization.
Label
Im überwachten maschinellen Lernen ist das der „Antwort“- oder „Ergebnis“-Teil eines Beispiels.
Jedes beispielhafte Element mit Label besteht aus einem oder mehreren Features und einem Label. In einem Dataset zur Spamerkennung wäre das Label beispielsweise wahrscheinlich entweder „Spam“ oder „Kein Spam“. In einem Dataset zu Niederschlagsmengen könnte das Label die Menge an Regen sein, die in einem bestimmten Zeitraum gefallen ist.
Weitere Informationen finden Sie unter Supervised Learning in Introduction to Machine Learning.
Beispiel mit Label
Ein Beispiel, das ein oder mehrere Merkmale und ein Label enthält. In der folgenden Tabelle sind beispielsweise drei gelabelte Beispiele aus einem Modell zur Hausbewertung aufgeführt, die jeweils drei Features und ein Label enthalten:
| Anzahl der Schlafzimmer | Anzahl der Badezimmer | Alter des Hauses | Hauspreis (Label) |
|---|---|---|---|
| 3 | 2 | 15 | 345.000 $ |
| 2 | 1 | 72 | 179.000 $ |
| 4 | 2 | 34 | 392.000 $ |
Beim überwachten maschinellen Lernen> werden Modelle mit gelabelten Beispielen trainiert und Vorhersagen für nicht gelabelte Beispiele getroffen.
Stellen Sie ein gelabeltes Beispiel nicht gelabelten Beispielen gegenüber.
Weitere Informationen finden Sie unter Supervised Learning in Introduction to Machine Learning.
Lambda
Synonym für Regularisierungsrate.
Lambda ist ein überlasteter Begriff. Hier konzentrieren wir uns auf die Definition des Begriffs im Kontext von Regularisierung.
Layer
Eine Gruppe von Neuronen in einem neuronalen Netzwerk. Im Folgenden sind drei gängige Arten von Layern aufgeführt:
- Die Eingabeschicht, die Werte für alle Features bereitstellt.
- Eine oder mehrere verborgene Schichten, die nicht lineare Beziehungen zwischen den Features und dem Label finden.
- Die Ausgabeschicht, die die Vorhersage liefert.
Die folgende Abbildung zeigt beispielsweise ein neuronales Netzwerk mit einer Eingabeschicht, zwei verborgenen Schichten und einer Ausgabeschicht:
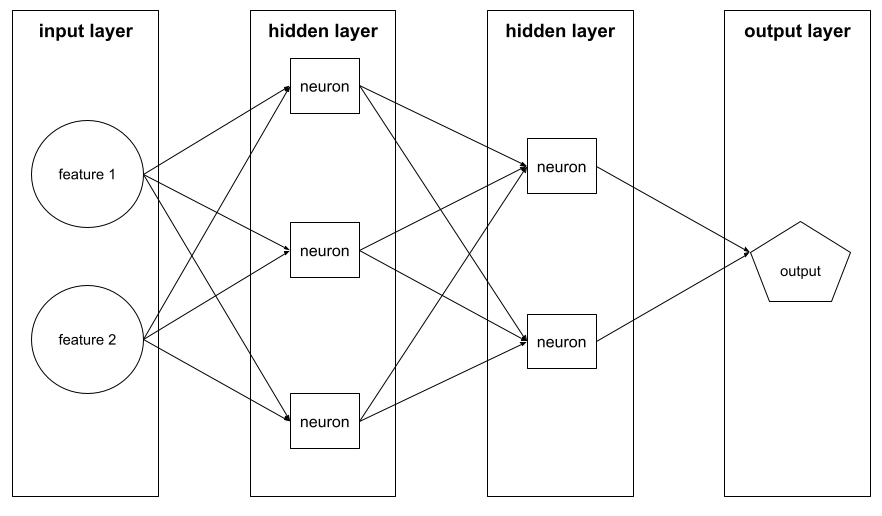
In TensorFlow sind Ebenen auch Python-Funktionen, die Tensoren und Konfigurationsoptionen als Eingabe verwenden und andere Tensoren als Ausgabe erzeugen.
Lernrate
Eine Gleitkommazahl, die dem Gradientenabstiegsalgorithmus angibt, wie stark Gewichte und Bias bei jeder Iteration angepasst werden sollen. Bei einer Lernrate von 0,3 werden Gewichte und Bias beispielsweise dreimal stärker angepasst als bei einer Lernrate von 0,1.
Die Lernrate ist ein wichtiger Hyperparameter. Wenn Sie die Lernrate zu niedrig festlegen, dauert das Training zu lange. Wenn Sie die Lernrate zu hoch einstellen, hat der Gradientenabstieg oft Schwierigkeiten, Konvergenz zu erreichen.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Hyperparameter.
Linear
Eine Beziehung zwischen zwei oder mehr Variablen, die nur durch Addition und Multiplikation dargestellt werden kann.
Die Darstellung einer linearen Beziehung ist eine Linie.
Im Gegensatz dazu steht die nicht lineare.
Lineares Modell
Ein Modell, das jedem Feature eine Gewichtung zuweist, um Vorhersagen zu treffen. Lineare Modelle enthalten auch einen Bias. Im Gegensatz dazu ist die Beziehung von Features zu Vorhersagen in Deep-Learning-Modellen in der Regel nicht linear.
Lineare Modelle sind in der Regel einfacher zu trainieren und besser interpretierbar als Deep-Learning-Modelle. Mit Deep-Learning-Modellen lassen sich jedoch komplexe Beziehungen zwischen Features erkennen.
Lineare Regression und logistische Regression sind zwei Arten von linearen Modellen.
lineare Regression
Ein Typ von Machine-Learning-Modell, bei dem beides zutrifft:
- Das Modell ist ein lineares Modell.
- Die Vorhersage ist ein Gleitkommawert. (Dies ist der Regressions-Teil der linearen Regression.)
Stellen Sie die lineare Regression der logistischen Regression gegenüber. Stellen Sie außerdem die Regression der Kontrastvariablen der Klassifizierung gegenüber.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression.
logistische Regression
Ein Typ von Regressionsmodell, mit dem eine Wahrscheinlichkeit vorhergesagt wird. Logistische Regressionsmodelle haben die folgenden Merkmale:
- Das Label ist kategorial. Der Begriff „logistische Regression“ bezieht sich in der Regel auf die binäre logistische Regression, d. h. auf ein Modell, das Wahrscheinlichkeiten für Labels mit zwei möglichen Werten berechnet. Eine weniger häufige Variante, die multinominale logistische Regression, berechnet Wahrscheinlichkeiten für Labels mit mehr als zwei möglichen Werten.
- Die Verlustfunktion während des Trainings ist Log Loss. (Mehrere Log Loss-Einheiten können parallel für Labels mit mehr als zwei möglichen Werten platziert werden.)
- Das Modell hat eine lineare Architektur und kein neuronales Deep-Learning-Netzwerk. Der Rest dieser Definition gilt jedoch auch für Deep-Modelle, die Wahrscheinlichkeiten für kategorische Labels vorhersagen.
Nehmen wir beispielsweise ein logistisches Regressionsmodell, das die Wahrscheinlichkeit berechnet, dass eine eingegebene E‑Mail entweder Spam oder kein Spam ist. Angenommen, das Modell sagt während der Inferenz 0,72 voraus. Das Modell schätzt also Folgendes:
- Die Wahrscheinlichkeit, dass die E‑Mail Spam ist, liegt bei 72 %.
- Die Wahrscheinlichkeit, dass die E-Mail kein Spam ist, liegt bei 28 %.
Ein logistisches Regressionsmodell verwendet die folgende zweistufige Architektur:
- Das Modell generiert eine Rohvorhersage (y') durch Anwenden einer linearen Funktion von Eingabefeatures.
- Das Modell verwendet diese Rohvorhersage als Eingabe für eine Sigmoid-Funktion, die die Rohvorhersage in einen Wert zwischen 0 und 1 (ausschließlich) konvertiert.
Wie bei jedem Regressionsmodell wird auch bei einem logistischen Regressionsmodell eine Zahl vorhergesagt. Diese Zahl wird jedoch in der Regel wie folgt Teil eines binären Klassifizierungsmodells:
- Wenn die vorhergesagte Zahl größer als der Klassifizierungsschwellenwert ist, sagt das binäre Klassifizierungsmodell die positive Klasse vorher.
- Wenn die vorhergesagte Zahl kleiner als der Klassifizierungsschwellenwert ist, sagt das binäre Klassifizierungsmodell die negative Klasse vorher.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Logistische Regression.
Logarithmischer Verlust
Die Verlustfunktion, die in der binären logistischen Regression verwendet wird.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Logistische Regression: Verlust und Regularisierung.
Log-Odds
Der Logarithmus der Chance eines Ereignisses.
Niederlage
Beim Training eines überwachten Modells wird gemessen, wie weit die Vorhersage eines Modells von seinem Label entfernt ist.
Mit einer Verlustfunktion wird der Verlust berechnet.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Verlust.
Verlustkurve
Ein Diagramm des Verlusts als Funktion der Anzahl der Trainingsiterationen. Das folgende Diagramm zeigt eine typische Verlustkurve:
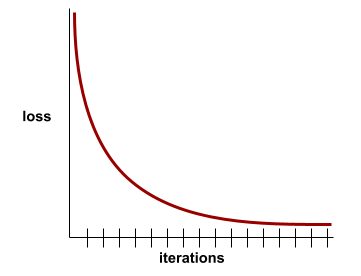
Anhand von Verlustkurven können Sie feststellen, wann Ihr Modell konvergiert oder überangepasst ist.
In Verlustkurven können alle folgenden Arten von Verlust dargestellt werden:
Siehe auch Verallgemeinerungskurve.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Overfitting: Interpreting loss curves.
Verlustfunktion
Während des Trainings oder Tests wird eine mathematische Funktion verwendet, mit der der Verlust für einen Batch von Beispielen berechnet wird. Eine Verlustfunktion gibt einen niedrigeren Verlust für Modelle zurück, die gute Vorhersagen treffen, als für Modelle, die schlechte Vorhersagen treffen.
Das Ziel des Trainings besteht in der Regel darin, den Verlust zu minimieren, der von einer Verlustfunktion zurückgegeben wird.
Es gibt viele verschiedene Arten von Verlustfunktionen. Wählen Sie die geeignete Verlustfunktion für den Typ des Modells aus, das Sie erstellen. Beispiel:
- L2-Verlust (oder mittlerer quadratischer Fehler) ist die Verlustfunktion für die lineare Regression.
- Logarithmischer Verlust ist die Verlustfunktion für die logistische Regression.
M
Machine Learning
Ein Programm oder System, das ein Modell mit Eingabedaten trainiert. Das trainierte Modell kann für (komplett) neue Daten nützliche Vorhersagen treffen, die aus derselben Verteilung stammen wie die Daten, die zum Trainieren des Modells verwendet wurden.
Machine Learning bezieht sich auch auf den Forschungsbereich, der sich mit diesen Programmen oder Systemen befasst.
Weitere Informationen finden Sie im Kurs Einführung in maschinelles Lernen.
Mehrheitsklasse
Das häufigere Label in einem Dataset mit unausgewogenen Klassen. Wenn ein Dataset beispielsweise 99% negative Labels und 1% positive Labels enthält, sind die negativen Labels die Mehrheitsklasse.
Kontrast zur Minderheitsklasse.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Datasets: Imbalanced datasets.
Mini-Batch
Eine kleine, zufällig ausgewählte Teilmenge eines Batch, die in einer Iteration verarbeitet wird. Die Batchgröße eines Minibatches liegt in der Regel zwischen 10 und 1.000 Beispielen.
Angenommen, der gesamte Trainingsdatensatz (der vollständige Batch) besteht aus 1.000 Beispielen. Angenommen, Sie legen die Batchgröße jedes Mini-Batch auf 20 fest. Daher wird in jeder Iteration der Verlust für 20 zufällige der 1.000 Beispiele ermittelt und die Gewichte und Biasse entsprechend angepasst.
Es ist viel effizienter, den Verlust für einen Mini-Batch zu berechnen als für alle Beispiele im vollständigen Batch.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Hyperparameter.
Minderheitsklasse
Das weniger häufige Label in einem Dataset mit unausgeglichenen Klassen. Wenn ein Dataset beispielsweise 99% negative und 1% positive Labels enthält, sind die positiven Labels die Minderheitsklasse.
Kontrast zur Mehrheitsklasse.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Datasets: Imbalanced datasets.
Modell
Im Allgemeinen ist das jedes mathematische Konstrukt, das Eingabedaten verarbeitet und eine Ausgabe zurückgibt. Anders ausgedrückt: Ein Modell ist die Menge der Parameter und der Struktur, die für ein System erforderlich sind, um Vorhersagen zu treffen. Beim überwachten maschinellen Lernen wird ein Beispiel als Eingabe verwendet und eine Vorhersage als Ausgabe abgeleitet. Innerhalb des überwachten maschinellen Lernens unterscheiden sich die Modelle etwas. Beispiel:
- Ein lineares Regressionsmodell besteht aus einer Reihe von Gewichten und einem Bias.
- Ein Modell für neuronale Netzwerke besteht aus:
- Eine Reihe von verborgenen Ebenen, die jeweils ein oder mehrere Neuronen enthalten.
- Die Gewichte und der Bias, die mit jedem Neuron verknüpft sind.
- Ein Entscheidungsbaummodell besteht aus:
- Die Form des Baums, d. h. das Muster, in dem die Bedingungen und Blätter verbunden sind.
- Die Bedingungen und Blätter.
Sie können ein Modell speichern, wiederherstellen oder Kopien davon erstellen.
Beim unüberwachten maschinellen Lernen werden ebenfalls Modelle generiert, in der Regel eine Funktion, die ein Eingabebeispiel dem am besten geeigneten Cluster zuordnen kann.
Klassifizierung mit mehreren Klassen
Beim überwachten Lernen ein Klassifizierungsproblem, bei dem das Dataset mehr als zwei Klassen von Labels enthält. Die Labels im Iris-Dataset müssen beispielsweise einer der folgenden drei Klassen entsprechen:
- Iris setosa
- Iris virginica
- Iris versicolor
Ein Modell, das mit dem Iris-Dataset trainiert wurde und den Iris-Typ für neue Beispiele vorhersagt, führt eine Klassifizierung mit mehreren Klassen durch.
Klassifizierungsprobleme, bei denen genau zwei Klassen unterschieden werden, sind binäre Klassifizierungsmodelle. Ein E‑Mail-Modell, das entweder Spam oder Kein Spam vorhersagt, ist beispielsweise ein binäres Klassifizierungsmodell.
Bei Clustering-Problemen bezieht sich die Klassifizierung mit mehreren Klassen auf mehr als zwei Cluster.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Neuronale Netze: Multiklassenklassifizierung.
N
negative Klasse
Bei der binären Klassifizierung wird eine Klasse als positiv und die andere als negativ bezeichnet. Die positive Klasse ist das Ding oder Ereignis, auf das das Modell testet, und die negative Klasse ist die andere Möglichkeit. Beispiel:
- Die negative Klasse in einem medizinischen Test könnte „kein Tumor“ sein.
- Die negative Klasse in einem Klassifizierungsmodell für E‑Mails könnte „Kein Spam“ sein.
Kontrast zur positiven Klasse.
neuronales Netzwerk
Ein Modell mit mindestens einer verborgenen Ebene. Ein neuronales Deep-Learning-Netzwerk ist eine Art von neuronalem Netzwerk mit mehr als einer verborgenen Ebene. Das folgende Diagramm zeigt beispielsweise ein tiefes neuronales Netzwerk mit zwei verborgenen Schichten.
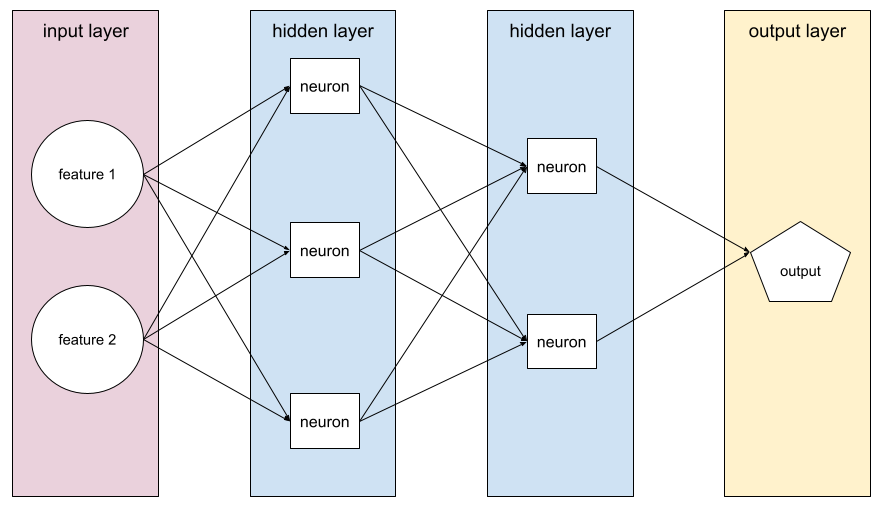
Jedes Neuron in einem neuronalen Netzwerk ist mit allen Knoten in der nächsten Schicht verbunden. Im obigen Diagramm ist zu sehen, dass jede der drei Neuronen in der ersten verborgenen Schicht separat mit beiden Neuronen in der zweiten verborgenen Schicht verbunden ist.
Neuronale Netzwerke, die auf Computern implementiert werden, werden manchmal als künstliche neuronale Netzwerke bezeichnet, um sie von neuronalen Netzwerken in Gehirnen und anderen Nervensystemen zu unterscheiden.
Einige neuronale Netze können extrem komplexe nichtlineare Beziehungen zwischen verschiedenen Features und dem Label nachbilden.
Siehe auch Convolutional Neural Network (CNN) und Recurrent Neural Network (RNN).
Weitere Informationen finden Sie im Machine Learning Crash Course unter Neuronale Netze.
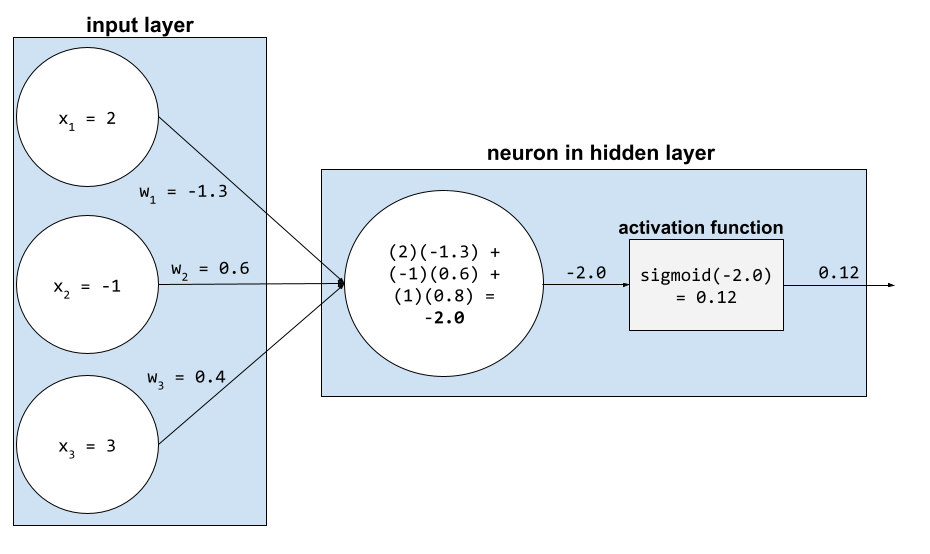
Neuron
Im Machine Learning eine separate Einheit in einer verdeckten Schicht eines neuronalen Netzwerks. Jedes Neuron führt die folgenden zwei Schritte aus:
- Berechnet die gewichtete Summe der Eingabewerte, die mit ihren entsprechenden Gewichten multipliziert werden.
- Übergibt die gewichtete Summe als Eingabe an eine Aktivierungsfunktion.
Ein Neuron in der ersten verborgenen Schicht akzeptiert Eingaben aus den Feature-Werten in der Eingabeschicht. Ein Neuron in einer beliebigen verborgenen Schicht nach der ersten akzeptiert Eingaben von den Neuronen in der vorherigen verborgenen Schicht. Ein Neuron in der zweiten verborgenen Ebene akzeptiert beispielsweise Eingaben von den Neuronen in der ersten verborgenen Ebene.
Die folgende Abbildung zeigt zwei Neuronen und ihre Eingaben.
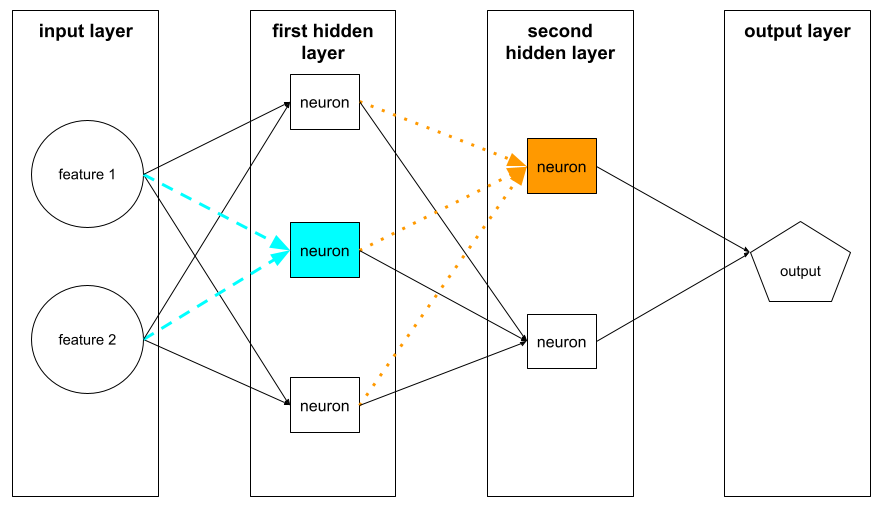
Ein Neuron in einem neuronalen Netzwerk ahmt das Verhalten von Neuronen im Gehirn und anderen Teilen des Nervensystems nach.
Knoten (neuronales Netzwerk)
Ein Neuron in einer versteckten Schicht.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Neuronale Netze.
nicht linear
Eine Beziehung zwischen zwei oder mehr Variablen, die nicht nur durch Addition und Multiplikation dargestellt werden kann. Ein linearer Zusammenhang kann als Linie dargestellt werden, ein nichtlinearer Zusammenhang nicht. Betrachten Sie beispielsweise zwei Modelle, die jeweils ein einzelnes Feature mit einem einzelnen Label in Beziehung setzen. Das Modell auf der linken Seite ist linear, das Modell auf der rechten Seite ist nicht linear:

Im Machine Learning Crash Course finden Sie unter Neuronale Netze: Knoten und verborgene Schichten weitere Informationen zum Experimentieren mit verschiedenen Arten von nichtlinearen Funktionen.
Nichtstationarität
Ein Merkmal, dessen Werte sich über eine oder mehrere Dimensionen hinweg ändern, in der Regel über die Zeit. Hier einige Beispiele für Nichtstationarität:
- Die Anzahl der in einem bestimmten Geschäft verkauften Badeanzüge variiert je nach Jahreszeit.
- Die Menge einer bestimmten Frucht, die in einer bestimmten Region geerntet wird, ist einen Großteil des Jahres null, aber für einen kurzen Zeitraum groß.
- Aufgrund des Klimawandels verschieben sich die jährlichen Durchschnittstemperaturen.
Kontrast zur Stationarität.
Normalisierung
Im Allgemeinen wird dabei der tatsächliche Wertebereich einer Variablen in einen Standardwertebereich konvertiert, z. B.:
- –1 bis +1
- 0 bis 1
- Z-Werte (ungefähr -3 bis +3)
Angenommen, der tatsächliche Wertebereich eines bestimmten Merkmals liegt zwischen 800 und 2.400. Im Rahmen des Feature Engineering können Sie die tatsächlichen Werte auf einen Standardbereich wie -1 bis +1 normalisieren.
Die Normalisierung ist eine häufige Aufgabe beim Feature Engineering. Modelle werden in der Regel schneller trainiert und liefern bessere Vorhersagen, wenn alle numerischen Features im Feature-Vektor ungefähr denselben Bereich haben.
Weitere Informationen finden Sie unter Z-Score-Normalisierung.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Numerische Daten: Normalisierung.
Numerische Daten
Features, die als Ganzzahlen oder reelle Zahlen dargestellt werden. Bei einem Modell zur Bewertung von Häusern würde die Größe eines Hauses (in Quadratfuß oder Quadratmetern) wahrscheinlich als numerische Daten dargestellt. Wenn Sie ein Feature als numerische Daten darstellen, bedeutet das, dass die Werte des Features eine mathematische Beziehung zum Label haben. Die Anzahl der Quadratmeter in einem Haus steht wahrscheinlich in einem mathematischen Verhältnis zum Wert des Hauses.
Nicht alle Ganzzahldaten sollten als numerische Daten dargestellt werden. Beispielsweise sind Postleitzahlen in einigen Teilen der Welt Ganzzahlen. Ganzzahlige Postleitzahlen sollten jedoch nicht als numerische Daten in Modellen dargestellt werden. Das liegt daran, dass eine Postleitzahl von 20000 nicht doppelt so (oder halb so) wirkungsvoll ist wie eine Postleitzahl von 10000. Außerdem korrelieren unterschiedliche Postleitzahlen zwar mit unterschiedlichen Immobilienwerten, aber wir können nicht davon ausgehen, dass Immobilienwerte mit der Postleitzahl 20000 doppelt so wertvoll sind wie Immobilienwerte mit der Postleitzahl 10000.
Postleitzahlen sollten stattdessen als kategorische Daten dargestellt werden.
Numerische Merkmale werden manchmal auch als kontinuierliche Merkmale bezeichnet.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Mit numerischen Daten arbeiten.
O
offline
Synonym für static.
Offlineinferenz
Der Prozess, bei dem ein Modell einen Batch von Vorhersagen generiert und diese Vorhersagen dann im Cache speichert. Apps können dann auf die abgeleitete Vorhersage aus dem Cache zugreifen, anstatt das Modell noch einmal auszuführen.
Angenommen, ein Modell generiert alle vier Stunden lokale Wettervorhersagen (Prognosen). Nach jedem Modelllauf werden alle lokalen Wettervorhersagen im System zwischengespeichert. Wetter-Apps rufen die Vorhersagen aus dem Cache ab.
Die Offline-Inferenz wird auch als statische Inferenz bezeichnet.
Im Gegensatz dazu steht die Onlineinferenz. Weitere Informationen finden Sie im Machine Learning Crash Course unter Production ML systems: Static versus dynamic inference.
One-Hot-Codierung
Kategorische Daten werden als Vektor dargestellt, in dem:
- Ein Element ist auf 1 gesetzt.
- Alle anderen Elemente werden auf 0 gesetzt.
Die One-Hot-Codierung wird häufig verwendet, um Strings oder Kennungen mit einer endlichen Anzahl möglicher Werte darzustellen.
Angenommen, ein bestimmtes kategorisches Feature namens Scandinavia hat fünf mögliche Werte:
- „Dänemark“
- „Schweden“
- „Norwegen“
- „Finnland“
- „Island“
Die fünf Werte könnten so als One-Hot-Codierung dargestellt werden:
| Land | Vektor | ||||
|---|---|---|---|---|---|
| „Dänemark“ | 1 | 0 | 0 | 0 | 0 |
| „Schweden“ | 0 | 1 | 0 | 0 | 0 |
| „Norwegen“ | 0 | 0 | 1 | 0 | 0 |
| „Finnland“ | 0 | 0 | 0 | 1 | 0 |
| „Island“ | 0 | 0 | 0 | 0 | 1 |
Dank der One-Hot-Codierung kann ein Modell auf Grundlage der einzelnen Länder unterschiedliche Verbindungen lernen.
Die Darstellung eines Merkmals als numerische Daten ist eine Alternative zur One-Hot-Codierung. Leider ist es nicht sinnvoll, die skandinavischen Länder numerisch darzustellen. Betrachten Sie beispielsweise die folgende numerische Darstellung:
- „Denmark“ ist 0
- „Schweden“ ist 1
- „Norwegen“ ist 2
- „Finnland“ ist 3
- „Island“ ist 4
Bei der numerischen Codierung würde ein Modell die Rohzahlen mathematisch interpretieren und versuchen, anhand dieser Zahlen zu trainieren. Island ist aber nicht doppelt so viel (oder halb so viel) wie Norwegen, daher würde das Modell zu seltsamen Schlussfolgerungen kommen.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Categorical data: Vocabulary and one-hot encoding.
One-vs.-All
Bei einem Klassifizierungsproblem mit N Klassen besteht eine Lösung aus N separaten binären Klassifizierungsmodellen – einem binären Klassifizierungsmodell für jedes mögliche Ergebnis. Angenommen, Sie haben ein Modell, das Beispiele als Tier, Pflanze oder Mineral klassifiziert. Eine One-vs.-All-Lösung würde die folgenden drei separaten binären Klassifizierungsmodelle bereitstellen:
- Tier oder kein Tier
- Gemüse oder nicht
- mineralisch oder nicht mineralisch
online
Synonym für dynamisch.
Onlineinferenz
Vorhersagen werden auf Anfrage generiert. Angenommen, eine App übergibt Eingaben an ein Modell und sendet eine Anfrage für eine Vorhersage. Ein System, das Onlineinferenz verwendet, reagiert auf die Anfrage, indem es das Modell ausführt und die Vorhersage an die App zurückgibt.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Production ML systems: Static versus dynamic inference.
Ausgabeschicht
Die „letzte“ Ebene eines neuronalen Netzwerks. Die Ausgabeschicht enthält die Vorhersage.
Die folgende Abbildung zeigt ein kleines Deep Neural Network mit einer Eingabeschicht, zwei verborgenen Schichten und einer Ausgabeschicht:
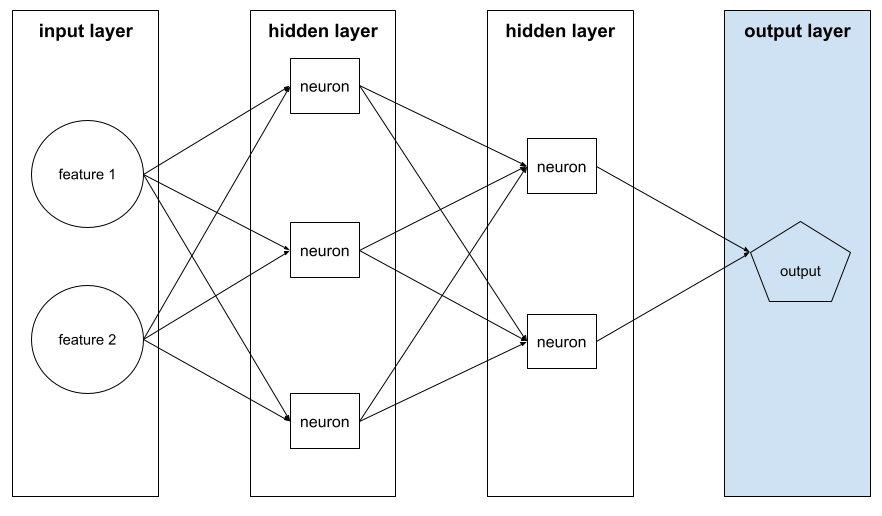
Überanpassung
Ein Modell erstellen, das so genau mit den Trainingsdaten übereinstimmt, dass es keine korrekten Vorhersagen für neue Daten treffen kann.
Regularisierung kann Overfitting reduzieren. Das Training mit einem großen und vielfältigen Trainingssatz kann auch eine Überanpassung reduzieren.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Overfitting.
P
pandas
Eine spaltenorientierte Datenanalyse-API, die auf numpy basiert. Viele Frameworks für maschinelles Lernen, darunter TensorFlow, unterstützen Pandas-Datenstrukturen als Eingaben. Weitere Informationen finden Sie in der pandas-Dokumentation.
Parameter
Die Gewichtungen und Biases, die ein Modell während des Trainings lernt. In einem linearen Regressionsmodell bestehen die Parameter beispielsweise aus dem Bias (b) und allen Gewichten (w1, w2 usw.) in der folgenden Formel:
Im Gegensatz dazu sind Hyperparameter die Werte, die Sie (oder ein Hyperparameter-Abstimmungsdienst) für das Modell bereitstellen. Die Lernrate ist beispielsweise ein Hyperparameter.
positive Klasse
Die Klasse, die Sie testen.
Die positive Klasse in einem Krebsmodell könnte beispielsweise „Tumor“ sein. Die positive Klasse in einem E-Mail-Klassifizierungsmodell kann beispielsweise „Spam“ sein.
Im Gegensatz zur negativen Klasse.
Nachbearbeitung
Die Ausgabe eines Modells wird nach dem Ausführen des Modells angepasst. Mit der Nachbearbeitung lassen sich Fairness-Einschränkungen durchsetzen, ohne die Modelle selbst zu ändern.
Beispielsweise kann die Nachbearbeitung auf ein binäres Klassifikationsmodell angewendet werden, indem ein Klassifikationsschwellenwert festgelegt wird, sodass die Chancengleichheit für ein Attribut aufrechterhalten wird. Dazu wird geprüft, ob die Rate der richtig positiven Ergebnisse für alle Werte dieses Attributs gleich ist.
Precision
Ein Messwert für Klassifizierungsmodelle, der die folgende Frage beantwortet:
Wenn das Modell die positive Klasse vorhergesagt hat, wie viel Prozent der Vorhersagen waren richtig?
Hier ist die Formel:
Dabei gilt:
- „Richtig positiv“ bedeutet, dass das Modell die positive Klasse richtig vorhergesagt hat.
- „Falsch positiv“ bedeutet, dass das Modell die positive Klasse fälschlicherweise vorhergesagt hat.
Angenommen, ein Modell hat 200 positive Vorhersagen getroffen. Von diesen 200 positiven Vorhersagen:
- 150 Ergebnisse waren richtig positiv.
- 50 davon waren Fehlalarme.
In diesem Fall gilt:
Genauigkeit und Trefferquote im Vergleich.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Klassifizierung: Genauigkeit, Trefferquote, Präzision und zugehörige Messwerte.
Vorhersage-
Die Ausgabe eines Modells. Beispiel:
- Die Vorhersage eines binären Klassifizierungsmodells ist entweder die positive oder die negative Klasse.
- Die Vorhersage eines Klassifizierungsmodells mit mehreren Klassen ist eine Klasse.
- Die Vorhersage eines linearen Regressionsmodells ist eine Zahl.
Proxy-Labels
Daten, mit denen Labels angenähert werden, die in einem Dataset nicht direkt verfügbar sind.
Angenommen, Sie müssen ein Modell trainieren, um den Stresspegel von Mitarbeitern vorherzusagen. Ihr Dataset enthält viele Vorhersagefunktionen, aber kein Label mit dem Namen Stressniveau. Sie lassen sich nicht entmutigen und wählen „Arbeitsunfälle“ als Proxy-Label für das Stressniveau aus. Denn Mitarbeiter, die unter hohem Stress stehen, haben mehr Unfälle als entspannte Mitarbeiter. Oder doch? Vielleicht steigen und sinken Arbeitsunfälle aus mehreren Gründen.
Nehmen wir als zweites Beispiel an, Sie möchten, dass Regnet es? ein boolesches Label für Ihren Datensatz ist, Ihr Datensatz aber keine Regendaten enthält. Wenn Fotos verfügbar sind, können Sie Bilder von Personen mit Regenschirmen als Proxy-Label für Regnet es? verwenden. Ist das ein guter Proxy-Label? Möglicherweise, aber Menschen in einigen Kulturen verwenden Regenschirme eher zum Schutz vor der Sonne als vor Regen.
Proxy-Labels sind oft unvollkommen. Wählen Sie nach Möglichkeit tatsächliche Labels anstelle von Proxy-Labels aus. Wenn kein tatsächliches Label vorhanden ist, wählen Sie das Proxy-Label sehr sorgfältig aus und entscheiden Sie sich für das am wenigsten schlechte Proxy-Label.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Datasets: Labels.
R
RAG
Abkürzung für Retrieval-Augmented Generation.
Bewerter
Eine Person, die Labels für Beispiele bereitstellt. „Annotator“ ist eine andere Bezeichnung für „Rater“.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Kategorische Daten: Häufige Probleme.
Rückruf
Ein Messwert für Klassifizierungsmodelle, der die folgende Frage beantwortet:
Wenn die Ground Truth die positive Klasse war, bei wie viel Prozent der Vorhersagen hat das Modell die positive Klasse richtig erkannt?
Hier ist die Formel:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
Dabei gilt:
- „Richtig positiv“ bedeutet, dass das Modell die positive Klasse richtig vorhergesagt hat.
- „Falsch negativ“ bedeutet, dass das Modell fälschlicherweise die negative Klasse vorhergesagt hat.
Angenommen, Ihr Modell hat 200 Vorhersagen für Beispiele getroffen, für die die Grundwahrheit die positive Klasse war. Von diesen 200 Vorhersagen:
- 180 Ergebnisse waren richtig positiv.
- 20 Ergebnisse waren falsch negativ.
In diesem Fall gilt:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
Rektifizierte lineare Einheit (ReLU)
Eine Aktivierungsfunktion mit dem folgenden Verhalten:
- Wenn die Eingabe negativ oder null ist, ist die Ausgabe 0.
- Wenn die Eingabe positiv ist, entspricht die Ausgabe der Eingabe.
Beispiel:
- Wenn die Eingabe -3 ist, ist die Ausgabe 0.
- Wenn die Eingabe +3 ist, ist die Ausgabe 3,0.
Hier ist ein Diagramm von ReLU:
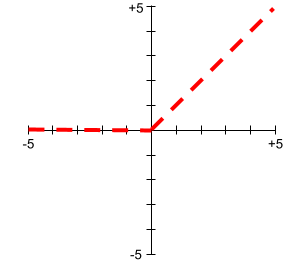
ReLU ist eine sehr beliebte Aktivierungsfunktion. Trotz ihres einfachen Verhaltens ermöglicht ReLU einem neuronalen Netzwerk, nichtlineare Beziehungen zwischen Features und dem Label zu lernen.
Regressionsmodell
Ein Modell, das eine numerische Vorhersage generiert. Im Gegensatz dazu wird bei einem Klassifizierungsmodell eine Vorhersage für die Klasse generiert. Beispiele für Regressionsmodelle:
- Ein Modell, das den Wert eines bestimmten Hauses in Euro vorhersagt,z. B. 423.000 €.
- Ein Modell, das die Lebenserwartung eines bestimmten Baums in Jahren vorhersagt, z. B. 23,2.
- Ein Modell, das die Menge an Regen in Zoll vorhersagt, die in den nächsten sechs Stunden in einer bestimmten Stadt fallen wird, z. B. 0,18.
Zwei gängige Arten von Regressionsmodellen sind:
- Lineare Regression: Hier wird die Linie ermittelt, die am besten zu den Labelwerten und Features passt.
- Logistische Regression: Hier wird eine Wahrscheinlichkeit zwischen 0,0 und 1,0 generiert, die von einem System in der Regel einer Klassenprognose zugeordnet wird.
Nicht jedes Modell, das numerische Vorhersagen ausgibt, ist ein Regressionsmodell. In einigen Fällen ist eine numerische Vorhersage eigentlich nur ein Klassifizierungsmodell mit numerischen Klassennamen. Ein Modell, mit dem eine numerische Postleitzahl vorhergesagt wird, ist beispielsweise ein Klassifikationsmodell und kein Regressionsmodell.
Regularisierung
Jeder Mechanismus, der Overfitting reduziert. Beliebte Arten der Regularisierung sind:
- L1-Regularisierung
- L2-Regularisierung
- Dropout-Regularisierung
- Vorzeitiger Stopp: Dies ist keine formale Regularisierungsmethode, kann aber eine Überanpassung effektiv einschränken.
Regularisierung kann auch als die Strafe für die Komplexität eines Modells definiert werden.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Overfitting: Model complexity.
Regularisierungsrate
Eine Zahl, die die relative Wichtigkeit der Regularisierung während des Trainings angibt. Wenn Sie die Regularisierungsrate erhöhen, wird die Überanpassung reduziert, die Vorhersagekraft des Modells kann jedoch abnehmen. Wenn Sie die Regularisierungsrate verringern oder weglassen, steigt das Risiko von Overfitting.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Overfitting: L2 regularization.
ReLU
Abkürzung für Rectified Linear Unit (rektifizierte Lineareinheit).
Retrieval-Augmented Generation (RAG)
Eine Technik zur Verbesserung der Qualität der Ausgabe von Large Language Models (LLMs) durch die Fundierung mit Wissensquellen, die nach dem Training des Modells abgerufen werden. RAG verbessert die Genauigkeit von LLM-Antworten, indem das trainierte LLM Zugriff auf Informationen erhält, die aus vertrauenswürdigen Wissensdatenbanken oder Dokumenten abgerufen werden.
Häufige Gründe für die Verwendung von Retrieval-Augmented Generation sind:
- Die faktische Richtigkeit der vom Modell generierten Antworten erhöhen.
- Dem Modell Zugriff auf Wissen geben, mit dem es nicht trainiert wurde.
- Das Wissen ändern, das das Modell verwendet.
- Das Modell kann Quellen zitieren.
Angenommen, eine Chemie-App verwendet die PaLM API, um Zusammenfassungen zu Nutzeranfragen zu generieren. Wenn das Backend der App eine Anfrage empfängt, passiert Folgendes:
- Sucht nach Daten, die für die Anfrage des Nutzers relevant sind, und ruft sie ab.
- Hängt die relevanten Chemie-Daten an die Nutzeranfrage an („erweitert“).
- Weist das LLM an, eine Zusammenfassung auf Grundlage der angehängten Daten zu erstellen.
ROC-Kurve (Receiver Operating Characteristic)
Ein Diagramm der Richtig-Positiv-Rate im Vergleich zur Falsch-Positiv-Rate für verschiedene Klassifizierungsschwellenwerte bei der binären Klassifizierung.
Die Form einer ROC-Kurve gibt Aufschluss darüber, wie gut ein binäres Klassifikationsmodell positive von negativen Klassen trennen kann. Angenommen, ein binäres Klassifizierungsmodell trennt alle negativen Klassen perfekt von allen positiven Klassen:
Die ROC-Kurve für das vorherige Modell sieht so aus:
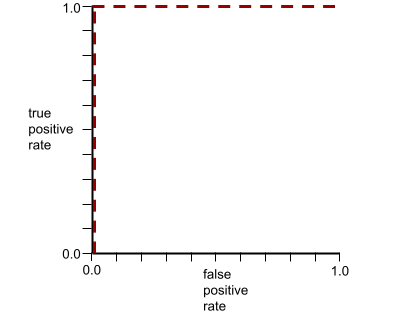
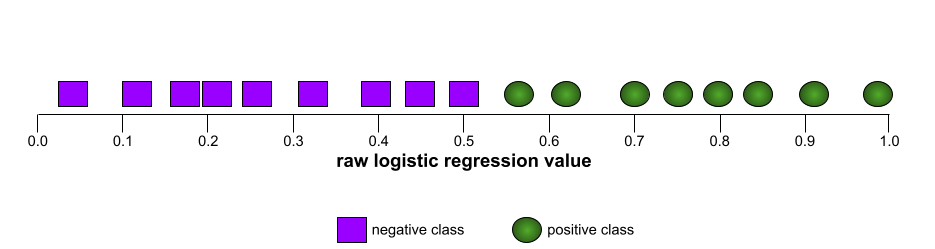
Im Gegensatz dazu zeigt die folgende Abbildung die Rohwerte der logistischen Regression für ein schlechtes Modell, das negative Klassen überhaupt nicht von positiven Klassen trennen kann:
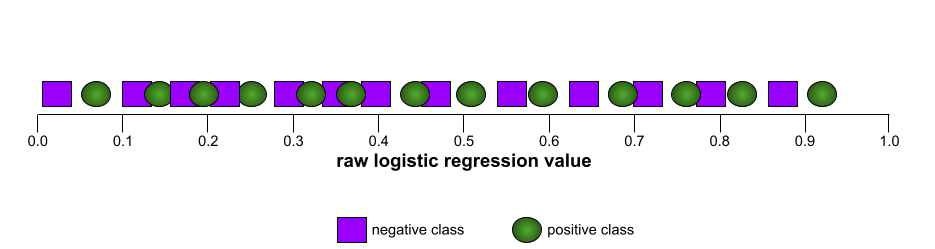
Die ROC-Kurve für dieses Modell sieht so aus:
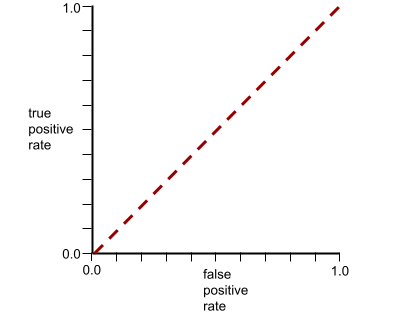
In der realen Welt trennen die meisten binären Klassifizierungsmodelle positive und negative Klassen bis zu einem gewissen Grad, aber in der Regel nicht perfekt. Eine typische ROC-Kurve liegt also irgendwo zwischen den beiden Extremen:
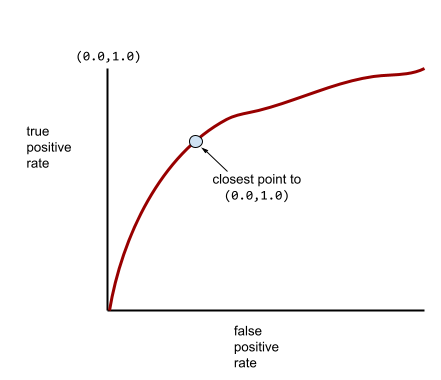
Der Punkt auf einer ROC-Kurve, der theoretisch am nächsten an (0,0,1,0) liegt, gibt den idealen Klassifizierungsschwellenwert an. Die Auswahl des idealen Klassifizierungsschwellenwerts wird jedoch von mehreren anderen realen Problemen beeinflusst. Falsch negative Ergebnisse verursachen beispielsweise möglicherweise viel mehr Probleme als falsch positive Ergebnisse.
Ein numerischer Messwert namens AUC fasst die ROC-Kurve in einem einzelnen Gleitkommawert zusammen.
Wurzel der mittleren Fehlerquadratsumme (RMSE)
Die Quadratwurzel der mittleren quadratischen Abweichung.
S
Sigmoidfunktion
Eine mathematische Funktion, die einen Eingabewert in einen eingeschränkten Bereich „quetscht“, in der Regel 0 bis 1 oder -1 bis +1. Das heißt, Sie können eine beliebige Zahl (2, eine Million, eine negative Milliarde usw.) an eine Sigmoidfunktion übergeben und die Ausgabe liegt trotzdem im eingeschränkten Bereich. Ein Diagramm der Sigmoid-Aktivierungsfunktion sieht so aus:

Die Sigmoid-Funktion hat im Bereich des maschinellen Lernens mehrere Anwendungsbereiche, darunter:
- Umwandlung der Rohausgabe eines logistischen Regressionsmodells oder multinomialen Regressionsmodells in eine Wahrscheinlichkeit.
- Als Aktivierungsfunktion in einigen neuronalen Netzwerken.
Softmax-Funktion
Eine Funktion, die Wahrscheinlichkeiten für jede mögliche Klasse in einem Klassifizierungsmodell mit mehreren Klassen bestimmt. Die Wahrscheinlichkeiten ergeben zusammen genau 1,0. In der folgenden Tabelle sehen Sie ein Beispiel dafür, wie mit der Softmax-Funktion verschiedene Wahrscheinlichkeiten verteilt werden:
| Das Bild ist ein… | Probability |
|---|---|
| Hund | 0,85 |
| Katze | .13 |
| Pferd | .02 |
Softmax wird auch als Full Softmax bezeichnet.
Im Gegensatz dazu steht das Auswählen von Kandidaten.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Neuronale Netze: Multiklassenklassifizierung.
dünnbesetztes Feature
Ein Attribut, dessen Werte überwiegend null oder leer sind. Ein Feature, das einen einzelnen Wert von 1 und eine Million Werte von 0 enthält, ist beispielsweise spärlich. Im Gegensatz dazu hat ein dichtes Feature Werte, die überwiegend nicht null oder leer sind.
Beim maschinellen Lernen ist eine überraschend große Anzahl von Features spärlich. Kategoriale Merkmale sind in der Regel spärliche Merkmale. Von den 300 möglichen Baumarten in einem Wald kann ein einzelnes Beispiel beispielsweise nur einen Ahornbaum identifizieren. Oder von den Millionen möglicher Videos in einer Videobibliothek könnte ein einzelnes Beispiel nur „Casablanca“ identifizieren.
In einem Modell werden spärliche Merkmale in der Regel mit One-Hot-Codierung dargestellt. Wenn die One-Hot-Codierung groß ist, können Sie für mehr Effizienz eine Einbettungsebene über die One-Hot-Codierung legen.
dünnbesetzte Darstellung
Es werden nur die Positionen von Elementen ungleich null in einem spärlichen Feature gespeichert.
Angenommen, ein kategoriales Feature namens species identifiziert die 36 Baumarten in einem bestimmten Wald. Nehmen Sie außerdem an, dass jedes Beispiel nur eine einzelne Art identifiziert.
Sie könnten einen One-Hot-Vektor verwenden, um die Baumart in jedem Beispiel darzustellen.
Ein One-Hot-Vektor würde eine einzelne 1 (zur Darstellung der jeweiligen Baumart in diesem Beispiel) und 35 0 (zur Darstellung der 35 Baumarten, die nicht in diesem Beispiel enthalten sind) enthalten. Die One-Hot-Darstellung von maple könnte also so aussehen:

Alternativ würde die spärliche Darstellung einfach die Position der jeweiligen Art angeben. Wenn maple an Position 24 steht, wäre die spärliche Darstellung von maple einfach:
24
Die dünnbesetzte Darstellung ist viel kompakter als die One-Hot-Darstellung.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Mit kategorischen Daten arbeiten.
dünnbesetzter Vektor
Ein Vektor, dessen Werte größtenteils Nullen sind. Siehe auch Sparsamer Feature und Sparsity.
Quadratischer Verlust
Synonym für L2-Verlust.
Statisch
Etwas, das einmalig statt kontinuierlich erledigt wird. Die Begriffe statisch und offline sind Synonyme. Im Folgenden finden Sie einige gängige Anwendungsfälle für statisch und offline im Bereich des maschinellen Lernens:
- Ein statisches Modell (oder Offline-Modell) wird einmal trainiert und dann für eine Weile verwendet.
- Statisches Training (oder Offlinetraining) ist der Prozess des Trainings eines statischen Modells.
- Statische Inferenzen (oder Offline-Inferenzen) sind ein Prozess, bei dem ein Modell jeweils einen Batch von Vorhersagen generiert.
Im Gegensatz dazu steht dynamisch.
Statische Inferenz
Synonym für Offlineinferenz.
Stationarität
Ein Feature, dessen Werte sich über eine oder mehrere Dimensionen hinweg nicht ändern, in der Regel über die Zeit. Ein Feature, dessen Werte 2021 und 2023 ungefähr gleich sind, weist beispielsweise Stationarität auf.
In der Praxis weisen nur sehr wenige Merkmale Stationarität auf. Selbst Merkmale, die für Stabilität stehen (z. B. der Meeresspiegel), ändern sich im Laufe der Zeit.
Im Gegensatz dazu steht die Nicht-Stationarität.
Stochastic Gradient Descent (SGD)
Ein Gradientenabstieg-Algorithmus, bei dem die Batchgröße 1 ist. Mit anderen Worten: SGD wird anhand eines einzelnen Beispiels trainiert, das gleichmäßig zufällig aus einem Trainingsset ausgewählt wird.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Hyperparameter.
überwachtes maschinelles Lernen
Training eines Modells anhand von Features und den entsprechenden Labels. Überwachtes maschinelles Lernen ist vergleichbar mit dem Erlernen eines Themas durch das Bearbeiten einer Reihe von Fragen und der entsprechenden Antworten. Nachdem ein Schüler/Student die Zuordnung zwischen Fragen und Antworten beherrscht, kann er Antworten auf neue (noch nie gesehene) Fragen zum selben Thema geben.
Unüberwachtes maschinelles Lernen
Weitere Informationen finden Sie im Kurs „Einführung in ML“ unter Supervised Learning.
synthetisches Feature
Ein Feature, das nicht zu den Eingabe-Features gehört, sondern aus einem oder mehreren von ihnen zusammengestellt wird. Es gibt verschiedene Methoden zum Erstellen synthetischer Features, darunter:
- Kontinuierliches Feature in Bereichs-Bins aufteilen:
- Feature Cross erstellen
- Multiplikation (oder Division) eines Featurewerts mit anderen Featurewerten oder mit sich selbst. Wenn
aundbbeispielsweise Eingabefeatures sind, sind die folgenden Beispiele für synthetische Features:- ab
- a2
- Anwenden einer transzendenten Funktion auf einen Attributwert. Wenn
cbeispielsweise ein Eingabe-Feature ist, sind die folgenden Beispiele für synthetische Features:- sin(c)
- ln(c)
Funktionen, die nur durch Normalisieren oder Skalieren erstellt werden, gelten nicht als synthetische Funktionen.
T
Testverlust
Ein Messwert, der den Verlust eines Modells im Vergleich zum Test-Dataset darstellt. Beim Erstellen eines Modells versuchen Sie in der Regel, den Testverlust zu minimieren. Das liegt daran, dass ein geringer Testverlust ein stärkeres Qualitätssignal ist als ein geringer Trainingsverlust oder ein geringer Validierungsverlust.
Eine große Lücke zwischen Testverlust und Trainings- oder Validierungsverlust deutet manchmal darauf hin, dass Sie die Regularisierungsrate erhöhen müssen.
Training
Der Prozess, bei dem die idealen Parameter (Gewichtungen und Bias) eines Modells ermittelt werden. Während des Trainings liest ein System Beispiele ein und passt die Parameter nach und nach an. Beim Training wird jedes Beispiel einige Male bis hin zu Milliarden Mal verwendet.
Weitere Informationen finden Sie im Kurs „Einführung in ML“ unter Supervised Learning.
Trainingsverlust
Ein Messwert, der den Verlust eines Modells während eines bestimmten Trainingsdurchlaufs darstellt. Angenommen, die Verlustfunktion ist Mean Squared Error. Vielleicht beträgt der Trainingsverlust (der mittlere quadratische Fehler) für die 10.Iteration 2,2 und der Trainingsverlust für die 100.Iteration 1,9.
In einer Verlustkurve wird der Trainingsverlust im Verhältnis zur Anzahl der Iterationen dargestellt. Eine Verlustkurve kann folgende Hinweise zum Training geben:
- Ein abwärts gerichteter Verlauf deutet darauf hin, dass sich das Modell verbessert.
- Ein Aufwärtstrend bedeutet, dass das Modell schlechter wird.
- Eine flache Steigung bedeutet, dass das Modell konvergiert ist.
Das folgende etwas idealisierte Verlustkurvenbeispiel zeigt:
- Ein steiler Abwärtstrend in den ersten Iterationen, der auf eine schnelle Verbesserung des Modells hindeutet.
- Ein allmählich abflachender (aber immer noch abwärts gerichteter) Verlauf bis kurz vor dem Ende des Trainings, was auf eine kontinuierliche Verbesserung des Modells hinweist, wenn auch etwas langsamer als in den ersten Iterationen.
- Ein flacher Abfall gegen Ende des Trainings, der auf Konvergenz hindeutet.
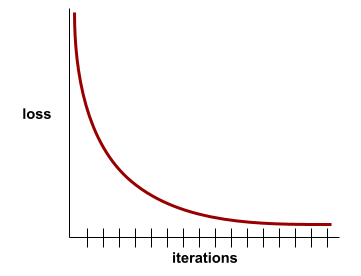
Der Trainingsverlust ist zwar wichtig, aber sehen Sie sich auch die Generalisierung an.
Abweichungen zwischen Training und Bereitstellung
Der Unterschied zwischen der Leistung eines Modells während des Trainings und der Leistung desselben Modells während der Bereitstellung.
Trainings-Dataset
Die Teilmenge des Datasets, die zum Trainieren eines Modells verwendet wird.
Traditionell werden Beispiele im Dataset in die folgenden drei unterschiedlichen Teilmengen unterteilt:
- ein Trainings-Dataset
- ein Validierungs-Dataset
- ein Test-Dataset
Idealerweise sollte jedes Beispiel im Dataset nur zu einer der oben genannten Teilmengen gehören. Ein einzelnes Beispiel sollte beispielsweise nicht sowohl zum Trainings- als auch zum Validierungs-Dataset gehören.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Datasets: Dividing the original dataset.
richtig negativ (RN)
Ein Beispiel, in dem das Modell die negative Klasse richtig vorhersagt. Das Modell leitet beispielsweise ab, dass eine bestimmte E‑Mail-Nachricht kein Spam ist, und diese E‑Mail-Nachricht ist tatsächlich kein Spam.
Richtig positiv (TP)
Ein Beispiel, in dem das Modell die positive Klasse richtig vorhersagt. Das Modell leitet beispielsweise ab, dass eine bestimmte E‑Mail-Nachricht Spam ist, und diese E‑Mail-Nachricht ist tatsächlich Spam.
Rate richtig positiver Ergebnisse (True Positive Rate, TPR)
Synonym für Rückruf. Das bedeutet:
Die Rate richtig positiver Ergebnisse ist die Y-Achse in einer ROC-Kurve.
U
Unteranpassung
Ein Modell mit schlechter Vorhersagefähigkeit erstellen, weil das Modell die Komplexität der Trainingsdaten nicht vollständig erfasst hat. Unteranpassung kann viele Ursachen haben, darunter:
- Das Training basiert auf den falschen Funktionen.
- Das Training wurde für zu wenige Epochen oder mit einer zu niedrigen Lernrate durchgeführt.
- Training mit einer zu hohen Regularisierungsrate.
- Zu wenige versteckte Ebenen in einem tiefen neuronalen Netzwerk.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Overfitting.
Beispiel ohne Label
Ein Beispiel, das Merkmale, aber kein Label enthält. In der folgenden Tabelle sind beispielsweise drei nicht gelabelte Beispiele aus einem Modell zur Hausbewertung aufgeführt, die jeweils drei Features, aber keinen Hauswert enthalten:
| Anzahl der Schlafzimmer | Anzahl der Badezimmer | Alter des Hauses |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
Beim überwachten maschinellen Lernen> werden Modelle mit gelabelten Beispielen trainiert und Vorhersagen für nicht gelabelte Beispiele getroffen.
Beim halbüberwachten und unbeaufsichtigten Lernen werden während des Trainings Beispiele ohne Labels verwendet.
Stellen Sie ein Beispiel ohne Label einem Beispiel mit Label gegenüber.
unüberwachtes maschinelles Lernen
Ein Modell wird trainiert, um Muster in einem Dataset zu finden, in der Regel einem Dataset ohne Labels.
Die häufigste Anwendung von unbeaufsichtigtem maschinellem Lernen ist das Clustern von Daten in Gruppen ähnlicher Beispiele. Beispielsweise kann ein unbeaufsichtigter Algorithmus für maschinelles Lernen Songs anhand verschiedener Eigenschaften der Musik gruppieren. Die resultierenden Cluster können als Eingabe für andere Machine-Learning-Algorithmen dienen, z. B. für einen Musikempfehlungsdienst. Clustering kann hilfreich sein, wenn nützliche Labels nur in geringer Anzahl oder gar nicht vorhanden sind. In Bereichen wie Missbrauch und Betrug können Cluster beispielsweise dazu beitragen, dass Menschen die Daten besser verstehen.
Überwachtes maschinelles Lernen
Weitere Informationen finden Sie im Kurs „Einführung in ML“ unter Was ist maschinelles Lernen?.
V
Validierung
Die erste Bewertung der Qualität eines Modells. Bei der Validierung wird die Qualität der Vorhersagen eines Modells anhand des Validierungssets überprüft.
Da sich das Validierungs-Dataset vom Trainings-Dataset unterscheidet, kann durch die Validierung Überanpassung vermieden werden.
Die Bewertung des Modells anhand des Validierungssets kann als erste Testrunde betrachtet werden, die Bewertung des Modells anhand des Testsets als zweite Testrunde.
Validierungsverlust
Eine Messwert, die den Verlust eines Modells im Validierungs-Dataset während eines bestimmten Trainingsdurchlaufs darstellt.
Siehe auch Verallgemeinerungskurve.
Validierungs-Dataset
Die Teilmenge des Datasets, mit der eine erste Bewertung eines trainierten Modells durchgeführt wird. Normalerweise wird das trainierte Modell mehrmals anhand des Validierungssets bewertet, bevor es anhand des Testsets bewertet wird.
Normalerweise werden die Beispiele im Dataset in die folgenden drei unterschiedlichen Teilmengen unterteilt:
- ein Trainings-Dataset
- ein Validierungs-Dataset
- ein Test-Dataset
Idealerweise sollte jedes Beispiel im Dataset nur zu einer der oben genannten Teilmengen gehören. Ein einzelnes Beispiel sollte beispielsweise nicht sowohl zum Trainings- als auch zum Validierungs-Dataset gehören.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Datasets: Dividing the original dataset.
W
Gewicht
Ein Wert, der von einem Modell mit einem anderen Wert multipliziert wird. Training ist der Prozess, bei dem die idealen Gewichte eines Modells bestimmt werden. Bei der Inferenz werden diese gelernten Gewichte verwendet, um Vorhersagen zu treffen.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression.
gewichtete Summe
Die Summe aller relevanten Eingabewerte multipliziert mit ihren entsprechenden Gewichten. Angenommen, die relevanten Eingaben bestehen aus Folgendem:
| Eingabewert | Gewichtung der Eingabe |
| 2 | –1,3 |
| -1 | 0,6 |
| 3 | 0,4 |
Die gewichtete Summe ist also:
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
Eine gewichtete Summe ist das Eingabeargument für eine Aktivierungsfunktion.
Z
Z-Score-Normalisierung
Eine Skalierungsmethode, bei der ein roher Feature-Wert durch einen Gleitkommawert ersetzt wird, der die Anzahl der Standardabweichungen vom Mittelwert dieses Features darstellt. Nehmen wir als Beispiel ein Feature mit einem Mittelwert von 800 und einer Standardabweichung von 100. In der folgenden Tabelle sehen Sie, wie der Rohwert durch die Z-Score-Normalisierung dem Z-Score zugeordnet wird:
| Unverarbeiteter Wert | Z-Transformation |
|---|---|
| 800 | 0 |
| 950 | +1,5 |
| 575 | -2,25 |
Das Machine-Learning-Modell wird dann anhand der Z-Werte für dieses Merkmal und nicht anhand der Rohwerte trainiert.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Numerische Daten: Normalisierung.