Ta strona zawiera terminy z glosariusza podstaw uczenia maszynowego. Aby wyświetlić wszystkie terminy z glosariusza, kliknij tutaj.
A
dokładność
Liczba prawidłowych prognoz klasyfikacji podzielona przez łączną liczbę prognoz. Czyli:
Na przykład model, który dokonał 40 prawidłowych i 10 nieprawidłowych prognoz, ma dokładność:
Klasyfikacja binarna podaje konkretne nazwy różnych kategorii prawidłowych prognoz i nieprawidłowych prognoz. Wzór na dokładność w przypadku klasyfikacji binarnej jest taki:
gdzie:
- TP to liczba wyników prawdziwie pozytywnych (poprawnych prognoz).
- TN to liczba wyników prawdziwie negatywnych (prawidłowych prognoz).
- FP to liczba fałszywie pozytywnych wyników (nieprawidłowych prognoz).
- FN to liczba wyników fałszywie negatywnych (nieprawidłowych prognoz).
Porównaj dokładność z precyzją i czułością.
Więcej informacji znajdziesz w sekcji Klasyfikacja: dokładność, czułość, precyzja i powiązane dane w kursie Machine Learning Crash Course.
funkcja aktywacji,
Funkcja, która umożliwia sieciom neuronowym uczenie się nieliniowych (złożonych) zależności między cechami a etykietą.
Popularne funkcje aktywacji to:
Wykresy funkcji aktywacji nigdy nie są pojedynczymi liniami prostymi. Na przykład wykres funkcji aktywacji ReLU składa się z 2 linii prostych:

Wykres funkcji aktywacji sigmoid wygląda tak:

Więcej informacji znajdziesz w sekcji Sieci neuronowe: funkcje aktywacji w kursie Machine Learning Crash Course.
sztuczna inteligencja
Program lub model niebędący człowiekiem, który potrafi wykonywać złożone zadania. Na przykład program lub model, który tłumaczy tekst, albo program lub model, który identyfikuje choroby na podstawie zdjęć radiologicznych, wykazują cechy sztucznej inteligencji.
Formalnie uczenie maszynowe jest poddziedziną sztucznej inteligencji. Jednak w ostatnich latach niektóre organizacje zaczęły używać terminów sztuczna inteligencja i uczenie maszynowe zamiennie.
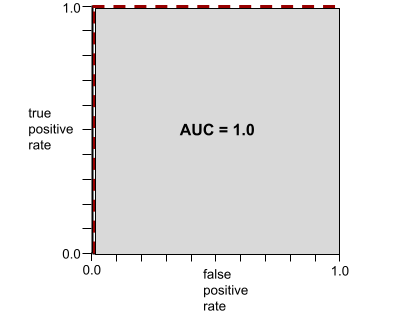
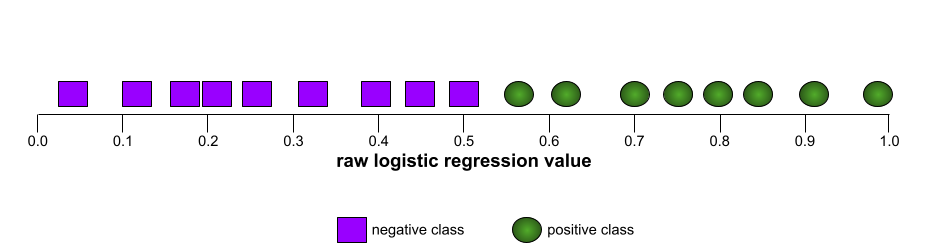
AUC (obszar pod krzywą ROC)
Liczba z zakresu od 0,0 do 1,0 reprezentująca zdolność modelu klasyfikacji binarnej do rozdzielania klas pozytywnych od klas negatywnych. Im bliżej wartości 1,0 jest AUC, tym lepiej model rozróżnia klasy.
Na przykład poniższa ilustracja przedstawia model klasyfikacji, który doskonale rozdziela klasy pozytywne (zielone owale) od klas negatywnych (fioletowe prostokąty). Ten nierealistycznie doskonały model ma wartość AUC równą 1,0:

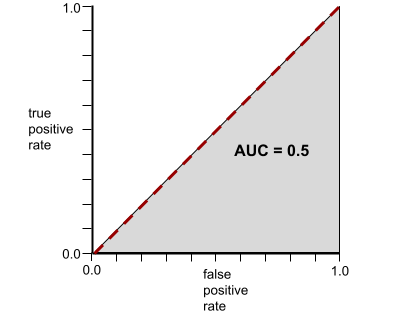
Z kolei poniższa ilustracja przedstawia wyniki modelu klasyfikacji, który generował losowe wyniki. Ten model ma wartość AUC 0,5:

Tak, poprzedni model ma wartość AUC 0,5, a nie 0,0.
Większość modeli znajduje się gdzieś pomiędzy tymi dwoma skrajnościami. Na przykład poniższy model w pewnym stopniu rozdziela wartości pozytywne od negatywnych, dlatego ma wartość AUC między 0,5 a 1,0:

AUC ignoruje każdą wartość ustawioną dla progu klasyfikacji. Zamiast tego AUC uwzględnia wszystkie możliwe progi klasyfikacji.
Więcej informacji znajdziesz w sekcji Klasyfikacja: ROC i AUC w szybkim szkoleniu z uczenia maszynowego.
B
propagacja wsteczna
Algorytm, który implementuje metodę gradientu prostego w sieciach neuronowych.
Trenowanie sieci neuronowej obejmuje wiele iteracji tego dwuetapowego cyklu:
- Podczas przejścia w przód system przetwarza partię przykładów, aby uzyskać prognozy. System porównuje każdą prognozę z wartością każdej etykiety. Różnica między prognozą a wartością etykiety to funkcja straty dla tego przykładu. System sumuje straty dla wszystkich przykładów, aby obliczyć całkowitą stratę dla bieżącej partii.
- Podczas przejścia wstecznego (propagacji wstecznej) system zmniejsza straty, dostosowując wagi wszystkich neuronów we wszystkich warstwach ukrytych.
Sieci neuronowe często zawierają wiele neuronów w wielu warstwach ukrytych. Każdy z tych neuronów przyczynia się do ogólnej utraty w inny sposób. Algorytm propagacji wstecznej określa, czy zwiększyć, czy zmniejszyć wagi przypisane do poszczególnych neuronów.
Tempo uczenia się to mnożnik, który określa stopień, w jakim każda iteracja wsteczna zwiększa lub zmniejsza każdą wagę. Duże tempo uczenia się zwiększy lub zmniejszy każdą wagę bardziej niż małe tempo uczenia się.
W terminologii rachunku różniczkowego propagacja wsteczna wykorzystuje regułę łańcuchową. Oznacza to, że propagacja wsteczna oblicza pochodną cząstkową błędu względem każdego parametru.
Jeszcze kilka lat temu specjaliści ds. uczenia maszynowego musieli pisać kod, aby wdrożyć propagację wsteczną. Nowoczesne interfejsy API ML, takie jak Keras, implementują propagację wsteczną. Uff...
Więcej informacji znajdziesz w sekcji Sieci neuronowe w Szybkim szkoleniu z uczenia maszynowego.
wsad
Zestaw przykładów używanych w jednej iteracji trenowania. Rozmiar wsadu określa liczbę przykładów w wsadzie.
Wyjaśnienie, jak partia jest powiązana z epoką, znajdziesz w tym artykule.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
wielkość wsadu
Liczba przykładów w partii. Jeśli na przykład rozmiar partii wynosi 100, model przetwarza 100 przykładów na iterację.
Oto popularne strategie dotyczące wielkości wsadu:
- Stochastyczny spadek wzdłuż gradientu (SGD), w którym rozmiar partii wynosi 1.
- Pełny wsad, w którym rozmiar wsadu jest równy liczbie przykładów w całym zbiorze treningowym. Jeśli np. zbiór treningowy zawiera milion przykładów, rozmiar partii będzie wynosić milion przykładów. Pełna partia jest zwykle nieefektywną strategią.
- mini-batch, w którym rozmiar partii wynosi zwykle od 10 do 1000. Mini-batch to zwykle najbardziej efektywna strategia.
Więcej informacji znajdziesz poniżej:
- Produkcyjne systemy uczenia maszynowego: wnioskowanie statyczne a dynamiczne w szybkim szkoleniu z uczenia maszynowego.
- Poradnik dotyczący dostrajania głębokiego uczenia
uprzedzenia (etyka/bezstronność),
1. Tworzenie stereotypów lub faworyzowanie określonych rzeczy, ludzi lub grup względem innych. Te odchylenia mogą wpływać na zbieranie i interpretowanie danych, projektowanie systemu oraz sposób, w jaki użytkownicy z nim wchodzą w interakcje. Formy tego typu błędu:
- błąd automatyzacji
- efekt potwierdzenia
- błąd eksperymentatora
- błąd uogólnienia
- nieświadome uprzedzenia
- stronniczość wewnątrzgrupowa,
- błąd jednorodności grupy obcej,
2. Błąd systematyczny wprowadzony przez procedurę próbkowania lub raportowania. Formy tego typu błędu:
- błąd pokrycia
- błąd braku odpowiedzi,
- błąd związany z udziałem
- błąd raportowania,
- błąd próbkowania
- błąd doboru
Nie należy go mylić z terminem „uprzedzenie” w modelach uczenia maszynowego ani z uprzedzeniem w prognozach.
Więcej informacji znajdziesz w sekcji Sprawiedliwość: rodzaje odchyleń w kursie Machine Learning Crash Course.
wyraz wolny (matematyka) lub wyraz wolny
Punkt przecięcia lub przesunięcie względem punktu początkowego. Uprzedzenie to parametr w modelach uczenia maszynowego, który jest oznaczany jednym z tych symboli:
- b
- w0
Na przykład w tej formule wyraz b oznacza odchylenie:
W przypadku prostej dwuwymiarowej odchylenie oznacza po prostu „punkt przecięcia z osią Y”. Na przykład odchylenie prostej na poniższej ilustracji wynosi 2.
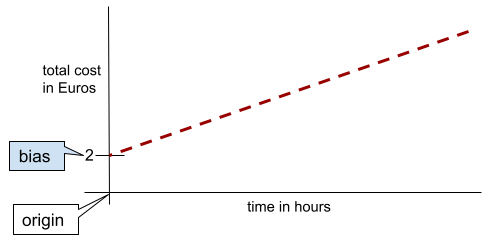
Występuje odchylenie, ponieważ nie wszystkie modele zaczynają się od punktu początkowego (0,0). Załóżmy na przykład, że wejście do parku rozrywki kosztuje 2 PLN, a każda dodatkowa godzina pobytu klienta to 0,5 PLN. Dlatego model mapujący koszt całkowity ma odchylenie równe 2, ponieważ najniższy koszt to 2 euro.
Uprzedzeń nie należy mylić z uprzedzeniami w kontekście etyki i obiektywności ani z uprzedzeniami w prognozach.
Więcej informacji znajdziesz w sekcji Regresja liniowa w szybkim szkoleniu z uczenia maszynowego.
klasyfikacja binarna,
Typ zadania klasyfikacji, które przewiduje jedną z 2 wzajemnie wykluczających się klas:
Na przykład te 2 modele uczenia maszynowego wykonują klasyfikację binarną:
- Model, który określa, czy wiadomości e-mail to spam (klasa pozytywna) czy nie spam (klasa negatywna).
- Model, który ocenia objawy medyczne, aby określić, czy dana osoba ma konkretną chorobę (klasa pozytywna), czy nie (klasa negatywna).
Porównaj z klasyfikacją wieloklasową.
Zobacz też regresję logistyczną i próg klasyfikacji.
Więcej informacji znajdziesz w sekcji Klasyfikacja w Szybkim szkoleniu z uczenia maszynowego.
skategoryzowanie w przedziałach
Przekształcanie pojedynczej cechy w wiele cech binarnych, zwanych zasobnikami lub przedziałami, zwykle na podstawie zakresu wartości. Przycięta cecha jest zwykle cechą ciągłą.
Na przykład zamiast przedstawiać temperaturę jako pojedynczą ciągłą cechę zmiennoprzecinkową, możesz podzielić zakresy temperatur na odrębne przedziały, takie jak:
- „Zimno” to temperatura ≤ 10°C.
- Przedział „umiarkowany” to 11–24 stopnie Celsjusza.
- „Ciepło” to temperatura ≥ 25°C.
Model będzie traktować każdą wartość w tym samym przedziale identycznie. Na przykład wartości 13 i 22 należą do tego samego przedziału klimatu umiarkowanego, więc model traktuje je identycznie.
Więcej informacji znajdziesz w sekcji Dane liczbowe: dzielenie na przedziały w szybkim szkoleniu z systemów uczących się.
C
dane kategorialne,
Cechy mające określony zestaw możliwych wartości. Rozważmy na przykład cechę kategorialną o nazwie traffic-light-state, która może przyjmować tylko jedną z tych 3 wartości:
redyellowgreen
Przedstawiając traffic-light-state jako cechę kategorialną, model może się nauczyć różnych wpływów red, green i yellow na zachowanie kierowcy.
Funkcje kategorialne są czasami nazywane funkcjami dyskretnymi.
Kontrast z danymi liczbowymi.
Więcej informacji znajdziesz w sekcji Praca z danymi kategorialnymi w kursie Machine Learning Crash Course.
klasa
Kategoria, do której może należeć etykieta. Na przykład:
- W modelu klasyfikacji binarnej, który wykrywa spam, 2 klasy mogą być oznaczone jako spam i nie spam.
- W modelu klasyfikacji wieloklasowej, który identyfikuje rasy psów, klasy mogą być pudel, beagle, mops itp.
Model klasyfikacji prognozuje klasę. Z kolei model regresji prognozuje liczbę, a nie klasę.
Więcej informacji znajdziesz w sekcji Klasyfikacja w Szybkim szkoleniu z uczenia maszynowego.
model klasyfikacji,
Model, którego prognozą jest klasa. Na przykład modelami klasyfikacji są:
- Model, który przewiduje język zdania wejściowego (francuski? hiszpański? włoski?).
- Model, który przewiduje gatunek drzewa (klon? Dąb? Baobab?).
- Model, który prognozuje klasę pozytywną lub negatywną dla określonego stanu zdrowia.
Modele regresji przewidują liczby, a nie klasy.
Dwa popularne rodzaje modeli klasyfikacji to:
próg klasyfikacji
W klasyfikacji binarnej liczba z zakresu od 0 do 1, która przekształca surowe dane wyjściowe modelu regresji logistycznej w prognozę klasy pozytywnej lub klasy negatywnej. Pamiętaj, że próg klasyfikacji to wartość wybierana przez człowieka, a nie wartość wybierana podczas trenowania modelu.
Model regresji logistycznej zwraca wartość surową z zakresu od 0 do 1. Następnie:
- Jeśli ta wartość surowa jest większa od progu klasyfikacji, prognozowana jest klasa pozytywna.
- Jeśli ta wartość surowa jest mniejsza od progu klasyfikacji, przewidywana jest klasa negatywna.
Załóżmy na przykład, że próg klasyfikacji wynosi 0,8. Jeśli wartość surowa wynosi 0,9, model prognozuje klasę pozytywną. Jeśli wartość surowa wynosi 0,7, model prognozuje klasę negatywną.
Wybór progu klasyfikacji ma duży wpływ na liczbę wyników fałszywie pozytywnych i wyników fałszywie negatywnych.
Więcej informacji znajdziesz w sekcji Progi i macierz pomyłek w szybkim szkoleniu z uczenia maszynowego.
klasyfikator
Potoczne określenie modelu klasyfikacji.
zbiór danych z nierównomiernym rozkładem klas,
Zbiór danych do klasyfikacji, w którym łączna liczba etykiet każdej klasy znacznie się różni. Rozważmy na przykład zbiór danych klasyfikacji binarnej, którego 2 etykiety są podzielone w ten sposób:
- 1 000 000 etykiet wartości ujemnych
- 10 etykiet wartości dodatnich
Stosunek etykiet negatywnych do pozytywnych wynosi 100 tys. do 1, więc jest to zbiór danych z nierównowagą klas.
Natomiast ten zbiór danych jest zrównoważony pod względem klas, ponieważ stosunek etykiet negatywnych do pozytywnych jest stosunkowo bliski 1:
- 517 etykiet wartości ujemnych
- 483 etykiety wartości dodatnich
Zbiory danych z wieloma klasami mogą też być niezrównoważone pod względem klas. Na przykład ten wieloklasowy zbiór danych do klasyfikacji jest również niezrównoważony, ponieważ jedna etykieta ma znacznie więcej przykładów niż pozostałe dwie:
- 1 000 000 etykiet z klasą „zielony”
- 200 etykiet z klasą „fioletowy”
- 350 etykiet z klasą „pomarańczowy”
Trenowanie zbiorów danych z nierównomiernym rozkładem klas może być szczególnie trudne. Więcej informacji znajdziesz w sekcji Niezrównoważone zbiory danych w kursie Machine Learning Crash Course.
Zobacz też entropię, klasę większościową i klasę mniejszościową.
obcinanie,
Technika radzenia sobie z wartościami odstającymi, która polega na wykonaniu jednej lub obu tych czynności:
- Zmniejszanie wartości cechy, które są większe niż maksymalny próg, do tego progu.
- Zwiększanie wartości cech, które są mniejsze niż próg minimalny, do tego progu.
Załóżmy na przykład, że <0,5% wartości dla danej cechy wypada poza zakresem 40–60. W takim przypadku możesz wykonać te czynności:
- Wszystkie wartości powyżej 60 (maksymalnego progu) zostaną przycięte do 60.
- Wszystkie wartości poniżej 40 (minimalnego progu) zostaną zaokrąglone do 40.
Wartości odstające mogą uszkodzić modele, czasami powodując przepełnienie wag podczas trenowania. Niektóre wartości odstające mogą też znacznie zaniżać wskaźniki takie jak dokładność. Ograniczanie jest powszechną techniką ograniczania szkód.
Obcinanie gradientu wymusza podczas trenowania wartości gradientu w wyznaczonym zakresie.
Więcej informacji znajdziesz w sekcji Dane liczbowe: normalizacja w kursie Machine Learning Crash Course.
tablica pomyłek,
Tabela N×N, która podsumowuje liczbę prawidłowych i nieprawidłowych prognoz dokonanych przez model klasyfikacji. Rozważmy na przykład tę tablicę pomyłek dla modelu klasyfikacji binarnej:
| Guz (prognozowany) | Non-Tumor (predicted) | |
|---|---|---|
| Guz (dane podstawowe) | 18 (TP) | 1 (FN) |
| Brak nowotworu (dane podstawowe) | 6 (FP) | 452 (TN) |
Z powyższej tablicy pomyłek wynika, że:
- Spośród 19 prognoz, w których dane podstawowe wskazywały na nowotwór, model prawidłowo sklasyfikował 18 przypadków, a nieprawidłowo – 1.
- Spośród 458 prognoz, w których dane podstawowe (ground truth) wskazywały na brak guza, model prawidłowo sklasyfikował 452 prognozy, a nieprawidłowo – 6.
Tablica pomyłek w przypadku problemu z klasyfikacją wieloklasową może pomóc w wykrywaniu wzorców błędów. Rozważmy na przykład tę macierz pomyłek dla modelu klasyfikacji wieloklasowej, który klasyfikuje 3 różne rodzaje irysów (Virginica, Versicolor i Setosa). Gdy danymi podstawowymi była odmiana Virginica, tablica pomyłek pokazuje, że model znacznie częściej błędnie przewidywał odmianę Versicolor niż Setosa:
| Setosa (przewidywany) | Versicolor (prognozowane) | Virginica (przewidywane) | |
|---|---|---|---|
| Setosa (dane podstawowe) | 88 | 12 | 0 |
| Versicolor (dane podstawowe) | 6 | 141 | 7 |
| Virginica (dane podstawowe) | 2 | 27 | 109 |
Innym przykładem może być macierz pomyłek, która pokazuje, że model wytrenowany do rozpoznawania odręcznych cyfr ma tendencję do błędnego przewidywania cyfry 9 zamiast 4 lub cyfry 1 zamiast 7.
Macierze pomyłek zawierają wystarczająco dużo informacji, aby obliczyć różne wskaźniki skuteczności, w tym precyzję i czułość.
cecha ciągła,
Cechy zmiennoprzecinkowe z nieskończonym zakresem możliwych wartości, np. temperatura lub waga.
Kontrast z funkcją dyskretną.
zbieżność
Stan osiągany, gdy wartości funkcji straty zmieniają się bardzo nieznacznie lub wcale z każdą iteracją. Na przykład ta krzywa strat sugeruje zbieżność po około 700 iteracjach:
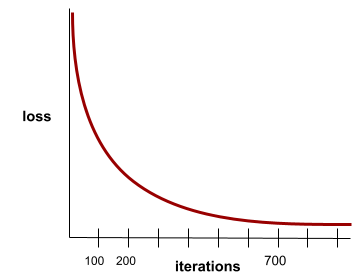
Model zbiega się, gdy dodatkowe trenowanie nie poprawia jego działania.
W uczeniu głębokim wartości funkcji straty czasami pozostają stałe lub prawie stałe przez wiele iteracji, zanim w końcu zaczną maleć. Podczas długiego okresu stałych wartości funkcji straty możesz tymczasowo odnieść fałszywe wrażenie zbieżności.
Zobacz też wczesne zatrzymanie.
Więcej informacji znajdziesz w sekcji Zbieżność modelu i krzywe funkcji straty w kursie Machine Learning Crash Course.
D
[struktura] DataFrame
Popularny typ danych pandas do reprezentowania zbiorów danych w pamięci.
DataFrame jest analogiczny do tabeli lub arkusza kalkulacyjnego. Każda kolumna obiektu DataFrame ma nazwę (nagłówek), a każdy wiersz jest identyfikowany przez unikalny numer.
Każda kolumna w obiekcie DataFrame jest uporządkowana jak tablica dwuwymiarowa, z tym wyjątkiem, że każdej kolumnie można przypisać własny typ danych.
Zobacz też oficjalną stronę referencyjną pandas.DataFrame.
zbiór danych
Zbiór surowych danych, zwykle (ale nie tylko) zorganizowanych w jednym z tych formatów:
- arkusz kalkulacyjny,
- plik w formacie CSV (wartości rozdzielane przecinkami);
model głęboki,
Sieć neuronowa zawierająca więcej niż jedną warstwę ukrytą.
Model głęboki jest też nazywany głęboką siecią neuronową.
Kontrast z modelem szerokim.
gęsta cecha,
Cechą, w której większość lub wszystkie wartości są niezerowe, jest zwykle tensor wartości zmiennoprzecinkowych. Na przykład ten 10-elementowy tensor jest gęsty, ponieważ 9 jego wartości jest niezerowych:
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
Kontrast z rzadką cechą.
głębokość
Suma tych elementów w sieci neuronowej:
- liczba warstw ukrytych,
- liczbę warstw wyjściowych, która zwykle wynosi 1;
- liczba warstw wektorów dystrybucyjnych;
Na przykład sieć neuronowa z 5 warstwami ukrytymi i 1 warstwą wyjściową ma głębokość 6.
Zwróć uwagę, że warstwa wejściowa nie wpływa na głębokość.
cecha dyskretna,
Cechę z skończonym zbiorem możliwych wartości. Na przykład cecha, której wartości mogą być tylko zwierzę, roślina lub minerał, jest cechą dyskretną (lub kategorialną).
Kontrast z cechą ciągłą.
dynamiczny
Czynność wykonywana często lub w sposób ciągły. W uczeniu maszynowym terminy dynamiczny i online są synonimami. Oto typowe zastosowania terminów dynamiczny i online w uczeniu maszynowym:
- Model dynamiczny (lub model online) to model, który jest często lub stale ponownie trenowany.
- Szkolenie dynamiczne (lub szkolenie online) to proces trenowania często lub w sposób ciągły.
- Wnioskowanie dynamiczne (lub wnioskowanie online) to proces generowania prognoz na żądanie.
model dynamiczny,
Model, który jest często (a nawet ciągle) ponownie trenowany. Model dynamiczny to „uczeń przez całe życie”, który stale dostosowuje się do zmieniających się danych. Model dynamiczny jest też nazywany modelem online.
Kontrast z modelem statycznym.
E
wczesne zatrzymanie,
Metoda regularyzacji polegająca na zakończeniu trenowania zanim strata trenowania przestanie maleć. W przypadku wczesnego zatrzymania celowo przerywasz trenowanie modelu, gdy strata w zbiorze danych weryfikacyjnych zaczyna rosnąć, czyli gdy pogarsza się skuteczność uogólniania.
Kontrastuje z wcześniejszym wyjściem.
warstwa wektora dystrybucyjnego
Specjalna warstwa ukryta, która trenuje na podstawie wielowymiarowej cechy kategorycznej, aby stopniowo uczyć się wektora dystrybucyjnego o mniejszej liczbie wymiarów. Warstwa wektorów dystrybucyjnych umożliwia sieci neuronowej znacznie wydajniejsze trenowanie niż w przypadku trenowania tylko na podstawie wielowymiarowej cechy kategorialnej.
Na przykład Earth obsługuje obecnie około 73 tys. gatunków drzew. Załóżmy, że gatunek drzewa jest cechą w Twoim modelu,więc warstwa wejściowa modelu zawiera wektor kodowania 1-z-N o długości 73 000 elementów.
Na przykład znak baobab może być reprezentowany w ten sposób:

Tablica zawierająca 73 tys. elementów jest bardzo długa. Jeśli nie dodasz do modelu warstwy osadzania, trenowanie będzie bardzo czasochłonne ze względu na mnożenie 72 999 zer. Możesz na przykład wybrać warstwę wektorów dystrybucyjnych składającą się z 12 wymiarów. W rezultacie warstwa osadzania będzie stopniowo uczyć się nowego wektora osadzania dla każdego gatunku drzewa.
W niektórych sytuacjach haszowanie jest rozsądną alternatywą dla warstwy osadzania.
Więcej informacji znajdziesz w sekcji Osadzanie w Szybkim szkoleniu z uczenia maszynowego.
początek epoki : epoka
Pełne przejście treningowe przez cały zbiór treningowy, w którym każdy przykład został przetworzony raz.
Epoka to N/rozmiar wsadu iteracji trenowania, gdzie N to całkowita liczba przykładów.
Załóżmy na przykład, że:
- Zbiór danych składa się z 1000 przykładów.
- Rozmiar wsadu to 50 przykładów.
Dlatego jedna epoka wymaga 20 iteracji:
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
przykład
Wartości jednego wiersza cech i ewentualnie etykiety. Przykłady w uczeniu nadzorowanym dzielą się na 2 ogólne kategorie:
- Przykład z etykietą składa się z co najmniej 1 cechy i etykiety. Podczas trenowania używane są przykłady z etykietami.
- Nieoznakowany przykład składa się z co najmniej 1 cechy, ale nie ma etykiety. Przykłady bez etykiet są używane podczas wnioskowania.
Załóżmy na przykład, że trenujesz model, który ma określać wpływ warunków pogodowych na wyniki testów uczniów. Oto 3 przykłady z etykietami:
| Funkcje | Etykieta | ||
|---|---|---|---|
| Temperatura | wilgotność, | Ciśnienie | Wynik testu |
| 15 | 47 | 998 | Dobry |
| 19 | 34 | 1020 | Świetna |
| 18 | 92 | 1012 | Niska |
Oto 3 przykłady bez etykiet:
| Temperatura | wilgotność, | Ciśnienie | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
Wiersz zbioru danych jest zwykle nieprzetworzonym źródłem przykładu. Oznacza to, że przykład zwykle składa się z podzbioru kolumn w zbiorze danych. Ponadto cechy w przykładzie mogą też obejmować cechy syntetyczne, takie jak kombinacje cech.
Więcej informacji znajdziesz w sekcji Uczenie nadzorowane w kursie Wprowadzenie do uczenia maszynowego.
P
wynik fałszywie negatywny (FN),
Przykład, w którym model błędnie przewiduje klasę negatywną. Na przykład model przewiduje, że dana wiadomość e-mail nie jest spamem (klasa negatywna), ale w rzeczywistości jest spamem.
wynik fałszywie pozytywny (FP),
Przykład, w którym model błędnie przewiduje klasę pozytywną. Na przykład model przewiduje, że dana wiadomość e-mail to spam (klasa pozytywna), ale w rzeczywistości nie jest to spam.
Więcej informacji znajdziesz w sekcji Progi i macierz pomyłek w szybkim szkoleniu z uczenia maszynowego.
współczynnik wyników fałszywie pozytywnych (FPR),
Odsetek rzeczywistych przykładów negatywnych, dla których model błędnie przewidział klasę pozytywną. Współczynnik fałszywie dodatnich wyników oblicza się według tego wzoru:
Współczynnik wyników fałszywie pozytywnych jest osią X na krzywej ROC.
Więcej informacji znajdziesz w sekcji Klasyfikacja: ROC i AUC w szybkim szkoleniu z uczenia maszynowego.
cecha [in context of machine learning]
Zmienna wejściowa modelu uczenia maszynowego. Przykład składa się z co najmniej 1 cechy. Załóżmy na przykład, że trenujesz model, aby określić wpływ warunków pogodowych na wyniki testów uczniów. W tabeli poniżej znajdziesz 3 przykłady, z których każdy zawiera 3 cechy i 1 etykietę:
| Funkcje | Etykieta | ||
|---|---|---|---|
| Temperatura | wilgotność, | Ciśnienie | Wynik testu |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
Kontrast z etykietą.
Więcej informacji znajdziesz w sekcji Uczenie z nadzorem w kursie Wprowadzenie do uczenia maszynowego.
kombinacja cech,
Cechy syntetyczne utworzone przez „skrzyżowanie” cech kategorycznych lub podzielonych na przedziały.
Rozważmy na przykład model „prognozowania nastroju”, który przedstawia temperaturę w jednym z tych 4 przedziałów:
freezingchillytemperatewarm
i przedstawia prędkość wiatru w jednym z tych 3 zakresów:
stilllightwindy
Bez kombinacji cech model liniowy trenuje się niezależnie na podstawie każdego z 7 wcześniejszych różnych przedziałów. Model trenuje więc np. na freezing niezależnie od trenowania np. na windy.
Możesz też utworzyć kombinację cech temperatury i prędkości wiatru. Ta syntetyczna cecha miałaby 12 możliwych wartości:
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
Dzięki kombinacjom cech model może się nauczyć różnic w nastroju między freezing-windy dniem a freezing-still dniem.
Jeśli utworzysz syntetyczną funkcję z 2 funkcji, z których każda ma wiele różnych przedziałów, wynikowa kombinacja funkcji będzie miała ogromną liczbę możliwych kombinacji. Jeśli na przykład jedna funkcja ma 1000 grup, a druga 2000 grup, to wynikowa kombinacja funkcji ma 2 000 000 grup.
Formalnie krzyżowanie to iloczyn kartezjański.
Kombinacje cech są najczęściej używane w modelach liniowych, a rzadko w sieciach neuronowych.
Więcej informacji znajdziesz w artykule Dane kategorialne: kombinacje cech w Szybkim szkoleniu z systemów uczących się.
ekstrakcja wyróżników
Proces obejmujący te kroki:
- określanie, które funkcje mogą być przydatne podczas trenowania modelu;
- przekształcanie nieprzetworzonych danych ze zbioru danych w skuteczne wersje tych funkcji;
Możesz na przykład uznać, że temperature to przydatna funkcja. Następnie możesz poeksperymentować z podziałem na przedziały, aby zoptymalizować to, czego model może się nauczyć z różnych temperature zakresów.
Inżynieria cech jest czasami nazywana ekstrakcją cech lub featurizacją.
Więcej informacji znajdziesz w sekcji Dane liczbowe: jak model przetwarza dane za pomocą wektorów cech w kursie Machine Learning Crash Course.
zestaw funkcji,
Grupa cech, na podstawie których trenowany jest Twój model systemu uczącego się. Na przykład prosty zestaw cech modelu, który prognozuje ceny mieszkań, może składać się z kodu pocztowego, wielkości nieruchomości i jej stanu.
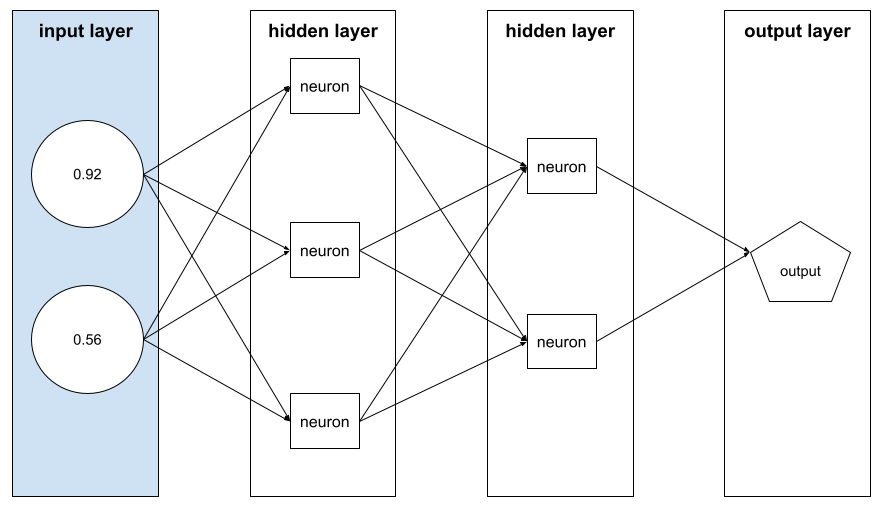
wektor cech,
Tablica wartości cechy składająca się z przykładu. Wektor cech jest używany jako dane wejściowe podczas trenowania i wnioskowania. Na przykład wektor cech modelu z 2 oddzielnymi cechami może wyglądać tak:
[0.92, 0.56]
Każdy przykład zawiera inne wartości wektora cech, więc wektor cech dla następnego przykładu może wyglądać tak:
[0.73, 0.49]
Inżynieria cech określa, jak reprezentować cechy w wektorze cech. Na przykład binarna cecha kategorialna z 5 możliwymi wartościami może być reprezentowana za pomocą kodowania 1-z-N. W tym przypadku część wektora cech dla danego przykładu będzie się składać z czterech zer i jednej wartości 1,0 na trzeciej pozycji:
[0.0, 0.0, 1.0, 0.0, 0.0]
Załóżmy na przykład, że model składa się z 3 cech:
- binarna cecha kategorialna z 5 możliwymi wartościami reprezentowanymi za pomocą kodowania 1-z-N, np.
[0.0, 1.0, 0.0, 0.0, 0.0]; - kolejną binarną cechę kategorialną z 3 możliwymi wartościami reprezentowanymi za pomocą kodowania 1 z n, np.
[0.0, 0.0, 1.0]. - cecha zmiennoprzecinkowa, np.
8.3.
W tym przypadku wektor cech każdego przykładu będzie reprezentowany przez 9 wartości. Biorąc pod uwagę przykładowe wartości z poprzedniej listy, wektor cech będzie wyglądać tak:
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
Więcej informacji znajdziesz w sekcji Dane liczbowe: jak model przetwarza dane za pomocą wektorów cech w kursie Machine Learning Crash Course.
pętla informacji zwrotnych
W uczeniu maszynowym sytuacja, w której prognozy modelu wpływają na dane treningowe tego samego lub innego modelu. Na przykład model, który rekomenduje filmy, będzie wpływać na to, jakie filmy widzą użytkownicy, co z kolei będzie miało wpływ na kolejne modele rekomendacji filmów.
Więcej informacji znajdziesz w sekcji Produkcyjne systemy uczenia maszynowego: pytania, które warto zadać w kursie Machine Learning Crash Course.
G
uogólnienie
Zdolność modelu do tworzenia prawidłowych prognoz na podstawie nowych, wcześniej niewidzianych danych. Model, który potrafi uogólniać, jest przeciwieństwem modelu, który jest przetrenowany.
Więcej informacji znajdziesz w sekcji Uogólnianie w szybkim szkoleniu z uczenia maszynowego.
krzywa generalizacji,
Wykres utraty treningowej i utraty walidacyjnej w funkcji liczby iteracji.
Krzywa uogólnienia może pomóc w wykryciu możliwego przetrenowania. Na przykład poniższa krzywa uogólnienia sugeruje przetrenowanie, ponieważ ostatecznie strata w przypadku weryfikacji staje się znacznie większa niż strata w przypadku trenowania.
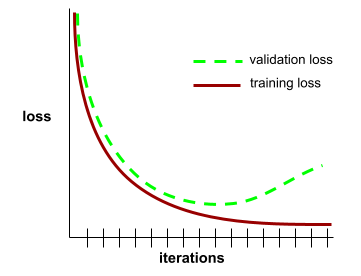
Więcej informacji znajdziesz w sekcji Uogólnianie w szybkim szkoleniu z uczenia maszynowego.
spadek wzdłuż gradientu
Technika matematyczna służąca do minimalizowania straty. Metoda gradientu prostego iteracyjnie dostosowuje wagi i odchylenia, stopniowo znajdując najlepszą kombinację, która minimalizuje straty.
Metoda gradientu prostego jest starsza od uczenia maszynowego – i to znacznie.
Więcej informacji znajdziesz w sekcji Regresja liniowa: metoda gradientowa w kursie Machine Learning Crash Course.
dane podstawowe,
Rzeczywistość.
co faktycznie się wydarzyło.
Rozważmy na przykład model klasyfikacji binarnej, który przewiduje, czy student pierwszego roku ukończy studia w ciągu 6 lat. Dane podstawowe dla tego modelu to informacja, czy uczeń ukończył studia w ciągu 6 lat.
H
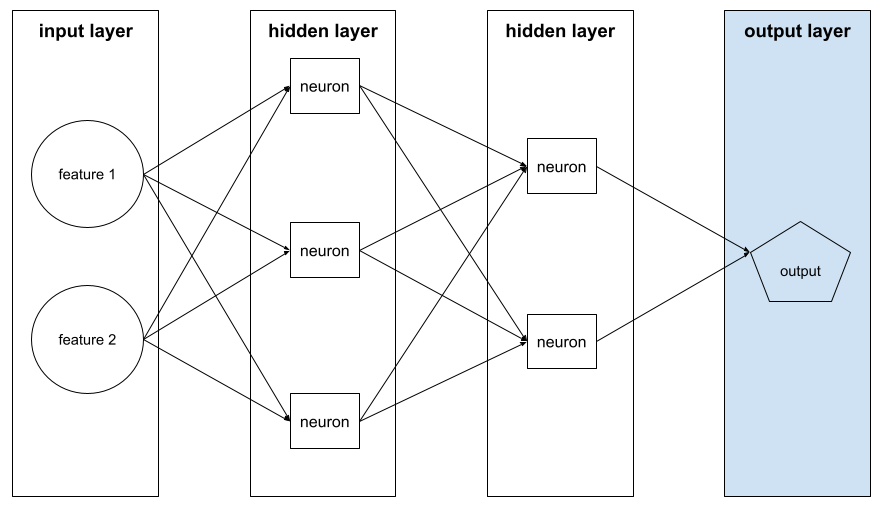
warstwa ukryta
Warstwa w sieci neuronowej między warstwą wejściową (cechy) a warstwą wyjściową (prognoza). Każda warstwa ukryta składa się z co najmniej 1 neuronu. Na przykład ta sieć neuronowa zawiera 2 warstwy ukryte: pierwszą z 3 neuronami i drugą z 2 neuronami:
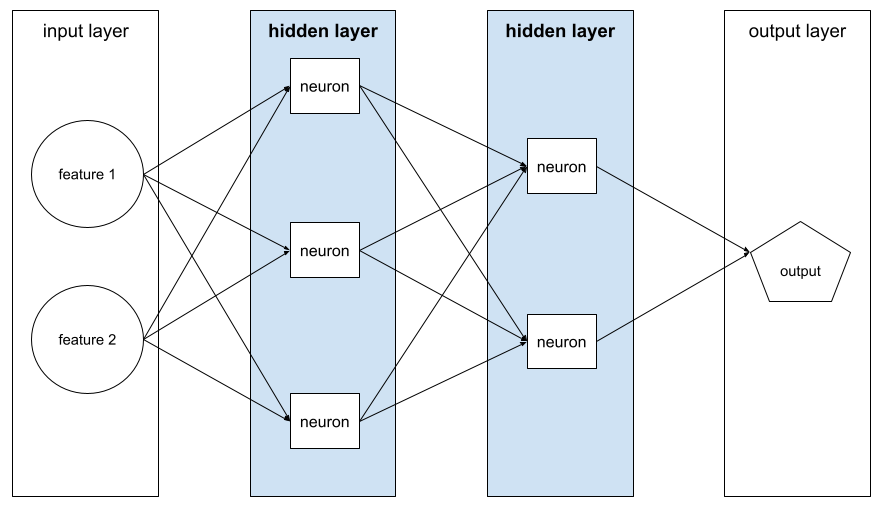
Głęboka sieć neuronowa zawiera więcej niż jedną warstwę ukrytą. Na przykład ilustracja powyżej przedstawia głęboką sieć neuronową, ponieważ model zawiera 2 warstwy ukryte.
Więcej informacji znajdziesz w sekcji Sieci neuronowe: węzły i warstwy ukryte w kursie Machine Learning Crash Course.
hiperparametr
Zmienne, które Ty lub usługa dostrajania hiperparametrówdostosowuje podczas kolejnych uruchomień trenowania modelu. Na przykład szybkość uczenia jest hiperparametrem. Przed jedną sesją trenowania możesz ustawić współczynnik uczenia na 0,01. Jeśli uznasz, że wartość 0,01 jest zbyt wysoka, możesz ustawić współczynnik uczenia na 0,003 w przypadku następnej sesji treningowej.
Z kolei parametry to różne wagi i odchylenia, których model uczy się podczas trenowania.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
I
niezależne i identycznie rozłożone (i.i.d.)
Dane pochodzące z rozkładu, który się nie zmienia, a każda wylosowana wartość nie zależy od wartości wylosowanych wcześniej. Rozkład i.i.d. jest gazem idealnym uczenia maszynowego – przydatną konstrukcją matematyczną, która jednak prawie nigdy nie występuje w rzeczywistości. Na przykład rozkład odwiedzających stronę internetową może być niezależny i identyczny w krótkim przedziale czasu, tzn. rozkład nie zmienia się w tym krótkim przedziale czasu, a wizyta jednej osoby jest na ogół niezależna od wizyty innej osoby. Jeśli jednak rozszerzysz ten przedział czasu, mogą się pojawić różnice sezonowe w liczbie odwiedzających stronę.
Zobacz też niestacjonarność.
wnioskowanie
W tradycyjnym uczeniu maszynowym proces prognozowania polegający na zastosowaniu wytrenowanego modelu do nieoznaczonych przykładów. Więcej informacji znajdziesz w module Uczenie z nadzorem w kursie Wprowadzenie do uczenia maszynowego.
W dużych modelach językowych wnioskowanie to proces polegający na używaniu wytrenowanego modelu do generowania odpowiedzi na prompta.
W statystyce wnioskowanie ma nieco inne znaczenie. Szczegółowe informacje znajdziesz w artykule w Wikipedii na temat wnioskowania statystycznego.
warstwa wejściowa
Warstwa sieci neuronowej, która zawiera wektor cech. Oznacza to, że warstwa wejściowa dostarcza przykłady na potrzeby trenowania lub wnioskowania. Na przykład warstwa wejściowa w tym przykładzie sieci neuronowej składa się z 2 cech:
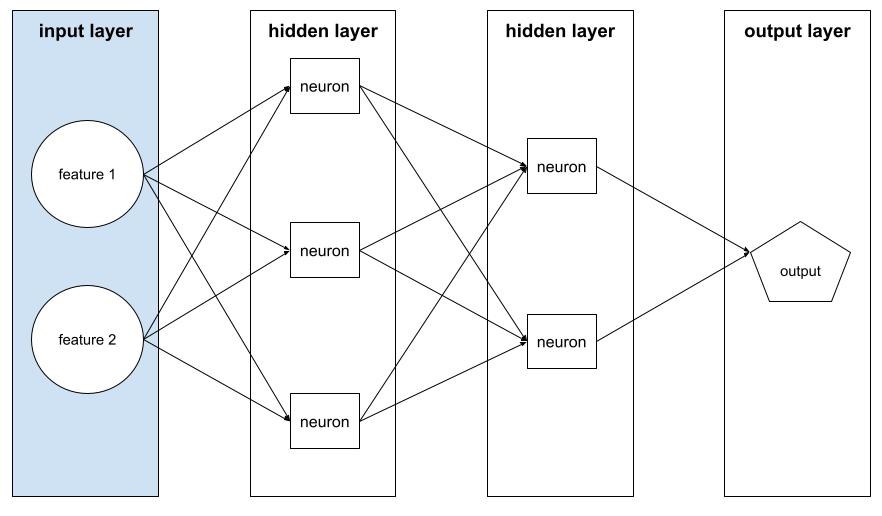
interpretowalność,
Możliwość wyjaśnienia lub przedstawienia rozumowania modelu uczenia maszynowego w sposób zrozumiały dla człowieka.
Na przykład większość modeli regresji liniowej jest bardzo łatwa do interpretacji. (Wystarczy spojrzeć na wytrenowane wagi dla każdej cechy). Las decyzji jest też bardzo łatwy do interpretacji. Interpretowalność niektórych modeli wymaga jednak rozbudowanej wizualizacji.
Do interpretowania modeli ML możesz używać narzędzia do analizowania interpretowalności (LIT).
iteracja
Pojedyncza aktualizacja parametrów modelu, czyli wag i odchyleń modelu, podczas trenowania. Rozmiar wsadu określa, ile przykładów model przetwarza w jednej iteracji. Jeśli na przykład rozmiar partii wynosi 20, model przetwarza 20 przykładów przed dostosowaniem parametrów.
Podczas trenowania sieci neuronowej pojedyncza iteracja obejmuje 2 przejścia:
- Przejście w przód w celu oceny utraty w przypadku pojedynczej partii.
- Przejście wsteczne (propagacja wsteczna) w celu dostosowania parametrów modelu na podstawie wartości funkcji straty i tempa uczenia się.
Więcej informacji znajdziesz w sekcji Spadek gradientu w szybkim szkoleniu z uczenia maszynowego.
L
Regularyzacja L0
Rodzaj regularyzacji, która nakłada karę na łączną liczbę niezerowych wag w modelu. Na przykład model z 11 wagami o wartości różnej od zera zostanie ukarany bardziej niż podobny model z 10 wagami o wartości różnej od zera.
Regularyzacja L0 jest czasami nazywana regularyzacją normy L0.
Utrata sygnału L1
Funkcja straty, która oblicza wartość bezwzględną różnicy między rzeczywistymi wartościami etykiet a wartościami przewidywanymi przez model. Na przykład poniżej przedstawiamy obliczenia utraty L1 dla partii 5 przykładów:
| Rzeczywista wartość przykładu | Wartość prognozowana przez model | Wartość bezwzględna różnicy |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = utrata L1 | ||
Funkcja straty L1 jest mniej wrażliwa na wartości odstające niż funkcja straty L2.
Średni błąd bezwzględny to średnia strata L1 na przykład.
Więcej informacji znajdziesz w sekcji Regresja liniowa: funkcja straty w kursie Machine Learning Crash Course.
regularyzacja L1,
Rodzaj regularyzacji, która powoduje nakładanie kar na wagi proporcjonalnie do sumy wartości bezwzględnych wag. Regularyzacja L1 pomaga sprowadzić wagi nieistotnych lub mało istotnych cech do dokładnie 0. Cechę o wadze 0 można uznać za usuniętą z modelu.
Kontrast z regularyzacją L2.
Funkcja straty L2
Funkcja straty, która oblicza kwadrat różnicy między rzeczywistymi wartościami etykiet a wartościami przewidywanymi przez model. Oto przykład obliczania straty L2 dla partii pięciu przykładów:
| Rzeczywista wartość przykładu | Wartość prognozowana przez model | Kwadrat delty |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = przegrana L2 | ||
Ze względu na podnoszenie do kwadratu funkcja straty L2 wzmacnia wpływ wartości odstających. Oznacza to, że funkcja straty L2 reaguje silniej na nieprawidłowe prognozy niż funkcja straty L1. Na przykład funkcja straty L1 dla poprzedniej partii wyniesie 8, a nie 16. Zwróć uwagę, że 1 wartość odstająca odpowiada za 9 z 16 wartości.
Modele regresji zwykle używają funkcji utraty L2.
Błąd średniokwadratowy to średnia strata L2 na przykład. Strata kwadratowa to inna nazwa straty L2.
Więcej informacji znajdziesz w sekcji Regresja logistyczna: funkcja straty i regularyzacja w kursie Machine Learning Crash Course.
regularyzacja L2,
Rodzaj regularyzacji, która powoduje nakładanie kar na wagi proporcjonalnie do sumy kwadratów wag. Regularyzacja L2 pomaga zbliżyć wagi wartości odstających (o wysokich wartościach dodatnich lub niskich wartościach ujemnych) do 0, ale nie do 0. Cechy o wartościach bardzo bliskich 0 pozostają w modelu, ale nie mają dużego wpływu na jego prognozę.
Regularyzacja L2 zawsze poprawia generalizację w modelach liniowych.
Kontrast z regularyzacją L1.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie: regularyzacja L2 w szybkim szkoleniu z uczenia maszynowego.
etykieta
W uczeniu maszynowym nadzorowanym „odpowiedź” lub „wynik” w przykładzie.
Każdy przykład z etykietą składa się z co najmniej 1 cechy i etykiety. Na przykład w zbiorze danych do wykrywania spamu etykieta będzie prawdopodobnie miała wartość „spam” lub „nie spam”. W zbiorze danych o opadach deszczu etykietą może być ilość deszczu, która spadła w określonym czasie.
Więcej informacji znajdziesz w sekcji Uczenie nadzorowane w artykule Wprowadzenie do uczenia maszynowego.
przykład oznaczony etykietą,
Przykład zawierający co najmniej 1 cechę i etykietę. Na przykład poniższa tabela zawiera 3 przykłady z etykietami z modelu wyceny domu. Każdy z nich ma 3 cechy i 1 etykietę:
| Liczba sypialni | Liczba łazienek | Wiek domu | Cena domu (etykieta) |
|---|---|---|---|
| 3 | 2 | 15 | 345 tys. zł |
| 2 | 1 | 72 | 179 000 USD |
| 4 | 2 | 34 | 392 000 USD |
W nadzorowanym uczeniu maszynowym modele są trenowane na oznaczonych przykładach i dokonują prognoz na podstawie nieoznaczonych przykładów.
Porównaj przykłady z etykietami z przykładami bez etykiet.
Więcej informacji znajdziesz w sekcji Uczenie nadzorowane w artykule Wprowadzenie do uczenia maszynowego.
lambda
Synonim współczynnika regularyzacji.
Lambda to termin wieloznaczny. Skupiamy się tu na definicji tego terminu w kontekście regularyzacji.
warstwa
Zbiór neuronów w sieci neuronowej. Oto 3 najpopularniejsze rodzaje warstw:
- Warstwa wejściowa, która zawiera wartości wszystkich cech.
- Co najmniej 1 ukryta warstwa, która wykrywa nieliniowe zależności między cechami a etykietą.
- Warstwa wyjściowa, która zawiera prognozę.
Na przykład poniższa ilustracja przedstawia sieć neuronową z 1 warstwą wejściową, 2 warstwami ukrytymi i 1 warstwą wyjściową:
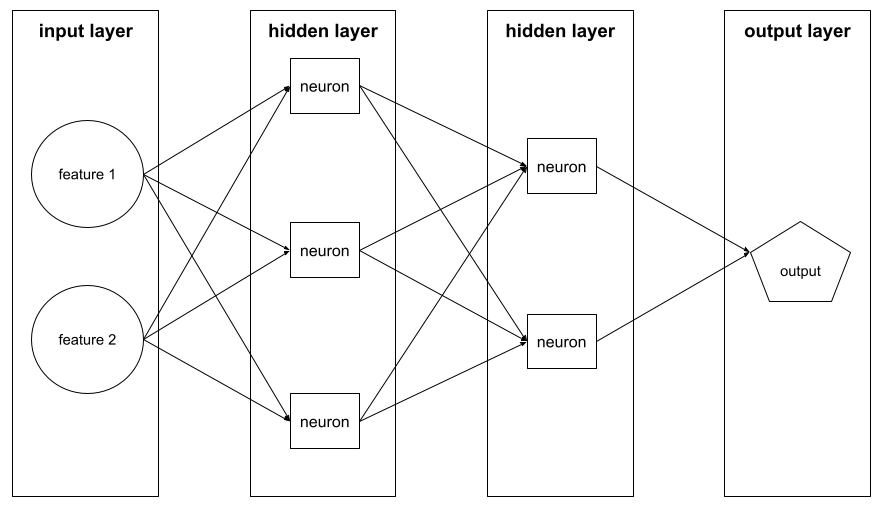
W TensorFlow warstwy to również funkcje Pythona, które przyjmują jako dane wejściowe tensory i opcje konfiguracji, a jako dane wyjściowe generują inne tensory.
tempo uczenia się
Liczba zmiennoprzecinkowa, która informuje algorytm spadku gradientu, jak silnie dostosowywać wagi i odchylenia w każdej iteracji. Na przykład współczynnik uczenia 0,3 dostosowuje wagi i odchylenia 3 razy skuteczniej niż współczynnik uczenia 0,1.
Tempo uczenia się to kluczowy hiperparametr. Jeśli ustawisz zbyt niską szybkość uczenia się, trenowanie potrwa zbyt długo. Jeśli ustawisz zbyt wysokie tempo uczenia się, metoda gradientu prostego często ma problemy z osiągnięciem konwergencji.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
jednostajne
Zależność między co najmniej 2 zmiennymi, którą można przedstawić wyłącznie za pomocą dodawania i mnożenia.
Wykres zależności liniowej to linia.
Kontrast z nieliniowymi.
model liniowy,
Model, który przypisuje jedną wagę do każdej cechy, aby tworzyć prognozy. (Modele liniowe również uwzględniają tendencyjność). Z kolei w modelach głębokich relacja między cechami a prognozami jest zwykle nieliniowa.
Modele liniowe są zwykle łatwiejsze do wytrenowania i bardziej zrozumiałe niż modele głębokie. Modele głębokie mogą jednak nauczyć się złożonych relacji między cechami.
Regresja liniowa i regresja logistyczna to 2 rodzaje modeli liniowych.
regresja liniowa,
Rodzaj modelu uczenia maszynowego, w którym spełnione są oba te warunki:
- Model jest modelem liniowym.
- Prognoza to liczba zmiennoprzecinkowa. (Jest to część regresji regresji liniowej).
Porównaj regresję liniową z regresją logistyczną. Porównaj też regresję z klasyfikacją.
Więcej informacji znajdziesz w sekcji Regresja liniowa w szybkim szkoleniu z uczenia maszynowego.
regresja logistyczna
Rodzaj modelu regresji, który prognozuje prawdopodobieństwo. Modele regresji logistycznej mają te cechy:
- Etykieta jest kategoryczna. Termin regresja logistyczna zwykle odnosi się do binarnej regresji logistycznej, czyli modelu, który oblicza prawdopodobieństwa etykiet o 2 możliwych wartościach. Mniej popularny wariant, wielomianowa regresja logistyczna, oblicza prawdopodobieństwa etykiet z więcej niż 2 możliwymi wartościami.
- Funkcja straty podczas trenowania to Log Loss. (W przypadku etykiet z więcej niż 2 możliwymi wartościami można umieścić równolegle kilka jednostek Log Loss).
- Model ma architekturę liniową, a nie głęboką sieć neuronową. Pozostała część tej definicji dotyczy jednak również modeli głębokich, które prognozują prawdopodobieństwa etykiet kategorialnych.
Rozważmy na przykład model regresji logistycznej, który oblicza prawdopodobieństwo, że e-mail jest spamem lub nie. Załóżmy, że podczas wnioskowania model prognozuje wartość 0,72. Dlatego model szacuje:
- 72% – prawdopodobieństwo, że e-mail jest spamem.
- 28% – prawdopodobieństwo, że e-mail nie jest spamem.
Model regresji logistycznej wykorzystuje tę dwuetapową architekturę:
- Model generuje prognozę pierwotną (y') przez zastosowanie funkcji liniowej cech wejściowych.
- Model używa tej surowej prognozy jako danych wejściowych funkcji sigmoidalnej, która przekształca surową prognozę w wartość z przedziału (0, 1).
Podobnie jak każdy model regresji, model regresji logistycznej prognozuje liczbę. Zwykle jednak liczba ta staje się częścią modelu klasyfikacji binarnej w ten sposób:
- Jeśli przewidywana liczba jest większa niż próg klasyfikacji, model klasyfikacji binarnej prognozuje klasę pozytywną.
- Jeśli przewidywana liczba jest mniejsza niż próg klasyfikacji, model klasyfikacji binarnej prognozuje klasę negatywną.
Więcej informacji znajdziesz w sekcji Regresja logistyczna w szybkim szkoleniu z systemów uczących się.
Logarytmiczna funkcja straty
Funkcja straty używana w przypadku binarnej regresji logistycznej.
Więcej informacji znajdziesz w sekcji Regresja logistyczna: funkcja straty i regularyzacja w kursie Machine Learning Crash Course.
log-odds
Logarytm szans wystąpienia danego zdarzenia.
strata
Podczas trenowania modelu nadzorowanego miara odległości prognozy modelu od jego etykiety.
Funkcja straty oblicza stratę.
Więcej informacji znajdziesz w sekcji Regresja liniowa: funkcja straty w kursie Machine Learning Crash Course.
krzywa strat,
Wykres utraty jako funkcji liczby iteracji treningowych. Poniższy wykres przedstawia typową krzywą utraty:
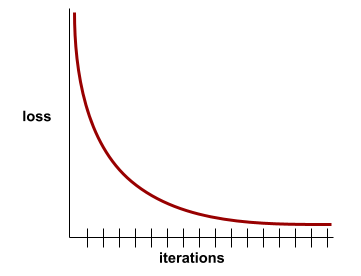
Krzywe funkcji straty mogą pomóc Ci określić, kiedy model zbiega się lub nadmiernie dopasowuje się.
Krzywe strat mogą przedstawiać wszystkie te rodzaje strat:
Zobacz też krzywą generalizacji.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie: interpretowanie krzywych funkcji straty w kursie Machine Learning Crash Course.
funkcja straty,
Podczas trenowania lub testowania funkcja matematyczna, która oblicza stratę na partii przykładów. Funkcja straty zwraca mniejszą stratę w przypadku modeli, które generują dobre prognozy, niż w przypadku modeli, które generują złe prognozy.
Celem trenowania jest zwykle minimalizowanie straty zwracanej przez funkcję straty.
Istnieje wiele różnych rodzajów funkcji straty. Wybierz odpowiednią funkcję straty dla rodzaju tworzonego modelu. Na przykład:
- Funkcja straty L2 (lub średnia kwadratowa błędów) to funkcja straty dla regresji liniowej.
- Log Loss to funkcja straty dla regresji logistycznej.
M
systemy uczące się
To programy lub systemy, które trenują model na podstawie danych wejściowych. Wytrenowany model może tworzyć przydatne prognozy na podstawie nowych (wcześniej niewykorzystanych) danych pobranych z tego samego rozkładu co dane użyte do trenowania modelu.
Uczenie maszynowe to także dziedzina nauki zajmująca się tymi programami lub systemami.
Więcej informacji znajdziesz w kursie Wprowadzenie do uczenia maszynowego.
klasa większościowa,
Etykieta, która występuje częściej w zbiorze danych z niezrównoważonymi klasami. Na przykład w zbiorze danych zawierającym 99% etykiet negatywnych i 1% etykiet pozytywnych etykiety negatywne stanowią klasę większościową.
Kontrast z klasą mniejszościową.
Więcej informacji znajdziesz w sekcji Zbiory danych: niezrównoważone zbiory danych w kursie Machine Learning Crash Course.
mini-batch
Mały, losowo wybrany podzbiór partii przetwarzanej w ramach jednej iteracji. Rozmiar pakietu mini-pakietu wynosi zwykle od 10 do 1000 przykładów.
Załóżmy na przykład, że cały zbiór treningowy (pełna partia) składa się z 1000 przykładów. Załóżmy, że ustawisz rozmiar partii każdej mini-partii na 20. Dlatego w każdej iteracji określa utratę na podstawie losowych 20 przykładów z 1000, a następnie odpowiednio dostosowuje wagi i odchylenia.
Obliczanie funkcji straty na podstawie mini-wsadu jest znacznie wydajniejsze niż obliczanie jej na podstawie wszystkich przykładów w pełnym wsadzie.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
klasa mniejszościowa,
Mniej popularna etykieta w zbiorze danych z nierównomiernym rozkładem klas. Na przykład w zbiorze danych zawierającym 99% etykiet negatywnych i 1% etykiet pozytywnych etykiety pozytywne stanowią klasę mniejszościową.
Kontrast z klasą większościową.
Więcej informacji znajdziesz w sekcji Zbiory danych: niezrównoważone zbiory danych w kursie Machine Learning Crash Course.
model
Ogólnie rzecz biorąc, jest to dowolna konstrukcja matematyczna, która przetwarza dane wejściowe i zwraca dane wyjściowe. Inaczej mówiąc, model to zbiór parametrów i struktury potrzebnych systemowi do tworzenia prognoz. W nadzorowanym uczeniu maszynowym model przyjmuje przykład jako dane wejściowe i wyciąga prognozę jako dane wyjściowe. W przypadku uczenia maszynowego z nadzorem modele nieco się różnią. Na przykład:
- Model regresji liniowej składa się z zestawu wag i wartości progowej.
- Model sieci neuronowej składa się z:
- Zestaw warstw ukrytych, z których każda zawiera co najmniej 1 neuron.
- wagi i odchylenia powiązane z każdym neuronem;
- Model drzewa decyzyjnego składa się z:
- Kształt drzewa, czyli wzorzec, w którym połączone są warunki i liście.
- The conditions and leaves.
Możesz zapisywać, przywracać i kopiować modele.
Uczenie maszynowe bez nadzoru również generuje modele, zwykle funkcję, która może mapować przykładowe dane wejściowe na najbardziej odpowiednią grupę.
klasyfikacja wieloklasowa,
W uczeniu nadzorowanym problem klasyfikacji, w którym zbiór danych zawiera więcej niż 2 klasy etykiet. Na przykład etykiety w zbiorze danych Iris muszą należeć do jednej z tych 3 klas:
- Iris setosa
- Iris virginica
- Iris versicolor
Model wytrenowany na zbiorze danych Iris, który prognozuje typ irysa na podstawie nowych przykładów, wykonuje klasyfikację wieloklasową.
Z kolei problemy klasyfikacji, które rozróżniają dokładnie 2 klasy, są binarnymi modelami klasyfikacji. Na przykład model e-maila, który przewiduje, czy e-mail jest spamem, czy nie jest spamem, to model klasyfikacji binarnej.
W przypadku problemów z klastrowaniem klasyfikacja wieloklasowa odnosi się do więcej niż 2 klastrów.
Więcej informacji znajdziesz w sekcji Sieci neuronowe: klasyfikacja wieloklasowa w kursie Machine Learning Crash Course.
N
klasa wyników negatywnych,
W klasyfikacji binarnej jedna klasa jest określana jako pozytywna, a druga jako negatywna. Klasa pozytywna to rzecz lub zdarzenie, które model testuje, a klasa negatywna to inna możliwość. Na przykład:
- Klasa negatywna w teście medycznym może oznaczać „brak guza”.
- Klasa negatywna w modelu klasyfikacji e-maili może być oznaczona jako „nie spam”.
Porównaj z klasą wyników pozytywnych.
sieć neuronowa
Model zawierający co najmniej 1 warstwę ukrytą. Głęboka sieć neuronowa to rodzaj sieci neuronowej zawierającej więcej niż jedną warstwę ukrytą. Na przykład poniższy diagram przedstawia głęboką sieć neuronową zawierającą 2 ukryte warstwy.
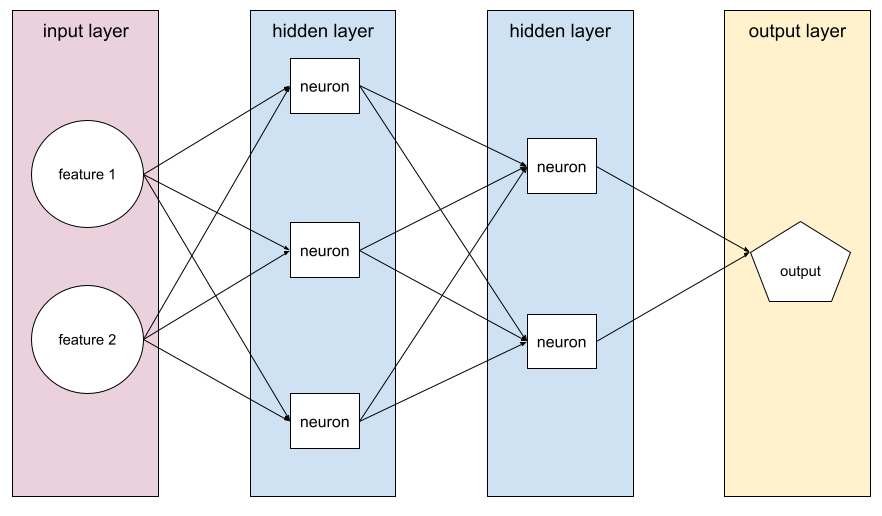
Każdy neuron w sieci neuronowej łączy się ze wszystkimi węzłami w następnej warstwie. Na przykład na powyższym diagramie widać, że każdy z 3 neuronów w pierwszej warstwie ukrytej jest połączony oddzielnie z każdym z 2 neuronów w drugiej warstwie ukrytej.
Sieci neuronowe zaimplementowane na komputerach są czasami nazywane sztucznymi sieciami neuronowymi, aby odróżnić je od sieci neuronowych występujących w mózgu i innych układach nerwowych.
Niektóre sieci neuronowe mogą naśladować bardzo złożone nieliniowe zależności między różnymi cechami a etykietą.
Zobacz też splotową sieć neuronową i rekurencyjną sieć neuronową.
Więcej informacji znajdziesz w sekcji Sieci neuronowe w Szybkim szkoleniu z uczenia maszynowego.
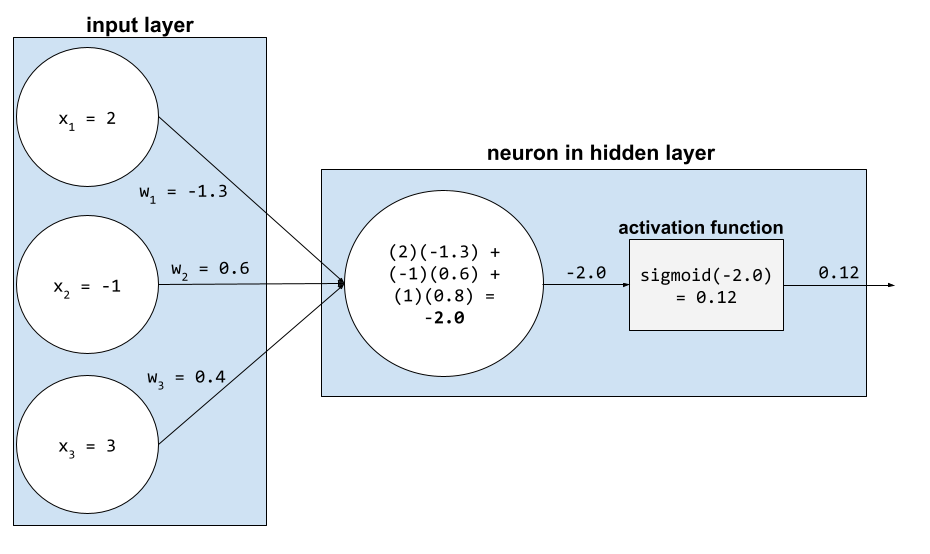
neuron,
W uczeniu maszynowym jest to odrębna jednostka w warstwie ukrytej sieci neuronowej. Każdy neuron wykonuje te 2 czynności:
- Oblicza sumę ważoną wartości wejściowych pomnożonych przez odpowiednie wagi.
- Przekazuje sumę ważoną jako dane wejściowe do funkcji aktywacji.
Neuron w pierwszej warstwie ukrytej przyjmuje dane wejściowe z wartości cech w warstwie wejściowej. Neuron w dowolnej warstwie ukrytej za pierwszą przyjmuje dane wejściowe z neuronów w poprzedniej warstwie ukrytej. Na przykład neuron w 2. warstwie ukrytej przyjmuje dane wejściowe z neuronów w 1. warstwie ukrytej.
Ilustracja poniżej przedstawia 2 neurony i ich dane wejściowe.
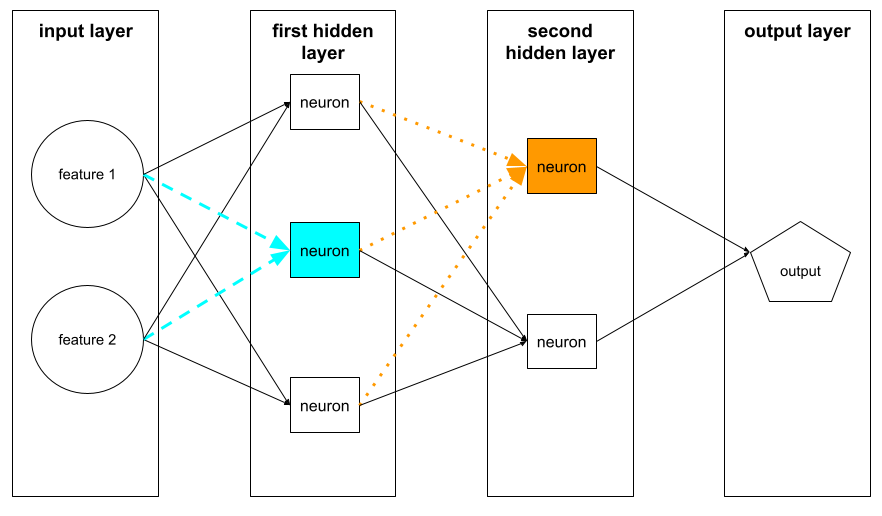
Neuron w sieci neuronowej naśladuje zachowanie neuronów w mózgu i innych częściach układu nerwowego.
węzeł (sieć neuronowa)
Więcej informacji znajdziesz w sekcji Sieci neuronowe w Szybkim szkoleniu z uczenia maszynowego.
nieliniowy,
Zależność między co najmniej 2 zmiennymi, której nie można przedstawić wyłącznie za pomocą dodawania i mnożenia. Relację liniową można przedstawić jako linię, a relacji nieliniowej nie można. Rozważmy na przykład 2 modele, z których każdy wiąże jedną cechę z jedną etykietą. Model po lewej stronie jest liniowy, a model po prawej stronie jest nieliniowy:

W sekcji Sieci neuronowe: węzły i warstwy ukryte w kursie Machine Learning Crash Course możesz eksperymentować z różnymi rodzajami funkcji nieliniowych.
niestacjonarność
Cecha, której wartości zmieniają się w co najmniej 1 wymiarze, zwykle w czasie. Oto przykłady niestacjonarności:
- Liczba sprzedanych kostiumów kąpielowych w danym sklepie różni się w zależności od pory roku.
- Ilość określonego owocu zebranego w danym regionie jest przez większą część roku zerowa, ale przez krótki okres bardzo duża.
- Ze względu na zmiany klimatu średnie roczne temperatury ulegają zmianie.
Kontrast z stacjonarnością.
normalizacja,
Ogólnie rzecz biorąc, proces przekształcania rzeczywistego zakresu wartości zmiennej w standardowy zakres wartości, np.:
- -1 do +1
- Od 0 do 1
- Wyniki z (w przybliżeniu od -3 do +3)
Załóżmy na przykład, że rzeczywisty zakres wartości pewnej cechy to 800–2400. W ramach inżynierii cech możesz znormalizować rzeczywiste wartości do standardowego zakresu, np. od -1 do +1.
Normalizacja to powszechne zadanie w inżynierii cech. Modele zwykle trenują szybciej (i generują lepsze prognozy), gdy każda cecha numeryczna w wektorze cech ma mniej więcej ten sam zakres.
Zobacz też normalizację wyniku z.
Więcej informacji znajdziesz w sekcji Dane liczbowe: normalizacja w kursie Machine Learning Crash Course.
dane liczbowe,
Cechy reprezentowane jako liczby całkowite lub rzeczywiste. Na przykład model wyceny domu prawdopodobnie będzie reprezentować wielkość domu (w stopach lub metrach kwadratowych) jako dane liczbowe. Przedstawienie cechy jako danych liczbowych oznacza, że wartości cechy mają matematyczny związek z etykietą. Oznacza to, że liczba metrów kwadratowych w domu prawdopodobnie ma pewien związek matematyczny z jego wartością.
Nie wszystkie dane całkowite powinny być reprezentowane jako dane liczbowe. Na przykład kody pocztowe w niektórych częściach świata są liczbami całkowitymi, ale nie powinny być reprezentowane w modelach jako dane liczbowe. Dzieje się tak, ponieważ kod pocztowy 20000 nie jest 2 razy (ani o połowę) skuteczniejszy niż kod pocztowy 10000. Ponadto, chociaż różne kody pocztowe są powiązane z różnymi wartościami nieruchomości, nie możemy zakładać, że wartości nieruchomości w przypadku kodu pocztowego 20000 są 2 razy większe niż w przypadku kodu pocztowego 10000.
Kody pocztowe powinny być reprezentowane jako dane jakościowe.
Cechy liczbowe są czasami nazywane cechami ciągłymi.
Więcej informacji znajdziesz w sekcji Praca z danymi liczbowymi w kursie Machine Learning Crash Course.
O
offline
Synonim słowa statyczny.
wnioskowanie offline,
Proces generowania przez model partii prognoz i następnie zapisywania ich w pamięci podręcznej. Aplikacje mogą wtedy uzyskać dostęp do wywnioskowanej prognozy z pamięci podręcznej, zamiast ponownie uruchamiać model.
Rozważmy na przykład model, który generuje lokalne prognozy pogody (prognozy) co 4 godziny. Po każdym uruchomieniu modelu system zapisuje w pamięci podręcznej wszystkie lokalne prognozy pogody. Aplikacje pogodowe pobierają prognozy z pamięci podręcznej.
Wnioskowanie offline jest też nazywane wnioskowaniem statycznym.
Kontrast z wnioskowaniem online. Więcej informacji znajdziesz w sekcji Produkcyjne systemy uczenia maszynowego: wnioskowanie statyczne a dynamiczne w kursie Machine Learning Crash Course.
kodowanie 1 z n,
Reprezentowanie danych kategorialnych jako wektora, w którym:
- Jeden element jest ustawiony na 1.
- Wszystkie pozostałe elementy są ustawione na 0.
Kodowanie 1-z-N jest często używane do reprezentowania ciągów znaków lub identyfikatorów, które mają skończony zbiór możliwych wartości.
Załóżmy na przykład, że pewna cecha kategorialna o nazwie Scandinavia ma 5 możliwych wartości:
- "Dania"
- „Szwecja”
- „Norwegia”
- „Finlandia”
- „Islandia”
Kodowanie 1-z-N może przedstawiać każdą z 5 wartości w ten sposób:
| Kraj | Wektor | ||||
|---|---|---|---|---|---|
| "Dania" | 1 | 0 | 0 | 0 | 0 |
| „Szwecja” | 0 | 1 | 0 | 0 | 0 |
| „Norwegia” | 0 | 0 | 1 | 0 | 0 |
| „Finlandia” | 0 | 0 | 0 | 1 | 0 |
| „Islandia” | 0 | 0 | 0 | 0 | 1 |
Dzięki kodowaniu 1-z-N model może nauczyć się różnych powiązań na podstawie każdego z 5 krajów.
Przedstawienie cechy jako danych liczbowych jest alternatywą dla kodowania 1 z n. Niestety przedstawianie krajów skandynawskich w formie liczbowej nie jest dobrym pomysłem. Na przykład:
- „Dania” to 0
- „Szwecja” to 1
- „Norwegia” to 2
- „Finland” to 3
- „Islandia” to 4
W przypadku kodowania numerycznego model interpretuje surowe liczby matematycznie i próbuje trenować na ich podstawie. Jednak Islandia nie jest w rzeczywistości 2 razy większa (ani 2 razy mniejsza) od Norwegii, więc model wyciągnąłby dziwne wnioski.
Więcej informacji znajdziesz w sekcji Dane kategorialne: słownictwo i kodowanie 1-z-N w kursie Machine Learning Crash Course.
jeden kontra reszta
W przypadku problemu klasyfikacji z N klasami rozwiązanie składające się z N osobnych modeli klasyfikacji binarnej – po jednym modelu klasyfikacji binarnej dla każdego możliwego wyniku. Na przykład w przypadku modelu, który klasyfikuje przykłady jako zwierzę, roślinę lub minerał, rozwiązanie typu „jeden kontra reszta” zapewni te 3 osobne binarne modele klasyfikacji:
- zwierzę lub nie zwierzę,
- warzywo a nie warzywo,
- mineralne lub nie
online
Synonim słowa dynamiczny.
wnioskowanie online,
Generowanie prognoz na żądanie. Załóżmy na przykład, że aplikacja przekazuje dane wejściowe do modelu i wysyła żądanie prognozy. System korzystający z wnioskowania online odpowiada na żądanie, uruchamiając model (i zwracając prognozę do aplikacji).
W przeciwieństwie do wnioskowania offline.
Więcej informacji znajdziesz w sekcji Produkcyjne systemy uczenia maszynowego: wnioskowanie statyczne a dynamiczne w kursie Machine Learning Crash Course.
warstwa wyjściowa,
„Ostatnia” warstwa sieci neuronowej. Warstwa wyjściowa zawiera prognozę.
Ilustracja poniżej przedstawia małą głęboką sieć neuronową z warstwą wejściową, 2 warstwami ukrytymi i warstwą wyjściową:
nadmierne dopasowanie
Tworzenie modelu, który jest tak ściśle dopasowany do danych treningowych, że nie jest w stanie dokonywać prawidłowych prognoz na podstawie nowych danych.
Regularyzacja może zmniejszyć przeuczenie. Trenowanie na dużym i zróżnicowanym zbiorze treningowym może również zmniejszyć przeuczenie.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie w szybkim szkoleniu z uczenia maszynowego.
P
pandy
Interfejs API do analizy danych zorientowany na kolumny, oparty na bibliotece numpy. Wiele platform uczenia maszynowego, w tym TensorFlow, obsługuje struktury danych pandas jako dane wejściowe. Szczegóły znajdziesz w dokumentacji biblioteki pandas.
parametr
Wagi i odchylenia, których model uczy się podczas trenowania. Na przykład w modelu regresji liniowej parametry to wyraz wolny (b) i wszystkie wagi (w1, w2 itd.) w tej formule:
Natomiast hiperparametry to wartości, które Ty (lub usługa dostrajania hiperparametrów) przekazujesz do modelu. Na przykład szybkość uczenia się jest hiperparametrem.
klasa wyników pozytywnych,
Klasa, dla której przeprowadzasz test.
Na przykład klasą pozytywną w modelu do wykrywania raka może być „guz”. Klasą pozytywną w modelu klasyfikacji e-maili może być „spam”.
Porównaj z klasą wyników negatywnych.
przetwarzanie końcowe,
Dostosowywanie danych wyjściowych modelu po jego uruchomieniu. Przetwarzanie końcowe może służyć do wymuszania ograniczeń dotyczących sprawiedliwości bez modyfikowania samych modeli.
Na przykład można zastosować przetwarzanie końcowe w przypadku modelu klasyfikacji binarnej, ustawiając próg klasyfikacji w taki sposób, aby równość szans była zachowana w przypadku danego atrybutu. W tym celu należy sprawdzić, czy odsetek prawdziwie pozytywnych wyników jest taki sam dla wszystkich wartości tego atrybutu.
precyzja
Miara dla modeli klasyfikacji, która odpowiada na to pytanie:
Gdy model przewidział klasę pozytywną, jaki odsetek prognoz był prawidłowy?
Oto wzór:
gdzie:
- Prawdziwie pozytywny wynik oznacza, że model prawidłowo przewidział klasę pozytywną.
- Fałszywie pozytywny wynik oznacza, że model błędnie przewidział klasę pozytywną.
Załóżmy na przykład, że model wygenerował 200 prognoz pozytywnych. Z tych 200 pozytywnych prognoz:
- 150 z nich to wyniki prawdziwie pozytywne.
- 50 z nich to wyniki fałszywie pozytywne.
W tym przypadku:
Porównaj z dokładnością i czułością.
Więcej informacji znajdziesz w sekcji Klasyfikacja: dokładność, czułość, precyzja i powiązane dane w kursie Machine Learning Crash Course.
prognoza
Dane wyjściowe modelu. Na przykład:
- Prognoza modelu klasyfikacji binarnej to klasa pozytywna lub negatywna.
- Prognoza modelu klasyfikacji wieloklasowej to jedna klasa.
- Prognoza modelu regresji liniowej to liczba.
etykiety proxy,
Dane używane do przybliżania etykiet, które nie są bezpośrednio dostępne w zbiorze danych.
Załóżmy na przykład, że musisz wytrenować model do prognozowania poziomu stresu pracowników. Twój zbiór danych zawiera wiele funkcji predykcyjnych, ale nie zawiera etykiety o nazwie stress level. Nie zrażasz się tym i wybierasz „wypadki w miejscu pracy” jako etykietę zastępczą dla poziomu stresu. W końcu pracownicy poddani silnemu stresowi częściej ulegają wypadkom niż ci, którzy są spokojni. A może jednak? Może się okazać, że wypadki w miejscu pracy wzrastają i maleją z różnych powodów.
Inny przykład: załóżmy, że chcesz, aby etykieta logiczna is it raining? (czy pada deszcz?) była częścią Twojego zbioru danych, ale nie zawiera on danych o deszczu. Jeśli dostępne są zdjęcia, możesz uznać zdjęcia osób z parasolami za etykietę zastępczą dla pytania czy pada deszcz? Czy to dobra etykieta zastępcza? Być może, ale w niektórych kulturach ludzie częściej noszą parasole, aby chronić się przed słońcem niż przed deszczem.
Etykiety zastępcze są często niedoskonałe. W miarę możliwości wybieraj rzeczywiste etykiety zamiast etykiet zastępczych. Jeśli jednak brakuje rzeczywistej etykiety, bardzo starannie wybierz etykietę zastępczą, wybierając najmniej szkodliwą z nich.
Więcej informacji znajdziesz w sekcji Zbiory danych: etykiety w szybkim szkoleniu z systemów uczących się.
R
RAG
Skrót od generowania wspomaganego wyszukiwaniem.
oceniający,
Osoba, która przypisuje etykiety do przykładów. „Annotator” to inna nazwa oceniającego.
Więcej informacji znajdziesz w module Dane kategorialne: typowe problemy w kursie Machine Learning Crash Course.
wycofanie
Miara dla modeli klasyfikacji, która odpowiada na to pytanie:
Gdy dane podstawowe należały do klasy pozytywnej, jaki odsetek prognoz został przez model prawidłowo zidentyfikowany jako klasa pozytywna?
Oto wzór:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
gdzie:
- Prawdziwie pozytywny wynik oznacza, że model prawidłowo przewidział klasę pozytywną.
- Fałszywie negatywny wynik oznacza, że model błędnie przewidział klasę negatywną.
Załóżmy na przykład, że model dokonał 200 prognoz na podstawie przykładów, w których prawdziwa klasa to klasa pozytywna. Z tych 200 prognoz:
- 180 z nich to wyniki prawdziwie pozytywne.
- 20 z nich to wyniki fałszywie negatywne.
W tym przypadku:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
Więcej informacji znajdziesz w artykule Klasyfikacja: dokładność, czułość, precyzja i powiązane dane.
Jednostka liniowa z progowaniem (ReLU)
Funkcja aktywacji o tym działaniu:
- Jeśli dane wejściowe są ujemne lub równe zero, dane wyjściowe wynoszą 0.
- Jeśli dane wejściowe są dodatnie, dane wyjściowe są równe danym wejściowym.
Na przykład:
- Jeśli dane wejściowe to -3, dane wyjściowe to 0.
- Jeśli dane wejściowe to +3, dane wyjściowe to 3,0.
Oto wykres funkcji ReLU:
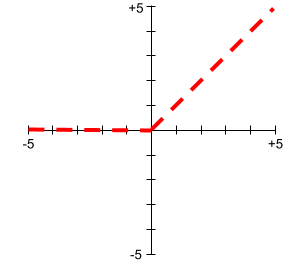
ReLU to bardzo popularna funkcja aktywacji. Pomimo prostego działania funkcja ReLU umożliwia sieci neuronowej uczenie się nieliniowych zależności między cechami a etykietą.
model regresji,
Nieformalnie: model, który generuje prognozę liczbową. (Dla porównania model klasyfikacji generuje prognozę klasy). Na przykład wszystkie te modele to modele regresji:
- Model, który prognozuje wartość określonego domu w euro,np. 423 000.
- Model, który prognozuje średnią długość życia danego drzewa w latach, np.23,2.
- Model, który prognozuje ilość deszczu w calach, jaka spadnie w danym mieście w ciągu najbliższych 6 godzin, np.0,18.
Dwa najpopularniejsze rodzaje modeli regresji to:
- Regresja liniowa, która znajduje linię najlepiej dopasowującą wartości etykiet do cech.
- Regresja logistyczna, która generuje prawdopodobieństwo z przedziału od 0,0 do 1,0, które system zwykle mapuje na prognozę klasy.
Nie każdy model, który generuje prognozy liczbowe, jest modelem regresji. W niektórych przypadkach prognoza numeryczna jest w rzeczywistości modelem klasyfikacji, który ma numeryczne nazwy klas. Na przykład model, który prognozuje numeryczny kod pocztowy, jest modelem klasyfikacji, a nie modelem regresji.
regularyzacja
Każdy mechanizm, który zmniejsza nadmierne dopasowanie. Popularne typy regularyzacji to:
- Regularyzacja L1
- Regularyzacja L2
- regularyzacja przez wyłączanie,
- wczesne zatrzymanie (nie jest to formalna metoda regularyzacji, ale może skutecznie ograniczać przetrenowanie);
Regularyzację można też zdefiniować jako karę za złożoność modelu.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie: złożoność modelu w kursie Machine Learning Crash Course.
współczynnik regularyzacji
Liczba określająca względne znaczenie regularyzacji podczas trenowania. Zwiększenie współczynnika regularyzacji zmniejsza nadmierne dopasowanie, ale może zmniejszyć moc predykcyjną modelu. Z kolei zmniejszenie lub pominięcie współczynnika regularyzacji zwiększa przetrenowanie.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie: regularyzacja L2 w szybkim szkoleniu z uczenia maszynowego.
ReLU
Skrót od Rectified Linear Unit.
generowanie wspomagane wyszukiwaniem
Technika poprawiająca jakość danych wyjściowych dużego modelu językowego (LLM) poprzez powiązanie ich ze źródłami wiedzy pobranymi po wytrenowaniu modelu. RAG zwiększa dokładność odpowiedzi LLM, zapewniając wytrenowanemu modelowi LLM dostęp do informacji pobranych z zaufanych baz wiedzy lub dokumentów.
Najczęstsze powody korzystania z generowania z wyszukiwaniem to:
- Zwiększanie dokładności generowanych przez model odpowiedzi.
- Udostępnianie modelowi wiedzy, na której nie został wytrenowany.
- zmieniać wiedzę, z której korzysta model;
- umożliwienie modelowi cytowania źródeł;
Załóżmy na przykład, że aplikacja do chemii korzysta z interfejsu PaLM API do generowania podsumowań związanych z zapytaniami użytkowników. Gdy backend aplikacji otrzyma zapytanie:
- Wyszukuje (czyli „pobiera”) dane pasujące do zapytania użytkownika.
- Dołącza („wzbogaca”) odpowiednie dane chemiczne do zapytania użytkownika.
- Instruuje model LLM, aby utworzył podsumowanie na podstawie dołączonych danych.
Krzywa charakterystyki operacyjnej odbiornika (ROC)
Wykres przedstawiający odsetek prawdziwie pozytywnych wyników w porównaniu z odsetkiem fałszywie pozytywnych wyników dla różnych progów klasyfikacji w klasyfikacji binarnej.
Kształt krzywej ROC wskazuje na zdolność modelu klasyfikacji binarnej do oddzielania klas pozytywnych od negatywnych. Załóżmy na przykład, że binarny model klasyfikacji doskonale oddziela wszystkie klasy negatywne od wszystkich klas pozytywnych:
Krzywa ROC poprzedniego modelu wygląda tak:
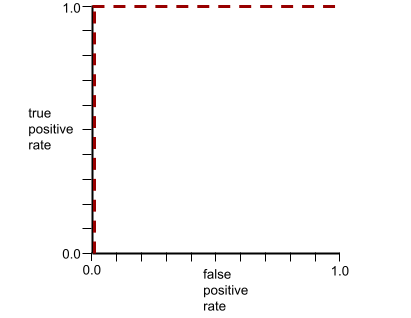
Z kolei na poniższej ilustracji przedstawiono surowe wartości regresji logistycznej w przypadku bardzo słabego modelu, który w ogóle nie potrafi odróżnić klas negatywnych od pozytywnych:
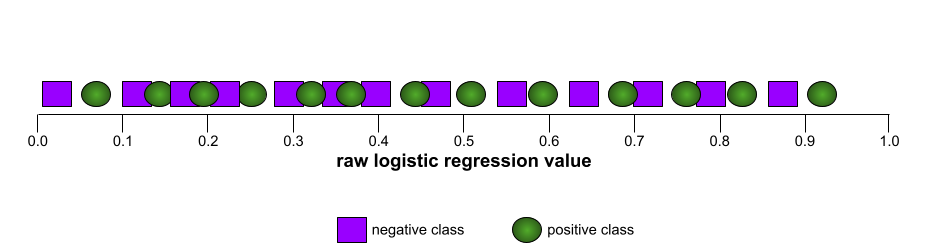
Krzywa ROC tego modelu wygląda tak:
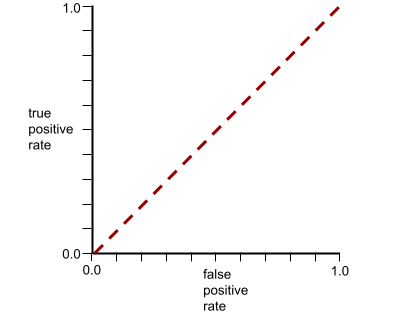
W rzeczywistości większość modeli klasyfikacji binarnej w pewnym stopniu rozdziela klasy pozytywne i negatywne, ale zwykle nie robi tego idealnie. Typowa krzywa ROC znajduje się więc gdzieś pomiędzy tymi dwoma skrajnościami:
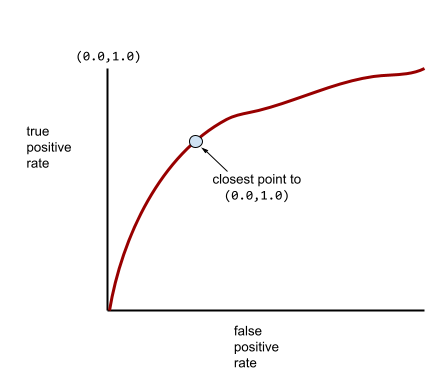
Punkt na krzywej ROC najbliższy punktowi (0,0, 1,0) teoretycznie określa idealny próg klasyfikacji. Na wybór idealnego progu klasyfikacji wpływa jednak kilka innych problemów z rzeczywistego świata. Na przykład fałszywe negatywy mogą być znacznie bardziej uciążliwe niż fałszywe pozytywy.
Podsumowaniem krzywej ROC jest wartość liczbowa o nazwie AUC, która jest pojedynczą liczbą zmiennoprzecinkową.
Średnia kwadratowa błędów (RMSE)
Pierwiastek kwadratowy z błędu średniokwadratowego.
S
funkcja sigmoid
Funkcja matematyczna, która „ściska” wartość wejściową do ograniczonego zakresu, zwykle od 0 do 1 lub od -1 do +1. Oznacza to, że możesz przekazać do funkcji sigmoidalnej dowolną liczbę (2, milion, minus miliard itp.), a wynik nadal będzie mieścił się w określonym zakresie. Wykres funkcji aktywacji sigmoid wygląda tak:

Funkcja sigmoid ma kilka zastosowań w uczeniu maszynowym, m.in.:
- Przekształcanie surowych danych wyjściowych modelu regresji logistycznej lub regresji wielomianowej w prawdopodobieństwo.
- Pełni funkcję funkcji aktywacji w niektórych sieciach neuronowych.
funkcja softmax
Funkcja, która określa prawdopodobieństwa dla każdej możliwej klasy w modelu klasyfikacji wieloklasowej. Suma prawdopodobieństw wynosi dokładnie 1,0. Na przykład w tabeli poniżej pokazujemy, jak funkcja softmax rozdziela różne prawdopodobieństwa:
| Obraz jest… | Prawdopodobieństwo |
|---|---|
| pies | 0,85 |
| kot | 0,13 |
| koń | 0,02 |
Funkcja softmax jest też nazywana pełną funkcją softmax.
Porównaj z próbkowaniem kandydatów.
Więcej informacji znajdziesz w sekcji Sieci neuronowe: klasyfikacja wieloklasowa w kursie Machine Learning Crash Course.
rzadka cecha,
Cechy, których wartości są w większości zerowe lub puste. Na przykład cecha zawierająca jedną wartość 1 i milion wartości 0 jest rzadka. Z kolei gęsta cecha ma wartości, które w większości nie są zerowe ani puste.
W uczeniu maszynowym zaskakująco wiele cech to cechy rzadkie. Funkcje kategorialne są zwykle rzadkie. Na przykład spośród 300 gatunków drzew rosnących w lesie pojedynczy przykład może wskazywać tylko klon. Lub z milionów możliwych filmów w bibliotece filmów pojedynczy przykład może identyfikować tylko „Casablancę”.
W modelu cechy rzadkie są zwykle reprezentowane za pomocą kodowania 1 z n. Jeśli kodowanie 1 z n jest duże, możesz umieścić na nim warstwę wektora dystrybucyjnego, aby zwiększyć wydajność.
rozproszona reprezentacja,
Przechowywanie tylko pozycji elementów o wartościach różnych od zera w rzadkim wektorze cech.
Załóżmy na przykład, że cecha kategorialna o nazwie species identyfikuje 36
gatunków drzew w określonym lesie. Załóżmy też, że każdy przykład identyfikuje tylko jeden gatunek.
W każdym przykładzie możesz użyć wektora typu one-hot do reprezentowania gatunku drzewa.
Wektor typu one-hot zawierałby jedną wartość 1 (reprezentującą w tym przykładzie konkretny gatunek drzewa) i 35 wartości 0 (reprezentujących 35 gatunków drzew, które nie występują w tym przykładzie). Reprezentacja maple w formie kodowania 1-z-N może wyglądać tak:

Alternatywnie rzadka reprezentacja po prostu identyfikuje pozycję danego gatunku. Jeśli maple znajduje się na pozycji 24, rzadka reprezentacja maple będzie wyglądać tak:
24
Zwróć uwagę, że rzadka reprezentacja jest znacznie bardziej zwarta niż reprezentacja typu one-hot.
Więcej informacji znajdziesz w sekcji Praca z danymi kategorialnymi w kursie Machine Learning Crash Course.
wektor rzadki,
Wektor, którego wartości to w większości zera. Zobacz też rzadkie i rzadkość.
strata kwadratowa,
Synonim terminu utrata L2.
statyczne
Coś, co jest wykonywane raz, a nie w sposób ciągły. Terminy statyczny i offline są synonimami. Oto typowe zastosowania statycznych i offline w uczeniu maszynowym:
- Model statyczny (lub model offline) to model, który jest trenowany raz, a potem używany przez pewien czas.
- Trenowanie statyczne (lub trenowanie offline) to proces trenowania modelu statycznego.
- Wnioskowanie statyczne (lub wnioskowanie offline) to proces, w którym model generuje partię prognoz naraz.
Kontrast z dynamicznym.
wnioskowanie statyczne,
Synonim terminu wnioskowanie offline.
stacjonarność,
Cechy, których wartości nie zmieniają się w przypadku co najmniej jednego wymiaru, zwykle czasu. Na przykład cecha, której wartości w 2021 r. i 2023 r. są podobne, wykazuje stacjonarność.
W rzeczywistości bardzo niewiele cech wykazuje stacjonarność. Nawet cechy synonimiczne ze stabilnością (np. poziom morza) zmieniają się z czasem.
Porównaj z niestacjonarnością.
stochastyczny spadek wzdłuż gradientu (SGD),
Algorytm spadku gradientowego, w którym rozmiar partii wynosi 1. Innymi słowy, SGD trenuje na jednym przykładzie wybranym losowo z zbioru treningowego.
Więcej informacji znajdziesz w sekcji Regresja liniowa: hiperparametry w kursie Machine Learning Crash Course.
nadzorowane uczenie maszynowe
Trenowanie modelu na podstawie cech i odpowiadających im etykiet. Uczenie nadzorowane jest podobne do uczenia się danego przedmiotu przez studiowanie zestawu pytań i odpowiedzi. Po opanowaniu mapowania pytań i odpowiedzi uczeń może udzielać odpowiedzi na nowe (nigdy wcześniej nie widziane) pytania dotyczące tego samego tematu.
Porównaj z nienadzorowanym uczeniem maszynowym.
Więcej informacji znajdziesz w sekcji dotyczącej uczenia nadzorowanego w kursie Wprowadzenie do uczenia maszynowego.
cecha syntetyczna,
Cechy, których nie ma wśród cech wejściowych, ale które są tworzone na podstawie co najmniej jednej z nich. Metody tworzenia cech syntetycznych obejmują:
- Podział cechy ciągłej na zasobniki zakresu.
- Tworzenie kombinacji cech.
- Mnożenie (lub dzielenie) jednej wartości cechy przez inne wartości cech lub przez samą siebie. Jeśli np.
aibsą cechami wejściowymi, to przykłady cech syntetycznych to:- ab
- a2
- Zastosowanie funkcji transcendentalnej do wartości cechy. Jeśli np.
cjest cechą wejściową, to przykłady cech syntetycznych to:- sin(c)
- ln(c)
Funkcje utworzone przez normalizację lub skalowanie nie są uznawane za funkcje syntetyczne.
T
strata testowa
Wartość reprezentująca stratę modelu w odniesieniu do zbioru testowego. Podczas tworzenia modelu zwykle starasz się zminimalizować utratę w teście. Dzieje się tak, ponieważ niski błąd testowy jest silniejszym sygnałem jakości niż niski błąd trenowania lub niski błąd weryfikacji.
Duża różnica między stratą na zbiorze testowym a stratą na zbiorze treningowym lub walidacyjnym może sugerować, że musisz zwiększyć współczynnik regularyzacji.
szkolenie
Proces określania optymalnych parametrów (wag i odchyleń) tworzących model. Podczas trenowania system odczytuje przykłady i stopniowo dostosowuje parametry. Podczas trenowania każdy przykład jest wykorzystywany od kilku do miliardów razy.
Więcej informacji znajdziesz w sekcji dotyczącej uczenia nadzorowanego w kursie Wprowadzenie do uczenia maszynowego.
strata podczas trenowania,
Wskaźnik reprezentujący stratę modelu podczas konkretnej iteracji trenowania. Załóżmy na przykład, że funkcja straty to błąd średniokwadratowy. Załóżmy, że strata treningowa (średni błąd kwadratowy) w 10 iteracji wynosi 2,2, a w 100 iteracji – 1,9.
Krzywa straty przedstawia stratę podczas trenowania w zależności od liczby iteracji. Krzywa straty zawiera następujące wskazówki dotyczące trenowania:
- Spadek oznacza, że model się poprawia.
- Wznosząca się linia oznacza, że model się pogarsza.
- Płaska krzywa oznacza, że model osiągnął zbieżność.
Na przykład poniższa nieco wyidealizowana krzywa strat pokazuje:
- Strome nachylenie w dół w początkowych iteracjach, co oznacza szybką poprawę modelu.
- Stopniowo spłaszczająca się (ale nadal opadająca) krzywa aż do końca trenowania, co oznacza dalsze ulepszanie modelu w nieco wolniejszym tempie niż w początkowych iteracjach.
- Płaski spadek pod koniec szkolenia, co sugeruje zbieżność.
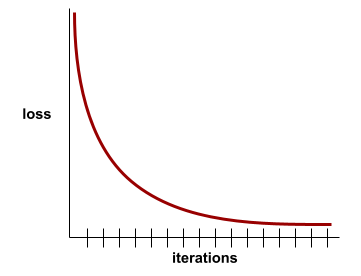
Chociaż strata podczas trenowania jest ważna, zobacz też uogólnianie.
zniekształcenie między trenowaniem a zastosowaniem praktycznym
Różnica między skutecznością modelu podczas trenowania a skutecznością tego samego modelu podczas wdrażania.
zbiór treningowy,
Podzbiór zbioru danych używany do trenowania modelu.
Przykłady w zbiorze danych są zwykle dzielone na 3 odrębne podzbiory:
- zbiór treningowy,
- zbiór walidacyjny,
- zbiór testowy,
Najlepiej, aby każdy przykład w zbiorze danych należał tylko do jednego z powyższych podzbiorów. Na przykład pojedynczy przykład nie powinien należeć zarówno do zbioru treningowego, jak i do zbioru do weryfikacji.
Więcej informacji znajdziesz w sekcji Zbiory danych: dzielenie pierwotnego zbioru danych w szybkim szkoleniu z uczenia maszynowego.
wynik prawdziwie negatywny (TN)
Przykład, w którym model prawidłowo przewiduje klasę negatywną. Na przykład model wnioskuje, że dany e-mail nie jest spamem, i rzeczywiście nie jest spamem.
wynik prawdziwie pozytywny (TP),
Przykład, w którym model prawidłowo prognozuje klasę pozytywną. Na przykład model wnioskuje, że dany e-mail to spam, i rzeczywiście tak jest.
współczynnik wyników prawdziwie pozytywnych (TPR)
Synonim słowa wycofanie. Czyli:
Współczynnik wyników prawdziwie pozytywnych jest osią Y na krzywej ROC.
U
niedopasowanie
Utworzenie modelu o słabych możliwościach prognozowania, ponieważ nie w pełni uchwycił on złożoności danych treningowych. Niedopasowanie może być spowodowane wieloma problemami, w tym:
- Trenowanie na niewłaściwym zestawie cech.
- Trenowanie przez zbyt małą liczbę epok lub przy zbyt niskim współczynniku uczenia się.
- Trenowanie z zbyt wysokim współczynnikiem regularyzacji.
- Zbyt mała liczba warstw ukrytych w głębokiej sieci neuronowej.
Więcej informacji znajdziesz w sekcji Nadmierne dopasowanie w szybkim szkoleniu z uczenia maszynowego.
nieoznaczony przykład,
Przykład, który zawiera funkcje, ale nie ma etykiety. Na przykład w tabeli poniżej przedstawiono 3 nieoznaczone przykłady z modelu wyceny domu. Każdy z nich ma 3 cechy, ale nie ma wartości domu:
| Liczba sypialni | Liczba łazienek | Wiek domu |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
W nadzorowanym uczeniu maszynowym modele są trenowane na oznaczonych przykładach i dokonują prognoz na podstawie nieoznaczonych przykładów.
W uczeniu częściowo nadzorowanym i nienadzorowanym podczas trenowania używane są przykłady bez etykiet.
Porównaj nieoznaczony przykład z oznaczonym przykładem.
nienadzorowane uczenie maszynowe
Trenowanie modelu w celu znajdowania wzorców w zbiorze danych, zwykle w zbiorze danych bez etykiet.
Najczęstszym zastosowaniem nienadzorowanego uczenia maszynowego jest grupowanie danych w grupy podobnych przykładów. Na przykład algorytm uczenia maszynowego bez nadzoru może grupować utwory na podstawie różnych właściwości muzyki. Powstałe klastry mogą być danymi wejściowymi dla innych algorytmów uczenia maszynowego (np. dla usługi rekomendacji muzyki). Grupowanie może być przydatne, gdy brakuje przydatnych etykiet. Na przykład w przypadku domen takich jak przeciwdziałanie nadużyciom i oszustwom klastry mogą pomóc ludziom lepiej zrozumieć dane.
Porównaj z nadzorowanym uczeniem maszynowym.
Więcej informacji znajdziesz w sekcji Czym jest uczenie maszynowe? w kursie Wprowadzenie do uczenia maszynowego.
V
walidacja
Wstępna ocena jakości modelu. Weryfikacja sprawdza jakość prognoz modelu na podstawie zbioru weryfikacyjnego.
Ponieważ zbiór weryfikacyjny różni się od zbioru treningowego, weryfikacja pomaga zapobiegać przetrenowaniu.
Ocenę modelu na podstawie zbioru walidacyjnego możesz traktować jako pierwszą rundę testów, a ocenę modelu na podstawie zbioru testowego jako drugą rundę testów.
strata weryfikacji,
Metryka reprezentująca stratę modelu w zbiorze weryfikacyjnym podczas konkretnej iteracji trenowania.
Zobacz też krzywą generalizacji.
zbiór walidacyjny,
Podzbiór zbioru danych, który przeprowadza wstępną ocenę wytrenowanego modelu. Zwykle wytrenowany model jest oceniany na podstawie zbioru walidacyjnego kilka razy, zanim zostanie oceniony na podstawie zbioru testowego.
Zwykle przykłady w zbiorze danych dzieli się na 3 odrębne podzbiory:
- zbiór treningowy,
- zbiór walidacyjny,
- zbiór testowy,
Najlepiej, aby każdy przykład w zbiorze danych należał tylko do jednego z powyższych podzbiorów. Na przykład pojedynczy przykład nie powinien należeć zarówno do zbioru treningowego, jak i do zbioru do weryfikacji.
Więcej informacji znajdziesz w sekcji Zbiory danych: dzielenie pierwotnego zbioru danych w szybkim szkoleniu z uczenia maszynowego.
W
waga
Wartość, przez którą model mnoży inną wartość. Trenowanie to proces określania idealnych wag modelu. Wnioskowanie to proces wykorzystywania tych wyuczonych wag do prognozowania.
Więcej informacji znajdziesz w sekcji Regresja liniowa w szybkim szkoleniu z uczenia maszynowego.
suma ważona
Suma wszystkich odpowiednich wartości wejściowych pomnożonych przez odpowiadające im wagi. Załóżmy na przykład, że odpowiednie dane wejściowe to:
| wartość wejściowa, | waga wejściowa |
| 2 | -1,3 |
| -1 | 0,6 |
| 3 | 0,4 |
Suma ważona wynosi więc:
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
Suma ważona jest argumentem wejściowym funkcji aktywacji.
Z
Normalizacja standaryzacji Z
Technika skalowania, która zastępuje surową wartość cechy wartością zmiennoprzecinkową reprezentującą liczbę odchyleń standardowych od średniej tej cechy. Weźmy na przykład cechę, której średnia wynosi 800, a odchylenie standardowe – 100. W tabeli poniżej pokazujemy, jak normalizacja za pomocą wyniku z (Z-score) przekształca wartość surową w wynik z:
| Wartość nieprzetworzona | Standaryzacja Z |
|---|---|
| 800 | 0 |
| 950 | +1,5 |
| 575 | -2,25 |
Model uczenia maszynowego jest następnie trenowany na podstawie wyników z-score dla tej cechy, a nie na podstawie wartości surowych.
Więcej informacji znajdziesz w sekcji Dane liczbowe: normalizacja w kursie Machine Learning Crash Course.