機器學習詞彙：指標

本頁面包含指標詞彙表。如要查看所有詞彙，請按這裡。

A

精確度

#fundamentals

#指標

正確分類預測次數除以預測總次數。也就是：

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

舉例來說，如果模型做出 40 項正確預測和 10 項錯誤預測，準確率為：

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

二元分類會為正確預測和不正確預測的不同類別提供特定名稱。因此，二元分類的準確度公式如下：

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

其中：

• TP 是真陽性 (正確預測) 的數量。
• TN 是真陰性 (正確預測) 的數量。
• FP 是偽陽性 (不正確預測) 的數量。
• FN 是偽陰性 (不正確預測) 的數量。

比較準確率與精確度和喚回度的異同。

按一下圖示，即可查看準確度和類別不平衡資料集的詳細資料。

雖然準確率在某些情況下是很有價值的指標，但在其他情況下卻可能造成誤導。請注意，準確度通常不適合用來評估處理類別不平衡資料集的分類模型。

舉例來說，假設某個亞熱帶城市每世紀只會下雪 25 天，由於無雪天數 (負類別) 遠多於有雪天數 (正類別)，因此這個城市的降雪資料集屬於不平衡資料集。假設有個二元分類模型每天都會預測是否會下雪，但每天都只預測「不會下雪」。這個模型非常準確，但沒有預測能力。 下表摘要列出百年預測結果：

類別	數字
TP	0
TN	36499
FP	0
FN	25

因此，這個模型的準確度為：

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

雖然 99.93% 的準確率看起來非常驚人，但模型實際上沒有預測能力。

對於在類別不平衡資料集上訓練的模型，精確度和喚回度通常比準確率更有用。

---

詳情請參閱機器學習速成課程中的「分類：準確度、喚回率、精確度和相關指標」。

PR 曲線下面積

#指標

請參閱「PR AUC (PR 曲線下的面積)」。

ROC 曲線下面積

#指標

請參閱 AUC (ROC 曲線下面積)。

AUC (ROC 曲線下面積)

#fundamentals

#指標

介於 0.0 和 1.0 之間的數字，代表二元分類模型區分正類和負類的能力。AUC 越接近 1.0，代表模型區分各類別的能力越好。

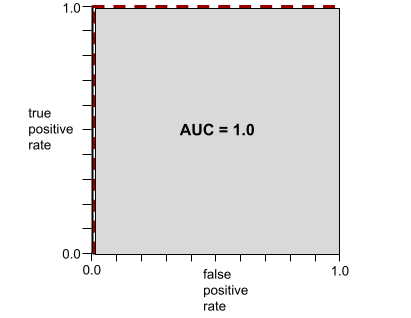
舉例來說，下圖顯示分類模型完美區分正類 (綠色橢圓) 和負類 (紫色矩形)。這個不切實際的完美模型 AUC 值為 1.0：

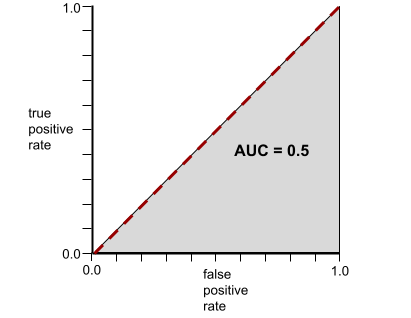
反之，下圖顯示分類模型產生隨機結果時的結果。這個模型的 AUC 為 0.5：

是，前一個模型的 AUC 為 0.5，而非 0.0。

大多數模型都介於這兩個極端之間。舉例來說，下列模型會將正向和負向結果分開，因此 AUC 值介於 0.5 和 1.0 之間：

AUC 會忽略您為分類閾值設定的任何值。AUC 則會考量所有可能的分類門檻。

按一下圖示，瞭解 AUC 和 ROC 曲線之間的關係。

AUC 代表 ROC 曲線下的面積。舉例來說，如果模型能完美區分正類和負類，ROC 曲線會如下所示：

AUC 是上圖中灰色區域的面積。 在這個特殊情況下，面積就是灰色區域的長度 (1.0) 乘以寬度 (1.0)。因此，1.0 和 1.0 的乘積會產生 AUC 值 1.0，這是最高的 AUC 分數。

反之，如果分類模型完全無法區分類別，ROC 曲線如下。這個灰色區域的面積為 0.5。

更典型的 ROC 曲線大致如下所示：

手動計算這條曲線下的面積非常費力，因此通常會由程式計算大多數 AUC 值。

---

按一下圖示，即可查看 AUC 的正式定義。

AUC 是指分類模型認為隨機挑選的正向樣本確實為正向的機率，比隨機挑選的負向樣本為正向的機率還要高。

---

詳情請參閱機器學習速成課程中的「分類：ROC 和 AUC」。

k 的平均精確度

#指標

這項指標會彙整模型在單一提示中的成效，並產生排序結果，例如書籍建議的編號清單。k 的平均精確度，就是每個相關結果的 k 精確度值的平均值。因此，k 的平均精確度公式為：

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

其中：

• \(n\) 是清單中相關項目的數量。

與 recall@k 對比。

注意： k 的平均精確度會評估單一提示的輸出內容。使用 k 值的平均精確度，評估模型在許多不同提示下的輸出品質。

注意： 有些人會將 k 值的平均精確度簡稱為平均精確度。

按一下圖示即可聆聽範例

假設大型語言模型收到下列查詢：

List the 6 funniest movies of all time in order.

大型語言模型會傳回下列清單：

1. 將軍
2. 辣妹過招
3. Platoon
4. 《伴娘我最大》
5. 大國民
6. This is Spinal Tap

傳回清單中的四部電影非常有趣 (也就是相關)，但有兩部是劇情片 (不相關)。下表詳細列出結果：

位置	電影	是否相關？	前 k 項的精確度
1	將軍	是	1.0
2	辣妹過招	是	1.0
3	Platoon	否	不相關
4	《伴娘我最大》	是	0.75
5	大國民	否	不相關
6	This is Spinal Tap	是	0.67

相關結果數量為 4。因此，您可以按照以下方式計算 6 的平均精確度：

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

基準

#指標

用來做為參考點的模型，可比較另一個模型 (通常是較複雜的模型) 的效能。舉例來說，邏輯迴歸模型可能適合作為深層模型的良好基準。

針對特定問題，基準可協助模型開發人員量化新模型必須達成的最低預期成效，新模型才能派上用場。

C

費用

#指標

loss 的同義詞。

反事實公平性

#responsible

#指標

這項公平性指標會檢查分類模型是否會為某位使用者產生結果，並為與該使用者完全相同 (但一或多項敏感屬性除外) 的使用者產生相同結果。評估分類模型的反事實公平性，是找出模型中潛在偏差來源的方法之一。

詳情請參閱下列任一文章：

• 公平性：機器學習密集課程中的反事實公平性。
• When Worlds Collide：在公平性中整合不同的反事實假設

交叉熵

#指標

對數損失的一般化，適用於多重分類問題。交叉熵可量化兩種機率分布之間的差異。另請參閱 困惑度。

累積分佈函式 (CDF)

#指標

這個函式會定義小於或等於目標值的樣本頻率。舉例來說，請考慮連續值的常態分布。 CDF 會告訴您，大約 50% 的樣本應小於或等於平均值，大約 84% 的樣本應小於或等於平均值加上一個標準差。

D

群體均等

#responsible

#指標

如果模型分類結果不取決於特定敏感屬性，即符合公平性指標。

舉例來說，如果小人國人和大人國人都申請進入格魯布達布德里布大學，只要兩國人錄取率相同，就可達到人口統計均等，無論其中一組的平均資格是否優於另一組。

與均等機率和機會均等形成對比，後兩者允許分類結果匯總取決於私密屬性，但不允許特定基本事實標籤的分類結果取決於私密屬性。如要查看視覺化資料，瞭解在盡量達到人口統計資料同等性時的取捨考量，請參閱「以更智慧的機器學習對抗歧視」。

詳情請參閱機器學習速成課程中的「公平性：人口統計均等」。

E

推土機距離 (EMD)

#指標

用來評估兩個分布的相對相似度。 地球移動距離越小，表示分布越相似。

編輯距離

#指標

用來測量兩個字串的相似程度。 在機器學習中，編輯距離有以下用途：

• 編輯距離很容易計算。
• 編輯距離可比較兩個已知相似的字串。
• 編輯距離可判斷不同字串與指定字串的相似程度。

編輯距離有多種定義，每種定義都使用不同的字串作業。請參閱 Levenshtein 距離範例。

實證累積分佈函式 (eCDF 或 EDF)

#指標

根據實際資料集中的實證測量結果，建立累積分布函數。沿著 x 軸的任何一點，函式的值都是資料集中小於或等於指定值的觀測值比例。

熵

#df

#指標

在 資訊理論中，熵是用來描述機率分布的不可預測程度。或者，熵也可以定義為每個樣本所含的資訊量。當隨機變數的所有值都同樣可能發生時，分配的熵最高。

如果集合有兩個可能的值「0」和「1」(例如二元分類問題中的標籤)，則熵的公式如下：

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

其中：

• H 是熵。
• p 是「1」範例的分數。
• q 是「0」範例的分數。請注意，q = (1 - p)
• 記錄通常是記錄 ₂。在本例中，熵單位為位元。

舉例來說，假設：

• 100 個範例包含值「1」
• 300 個範例包含值「0」

因此，熵值為：

• p = 0.25
• q = 0.75
• H = (-0.25)log₂(0.25) - (0.75)log₂(0.75) = 每個範例 0.81 位元

如果資料集完全平衡 (例如 200 個「0」和 200 個「1」)，每個樣本的熵為 1.0 位元。當集合變得越不平衡，其熵值就會越接近 0.0。

在決策樹中，熵有助於制定資訊增益，協助分割器在分類決策樹成長期間選取條件。

比較熵值與：

• 吉尼不純度
• 交叉熵損失函式

熵通常稱為「香農熵」。

詳情請參閱「Exact splitter for binary classification with numerical features」(使用精確分割器搭配數值特徵進行二元分類) 課程。

機會平等

#responsible

#指標

公平性指標：評估模型是否能對敏感屬性的所有值，做出同樣準確的預測。換句話說，如果模型的理想結果是正類，目標就是讓所有群組的真陽性率相同。

機會均等與均等勝算有關，兩者都要求所有群組的真陽率和偽陽率相同。

假設 Glubbdubdrib 大學的嚴格數學課程同時招收小人國和大人國的學生。Lilliputians 的中學提供紮實的數學課程，絕大多數學生都有資格參加大學課程。Brobdingnagians 的中學完全不提供數學課程，因此合格的學生少得多。如果無論學生是小人國人還是大人國人，只要符合資格，錄取機率都相同，則就國籍 (小人國或大人國) 而言，偏好的「錄取」標籤即符合機會均等原則。

舉例來說，假設有 100 位小人國人和 100 位大人國人申請進入 Glubbdubdrib 大學，而入學決定如下：

表 1. Lilliputian 申請者 (90% 符合資格)

	晉級	不合格
已錄取	45	3
已遭拒	45	7
總計	90	10
符合資格的學生錄取百分比：45/90 = 50% 不符合資格的學生遭拒百分比：7/10 = 70% 小人國學生總錄取百分比：(45+3)/100 = 48%

 

表 2. Brobdingnagian 申請者 (10% 符合資格)：

	晉級	不合格
已錄取	5	9
已遭拒	5	81
總計	10	90
符合資格的學生錄取率：5/10 = 50% 不符合資格的學生拒絕率：81/90 = 90% Brobdingnagian 學生總錄取率：(5+9)/100 = 14%

上述例子符合接受合格學生的機會均等原則，因為合格的 Lilliputians 和 Brobdingnagians 都有 50% 的入學機會。

雖然滿足機會均等，但下列兩項公平性指標不符合條件：

• 群體均等：小人國人和大人國人進入大學的比例不同；小人國學生有 48% 能進入大學，但大人國學生只有 14% 能進入大學。
• 均等機會：符合資格的 Lilliputian 和 Brobdingnagian 學生都有相同的入學機會，但額外限制 (不符合資格的 Lilliputian 和 Brobdingnagian 學生都有相同的拒絕機會) 並不符合。不符合資格的 Lilliputian 遭拒率為 70%，不符合資格的 Brobdingnagian 遭拒率則為 90%。

詳情請參閱機器學習速成課程中的「公平性：機會均等」。

等化勝算

#responsible

#指標

這項公平性指標可評估模型是否能針對敏感屬性的所有值，對正類和負類做出同樣準確的預測，而不僅限於其中一類。換句話說，所有群組的真陽率和偽陰率應相同。

均等機會與機會均等有關，後者只著重於單一類別 (正或負) 的錯誤率。

舉例來說，假設 Glubbdubdrib 大學的嚴格數學課程同時招收小人國和大腳國的學生。Lilliputians 的中學提供完善的數學課程，絕大多數學生都符合大學課程的資格。Brobdingnagian 的中學完全沒有數學課，因此合格的學生少得多。只要申請人符合資格，無論是小人國或大人國的人，都有同等機會獲准加入該計畫，若不符合資格，則有同等機會遭到拒絕，即滿足均等機會條件。

假設有 100 名小人國人和 100 名大人國人申請進入 Glubbdubdrib 大學，而入學決定如下：

表 3. Lilliputian 申請者 (90% 符合資格)

	晉級	不合格
已錄取	45	2
已遭拒	45	8
總計	90	10
符合資格的學生錄取百分比：45/90 = 50% 不符合資格的學生遭拒百分比：8/10 = 80% 小人國學生總錄取百分比：(45+2)/100 = 47%

 

表 4. Brobdingnagian 申請者 (10% 符合資格)：

	晉級	不合格
已錄取	5	18
已遭拒	5	72
總計	10	90
符合資格的學生錄取率：5/10 = 50% 不符合資格的學生拒絕率：72/90 = 80% Brobdingnagian 學生總錄取率：(5+18)/100 = 23%

由於符合資格的 Lilliputian 和 Brobdingnagian 學生都有 50% 的入學機會，不符合資格的學生則有 80% 的機率遭到拒絕，因此滿足了均等機率條件。

注意： 雖然這裡符合均等機率，但客層均等不符合。Lilliputian 和 Brobdingnagian 學生以不同比率進入 Glubbdubdrib 大學；47% 的 Lilliputian 學生獲准入學，而 Brobdingnagian 學生則有 23% 獲准入學。

「機會均等」的正式定義請參閱「Equality of Opportunity in Supervised Learning」(監督式學習中的機會均等) 一文，如下所示：「如果預測值 Ŷ 和受保護屬性 A 相互獨立，且以 Y 為條件，則預測值 Ŷ 會滿足受保護屬性 A 和結果 Y 的機會均等條件。」

注意： 請將「機會均等」與較寬鬆的「機會均等」指標進行比較。

evals

#generativeAI

#指標

主要用來做為大型語言模型評估的縮寫。 廣義來說，評估是任何形式的評估縮寫。

評估

#generativeAI

#指標

評估模型品質或比較不同模型成效的程序。

如要評估監督式機器學習模型，通常會根據驗證集和測試集進行評估。評估 LLM 通常需要進行更廣泛的品質和安全評估。

F

F₁

#指標

「匯總」二元分類指標，同時依據精確度和喚回度。公式如下：

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

按一下圖示即可查看範例。

假設精確度和召回率的值如下：

• 精確度 = 0.6
• recall = 0.4

F₁ 的計算方式如下：

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

當精確度和召回率相當接近時 (如上例所示)，F₁ 會接近兩者的平均值。如果精確度和召回率差異顯著，F₁ 會較接近較低的值。例如：

• 精確度 = 0.9
• recall = 0.1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

公平性指標

#responsible

#指標

可衡量的「公平性」數學定義。常用的公平性指標包括：

• 等化勝算
• 預測對等性
• 反事實公平性
• 群體均等

許多公平性指標互斥，請參閱公平性指標互相衝突。

偽陰性 (FN)

#fundamentals

#指標

模型錯誤預測負類的例子。舉例來說，模型預測某封電子郵件不是垃圾郵件 (負面類別)，但該郵件實際上是垃圾郵件。

偽陰率

#指標

模型錯誤預測為負類的實際正類範例比例。下列公式可計算偽陰性率：

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

詳情請參閱機器學習速成課程中的「門檻和混淆矩陣」。

偽陽性 (FP)

#fundamentals

#指標

舉例來說，模型錯誤預測正類。舉例來說，模型預測特定電子郵件是垃圾郵件 (正類)，但該電子郵件其實不是垃圾郵件。

詳情請參閱機器學習速成課程中的「門檻和混淆矩陣」。

偽陽率 (FPR)

#fundamentals

#指標

模型錯誤預測為正類的實際負例比例。下列公式可計算出誤報率：

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

偽陽率是 ROC 曲線的 x 軸。

詳情請參閱機器學習速成課程中的「分類：ROC 和 AUC」。

特徵重要性

#df

#指標

變數重要性的同義詞。

基礎模型

#generativeAI

#指標

這類模型經過訓練，可處理大量多樣的訓練集，是極為龐大的預先訓練模型。基礎模型可以執行下列兩項操作：

• 能妥善回應各種要求。
• 做為額外微調或其他自訂作業的基礎模型。

換句話說，基礎模型在一般情況下已具備強大功能，但可進一步自訂，以更有效率地完成特定工作。

成功次數比例

#generativeAI

#指標

用於評估機器學習模型生成文字的指標。 成功率是指「成功」生成的文字輸出內容數量，除以生成的文字輸出內容總數。舉例來說，如果大型語言模型生成 10 個程式碼區塊，其中 5 個成功，則成功率為 50%。

雖然成功率在整個統計領域都很有用，但在 ML 中，這項指標主要用於評估可驗證的任務，例如程式碼生成或數學問題。

G

吉尼不純度

#df

#指標

與熵類似的指標。分割器 會使用從吉尼不純度或熵值衍生的值，組成用於分類條件的決策樹。 資訊增益是從熵值衍生而來。從吉尼不純度衍生的指標，目前沒有普遍接受的同義詞；不過，這個未命名的指標與資訊增益同樣重要。

吉尼不純度也稱為「吉尼係數」，或簡稱「吉尼」。

按一下圖示，即可查看吉尼不純度的數學詳細資料。

吉尼不純度是指從相同分布中取得的新資料片段遭到錯誤分類的機率。如果一組資料有兩個可能值「0」和「1」(例如二元分類問題中的標籤)，則可使用下列公式計算該組資料的吉尼不純度：

   I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

其中：

• I 是吉尼不純度。
• p 是「1」範例的分數。
• q 是「0」範例的分數。請注意，q = 1-p

舉例來說，請看以下資料集：

• 100 個標籤 (占資料集的 0.25) 包含值「1」
• 300 個標籤 (占資料集的 0.75) 包含「0」值

因此，吉尼不純度為：

• p = 0.25
• q = 0.75
• I = 1 - (0.25² + 0.75²) = 0.375

因此，來自相同資料集的隨機標籤有 37.5% 的機率會遭到錯誤分類，有 62.5% 的機率會正確分類。

如果標籤完全平衡 (例如 200 個「0」和 200 個「1」)，基尼不純度為 0.5。如果標籤極度不平衡，基尼不純度會接近 0.0。

---

H

轉折損失

#指標

一系列用於分類的損失函式，旨在找出與每個訓練範例盡可能遠的決策邊界，進而盡量擴大範例與邊界之間的間隔。KSVM 使用鉸鏈損失 (或平方鉸鏈損失等相關函式)。如果是二元分類，鉸鏈損失函式的定義如下：

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

其中 y 是實際標籤 (-1 或 +1)，y' 則是分類模型的原始輸出內容：

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

因此，鉸鏈損失與 (y * y') 的關係圖如下所示：

I

公平性指標互相衝突

#responsible

#指標

某些公平性概念互不相容，無法同時滿足。因此，沒有單一通用的指標可用於量化公平性，並套用至所有機器學習問題。

雖然這可能令人沮喪，但公平性指標不相容並不代表公平性工作毫無成果。而是建議根據特定機器學習問題的發生情境來定義公平性，以避免發生與應用實例相關的危害。

如要進一步瞭解公平性指標互相衝突的問題，請參閱「公平性的(不)可能性」。

個人公平性

#responsible

#指標

這項公平性指標會檢查類似的個人是否獲得類似的分類結果。舉例來說，Brobdingnagian Academy 可能想確保成績和標準化測驗分數相同的兩名學生，獲得入學許可的機率相同，以滿足個人公平性。

請注意，個別公平性完全取決於您如何定義「相似性」(在本例中為成績和測驗分數)，如果相似性指標遺漏重要資訊 (例如學生的課程嚴謹程度)，您可能會引發新的公平性問題。

如要進一步瞭解個別公平性，請參閱「透過認知實現公平性」。

資訊增益

#df

#指標

在決策樹林中，節點的熵與其子項節點熵的加權 (依範例數量) 總和之間的差異。節點的熵是該節點中範例的熵。

舉例來說，請考量下列熵值：

• 父節點的熵 = 0.6
• 一個子節點的熵，有 16 個相關範例 = 0.2
• 另一個子節點的熵 (24 個相關範例) = 0.1

因此，40% 的範例位於一個子節點，60% 位於另一個子節點。因此：

• 子節點的加權熵總和 = (0.4 * 0.2) + (0.6 * 0.1) = 0.14

因此，資訊增益為：

• 資訊增益 = 父項節點的熵 - 子項節點的加權熵總和
• 資訊增益 = 0.6 - 0.14 = 0.46

大多數分割器會盡量建立條件，以獲得最多資訊。

資料標註一致性

#指標

這項指標可衡量資料標註人員執行工作時，判定一致的頻率。 如果評估人員意見不一致，可能需要改善工作指示。有時也稱為「標註者間一致性」或「評估者間信度」。另請參閱 Cohen 的 Kappa，這是最常用的評估者間一致性測量方法之一。

詳情請參閱機器學習速成課程中的「類別資料：常見問題」。

L

L₁ 損失

#fundamentals

#指標

損失函式，用於計算實際標籤值與模型預測值之間的絕對差異。舉例來說，以下是五個範例的批次 L₁ 損失計算：

範例的實際值	模型預測值	差異的絕對值
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 損失

相較於 L₂ 損失，L₁ 損失對離群值的敏感度較低。

平均絕對誤差是每個樣本的平均 L₁ 損失。

按一下圖示即可查看正式數學式。

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

其中：

• $n$ 是範例數。
• $y$ 是標籤的實際值。
• $\hat{y}$ 是模型預測的 $y$ 值。

---

詳情請參閱機器學習速成課程中的「線性迴歸：損失」。

L₂ 損失

#fundamentals

#指標

損失函式：計算實際標籤值與模型預測值之間的差異平方。舉例來說，以下是五個範例的批次 L₂ 損失計算：

範例的實際值	模型預測值	Delta 的平方
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = L2 損失

由於平方運算，L₂ 損失會放大離群值的影響。也就是說，相較於 L₁ 損失，L₂ 損失對錯誤預測的反應更強烈。舉例來說，前述批次的 L₁ 損失會是 8 而不是 16。請注意，單一離群值就占了 16 個中的 9 個。

迴歸模型通常會使用 L₂ 損失做為損失函式。

均方誤差是每個樣本的平均 L₂ 損失。平方損失是 L₂ 損失的別名。

按一下圖示即可查看正式數學式。

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

其中：

• $n$ 是範例數。
• $y$ 是標籤的實際值。
• $\hat{y}$ 是模型預測的 $y$ 值。

---

詳情請參閱機器學習速成課程中的「邏輯迴歸：損失和正規化」。

LLM 評估

#generativeAI

#指標

用來評估大型語言模型 (LLM) 效能的一組指標和基準。概略來說，LLM 評估作業：

• 協助研究人員找出需要改進的大型語言模型。
• 有助於比較不同 LLM，並找出最適合特定工作的 LLM。
• 確保 LLM 安全無虞且符合道德規範。

詳情請參閱機器學習速成課程中的大型語言模型 (LLM)。

損失

#fundamentals

#指標

在訓練監督式模型時，會測量模型預測與標籤之間的差距。

損失函數會計算損失。

詳情請參閱機器學習速成課程中的「線性迴歸：損失」。

損失函數

#fundamentals

#指標

在訓練或測試期間，計算批次範例損失的數學函式。如果模型預測結果良好，損失函式會傳回較低的損失值；如果模型預測結果不佳，則會傳回較高的損失值。

訓練的目標通常是盡量減少損失函式傳回的損失。

損失函數的種類繁多，請為您要建構的模型類型選擇適當的損失函數。例如：

• L₂ 損失 (或均方誤差) 是線性迴歸的損失函式。
• 對數損失是邏輯迴歸的損失函數。

M

平均絕對誤差 (MAE)

#指標

使用 L₁ 損失時，每個樣本的平均損失。平均絕對誤差的計算方式如下：

1. 計算批次的 L₁ 損失。
2. 將 L₁ 損失除以批次中的樣本數。

按一下圖示即可查看正式數學式。

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

其中：

• $n$ 是範例數。
• $y$ 是標籤的實際值。
• $\hat{y}$ 是模型預測的 $y$ 值。

---

舉例來說，請考慮下列五個範例批次的 L₁ 損失計算：

範例的實際值	模型預測值	損失 (實際值與預測值之間的差異)
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 損失

因此，L₁ 損失為 8，範例數為 5。因此，平均絕對誤差為：

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

請比較平均絕對誤差與均方誤差和均方根誤差。

前 k 項的平均精確度平均值 (mAP@k)

#generativeAI

#指標

驗證資料集中所有「k 處的平均精確度」分數的統計平均值。在 k 處使用平均精確度，可判斷推薦系統產生的建議品質。

雖然「平均值」一詞聽起來有些多餘，但這個指標名稱很合適。畢竟這項指標會找出多個「k 處的平均精確度」值。

按一下圖示即可查看範例。

假設您建構的推薦系統會為每位使用者產生個人化的推薦小說清單。根據所選使用者的意見回饋，計算下列五個 k 分數的平均精確度 (每個使用者一個分數)：

• 0.73
• 0.77
• 0.67
• 0.82
• 0.76

因此，K 的平均精確度平均值為：

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

均方誤差 (MSE)

#指標

使用 L₂ 損失時，每個樣本的平均損失。均方誤差的計算方式如下：

1. 計算批次的 L₂ 損失。
2. 將 L₂ 損失除以批次中的樣本數。

按一下圖示即可查看正式數學式。

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ where:

• $n$ 是範例數。
• $y$ 是標籤的實際值。
• $\hat{y}$ 是模型對 $y$ 的預測結果。

---

舉例來說，請看下列五個樣本批次的損失：

實際值	模型預測	損失	平方損失
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			16 = L2 損失

因此，均方誤差為：

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

均方誤差是常見的訓練最佳化工具，特別適用於線性迴歸。

請比較均方誤差與平均絕對誤差和均方根誤差。

TensorFlow Playground 使用均方差計算損失值。

按一下圖示即可查看離群值的詳細資料。

離群值會大幅影響均方誤差。 舉例來說，損失 1 的平方損失為 1，但損失 3 的平方損失為 9。在上表中，損失 3 個帳戶的範例約占均方差的 56%，而損失 1 個帳戶的範例則只占均方差的 6%。

與均方誤差相比，離群值對平均絕對誤差的影響較小。舉例來說，如果只損失 3 個帳戶，平均絕對誤差就只會增加約 38%。

裁剪是避免極端離群值損害模型預測能力的方法之一。

---

指標

#TensorFlow

#指標

您重視的統計資料。

目標是機器學習系統嘗試最佳化的指標。

指標 API (tf.metrics)

#指標

用於評估模型的 TensorFlow API。舉例來說，tf.metrics.accuracy 可判斷模型的預測結果與標籤相符的頻率。

minimax loss

#指標

生成對抗網路的損失函式，以生成資料和真實資料的分布之間的交叉熵為依據。

第一篇論文使用極小極大損失來描述生成對抗網路。

詳情請參閱「生成對抗網路」課程中的損失函式。

模型容量

#指標

模型可學習的問題複雜程度。模型能學習的問題越複雜，模型的能力就越高。模型容量通常會隨著模型參數數量增加。如要瞭解分類模型容量的正式定義，請參閱「VC 維度」。

否

負類

#fundamentals

#指標

在二元分類中，一個類別稱為「正類」，另一個類別則稱為「負類」。正類是模型測試的項目或事件，負類則是其他可能性。例如：

• 醫療檢測中的負面類別可能是「非腫瘤」。
• 在電子郵件分類模型中，負面類別可能是「非垃圾郵件」。

與正類形成對比。

O

目標

#指標

演算法嘗試最佳化的指標。

目標函式

#指標

模型要盡量提升的數學公式或指標。 舉例來說，線性迴歸的目標函式通常是均方損失。因此，訓練線性迴歸模型時，訓練目標是盡量減少均方損失。

在某些情況下，目標是盡量提高目標函式。舉例來說，如果目標函式是準確度，目標就是盡可能提高準確度。

另請參閱「損失」。

P

pass at k (pass@k)

#指標

這項指標用於判斷大型語言模型生成的程式碼 (例如 Python) 品質。 具體來說，pass@k 會告訴您，在 k 個生成的程式碼區塊中，至少有一個程式碼區塊通過所有單元測試的機率。

大型語言模型通常難以針對複雜的程式設計問題生成優質程式碼。軟體工程師會提示大型語言模型，針對同一問題生成多個 (k) 解決方案，藉此解決這個問題。接著，軟體工程師會針對單元測試，測試每項解決方案。k 的通過計算取決於單元測試的結果：

• 如果一或多個解決方案通過單元測試，則 LLM 通過該程式碼生成挑戰。
• 如果沒有任何解決方案通過單元測試，LLM 就會失敗，無法完成程式碼生成挑戰。

k 的傳遞公式如下：

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

一般而言，k 值越高，通過 k 分數就越高；不過，k 值越高，需要的大型語言模型和單元測試資源就越多。

按一下圖示即可聆聽範例。

假設軟體工程師要求大型語言模型為 n=50 個程式設計難題生成 k=10 個解決方案。結果如下：

• 30 次
• 20 次失敗

因此，10 分的及格分數為：

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

performance

#指標

多載字詞，含義如下：

• 軟體工程中的標準意義。也就是說，這段軟體執行的速度 (或效率) 有多快？
• 機器學習中的意義。這裡的「成效」會回答下列問題：這個模型有多正確？也就是說，模型的預測結果有多準確？

排列變數重要性

#df

#指標

一種變數重要性，用於評估模型在特徵值經過排列後，預測錯誤率的增幅。排序變數重要性是與模型無關的指標。

困惑度

#指標

用來評估模型完成工作的程度。舉例來說，假設您的工作是讀取使用者在手機鍵盤上輸入的字詞前幾個字母，並提供可能的完成字詞清單。這項工作的困惑度 P 大約是您需要提供的猜測次數，才能讓清單包含使用者嘗試輸入的實際字詞。

複雜度與交叉熵的關係如下：

$$P= 2^{-\text{cross entropy}}$$

正類

#fundamentals

#指標

您要測試的類別。

舉例來說，癌症模型中的正向類別可能是「腫瘤」。 電子郵件分類模型中的正類可能是「垃圾郵件」。

與負類形成對比。

按一下圖示即可查看其他附註。

「陽性類別」一詞可能會造成混淆，因為許多檢測的「陽性」結果通常是不良結果。舉例來說，許多醫療檢測中的陽性類別對應到腫瘤或疾病。一般來說，您會希望醫生告訴您「恭喜！您的檢測結果為陰性。」 無論如何，正向類別是測試要尋找的事件。

誠然，您同時測試正向和負向類別。

---

PR AUC (PR 曲線下面積)

#指標

內插精確度和喚回度曲線下的面積，是透過繪製不同分類門檻值的 (喚回度、精確度) 點取得。

精確性

#fundamentals

#指標

分類模型的指標，可用來回答下列問題：

模型預測正類時，預測正確的百分比是多少？

公式如下：

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

其中：

• 真陽性是指模型正確預測正類。
• 偽陽性是指模型錯誤預測正類。

舉例來說，假設模型做出 200 項正向預測。在這 200 項正向預測中：

• 其中 150 個是真陽性。
• 其中 50 個是誤報。

在這種情況下：

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

與準確率和喚回度形成對比。

詳情請參閱機器學習速成課程中的「分類：準確度、喚回率、精確度和相關指標」。

前 k 項的查準率 (precision@k)

#指標

用於評估排序 (依序排列) 項目清單的指標。 k 的精確度會指出該清單中前 k 個項目與「相關」的比例。也就是：

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

k 的值必須小於或等於傳回清單的長度。 請注意，傳回清單的長度不屬於計算範圍。

關聯性通常是主觀的，即使是人工評估人員也經常對哪些項目具有關聯性意見不合。

比較時段：

• k 的平均精確度
• k 的平均精確度平均值

按一下圖示即可查看範例。

假設大型語言模型收到下列查詢：

List the 6 funniest movies of all time in order.

大型語言模型會傳回下表前兩欄顯示的清單：

位置	電影	是否相關？
1	將軍	是
2	辣妹過招	是
3	Platoon	否
4	《伴娘我最大》	是
5	大國民	否
6	This is Spinal Tap	是

前三部電影中有兩部相關，因此精確度為 3 時：

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

前五部電影中有三部非常搞笑，因此精確度為 5：

$$\text{precision at 5} = \frac{\text{3}} {\text{5}} = 0.6$$

---

精確度與喚回度曲線

#指標

在不同分類門檻下，精確度與喚回度的曲線。

預測偏誤

#指標

這個值表示資料集中預測平均值與標籤平均值之間的差距。

請勿與機器學習模型中的偏誤項混淆，也不要與倫理和公平性方面的偏誤混淆。

預測同位性

#responsible

#指標

公平性指標：檢查特定分類模型的準確率是否對所考量的子群組一視同仁。

舉例來說，如果模型預測大學錄取結果時，對小人國人和大人國人的預測精確度相同，就符合國籍的預測均等性。

預測同價有時也稱為「預測同價率」。

如要進一步瞭解預測均等性，請參閱「公平性定義說明」(第 3.2.1 節)。

預測價格一致性

#responsible

#指標

預測同位的別名。

機率密度函式

#指標

這個函式會找出資料樣本完全符合特定值的頻率。如果資料集的值是連續的浮點數，就很少會出現完全相符的情況。不過，從值 x 到值 y整合機率密度函式，會產生 x 和 y 之間資料樣本的預期頻率。

舉例來說，假設常態分布的平均值為 200，標準差為 30。如要判斷落在 211.4 到 218.7 範圍內的資料樣本預期頻率，可以整合常態分布的機率密度函式 (從 211.4 到 218.7)。

R

召回

#fundamentals

#指標

分類模型的指標，可用來回答下列問題：

當基準真相為正類時，模型正確識別為正類的預測百分比是多少？

公式如下：

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

其中：

• 真陽性是指模型正確預測正類。
• 偽陰性表示模型錯誤預測為負類。

舉例來說，假設模型對基準真相為正類的樣本做出 200 項預測。在這 200 項預測中：

• 其中 180 個是真陽性。
• 其中 20 個是偽陰性。

在這種情況下：

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

按一下不平衡資料集相關附註的圖示。

如果分類模型中正類別很少見，則召回率特別有助於判斷模型的預測能力。舉例來說，假設有類別不平衡的資料集，其中某種疾病的正類只出現在一百萬名患者中的 10 位。假設您的模型進行了五百萬次預測，並產生下列結果：

• 30 個真陽性
• 20 個偽陰性
• 4,999,000 個真陰性
• 950 個誤報

因此，這個模型的喚回率為：

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

相較之下，這個模型的準確率為：

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

高準確率看起來很厲害，但其實沒有意義。 對於類別不平衡的資料集，喚回度比準確度更有用。

---

詳情請參閱「分類：準確度、查全率、查準率和相關指標」。

前 k 項的召回率 (recall@k)

#指標

這項指標用於評估系統，該系統會輸出排序 (依序) 的項目清單。「前 k 項的召回率」k 是指在該清單的前 k 個項目中，相關項目所占的分數，計算方式為相關項目數除以傳回的相關項目總數。

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

對比度與 k 的精確度。

按一下圖示即可查看範例。

假設大型語言模型收到下列查詢：

List the 10 funniest movies of all time in order.

大型語言模型會傳回前兩欄顯示的清單：

位置	電影	是否相關？
1	將軍	是
2	辣妹過招	是
3	Platoon	否
4	《伴娘我最大》	是
5	This is Spinal Tap	是
6	飛機！	是
7	土撥鼠日	是
8	蒙提蟒蛇與聖杯	是
9	奧本海默	否
10	Clueless	是

上述清單中有八部電影非常搞笑，因此是「清單中的相關項目」。因此，在所有 k 的召回率計算中，8 都會是分母。那分子呢？嗯，前 4 個項目中有 3 個相關，因此在 4 個項目中的召回率為：

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

前 8 部電影中有 7 部非常有趣，因此回想率為：

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

ROC 曲線

#fundamentals

#指標

二元分類中，不同分類閾值的真陽率與偽陽率圖表。

ROC 曲線的形狀代表二元分類模型區分正類和負類的能力。舉例來說，假設二元分類模型完美區分了所有負類和正類：

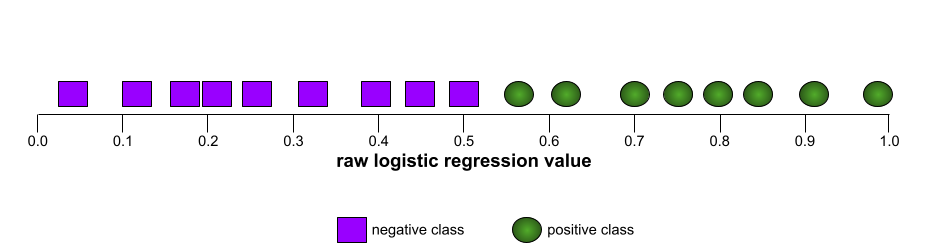
上述模型的 ROC 曲線如下所示：

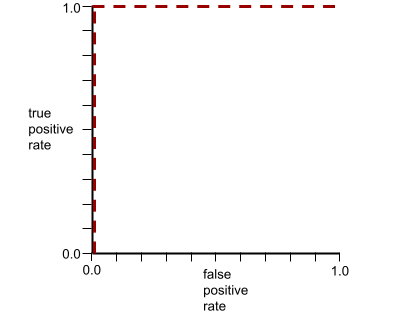
相較之下，下圖繪製了原始邏輯迴歸值，代表模型效能不佳，完全無法區分負面類別和正面類別：

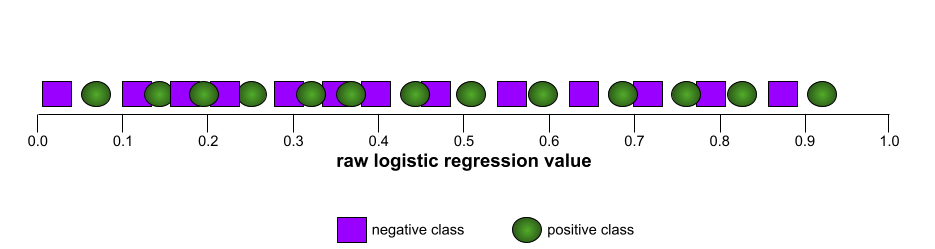
這個模型的 ROC 曲線如下所示：

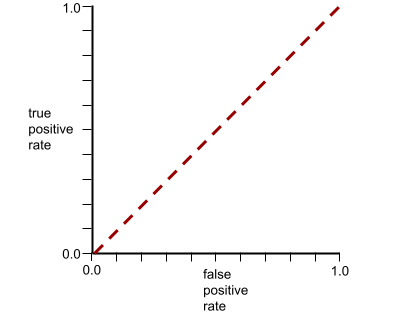
同時，在現實世界中，大多數二元分類模型都會在某種程度上區分正類和負類，但通常不會完美區分。因此，典型的 ROC 曲線會落在兩個極端之間：

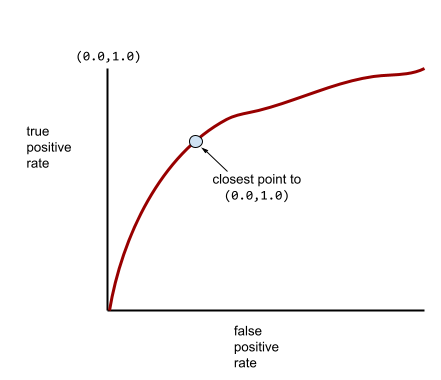
ROC 曲線最接近 (0.0,1.0) 的點，理論上會找出理想的分類門檻。不過，其他幾個現實世界的問題會影響理想分類門檻的選取。舉例來說，偽陰性造成的困擾可能遠大於偽陽性。

AUC 是用來彙整 ROC 曲線的數值指標，會以單一浮點數值表示。

均方根誤差 (RMSE)

#fundamentals

#指標

均方誤差的平方根。

ROUGE (喚回度導向的摘要評估研究)

#指標

這是一系列指標，用於評估自動摘要和機器翻譯模型。ROUGE 指標會判斷參考文字與機器學習模型生成的文字重疊的程度。ROUGE 系列的每個成員都會以不同的方式測量重疊程度。ROUGE 分數越高，表示參考文字與生成文字的相似度越高。

每個 ROUGE 系列成員通常會產生下列指標：

• 精確度
• 喚回度
• F₁

注意： ROUGE 使用精確度和召回率的方式，與傳統精確度和召回率略有不同。

詳情和範例請參閱：

• ROUGE-L
• ROUGE-N
• ROUGE-S

注意： BLEU 和 BLEURT 會針對準確度進行最佳化，而 ROUGE 則會針對召回率進行最佳化。 因此，BLEU 和 BLEURT 更適合用來評估機器翻譯 (因為重點在於精確度)，而 ROUGE 更適合用來評估摘要製作 (因為重點在於喚回度)。

ROUGE-L

#指標

ROUGE 系列的指標，著重於參考文字和生成文字中最長共同子序列的長度。下列公式會計算 ROUGE-L 的召回率和精確度：

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

然後使用 F₁ 將 ROUGE-L 喚回率和 ROUGE-L 精確度匯總為單一指標：

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

按一下圖示，查看 ROUGE-L 的計算範例。

請參考下列參考文字和生成的文字。

類別	製作人是誰？	文字
參考文字	人工翻譯	我想瞭解各種事物。
生成的文字	機器學習模型	我想學習許多事物。

因此：

• 最長共同子序列為 5 (I want to of things)
• 參考文字的字數為 9。
• 生成文字中的字數為 7。

因此：

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

ROUGE-L 會忽略參考文字和生成文字中的任何換行符，因此最長共同子序列可能會跨越多個句子。如果參考文字和生成的文字包含多個句子，一般來說，ROUGE-Lsum (ROUGE-L 的變體) 是較好的指標。ROUGE-Lsum 會判斷段落中每個句子的最長共同子序列，然後計算這些最長共同子序列的平均值。

按一下圖示，查看 ROUGE-Lsum 的計算範例。

請參考下列參考文字和生成的文字。

類別	製作人是誰？	文字
參考文字	人工翻譯	火星表面乾燥，幾乎所有水都位於地底深處。
生成的文字	機器學習模型	火星表面乾燥，不過，絕大多數的水都在地下。

因此：

	第一句	第二句
最長共同序列	2 (火星乾燥)	3 (水在地下)
參考文字的句子長度	6	7
生成文字的句子長度	5	8

因此：

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#指標

ROUGE 系列指標集，用於比較參考文字和生成文字中特定大小的共用 N 元語。例如：

• ROUGE-1 會計算參考文字和生成文字中共同的符記數量。
• ROUGE-2 會計算參考文字和生成文字中二元語法 (2 元語法) 的數量。
• ROUGE-3 會測量參考文字和生成文字中，共用的三元語法 (3 元語法) 數量。

您可以使用下列公式，計算 ROUGE-N 系列中任何成員的 ROUGE-N 召回率和 ROUGE-N 精確度：

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

接著，您可以使用 F₁，將 ROUGE-N 喚回率和 ROUGE-N 精確度匯總為單一指標：

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

按一下圖示即可聆聽範例。

假設您決定使用 ROUGE-2，評估機器學習模型與人類翻譯員的翻譯成效。

類別	製作人是誰？	文字	雙連詞
參考文字	人工翻譯	我想瞭解各種事物。	我想瞭解各種事物
生成的文字	機器學習模型	我想學習許多事物。	I want, want to, to learn, learn plenty, plenty of, of things

因此：

• 相符的 2-gram 數量為 3 個 (「I want」、「want to」和「of things」)。
• 參考文字中的 2-gram 數量為 8。
• 生成文字中的 2-gram 數量為 6。

因此：

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#指標

寬容形式的 ROUGE-N，可啟用 skip-gram 比對。也就是說，ROUGE-N 只會計算完全相符的 N 元語法，但 ROUGE-S 也會計算以一或多個字詞分隔的 N 元語法。舉例來說，您可以嘗試：

• 參考文字：白雲
• 生成的文字：白色捲雲

計算 ROUGE-N 時，2-gram「White clouds」與「White billowing clouds」不符。不過，在計算 ROUGE-S 時，「White clouds」(白雲)確實與「White billowing clouds」(白雲朵朵)相符。

R 平方

#指標

迴歸指標，指出標籤的變異程度是由個別特徵或特徵集所造成。R 平方值介於 0 到 1 之間，解讀方式如下：

• R 平方值為 0 表示標籤的變異與特徵集無關。
• R 平方值為 1 表示標籤的所有變異都是由特徵集所致。
• 介於 0 和 1 之間的 R 平方值，表示可從特定特徵或特徵集預測標籤變異的程度。舉例來說，R 平方值為 0.10 表示標籤的變異數有 10% 是由特徵集造成，R 平方值為 0.20 表示有 20% 是由特徵集造成，依此類推。

R 平方是模型預測值與真值之間的皮爾森相關係數平方。

日

計分

#指標

推薦系統的一部分，可為候選項目生成階段產生的每個項目提供值或排名。

相似度指標

#clustering

#指標

在分群演算法中，用來判斷任意兩個樣本相似程度的指標。

稀疏度

#指標

向量或矩陣中設為零 (或空值) 的元素數量，除以該向量或矩陣中的項目總數。舉例來說，假設有 100 個元素的矩陣，其中 98 個儲存格包含零。稀疏程度的計算方式如下：

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

特徵稀疏性是指特徵向量的稀疏性；模型稀疏性是指模型權重的稀疏性。

平方轉折損失

#指標

轉折損失的平方。平方轉折損失對離群值的懲罰比一般轉折損失更嚴厲。

平方損失

#fundamentals

#指標

L₂ 損失 的同義詞。

T

測試損失

#fundamentals

#指標

代表模型對測試集的損失的指標。建構模型時，您通常會盡量減少測試損失。這是因為相較於低訓練損失或低驗證損失，低測試損失是更強大的品質信號。

如果測試損失與訓練損失或驗證損失之間存在巨大差距，有時表示您需要提高正規化率。

前 k 項準確率

#指標

在生成的清單中，前 k 個位置顯示「目標標籤」的百分比。清單可以是個人化建議，也可以是依 softmax 排序的項目清單。

Top-k 準確率也稱為「k 準確率」。

注意： 目標標籤可以是任何類別 (不一定是基本事實類別)，因此前 k 名準確率不一定等同於傳統的準確率。

按一下圖示即可聆聽範例。

假設有個機器學習系統會根據樹葉圖片，使用 Softmax 識別樹木的機率。下表顯示從五張輸入樹狀結構圖片產生的輸出清單。每個資料列都包含目標標籤和最有可能的五棵樹。舉例來說，如果目標標籤是「楓樹」，機器學習模型會將「榆樹」識別為最有可能的樹木，將「橡樹」識別為第二有可能的樹木，依此類推。

目標標籤	1	2	3	4	5
Maple	elm	橡木	楓木	山毛櫸	楊木
山茱萸	橡木	dogwood	楊木	Hickory	Maple
橡木	oak	椴木	locust	赤楊	Linden
Linden	Maple	paw-paw	橡木	椴木	楊木
橡木	locust	Linden	oak	Maple	paw-paw

目標標籤只會在第一個位置出現一次，因此前 1 名準確率為：

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

目標標籤四次出現在前三名位置，因此前 3 名準確度為：

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

毒性

#指標

內容是否辱罵、威脅或令人反感。許多機器學習模型都能辨識及評估毒性。這類模型大多會根據多項參數 (例如濫用語言的程度和威脅性語言的程度) 判斷毒性。

訓練損失

#fundamentals

#指標

代表模型在特定訓練疊代期間的損失指標。舉例來說，假設損失函式為平均平方誤差。舉例來說，第 10 次疊代的訓練損失 (均方誤差) 為 2.2，第 100 次疊代的訓練損失為 1.9。

損失曲線會繪製訓練損失與疊代次數的關係圖。損失曲線可提供下列訓練提示：

• 如果斜率向下，表示模型正在進步。
• 如果斜率向上，表示模型品質正在變差。
• 平緩的斜率表示模型已達到收斂。

舉例來說，以下是經過某種程度理想化的損失曲線，顯示：

• 在初期反覆執行階段，斜率大幅下降，表示模型快速進步。
• 斜率逐漸趨緩 (但仍向下)，直到訓練接近尾聲為止，這表示模型持續進步，但速度比初期反覆運算時稍慢。
• 訓練結束時的斜率平緩，表示模型已收斂。

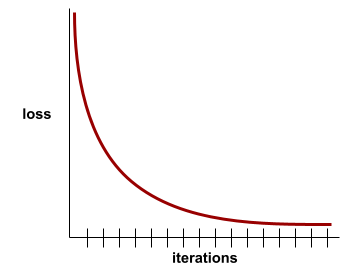
雖然訓練損失很重要，但請參閱泛化。

真陰性 (TN)

#fundamentals

#指標

舉例來說，模型正確預測負類。舉例來說，模型推斷某封電子郵件不是垃圾郵件，而該電子郵件確實不是垃圾郵件。

真陽性 (TP)

#fundamentals

#指標

舉例來說，模型正確預測正類。舉例來說，模型推斷特定電子郵件是垃圾郵件，而該電子郵件確實是垃圾郵件。

真陽率 (TPR)

#fundamentals

#指標

recall 的同義詞。也就是：

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

真陽率是 ROC 曲線的 y 軸。

V

驗證損失

#fundamentals

#指標

代表模型在特定訓練疊代期間，於驗證集上的損失指標。

另請參閱一般化曲線。

變數重要性

#df

#指標

一組分數，代表各特徵對模型的重要性。

舉例來說，假設您要使用決策樹估算房價。假設這個決策樹使用三項特徵：尺寸、年齡和風格。如果計算出三個特徵的變數重要性為 {size=5.8, age=2.5, style=4.7}，則對決策樹而言，大小比年齡或風格更重要。

變數重要性指標有很多種，可讓 ML 專家瞭解模型的不同層面。

W

Wasserstein 損失

#指標

這是生成對抗網路中常用的損失函式之一，根據生成資料和真實資料分布之間的地球移動距離計算得出。