機械学習の用語集: 指標

このページには、指標の用語集が記載されています。用語集のすべての用語については、こちらをクリックしてください。

A

accuracy

#fundamentals

#Metric

分類予測の正解の数を予測の総数で割った数。具体的には、次のことが求められます。

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

たとえば、40 個の正しい予測と 10 個の誤った予測を行ったモデルの精度は次のようになります。

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

バイナリ分類では、正しい予測と誤った予測のさまざまなカテゴリに固有の名前が付けられます。したがって、二項分類の精度の式は次のようになります。

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

ここで

• TP は、真陽性（正しい予測）の数です。
• TN は真陰性（正しい予測）の数です。
• FP は偽陽性（誤った予測）の数です。
• FN は偽陰性（誤った予測）の数です。

精度と適合率、再現率を比較対照します。

アイコンをクリックすると、精度とクラス不均衡データセットの詳細が表示されます。

精度は、状況によっては有用な指標ですが、誤解を招く可能性もあります。特に、精度は通常、クラス不均衡データセットを処理する分類モデルを評価するのに適した指標ではありません。

たとえば、ある亜熱帯の都市で雪が降るのは 1 世紀に 25 日だけだとします。雪が降らない日（負のクラス）は雪が降る日（正のクラス）よりもはるかに多いため、この都市の雪のデータセットはクラスの不均衡があります。毎日雪が降るか降らないかを予測するはずのバイナリ分類モデルが、毎日「雪が降らない」と予測しているとします。このモデルは非常に正確ですが、予測能力はありません。次の表に、100 年間の予測の結果をまとめます。

カテゴリ	数値
TP	0
TN	36499
FP	0
FN	25

したがって、このモデルの精度は次のようになります。

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

99.93% の精度は非常に高いように見えますが、実際にはこのモデルには予測力はありません。

適合率と再現率は、通常、クラス不均衡データセットでトレーニングされたモデルを評価する場合、精度よりも有用な指標です。

---

詳細については、ML 集中講座の分類: 正確度、再現率、適合率、関連指標をご覧ください。

PR 曲線下面積

#Metric

PR AUC（PR 曲線の下の面積）をご覧ください。

ROC 曲線下面積

#Metric

AUC（ROC 曲線の下の面積）をご覧ください。

AUC（ROC 曲線の下の面積）

#fundamentals

#Metric

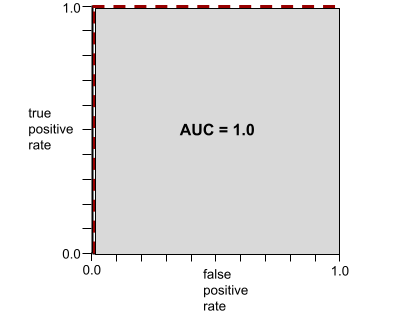
陽性クラスと陰性クラスを分離するバイナリ分類モデルの能力を表す 0.0 ～ 1.0 の数値。AUC が 1.0 に近いほど、クラスを互いに分離するモデルの能力が優れています。

たとえば、次の図は、陽性クラス（緑色の楕円）と陰性クラス（紫色の長方形）を完全に分離する分類モデルを示しています。この非現実的な完全なモデルの AUC は 1.0 です。

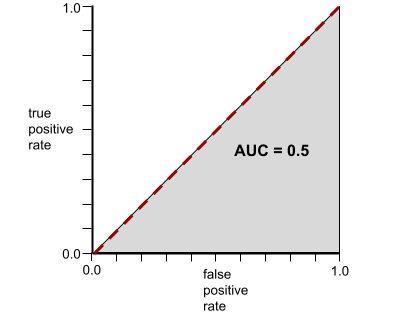
一方、次の図は、ランダムな結果を生成した分類モデルの結果を示しています。このモデルの AUC は 0.5 です。

はい。上記のモデルの AUC は 0.0 ではなく 0.5 です。

ほとんどのモデルは、この 2 つの極端なモデルの中間に位置します。たとえば、次のモデルは陽性と陰性をある程度分離しているため、AUC は 0.5 ～ 1.0 の範囲になります。

AUC は、分類しきい値に設定した値を無視します。AUC は、可能なすべての分類しきい値を考慮します。

アイコンをクリックして、AUC と ROC 曲線との関係を確認します。

AUC は、ROC 曲線の下の面積を表します。たとえば、陽性と陰性を完全に分離するモデルの ROC 曲線は次のようになります。

AUC は、上の図のグレーの領域の面積です。この特殊なケースでは、面積はグレーの領域の長さ（1.0）にグレーの領域の幅（1.0）を掛けたものになります。したがって、1.0 と 1.0 の積は AUC が 1.0 になり、これは可能な限り高い AUC スコアです。

逆に、クラスをまったく分離できない分類モデルの ROC 曲線は次のようになります。このグレーの領域の面積は 0.5 です。

一般的な ROC 曲線は次のようになります。

この曲線の下の面積を手動で計算するのは大変なため、通常はプログラムでほとんどの AUC 値を計算します。

---

アイコンをクリックすると、AUC のより正式な定義が表示されます。

AUC は、無作為に選択した陽性のサンプルが陽性に分類される確率が、無作為に選択した陰性のサンプルが陽性に分類される確率よりも高い可能性を表します。

---

詳細については、ML 集中講座の分類: ROC と AUC をご覧ください。

k における平均適合率

#Metric

ランク付けされた結果（書籍の推奨事項の番号付きリストなど）を生成する単一のプロンプトに対するモデルのパフォーマンスを要約する指標。k における平均適合率は、各関連結果の k における適合率の値の平均です。したがって、k における平均適合率の式は次のようになります。

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

ここで

• \(n\) は、リスト内の関連アイテムの数です。

k でのリコールとのコントラスト。

注: k での平均適合率は、単一のプロンプトの出力を評価します。k での平均適合率を使用して、さまざまなプロンプトに対するモデルの出力の品質を評価します。

注: k での平均適合率を単に平均適合率と略す人もいます。

アイコンをクリックして例を確認

大規模言語モデルに次のクエリが与えられたとします。

List the 6 funniest movies of all time in order.

大規模言語モデルは次のリストを返します。

1. The General
2. Mean Girls
3. Platoon
4. ブライズメイズ 史上最悪のウェディングプラン
5. Citizen Kane
6. This is Spinal Tap

返されたリストの 4 本の映画は非常に面白い（つまり、関連性がある）が、2 本の映画はドラマ（関連性がない）である。次の表に結果の詳細を示します。

位置	映画	関連性があるか？	適合率 k
1	The General	○	1.0
2	Mean Girls	○	1.0
3	Platoon	いいえ	関連性がない
4	ブライズメイズ 史上最悪のウェディングプラン	○	0.75
5	Citizen Kane	いいえ	関連性がない
6	This is Spinal Tap	○	0.67

関連性の高い結果の数は 4 です。したがって、6 での平均適合率は次のように計算できます。

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

ベースライン

#Metric

別のモデル（通常はより複雑なモデル）のパフォーマンスを比較評価するための基準点として使用されるモデル。たとえば、ロジスティック回帰モデルは、ディープ ラーニング モデルの優れたベースラインとして機能します。

特定の問題に関して、ベースラインは、新しいモデルが有用であるために新しいモデルが達成する必要があるパフォーマンスの最小期待値をモデル デベロッパーが定量化するのに役立ちます。

C

費用

#Metric

損失と同義。

反事実的公平性

#responsible

#Metric

1 つ以上の機密属性を除き、最初の個人と同一の別の個人に対して、分類モデルが同じ結果を生成するかどうかを確認する公平性指標。反事実的公平性について分類モデルを評価することは、モデル内の潜在的なバイアスの原因を特定する 1 つの方法です。

詳しくは、次のいずれかをご覧ください。

• 機械学習集中講座の公平性: 反事実的公平性。
• When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness（英語）

交差エントロピー

#Metric

対数損失をマルチクラス分類問題に一般化したものです。交差エントロピーは、2 つの確率分布間の差を定量化します。パープレキシティもご覧ください。

累積分布関数（CDF）

#Metric

目標値以下のサンプルの頻度を定義する関数。たとえば、連続値の正規分布を考えてみましょう。CDF は、サンプルの約 50% が平均値以下であり、サンプルの約 84% が平均値より 1 標準偏差大きい値以下であることを示します。

D

人口学的等価性

#responsible

#Metric

モデルの分類結果が特定の機密属性に依存しない場合に満たされる公平性指標。

たとえば、リリパット人とブロブディンナグ人が Glubbdubdrib 大学に申し込んだ場合、リリパット人の合格率とブロブディンナグ人の合格率が同じであれば、一方のグループが他方よりも平均的に資格があるかどうかに関係なく、人口統計学的パリティが達成されます。

均等化されたオッズと機会の平等とは対照的です。これらは、分類結果の集計が機密属性に依存することを許可しますが、特定のグラウンド トゥルース ラベルの分類結果が機密属性に依存することを許可しません。人口統計学的パリティの最適化におけるトレードオフを視覚化したものについては、「よりスマートな機械学習による差別の是正」をご覧ください。

詳細については、ML 集中講座の公平性: 人口統計学的パリティをご覧ください。

E

アース ムーバー距離（EMD）

#Metric

2 つの分布の相対的な類似度を測定します。アース ムーバー距離が小さいほど、分布の類似性が高くなります。

編集距離

#Metric

2 つのテキスト文字列の類似性を測定します。機械学習では、編集距離は次の理由で役立ちます。

• 編集距離は簡単に計算できます。
• 編集距離は、互いに類似していることがわかっている 2 つの文字列を比較できます。
• 編集距離を使用すると、異なる文字列が特定の文字列にどの程度類似しているかを判断できます。

編集距離にはいくつかの定義があり、それぞれ異なる文字列操作を使用します。例については、レーベンシュタイン距離をご覧ください。

経験累積分布関数（eCDF または EDF）

#Metric

実際のデータセットの実測値に基づく累積分布関数。X 軸上の任意の点における関数の値は、指定された値以下のデータセット内の観測値の割合です。

エントロピー

#df

#Metric

情報理論では、確率分布の予測不可能性を説明します。また、エントロピーは、各例に含まれる情報量としても定義されます。分布のエントロピーが最大になるのは、確率変数のすべての値が等しい確率で発生する場合です。

2 つの値「0」と「1」を持つセットのエントロピー（たとえば、バイナリ分類問題のラベル）は、次の式で表されます。

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

ここで

• H はエントロピーです。
• p は「1」の例の割合です。
• q は「0」の例の割合です。q = (1 - p) であることに注意してください。
• log は通常 log₂ です。この場合、エントロピー単位はビットです。

たとえば、次のように仮定します。

• 100 個の例に値「1」が含まれている
• 300 個の例に値「0」が含まれている

したがって、エントロピー値は次のようになります。

• p = 0.25
• q = 0.75
• H = (-0.25)log₂(0.25) - (0.75)log₂(0.75) = 1 例あたり 0.81 ビット

完全にバランスの取れたセット（たとえば、200 個の「0」と 200 個の「1」）のエントロピーは、例あたり 1.0 ビットになります。セットのバランスが崩れるほど、エントロピーは 0.0 に近づきます。

決定木では、エントロピーは情報ゲインの定式化に役立ち、スプリッタが分類決定木の成長中に条件を選択するのに役立ちます。

エントロピーを以下と比較します。

• ジニ不純度
• 交差エントロピー損失関数

エントロピーは、シャノンのエントロピーと呼ばれることもあります。

詳細については、Decision Forests コースの数値特徴を使用したバイナリ分類の正確な分割ツールをご覧ください。

機会の平等

#responsible

#Metric

モデルが機密属性のすべての値について望ましい結果を平等に予測しているかどうかを評価する公平性指標。つまり、モデルの望ましい結果が陽性クラスの場合、すべてのグループで真陽性率が同じになることが目標となります。

機会の平等は、均等化されたオッズに関連しています。これは、すべてのグループで真陽性率と偽陽性率の両方が同じであることを必要とします。

Glubbdubdrib 大学が、リリパット人とブロブディンナグ人を厳格な数学プログラムに受け入れたとします。リリパットのセカンダリー スクールでは、数学の授業の充実したカリキュラムが提供されており、生徒のほとんどが大学プログラムの資格を取得しています。ブロブディンナグの高校では数学の授業がまったく提供されていないため、資格のある生徒ははるかに少なくなっています。リリパット人かブロブディンナグ人かに関係なく、有資格の学生が同じ確率で入学できる場合、国籍（リリパット人かブロブディンナグ人か）に関して「合格」という優先ラベルの機会均等性が満たされます。

たとえば、Glubbdubdrib 大学に 100 人の Lilliputians と 100 人の Brobdingnagians が応募し、次のように入学が決定されるとします。

表 1. リリパットの応募者（90% が資格あり）

	リードの精査が完了	見込みなし
Admitted	45	3
不承認	45	7
合計	90	10
合格した資格のある学生の割合: 45/90 = 50% 不合格になった資格のない学生の割合: 7/10 = 70% 合格したリリパット人の学生の割合: (45+3)/100 = 48%

 

表 2. Brobdingnagian の応募者（10% が資格あり）:

	リードの精査が完了	見込みなし
Admitted	5	9
不承認	5	81
合計	10	90
入学を許可された資格のある学生の割合: 5/10 = 50% 入学を拒否された資格のない学生の割合: 81/90 = 90% 入学を許可された Brobdingnagian 学生の合計割合: (5+9)/100 = 14%

上記の例では、リリパット人とブロブディンナグ人がどちらも 50% の確率で入学できるため、有資格の学生の入学機会の平等が満たされています。

機会均等性は満たされていますが、次の 2 つの公平性指標は満たされていません。

• 人口統計学的パリティ: リリパット人とブロブディンナグ人が異なる割合で大学に入学している。リリパット人の学生の 48% が入学しているが、ブロブディンナグ人の学生は 14% しか入学していない。
• 均等オッズ: 資格のあるリリパット人とブロブディンナグ人が同じ確率で入学できる一方で、資格のないリリパット人とブロブディンナグ人が同じ確率で不合格になるという追加の制約は満たされません。不適格な Lilliputian の拒否率は 70% ですが、不適格な Brobdingnagian の拒否率は 90% です。

詳細については、ML 集中講座の公平性: 機会の平等をご覧ください。

均等オッズ

#responsible

#Metric

モデルがポジティブ クラスとネガティブ クラスの両方に関して、機密属性のすべての値に対して結果を平等に予測しているかどうかを評価する公平性指標。一方のクラスのみを排他的に評価するものではありません。つまり、すべてのグループで真陽性率と偽陰性率が同じである必要があります。

均等オッズは、単一のクラス（正または負）のエラー率のみに焦点を当てた機会の平等に関連しています。

たとえば、Glubbdubdrib 大学がリリパット人とブロブディンナグ人を厳格な数学プログラムに受け入れているとします。リリパットの高校では、数学の授業のカリキュラムが充実しており、ほとんどの生徒が大学プログラムの資格を取得しています。Brobdingnagians の中等学校では数学の授業がまったく提供されていないため、資格のある生徒ははるかに少なくなっています。応募者がリリパット人であろうとブロブディンナグ人であろうと、資格があればプログラムに合格する可能性は同じであり、資格がなければ不合格になる可能性も同じである場合、均等なオッズが満たされます。

リリパット人とブロブディンナグ人がそれぞれ 100 人ずつ Glubbdubdrib 大学に入学を申し込んだとします。入学の可否は次のように決定されます。

表 3: リリパットの応募者（90% が資格あり）

	リードの精査が完了	見込みなし
Admitted	45	2
不承認	45	8
合計	90	10
入学が許可された資格のある学生の割合: 45/90 = 50% 入学が許可されなかった資格のない学生の割合: 8/10 = 80% 入学が許可されたリリパット人の学生の合計割合: (45+2)/100 = 47%

 

表 4. Brobdingnagian の応募者（10% が資格あり）:

	リードの精査が完了	見込みなし
Admitted	5	18
不承認	5	72
合計	10	90
合格した資格のある学生の割合: 5/10 = 50% 不合格になった資格のない学生の割合: 72/90 = 80% 合格したブロブディンナグ人の学生の割合: (5+18)/100 = 23%

リリパット人とブロブディンナグ人の両方で、合格した学生の 50% が合格し、不合格の学生の 80% が不合格になるため、均等なオッズが満たされています。

注: ここでは均等なオッズが満たされていますが、人口統計学的パリティは満たされていません。リリパットの学生とブロブディンナグの学生は、グルブダブドリブ大学に異なる割合で入学します。リリパットの学生の 47% が入学し、ブロブディンナグの学生の 23% が入学します。

均等なオッズは、「Equality of Opportunity in Supervised Learning」で次のように正式に定義されています。「予測子 Ŷ は、Y を条件として Ŷ と A が独立している場合、保護属性 A と結果 Y に関して均等なオッズを満たします。」

注: 等しいオッズと、より緩和された機会均等指標を比較します。

evals

#generativeAI

#Metric

主に LLM 評価の略語として使用されます。広義には、evals は、評価のあらゆる形式の略語です。

評価

#generativeAI

#Metric

モデルの品質を測定したり、異なるモデルを比較したりするプロセス。

教師あり機械学習モデルを評価するには、通常、検証セットとテストセットに対してモデルを評価します。LLM の評価では、通常、品質と安全性のより広範な評価が行われます。

F

F₁

#Metric

適合率と再現率の両方に依存する「ロールアップ」2 値分類指標。式は次のとおりです。

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

アイコンをクリックして例をご覧ください。

適合率と再現率が次の値であるとします。

• precision = 0.6
• recall = 0.4

F₁ は次のように計算します。

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

適合率と再現率がかなり類似している場合（前の例のように）、F₁ はそれらの平均値に近くなります。適合率と再現率の差が大きい場合、F₁ は小さい値に近づきます。次に例を示します。

• precision = 0.9
• 再現率 = 0.1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

公平性指標

#responsible

#Metric

測定可能な「公平性」の数学的定義。よく使用される公平性指標には、次のようなものがあります。

• 均等なオッズ
• 予測のパリティ
• 反事実的公平性
• 人口学的等価性

公平性に関する指標の多くは相互に排他的です。公平性に関する指標の不整合をご覧ください。

偽陰性（FN）

#fundamentals

#Metric

モデルが陰性クラスを誤って予測した例。たとえば、特定のメール メッセージがスパムではない（負のクラス）と予測されたが、そのメール メッセージが実際にはスパムである場合などです。

偽陰性率

#Metric

モデルが誤って陰性クラスを予測した実際の陽性例の割合。次の式は、偽陰性率を計算します。

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

詳細については、ML 集中講座のしきい値と混同行列をご覧ください。

偽陽性（FP）

#fundamentals

#Metric

モデルが陽性クラスを誤って予測した例。たとえば、特定のメール メッセージがスパム（ポジティブ クラス）であるとモデルが予測したが、そのメール メッセージは実際にはスパムではない場合などです。

詳細については、ML 集中講座のしきい値と混同行列をご覧ください。

偽陽性率（FPR）

#fundamentals

#Metric

モデルが陽性クラスを誤って予測した実際の陰性例の割合。次の式は、偽陽性率を計算します。

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

偽陽性率は、ROC 曲線の X 軸です。

詳細については、ML 集中講座の分類: ROC と AUC をご覧ください。

特徴の重要度

#df

#Metric

変数の重要度と同義。

基盤モデル

#generativeAI

#Metric

膨大で多様なトレーニング セットでトレーニングされた、非常に大規模な事前トレーニング済みモデル。基盤モデルは、次の両方を行うことができます。

• 幅広いリクエストに適切に対応する。
• 追加のファインチューニングやその他のカスタマイズのベースモデルとして機能します。

つまり、基盤モデルは一般的な意味ですでに非常に有能ですが、特定のタスクに対してさらに有用になるようにカスタマイズできます。

成功の割合

#generativeAI

#Metric

ML モデルの生成されたテキストを評価するための指標。成功の割合は、生成されたテキスト出力の総数で「成功」した生成テキスト出力の数を割った値です。たとえば、大規模言語モデルが 10 個のコードブロックを生成し、そのうち 5 個が成功した場合、成功率は 50% になります。

成功率の指標は統計全体で広く使用されていますが、ML では主にコード生成や数学の問題などの検証可能なタスクの測定に役立ちます。

G

ジニ不純度

#df

#Metric

エントロピーに似た指標。スプリッタは、ジニ不純度またはエントロピーから導出された値を使用して、分類の決定木の条件を構成します。情報ゲインはエントロピーから導出されます。ジニ不純度から導出された指標に、一般的に受け入れられている同等の用語はありません。ただし、この名前のない指標は情報ゲインと同じくらい重要です。

ジニ不純度は、ジニ係数または単にジニとも呼ばれます。

アイコンをクリックすると、ジニ不純度に関する数学的な詳細が表示されます。

ジニ不純度は、同じ分布から取得した新しいデータを誤分類する確率です。2 つの値「0」と「1」を持つセットのジニ不純度（バイナリ分類問題のラベルなど）は、次の式で計算されます。

   I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

ここで

• I はジニ不純度です。
• p は「1」の例の割合です。
• q は「0」の例の割合です。q = 1-p

たとえば、次のデータセットについて考えてみましょう。

• 100 個のラベル（データセットの 0.25）に値「1」が含まれています。
• 300 個のラベル（データセットの 0.75）に値「0」が含まれている

したがって、ジニ不純度は次のようになります。

• p = 0.25
• q = 0.75
• I = 1 - (0.25² + 0.75²) = 0.375

したがって、同じデータセットからランダムに選択されたラベルが誤分類される確率は 37.5%、正しく分類される確率は 62.5% になります。

完全にバランスの取れたラベル（たとえば、200 個の「0」と 200 個の「1」）のジニ不純度は 0.5 になります。不均衡なラベルの場合、ジニ不純度は 0.0 に近い値になります。

---

H

ヒンジ損失

#Metric

分類用の損失関数のファミリー。各トレーニング例から可能な限り離れた決定境界を見つけ、例と境界の間のマージンを最大化するように設計されています。KSVM はヒンジ損失（または 2 乗ヒンジ損失などの関連関数）を使用します。バイナリ分類の場合、ヒンジ損失関数は次のように定義されます。

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

ここで、y は -1 または +1 の真のラベル、y' は分類モデルの未加工の出力です。

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

したがって、ヒンジ損失と（y * y'）のプロットは次のようになります。

I

公平性に関する指標の不整合

#responsible

#Metric

公平性の概念の中には、相互に両立せず、同時に満たすことができないものがあるという考え方。そのため、すべての ML 問題に適用できる公平性を定量化するための単一の普遍的な指標はありません。

これは落胆するようなことかもしれませんが、公平性の指標の不整合は、公平性の取り組みが無駄であることを意味するものではありません。代わりに、公平性は特定の ML 問題のコンテキストに沿って定義し、そのユースケースに固有の危害を防ぐことを目標にする必要があることを示唆しています。

公平性指標の非互換性について詳しくは、「公平性の（不）可能性について」をご覧ください。

個人の公平性

#responsible

#Metric

類似した個人が同様に分類されているかどうかを確認する公平性指標。たとえば、Brobdingnagian Academy は、成績と標準テストのスコアが同じ 2 人の生徒が同じ確率で入学できるようにすることで、個人の公平性を満たしたいと考えているかもしれません。

個人の公平性は「類似性」（この場合は成績とテストの点数）の定義に完全に依存します。類似性指標に重要な情報（生徒のカリキュラムの厳しさなど）が欠落していると、新たな公平性の問題が生じる可能性があります。

個人の公平性について詳しくは、「認識による公平性」をご覧ください。

情報利得

#df

#Metric

決定フォレストでは、ノードのエントロピーと、子ノードのエントロピーの重み付け（例の数による）された合計の差。ノードのエントロピーは、そのノード内の例のエントロピーです。

たとえば、次のエントロピー値を考えてみましょう。

• 親ノードのエントロピー = 0.6
• 16 個の関連する例を含む 1 つの子ノードのエントロピー = 0.2
• 関連する例が 24 個ある別の子ノードのエントロピー = 0.1

したがって、例の 40% は一方の子ノードにあり、60% はもう一方の子ノードにあります。そのため、次のようになります。

• 子ノードの重み付きエントロピーの合計 = (0.4 × 0.2) + (0.6 × 0.1) = 0.14

したがって、情報利得は次のようになります。

• 情報利得 = 親ノードのエントロピー - 子ノードの重み付きエントロピーの合計
• 情報利得 = 0.6 - 0.14 = 0.46

ほとんどの分割器は、情報ゲインを最大化する条件を作成しようとします。

inter-rater agreement（採点者間の一致度）

#Metric

タスクの実行時に人間の評価者が一致する頻度を測定します。評価者が同意しない場合は、タスクの手順を改善する必要があるかもしれません。アノテーター間一致度または評価者間信頼性とも呼ばれます。最も一般的な評価者間一致度の測定方法の 1 つである Cohen のカッパ係数もご覧ください。

詳細については、ML 集中講座のカテゴリデータ: 一般的な問題をご覧ください。

L

L₁ 損失

#fundamentals

#Metric

実際のラベル値とモデルが予測する値の差の絶対値を計算する損失関数。たとえば、5 つの例のバッチの L₁ 損失の計算は次のようになります。

例の実際の値	モデルの予測値	デルタの絶対値
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 損失

L₁ 損失は、L₂ 損失よりも外れ値の影響を受けにくいです。

平均絶対誤差は、例ごとの L₁ 損失の平均です。

アイコンをクリックすると、数式が表示されます。

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

ここで

• $n$ はサンプル数です。
• $y$ はラベルの実際の値です。
• $\hat{y}$ は、モデルが $y$ に対して予測する値です。

---

詳細については、ML 集中講座の線形回帰: 損失をご覧ください。

L₂ 損失

#fundamentals

#Metric

実際のラベル値とモデルが予測する値の差の二乗を計算する損失関数。たとえば、5 つの例のバッチの L₂ 損失の計算は次のようになります。

例の実際の値	モデルの予測値	デルタの二乗
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = L2 損失

2 乗するため、L₂ 損失は外れ値の影響を増幅します。つまり、L₂ 損失は、L₁ 損失よりも悪い予測に強く反応します。たとえば、前のバッチの L₁ 損失は 16 ではなく 8 になります。16 個のうち 9 個が 1 つの外れ値で占められていることに注目してください。

回帰モデルでは、通常、損失関数として L₂ 損失が使用されます。

平均二乗誤差は、例ごとの L₂ 損失の平均です。二乗損失は、L₂ 損失の別名です。

アイコンをクリックすると、数式が表示されます。

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

ここで

• $n$ はサンプル数です。
• $y$ はラベルの実際の値です。
• $\hat{y}$ は、モデルが $y$ に対して予測する値です。

---

詳細については、ML 集中講座のロジスティック回帰: 損失と正則化をご覧ください。

LLM 評価（eval）

#generativeAI

#Metric

大規模言語モデル（LLM）のパフォーマンスを評価するための指標とベンチマークのセット。LLM の評価は、大まかに次のようになります。

• 研究者が LLM の改善が必要な領域を特定するのに役立ちます。
• さまざまな LLM を比較し、特定のタスクに最適な LLM を特定するのに役立ちます。
• LLM の使用が安全で倫理的であることを確認します。

詳細については、ML 集中講座の大規模言語モデル（LLM）をご覧ください。

損失

#fundamentals

#Metric

教師ありモデルのトレーニングで、モデルの予測がラベルからどのくらい離れているかを表す指標。

損失関数は損失を計算します。

詳細については、ML 集中講座の線形回帰: 損失をご覧ください。

損失関数

#fundamentals

#Metric

トレーニングまたはテスト中に、例のバッチの損失を計算する数学関数。損失関数は、予測が悪いモデルよりも予測がよいモデルに対して、より低い損失を返します。

通常、トレーニングの目標は、損失関数が返す損失を最小限に抑えることです。

損失関数にはさまざまな種類があります。構築するモデルの種類に適した損失関数を選択します。次に例を示します。

• L₂ 損失（または平均二乗誤差）は、線形回帰の損失関数です。
• 対数損失は、ロジスティック回帰の損失関数です。

M

平均絶対誤差（MAE）

#Metric

L₁ 損失が使用されている場合の、例ごとの平均損失。平均絶対誤差は次のように計算します。

1. バッチの L₁ 損失を計算します。
2. L₁ 損失をバッチ内のサンプル数で割ります。

アイコンをクリックすると、数式が表示されます。

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

ここで

• $n$ はサンプル数です。
• $y$ はラベルの実際の値です。
• $\hat{y}$ は、モデルが $y$ に対して予測する値です。

---

たとえば、次の 5 つの例のバッチで L₁ 損失を計算することを考えます。

例の実際の値	モデルの予測値	損失（実測値と予測値の差）
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 損失

したがって、L₁ 損失は 8 で、サンプル数は 5 です。したがって、平均絶対誤差は次のようになります。

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

平均絶対誤差と平均二乗誤差、二乗平均平方根誤差を比較します。

k での平均適合率の平均（mAP@k）

#generativeAI

#Metric

検証データセット全体でのすべてのk における平均適合率スコアの統計的平均。k における平均適合率の用途の一つは、レコメンデーション システムによって生成された推奨事項の品質を判断することです。

「平均平均」というフレーズは冗長に聞こえますが、指標の名前としては適切です。この指標は、複数の k における平均適合率の値の平均を求めるためです。

アイコンをクリックすると、例が表示されます。

各ユーザーにパーソナライズされたおすすめの小説のリストを生成するレコメンデーション システムを構築するとします。選択したユーザーからのフィードバックに基づいて、次の 5 つの平均適合率（k）スコア（ユーザーごとに 1 つのスコア）を計算します。

• 0.73
• 0.77
• 0.67
• 0.82
• 0.76

したがって、K における平均適合率の平均は次のようになります。

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

平均二乗誤差（MSE）

#Metric

L₂ 損失が使用されている場合の、例あたりの平均損失。平均二乗誤差は次のように計算します。

1. バッチの L₂ 損失を計算します。
2. L₂ 損失をバッチ内のサンプル数で割ります。

アイコンをクリックすると、数式が表示されます。

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ ここで:

• $n$ はサンプル数です。
• $y$ はラベルの実際の値です。
• $\hat{y}$ は $y$ に対するモデルの予測です。

---

たとえば、次の 5 つの例のバッチの損失について考えてみましょう。

実際の値	モデルの予測	損失	二乗損失
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			16 = L2 損失

したがって、平均二乗誤差は次のようになります。

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

平均二乗誤差は、特に線形回帰でよく使用されるトレーニング オプティマイザーです。

平均二乗誤差と平均絶対誤差、二乗平均平方根誤差を比較します。

TensorFlow Playground では、平均二乗誤差を使用して損失値を計算します。

アイコンをクリックすると、外れ値の詳細が表示されます。

外れ値は平均二乗誤差に大きな影響を与えます。たとえば、損失が 1 の場合、二乗損失は 1 ですが、損失が 3 の場合、二乗損失は 9 になります。上の表では、3 つのアカウントの損失がある例は平均二乗誤差の約 56% を占めていますが、1 つのアカウントの損失がある例はそれぞれ平均二乗誤差の 6% しか占めていません。

外れ値は、平均二乗誤差ほど平均絶対誤差に影響しません。たとえば、3 つのアカウントの損失は、平均絶対誤差の約 38% にすぎません。

クリッピングは、極端な外れ値がモデルの予測能力を損なうのを防ぐ方法の 1 つです。

---

指標

#TensorFlow

#Metric

重視すべき統計情報。

目標は、ML システムが最適化しようとする指標です。

指標 API（tf.metrics）

#Metric

モデルを評価するための TensorFlow API。たとえば、tf.metrics.accuracy は、モデルの予測がラベルと一致する頻度を決定します。

ミニマックス損失

#Metric

生成されたデータと実際のデータの分布間のクロスエントロピーに基づく、敵対的生成ネットワークの損失関数。

ミニマックス損失は、最初の論文で敵対的生成ネットワークを説明するために使用されています。

詳細については、Generative Adversarial Networks コースの損失関数をご覧ください。

モデル容量

#Metric

モデルが学習できる問題の複雑さ。モデルが学習できる問題が複雑であるほど、モデルの容量は大きくなります。通常、モデルの容量はモデル パラメータの数とともに増加します。分類モデルの容量の正式な定義については、VC 次元をご覧ください。

N

陰性クラス

#fundamentals

#Metric

バイナリ分類では、一方のクラスを「陽性」、もう一方のクラスを「陰性」と呼びます。陽性クラスはモデルがテストしているものまたはイベントであり、陰性クラスはそれ以外の可能性です。次に例を示します。

• 医学検査の陰性クラスは「腫瘍なし」などになります。
• メールの分類モデルの負のクラスは「迷惑メールではない」です。

ポジティブ クラスと対照的です。

O

目標

#Metric

アルゴリズムが最適化しようとしている指標。

目的関数

#Metric

モデルの最適化対象とする数式または指標。たとえば、線形回帰の目的関数は、通常は平均二乗損失です。したがって、線形回帰モデルをトレーニングするときは、平均二乗損失を最小限に抑えることが目標となります。

場合によっては、目的関数を最大化することが目標になります。たとえば、目的関数が精度の場合、目標は精度を最大化することです。

損失もご覧ください。

P

pass at k（pass@k）

#Metric

大規模言語モデルが生成するコード（Python など）の品質を判断する指標。具体的には、pass at k は、生成された k 個のコードブロックのうち、少なくとも 1 つの生成されたコードブロックがすべての単体テストに合格する可能性を示します。

大規模言語モデルは、複雑なプログラミング問題に対して適切なコードを生成するのが難しいことがよくあります。ソフトウェア エンジニアは、大規模言語モデルに同じ問題に対する複数の（k 個の）ソリューションを生成するように指示することで、この問題に対応します。次に、ソフトウェア エンジニアが各ソリューションを単体テストでテストします。k での合格の計算は、単体テストの結果によって異なります。

• これらのソリューションのいずれかが単体テストに合格した場合、LLM はそのコード生成チャレンジに合格します。
• どのソリューションも単体テストに合格しない場合、LLM はそのコード生成チャレンジに失敗します。

k でのパスの式は次のとおりです。

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

一般に、k の値が大きいほど、pass at k スコアが高くなります。ただし、k の値が大きいほど、大規模言語モデルと単体テストのリソースが必要になります。

アイコンをクリックして例を確認します。

ソフトウェア エンジニアが大規模言語モデルに、n=50 個の難しいコーディング問題に対する k=10 個のソリューションを生成するように依頼したとします。結果は次のとおりです。

• 30 回のパス
• 20 件の不合格

したがって、スコア 10 での合格は次のようになります。

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

パフォーマンス

#Metric

次の意味を持つオーバーロードされた用語:

• ソフトウェア エンジニアリングにおける標準的な意味。つまり、このソフトウェアはどのくらいの速さ（または効率）で実行されるかということです。
• ML における意味。ここで、パフォーマンスは「このモデルはどの程度正確か？」という質問に答えます。つまり、モデルの予測はどの程度正確かということです。

permutation variable importances

#df

#Metric

特徴量の値を並べ替えた後のモデルの予測誤差の増加を評価する変数重要度の一種。順列変数重要度は、モデルに依存しない指標です。

パープレキシティ

#Metric

モデルがタスクをどの程度達成しているかを測定する指標の 1 つ。たとえば、ユーザーがスマートフォンのキーボードで入力している単語の最初の数文字を読み取り、候補となる補完単語のリストを表示するタスクがあるとします。このタスクのパープレキシティ P は、ユーザーが入力しようとしている実際の単語をリストに含めるために必要な推測の数にほぼ等しくなります。

パープレキシティは、次のように交差エントロピーに関連しています。

$$P= 2^{-\text{cross entropy}}$$

陽性クラス

#fundamentals

#Metric

テスト対象のクラス。

たとえば、がんモデルのポジティブ クラスは「腫瘍」になります。メールの分類モデルのポジティブ クラスは「迷惑メール」になる可能性があります。

陰性クラスと比較してください。

アイコンをクリックすると、追加のメモが表示されます。

多くのテストでは「陽性」の結果は望ましくない結果であることが多いため、「陽性クラス」という用語は混乱を招く可能性があります。たとえば、多くの医療検査で陽性クラスは腫瘍や病気に対応します。一般的に、医師には「おめでとうございます。検査結果は陰性でした。」 いずれにしても、ポジティブ クラスはテストで検出するイベントです。

確かに、同時にポジティブ クラスとネガティブ クラスの両方をテストしています。

---

PR AUC（PR 曲線の下の面積）

#Metric

さまざまな分類しきい値の値に対して（再現率、適合率）の点をプロットして得られた、補間された適合率 / 再現率曲線の下の面積。

precision

#fundamentals

#Metric

「全陽性のラベルの中でモデルが正しく識別したラベルの数は？」という質問に回答する分類モデルの指標。

モデルが陽性クラスを予測したとき、予測が正しかった割合はどのくらいですか？

式は次のとおりです。

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

ここで

• 真陽性とは、モデルが陽性のクラスを正しく予測したことを意味します。
• 偽陽性とは、モデルが陽性クラスを誤って予測したことを意味します。

たとえば、モデルが 200 件のポジティブ予測を行ったとします。この 200 件の正の予測のうち:

• 150 件が真陽性でした。
• 50 件は誤検知でした。

この例の場合は、次のようになります。

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

精度と再現率と比較してください。

詳細については、ML 集中講座の分類: 正確度、再現率、適合率、関連指標をご覧ください。

k での適合率（precision@k）

#Metric

ランク付けされた（順序付けされた）アイテムのリストを評価するための指標。Precision at k は、そのリストの最初の k 個の項目のうち「関連性がある」項目の割合を示します。具体的には、次のことが求められます。

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

k の値は、返されるリストの長さ以下にする必要があります。返されるリストの長さは計算に含まれません。

関連性は主観的なことが多く、人間の評価者でさえ、どの項目が関連しているかについて意見が一致しないことがよくあります。

比較対象日:

• k における平均適合率
• k における平均適合率

アイコンをクリックすると、例が表示されます。

大規模言語モデルに次のクエリが与えられたとします。

List the 6 funniest movies of all time in order.

大規模言語モデルは、次の表の最初の 2 つの列に示すリストを返します。

位置	映画	関連性があるか？
1	The General	○
2	Mean Girls	○
3	Platoon	いいえ
4	ブライズメイズ 史上最悪のウェディングプラン	○
5	Citizen Kane	いいえ
6	This is Spinal Tap	○

最初の 3 つの映画のうち 2 つが関連性があるため、精度は 3 です。

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

最初の 5 本の映画のうち 3 本が非常に面白いので、精度 @ 5 は次のようになります。

$$\text{precision at 5} = \frac{\text{3}} {\text{5}} = 0.6$$

---

適合率と再現率の曲線

#Metric

さまざまな分類しきい値における適合率と再現率の曲線。

予測バイアス

#Metric

データセット内の予測の平均とラベルの平均との差を示す値。

ML モデルのバイアス項や、倫理と公平性のバイアスとは異なります。

予測のパリティ

#responsible

#Metric

特定の分類モデルについて、考慮対象のサブグループの適合率が同等かどうかをチェックする公平性指標。

たとえば、大学の合格を予測するモデルの場合、リリパット人とブロブディンナグ人の適合率が同じであれば、国籍に関する予測パリティを満たします。

予測パリティは、予測率パリティとも呼ばれます。

予測パリティの詳細については、「公平性の定義の説明」（セクション 3.2.1）をご覧ください。

予測料金同等性

#responsible

#Metric

予測パリティの別名。

確率密度関数

#Metric

特定の値を正確に持つデータサンプルの頻度を特定する関数。データセットの値が連続する浮動小数点数の場合、完全一致はほとんど発生しません。ただし、値 x から値 y までの確率密度関数を積分すると、x と y の間のデータサンプル数の期待値が得られます。

たとえば、平均が 200 で標準偏差が 30 の正規分布を考えてみましょう。211.4 ～ 218.7 の範囲に収まるデータサンプルが予想される頻度を特定するには、正規分布の確率密度関数を 211.4 ～ 218.7 の範囲で積分します。

R

recall

#fundamentals

#Metric

「全陽性のラベルの中でモデルが正しく識別したラベルの数は？」という質問に回答する分類モデルの指標。

グラウンド トゥルースが陽性クラスだった場合、モデルが陽性クラスとして正しく識別した予測の割合はどのくらいですか？

式は次のとおりです。

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

ここで

• 真陽性とは、モデルが陽性のクラスを正しく予測したことを意味します。
• 偽陰性とは、モデルが陰性クラスを誤って予測したことを意味します。

たとえば、モデルがグラウンド トゥルースが陽性クラスである例について 200 件の予測を行ったとします。これらの 200 個の予測のうち:

• 180 件が真陽性でした。
• 20 件は偽陰性でした。

この例の場合は、次のようになります。

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

クラス不均衡データセットに関するメモのアイコンをクリックします。

再現率は、陽性クラスがまれな分類モデルの予測能力を判断するのに特に役立ちます。たとえば、特定の病気の陽性クラスが 100 万人の患者のうち 10 人にしか発生しないクラス不均衡データセットを考えてみましょう。モデルが 500 万件の予測を行い、次の結果が得られたとします。

• 30 個の真陽性
• 20 個の偽陰性
• 4,999,000 件の真陰性
• 950 件の誤検出

したがって、このモデルの再現率は次のようになります。

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

一方、このモデルの精度は次のとおりです。

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

この高い精度の値は印象的ですが、本質的には意味がありません。再現率は、クラスの不均衡なデータセットでは精度よりもはるかに有用な指標です。

---

詳細については、分類: 精度、再現率、適合率、関連指標をご覧ください。

上位 k 件の再現率（recall@k）

#Metric

ランク付けされた（順序付けされた）アイテムのリストを出力するシステムを評価するための指標。再現率（k）は、返された関連アイテムの総数のうち、リストの最初の k 個のアイテムに含まれる関連アイテムの割合を示します。

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

k での精度とのコントラスト。

アイコンをクリックすると、例が表示されます。

大規模言語モデルに次のクエリが与えられたとします。

List the 10 funniest movies of all time in order.

大規模言語モデルは、最初の 2 つの列に示すリストを返します。

位置	映画	関連性があるか？
1	The General	○
2	Mean Girls	○
3	Platoon	いいえ
4	ブライズメイズ 史上最悪のウェディングプラン	○
5	This is Spinal Tap	○
6	飛行機！	○
7	Groundhog Day	○
8	モンティ パイソン アンド ホーリー グレイル	○
9	Oppenheimer	いいえ
10	Clueless	○

上記のリストにある 8 本の映画は非常に面白いので、「リスト内の関連アイテム」です。したがって、k でのリコールのすべての計算で、8 が分母になります。分子はどうでしょうか。最初の 4 つのアイテムのうち 3 つが関連性があるため、再現率（4）は次のようになります。

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

最初の 8 本の映画のうち 7 本が非常に面白いので、リコールは 8 です。

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

ROC（受信者操作特性）曲線

#fundamentals

#Metric

バイナリ分類におけるさまざまな分類しきい値に対する真陽性率と偽陽性率のグラフ。

ROC 曲線の形状は、陽性クラスと陰性クラスを分離するバイナリ分類モデルの能力を示します。たとえば、バイナリ分類モデルがすべての陰性クラスとすべての陽性クラスを完全に分離するとします。

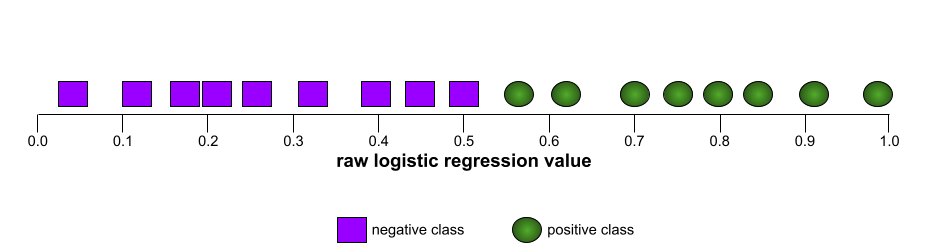
上記のモデルの ROC 曲線は次のようになります。

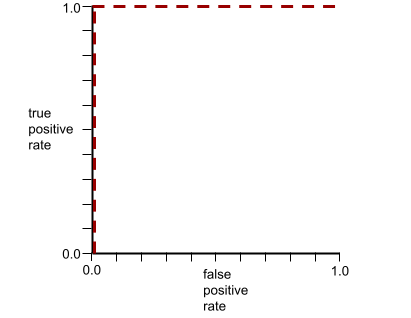
一方、次の図は、負のクラスと正のクラスをまったく分離できないひどいモデルのロジスティック回帰の生値をグラフ化したものです。

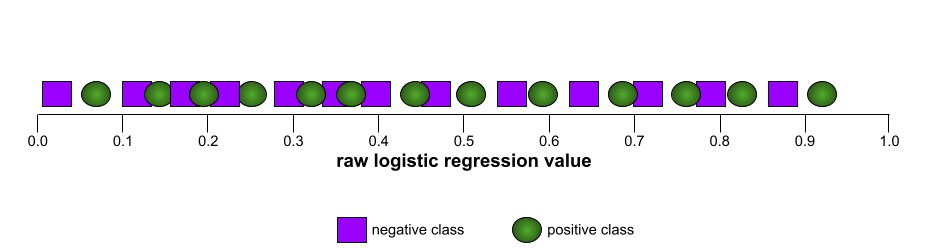
このモデルの ROC 曲線は次のようになります。

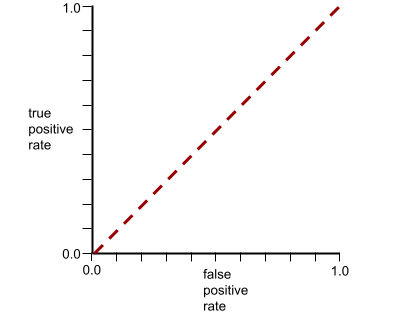
一方、現実の世界では、ほとんどのバイナリ分類モデルは陽性クラスと陰性クラスをある程度分離しますが、完全に分離することは通常ありません。したがって、一般的な ROC 曲線は、次の 2 つの極端なケースの中間に位置します。

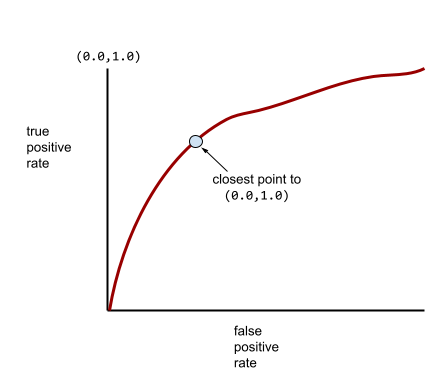
ROC 曲線上の点のうち、(0.0,1.0) に最も近い点が、理論上は理想的な分類しきい値を特定します。ただし、理想的な分類しきい値の選択には、他のいくつかの現実世界の問題が影響します。たとえば、偽陰性の方が偽陽性よりもはるかに大きな問題を引き起こす可能性があります。

AUC という数値指標は、ROC 曲線を単一の浮動小数点値に要約します。

二乗平均平方根誤差（RMSE）

#fundamentals

#Metric

平均二乗誤差の平方根。

ROUGE（Recall-Oriented Understudy for Gisting Evaluation）

#Metric

自動要約モデルと機械翻訳モデルを評価する指標のファミリー。ROUGE 指標は、参照テキストが ML モデルの生成テキストとどの程度重複しているかを判断します。ROUGE ファミリーの各メンバーは、重複を異なる方法で測定します。ROUGE スコアが高いほど、参照テキストと生成されたテキストの類似性が高いことを示します。

通常、ROUGE ファミリーの各メンバーは次の指標を生成します。

• 適合率
• 再現率
• F₁

注: ROUGE では、従来の 適合率と再現率とは若干異なる方法で適合率と再現率が使用されます。

詳細と例については、以下をご覧ください。

• ROUGE-L
• ROUGE-N
• ROUGE-S

注: BLEU と BLEURT は適合率を最適化しますが、ROUGE は再現率を最適化します。したがって、BLEU と BLEURT は機械翻訳の評価に適した指標であり（精度に重点が置かれているため）、ROUGE は要約に適した指標です（再現率に重点が置かれているため）。

ROUGE-L

#Metric

ROUGE ファミリーのメンバーで、参照テキストと生成されたテキストの最長共通部分列の長さに焦点を当てています。次の式は、ROUGE-L の再現率と適合率を計算します。

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

次に、F₁ を使用して、ROUGE-L 再現率と ROUGE-L 適合率を 1 つの指標にロールアップできます。

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

ROUGE-L の計算例のアイコンをクリックします。

次の参照テキストと生成されたテキストについて考えてみましょう。

カテゴリ	制作会社	テキスト
参照テキスト	人間の翻訳者	さまざまなことを理解したい。
生成されたテキスト	ML モデル	たくさんのことを学びたい。

したがって、次のコマンドを実行します。

• 最長共通部分列は 5（I want to of things）です。
• 参照テキストの単語数は 9 です。
• 生成されたテキストの単語数は 7 です。

したがって、次のようになります。

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

ROUGE-L は、参照テキストと生成されたテキストの改行を無視するため、最長共通部分列が複数の文にまたがる可能性があります。参照テキストと生成されたテキストに複数の文が含まれている場合は、一般的に ROUGE-Lsum と呼ばれる ROUGE-L のバリエーションの方が優れた指標になります。ROUGE-Lsum は、パッセージ内の各文の最長共通部分列を特定し、それらの最長共通部分列の平均を計算します。

アイコンをクリックすると、ROUGE-Lsum の計算例が表示されます。

次の参照テキストと生成されたテキストについて考えてみましょう。

カテゴリ	制作会社	テキスト
参照テキスト	人間の翻訳者	火星の表面は乾燥しています。水はほとんどが地下深くにあります。
生成されたテキスト	ML モデル	火星の表面は乾燥しています。ただし、水の大部分は地下にあります。

そのため、以下のコマンドを実行します。

	First sentence	2 文目
最長共通シーケンス	2（火星乾燥）	3（水が地下にある）
参照テキストの文の長さ	6	7
生成されたテキストの文の長さ	5	8

したがって、次のようになります。

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#Metric

ROUGE ファミリー内の指標のセット。参照テキストと生成されたテキストの特定のサイズの共有 N グラムを比較します。次に例を示します。

• ROUGE-1 は、参照テキストと生成されたテキストで共有されているトークンの数を測定します。
• ROUGE-2 は、参照テキストと生成されたテキストで共有されるバイグラム（2 グラム）の数を測定します。
• ROUGE-3 は、参照テキストと生成されたテキストで共有されているトライグラム（3 グラム）の数を測定します。

次の数式を使用すると、ROUGE-N ファミリーの任意のメンバーの ROUGE-N 再現率と ROUGE-N 適合率を計算できます。

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

次に、F₁ を使用して、ROUGE-N 再現率と ROUGE-N 適合率を 1 つの指標にロールアップできます。

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

アイコンをクリックして例を確認します。

たとえば、人間の翻訳者と比較して ML モデルの翻訳の有効性を測定するために ROUGE-2 を使用するとします。

カテゴリ	制作会社	テキスト	バイグラム
参照テキスト	人間の翻訳者	さまざまなことを理解したい。	さまざまなことを理解したい
生成されたテキスト	ML モデル	たくさんのことを学びたい。	I want, want to, to learn, learn plenty, plenty of, of things

したがって、次のコマンドを実行します。

• 一致する 2 グラムの数は 3（I want、want to、of things）です。
• 参照テキスト内の 2 グラムの数は 8 です。
• 生成されたテキストの 2 グラムの数は 6 です。

したがって、次のようになります。

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#Metric

スキップグラム マッチングを可能にする ROUGE-N の寛容な形式。つまり、ROUGE-N は完全に一致する N グラムのみをカウントしますが、ROUGE-S は 1 つ以上の単語で区切られた N グラムもカウントします。たとえば、次の点を考えます。

• 参照テキスト: 白い雲
• 生成されたテキスト: 白い雲が湧き上がっている

ROUGE-N を計算する場合、2 グラムの「白い雲」は「白いもくもくとした雲」と一致しません。ただし、ROUGE-S を計算する際は、白い雲は白い積雲と一致します。

決定係数

#Metric

ラベルの分散が個々の特徴量または特徴量セットにどの程度起因するかを示す回帰指標。決定係数は 0 ～ 1 の値で、次のように解釈できます。

• 決定係数 0 は、その特徴量セットがラベルの分散にまったく寄与していないことを意味します。
• 決定係数 1 は、ラベルの分散のすべてがその特徴量セットによるものであることを意味します。
• 0 ～ 1 の決定係数は、ラベルの分散が特定の特徴量または特徴量セットからどの程度予測可能であるかを示します。たとえば、決定係数が 0.10 の場合、ラベルの分散の 10% が特徴量セットによるものであることを意味します。決定係数が 0.20 の場合、20% が特徴量セットによるものであることを意味します。

決定係数は、モデルが予測した値とグラウンド トゥルースの間のピアソン相関係数の 2 乗です。

S

得点

#Metric

候補生成フェーズで生成された各アイテムの値またはランキングを提供するレコメンデーション システムの一部。

類似性指標

#clustering

#Metric

クラスタリング アルゴリズムで、2 つの例がどの程度類似しているかを判断するために使用される指標。

スパース性

#Metric

ベクトルまたは行列でゼロ（または null）に設定された要素の数を、そのベクトルまたは行列のエントリの総数で割った値。たとえば、98 個のセルに 0 が含まれる 100 要素の行列について考えてみましょう。スパース性の計算は次のとおりです。

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

特徴量のスパース性は特徴ベクトル内のスパース性を指し、モデルのスパース性はモデルの重みのスパース性を指します。

二乗ヒンジ損失

#Metric

ヒンジ損失の 2 乗。2 乗ヒンジ損失は、通常のヒンジ損失よりも外れ値に厳しいペナルティを科します。

二乗損失

#fundamentals

#Metric

L₂ 損失と同義。

T

テスト損失

#fundamentals

#Metric

テストセットに対するモデルの損失を表す指標。モデルを構築する場合、通常はテスト損失を最小限に抑えようとします。これは、テスト損失が小さいほど、トレーニング損失や検証損失が小さい場合よりも品質シグナルが強くなるためです。

テスト損失とトレーニング損失または検証損失の間に大きな差がある場合は、正則化率を上げる必要があることを示している場合があります。

上位 k の精度

#Metric

生成されたリストの最初の k 個の位置に「ターゲット ラベル」が表示される割合。リストは、パーソナライズされたおすすめや、softmaxで並べ替えられたアイテムのリストなどです。

上位 k の精度は、k での精度とも呼ばれます。

注: ターゲット ラベルは任意のクラス（必ずしもグラウンド トゥルース クラスである必要はありません）であるため、上位 k の精度は必ずしも従来の精度と同等ではありません。

アイコンをクリックして例を確認します。

Softmax を使用して、木の葉の写真に基づいて木の確率を特定する ML システムを考えてみましょう。次の表に、5 つの入力ツリー画像から生成された出力リストを示します。各行には、ターゲット ラベルと、最も可能性の高い 5 つのツリーが含まれています。たとえば、ターゲット ラベルが maple の場合、機械学習モデルは elm を最も可能性の高い木、oak を 2 番目に可能性の高い木として識別しました。

ターゲット ラベル	1	2	3	4	5
カエデ	elm	オーク	maple	ブナ	ポプラ
ハナミズキ	オーク	dogwood	ポプラ	Hickory	カエデ
オーク	oak	バスウッド	locust	ハンノキ	Linden
Linden	カエデ	paw-paw	オーク	バスウッド	ポプラ
オーク	locust	Linden	oak	カエデ	paw-paw

ターゲット ラベルは最初の位置に 1 回だけ表示されるため、上位 1 の精度は次のようになります。

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

ターゲット ラベルが上位 3 つの位置のいずれかに 4 回表示されるため、上位 3 つの精度は次のようになります。

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

有害

#Metric

コンテンツが誹謗中傷、脅迫、不快な内容である度合い。多くの ML モデルは、有害性を特定して測定できます。これらのモデルのほとんどは、暴言のレベルや脅迫的な言葉のレベルなど、複数のパラメータに沿って有害性を特定します。

トレーニングの損失

#fundamentals

#Metric

特定のトレーニング反復処理中のモデルの損失を表す指標。たとえば、損失関数が平均二乗誤差であるとします。たとえば、10 回目の反復のトレーニング損失（平均二乗誤差）が 2.2 で、100 回目の反復のトレーニング損失が 1.9 であるとします。

損失曲線は、トレーニングの損失と反復回数をプロットしたものです。損失曲線は、トレーニングについて次のヒントを提供します。

• 右下がりの傾斜は、モデルが改善されていることを意味します。
• 上向きの傾斜は、モデルが悪化していることを意味します。
• 傾斜が平らな場合は、モデルが収束に達したことを意味します。

たとえば、次のやや理想化された損失曲線は、次のようになります。

• 初期の反復で急激な下降勾配が見られる。これは、モデルが急速に改善していることを意味します。
• トレーニングの終了近くまで徐々に平坦になる（ただし、まだ下降している）傾斜。これは、最初の反復処理よりもやや遅いペースでモデルの改善が継続していることを意味します。
• トレーニングの終わりに近づくにつれて傾斜が平らになり、収束を示しています。

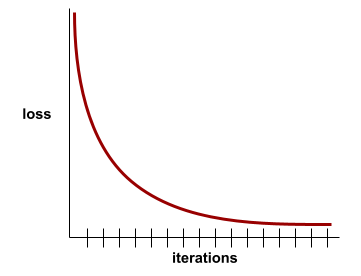
トレーニング損失は重要ですが、汎化もご覧ください。

真陰性（TN）

#fundamentals

#Metric

モデルが陰性クラスを正しく予測した例。たとえば、特定のメール メッセージが迷惑メールではないとモデルが推論し、そのメール メッセージが実際に迷惑メールではない場合です。

真陽性（TP）

#fundamentals

#Metric

モデルが陽性クラスを正しく予測した例。たとえば、特定のメール メッセージがスパムであるとモデルが推論し、そのメール メッセージが実際にスパムである場合です。

真陽性率（TPR）

#fundamentals

#Metric

再現率と同義。具体的には、次のことが求められます。

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

真陽性率は、ROC 曲線の Y 軸です。

V

検証損失

#fundamentals

#Metric

トレーニングの特定の反復中に、検証セットでのモデルの損失を表す指標。

汎化曲線もご覧ください。

変数の重要度

#df

#Metric

各特徴のモデルに対する相対的な重要度を示すスコアのセット。

たとえば、住宅価格を推定する決定木について考えてみましょう。この決定木では、サイズ、年齢、スタイルの 3 つの特徴を使用するとします。3 つの特徴の変数重要度のセットが {size=5.8, age=2.5, style=4.7} と計算された場合、サイズは年齢やスタイルよりも決定木にとって重要です。

さまざまな変数重要度指標があり、ML の専門家はモデルのさまざまな側面について知ることができます。

W

Wasserstein 損失

#Metric

敵対的生成ネットワークで一般的に使用される損失関数の 1 つ。生成されたデータの分布と実際のデータの間のアース ムーバー距離に基づいています。