मशीन लर्निंग की शब्दावली: मेट्रिक

इस पेज पर, मेट्रिक शब्दावली के शब्द दिए गए हैं. सभी शब्दावली के लिए, यहां क्लिक करें.

A

सटीक

#fundamentals

#Metric

सही क्लासिफ़िकेशन अनुमानों की संख्या को अनुमानों की कुल संख्या से भाग देने पर यह स्कोर मिलता है. यानी:

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

उदाहरण के लिए, अगर किसी मॉडल ने 40 सही और 10 गलत अनुमान लगाए हैं, तो उसकी सटीकता इस तरह से कैलकुलेट की जाएगी:

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

बाइनरी क्लासिफ़िकेशन में, सही अनुमानों और गलत अनुमानों की अलग-अलग कैटगरी के लिए खास नाम दिए गए हैं. इसलिए, बाइनरी क्लासिफ़िकेशन के लिए सटीक नतीजे का फ़ॉर्मूला यह है:

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

कहां:

• टीपी, ट्रू पॉज़िटिव (सही अनुमान) की संख्या है.
• TN, ट्रू नेगेटिव (सही अनुमान) की संख्या है.
• एफ़पी, फ़ॉल्स पॉज़िटिव (गलत अनुमान) की संख्या है.
• FN, फ़ॉल्स निगेटिव (गलत अनुमान) की संख्या है.

प्रिसिज़न और रीकॉल के साथ, सटीकता की तुलना करें और इनके बीच अंतर बताएं.

सटीकता और क्लास-इंबैलेंस वाले डेटासेट के बारे में ज़्यादा जानने के लिए, आइकॉन पर क्लिक करें.

कुछ मामलों में यह मेट्रिक काम की होती है, लेकिन अन्य मामलों में यह सटीक जानकारी नहीं देती. खास तौर पर, एक्यूरेसी आम तौर पर उन क्लासिफ़िकेशन मॉडल का आकलन करने के लिए एक खराब मेट्रिक होती है जो क्लास-इंबैलेंस वाले डेटासेट को प्रोसेस करते हैं.

उदाहरण के लिए, मान लें कि किसी उपोष्णकटिबंधीय शहर में, हर सदी में सिर्फ़ 25 दिन बर्फ़बारी होती है. इस शहर में, बर्फ़बारी वाले दिनों (पॉज़िटिव क्लास) की तुलना में बर्फ़बारी न होने वाले दिनों (नेगेटिव क्लास) की संख्या बहुत ज़्यादा है. इसलिए, इस शहर के लिए बर्फ़बारी का डेटासेट, क्लास-इंबैलेंस वाला है. मान लें कि एक बाइनरी क्लासिफ़िकेशन मॉडल है. इसे हर दिन यह अनुमान लगाना है कि बर्फ़बारी होगी या नहीं. हालांकि, यह हर दिन सिर्फ़ "बर्फ़बारी नहीं होगी" का अनुमान लगाता है. यह मॉडल बहुत सटीक है, लेकिन इसमें अनुमान लगाने की क्षमता नहीं है. यहां दी गई टेबल में, 100 साल के अनुमानों के नतीजों की खास जानकारी दी गई है:

कैटगरी	नंबर
TP	0
TN	36499
एफ़पी	0
FN	25

इसलिए, इस मॉडल के सटीक होने की संभावना यह है:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

हालांकि, 99.93% सटीकता का प्रतिशत बहुत अच्छा लगता है, लेकिन मॉडल में अनुमान लगाने की क्षमता नहीं है.

क्लास-इंबैलेंस वाले डेटासेट पर ट्रेन किए गए मॉडल का आकलन करने के लिए, सटीकता की तुलना में सटीक नतीजे और वापस बुलाना आम तौर पर ज़्यादा काम की मेट्रिक होती हैं.

---

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में क्लासिफ़िकेशन: सटीक, रीकॉल, प्रेसिज़न, और इनसे जुड़ी मेट्रिक देखें.

पीआर कर्व के नीचे का एरिया

#Metric

पीआर एयूसी (पीआर कर्व के नीचे का हिस्सा) देखें.

आरओसी कर्व के नीचे का क्षेत्र

#Metric

AUC (ROC कर्व के नीचे का हिस्सा) देखें.

AUC (आरओसी कर्व के नीचे का हिस्सा)

#fundamentals

#Metric

यह 0.0 से 1.0 के बीच की एक संख्या होती है. यह बाइनरी क्लासिफ़िकेशन मॉडल की, पॉज़िटिव क्लास को नेगेटिव क्लास से अलग करने की क्षमता को दिखाती है. एयूसी की वैल्यू 1.0 के जितनी ज़्यादा करीब होगी, मॉडल की परफ़ॉर्मेंस उतनी ही बेहतर होगी.

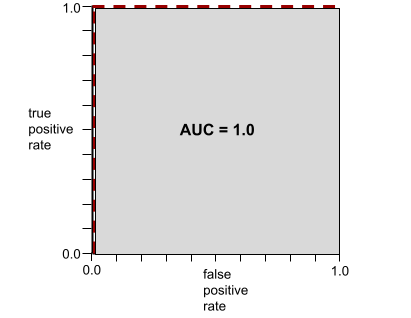
उदाहरण के लिए, यहां दी गई इमेज में एक क्लासिफ़िकेशन मॉडल दिखाया गया है. यह पॉज़िटिव क्लास (हरे रंग के ओवल) को नेगेटिव क्लास (बैंगनी रंग के आयत) से अलग करता है. इस मॉडल का एयूसी 1.0 है, जो कि काफ़ी अच्छा है:

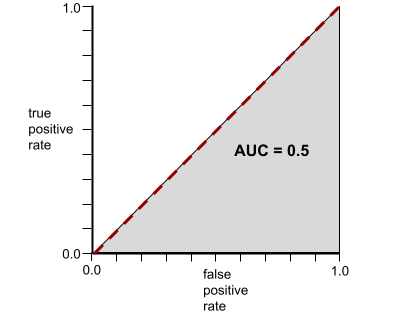
इसके उलट, यहां दिए गए उदाहरण में, क्लासिफ़िकेशन मॉडल के नतीजे दिखाए गए हैं. इस मॉडल ने रैंडम नतीजे जनरेट किए हैं. इस मॉडल का एयूसी 0.5 है:

हां, पिछले मॉडल का एयूसी 0.5 है, न कि 0.0.

ज़्यादातर मॉडल, इन दोनों के बीच में कहीं होते हैं. उदाहरण के लिए, यहां दिया गया मॉडल, पॉज़िटिव और नेगेटिव वैल्यू को कुछ हद तक अलग करता है. इसलिए, इसका एयूसी 0.5 और 1.0 के बीच है:

एयूसी, क्लासिफ़िकेशन थ्रेशोल्ड के लिए सेट की गई किसी भी वैल्यू को अनदेखा करता है. इसके बजाय, एयूसी, क्लासिफ़िकेशन के सभी संभावित थ्रेशोल्ड पर विचार करता है.

एयूसी और आरओसी कर्व के बीच के संबंध के बारे में जानने के लिए, आइकॉन पर क्लिक करें.

AUC, ROC कर्व के नीचे के क्षेत्र को दिखाता है. उदाहरण के लिए, किसी ऐसे मॉडल के लिए आरओसी कर्व यहां दिया गया है जो पॉज़िटिव और नेगेटिव को पूरी तरह से अलग करता है:

एयूसी, ऊपर दिए गए इलस्ट्रेशन में ग्रे रंग वाला हिस्सा है. इस खास मामले में, क्षेत्रफल निकालने के लिए ग्रे क्षेत्र की लंबाई (1.0) को ग्रे क्षेत्र की चौड़ाई (1.0) से गुणा किया जाता है. इसलिए, 1.0 और 1.0 का प्रॉडक्ट, एयूसी के तौर पर ठीक 1.0 देता है. यह एयूसी का सबसे ज़्यादा स्कोर है.

इसके उलट, क्लासिफ़िकेशन मॉडल के लिए आरओसी कर्व, क्लास को अलग नहीं कर सकता. यह इस तरह दिखता है. इस ग्रे रंग के क्षेत्र का क्षेत्रफल 0.5 है.

एक सामान्य आरओसी कर्व, कुछ ऐसा दिखता है:

इस कर्व के नीचे के एरिया का हिसाब मैन्युअल तरीके से लगाना मुश्किल होता है. इसलिए, आम तौर पर कोई प्रोग्राम ज़्यादातर एयूसी वैल्यू का हिसाब लगाता है.

---

एयूसी की ज़्यादा औपचारिक परिभाषा के लिए, आइकॉन पर क्लिक करें.

एयूसी, इस बात की संभावना है कि क्लासिफ़िकेशन मॉडल को इस बात का ज़्यादा भरोसा होगा कि रैंडम तरीके से चुना गया पॉज़िटिव उदाहरण, असल में पॉज़िटिव है. इसके बजाय, रैंडम तरीके से चुना गया नेगेटिव उदाहरण पॉज़िटिव है.

---

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में क्लासिफ़िकेशन: आरओसी और एयूसी देखें.

k पर औसत प्रीसिज़न

#Metric

यह एक ऐसी मेट्रिक है जो किसी एक प्रॉम्प्ट पर मॉडल की परफ़ॉर्मेंस की खास जानकारी देती है. यह मेट्रिक, रैंक किए गए नतीजे जनरेट करती है. जैसे, किताबों के सुझावों की नंबर वाली सूची. k पर औसत सटीक नतीजे, हर काम के नतीजे के लिए k पर सटीक नतीजे वैल्यू का औसत होता है. इसलिए, k पर औसत सटीक स्कोर का फ़ॉर्मूला यह है:

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

कहां:

• \(n\) सूची में मौजूद काम के आइटम की संख्या है.

इसकी तुलना k पर वापस मंगाना से करें.

ध्यान दें: k पर औसत सटीक नतीजे, एक प्रॉम्प्ट के आउटपुट का आकलन करते हैं. कई अलग-अलग प्रॉम्प्ट के लिए, मॉडल के आउटपुट की क्वालिटी का आकलन करने के लिए, k पर औसत सटीक दर का इस्तेमाल करें.

ध्यान दें: कुछ लोग k पर औसत सटीक दर को छोटा करके, सिर्फ़ औसत सटीक दर कहते हैं.

उदाहरण के लिए, आइकॉन पर क्लिक करें

मान लें कि लार्ज लैंग्वेज मॉडल को यह क्वेरी दी गई है:

List the 6 funniest movies of all time in order.

इसके बाद, लार्ज लैंग्वेज मॉडल से यह सूची मिलती है:

1. द जनरल
2. Mean Girls
3. Platoon
4. दुल्हन की सहेलियां
5. सिटीज़न केन
6. This is Spinal Tap

जवाब में मिली सूची में से चार फ़िल्में बहुत मज़ेदार हैं. इसका मतलब है कि वे क्वेरी के हिसाब से सही हैं. हालांकि, दो फ़िल्में ड्रामा हैं, जो क्वेरी के हिसाब से सही नहीं हैं. इस टेबल में, नतीजों के बारे में ज़्यादा जानकारी दी गई है:

स्थिति	मूवी	क्या यह काम का है?	के पर प्रीसिज़न
1	द जनरल	हां	1.0
2	Mean Girls	हां	1.0
3	Platoon	नहीं	काम का नहीं है
4	दुल्हन की सहेलियां	हां	0.75
5	सिटीज़न केन	नहीं	काम का नहीं है
6	This is Spinal Tap	हां	0.67

काम के नतीजों की संख्या 4 है. इसलिए, 6 पर औसत सटीक जानकारी का हिसाब इस तरह लगाया जा सकता है:

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

आधारभूत

#Metric

मॉडल का इस्तेमाल, रेफ़रंस पॉइंट के तौर पर किया जाता है. इससे यह तुलना की जाती है कि कोई दूसरा मॉडल (आम तौर पर, ज़्यादा जटिल मॉडल) कैसा परफ़ॉर्म कर रहा है. उदाहरण के लिए, लॉजिस्टिक रिग्रेशन मॉडल, डीप मॉडल के लिए एक अच्छा बेसलाइन मॉडल हो सकता है.

किसी समस्या के लिए, बेसलाइन से मॉडल डेवलपर को यह तय करने में मदद मिलती है कि नए मॉडल को कम से कम कितनी परफ़ॉर्मेंस देनी चाहिए, ताकि वह काम का साबित हो सके.

C

लागत

#Metric

नुकसान के लिए समानार्थी शब्द.

काउंटरफ़ैक्चुअल फ़ेयरनेस

#responsible

#Metric

यह एक निष्पक्षता मेट्रिक है. इससे यह पता चलता है कि क्या क्लासिफ़िकेशन मॉडल, एक व्यक्ति के लिए वही नतीजा देता है जो वह दूसरे व्यक्ति के लिए देता है. हालांकि, दूसरा व्यक्ति पहले व्यक्ति जैसा ही होता है. इसमें एक या उससे ज़्यादा संवेदनशील एट्रिब्यूट को छोड़कर, बाकी सभी एट्रिब्यूट एक जैसे होते हैं. क्लासिफ़िकेशन मॉडल का आकलन करके, यह पता लगाया जा सकता है कि मॉडल में भेदभाव के संभावित सोर्स कौनसे हैं.

ज़्यादा जानकारी के लिए, इनमें से कोई एक लेख पढ़ें:

• मशीन लर्निंग क्रैश कोर्स में, निष्पक्षता: काउंटरफ़ैक्चुअल निष्पक्षता के बारे में जानें.
• When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness

क्रॉस-एंट्रॉपी

#Metric

यह लॉग लॉस का सामान्यीकरण है. इसका इस्तेमाल एक से ज़्यादा क्लास वाले क्लासिफ़िकेशन की समस्याओं को हल करने के लिए किया जाता है. क्रॉस-एंट्रॉपी, दो प्रायिकता बंटनों के बीच के अंतर को मेज़र करती है. perplexity भी देखें.

क्यूमुलेटिव डिस्ट्रीब्यूशन फ़ंक्शन (सीडीएफ़)

#Metric

यह फ़ंक्शन, टारगेट वैल्यू से कम या उसके बराबर सैंपल की फ़्रीक्वेंसी तय करता है. उदाहरण के लिए, लगातार वैल्यू के सामान्य डिस्ट्रिब्यूशन पर विचार करें. सीडीएफ़ से पता चलता है कि लगभग 50% सैंपल, औसत से कम या उसके बराबर होने चाहिए. साथ ही, लगभग 84% सैंपल, औसत से एक स्टैंडर्ड डेविएशन से कम या उसके बराबर होने चाहिए.

D

डेमोग्राफ़िक पैरिटी

#responsible

#Metric

यह एक निष्पक्षता मेट्रिक है. अगर किसी मॉडल के क्लासिफ़िकेशन के नतीजे, दिए गए संवेदनशील एट्रिब्यूट पर निर्भर नहीं करते हैं, तो यह मेट्रिक पूरी होती है.

उदाहरण के लिए, अगर ग्लबडबड्रिब यूनिवर्सिटी में लिलीपुटियन और ब्रॉबडिंगनैगियन, दोनों आवेदन करते हैं, तो डेमोग्राफ़िक पैरिटी तब हासिल होती है, जब लिलीपुटियन और ब्रॉबडिंगनैगियन, दोनों को बराबर संख्या में दाखिला मिलता है. भले ही, एक ग्रुप दूसरे ग्रुप की तुलना में ज़्यादा योग्य हो.

इसकी तुलना समान अवसर और समान संभावना से करें. ये दोनों, क्लासिफ़िकेशन के कुल नतीजों को संवेदनशील एट्रिब्यूट पर निर्भर रहने की अनुमति देते हैं. हालांकि, ये ग्राउंड ट्रुथ के कुछ खास लेबल के लिए, क्लासिफ़िकेशन के नतीजों को संवेदनशील एट्रिब्यूट पर निर्भर रहने की अनुमति नहीं देते. डेमोग्राफ़िक समानता के लिए ऑप्टिमाइज़ करते समय, ट्रेडऑफ़ के बारे में जानने के लिए, "स्मार्ट मशीन लर्निंग की मदद से भेदभाव को खत्म करना" लेख में दिया गया विज़ुअलाइज़ेशन देखें.

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में निष्पक्षता: डेमोग्राफ़िक समानता देखें.

E

अर्थ मूवर की दूरी (ईएमडी)

#Metric

यह दो डिस्ट्रीब्यूशन के बीच की समानता को मेज़र करता है. अर्थ मूवर की दूरी जितनी कम होगी, डिस्ट्रिब्यूशन उतना ही मिलता-जुलता होगा.

एडिट डिस्टेंस

#Metric

इससे यह पता चलता है कि दो टेक्स्ट स्ट्रिंग एक-दूसरे से कितनी मिलती-जुलती हैं. मशीन लर्निंग में, एडिट डिस्टेंस इन वजहों से काम का होता है:

• एडिट डिस्टेंस का हिसाब लगाना आसान होता है.
• एडिट डिस्टेंस की मदद से, एक-दूसरे से मिलती-जुलती दो स्ट्रिंग की तुलना की जा सकती है.
• एडिट डिस्टेंस से यह पता लगाया जा सकता है कि अलग-अलग स्ट्रिंग, किसी दी गई स्ट्रिंग से कितनी मिलती-जुलती हैं.

एडिट डिस्टेंस की कई परिभाषाएं मौजूद हैं. हर परिभाषा में अलग-अलग स्ट्रिंग ऑपरेशन का इस्तेमाल किया जाता है. उदाहरण के लिए, लेवेंश्टाइन दूरी देखें.

अनुभवजन्य संचयी बंटन फ़ंक्शन (ईसीडीएफ़ या ईडीएफ़)

#Metric

यह क्यूमुलेटिव डिस्ट्रिब्यूशन फ़ंक्शन है. यह किसी असल डेटासेट से मिले अनुभवजन्य मेज़रमेंट पर आधारित होता है. x-ऐक्सिस पर किसी भी पॉइंट पर फ़ंक्शन की वैल्यू, डेटासेट में मौजूद उन ऑब्ज़र्वेशन का फ़्रैक्शन होती है जो तय की गई वैल्यू से कम या उसके बराबर होती हैं.

एन्ट्रॉपी

#df

#Metric

सूचना सिद्धांत में, यह बताया जाता है कि किसी संभावना वितरण का अनुमान लगाना कितना मुश्किल है. इसके अलावा, एन्ट्रापी को इस तरह भी परिभाषित किया जाता है कि हर उदाहरण में कितनी जानकारी शामिल है. किसी डिस्ट्रिब्यूशन की एंट्रॉपी सबसे ज़्यादा तब होती है, जब रैंडम वैरिएबल की सभी वैल्यू की संभावना बराबर होती है.

दो संभावित वैल्यू "0" और "1" वाले सेट की एंट्रॉपी (उदाहरण के लिए, बाइनरी क्लासिफ़िकेशन की समस्या में लेबल) का फ़ॉर्मूला यह है:

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

कहां:

• H एन्ट्रॉपी है.
• p, "1" उदाहरणों का फ़्रैक्शन है.
• q, "0" उदाहरणों का फ़्रैक्शन है. ध्यान दें कि q = (1 - p)
• लॉग आम तौर पर log₂ होता है. इस मामले में, एंट्रॉपी यूनिट एक बिट है.

उदाहरण के लिए, मान लें कि:

• 100 उदाहरणों में "1" वैल्यू मौजूद है
• 300 उदाहरणों में वैल्यू "0" मौजूद है

इसलिए, एंट्रॉपी की वैल्यू यह होगी:

• p = 0.25
• q = 0.75
• H = (-0.25)log₂(0.25) - (0.75)log₂(0.75) = 0.81 बिट प्रति उदाहरण

पूरी तरह से संतुलित सेट (उदाहरण के लिए, 200 "0" और 200 "1") में, हर उदाहरण के लिए एंट्रॉपी 1.0 बिट होगी. सेट के इंबैलेंस होने पर, उसकी एंट्रॉपी 0.0 की ओर बढ़ती है.

डिसिज़न ट्री में, एंट्रॉपी सूचना लाभ को फ़ॉर्म्युलेट करने में मदद करती है, ताकि स्प्लिटर, क्लासिफ़िकेशन डिसिज़न ट्री के बढ़ने के दौरान शर्तें चुन सके.

एंट्रॉपी की तुलना इससे करें:

• गिनी अशुद्धता
• क्रॉस-एंट्रॉपी लॉस फ़ंक्शन

एंट्रॉपी को अक्सर शैनन की एंट्रॉपी कहा जाता है.

ज़्यादा जानकारी के लिए, फ़ैसले लेने वाले फ़ॉरेस्ट कोर्स में संख्यात्मक सुविधाओं के साथ बाइनरी क्लासिफ़िकेशन के लिए सटीक स्प्लिटर देखें.

समान अवसर

#responsible

#Metric

निष्पक्षता मेट्रिक का इस्तेमाल यह आकलन करने के लिए किया जाता है कि कोई मॉडल, संवेदनशील एट्रिब्यूट की सभी वैल्यू के लिए, एक जैसा और सही अनुमान लगा रहा है या नहीं. दूसरे शब्दों में कहें, तो अगर किसी मॉडल के लिए पॉज़िटिव क्लास सबसे सही नतीजा है, तो सभी ग्रुप के लिए ट्रू पॉज़िटिव रेट एक जैसा होना चाहिए.

अवसर की समानता, समान ऑड्स से जुड़ी होती है. इसके लिए, यह ज़रूरी है कि सभी ग्रुप के लिए, दोनों ट्रू पॉज़िटिव रेट और फ़ॉल्स पॉज़िटिव रेट एक जैसे हों.

मान लें कि ग्लबडबड्रिब यूनिवर्सिटी, गणित के एक मुश्किल प्रोग्राम में लिलीपुटियन और ब्रॉबडिंगनैगियन, दोनों को दाखिला देती है. लिलिपुटियन के सेकंडरी स्कूलों में, गणित की क्लास के लिए एक मज़बूत पाठ्यक्रम उपलब्ध कराया जाता है. साथ ही, ज़्यादातर छात्र-छात्राएं यूनिवर्सिटी प्रोग्राम के लिए ज़रूरी शर्तें पूरी करते हैं. ब्रॉबडिंगनैग के सेकंडरी स्कूलों में गणित की क्लास नहीं होती हैं. इसलिए, वहां के बहुत कम छात्र-छात्राएं गणित की परीक्षा पास कर पाते हैं. अगर योग्य छात्र-छात्राओं को उनकी राष्ट्रीयता (लिलिपुटियन या ब्रॉबडिंगनैगियन) के आधार पर भेदभाव किए बिना बराबर मौके दिए जाते हैं, तो यह माना जाएगा कि "स्वीकार किया गया" लेबल के लिए, अवसर की समानता की शर्त पूरी की गई है.

उदाहरण के लिए, मान लें कि ग्लबडबड्रिब यूनिवर्सिटी में 100 लिलिपुटियन और 100 ब्रॉबडिंगनैगियन ने आवेदन किया है. इसके बाद, एडमिशन के फ़ैसले इस तरह लिए जाते हैं:

पहली टेबल. छोटे कारोबारों के लिए आवेदन करने वाले लोग या कंपनियां (इनमें से 90% ने ज़रूरी शर्तें पूरी की हैं)

	क्वालिफ़ाई हुई	अयोग्य
स्वीकार किया गया	45	3
अस्वीकार किया गया	45	7
कुल	90	10
ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं में से चुने गए छात्र-छात्राओं का प्रतिशत: 45/90 = 50% ज़रूरी शर्तें पूरी न करने वाले छात्र-छात्राओं में से अस्वीकार किए गए छात्र-छात्राओं का प्रतिशत: 7/10 = 70% लिलिपुटियन स्कूल में चुने गए छात्र-छात्राओं का कुल प्रतिशत: (45+3)/100 = 48%

 

टेबल 2. बहुत ज़्यादा आवेदन करने वाले लोग (इनमें से 10% लोग ज़रूरी शर्तें पूरी करते हैं):

	क्वालिफ़ाई हुई	अयोग्य
स्वीकार किया गया	5	9
अस्वीकार किया गया	5	81
कुल	10	90
ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं में से दाखिला पाने वालों का प्रतिशत: 5/10 = 50% ज़रूरी शर्तें पूरी न करने वाले छात्र-छात्राओं में से दाखिला न पाने वालों का प्रतिशत: 81/90 = 90% ब्रॉबडिंगनैगियन छात्र-छात्राओं में से दाखिला पाने वालों का कुल प्रतिशत: (5+9)/100 = 14%

ऊपर दिए गए उदाहरणों में, ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं को बराबर का मौका दिया गया है. ऐसा इसलिए, क्योंकि ज़रूरी शर्तें पूरी करने वाले Lilliputians और Brobdingnagians, दोनों के पास 50% संभावना है कि उन्हें दाखिला मिल जाए.

अवसर की समानता की शर्त पूरी होती है, लेकिन निष्पक्षता से जुड़ी ये दो शर्तें पूरी नहीं होतीं:

• जनसांख्यिकी समानता: लिलिपुटियन और ब्रॉबडिंगनैगियन को अलग-अलग दरों पर यूनिवर्सिटी में दाखिला मिलता है; 48% लिलिपुटियन छात्र-छात्राओं को दाखिला मिलता है, लेकिन सिर्फ़ 14% ब्रॉबडिंगनैगियन छात्र-छात्राओं को दाखिला मिलता है.
• समान अवसर: ज़रूरी शर्तें पूरी करने वाले लिलीपुटियन और ब्रॉबडिंगनैगियन, दोनों तरह के छात्र-छात्राओं को दाखिला मिलने की संभावना बराबर होती है. हालांकि, ज़रूरी शर्तें पूरी न करने वाले लिलीपुटियन और ब्रॉबडिंगनैगियन, दोनों तरह के छात्र-छात्राओं को अस्वीकार किए जाने की संभावना बराबर होने की अतिरिक्त शर्त पूरी नहीं होती. ज़रूरी शर्तें पूरी न करने वाले Lilliputians के लिए, अस्वीकार किए जाने की दर 70% है. वहीं, ज़रूरी शर्तें पूरी न करने वाले Brobdingnagians के लिए, अस्वीकार किए जाने की दर 90% है.

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में निष्पक्षता: अवसर की समानता देखें.

ऑड बराबर करना

#responsible

#Metric

यह निष्पक्षता से जुड़ी मेट्रिक है. इससे यह आकलन किया जाता है कि कोई मॉडल, संवेदनशील एट्रिब्यूट की सभी वैल्यू के लिए, एक जैसे नतीजे दे रहा है या नहीं. साथ ही, यह भी आकलन किया जाता है कि मॉडल, पॉज़िटिव क्लास और नेगेटिव क्लास, दोनों के लिए एक जैसे नतीजे दे रहा है या नहीं. ऐसा नहीं होना चाहिए कि मॉडल, सिर्फ़ एक क्लास के लिए नतीजे दे रहा हो. दूसरे शब्दों में कहें, तो सभी ग्रुप के लिए ट्रू पॉज़िटिव रेट और फ़ॉल्स नेगेटिव रेट एक जैसा होना चाहिए.

समान अवसर, अवसर की समानता से जुड़ा है. यह सिर्फ़ एक क्लास (पॉज़िटिव या नेगेटिव) के लिए गड़बड़ी की दरों पर फ़ोकस करता है.

उदाहरण के लिए, मान लें कि ग्लबडबड्रिब यूनिवर्सिटी, गणित के एक मुश्किल प्रोग्राम में लिलीपुटियन और ब्रॉबडिंगनैगियन, दोनों को दाखिला देती है. लिलिपुटियन के सेकंडरी स्कूलों में, गणित की क्लास के लिए एक मज़बूत पाठ्यक्रम उपलब्ध कराया जाता है. साथ ही, ज़्यादातर छात्र-छात्राएं यूनिवर्सिटी प्रोग्राम के लिए ज़रूरी शर्तें पूरी करते हैं. ब्रॉबडिंगनैग के सेकंडरी स्कूलों में गणित की क्लास नहीं होती हैं. इसलिए, वहां के बहुत कम छात्र-छात्राएं गणित में पास हो पाते हैं. 'समान अवसर' की शर्त तब पूरी होती है, जब कोई भी व्यक्ति आवेदन करे, चाहे वह बौना हो या विशालकाय, अगर वह ज़रूरी शर्तें पूरी करता है, तो उसे प्रोग्राम में शामिल होने का समान अवसर मिलता है. वहीं, अगर वह ज़रूरी शर्तें पूरी नहीं करता है, तो उसे अस्वीकार किए जाने की संभावना भी समान होती है.

मान लें कि ग्लबडबड्रिब यूनिवर्सिटी में 100 लिलिपुटियन और 100 ब्रॉबडिंगनैगियन ने आवेदन किया है. साथ ही, एडमिशन के फ़ैसले इस तरह लिए गए हैं:

तीसरी टेबल. छोटे कारोबारों के लिए आवेदन करने वाले लोग या कंपनियां (इनमें से 90% ने ज़रूरी शर्तें पूरी की हैं)

	क्वालिफ़ाई हुई	अयोग्य
स्वीकार किया गया	45	2
अस्वीकार किया गया	45	8
कुल	90	10
ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं में से, दाखिला पाने वाले छात्र-छात्राओं का प्रतिशत: 45/90 = 50% ज़रूरी शर्तें पूरी न करने वाले छात्र-छात्राओं में से, दाखिला न पाने वाले छात्र-छात्राओं का प्रतिशत: 8/10 = 80% लिलिपुटियन स्कूल में दाखिला पाने वाले छात्र-छात्राओं का कुल प्रतिशत: (45+2)/100 = 47%

 

चौथी टेबल. बहुत ज़्यादा आवेदन करने वाले लोग (इनमें से 10% लोग ज़रूरी शर्तें पूरी करते हैं):

	क्वालिफ़ाई हुई	अयोग्य
स्वीकार किया गया	5	18
अस्वीकार किया गया	5	72
कुल	10	90
ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं में से चुने गए छात्र-छात्राओं का प्रतिशत: 5/10 = 50% ज़रूरी शर्तें पूरी न करने वाले छात्र-छात्राओं में से अस्वीकार किए गए छात्र-छात्राओं का प्रतिशत: 72/90 = 80% ब्रॉबडिंगनैगियन स्कूल में चुने गए छात्र-छात्राओं का कुल प्रतिशत: (5+18)/100 = 23%

'समान अवसर' सिद्धांत का पालन किया गया है, क्योंकि परीक्षा पास करने वाले लिलिपुटियन और ब्रॉबडिंग्नैगियन, दोनों छात्रों को 50% संभावना के साथ दाखिला मिल सकता है. वहीं, परीक्षा पास न करने वाले लिलिपुटियन और ब्रॉबडिंग्नैगियन, दोनों छात्रों को 80% संभावना के साथ अस्वीकार किया जा सकता है.

ध्यान दें: यहां समान अवसर की शर्त पूरी होती है, लेकिन डेमोग्राफ़िक पैरिटी की शर्त पूरी नहीं होती. लिलिपुटियन और ब्रॉबडिंगनैगियन छात्र-छात्राओं को ग्लबडबड्रिब यूनिवर्सिटी में अलग-अलग दरों पर दाखिला मिलता है. लिलिपुटियन छात्र-छात्राओं में से 47% को और ब्रॉबडिंगनैगियन छात्र-छात्राओं में से 23% को दाखिला मिलता है.

"Equality of Opportunity in Supervised Learning" में, इक्वल ऑड्स को इस तरह से औपचारिक तौर पर परिभाषित किया गया है: "अगर Ŷ और A, Y के आधार पर एक-दूसरे से अलग हैं, तो इसका मतलब है कि अनुमान लगाने वाले Ŷ ने सुरक्षित एट्रिब्यूट A और नतीजे Y के हिसाब से इक्वल ऑड्स की शर्त पूरी की है."

ध्यान दें: अवसर की समानता मेट्रिक की तुलना में, समान अवसर की संभावना के लिए ज़्यादा सख्त मानदंड होते हैं.

आकलन

#generativeAI

#Metric

इसका इस्तेमाल मुख्य रूप से, एलएलएम के आकलन के लिए किया जाता है. मोटे तौर पर, इवैल, इवैल्यूएशन का संक्षिप्त रूप है.

आकलन

#generativeAI

#Metric

किसी मॉडल की क्वालिटी को मेज़र करने या अलग-अलग मॉडल की तुलना करने की प्रोसेस.

सुपरवाइज़्ड मशीन लर्निंग मॉडल का आकलन करने के लिए, आम तौर पर इसकी तुलना मान्य डेटा सेट और टेस्ट डेटा सेट से की जाती है. एलएलएम का आकलन करने में आम तौर पर, क्वालिटी और सुरक्षा से जुड़े बड़े पैमाने पर आकलन शामिल होते हैं.

F

F₁

#Metric

यह एक "रोल-अप" बाइनरी क्लासिफ़िकेशन मेट्रिक है. यह प्रिसिज़न और रीकॉल, दोनों पर निर्भर करती है. यहां फ़ॉर्मूला दिया गया है:

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

उदाहरण देखने के लिए, आइकॉन पर क्लिक करें.

मान लें कि प्रिसिज़न और रीकॉल की वैल्यू ये हैं:

• प्रीसिज़न = 0.6
• recall = 0.4

F₁ को इस तरह कैलकुलेट किया जाता है:

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

जब प्रिसिज़न और रीकॉल काफ़ी हद तक एक जैसे होते हैं (जैसा कि ऊपर दिए गए उदाहरण में है), तो F₁ उनके औसत के करीब होता है. जब सटीक और रिकॉल वैल्यू में काफ़ी अंतर होता है, तो F₁ की वैल्यू कम होती है. उदाहरण के लिए:

• precision = 0.9
• recall = 0.1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

निष्पक्षता मेट्रिक

#responsible

#Metric

"निष्पक्षता" की गणितीय परिभाषा, जिसे मापा जा सकता है. आम तौर पर इस्तेमाल की जाने वाली निष्पक्षता मेट्रिक में ये शामिल हैं:

• बराबर किए गए ऑड्स
• अनुमानित समानता
• काउंटरफ़ैक्चुअल फ़ेयरनेस
• डेमोग्राफ़िक पैरिटी

निष्पक्षता से जुड़ी कई मेट्रिक एक-दूसरे से अलग होती हैं. निष्पक्षता से जुड़ी मेट्रिक का एक-दूसरे के साथ काम न करना लेख पढ़ें.

फ़ॉल्स नेगेटिव (FN)

#fundamentals

#Metric

इस उदाहरण में, मॉडल ने गलती से नेगेटिव क्लास का अनुमान लगाया है. उदाहरण के लिए, मॉडल यह अनुमान लगाता है कि कोई ईमेल मैसेज स्पैम नहीं है (नेगेटिव क्लास), लेकिन वह ईमेल मैसेज असल में स्पैम है.

खतरे को कम आंकने की दर

#Metric

यह असल पॉज़िटिव उदाहरणों का अनुपात है जिनके लिए मॉडल ने गलती से नेगेटिव क्लास का अनुमान लगाया. यहां दिया गया फ़ॉर्मूला, फ़ॉल्स नेगेटिव रेट का हिसाब लगाता है:

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में थ्रेशोल्ड और कन्फ़्यूज़न मैट्रिक्स देखें.

फ़ॉल्स पॉज़िटिव (FP)

#fundamentals

#Metric

ऐसा उदाहरण जिसमें मॉडल, पॉज़िटिव क्लास के बारे में गलत अनुमान लगाता है. उदाहरण के लिए, मॉडल का अनुमान है कि कोई ईमेल मैसेज स्पैम (पॉज़िटिव क्लास) है, लेकिन वह ईमेल मैसेज असल में स्पैम नहीं है.

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में थ्रेशोल्ड और कन्फ़्यूज़न मैट्रिक्स देखें.

फ़ॉल्स पॉज़िटिव रेट (एफ़पीआर)

#fundamentals

#Metric

यह असल नेगेटिव उदाहरणों का अनुपात है जिनके लिए मॉडल ने गलती से पॉज़िटिव क्लास का अनुमान लगाया. यहां दिए गए फ़ॉर्मूले से, फ़ॉल्स पॉज़िटिव रेट का हिसाब लगाया जाता है:

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

फ़ॉल्स पॉज़िटिव रेट, आरओसी कर्व में x-ऐक्सिस होता है.

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में क्लासिफ़िकेशन: आरओसी और एयूसी देखें.

सुविधाओं की अहमियत

#df

#Metric

यह वैरिएबल के महत्व का समानार्थी शब्द है.

फ़ाउंडेशन मॉडल

#generativeAI

#Metric

यह एक बहुत बड़ा पहले से ट्रेन किया गया मॉडल है. इसे अलग-अलग तरह के ट्रेनिंग सेट पर ट्रेन किया गया है. फ़ाउंडेशन मॉडल, यहां दिए गए दोनों काम कर सकता है:

• अलग-अलग तरह के अनुरोधों के लिए सही जवाब दे सकता है.
• इसे अन्य फ़ाइन-ट्यूनिंग या पसंद के मुताबिक बनाने के लिए, बेसिक मॉडल के तौर पर इस्तेमाल किया जा सकता है.

दूसरे शब्दों में, फ़ाउंडेशन मॉडल सामान्य तौर पर पहले से ही बहुत कुछ कर सकता है. हालांकि, इसे किसी खास काम के लिए और भी ज़्यादा उपयोगी बनाने के लिए, अपनी पसंद के मुताबिक बनाया जा सकता है.

सफलताओं का फ़्रैक्शन

#generativeAI

#Metric

यह एमएल मॉडल के जनरेट किए गए टेक्स्ट का आकलन करने वाली मेट्रिक है. सफलता की दर, जनरेट किए गए "सफल" टेक्स्ट आउटपुट की संख्या को जनरेट किए गए टेक्स्ट आउटपुट की कुल संख्या से भाग देने पर मिलती है. उदाहरण के लिए, अगर किसी बड़े लैंग्वेज मॉडल ने कोड के 10 ब्लॉक जनरेट किए हैं, जिनमें से पांच सही हैं, तो सही कोड का फ़्रैक्शन 50% होगा.

हालांकि, सफलता की दर का इस्तेमाल आम तौर पर सभी तरह के आंकड़ों में किया जाता है. एमएल में, इस मेट्रिक का इस्तेमाल मुख्य रूप से ऐसे कामों को मेज़र करने के लिए किया जाता है जिनकी पुष्टि की जा सकती है. जैसे, कोड जनरेट करना या गणित की समस्याएं हल करना.

G

गिनी अशुद्धता

#df

#Metric

एंट्रॉपी से मिलती-जुलती मेट्रिक. स्प्लिटर, क्लासिफ़िकेशन डिसिज़न ट्री के लिए शर्तें बनाने के लिए, गिनी इंप्योरिटी या एंट्रॉपी से मिली वैल्यू का इस्तेमाल करते हैं. सूचना लाभ, एंट्रॉपी से मिलता है. गिनी अशुद्धता से निकाली गई मेट्रिक के लिए, कोई भी ऐसा शब्द नहीं है जिसे सभी लोग स्वीकार करते हों. हालांकि, बिना नाम वाली यह मेट्रिक, सूचना के फ़ायदे जितनी ही अहम होती है.

Gini अशुद्धता को Gini इंडेक्स या सिर्फ़ Gini भी कहा जाता है.

गिनी अशुद्धता के बारे में गणितीय जानकारी पाने के लिए, आइकॉन पर क्लिक करें.

गिनी अशुद्धता, एक ही डिस्ट्रिब्यूशन से लिए गए नए डेटा को गलत तरीके से क्लासिफ़ाई करने की संभावना होती है. दो संभावित वैल्यू "0" और "1" वाले सेट की गिनी अशुद्धता (उदाहरण के लिए, बाइनरी क्लासिफ़िकेशन की समस्या में लेबल) की गणना इस फ़ॉर्मूले से की जाती है:

   I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

कहां:

• I, गिनी अशुद्धता है.
• p, "1" उदाहरणों का फ़्रैक्शन है.
• q, "0" उदाहरणों का फ़्रैक्शन है. ध्यान दें कि q = 1-p

उदाहरण के लिए, इस डेटासेट पर ध्यान दें:

• 100 लेबल (डेटासेट का 0.25) में "1" वैल्यू मौजूद है
• 300 लेबल (डेटासेट का 0.75) में "0" वैल्यू शामिल है

इसलिए, गिनी अशुद्धता यह है:

• p = 0.25
• q = 0.75
• I = 1 - (0.25² + 0.75²) = 0.375

इसलिए, उसी डेटासेट के किसी रैंडम लेबल के गलत तरीके से क्लासिफ़ाई होने की संभावना 37.5% होगी. वहीं, सही तरीके से क्लासिफ़ाई होने की संभावना 62.5% होगी.

पूरी तरह से बैलेंस किए गए लेबल (उदाहरण के लिए, 200 "0" और 200 "1") के लिए, गिनी अशुद्धता 0.5 होगी. बहुत ज़्यादा असंतुलित लेबल के लिए, गिनी अशुद्धता 0.0 के आस-पास होगी.

---

H

हिंज लॉस

#Metric

क्लासिफ़िकेशन के लिए लॉस फ़ंक्शन का एक फ़ैमिली, जिसे डिसिज़न बाउंड्री को हर ट्रेनिंग उदाहरण से ज़्यादा से ज़्यादा दूरी पर रखने के लिए डिज़ाइन किया गया है. इससे उदाहरणों और बाउंड्री के बीच मार्जिन ज़्यादा से ज़्यादा हो जाता है. KSVM, हिंज लॉस (या इससे जुड़ा कोई फ़ंक्शन, जैसे कि स्क्वेयर्ड हिंज लॉस) का इस्तेमाल करते हैं. बाइनरी क्लासिफ़िकेशन के लिए, हिंज लॉस फ़ंक्शन को इस तरह से परिभाषित किया गया है:

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

यहां y, सही लेबल है. यह -1 या +1 हो सकता है. साथ ही, y', क्लासिफ़िकेशन मॉडल का रॉ आउटपुट है:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

इसलिए, हिंज लॉस बनाम (y * y') का प्लॉट इस तरह दिखता है:

I

निष्पक्षता से जुड़ी मेट्रिक का साथ में काम न करना

#responsible

#Metric

इस सिद्धांत के मुताबिक, निष्पक्षता के कुछ सिद्धांत एक-दूसरे के साथ काम नहीं करते और उन्हें एक साथ लागू नहीं किया जा सकता. इस वजह से, निष्पक्षता का आकलन करने के लिए कोई एक मेट्रिक नहीं है, जिसे एमएल से जुड़ी सभी समस्याओं पर लागू किया जा सके.

हालांकि, यह निराशाजनक लग सकता है, लेकिन निष्पक्षता की मेट्रिक के काम न करने का मतलब यह नहीं है कि निष्पक्षता के लिए की गई कोशिशें बेकार हैं. इसके बजाय, इसमें यह सुझाव दिया गया है कि किसी एमएल समस्या के लिए, निष्पक्षता को कॉन्टेक्स्ट के हिसाब से तय किया जाना चाहिए. साथ ही, इसका मकसद इस्तेमाल के उदाहरणों से होने वाले नुकसान को रोकना होना चाहिए.

निष्पक्षता की मेट्रिक के मेल न खाने के बारे में ज़्यादा जानकारी के लिए, "On the (im)possibility of fairness" लेख पढ़ें.

व्यक्तिगत निष्पक्षता

#responsible

#Metric

यह निष्पक्षता से जुड़ी मेट्रिक है. इससे यह पता चलता है कि क्या एक जैसे लोगों को एक ही कैटगरी में रखा गया है. उदाहरण के लिए, ब्रॉबडिंगनैगियन अकैडमी, व्यक्तिगत निष्पक्षता के सिद्धांत का पालन करना चाहती है. इसके लिए, वह यह पक्का करती है कि एक जैसे ग्रेड और स्टैंडर्डाइज़्ड टेस्ट स्कोर वाले दो छात्र-छात्राओं को दाखिला मिलने की संभावना बराबर हो.

ध्यान दें कि किसी व्यक्ति के साथ निष्पक्षता से व्यवहार करना पूरी तरह से इस बात पर निर्भर करता है कि आपने "समानता" को कैसे परिभाषित किया है. इस मामले में, ग्रेड और टेस्ट स्कोर. अगर समानता की मेट्रिक में ज़रूरी जानकारी शामिल नहीं है, तो निष्पक्षता से जुड़ी नई समस्याएं पैदा हो सकती हैं. जैसे, छात्र-छात्रा के पाठ्यक्रम की गंभीरता.

व्यक्तिगत निष्पक्षता के बारे में ज़्यादा जानकारी के लिए, "Fairness Through Awareness" देखें.

सूचना लाभ

#df

#Metric

डिसिज़न फ़ॉरेस्ट में, किसी नोड की एंट्रॉपी और उसके चाइल्ड नोड की एंट्रॉपी के वज़न (उदाहरणों की संख्या के हिसाब से) के योग के बीच का अंतर. किसी नोड की एंट्रॉपी, उस नोड में मौजूद उदाहरणों की एंट्रॉपी होती है.

उदाहरण के लिए, यहां दी गई एंट्रॉपी वैल्यू देखें:

• पैरंट नोड की एन्ट्रॉपी = 0.6
• काम के 16 उदाहरणों वाले एक चाइल्ड नोड की एंट्रॉपी = 0.2
• 24 काम के उदाहरणों वाले दूसरे चाइल्ड नोड की एंट्रॉपी = 0.1

इसलिए, 40% उदाहरण एक चाइल्ड नोड में हैं और 60% उदाहरण दूसरे चाइल्ड नोड में हैं. इसलिए:

• चाइल्ड नोड की वेटेड एन्ट्रॉपी का योग = (0.4 * 0.2) + (0.6 * 0.1) = 0.14

इसलिए, जानकारी में हुई बढ़ोतरी यह है:

• सूचना लाभ = पैरंट नोड की एन्ट्रॉपी - चाइल्ड नोड की वज़न के हिसाब से एन्ट्रॉपी का योग
• सूचना लाभ = 0.6 - 0.14 = 0.46

ज़्यादातर स्प्लिटर, शर्तें बनाने की कोशिश करते हैं, ताकि ज़्यादा से ज़्यादा जानकारी मिल सके.

इंटर-रेटर एग्रीमेंट

#Metric

यह मेज़रमेंट बताता है कि किसी टास्क को पूरा करते समय, ह्यूमन रेटर कितनी बार एक-दूसरे से सहमत होते हैं. अगर रेटिंग देने वाले लोग सहमत नहीं हैं, तो टास्क के निर्देशों में सुधार करना पड़ सकता है. इसे कभी-कभी इंटर-एनोटेटर एग्रीमेंट या इंटर-रेटर रिलायबिलिटी भी कहा जाता है. यह भी देखें कोहेन का कप्पा, जो दो लोगों के बीच सहमति का आकलन करने के सबसे लोकप्रिय तरीकों में से एक है.

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में कैटेगरी के हिसाब से डेटा: सामान्य समस्याएं देखें.

L

L₁ नुकसान

#fundamentals

#Metric

यह एक लॉस फ़ंक्शन है. यह असल लेबल वैल्यू और मॉडल की अनुमानित वैल्यू के बीच के अंतर की ऐब्सलूट वैल्यू कैलकुलेट करता है. उदाहरण के लिए, यहां पांच उदाहरणों के बैच के लिए, L₁ लॉस की गणना दी गई है:

उदाहरण की असल वैल्यू	मॉडल की अनुमानित वैल्यू	डेल्टा की ऐब्सलूट वैल्यू
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 नुकसान

L₁ लॉस, L₂ लॉस की तुलना में आउटलायर के लिए कम संवेदनशील होता है.

कुल गड़बड़ी का मध्यमान, हर उदाहरण के लिए औसत L₁ लॉस होता है.

गणित के फ़ॉर्मूले देखने के लिए, आइकॉन पर क्लिक करें.

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

where:

• $n$ उदाहरणों की संख्या है.
• $y$ लेबल की असल वैल्यू है.
• $\hat{y}$ वह वैल्यू है जिसका अनुमान मॉडल, $y$ के लिए लगाता है.

---

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में लीनियर रिग्रेशन: लॉस देखें.

L₂ नुकसान

#fundamentals

#Metric

यह एक लॉस फ़ंक्शन है. यह असल लेबल वैल्यू और मॉडल की अनुमानित वैल्यू के बीच के अंतर का स्क्वेयर कैलकुलेट करता है. उदाहरण के लिए, यहां पांच उदाहरणों के बैच के लिए, L₂ लॉस की गणना दी गई है:

उदाहरण की असल वैल्यू	मॉडल की अनुमानित वैल्यू	डेल्टा का स्क्वेयर
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = L2 लॉस

स्क्वेयर करने की वजह से, L₂ लॉस, आउटलायर के असर को बढ़ा देता है. इसका मतलब है कि खराब अनुमानों पर L₂ लॉस, L₁ लॉस की तुलना में ज़्यादा असर डालता है. उदाहरण के लिए, पिछले बैच के लिए L₁ लॉस, 16 के बजाय 8 होगा. ध्यान दें कि एक आउटलायर, 16 में से 9 के लिए ज़िम्मेदार है.

रिग्रेशन मॉडल, आम तौर पर लॉस फ़ंक्शन के तौर पर L₂ लॉस का इस्तेमाल करते हैं.

मीन स्क्वेयर्ड एरर, हर उदाहरण के लिए औसत L₂ लॉस होता है. स्क्वेयर्ड लॉस को L₂ लॉस भी कहा जाता है.

गणित के फ़ॉर्मूले देखने के लिए, आइकॉन पर क्लिक करें.

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

where:

• $n$ उदाहरणों की संख्या है.
• $y$ लेबल की असल वैल्यू है.
• $\hat{y}$ वह वैल्यू है जिसका अनुमान मॉडल, $y$ के लिए लगाता है.

---

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में लॉजिस्टिक रिग्रेशन: लॉस और रेगुलराइज़ेशन देखें.

एलएलएम के आकलन (इवैल)

#generativeAI

#Metric

यह मेट्रिक और बेंचमार्क का एक सेट है. इसका इस्तेमाल, लार्ज लैंग्वेज मॉडल (एलएलएम) की परफ़ॉर्मेंस का आकलन करने के लिए किया जाता है. एलएलएम के आकलन के लिए, ये काम किए जाते हैं:

• शोधकर्ताओं को उन क्षेत्रों की पहचान करने में मदद करना जहां एलएलएम को बेहतर बनाने की ज़रूरत है.
• इनसे अलग-अलग एलएलएम की तुलना करने और किसी टास्क के लिए सबसे अच्छे एलएलएम की पहचान करने में मदद मिलती है.
• यह पक्का करने में मदद करना कि एलएलएम का इस्तेमाल सुरक्षित और ज़िम्मेदारी से किया जा रहा है.

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में लार्ज लैंग्वेज मॉडल (एलएलएम) देखें.

हार

#fundamentals

#Metric

निगरानी वाले मॉडल की ट्रेनिंग के दौरान, यह मेज़रमेंट किया जाता है कि मॉडल का अनुमान, उसके लेबल से कितना अलग है.

लॉस फ़ंक्शन, लॉस का हिसाब लगाता है.

ज़्यादा जानकारी के लिए, Machine Learning Crash Course में लीनियर रिग्रेशन: लॉस देखें.

लॉस फ़ंक्शन

#fundamentals

#Metric

ट्रेनिंग या टेस्टिंग के दौरान, यह एक गणितीय फ़ंक्शन होता है. यह उदाहरणों के बैच के नुकसान का हिसाब लगाता है. लॉस फ़ंक्शन, अच्छी परफ़ॉर्मेंस वाले मॉडल के लिए कम लॉस दिखाता है. वहीं, खराब परफ़ॉर्मेंस वाले मॉडल के लिए ज़्यादा लॉस दिखाता है.

ट्रेनिंग का मकसद आम तौर पर, लॉस फ़ंक्शन से मिलने वाले नुकसान को कम करना होता है.

कई तरह के लॉस फ़ंक्शन मौजूद होते हैं. बनाए जा रहे मॉडल के हिसाब से, सही लॉस फ़ंक्शन चुनें. उदाहरण के लिए:

• L₂ लॉस या मीन स्क्वेयर्ड एरर, लीनियर रिग्रेशन के लिए लॉस फ़ंक्शन होता है.
• लॉग लॉस, लॉजिस्टिक्स रिग्रेशन के लिए लॉस फ़ंक्शन है.

M

मीन ऐब्सॉल्यूट एरर (MAE)

#Metric

L₁ लॉस का इस्तेमाल करने पर, हर उदाहरण के लिए औसत लॉस. कुल गड़बड़ी का मध्यमान इस तरह कैलकुलेट करें:

1. किसी बैच के लिए L₁ लॉस कैलकुलेट करें.
2. बैच में मौजूद उदाहरणों की संख्या से L₁ लॉस को भाग दें.

गणित के फ़ॉर्मूले देखने के लिए, आइकॉन पर क्लिक करें.

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

कहां:

• $n$ उदाहरणों की संख्या है.
• $y$ लेबल की असल वैल्यू है.
• $\hat{y}$ वह वैल्यू है जिसका अनुमान मॉडल, $y$ के लिए लगाता है.

---

उदाहरण के लिए, पांच उदाहरणों के इस बैच में L₁ नुकसान के कैलकुलेशन पर विचार करें:

उदाहरण की असल वैल्यू	मॉडल की अनुमानित वैल्यू	नुकसान (असल और अनुमानित वैल्यू के बीच का अंतर)
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 नुकसान

इसलिए, L₁ लॉस 8 है और उदाहरणों की संख्या 5 है. इसलिए, कुल गड़बड़ी का मध्यमान यह है:

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

मीन स्क्वेयर्ड एरर और रूट मीन स्क्वेयर्ड एरर के साथ, कॉन्ट्रास्ट मीन ऐब्सलूट एरर की तुलना करें.

k पर औसत सटीक दर (mAP@k)

#generativeAI

#Metric

यह पुष्टि करने वाले डेटासेट में, सभी k पर औसत सटीक स्कोर का सांख्यिकीय माध्य होता है. के पर औसत सटीक दर का इस्तेमाल, सुझाव देने वाले सिस्टम से जनरेट किए गए सुझावों की क्वालिटी का आकलन करने के लिए किया जाता है.

हालांकि, "औसत" शब्द का इस्तेमाल दो बार किया गया है, लेकिन मेट्रिक का नाम सही है. आखिरकार, यह मेट्रिक कई k पर औसत प्रेसिज़न वैल्यू का औसत निकालती है.

उदाहरण देखने के लिए, आइकॉन पर क्लिक करें.

मान लें कि आपने एक ऐसा सुझाव सिस्टम बनाया है जो हर उपयोगकर्ता के लिए, उसके हिसाब से सुझाए गए उपन्यासों की सूची जनरेट करता है. चुनिंदा उपयोगकर्ताओं से मिले सुझाव, शिकायत या राय के आधार पर, आपको के स्कोर पर औसत सटीक स्कोर की इन पांच वैल्यू का हिसाब लगाना है. हर उपयोगकर्ता के लिए एक स्कोर:

• 0.73
• 0.77
• 0.67
• 0.82
• 0.76

इसलिए, K पर औसत प्रिसिज़न का मतलब यह है:

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

मीन स्क्वेयर्ड एरर (एमएसई)

#Metric

L₂ लॉस का इस्तेमाल करने पर, हर उदाहरण के लिए औसत लॉस. मीन स्क्वेयर्ड एरर की गणना इस तरह करें:

1. किसी बैच के लिए L₂ लॉस की गणना करता है.
2. बैच में मौजूद उदाहरणों की संख्या से L₂ लॉस को भाग दें.

गणित के फ़ॉर्मूले देखने के लिए, आइकॉन पर क्लिक करें.

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ where:

• $n$ उदाहरणों की संख्या है.
• $y$ लेबल की असल वैल्यू है.
• $\hat{y}$, $y$ के लिए मॉडल का अनुमान है.

---

उदाहरण के लिए, पांच उदाहरणों के इस बैच में हुए नुकसान पर विचार करें:

वास्तविक मान	मॉडल का अनुमान	हार	स्क्वेयर्ड लॉस
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			16 = L2 लॉस

इसलिए, वर्ग में गड़बड़ी का माध्य यह है:

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

वर्ग में गड़बड़ी का माध्य, ट्रेनिंग के लिए इस्तेमाल किया जाने वाला एक लोकप्रिय ऑप्टिमाइज़र है. इसका इस्तेमाल खास तौर पर लीनियर रिग्रेशन के लिए किया जाता है.

मीन ऐब्सलूट एरर और रूट मीन स्क्वेयर्ड एरर के साथ कंट्रास्ट मीन स्क्वेयर्ड एरर की तुलना करें.

TensorFlow Playground, नुकसान की वैल्यू का हिसाब लगाने के लिए, माध्य वर्ग त्रुटि का इस्तेमाल करता है.

आउटलायर के बारे में ज़्यादा जानकारी देखने के लिए, आइकॉन पर क्लिक करें.

आउटलायर का असर, मीन स्क्वेयर्ड एरर पर बहुत ज़्यादा पड़ता है. उदाहरण के लिए, 1 का स्क्वेयर्ड लॉस 1 होता है, लेकिन 3 का स्क्वेयर्ड लॉस 9 होता है. ऊपर दी गई टेबल में, तीन खातों के नुकसान वाले उदाहरण में, माध्य वर्ग त्रुटि (एमएसई) का ~56% हिस्सा शामिल है. वहीं, एक खाते के नुकसान वाले हर उदाहरण में, माध्य वर्ग त्रुटि (एमएसई) का सिर्फ़ 6% हिस्सा शामिल है.

आउटलायर, मीन स्क्वेयर्ड एरर पर जितना असर डालते हैं उतना असर मीन ऐब्सॉल्यूट एरर पर नहीं डालते. उदाहरण के लिए, सिर्फ़ ~38% औसत निरपेक्ष गड़बड़ी के लिए, तीन खातों का नुकसान.

क्लिपिंग एक ऐसा तरीका है जिससे मॉडल की अनुमान लगाने की क्षमता को नुकसान पहुंचाने वाले एक्सट्रीम आउटलायर को रोका जा सकता है.

---

मीट्रिक

#TensorFlow

#Metric

वह आंकड़े जो आपके लिए अहम है.

मकसद एक ऐसी मेट्रिक होती है जिसे मशीन लर्निंग सिस्टम ऑप्टिमाइज़ करने की कोशिश करता है.

Metrics API (tf.metrics)

#Metric

मॉडल का आकलन करने के लिए TensorFlow API. उदाहरण के लिए, tf.metrics.accuracy से यह तय होता है कि मॉडल के अनुमान, लेबल से कितनी बार मेल खाते हैं.

minimax loss

#Metric

यह जनरेटिव ऐडवर्सैरियल नेटवर्क के लिए एक लॉस फ़ंक्शन है. यह जनरेट किए गए डेटा और असली डेटा के डिस्ट्रिब्यूशन के बीच क्रॉस-एंट्रॉपी पर आधारित होता है.

मिनिमैक्स लॉस का इस्तेमाल, पहले पेपर में जनरेटिव ऐडवर्सैरियल नेटवर्क के बारे में बताने के लिए किया गया था.

ज़्यादा जानकारी के लिए, जनरेटिव ऐडवर्सैरियल नेटवर्क कोर्स में लॉस फ़ंक्शन देखें.

मॉडल की क्षमता

#Metric

समस्याओं की जटिलता, जिसे मॉडल सीख सकता है. कोई मॉडल जितनी मुश्किल समस्याओं को हल करना सीख सकता है, उसकी क्षमता उतनी ही ज़्यादा होती है. मॉडल के पैरामीटर की संख्या बढ़ने पर, आम तौर पर मॉडल की क्षमता बढ़ जाती है. क्लासिफ़िकेशन मॉडल की क्षमता की औपचारिक परिभाषा के लिए, वीसी डाइमेंशन देखें.

नहीं

नेगेटिव क्लास

#fundamentals

#Metric

बाइनरी क्लासिफ़िकेशन में, एक क्लास को पॉज़िटिव और दूसरी क्लास को नेगेटिव कहा जाता है. पॉज़िटिव क्लास, वह चीज़ या इवेंट होता है जिसके लिए मॉडल की टेस्टिंग की जा रही है. वहीं, नेगेटिव क्लास, दूसरी संभावना होती है. उदाहरण के लिए:

• मेडिकल टेस्ट में नेगेटिव क्लास "ट्यूमर नहीं है" हो सकती है.
• ईमेल के क्लासिफ़िकेशन मॉडल में नेगेटिव क्लास "स्पैम नहीं है" हो सकती है.

पॉज़िटिव क्लास से तुलना करें.

O

कैंपेन का मकसद

#Metric

मेट्रिक, जिसे आपका एल्गोरिदम ऑप्टिमाइज़ करने की कोशिश कर रहा है.

ऑब्जेक्टिव फ़ंक्शन

#Metric

गणित का फ़ॉर्मूला या मेट्रिक जिसे मॉडल ऑप्टिमाइज़ करने की कोशिश करता है. उदाहरण के लिए, लीनियर रिग्रेशन के लिए ऑब्जेक्टिव फ़ंक्शन, आम तौर पर मीन स्क्वेयर्ड लॉस होता है. इसलिए, लीनियर रिग्रेशन मॉडल को ट्रेन करते समय, ट्रेनिंग का मकसद औसत स्क्वेयर्ड लॉस को कम करना होता है.

कुछ मामलों में, मकसद फ़ंक्शन को बढ़ाने का होता है. उदाहरण के लिए, अगर ऑब्जेक्टिव फ़ंक्शन सटीकता है, तो लक्ष्य सटीकता को ज़्यादा से ज़्यादा करना है.

नुकसान के बारे में भी जानें.

P

पास ऐट के (pass@k)

#Metric

यह एक मेट्रिक है. इससे यह पता चलता है कि लार्ज लैंग्वेज मॉडल ने किस क्वालिटी का कोड (उदाहरण के लिए, Python) जनरेट किया है. खास तौर पर, पास ऐट k से पता चलता है कि जनरेट किए गए k कोड ब्लॉक में से कम से कम एक कोड ब्लॉक, यूनिट की सभी जांचों को पास कर लेगा.

लार्ज लैंग्वेज मॉडल को अक्सर, प्रोग्रामिंग से जुड़ी मुश्किल समस्याओं के लिए अच्छा कोड जनरेट करने में परेशानी होती है. सॉफ़्टवेयर इंजीनियर इस समस्या को हल करने के लिए, लार्ज लैंग्वेज मॉडल को एक ही समस्या के कई (k) समाधान जनरेट करने के लिए प्रॉम्प्ट करते हैं. इसके बाद, सॉफ़्टवेयर इंजीनियर हर समाधान की यूनिट टेस्ट करते हैं. k पर पास होने की दर की कैलकुलेशन, यूनिट टेस्ट के नतीजे पर निर्भर करती है:

• अगर उन समाधानों में से एक या उससे ज़्यादा समाधान यूनिट टेस्ट पास कर लेते हैं, तो एलएलएम, कोड जनरेट करने से जुड़ी उस चुनौती को पास कर लेता है.
• अगर कोई भी समाधान यूनिट टेस्ट पास नहीं करता है, तो एलएलएम, कोड जनरेट करने की इस चुनौती में फ़ेल हो जाता है.

k पर पास होने का फ़ॉर्मूला यहां दिया गया है:

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

आम तौर पर, k की वैल्यू जितनी ज़्यादा होगी, पास ऐट k स्कोर उतना ही ज़्यादा होगा. हालांकि, k की वैल्यू ज़्यादा होने पर, बड़े लैंग्वेज मॉडल और यूनिट टेस्टिंग के लिए ज़्यादा संसाधनों की ज़रूरत होती है.

उदाहरण के लिए, आइकॉन पर क्लिक करें.

मान लें कि कोई सॉफ़्टवेयर इंजीनियर, लार्ज लैंग्वेज मॉडल से कोडिंग की n=50 मुश्किल समस्याओं के लिए k=10 समाधान जनरेट करने के लिए कहता है. ये रहे नतीजे:

• 30 पास
• 20 गड़बड़ियां

इसलिए, 10 के स्कोर पर पास होने की संभावना यह है:

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

प्रदर्शन

#Metric

इस शब्द के कई मतलब हैं:

• सॉफ़्टवेयर इंजीनियरिंग में इसका सामान्य मतलब. जैसे: यह सॉफ़्टवेयर कितनी तेज़ी से (या बेहतर तरीके से) काम करता है?
• मशीन लर्निंग में इसका मतलब. यहां परफ़ॉर्मेंस से इस सवाल का जवाब मिलता है: यह मॉडल कितना सही है? इसका मतलब है कि मॉडल के अनुमान कितने सटीक हैं?

पर्म्यूटेशन वैरिएबल के महत्व

#df

#Metric

यह वैरिएबल के महत्व का एक टाइप है. यह किसी मॉडल की अनुमान लगाने से जुड़ी गड़बड़ी में हुई बढ़ोतरी का आकलन करता है. ऐसा, फ़ीचर की वैल्यू को क्रम बदलने के बाद किया जाता है. परम्यूटेशन वैरिएबल इंपोर्टेंस, मॉडल से जुड़ी मेट्रिक नहीं है.

परप्लेक्सिटी

#Metric

यह इस बात का आकलन करता है कि मॉडल अपने टास्क को कितनी अच्छी तरह से पूरा कर रहा है. उदाहरण के लिए, मान लें कि आपको किसी शब्द के पहले कुछ अक्षरों को पढ़ना है. यह शब्द, कोई उपयोगकर्ता फ़ोन के कीबोर्ड पर टाइप कर रहा है. इसके बाद, आपको उस शब्द को पूरा करने के लिए संभावित शब्दों की सूची दिखानी है. इस टास्क के लिए परप्लेक्सिटी, P, का मतलब है कि आपको अनुमानित तौर पर इतने शब्द बताने होंगे, ताकि आपकी सूची में वह शब्द शामिल हो सके जिसे उपयोगकर्ता टाइप करने की कोशिश कर रहा है.

परप्लेक्सिटी, क्रॉस-एंट्रॉपी से इस तरह जुड़ी होती है:

$$P= 2^{-\text{cross entropy}}$$

पॉज़िटिव क्लास

#fundamentals

#Metric

वह क्लास जिसके लिए आपको टेस्ट करना है.

उदाहरण के लिए, कैंसर के मॉडल में पॉज़िटिव क्लास "ट्यूमर" हो सकती है. ईमेल क्लासिफ़िकेशन मॉडल में पॉज़िटिव क्लास "स्पैम" हो सकती है.

नेगेटिव क्लास से तुलना करें.

अन्य नोट के लिए, आइकॉन पर क्लिक करें.

पॉज़िटिव क्लास शब्द से भ्रम हो सकता है, क्योंकि कई टेस्ट के "पॉज़िटिव" नतीजे अक्सर अवांछित होते हैं. उदाहरण के लिए, कई मेडिकल टेस्ट में पॉज़िटिव क्लास, ट्यूमर या बीमारियों से जुड़ी होती है. आम तौर पर, आपको डॉक्टर से यह सुनने की उम्मीद होती है कि "बधाई हो! आपकी जांच के नतीजे नेगेटिव हैं." हालांकि, पॉज़िटिव क्लास वह इवेंट होता है जिसे टेस्ट में ढूंढने की कोशिश की जाती है.

हालांकि, एक साथ पॉज़िटिव और नेगेटिव, दोनों क्लास के लिए टेस्टिंग की जा रही है.

---

PR AUC (PR कर्व के नीचे का हिस्सा)

#Metric

इंटरपोलेट किए गए सटीकता-वापसी वक्र के नीचे का क्षेत्र. इसे वर्गीकरण थ्रेशोल्ड की अलग-अलग वैल्यू के लिए, (वापसी, सटीकता) पॉइंट को प्लॉट करके हासिल किया जाता है.

प्रीसिज़न

#fundamentals

#Metric

यह वर्गीकरण मॉडल के लिए एक मेट्रिक है. इससे इस सवाल का जवाब मिलता है:

जब मॉडल ने पॉज़िटिव क्लास का अनुमान लगाया, तो कितने प्रतिशत अनुमान सही थे?

यहां फ़ॉर्मूला दिया गया है:

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

कहां:

• ट्रू पॉज़िटिव का मतलब है कि मॉडल ने पॉज़िटिव क्लास का सही अनुमान लगाया है.
• फ़ॉल्स पॉज़िटिव का मतलब है कि मॉडल ने पॉज़िटिव क्लास का गलत अनुमान लगाया है.

उदाहरण के लिए, मान लें कि किसी मॉडल ने 200 पॉज़िटिव अनुमान लगाए. इन 200 पॉज़िटिव अनुमानों में से:

• इनमें से 150 सही पॉज़िटिव थे.
• इनमें से 50 फ़ॉल्स पॉज़िटिव थे.

इस मामले में:

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

इसकी तुलना सटीकता और रीकॉल से करें.

ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में क्लासिफ़िकेशन: सटीक, रीकॉल, प्रेसिज़न, और इनसे जुड़ी मेट्रिक देखें.

के पर सटीक (precision@k)

#Metric

यह मेट्रिक, रैंक की गई (क्रम से लगाई गई) आइटम की सूची का आकलन करने के लिए होती है. k पर सटीक होने का मतलब है कि सूची के पहले k आइटम में से कितने आइटम "काम के" हैं. यानी:

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

k की वैल्यू, दिखाई गई सूची की लंबाई से कम या इसके बराबर होनी चाहिए. ध्यान दें कि जवाब में मिली सूची की लंबाई, कैलकुलेशन का हिस्सा नहीं होती.

कोई आइटम कितना काम का है, यह अक्सर अलग-अलग लोगों के हिसाब से अलग-अलग होता है. यहां तक कि क्वालिटी का आकलन करने वाले विशेषज्ञ भी इस बात पर सहमत नहीं होते कि कौनसे आइटम काम के हैं.

इसके साथ तुलना करें:

• k पर औसत सटीक दर
• k पर औसत सटीक दर

उदाहरण देखने के लिए, आइकॉन पर क्लिक करें.

मान लें कि लार्ज लैंग्वेज मॉडल को यह क्वेरी दी गई है:

List the 6 funniest movies of all time in order.

इसके बाद, लार्ज लैंग्वेज मॉडल, नीचे दी गई टेबल के पहले दो कॉलम में दिखाई गई सूची दिखाता है:

स्थिति	मूवी	क्या यह काम का है?
1	द जनरल	हां
2	Mean Girls	हां
3	Platoon	नहीं
4	दुल्हन की सहेलियां	हां
5	सिटीज़न केन	नहीं
6	This is Spinal Tap	हां

शुरुआती तीन फ़िल्मों में से दो फ़िल्में काम की हैं. इसलिए, सटीक नतीजे दिखाने की क्षमता 3 है:

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

शुरुआती पांच फ़िल्मों में से तीन बहुत मज़ेदार हैं. इसलिए, 5 पर सटीक स्कोर यह है:

$$\text{precision at 5} = \frac{\text{3}} {\text{5}} = 0.6$$

---

प्रीसिज़न-रिकॉल कर्व

#Metric

यह अलग-अलग क्लासिफ़िकेशन थ्रेशोल्ड पर, सटीकता बनाम रिकॉल का कर्व होता है.

अनुमान में पक्षपात

#Metric

यह वैल्यू बताती है कि डेटासेट में, अनुमानों का औसत, लेबल के औसत से कितना अलग है.

इसे मशीन लर्निंग मॉडल में मौजूद बायस टर्म या नैतिकता और निष्पक्षता में मौजूद पूर्वाग्रह से भ्रमित न हों.

अनुमानित समानता

#responsible

#Metric

यह निष्पक्षता मेट्रिक है. इससे यह पता चलता है कि दिए गए क्लासिफ़िकेशन मॉडल के लिए, विचाराधीन सबग्रुप के लिए सटीकता की दरें बराबर हैं या नहीं.

उदाहरण के लिए, अगर कॉलेज में दाखिले का अनुमान लगाने वाले मॉडल का सटीक अनुमान लगाने का रेट, लिलिपुटियन और ब्रॉबडिंगनैगियन के लिए एक जैसा है, तो यह राष्ट्रीयता के लिए प्रेडिक्टिव पैरिटी की शर्त पूरी करेगा.

कभी-कभी, अनुमानित कीमत की समानता को अनुमानित कीमत की समानता भी कहा जाता है.

अनुमानित समानता के बारे में ज़्यादा जानकारी के लिए, "निष्पक्षता की परिभाषाएं समझाई गईं" (सेक्शन 3.2.1) देखें.

किराये की समानता के लिए अनुमानित दर

#responsible

#Metric

अनुमानित समानता का दूसरा नाम.

प्रोबैबिलिटी डेंसिटी फ़ंक्शन

#Metric

यह फ़ंक्शन, ठीक किसी वैल्यू वाले डेटा सैंपल की फ़्रीक्वेंसी का पता लगाता है. जब किसी डेटासेट की वैल्यू लगातार फ़्लोटिंग-पॉइंट नंबर होती हैं, तो एग्ज़ैक्ट मैच बहुत कम होते हैं. हालांकि, वैल्यू x से वैल्यू y तक प्रोबैबिलिटी डेंसिटी फ़ंक्शन को इंटिग्रेट करने पर, x और y के बीच डेटा सैंपल की अनुमानित फ़्रीक्वेंसी मिलती है.

उदाहरण के लिए, मान लें कि किसी नॉर्मल डिस्ट्रिब्यूशन का औसत 200 और स्टैंडर्ड डेविएशन 30 है. 211.4 से 218.7 की सीमा में आने वाले डेटा सैंपल की अनुमानित फ़्रीक्वेंसी का पता लगाने के लिए, सामान्य डिस्ट्रिब्यूशन के लिए प्रायिकता घनत्व फ़ंक्शन को 211.4 से 218.7 तक इंटिग्रेट किया जा सकता है.

R

रीकॉल

#fundamentals

#Metric

यह वर्गीकरण मॉडल के लिए एक मेट्रिक है. इससे इस सवाल का जवाब मिलता है:

जब ग्राउंड ट्रुथ, पॉज़िटिव क्लास थी, तब मॉडल ने कितने प्रतिशत अनुमानों को पॉज़िटिव क्लास के तौर पर सही तरीके से पहचाना?

यहां फ़ॉर्मूला दिया गया है:

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

कहां:

• ट्रू पॉज़िटिव का मतलब है कि मॉडल ने पॉज़िटिव क्लास का सही अनुमान लगाया है.
• फ़ॉल्स नेगेटिव का मतलब है कि मॉडल ने गलती से नेगेटिव क्लास का अनुमान लगाया है.

उदाहरण के लिए, मान लें कि आपके मॉडल ने उन उदाहरणों के लिए 200 अनुमान लगाए जिनके लिए ग्राउंड ट्रुथ पॉज़िटिव क्लास था. इन 200 अनुमानों में से:

• इनमें से 180 ट्रू पॉज़िटिव थे.
• इनमें से 20 फ़ॉल्स नेगेटिव थे.

इस मामले में:

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

क्लास के हिसाब से डेटासेट में अंतर होने के बारे में नोट देखने के लिए, आइकॉन पर क्लिक करें.

रिकॉल, खास तौर पर उन क्लासिफ़िकेशन मॉडल की अनुमान लगाने की क्षमता का पता लगाने के लिए उपयोगी होता है जिनमें पॉज़िटिव क्लास कम होती है. उदाहरण के लिए, क्लास-इंबैलेंस वाले डेटासेट पर विचार करें. इसमें किसी बीमारी के लिए पॉज़िटिव क्लास, 10 लाख में से सिर्फ़ 10 मरीज़ों में दिखती है. मान लें कि आपका मॉडल पांच करोड़ अनुमान लगाता है. इससे ये नतीजे मिलते हैं:

• 30 ट्रू पॉज़िटिव
• 20 फ़ॉल्स नेगेटिव
• 49,99,000 ट्रू नेगेटिव
• 950 फ़ॉल्स पॉज़िटिव

इसलिए, इस मॉडल का रिकॉल यह है:

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

इसके उलट, इस मॉडल की सटीकता यह है:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

सटीकता की यह ज़्यादा वैल्यू देखने में अच्छी लगती है, लेकिन इसका कोई मतलब नहीं है. क्लास-इंबैलेंस वाले डेटासेट के लिए, सटीकता की तुलना में रीकॉल ज़्यादा काम की मेट्रिक है.

---

ज़्यादा जानकारी के लिए, क्लासिफ़िकेशन: सटीकता, रिकॉल, सटीक और इससे जुड़ी मेट्रिक देखें.

recall at k (recall@k)

#Metric

यह मेट्रिक, उन सिस्टम का आकलन करने के लिए इस्तेमाल की जाती है जो आइटम की रैंक की गई (क्रम से लगाई गई) सूची दिखाते हैं. k पर रीकॉल से पता चलता है कि जवाब में मिले कुल काम के आइटम में से, सूची में मौजूद पहले k आइटम में कितने काम के आइटम हैं.

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

k पर सटीक जानकारी के साथ कंट्रास्ट करें.

उदाहरण देखने के लिए, आइकॉन पर क्लिक करें.

मान लें कि लार्ज लैंग्वेज मॉडल को यह क्वेरी दी गई है:

List the 10 funniest movies of all time in order.

इसके बाद, लार्ज लैंग्वेज मॉडल, पहले दो कॉलम में दिखाई गई सूची दिखाता है:

स्थिति	मूवी	क्या यह काम का है?
1	द जनरल	हां
2	Mean Girls	हां
3	Platoon	नहीं
4	दुल्हन की सहेलियां	हां
5	This is Spinal Tap	हां
6	हवाई जहाज़!	हां
7	ग्राउंडहॉग डे	हां
8	मॉन्टी पाइथन ऐंड द होली ग्रेल	हां
9	ऑपनहाइमर	नहीं
10	क्लूलेस	हां

ऊपर दी गई सूची में मौजूद आठ फ़िल्में बहुत मज़ेदार हैं. इसलिए, इन्हें "सूची में मौजूद काम के आइटम" माना जाता है. इसलिए, k पर रीकॉल के सभी कैलकुलेशन में, डिनॉमिनेटर 8 होगा. अंश के बारे में क्या जानकारी है? ठीक है, पहले चार आइटम में से तीन आइटम काम के हैं. इसलिए, चार आइटम में से तीन आइटम याद रखे गए.

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

शुरुआती आठ फ़िल्मों में से सात बहुत मज़ेदार हैं. इसलिए, आठ फ़िल्मों के बाद याद रहने की संभावना यह है:

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

आरओसी (रिसीवर ऑपरेटिंग कैरेक्टरिस्टिक) कर्व

#fundamentals

#Metric

यह बाइनरी क्लासिफ़िकेशन में, अलग-अलग क्लासिफ़िकेशन थ्रेशोल्ड के लिए, ट्रू पॉज़िटिव रेट बनाम फ़ॉल्स पॉज़िटिव रेट का ग्राफ़ है.

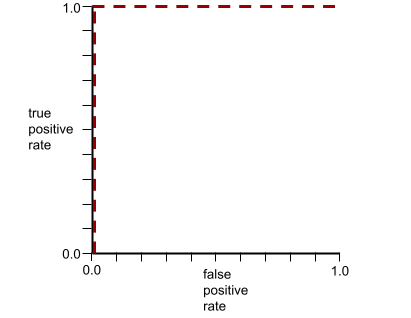
आरओसी कर्व का आकार, बाइनरी क्लासिफ़िकेशन मॉडल की पॉज़िटिव क्लास को नेगेटिव क्लास से अलग करने की क्षमता के बारे में बताता है. उदाहरण के लिए, मान लें कि बाइनरी क्लासिफ़िकेशन मॉडल, सभी नेगेटिव क्लास को सभी पॉज़िटिव क्लास से पूरी तरह अलग करता है:

ऊपर दिए गए मॉडल के लिए आरओसी कर्व ऐसा दिखता है:

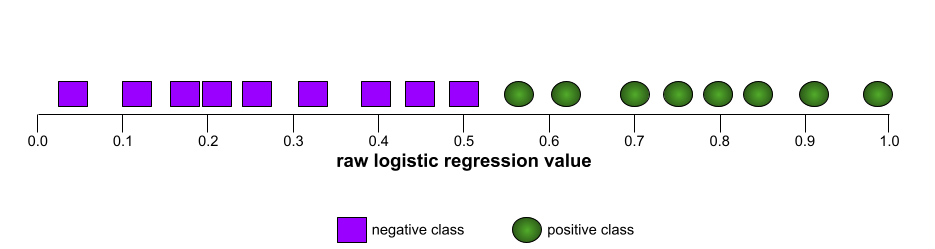
इसके उलट, इस इमेज में एक खराब मॉडल के लिए लॉजिस्टिक रिग्रेशन की रॉ वैल्यू दिखाई गई हैं. यह मॉडल, नेगेटिव क्लास को पॉज़िटिव क्लास से अलग नहीं कर सकता:

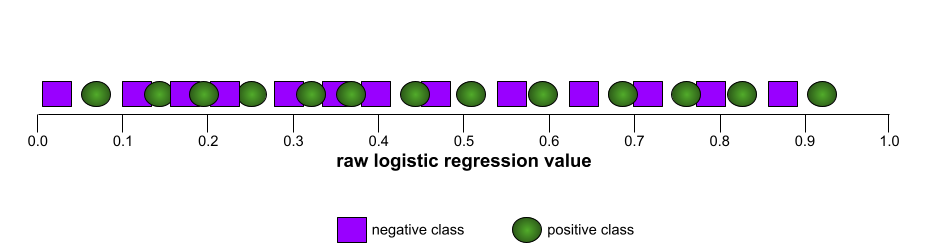
इस मॉडल के लिए आरओसी कर्व ऐसा दिखता है:

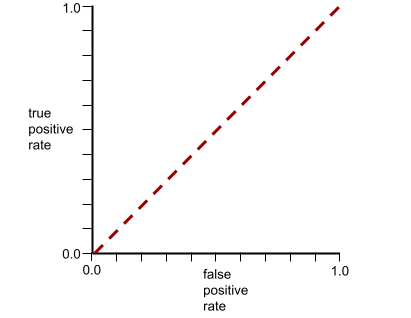
वहीं, असल दुनिया में ज़्यादातर बाइनरी क्लासिफ़िकेशन मॉडल, पॉज़िटिव और नेगेटिव क्लास को कुछ हद तक अलग करते हैं. हालांकि, वे आम तौर पर ऐसा पूरी तरह से नहीं कर पाते. इसलिए, एक सामान्य आरओसी कर्व, इन दोनों एक्सट्रीम के बीच कहीं होता है:

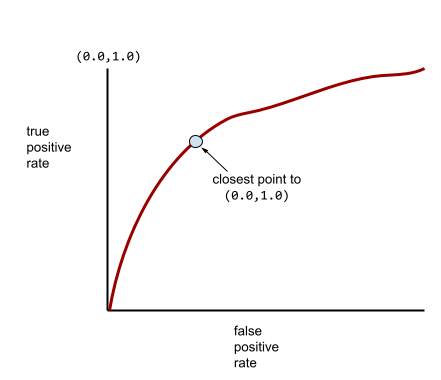
आरओसी कर्व पर (0.0,1.0) के सबसे करीब वाला पॉइंट, सैद्धांतिक तौर पर सबसे सही क्लासिफ़िकेशन थ्रेशोल्ड की पहचान करता है. हालांकि, असल दुनिया की कई अन्य समस्याएं, क्लासिफ़िकेशन के सही थ्रेशोल्ड को चुनने पर असर डालती हैं. उदाहरण के लिए, ऐसा हो सकता है कि गलत पहचान किए जाने से ज़्यादा नुकसान, पहचान न किए जाने से होता हो.

AUC नाम की संख्यात्मक मेट्रिक, आरओसी कर्व को एक फ़्लोटिंग-पॉइंट वैल्यू में बदल देती है.

रूट मीन स्क्वेयर्ड एरर (आरएमएसई)

#fundamentals

#Metric

यह मीन स्क्वेयर्ड एरर का वर्गमूल होता है.

ROUGE (रीकॉल-ओरिएंटेड अंडरस्टडी फ़ॉर गिस्टिंग इवैलुएशन)

#Metric

यह मेट्रिक का एक ग्रुप है. इससे, जवाब की खास जानकारी अपने-आप जनरेट होने और मशीन ट्रांसलेशन मॉडल का आकलन किया जाता है. ROUGE मेट्रिक से यह पता चलता है कि रेफ़रंस टेक्स्ट, एमएल मॉडल के जनरेट किए गए टेक्स्ट से कितना मिलता-जुलता है. ROUGE फ़ैमिली का हर सदस्य, ओवरलैप को अलग-अलग तरीके से मेज़र करता है. ROUGE स्कोर ज़्यादा होने का मतलब है कि रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में कम ROUGE स्कोर की तुलना में ज़्यादा समानता है.

ROUGE फ़ैमिली का हर सदस्य आम तौर पर ये मेट्रिक जनरेट करता है:

• स्पष्टता
• रीकॉल
• F₁

ध्यान दें: ROUGE, सटीकता और वापस बुलाना का इस्तेमाल, पारंपरिक सटीकता और वापस बुलाना से कुछ अलग तरीके से करता है.

ज़्यादा जानकारी और उदाहरणों के लिए, यहां जाएं:

• ROUGE-L
• ROUGE-N
• ROUGE-S

ध्यान दें: BLEU और BLEURT, सटीकता के लिए ऑप्टिमाइज़ होते हैं, जबकि ROUGE, रिकॉल के लिए ऑप्टिमाइज़ होता है. इसलिए, मशीन ट्रांसलेशन का आकलन करने के लिए BLEU और BLEURT बेहतर मेट्रिक हैं, क्योंकि इनका फ़ोकस सटीक जानकारी देने पर होता है. वहीं, खास जानकारी देने वाले कॉन्टेंट का आकलन करने के लिए ROUGE बेहतर मेट्रिक है, क्योंकि इसका फ़ोकस जानकारी को याद रखने पर होता है.

ROUGE-L

#Metric

यह ROUGE फ़ैमिली का सदस्य है. यह रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में सबसे लंबे कॉमन सबसीक्वेंस की लंबाई पर फ़ोकस करता है. यहां दिए गए फ़ॉर्मूले, ROUGE-L के लिए रीकॉल और सटीक होने का हिसाब लगाते हैं:

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

इसके बाद, ROUGE-L रीकॉल और ROUGE-L प्रेसिज़न को एक ही मेट्रिक में रोल अप करने के लिए, F₁ का इस्तेमाल किया जा सकता है:

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

ROUGE-L के हिसाब लगाने के उदाहरण के लिए, आइकॉन पर क्लिक करें.

यहां दिए गए रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट पर ध्यान दें.

कैटगरी	इसे किसने बनाया है?	टेक्स्ट
रेफ़रंस टेक्स्ट	मानवीय अनुवादक	मुझे कई तरह की चीज़ों के बारे में जानना है.
जनरेट किया गया टेक्स्ट	मशीन लर्निंग मॉडल	मुझे बहुत कुछ सीखना है.

इसलिए:

• सबसे लंबा कॉमन सबसीक्वेंस 5 है (I want to of things)
• रेफ़रंस टेक्स्ट में शब्दों की संख्या 9 है.
• जनरेट किए गए टेक्स्ट में शब्दों की संख्या 7 है.

इसलिए:

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

ROUGE-L, रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में मौजूद नई लाइनों को अनदेखा करता है. इसलिए, सबसे लंबा कॉमन सबसीक्वेंस एक से ज़्यादा वाक्यों में हो सकता है. जब रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में कई वाक्य शामिल होते हैं, तो आम तौर पर ROUGE-Lsum मेट्रिक बेहतर होती है. यह ROUGE-L का एक वैरिएंट है. ROUGE-Lsum, किसी पैसेज के हर वाक्य के लिए सबसे लंबे कॉमन सबसीक्वेंस का पता लगाता है. इसके बाद, उन सबसे लंबे कॉमन सबसीक्वेंस का औसत निकालता है.

ROUGE-Lsum के उदाहरण के तौर पर किए गए कैलकुलेशन के आइकॉन पर क्लिक करें.

यहां दिए गए रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट पर ध्यान दें.

कैटगरी	इसे किसने बनाया है?	टेक्स्ट
रेफ़रंस टेक्स्ट	मानवीय अनुवादक	मंगल ग्रह की सतह सूखी है. लगभग सारा पानी ज़मीन के नीचे है.
जनरेट किया गया टेक्स्ट	मशीन लर्निंग मॉडल	मंगल की सतह सूखी है. हालांकि, ज़्यादातर पानी ज़मीन के अंदर है.

इसलिए:

	First sentence	दूसरा वाक्य
सबसे लंबा कॉमन सीक्वेंस	2 (मंगल ग्रह की सूखी मिट्टी)	3 (पानी ज़मीन के नीचे है)
रेफ़रंस टेक्स्ट में वाक्य की लंबाई	6	7
जनरेट किए गए टेक्स्ट में वाक्य की लंबाई	5	8

इसलिए:

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#Metric

यह ROUGE फ़ैमिली की मेट्रिक का एक सेट है. यह रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में, एक तय साइज़ के शेयर किए गए N-ग्राम की तुलना करता है. उदाहरण के लिए:

• ROUGE-1, रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में शेयर किए गए टोकन की संख्या को मेज़र करता है.
• ROUGE-2, रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में, शेयर किए गए बिगराम (2-ग्राम) की संख्या को मेज़र करता है.
• ROUGE-3, रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में मौजूद, एक जैसे ट्रायग्राम (3-ग्राम) की संख्या को मेज़र करता है.

ROUGE-N फ़ैमिली के किसी भी सदस्य के लिए, ROUGE-N रीकॉल और ROUGE-N प्रेसिज़न का हिसाब लगाने के लिए, यहां दिए गए फ़ॉर्मूले इस्तेमाल किए जा सकते हैं:

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

इसके बाद, ROUGE-N recall और ROUGE-N precision को एक ही मेट्रिक में रोल अप करने के लिए, F₁ का इस्तेमाल किया जा सकता है:

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

उदाहरण के लिए, आइकॉन पर क्लिक करें.

मान लें कि आपको किसी मशीन लर्निंग मॉडल के अनुवाद की तुलना, किसी व्यक्ति के अनुवाद से करनी है. इसके लिए, आपको ROUGE-2 का इस्तेमाल करना है.

कैटगरी	इसे किसने बनाया है?	टेक्स्ट	बिगराम
रेफ़रंस टेक्स्ट	मानवीय अनुवादक	मुझे कई तरह की चीज़ों के बारे में जानना है.	मुझे, मुझे अलग-अलग, अलग-अलग तरह की, तरह की चीज़ों के बारे में, चीज़ों के बारे में जानना है
जनरेट किया गया टेक्स्ट	मशीन लर्निंग मॉडल	मुझे बहुत कुछ सीखना है.	मुझे, मुझे, सीखना है, सीखना है, बहुत कुछ, बहुत कुछ, के बारे में

इसलिए:

• मिलते-जुलते 2-ग्राम की संख्या 3 है (I want, want to, और of things).
• रेफ़रंस टेक्स्ट में 2-ग्राम की संख्या 8 है.
• जनरेट किए गए टेक्स्ट में 2-ग्राम की संख्या 6 है.

इसलिए:

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#Metric

यह ROUGE-N का एक ऐसा फ़ॉर्मूला है जो skip-gram मैचिंग को चालू करता है. इसका मतलब है कि ROUGE-N सिर्फ़ उन N-ग्राम की गिनती करता है जो पूरी तरह मैच करते हैं. हालांकि, ROUGE-S एक या उससे ज़्यादा शब्दों से अलग किए गए N-ग्राम की भी गिनती करता है. उदाहरण के लिए, आप नीचे दिया गया तरीका अपना सकते हैं:

• रेफ़रंस टेक्स्ट: सफ़ेद बादल
• जनरेट किया गया टेक्स्ट: सफ़ेद रंग के बादल

ROUGE-N का हिसाब लगाते समय, 2-ग्राम, सफ़ेद बादल, सफ़ेद बादल से मेल नहीं खाता. हालांकि, ROUGE-S का हिसाब लगाते समय, White clouds, White billowing clouds से मेल खाता है.

R-squared

#Metric

यह रिग्रेशन मेट्रिक है. इससे पता चलता है कि किसी लेबल में कितना बदलाव, किसी एक फ़ीचर या फ़ीचर सेट की वजह से हुआ है. R-स्क्वेयर्ड की वैल्यू 0 से 1 के बीच होती है. इसे इस तरह समझा जा सकता है:

• R-स्क्वेयर्ड की वैल्यू 0 होने का मतलब है कि लेबल में मौजूद किसी भी बदलाव की वजह, फ़ीचर सेट नहीं है.
• R-स्क्वेयर्ड की वैल्यू 1 होने का मतलब है कि किसी लेबल के सभी वैरिएशन, फ़ीचर सेट की वजह से हैं.
• R-स्क्वेयर्ड की वैल्यू 0 से 1 के बीच होती है. इससे पता चलता है कि किसी खास सुविधा या सुविधाओं के सेट से, लेबल के वैरिएशन का अनुमान कितना लगाया जा सकता है. उदाहरण के लिए, R-स्क्वेयर्ड की वैल्यू 0.10 का मतलब है कि लेबल में 10% वैरिएंस, फ़ीचर सेट की वजह से है. R-स्क्वेयर्ड की वैल्यू 0.20 का मतलब है कि 20% वैरिएंस, फ़ीचर सेट की वजह से है. इसी तरह, अन्य वैल्यू का मतलब भी निकाला जा सकता है.

आर-स्क्वेयर्ड, मॉडल की अनुमानित वैल्यू और ग्राउंड ट्रुथ के बीच पियर्सन कोरिलेशन कोएफ़िशिएंट का स्क्वेयर होता है.

S

स्कोरिंग

#Metric

सुझाव देने वाले सिस्टम का वह हिस्सा जो कैंडिडेट जनरेशन फ़ेज़ में तैयार किए गए हर आइटम के लिए वैल्यू या रैंकिंग देता है.

मिलते-जुलते डिज़ाइन

#clustering

#Metric

क्लस्टरिंग एल्गोरिदम में, इस मेट्रिक का इस्तेमाल यह तय करने के लिए किया जाता है कि कोई दो उदाहरण कितने मिलते-जुलते हैं.

कम जानकारी होना

#Metric

किसी वेक्टर या मैट्रिक्स में शून्य (या शून्य) पर सेट किए गए एलिमेंट की संख्या को उस वेक्टर या मैट्रिक्स में मौजूद कुल एंट्री की संख्या से भाग दिया जाता है. उदाहरण के लिए, 100 एलिमेंट वाली मैट्रिक्स पर विचार करें, जिसमें 98 सेल में शून्य है. विरलता का हिसाब इस तरह लगाया जाता है:

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

फ़ीचर स्पार्सिटी का मतलब, फ़ीचर वेक्टर की स्पार्सिटी से है; मॉडल स्पार्सिटी का मतलब, मॉडल के वेट की स्पार्सिटी से है.

स्क्वेयर्ड हिंज लॉस

#Metric

हिंज लॉस का स्क्वेयर. स्क्वेयर्ड हिंज लॉस, आउटलायर को सामान्य हिंज लॉस की तुलना में ज़्यादा नुकसान पहुंचाता है.

स्क्वेयर्ड लॉस

#fundamentals

#Metric

L₂ नुकसान के लिए समानार्थी शब्द.

T

टेस्ट लॉस

#fundamentals

#Metric

यह मेट्रिक, टेस्ट सेट के हिसाब से मॉडल के लॉस को दिखाती है. मॉडल बनाते समय, आम तौर पर टेस्ट लॉस को कम करने की कोशिश की जाती है. ऐसा इसलिए है, क्योंकि कम टेस्ट लॉस, कम ट्रेनिंग लॉस या कम वैलिडेशन लॉस की तुलना में ज़्यादा भरोसेमंद क्वालिटी सिग्नल होता है.

कभी-कभी, टेस्ट लॉस और ट्रेनिंग लॉस या पुष्टि करने के लॉस के बीच का अंतर यह बताता है कि आपको रेगुलराइज़ेशन रेट को बढ़ाना होगा.

टॉप-के ऐक्युरसी

#Metric

जनरेट की गई सूचियों की पहली k पोज़िशन में "टारगेट लेबल" के दिखने का प्रतिशत. ये सूचियां, आपकी दिलचस्पी के हिसाब से दिए गए सुझाव हो सकते हैं. इसके अलावा, ये softmax के हिसाब से क्रम में लगाए गए आइटम की सूची भी हो सकती हैं.

टॉप-k ऐक््यूरेसी को k पर ऐक््यूरेसी भी कहा जाता है.

ध्यान दें: टारगेट लेबल कोई भी क्लास हो सकती है. यह ज़रूरी नहीं कि वह ग्राउंड ट्रुथ क्लास हो. इसलिए, टॉप-के एक्यूरेसी हमेशा पारंपरिक एक्यूरेसी के बराबर नहीं होती.

उदाहरण के लिए, आइकॉन पर क्लिक करें.

मान लें कि मशीन लर्निंग सिस्टम, पेड़ की पत्तियों की तस्वीर के आधार पर पेड़ की संभावनाओं का पता लगाने के लिए, सॉफ़्टमैक्स का इस्तेमाल करता है. इस टेबल में, पांच इनपुट ट्री की तस्वीरों से जनरेट हुई आउटपुट सूचियां दिखाई गई हैं. हर लाइन में, टारगेट लेबल और पांच सबसे संभावित ट्री होते हैं. उदाहरण के लिए, जब टारगेट लेबल मेपल था, तब मशीन लर्निंग मॉडल ने एलम को सबसे ज़्यादा संभावना वाला पेड़, ओक को दूसरी सबसे ज़्यादा संभावना वाला पेड़, और इसी तरह अन्य पेड़ों की पहचान की.

टारगेट लेबल	1	2	3	4	5
मेपल	elm	ओक	maple	बीच	पॉप्लर
डॉगवुड	ओक	dogwood	पॉप्लर	Hickory	मेपल
ओक	oak	बासवुड	टिड्डी	ऑल्डर	Linden
Linden	मेपल	पॉ-पॉ	ओक	बासवुड	पॉप्लर
ओक	टिड्डी	Linden	oak	मेपल	पॉ-पॉ

टारगेट लेबल, पहली पोज़िशन पर सिर्फ़ एक बार दिखता है. इसलिए, टॉप-1 एक्यूरेसी यह है:

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

टारगेट लेबल, टॉप तीन में से किसी एक पोज़िशन पर चार बार दिखता है. इसलिए, टॉप-3 की सटीक जानकारी यह है:

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

बुरा बर्ताव

#Metric

कॉन्टेंट में किस हद तक गाली-गलौज, धमकी या आपत्तिजनक बातें शामिल हैं. मशीन लर्निंग के कई मॉडल, आपत्तिजनक कॉन्टेंट की पहचान कर सकते हैं और उसका आकलन कर सकते हैं. इनमें से ज़्यादातर मॉडल, कई पैरामीटर के आधार पर आपत्तिजनक कॉन्टेंट की पहचान करते हैं. जैसे, गाली-गलौज वाली भाषा का लेवल और धमकी देने वाली भाषा का लेवल.

ट्रेनिंग लॉस

#fundamentals

#Metric

यह मेट्रिक, ट्रेनिंग के किसी खास इटरेशन के दौरान मॉडल के लॉस को दिखाती है. उदाहरण के लिए, मान लें कि लॉस फ़ंक्शन Mean Squared Error है. ऐसा हो सकता है कि 10वें इटरेशन के लिए ट्रेनिंग लॉस (मीन स्क्वेयर्ड एरर) 2.2 हो और 100वें इटरेशन के लिए ट्रेनिंग लॉस 1.9 हो.

लॉस कर्व, ट्रेनिंग लॉस की तुलना में इटरेशन की संख्या को प्लॉट करता है. लॉस कर्व से, ट्रेनिंग के बारे में ये संकेत मिलते हैं:

• नीचे की ओर झुकी हुई लाइन का मतलब है कि मॉडल बेहतर हो रहा है.
• ऊपर की ओर जाती हुई ढलान का मतलब है कि मॉडल की परफ़ॉर्मेंस खराब हो रही है.
• स्लोप के फ़्लैट होने का मतलब है कि मॉडल कन्वर्जेंस पर पहुंच गया है.

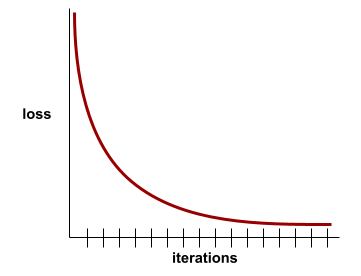
उदाहरण के लिए, यहां दिए गए लॉस कर्व में यह दिखाया गया है:

• शुरुआती इटरेशन के दौरान, नीचे की ओर तेज़ी से गिरता हुआ स्लोप. इससे पता चलता है कि मॉडल में तेज़ी से सुधार हो रहा है.
• ट्रेनिंग के आखिर तक, धीरे-धीरे कम होने वाला (लेकिन अब भी नीचे की ओर) स्लोप. इसका मतलब है कि मॉडल में सुधार जारी है, लेकिन शुरुआती इटरेशन की तुलना में कुछ हद तक धीमी गति से.
• ट्रेनिंग के आखिर में फ़्लैट स्लोप, जो कन्वर्जेंस का सुझाव देता है.

ट्रेनिंग लॉस अहम होता है. हालांकि, सामान्यीकरण के बारे में भी जानें.

ट्रू नेगेटिव (टीएन)

#fundamentals

#Metric

इस उदाहरण में, मॉडल ने नेगेटिव क्लास का सही अनुमान लगाया है. उदाहरण के लिए, मॉडल यह अनुमान लगाता है कि कोई ईमेल मैसेज स्पैम नहीं है और वह ईमेल मैसेज वाकई स्पैम नहीं है.

ट्रू पॉज़िटिव (टीपी)

#fundamentals

#Metric

ऐसा उदाहरण जिसमें मॉडल, पॉज़िटिव क्लास का सही अनुमान लगाता है. उदाहरण के लिए, मॉडल यह अनुमान लगाता है कि कोई ईमेल मैसेज स्पैम है और वह ईमेल मैसेज वाकई स्पैम है.

ट्रू पॉज़िटिव रेट (टीपीआर)

#fundamentals

#Metric

recall का समानार्थी शब्द. यानी:

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

ट्रू पॉज़िटिव रेट, आरओसी कर्व में y-ऐक्सिस होता है.

V

पुष्टि करने के दौरान होने वाला नुकसान

#fundamentals

#Metric

यह मेट्रिक, ट्रेनिंग के किसी इटरेशन के दौरान वैलिडेशन सेट पर मॉडल के लॉस को दिखाती है.

जनरलाइज़ेशन कर्व भी देखें.

वैरिएबल के महत्व

#df

#Metric

स्कोर का एक ऐसा सेट जो मॉडल के लिए हर फ़ीचर की अहमियत दिखाता है.

उदाहरण के लिए, डिसिज़न ट्री पर आधारित एक मॉडल लें, जो घर की कीमतों का अनुमान लगाता है. मान लें कि यह फ़ैसला लेने वाला ट्री, तीन सुविधाओं का इस्तेमाल करता है: साइज़, उम्र, और स्टाइल. अगर तीन सुविधाओं के लिए, वैरिएबल के महत्व का सेट {size=5.8, age=2.5, style=4.7} के तौर पर कैलकुलेट किया जाता है, तो साइज़, उम्र या स्टाइल की तुलना में फ़ैसले के ट्री के लिए ज़्यादा अहम होता है.

वैरिएबल की अहमियत को मेज़र करने वाली अलग-अलग मेट्रिक मौजूद हैं. इनसे एमएल विशेषज्ञों को मॉडल के अलग-अलग पहलुओं के बारे में जानकारी मिल सकती है.

W

Wasserstein loss

#Metric

यह लॉस फ़ंक्शन, जनरेटिव ऐडवर्सैरियल नेटवर्क में आम तौर पर इस्तेमाल किया जाता है. यह जनरेट किए गए डेटा और असली डेटा के डिस्ट्रिब्यूशन के बीच अर्थ मूवर डिस्टेंस पर आधारित होता है.