Makine Öğrenimi Terimleri Sözlüğü: Metrikler

Bu sayfada Metrik sözlüğü terimleri yer almaktadır. Tüm sözlük terimleri için burayı tıklayın.

A

doğruluk

#fundamentals

#Metric

Doğru sınıflandırma tahminlerinin sayısının toplam tahmin sayısına bölünmesiyle elde edilir. Yani:

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

Örneğin, 40 doğru ve 10 yanlış tahminde bulunan bir modelin doğruluğu şu şekilde olur:

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

İkili sınıflandırma, doğru tahminler ve yanlış tahminler kategorileri için belirli adlar sağlar. Bu nedenle, ikili sınıflandırma için doğruluk formülü aşağıdaki gibidir:

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

Bu örnekte:

• TP, doğru pozitif (doğru tahminler) sayısıdır.
• TN, doğru negatiflerin (doğru tahminler) sayısıdır.
• FP, yanlış pozitiflerin (yanlış tahminler) sayısıdır.
• FN, yanlış negatiflerin (yanlış tahminler) sayısıdır.

Doğruluğu hassasiyet ve geri çağırma ile karşılaştırın.

Doğruluk ve sınıf dengesizliği olan veri kümeleri hakkında ayrıntılı bilgi için simgeyi tıklayın.

Doğruluk, bazı durumlarda değerli bir metrik olsa da diğer durumlarda oldukça yanıltıcıdır. Doğruluk, özellikle sınıf dengesizliği olan veri kümelerini işleyen sınıflandırma modellerini değerlendirmek için genellikle uygun bir metrik değildir.

Örneğin, belirli bir subtropikal şehirde yüzyılda yalnızca 25 gün kar yağdığını varsayalım. Kar yağmayan günlerin (negatif sınıf) sayısı, kar yağdığı günlerin (pozitif sınıf) sayısından çok daha fazla olduğundan, bu şehir için kar veri kümesi sınıf dengesizliğine sahiptir. Her gün kar yağacak mı yoksa yağmayacak mı tahmininde bulunması gereken bir ikili sınıflandırma modelinin her gün "kar yağmayacak" tahmininde bulunduğunu düşünün. Bu model oldukça doğru ancak tahmin gücü yok. Aşağıdaki tabloda, bir asırlık tahminlerin sonuçları özetlenmektedir:

Kategori	Sayı
TP	0
TN	36499
FP	0
FN	25

Bu nedenle, modelin doğruluğu şöyledir:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

%99, 93 doğruluk oranı çok etkileyici görünse de modelin aslında tahmin gücü yoktur.

Sınıf dengesizliği olan veri kümeleri üzerinde eğitilmiş modelleri değerlendirirken hassasiyet ve geri çağırma genellikle doğruluktan daha kullanışlı metriklerdir.

---

Daha fazla bilgi için Makine Öğrenimine Giriş Kursu'ndaki Sınıflandırma: Doğruluk, geri çağırma, hassasiyet ve ilgili metrikler bölümüne bakın.

PR eğrisinin altındaki alan

#Metric

PR AUC (PR Eğrisinin Altındaki Alan) başlıklı makaleyi inceleyin.

ROC eğrisinin altındaki alan

#Metric

AUC (ROC eğrisinin altındaki alan) bölümüne bakın.

AUC (ROC eğrisinin altındaki alan)

#fundamentals

#Metric

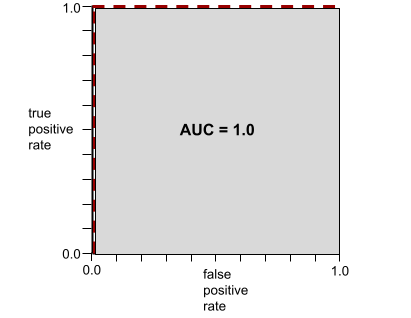
İkili sınıflandırma modelinin pozitif sınıfları negatif sınıflardan ayırma becerisini gösteren 0,0 ile 1,0 arasında bir sayı. AUC değeri 1, 0'a ne kadar yakın olursa modelin sınıfları birbirinden ayırma yeteneği o kadar iyi olur.

Örneğin, aşağıdaki resimde pozitif sınıfları (yeşil oval) negatif sınıflardan (mor dikdörtgen) mükemmel şekilde ayıran bir sınıflandırma modeli gösterilmektedir. Bu gerçekçi olmayan mükemmel modelin AUC değeri 1,0'dır:

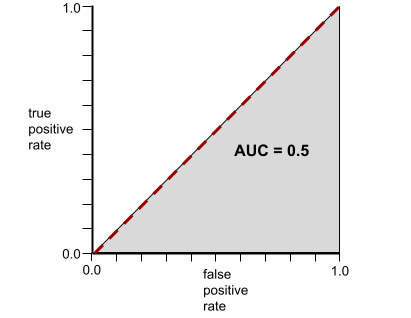
Buna karşılık, aşağıdaki resimde rastgele sonuçlar üreten bir sınıflandırma modelinin sonuçları gösterilmektedir. Bu modelin AUC değeri 0,5'tir:

Evet, önceki modelin AUC değeri 0,0 değil 0,5.

Çoğu model, iki uç nokta arasında bir yerdedir. Örneğin, aşağıdaki model pozitifleri negatiflerden biraz ayırır ve bu nedenle 0,5 ile 1,0 arasında bir AUC'ye sahiptir:

AUC, sınıflandırma eşiği için ayarladığınız tüm değerleri yoksayar. Bunun yerine AUC, olası tüm sınıflandırma eşiklerini dikkate alır.

AUC ve ROC eğrileri arasındaki ilişki hakkında bilgi edinmek için simgeyi tıklayın.

AUC, ROC eğrisinin altındaki alanı temsil eder. Örneğin, pozitifleri negatiflerden mükemmel şekilde ayıran bir modelin ROC eğrisi aşağıdaki gibi görünür:

AUC, önceki resimde gri bölgenin alanıdır. Bu alışılmadık durumda alan, gri bölgenin uzunluğu (1,0) ile gri bölgenin genişliğinin (1,0) çarpımıdır. Bu nedenle, 1,0 ile 1,0'ın çarpımı tam olarak 1,0 AUC değerini verir. Bu, mümkün olan en yüksek AUC puanıdır.

Buna karşılık, sınıfları hiç ayıramayan bir sınıflandırma modelinin ROC eğrisi aşağıdaki gibidir. Bu gri bölgenin alanı 0,5'tir.

Daha tipik bir ROC eğrisi yaklaşık olarak aşağıdaki gibi görünür:

Bu eğrinin altındaki alanı manuel olarak hesaplamak çok zahmetli bir iş olur. Bu nedenle, çoğu AUC değeri genellikle bir program tarafından hesaplanır.

---

AUC'nin daha resmi bir tanımı için simgeyi tıklayın.

AUC, sınıflandırma modelinin rastgele seçilen pozitif bir örneğin gerçekten pozitif olduğuna, rastgele seçilen negatif bir örneğin pozitif olduğuna kıyasla daha fazla güvenme olasılığıdır.

---

Daha fazla bilgi için Makine Öğrenimine Giriş Kursu'ndaki Sınıflandırma: ROC ve AUC başlıklı makaleyi inceleyin.

k'da ortalama hassasiyet

#Metric

Bir modelin, sıralanmış sonuçlar oluşturan tek bir istemdeki performansını özetleyen bir metrik (ör. kitap önerilerinin numaralandırılmış listesi). k'daki ortalama hassasiyet, her bir alakalı sonuç için k'daki hassasiyet değerlerinin ortalamasıdır. Bu nedenle, k'daki ortalama hassasiyet formülü şöyledir:

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

Bu örnekte:

• \(n\) , listedeki alakalı öğelerin sayısıdır.

k tuşunda geri çağırma ile karşılaştırın.

Not: k değerindeki ortalama kesinlik, tek istemin çıktısını değerlendirir. Bir modelin çıktısının kalitesini birçok farklı istemde değerlendirmek için k'da ortalama kesinliği kullanın.

Not: Bazı kişiler k'da ortalama kesinliği kısaca ortalama kesinlik olarak ifade eder.

Örnek için simgeyi tıklayın.

Bir büyük dil modeline aşağıdaki sorgunun verildiğini varsayalım:

List the 6 funniest movies of all time in order.

Büyük dil modeli aşağıdaki listeyi döndürür:

1. The General
2. Kötü
3. Platoon
4. Nedimeler
5. Yurttaş Kane
6. This is Spinal Tap

Döndürülen listedeki filmlerden dördü çok komik (yani alakalı), ikisi ise dram türünde (alakasız). Aşağıdaki tabloda sonuçlar ayrıntılı olarak açıklanmaktadır:

Konum	Film	Alakalı mı?	k değerinde hassasiyet
1	The General	Evet	1,0
2	Kötü	Evet	1,0
3	Platoon	Hayır	alakalı değil
4	Nedimeler	Evet	0,75
5	Yurttaş Kane	Hayır	alakalı değil
6	This is Spinal Tap	Evet	0,67

Alakalı sonuç sayısı 4'tür. Bu nedenle, ortalama kesinliği 6 olarak aşağıdaki şekilde hesaplayabilirsiniz:

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

referans değer

#Metric

Başka bir modelin (genellikle daha karmaşık bir model) ne kadar iyi performans gösterdiğini karşılaştırmak için referans noktası olarak kullanılan model. Örneğin, bir lojistik regresyon modeli, derin model için iyi bir referans değer olabilir.

Temel, belirli bir sorun için model geliştiricilerin yeni modelin faydalı olması için ulaşması gereken minimum beklenen performansı ölçmesine yardımcı olur.

C

maliyet

#Metric

Kaybın eş anlamlısı.

karşıolgusal adalet

#responsible

#Metric

Bir adalet metriği, bir sınıflandırma modelinin bir birey için aynı sonucu üretip üretmediğini kontrol eder. Bu birey, bir veya daha fazla hassas özellik dışında ilk bireyle aynıdır. Karşı olgusal adalet için bir sınıflandırma modelini değerlendirmek, modeldeki olası önyargı kaynaklarını ortaya çıkarmanın bir yöntemidir.

Daha fazla bilgi için aşağıdaki kaynaklardan birine bakın:

• Makine Öğrenimi Hızlandırılmış Kursu'nda Adalet: Karşıolgusal adalet.
• When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness

çapraz entropi

#Metric

Log Loss'un çok sınıflı sınıflandırma sorunlarına genelleştirilmiş halidir. Çapraz entropi, iki olasılık dağılımı arasındaki farkı ölçer. Ayrıca şaşırtıcılık konusuna da bakın.

kümülatif dağılım fonksiyonu (KDF)

#Metric

Hedef değerden küçük veya bu değere eşit örneklerin sıklığını tanımlayan bir işlev. Örneğin, sürekli değerlerin normal dağılımını ele alalım. Bir kümülatif dağılım fonksiyonu, örneklerin yaklaşık% 50'sinin ortalamadan küçük veya ortalamaya eşit olması gerektiğini ve örneklerin yaklaşık% 84'ünün ortalamanın bir standart sapma üzerinde olmaması gerektiğini gösterir.

D

demografik eşitlik

#responsible

#Metric

Bir modelin sınıflandırma sonuçları belirli bir hassas özelliğe bağlı değilse karşılanan bir adalet metriği.

Örneğin, hem Lilliputlular hem de Brobdingnaglılar Glubbdubdrib Üniversitesi'ne başvuruyorsa bir grubun ortalama olarak diğerinden daha nitelikli olup olmadığına bakılmaksızın, kabul edilen Lilliputluların yüzdesi ile kabul edilen Brobdingnaglıların yüzdesi aynı olduğunda demografik eşitlik sağlanır.

Eşitlenmiş olasılıklar ve fırsat eşitliği ile karşılaştırıldığında, bu kavramlar toplu sınıflandırma sonuçlarının hassas özelliklere bağlı olmasına izin verir ancak belirli gerçek etiketleri için sınıflandırma sonuçlarının hassas özelliklere bağlı olmasına izin vermez. Demografik eşitlik için optimizasyon yaparken yapılan fedakarlıkları inceleyen bir görselleştirme için "Daha akıllı makine öğrenimiyle ayrımcılığa karşı mücadele etme" başlıklı makaleye bakın.

Daha fazla bilgi için Makine Öğrenimi Hızlandırılmış Kursu'ndaki Adalet: demografik eşitlik bölümüne bakın.

E

toprak taşıma aracı mesafesi (EMD)

#Metric

İki dağıtımın göreli benzerliğinin ölçüsü. Toprak taşıma mesafesi ne kadar düşükse dağıtımlar o kadar benzerdir.

düzenleme mesafesi

#Metric

İki metin dizesinin birbirine ne kadar benzediğinin ölçüsü. Makine öğreniminde düzenleme mesafesi şu nedenlerle faydalıdır:

• Düzenleme mesafesini hesaplamak kolaydır.
• Düzenleme mesafesi, birbirine benzer olduğu bilinen iki dizeyi karşılaştırabilir.
• Düzenleme mesafesi, farklı dizelerin belirli bir dizeye ne kadar benzediğini belirleyebilir.

Düzenleme mesafesinin, her biri farklı dize işlemleri kullanan çeşitli tanımları vardır. Örnek için Levenshtein mesafesi başlıklı makaleyi inceleyin.

ampirik kümülatif dağılım işlevi (eCDF veya EDF)

#Metric

Gerçek bir veri kümesinden alınan kümülatif dağılım fonksiyonu deneysel ölçümlere dayanır. Fonksiyonun x ekseni boyunca herhangi bir noktadaki değeri, veri kümesindeki gözlemlerin belirtilen değerden küçük veya bu değere eşit olan kısmıdır.

entropi

#df

#Metric

Bilgi teorisinde, bir olasılık dağılımının ne kadar tahmin edilemez olduğunun açıklamasıdır. Alternatif olarak entropi, her bir örneğin ne kadar bilgi içerdiği şeklinde de tanımlanır. Bir dağılım, rastgele değişkenin tüm değerleri eşit olasılıklı olduğunda mümkün olan en yüksek entropiye sahiptir.

"0" ve "1" olmak üzere iki olası değere sahip bir kümenin entropisi (örneğin, ikili sınıflandırma problemindeki etiketler) aşağıdaki formüle sahiptir:

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

Bu örnekte:

• H, entropidir.
• p, "1" örneklerinin kesridir.
• q, "0" örneklerinin kesridir. q = (1 - p) olduğunu unutmayın.
• log genellikle log₂'dir. Bu durumda, entropi birimi bit'tir.

Örneğin, aşağıdakileri varsayalım:

• 100 örnekte "1" değeri var
• 300 örnekte "0" değeri var

Bu nedenle, entropi değeri şöyledir:

• p = 0,25
• q = 0,75
• H = (-0,25)log₂(0,25) - (0,75)log₂(0,75) = örnek başına 0,81 bit

Mükemmel dengelenmiş bir küme (örneğin, 200 "0" ve 200 "1") örneği başına 1,0 bit entropiye sahip olur. Bir küme dengesizleştiğinde entropisi 0, 0'a doğru hareket eder.

Karar ağaçlarında entropi, bölücünün sınıflandırma karar ağacının büyümesi sırasında koşulları seçmesine yardımcı olmak için bilgi kazancını formüle etmeye yardımcı olur.

Entropiyi şunlarla karşılaştırın:

• gini impurity
• Çapraz entropi kayıp fonksiyonu

Entropiye genellikle Shannon entropisi denir.

Daha fazla bilgi için Karar Ormanları kursundaki Sayısal özelliklerle ikili sınıflandırma için tam ayırıcı başlıklı makaleyi inceleyin.

fırsat eşitliği

#responsible

#Metric

Bir modelin, hassas özelliğin tüm değerleri için istenen sonucu eşit derecede iyi tahmin edip etmediğini değerlendirmek için kullanılan bir adalet metriği. Diğer bir deyişle, bir model için istenen sonuç pozitif sınıf ise amaç, gerçek pozitif oranının tüm gruplar için aynı olmasını sağlamaktır.

Fırsat eşitliği, eşitlenmiş olasılıklar ile ilgilidir. Bu da tüm gruplar için hem doğru pozitif oranlarının hem de yanlış pozitif oranlarının aynı olmasını gerektirir.

Glubbdubdrib Üniversitesi'nin hem Lilliputluları hem de Brobdingnaglıları zorlu bir matematik programına kabul ettiğini varsayalım. Lilliputluların ortaokullarında matematik derslerinden oluşan kapsamlı bir müfredat uygulanır ve öğrencilerin büyük çoğunluğu üniversite programına katılmaya hak kazanır. Brobdingnaglıların ortaokullarında matematik dersi verilmez ve sonuç olarak, öğrencilerin çok daha azı yeterli bilgiye sahiptir. Nitelikli öğrenciler, Lilliputlu veya Brobdingnaglı olmalarına bakılmaksızın eşit olasılıkla kabul ediliyorsa milliyet (Lilliputlu veya Brobdingnaglı) açısından "kabul edildi" tercih edilen etiketi için fırsat eşitliği sağlanmış olur.

Örneğin, Glubbdubdrib Üniversitesi'ne 100 Lilliputlu ve 100 Brobdingnaglı başvurduğunu ve kabul kararlarının aşağıdaki gibi verildiğini varsayalım:

Tablo 1. Lilliputian başvuru sahipleri (%90'ı nitelikli)

	Uygun	Uygun Değil
Kabul edildi	45	3
Reddedildi	45	7
Toplam	90	10
Kabul edilen nitelikli öğrenci yüzdesi: 45/90 =%50 Reddedilen niteliksiz öğrenci yüzdesi: 7/10 =%70 Kabul edilen toplam Lilliputlu öğrenci yüzdesi: (45+3)/100 = %48

 

Tablo 2. Brobdingnagian başvuru sahipleri (%10'u nitelikli):

	Uygun	Uygun Değil
Kabul edildi	5	9
Reddedildi	5	81
Toplam	10	90
Kabul edilen uygun öğrenci yüzdesi: 5/10 =%50 Reddedilen uygun olmayan öğrenci yüzdesi: 81/90 =%90 Kabul edilen toplam Brobdingnagian öğrenci yüzdesi: (5+9)/100 = %14

Yukarıdaki örnekler, nitelikli Lilliputluların ve Brobdingnaglıların kabul edilme şansı% 50 olduğundan nitelikli öğrencilerin kabulü için fırsat eşitliğini sağlar.

Fırsat eşitliği karşılanırken aşağıdaki iki adalet metriği karşılanmaz:

• Demografik eşitlik: Lilliputlular ve Brobdingnaglılar üniversiteye farklı oranlarda kabul ediliyor. Lilliputlu öğrencilerin% 48'i kabul edilirken Brobdingnaglı öğrencilerin yalnızca% 14'ü kabul ediliyor.
• Eşitlenmiş olasılıklar: Nitelikli Lilliput ve Brobdingnag öğrencileri kabul edilme konusunda eşit şansa sahip olsa da niteliksiz Lilliput ve Brobdingnag öğrencileri reddedilme konusunda eşit şansa sahip olma koşulu karşılanmaz. Uygun olmayan Lilliputluların reddedilme oranı% 70, uygun olmayan Brobdingnaglıların reddedilme oranı ise% 90'dır.

Daha fazla bilgi için Makine Öğrenimi Hızlandırılmış Kursu'ndaki Adalet: Fırsat eşitliği bölümüne bakın.

eşitlenmiş oranlar

#responsible

#Metric

Bir modelin, pozitif sınıf ve negatif sınıf ile ilgili olarak bir hassas özelliğin tüm değerleri için sonuçları eşit derecede iyi tahmin edip etmediğini değerlendirmek için kullanılan bir adalet metriği. Bu metrik, yalnızca bir sınıfı veya diğer sınıfı değerlendirmez. Başka bir deyişle, tüm gruplar için hem gerçek pozitif oranı hem de yanlış negatif oranı aynı olmalıdır.

Eşitlenmiş olasılık, yalnızca tek bir sınıfın (pozitif veya negatif) hata oranlarına odaklanan fırsat eşitliği ile ilgilidir.

Örneğin, Glubbdubdrib Üniversitesi'nin hem Lilliputluları hem de Brobdingnaglıları zorlu bir matematik programına kabul ettiğini varsayalım. Lilliputluların ortaokullarında matematik derslerinden oluşan sağlam bir müfredat uygulanır ve öğrencilerin büyük çoğunluğu üniversite programına katılmaya hak kazanır. Brobdingnaglıların ortaokullarında matematik dersleri verilmez ve sonuç olarak, öğrencilerinin çok daha azı niteliklidir. Başvuru sahibinin Lilliputian veya Brobdingnagian olması fark etmeksizin, nitelikli olması durumunda programa kabul edilme olasılığı eşit, nitelikli olmaması durumunda ise reddedilme olasılığı eşit olduğu sürece eşit olasılık koşulu karşılanmış olur.

Glubbdubdrib Üniversitesi'ne 100 Lilliputlu ve 100 Brobdingnaglı başvurduğunu ve kabul kararlarının aşağıdaki şekilde verildiğini varsayalım:

Tablo 3. Lilliputian başvuru sahipleri (%90'ı nitelikli)

	Uygun	Uygun Değil
Kabul edildi	45	2
Reddedildi	45	8
Toplam	90	10
Kabul edilen uygun öğrenci yüzdesi: 45/90 =%50 Reddedilen uygun olmayan öğrenci yüzdesi: 8/10 =%80 Toplamda kabul edilen Lilliputlu öğrenci yüzdesi: (45+2)/100 = %47

 

Tablo 4. Brobdingnagian başvuru sahipleri (%10'u nitelikli):

	Uygun	Uygun Değil
Kabul edildi	5	18
Reddedildi	5	72
Toplam	10	90
Kabul edilen nitelikli öğrenci yüzdesi: 5/10 =%50 Reddedilen niteliksiz öğrenci yüzdesi: 72/90 =%80 Kabul edilen Brobdingnagian öğrencilerin toplam yüzdesi: (5+18)/100 = %23

Uygun Lilliputian ve Brobdingnagian öğrencilerin kabul edilme şansı% 50, uygun olmayanların ise reddedilme şansı% 80 olduğundan eşit fırsat koşulu karşılanmaktadır.

Not: Burada eşit fırsat koşulu karşılanırken demografik eşitlik karşılanmaz. Lilliput ve Brobdingnag öğrencileri Glubbdubdrib Üniversitesi'ne farklı oranlarda kabul edilmektedir. Lilliput öğrencilerinin% 47'si, Brobdingnag öğrencilerinin ise% 23'ü kabul edilmektedir.

Eşitlenmiş olasılık, "Equality of Opportunity in Supervised Learning" (Denetimli Öğrenmede Fırsat Eşitliği) adlı makalede şu şekilde tanımlanır: "Ŷ tahmin edicisi, Y koşullu olarak Ŷ ve A bağımsızsa A korumalı özelliği ve Y sonucu açısından eşitlenmiş olasılığı karşılar."

Not: Eşitlenmiş şansları, daha rahat olan fırsat eşitliği metriğiyle karşılaştırın.

evals

#generativeAI

#Metric

Öncelikli olarak LLM değerlendirmeleri için kısaltma olarak kullanılır. Daha geniş bir ifadeyle evals, herhangi bir değerlendirme biçiminin kısaltmasıdır.

değerlendirme

#generativeAI

#Metric

Bir modelin kalitesini ölçme veya farklı modelleri birbiriyle karşılaştırma süreci.

Gözetimli makine öğrenimi modelini değerlendirmek için genellikle doğrulama kümesi ve test kümesi ile karşılaştırırsınız. LLM'leri değerlendirme genellikle daha kapsamlı kalite ve güvenlik değerlendirmelerini içerir.

C

F₁

#Metric

Hem hassasiyete hem de geri çağırmaya dayanan bir "toplama" ikili sınıflandırma metriği. Formül şu şekildedir:

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

Örnekleri görmek için simgeyi tıklayın.

Hassasiyet ve geri çağırmanın aşağıdaki değerlere sahip olduğunu varsayalım:

• precision = 0.6
• recall = 0.4

F₁'i aşağıdaki gibi hesaplarsınız:

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

Hassasiyet ve geri çağırma değerleri birbirine oldukça yakın olduğunda (bir önceki örnekte olduğu gibi) F₁, bu değerlerin ortalamasına yakındır. Kesinlik ve hatırlama önemli ölçüde farklı olduğunda F₁, daha düşük değere daha yakındır. Örneğin:

• precision = 0.9
• recall = 0.1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

adalet metriği

#responsible

#Metric

Ölçülebilir bir "adalet" tanımı. Sık kullanılan bazı adalet metrikleri şunlardır:

• eşitlenmiş oranlar
• tahmini eşitlik
• karşıolgusal adalet (counterfactual fairness)
• demografik eşitlik

Birçok adalet metriği birbirini dışlar. Adalet metriklerinin uyumsuzluğu başlıklı makaleyi inceleyin.

yanlış negatif (FN)

#fundamentals

#Metric

Modelin negatif sınıfı yanlışlıkla tahmin ettiği bir örnek. Örneğin, model belirli bir e-posta iletisinin spam olmadığını (negatif sınıf) tahmin ediyor ancak bu e-posta iletisi aslında spam.

yanlış negatif oranı

#Metric

Modelin yanlışlıkla negatif sınıfı tahmin ettiği gerçek pozitif örneklerin oranı. Aşağıdaki formül, yanlış negatif oranını hesaplar:

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

Daha fazla bilgi için Makine Öğrenimi Hızlandırılmış Kursu'ndaki Eşikler ve karmaşıklık matrisi bölümüne bakın.

yanlış pozitif (FP)

#fundamentals

#Metric

Modelin pozitif sınıfı yanlışlıkla tahmin ettiği bir örnek. Örneğin, model belirli bir e-posta iletisinin spam (pozitif sınıf) olduğunu tahmin ediyor ancak bu e-posta iletisi aslında spam değil.

Daha fazla bilgi için Makine Öğrenimi Hızlandırılmış Kursu'ndaki Eşikler ve karmaşıklık matrisi bölümüne bakın.

Yanlış pozitif oranı (FPR)

#fundamentals

#Metric

Modelin pozitif sınıfı yanlışlıkla tahmin ettiği gerçek negatif örneklerin oranı. Aşağıdaki formül, yanlış pozitif oranını hesaplar:

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

Yanlış pozitif oranı, ROC eğrisindeki x eksenidir.

Daha fazla bilgi için Makine Öğrenimine Giriş Kursu'ndaki Sınıflandırma: ROC ve AUC başlıklı makaleyi inceleyin.

özellik önem düzeyleri

#df

#Metric

Değişken önemleri ile eş anlamlıdır.

temel model

#generativeAI

#Metric

Çok büyük ve çeşitli bir eğitim kümesi üzerinde eğitilmiş çok büyük bir önceden eğitilmiş model. Temel model, aşağıdakilerin ikisini de yapabilir:

• Çok çeşitli isteklere iyi yanıt verme
• Ek ince ayar veya diğer özelleştirmeler için temel model olarak kullanılabilir.

Başka bir deyişle, temel model genel anlamda zaten çok yeteneklidir ancak belirli bir görev için daha da faydalı olacak şekilde özelleştirilebilir.

başarı oranı

#generativeAI

#Metric

Bir makine öğrenimi modelinin oluşturduğu metni değerlendirmek için kullanılan bir metrik. Başarı oranı, oluşturulan "başarılı" metin çıkışlarının sayısının, oluşturulan toplam metin çıkışı sayısına bölünmesiyle elde edilir. Örneğin, bir büyük dil modeli 10 kod bloğu oluşturduysa ve bunların beşi başarılı olduysa başarı oranı %50 olur.

Başarı oranı, istatistiklerde genel olarak faydalı olsa da makine öğreniminde bu metrik, öncelikli olarak kod oluşturma veya matematik problemleri gibi doğrulanabilir görevleri ölçmek için kullanılır.

G

Gini kirliliği

#df

#Metric

Entropiye benzer bir metrik. Ayırıcılar, sınıflandırma karar ağaçları için koşullar oluşturmak üzere gini kirliliğinden veya entropiden elde edilen değerleri kullanır. Bilgi kazancı, entropiden elde edilir. Gini kirliliğinden elde edilen metrik için evrensel olarak kabul edilen eşdeğer bir terim yoktur. Ancak bu adsız metrik, bilgi kazancı kadar önemlidir.

Gini kirliliğine Gini endeksi veya kısaca Gini de denir.

Gini kirliliğiyle ilgili matematiksel ayrıntılar için simgeyi tıklayın.

Gini kirliliği, aynı dağılımdan alınan yeni bir veri parçasının yanlış sınıflandırılma olasılığıdır. "0" ve "1" olmak üzere iki olası değeri olan bir kümenin Gini kirliliği (örneğin, ikili sınıflandırma problemindeki etiketler) aşağıdaki formülle hesaplanır:

   I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

Bu örnekte:

• I, Gini kirliliğidir.
• p, "1" örneklerinin kesridir.
• q, "0" örneklerinin kesridir. Unutmayın: q = 1-p

Örneğin, aşağıdaki veri kümesini ele alalım:

• 100 etikette (veri kümesinin %0,25'i) "1" değeri var.
• 300 etikette (veri kümesinin %0,75'i) "0" değeri var.

Bu nedenle, Gini kirliliği şöyledir:

• p = 0,25
• q = 0,75
• I = 1 - (0,25² + 0,75²) = 0,375

Dolayısıyla, aynı veri kümesinden rastgele bir etiketin yanlış sınıflandırılma olasılığı% 37,5, doğru sınıflandırılma olasılığı ise% 62,5 olur.

Mükemmel dengelenmiş bir etiketin (örneğin, 200 "0" ve 200 "1") Gini kirliliği 0,5 olur. Çok dengesiz bir etiketin gini kirliliği 0,0'a yakın olur.

---

H

menteşe kaybı

#Metric

Her bir eğitim örneğinden mümkün olduğunca uzak karar sınırını bulmak için tasarlanmış, sınıflandırma için bir kayıp işlevleri ailesi. Bu sayede, örnekler ile sınır arasındaki marj en üst düzeye çıkarılır. KSVM'ler, menteşe kaybını (veya kare menteşe kaybı gibi ilgili bir işlevi) kullanır. İkili sınıflandırma için menteşe kaybı işlevi aşağıdaki şekilde tanımlanır:

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

Burada y, -1 veya +1 olan gerçek etikettir ve y', sınıflandırma modelinin ham çıkışıdır:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

Sonuç olarak, menteşe kaybının (y * y') ile karşılaştırıldığı grafik aşağıdaki gibi görünür:

I

Adalet metriklerinin uyumsuzluğu

#responsible

#Metric

Bazı adalet kavramlarının birbiriyle uyumlu olmadığı ve aynı anda karşılanamayacağı fikri. Sonuç olarak, adalet kavramını ölçmek için tüm makine öğrenimi sorunlarına uygulanabilecek tek bir evrensel metrik yoktur.

Bu durum cesaret kırıcı olsa da adalet metriklerinin uyumsuzluğu, adalet için yapılan çalışmaların boşuna olduğu anlamına gelmez. Bunun yerine, adalet kavramının belirli bir makine öğrenimi sorunu için bağlamsal olarak tanımlanması gerektiğini ve kullanım alanlarına özgü zararları önlemenin amaçlandığını belirtir.

Adalet metriklerinin uyumsuzluğu hakkında daha ayrıntılı bir tartışma için "On the (im)possibility of fairness" (Adaletin (im)kansızlığı üzerine) başlıklı makaleyi inceleyin.

bireysel adalet

#responsible

#Metric

Benzer kişilerin benzer şekilde sınıflandırılıp sınıflandırılmadığını kontrol eden bir adalet metriği. Örneğin, Brobdingnagian Akademisi, aynı notlara ve standart test puanlarına sahip iki öğrencinin kabul edilme olasılığının eşit olmasını sağlayarak bireysel adaleti sağlamak isteyebilir.

Bireysel adalet kavramının tamamen "benzerliği" nasıl tanımladığınıza (bu durumda notlar ve test puanları) bağlı olduğunu ve benzerlik metriğiniz önemli bilgileri (ör. öğrencinin müfredatının zorluğu) kaçırırsa yeni adalet sorunları ortaya çıkarma riskiyle karşılaşabileceğinizi unutmayın.

Bireysel adalet hakkında daha ayrıntılı bilgi için "Farkındalıkla Adalet" başlıklı makaleyi inceleyin.

bilgi kazancı

#df

#Metric

Karar ağaçlarında, bir düğümün entropisi ile alt düğümlerinin entropisinin örnek sayısına göre ağırlıklı toplamı arasındaki fark. Bir düğümün entropisi, o düğümdeki örneklerin entropisidir.

Örneğin, aşağıdaki entropi değerlerini ele alalım:

• üst düğümün entropisi = 0,6
• 16 alakalı örneğe sahip bir alt düğümün entropisi = 0,2
• 24 alakalı örneği olan başka bir alt düğümün entropisi = 0,1

Bu nedenle, örneklerin% 40'ı bir alt düğümde, %60'ı ise diğer alt düğümdedir. Bu nedenle:

• alt düğümlerin ağırlıklı entropi toplamı = (0,4 * 0,2) + (0,6 * 0,1) = 0,14

Bu nedenle, bilgi kazancı şöyledir:

• bilgi kazancı = üst düğümün entropisi - alt düğümlerin ağırlıklı entropi toplamı
• bilgi kazancı = 0,6 - 0,14 = 0,46

Çoğu bölücü, bilgi kazanımını en üst düzeye çıkaran koşullar oluşturmayı amaçlar.

değerlendiriciler arası uyum

#Metric

İnsan derecelendirme uzmanlarının bir görevi yaparken ne sıklıkta aynı fikirde olduğunun ölçüsü. Değerlendirme uzmanları aynı fikirde değilse görev talimatlarının iyileştirilmesi gerekebilir. Bazen yorumcular arası anlaşma veya değerlendirmeler arası güvenilirlik olarak da adlandırılır. Ayrıca, en popüler gözlemciler arası anlaşma ölçümlerinden biri olan Cohen's kappa'ya bakın.

Daha fazla bilgi için Makine Öğrenimine Giriş Kursu'ndaki Kategorik veriler: Yaygın sorunlar bölümüne bakın.

L

L₁ kaybı

#fundamentals

#Metric

Gerçek etiket değerleri ile modelin tahmin ettiği değerler arasındaki farkın mutlak değerini hesaplayan bir kayıp işlevi. Örneğin, beş örnekten oluşan bir toplu işlem için L₁ kaybının hesaplanması aşağıda verilmiştir:

Örneğin gerçek değeri	Modelin tahmini değeri	Delta'nın mutlak değeri
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 kaybı

L₁ kaybı, L₂ kaybına kıyasla aykırı değerlere karşı daha az hassastır.

Ortalama mutlak hata, örnek başına ortalama _L1 kaybıdır.

Resmi matematiksel ifadeyi görmek için simgeyi tıklayın.

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

where:

• $n$, örnek sayısıdır.
• $y$, etiketin gerçek değeridir.
• $\hat{y}$, modelin $y$ için tahmin ettiği değerdir.

---

Daha fazla bilgi için Makine Öğrenimine Giriş Kursu'ndaki Doğrusal Regresyon: Kayıp bölümüne bakın.

L₂ kaybı

#fundamentals

#Metric

Gerçek etiket değerleri ile modelin tahmin ettiği değerler arasındaki farkın karesini hesaplayan bir kayıp işlevi. Örneğin, beş örnekten oluşan bir toplu işlem için L₂ kaybının hesaplanması aşağıda verilmiştir:

Örneğin gerçek değeri	Modelin tahmini değeri	Delta kare
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = L2 kaybı

Kare alma işlemi nedeniyle L₂ kaybı, aykırı değerlerin etkisini artırır. Yani L₂ kaybı, kötü tahminlere L₁ kaybından daha güçlü tepki verir. Örneğin, önceki toplu iş için L₁ kaybı 16 yerine 8 olur. 16 aykırı değerden 9'unun tek bir aykırı değerden kaynaklandığına dikkat edin.

Regresyon modelleri genellikle kayıp işlevi olarak L₂ kaybını kullanır.

Ortalama Karesel Hata, örnek başına ortalama _L2 kaybıdır. Kare kaybı, L₂ kaybının diğer adıdır.

Resmi matematiksel ifadeyi görmek için simgeyi tıklayın.

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

where:

• $n$, örnek sayısıdır.
• $y$, etiketin gerçek değeridir.
• $\hat{y}$, modelin $y$ için tahmin ettiği değerdir.

---

Daha fazla bilgi için Makine Öğrenimine Giriş Kursu'ndaki Lojistik regresyon: Kayıp ve düzenlileştirme bölümüne bakın.

LLM değerlendirmeleri (evals)

#generativeAI

#Metric

Büyük dil modellerinin (LLM'ler) performansını değerlendirmeye yönelik bir dizi metrik ve karşılaştırma. Özetle, LLM değerlendirmeleri:

• Araştırmacıların, LLM'lerin iyileştirilmesi gereken alanları belirlemesine yardımcı olun.
• Farklı büyük dil modellerini karşılaştırmak ve belirli bir görev için en iyi büyük dil modelini belirlemek amacıyla kullanılır.
• Büyük dil modellerinin güvenli ve etik bir şekilde kullanılmasını sağlamaya yardımcı olur.

Daha fazla bilgi için Makine Öğrenimi Hızlandırılmış Kursu'ndaki Büyük dil modelleri (LLM'ler) bölümüne bakın.

mağlubiyet

#fundamentals

#Metric

Gözetimli bir modelin eğitimi sırasında, modelin tahmininin etiketinden ne kadar uzak olduğunu gösteren bir ölçü.

Kayıp işlevi, kaybı hesaplar.

Daha fazla bilgi için Makine Öğrenimine Giriş Kursu'ndaki Doğrusal regresyon: Kayıp bölümüne bakın.

kayıp fonksiyonu

#fundamentals

#Metric

Eğitim veya test sırasında, bir örnek grubu üzerindeki kaybı hesaplayan matematiksel bir işlev. Bir kayıp işlevi, iyi tahminler yapan modeller için kötü tahminler yapan modellere göre daha düşük bir kayıp değeri döndürür.

Eğitimin amacı genellikle bir kayıp işlevinin döndürdüğü kaybı en aza indirmektir.

Birçok farklı türde kayıp fonksiyonu vardır. Oluşturduğunuz model türü için uygun kayıp işlevini seçin. Örneğin:

• L₂ kaybı (veya karesi alınmış ortalama hata), doğrusal regresyon için kayıp işlevidir.
• Log Loss, lojistik regresyon için kayıp işlevidir.

A

Ortalama mutlak hata (MAE)

#Metric

L₁ kaybı kullanıldığında örnek başına ortalama kayıp. Ortalama mutlak hatayı aşağıdaki şekilde hesaplayın:

1. Bir toplu iş için L₁ kaybını hesaplayın.
2. L₁ kaybını gruptaki örnek sayısına bölün.

Resmi matematiksel ifadeyi görmek için simgeyi tıklayın.

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

Bu örnekte:

• $n$, örnek sayısıdır.
• $y$, etiketin gerçek değeridir.
• $\hat{y}$, modelin $y$ için tahmin ettiği değerdir.

---

Örneğin, aşağıdaki beş örnekten oluşan toplu işlemde L₁ kaybının hesaplanmasını ele alalım:

Örneğin gerçek değeri	Modelin tahmini değeri	Kayıp (gerçek ve tahmin edilen değer arasındaki fark)
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = L1 kaybı

Bu nedenle, L₁ kaybı 8 ve örnek sayısı 5'tir. Bu nedenle, ortalama mutlak hata şöyledir:

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

Ortalama mutlak hatayı ortalama karesel hata ve kök ortalama karesel hata ile karşılaştırın.

k'da ortalama hassasiyet (mAP@k)

#generativeAI

#Metric

Bir doğrulama veri kümesindeki tüm k değerinde ortalama hassasiyet puanlarının istatistiksel ortalaması. k'da ortalama hassasiyetin bir kullanım alanı, öneri sistemi tarafından oluşturulan önerilerin kalitesini değerlendirmektir.

"Ortalama" ifadesi gereksiz gibi görünse de metriğin adı uygundur. Bu metrik, birden fazla k değerinde ortalama kesinlik değerinin ortalamasını bulur.

Örnek görmek için simgeyi tıklayın.

Her kullanıcı için kişiselleştirilmiş bir önerilen romanlar listesi oluşturan bir öneri sistemi oluşturduğunuzu varsayalım. Seçilen kullanıcılardan alınan geri bildirimlere göre aşağıdaki beş ortalama duyarlılık@k puanını hesaplarsınız (kullanıcı başına bir puan):

• 0,73
• 0,77
• 0,67
• 0,82
• 0,76

Bu nedenle, K'daki ortalama hassasiyet şu şekildedir:

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

Ortalama Karesel Hata (MSE)

#Metric

L₂ kaybı kullanıldığında örnek başına ortalama kayıp. Ortalama karesel hatayı aşağıdaki şekilde hesaplayın:

1. Bir toplu iş için L₂ kaybını hesaplayın.
2. L₂ kaybını toplu işteki örnek sayısına bölün.

Resmi matematiksel ifadeyi görmek için simgeyi tıklayın.

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ where:

• $n$, örnek sayısıdır.
• $y$, etiketin gerçek değeridir.
• $\hat{y}$, modelin $y$ için tahminidir.

---

Örneğin, aşağıdaki beş örneklik gruptaki kaybı göz önünde bulundurun:

Gerçek değer	Modelin tahmini	Kayıp	Karesel kayıp
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			16 = L2 kaybı

Bu nedenle, ortalama karesel hata şöyledir:

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

Ortalama karesel hata, özellikle doğrusal regresyon için popüler bir eğitim optimizasyon aracıdır.

Karesel ortalama hatayı ortalama mutlak hata ve kök ortalama kare hatası ile karşılaştırın.

TensorFlow Playground, kayıp değerlerini hesaplamak için ortalama kare hatayı kullanır.

Aykırı değerler hakkında daha fazla ayrıntı görmek için simgeyi tıklayın.

Aykırı değerler, Ortalama Karesel Hatayı büyük ölçüde etkiler. Örneğin, 1 kaybı 1'in karesi olan kayıptır ancak 3 kaybı 9'un karesi olan kayıptır. Önceki tabloda, yaklaşık% 56'lık bir Ortalama Karesel Hata için 3 hesap kaybı olan örnek, 1 hesap kaybı olan örneklerin her biri ise Ortalama Karesel Hata'nın yalnızca% 6'sını oluşturmaktadır.

Aykırı değerler, Ortalama Mutlak Hatayı Ortalama Karesel Hata kadar etkilemez. Örneğin, yalnızca ortalama mutlak hatanın yaklaşık% 38'i için 3 hesap kaybı.

Kırpma, uç değerlerin modelinizin tahmin yeteneğine zarar vermesini önlemenin bir yoludur.

---

metrik

#TensorFlow

#Metric

Önemsediğiniz bir istatistik.

Hedef, makine öğrenimi sisteminin optimize etmeye çalıştığı bir metriktir.

Metrics API (tf.metrics)

#Metric

Modelleri değerlendirmek için kullanılan bir TensorFlow API'si. Örneğin, tf.metrics.accuracy, bir modelin tahminlerinin etiketlerle ne sıklıkta eşleştiğini belirler.

minimax kaybı

#Metric

Üretilen verilerin dağıtımı ile gerçek veriler arasındaki çapraz entropiye dayalı olarak üretken karşıt ağlar için bir kayıp işlevi.

Minimax kaybı, üretken rakip ağları açıklamak için ilk makalede kullanılmıştır.

Daha fazla bilgi için Üretken Çekişmeli Ağlar kursundaki Kayıp İşlevleri bölümüne bakın.

model kapasitesi

#Metric

Bir modelin öğrenebileceği sorunların karmaşıklığı. Bir modelin öğrenebileceği sorunlar ne kadar karmaşıksa modelin kapasitesi de o kadar yüksek olur. Bir modelin kapasitesi genellikle model parametrelerinin sayısıyla artar. Sınıflandırma modeli kapasitesinin resmi tanımı için VC boyutu başlıklı makaleye bakın.

H

negatif sınıf

#fundamentals

#Metric

İkili sınıflandırmada bir sınıfa pozitif, diğerine ise negatif adı verilir. Pozitif sınıf, modelin test ettiği şey veya etkinliktir. Negatif sınıf ise diğer olasılıktır. Örneğin:

• Bir tıbbi testteki negatif sınıf "tümör yok" olabilir.
• Bir e-posta sınıflandırma modelindeki negatif sınıf "spam değil" olabilir.

Pozitif sınıfla karşılaştırın.

O

hedef

#Metric

Algoritmanızın optimize etmeye çalıştığı bir metrik.

amaç işlevi

#Metric

Bir modelin optimize etmeyi amaçladığı matematiksel formül veya metrik. Örneğin, doğrusal regresyon için amaç işlevi genellikle ortalama kare kaybıdır. Bu nedenle, doğrusal regresyon modeli eğitilirken eğitim, ortalama kare kaybını en aza indirmeyi amaçlar.

Bazı durumlarda amaç, hedef işlevi en üst düzeye çıkarmaktır. Örneğin, amaç işlevi doğruluksa hedef, doğruluğu en üst düzeye çıkarmaktır.

Ayrıca kayıp konusuna da bakın.

P

k'da pas (pass@k)

#Metric

Büyük dil modelinin oluşturduğu kodun (ör. Python) kalitesini belirleyen bir metrik. Daha spesifik olarak, k, oluşturulan k kod bloğundan en az birinin tüm birim testlerini geçme olasılığını gösterir.

Büyük dil modelleri, karmaşık programlama sorunları için genellikle iyi kod oluşturmakta zorlanır. Yazılım mühendisleri, büyük dil modelinden aynı sorun için birden fazla (k) çözüm üretmesini isteyerek bu soruna uyum sağlar. Ardından, yazılım mühendisleri çözümlerin her birini birim testlerine göre test eder. k'da geçme hesaplaması birim testlerinin sonucuna bağlıdır:

• Bu çözümlerden biri veya daha fazlası birim testini geçerse LLM, kod oluşturma görevini geçer.
• Çözümlerden hiçbiri birim testini geçemezse LLM, kod oluşturma görevinde başarısız olur.

k pası için formül aşağıdaki gibidir:

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

Genel olarak, k değerleri ne kadar yüksek olursa k'da geçme puanları da o kadar yüksek olur. Ancak k değerleri ne kadar yüksek olursa büyük dil modeli ve birim testi kaynakları da o kadar fazla gerekir.

Örnek için simgeyi tıklayın.

Bir yazılım mühendisinin, büyük bir dil modelinden n=50 zorlu kodlama sorunu için k=10 çözüm oluşturmasını istediğini varsayalım. Sonuçlar:

• 30 kart
• 20 Başarısız

Bu nedenle, 10 puanlık geçme notu:

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

performans

#Metric

Aşağıdaki anlamlara sahip aşırı yüklenmiş terim:

• Yazılım mühendisliğindeki standart anlam. Örneğin: Bu yazılım ne kadar hızlı (veya verimli) çalışıyor?
• Makine öğrenimindeki anlamı. Burada performans, şu soruyu yanıtlar: Bu model ne kadar doğru? Yani modelin tahminleri ne kadar iyi?

permütasyon değişkeni önemleri

#df

#Metric

Özellik değerleri permütasyonundan sonra bir modelin tahmin hatasındaki artışı değerlendiren bir değişken önem derecesi türü. Permütasyonlu değişken önemi, modelden bağımsız bir metriktir.

şaşkınlık

#Metric

Bir modelin görevini ne kadar iyi yerine getirdiğinin bir ölçüsüdür. Örneğin, görevinizin bir kullanıcının telefon klavyesinde yazdığı kelimenin ilk birkaç harfini okumak ve olası tamamlama kelimelerinin bir listesini sunmak olduğunu varsayalım. Bu görev için şaşkınlık (P), listenizin kullanıcının yazmaya çalıştığı gerçek kelimeyi içermesi için sunmanız gereken tahminlerin sayısıdır.

Perplexity, çapraz entropi ile şu şekilde ilişkilidir:

$$P= 2^{-\text{cross entropy}}$$

pozitif sınıf

#fundamentals

#Metric

Test ettiğiniz sınıf.

Örneğin, bir kanser modelindeki pozitif sınıf "tümör" olabilir. Bir e-posta sınıflandırma modelindeki pozitif sınıf "spam" olabilir.

Negatif sınıfla karşılaştırın.

Ek notlar için simgeyi tıklayın.

Birçok testin "pozitif" sonucu genellikle istenmeyen bir sonuç olduğundan pozitif sınıf terimi kafa karıştırıcı olabilir. Örneğin, birçok tıbbi testte pozitif sınıf, tümörlere veya hastalıklara karşılık gelir. Genel olarak, doktorun size "Tebrikler! Test sonuçlarınız negatif çıktı." Bununla birlikte, pozitif sınıf, testin bulmaya çalıştığı etkinliktir.

Açıkçası, hem pozitif hem de negatif sınıflar için aynı anda test yapıyorsunuz.

---

PR AUC (PR eğrisinin altındaki alan)

#Metric

Farklı sınıflandırma eşiği değerleri için (geri çağırma, hassasiyet) noktaları çizilerek elde edilen, enterpolasyonlu hassasiyet/geri çağırma eğrisinin altındaki alan.

precision

#fundamentals

#Metric

Aşağıdaki soruyu yanıtlayan sınıflandırma modelleri için bir metrik:

Model pozitif sınıfı tahmin ettiğinde tahminlerin yüzde kaçı doğruydu?

Formül şu şekildedir:

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

Bu örnekte:

• Gerçek pozitif, modelin pozitif sınıfı doğru tahmin ettiği anlamına gelir.
• Yanlış pozitif, modelin pozitif sınıfı yanlışlıkla tahmin ettiği anlamına gelir.

Örneğin, bir modelin 200 pozitif tahminde bulunduğunu varsayalım. Bu 200 pozitif tahminden:

• 150'si gerçek pozitifti.
• 50'si yanlış pozitifti.

Bu durumda:

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

Doğruluk ve geri çağırma ile karşılaştırın.

Daha fazla bilgi için Makine Öğrenimine Giriş Kursu'ndaki Sınıflandırma: Doğruluk, geri çağırma, hassasiyet ve ilgili metrikler bölümüne bakın.

k değerinde hassasiyet (precision@k)

#Metric

Sıralanmış (sıralı) öğe listesini değerlendirmek için kullanılan bir metrik. k'daki duyarlık, listedeki ilk k öğeden "alakalı" olanların oranını tanımlar. Yani:

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

k değeri, döndürülen listenin uzunluğundan küçük veya ona eşit olmalıdır. Döndürülen listenin uzunluğunun hesaplamaya dahil olmadığını unutmayın.

Alaka düzeyi genellikle özneldir. Hatta uzman insan değerlendiriciler bile hangi öğelerin alakalı olduğu konusunda çoğu zaman anlaşamaz.

Şununla karşılaştır:

• k'daki ortalama hassasiyet
• k değerinde ortalama hassasiyet

Örnek görmek için simgeyi tıklayın.

Bir büyük dil modeline aşağıdaki sorgunun verildiğini varsayalım:

List the 6 funniest movies of all time in order.

Büyük dil modeli, aşağıdaki tablonun ilk iki sütununda gösterilen listeyi döndürür:

Konum	Film	Alakalı mı?
1	The General	Evet
2	Kötü	Evet
3	Platoon	Hayır
4	Nedimeler	Evet
5	Yurttaş Kane	Hayır
6	This is Spinal Tap	Evet

İlk üç filmden ikisi alakalı olduğundan 3'teki kesinlik şöyledir:

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

İlk beş filmden üçü çok komik olduğundan 5'teki kesinlik şöyledir:

$$\text{precision at 5} = \frac{\text{3}} {\text{5}} = 0.6$$

---

hassasiyet-geri çağırma eğrisi

#Metric

Farklı sınıflandırma eşiklerinde hassasiyet ile geri çağırma arasındaki dengeyi gösteren bir eğri.

tahmin önyargısı

#Metric

Veri kümesindeki tahminlerin ortalaması ile etiketlerin ortalaması arasındaki farkı gösteren değer.

Makine öğrenimi modellerindeki yanlılık terimi veya etik ve adalet bağlamındaki yanlılıkla karıştırılmamalıdır.

tahmini eşitlik

#responsible

#Metric

Belirli bir sınıflandırma modeli için dikkate alınan alt gruplarda hassasiyet oranlarının eşdeğer olup olmadığını kontrol eden bir adalet metriği.

Örneğin, üniversite kabulünü tahmin eden bir model, Lilliputlular ve Brobdingnaglılar için kesinlik oranı aynıysa milliyet açısından tahmini eşitliği karşılar.

Tahmini fiyat paritesi bazen tahmini oran paritesi olarak da adlandırılır.

Tahmini eşitlik hakkında daha ayrıntılı bilgi için "Adalet Tanımları Açıklaması" (bölüm 3.2.1) başlıklı makaleyi inceleyin.

tahmini fiyat eşitliği

#responsible

#Metric

Tahmini eşlik için kullanılan başka bir ad.

olasılık yoğunluk fonksiyonu

#Metric

Tam olarak belirli bir değere sahip veri örneklerinin sıklığını belirleyen bir işlev. Bir veri kümesinin değerleri sürekli kayan nokta sayıları olduğunda tam eşleşmeler nadiren gerçekleşir. Ancak x değerinden y değerine kadar bir olasılık yoğunluk işlevinin entegrasyonu, x ile y arasındaki veri örneklerinin beklenen sıklığını verir.

Örneğin, ortalaması 200 ve standart sapması 30 olan normal bir dağılımı ele alalım. 211,4 ile 218,7 aralığına giren veri örneklerinin beklenen sıklığını belirlemek için normal dağılımın olasılık yoğunluk işlevini 211,4 ile 218,7 arasında entegre edebilirsiniz.

R

hatırlanabilirlik

#fundamentals

#Metric

Aşağıdaki soruyu yanıtlayan sınıflandırma modelleri için bir metrik:

Kesin referans pozitif sınıf olduğunda model, tahminlerin yüzde kaçını doğru şekilde pozitif sınıf olarak tanımladı?

Formül şu şekildedir:

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

Bu örnekte:

• Gerçek pozitif, modelin pozitif sınıfı doğru tahmin ettiği anlamına gelir.
• Yanlış negatif, modelin yanlışlıkla negatif sınıfı tahmin ettiği anlamına gelir.

Örneğin, modelinizin kesin referansın pozitif sınıf olduğu örnekler üzerinde 200 tahmin yaptığını varsayalım. Bu 200 tahminden:

• 180'i doğru pozitifti.
• 20'si yanlış negatifti.

Bu durumda:

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

Sınıf dengesizliği olan veri kümeleriyle ilgili notlar için simgeyi tıklayın.

Geri çağırma, özellikle pozitif sınıfın nadir olduğu sınıflandırma modellerinin tahmin gücünü belirlemek için kullanışlıdır. Örneğin, belirli bir hastalığın pozitif sınıfının bir milyon hastadan yalnızca 10'unda görüldüğü bir sınıf dengesizliği olan veri kümesini ele alalım. Modelinizin, aşağıdaki sonuçları veren beş milyon tahmin yaptığını varsayalım:

• 30 Gerçek Pozitif
• 20 Yanlış Negatif
• 4.999.000 Gerçek Negatif
• 950 yanlış pozitif

Bu modelin geri çağırma işlemi şu şekilde yapılır:

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

Buna karşılık, bu modelin doğruluğu:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

Bu yüksek doğruluk değeri etkileyici görünse de aslında anlamsızdır. Geri çağırma, sınıf dengesizliği olan veri kümeleri için doğruluktan çok daha kullanışlı bir metriktir.

---

Daha fazla bilgi için Sınıflandırma: Doğruluk, geri çağırma, hassasiyet ve ilgili metrikler başlıklı makaleyi inceleyin.

k değerinde geri çağırma (recall@k)

#Metric

Öğelerin sıralanmış (düzenli) listesini çıkaran sistemleri değerlendirmek için kullanılan bir metrik. k konumundaki hatırlama, döndürülen alakalı öğelerin toplam sayısı içindeki listede yer alan ilk k öğedeki alakalı öğelerin oranını tanımlar.

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

k ile kontrast oluşturun.

Örnek görmek için simgeyi tıklayın.

Bir büyük dil modeline aşağıdaki sorgunun verildiğini varsayalım:

List the 10 funniest movies of all time in order.

Büyük dil modeli, ilk iki sütunda gösterilen listeyi döndürür:

Konum	Film	Alakalı mı?
1	The General	Evet
2	Kötü	Evet
3	Platoon	Hayır
4	Nedimeler	Evet
5	This is Spinal Tap	Evet
6	Airplane!	Evet
7	Groundhog Day	Evet
8	Monty Python and the Holy Grail	Evet
9	Oppenheimer	Hayır
10	Clueless	Evet

Önceki listedeki sekiz film çok komik olduğu için "listedeki alakalı öğeler" olarak kabul edilir. Bu nedenle, k'daki tüm hatırlama hesaplamalarında payda 8 olur. Peki ya pay? İlk 4 öğeden 3'ü alakalı olduğundan 4 öğe için hatırlama oranı:

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

İlk 8 filmin 7'si çok komik. Bu nedenle 8. filmde hatırlama oranı:

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

ROC (alıcı çalışma özelliği) eğrisi

#fundamentals

#Metric

İkili sınıflandırmada farklı sınıflandırma eşikleri için gerçek pozitif oranı ile yanlış pozitif oranı arasındaki ilişkiyi gösteren grafik.

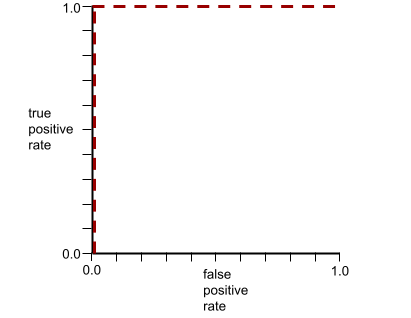
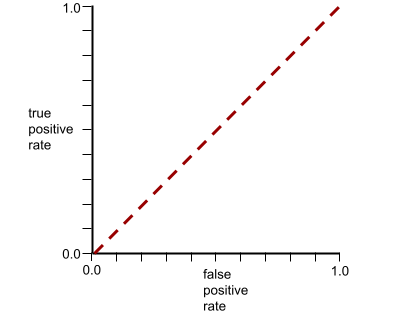
ROC eğrisinin şekli, ikili sınıflandırma modelinin pozitif sınıfları negatif sınıflardan ayırma yeteneğini gösterir. Örneğin, ikili sınıflandırma modelinin tüm negatif sınıfları tüm pozitif sınıflardan mükemmel şekilde ayırdığını varsayalım:

Önceki modelin ROC eğrisi aşağıdaki gibi görünür:

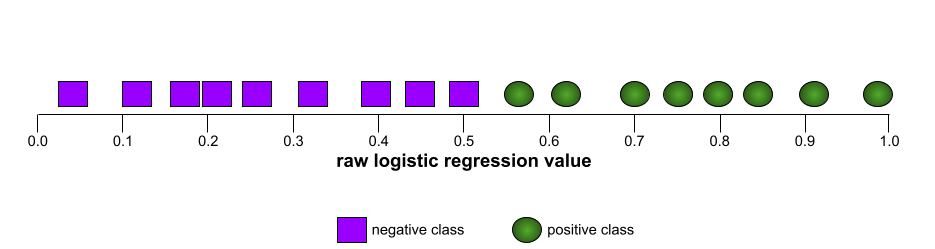
Buna karşılık, aşağıdaki resimde, negatif sınıfları pozitif sınıflardan hiç ayıramayan kötü bir modelin ham lojistik regresyon değerleri grafik olarak gösterilmektedir:

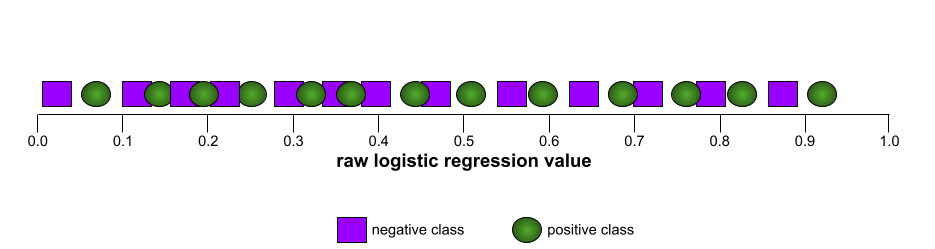
Bu modelin ROC eğrisi aşağıdaki gibi görünür:

Bu arada, gerçek hayatta çoğu ikili sınıflandırma modeli pozitif ve negatif sınıfları bir dereceye kadar ayırır ancak genellikle mükemmel bir şekilde değil. Bu nedenle, tipik bir ROC eğrisi iki uç nokta arasında bir yerde bulunur:

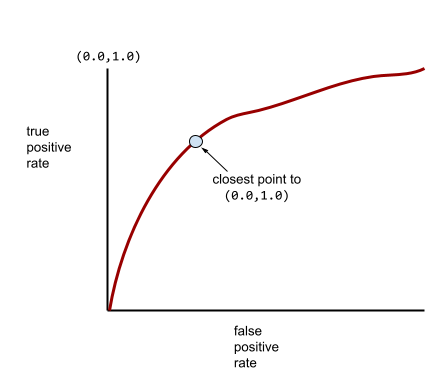
Bir ROC eğrisinde (0.0,1.0) noktasına en yakın olan nokta, teorik olarak ideal sınıflandırma eşiğini tanımlar. Ancak ideal sınıflandırma eşiğinin seçilmesini etkileyen başka gerçek dünya sorunları da vardır. Örneğin, yanlış negatif sonuçlar, yanlış pozitif sonuçlardan çok daha fazla sorun yaratabilir.

AUC adı verilen sayısal bir metrik, ROC eğrisini tek bir kayan nokta değeriyle özetler.

Kök Ortalama Kare Hatası (RMSE)

#fundamentals

#Metric

Ortalama karesel hatanın karekökü.

ROUGE (Recall-Oriented Understudy for Gisting Evaluation)

#Metric

Otomatik özetleme ve makine çevirisi modellerini değerlendiren bir metrik ailesi. ROUGE metrikleri, referans metnin bir makine öğrenimi modelinin oluşturduğu metinle ne kadar örtüştüğünü belirler. ROUGE ailesinin her üyesi, çakışmayı farklı şekilde ölçer. ROUGE puanları ne kadar yüksek olursa referans metin ile oluşturulan metin arasındaki benzerlik o kadar fazla olur.

Her ROUGE ailesi üyesi genellikle aşağıdaki metrikleri oluşturur:

• Hassasiyet
• Geri çağırma
• F₁

Not: ROUGE, hassasiyeti ve geri çağırmayı geleneksel hassasiyet ve geri çağırmadan biraz farklı şekilde kullanır.

Ayrıntılar ve örnekler için:

• ROUGE-L
• ROUGE-N
• ROUGE-S

Not: BLEU ve BLEURT, kesinlik için optimizasyon yaparken ROUGE, hatırlama için optimizasyon yapar. Dolayısıyla, BLEU ve BLEURT, makine çevirisini değerlendirmek için daha iyi metriklerdir (çünkü odak noktası hassasiyettir). ROUGE ise özetleme için daha iyi bir metriktir (çünkü odak noktası geri çağırmadır).

ROUGE-L

#Metric

ROUGE ailesinin bir üyesi, referans metin ve oluşturulan metindeki en uzun ortak alt dizinin uzunluğuna odaklanır. Aşağıdaki formüller, ROUGE-L için hatırlama ve kesinliği hesaplar:

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

Ardından, ROUGE-L geri çağırma ve ROUGE-L hassasiyetini tek bir metriğe toplamak için F₁'i kullanabilirsiniz:

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

ROUGE-L ile ilgili örnek hesaplama simgesini tıklayın.

Aşağıdaki referans metni ve oluşturulan metni inceleyin.

Kategori	Yapımcı kim?	Metin
Referans metin	Gerçek kişi çevirmen	Çok çeşitli konular hakkında bilgi edinmek istiyorum.
Oluşturulan metin	ML modeli	Birçok şey öğrenmek istiyorum.

Bu nedenle:

• En uzun ortak alt dizi 5'tir (I want to of things).
• Referans metindeki kelime sayısı 9.
• Oluşturulan metindeki kelime sayısı 7.

Sonuç olarak:

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

ROUGE-L, referans metindeki ve oluşturulan metindeki yeni satırları yok sayar. Bu nedenle, en uzun ortak alt dizi birden fazla cümleyi kapsayabilir. Referans metin ve oluşturulan metin birden fazla cümle içerdiğinde genellikle ROUGE-Lsum adı verilen ROUGE-L varyasyonu daha iyi bir metriktir. ROUGE-Lsum, bir pasajdaki her cümle için en uzun ortak alt diziyi belirler ve ardından bu en uzun ortak alt dizilerin ortalamasını hesaplar.

ROUGE-Lsum'un örnek hesaplaması için simgeyi tıklayın.

Aşağıdaki referans metni ve oluşturulan metni inceleyin.

Kategori	Yapımcı kim?	Metin
Referans metin	Gerçek kişi çevirmen	Mars'ın yüzeyi kurudur. Suyun neredeyse tamamı yerin derinliklerindedir.
Oluşturulan metin	ML modeli	Mars'ın yüzeyi kurudur. Ancak suyun büyük çoğunluğu yer altındadır.

Bu nedenle:

	İlk cümle	İkinci cümle
En uzun ortak dizi	2 (Mars dry)	3 (su yer altındadır)
Referans metnin cümle uzunluğu	6	7
Oluşturulan metnin cümle uzunluğu	5	8

Bu nedenle:

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#Metric

ROUGE ailesindeki bir dizi metrik, referans metin ve oluşturulan metindeki belirli boyuttaki ortak N-gramları karşılaştırır. Örneğin:

• ROUGE-1, referans metin ve oluşturulan metindeki ortak jeton sayısını ölçer.
• ROUGE-2, referans metin ve oluşturulan metindeki ortak bigram (2 gram) sayısını ölçer.
• ROUGE-3, referans metin ve oluşturulan metindeki ortak üçlü gram (3 gram) sayısını ölçer.

ROUGE-N ailesinin herhangi bir üyesi için ROUGE-N geri çağırma ve ROUGE-N kesinliğini hesaplamak üzere aşağıdaki formülleri kullanabilirsiniz:

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

Daha sonra, ROUGE-N geri çağırma ve ROUGE-N kesinliğini tek bir metrikte toplamak için F₁'i kullanabilirsiniz:

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

Örnek için simgeyi tıklayın.

Bir makine öğrenimi modelinin çevirisinin, bir çevirmenin çevirisine kıyasla ne kadar etkili olduğunu ölçmek için ROUGE-2'yi kullanmaya karar verdiğinizi varsayalım.

Kategori	Yapımcı kim?	Metin	Bigramlar
Referans metin	Gerçek kişi çevirmen	Çok çeşitli konular hakkında bilgi edinmek istiyorum.	I want, want to, to understand, understand a, a wide, wide variety, variety of, of things
Oluşturulan metin	ML modeli	Birçok şey öğrenmek istiyorum.	I want, want to, to learn, learn plenty, plenty of, of things

Bu nedenle:

• Eşleşen 2 gramlık birimlerin sayısı 3'tür (I want, want to ve of things).
• Referans metindeki 2 gramlık sayı 8'dir.
• Oluşturulan metindeki 2 gramlık kelime sayısı 6'dır.

Sonuç olarak:

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#Metric

ROUGE-N'nin, skip-gram eşleşmesine olanak tanıyan, daha esnek bir biçimidir. Yani ROUGE-N yalnızca tam olarak eşleşen N-gramları sayar ancak ROUGE-S, bir veya daha fazla kelimeyle ayrılmış N-gramları da sayar. Örneğin aşağıdakileri göz önünde bulundurabilirsiniz:

• referans metin: Beyaz bulutlar
• üretilen metin: Beyaz kabarık bulutlar

ROUGE-N hesaplanırken 2 gramlık Beyaz bulutlar, Beyaz kabaran bulutlar ile eşleşmez. Ancak ROUGE-S hesaplanırken Beyaz bulutlar, Beyaz kabarık bulutlar ile eşleşir.

R-kare

#Metric

Bir etiketteki varyasyonun ne kadarının tek bir özellikten veya bir özellik grubundan kaynaklandığını gösteren regresyon metriği. Belirleme katsayısı, 0 ile 1 arasında bir değerdir ve şu şekilde yorumlanabilir:

• 0 R kare değeri, bir varyasyonun hiçbirinin özellik kümesinden kaynaklanmadığı anlamına gelir.
• Belirleme katsayısının 1 olması, bir etiketin tüm varyasyonunun özellik grubundan kaynaklandığı anlamına gelir.
• 0 ile 1 arasındaki bir R kare değeri, etiketin varyasyonunun belirli bir özellikten veya özellik kümesinden ne ölçüde tahmin edilebileceğini gösterir. Örneğin, 0,10'luk bir R kare değeri, etiketteki varyansın yüzde 10'unun özellik kümesinden kaynaklandığı anlamına gelir. 0,20'lik bir R kare değeri, yüzde 20'sinin özellik kümesinden kaynaklandığı anlamına gelir.

Belirleme katsayısı, bir modelin tahmin ettiği değerler ile kesin referans arasındaki Pearson korelasyon katsayısının karesidir.

G

puanlama

#Metric

Öneri sisteminin, aday oluşturma aşamasında üretilen her öğe için bir değer veya sıralama sağlayan kısmı.

benzerlik ölçüsü

#clustering

#Metric

Kümeleme algoritmalarında, iki örneğin ne kadar benzer olduğunu belirlemek için kullanılan metrik.

seyreklik

#Metric

Bir vektör veya matriste sıfır (ya da boş) olarak ayarlanan öğe sayısının, söz konusu vektör veya matristeki toplam giriş sayısına bölünmesiyle elde edilen değer. Örneğin, 98 hücresinde sıfır bulunan 100 öğelik bir matrisi ele alalım. Seyrekliği hesaplama şekli şöyledir:

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

Özellik seyrekliği, özellik vektörünün seyrekliğini ifade ederken model seyrekliği, model ağırlıklarının seyrekliğini ifade eder.

kare menteşe kaybı

#Metric

Menteşe kaybının karesi. Karesel menteşe kaybı, aykırı değerleri normal menteşe kaybına kıyasla daha sert şekilde cezalandırır.

kare kaybı

#fundamentals

#Metric

L₂ kaybı ile eş anlamlıdır.

T

test kaybı

#fundamentals

#Metric

Bir modelin test kümesine karşı kaybını temsil eden bir metrik. Model oluştururken genellikle test kaybını en aza indirmeye çalışırsınız. Bunun nedeni, düşük test kaybının düşük eğitim kaybı veya düşük doğrulama kaybından daha güçlü bir kalite sinyali olmasıdır.

Test kaybı ile eğitim kaybı veya doğrulama kaybı arasında büyük bir fark olması bazen düzenlileştirme oranını artırmanız gerektiğini gösterir.

top-k doğruluğu

#Metric

Oluşturulan listelerin ilk k konumunda "hedef etiketin" görünme yüzdesi. Listeler, kişiselleştirilmiş öneriler veya softmax'a göre sıralanmış öğelerden oluşabilir.

Top-k doğruluğu, k'da doğruluk olarak da bilinir.

Not: Hedef etiketi herhangi bir sınıf olabilir (mutlaka gerçek sınıfı olmak zorunda değildir). Bu nedenle, top-k doğruluğu her zaman geleneksel doğruluğa eşdeğer değildir.

Örnek için simgeyi tıklayın.

Ağaç yapraklarının resmine göre ağaç olasılıklarını belirlemek için softmax kullanan bir makine öğrenimi sistemi düşünün. Aşağıdaki tabloda, beş giriş ağacı resminden oluşturulan çıkış listeleri gösterilmektedir. Her satırda bir hedef etiketi ve olasılığı en yüksek beş ağaç bulunur. Örneğin, hedef etiket maple olduğunda makine öğrenimi modeli, en olası ağaç olarak elm, ikinci en olası ağaç olarak oak vb. olarak tanımladı.

Hedef etiketi	1	2	3	4	5
Maple	elm	meşe	maple	kayın	kavak
kızılcık	meşe	dogwood	kavak	Hickory	Maple
meşe	meşe	ıhlamur ağacı	çekirge	alder	Linden
Linden	Maple	paw-paw	meşe	ıhlamur ağacı	kavak
meşe	çekirge	Linden	meşe	Maple	paw-paw

Hedef etiketi yalnızca bir kez ilk konumda göründüğünden ilk 1 doğruluk oranı şöyledir:

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

Hedef etiketi, ilk üç konumdan birinde dört kez göründüğünden ilk 3'teki doğruluk oranı şöyledir:

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

toksik

#Metric

İçeriğin kötüye kullanım, tehdit veya rahatsız edici olma derecesi Birçok makine öğrenimi modeli, toksisiteyi tanımlayıp ölçebilir. Bu modellerin çoğu, toksisiteyi birden fazla parametreye göre (ör. kötüye kullanım amaçlı dil düzeyi ve tehdit edici dil düzeyi) tanımlar.

eğitim kaybı

#fundamentals

#Metric

Belirli bir eğitim yinelemesi sırasında modelin kaybını temsil eden bir metrik. Örneğin, kayıp işlevinin ortalama kare hatası olduğunu varsayalım. Örneğin, 10.yinelemede eğitim kaybı (ortalama kare hatası) 2,2 ve 100.yinelemede eğitim kaybı 1,9 olabilir.

Kayıp eğrisi, eğitim kaybını yineleme sayısına karşı çizer. Bir kayıp eğrisi, eğitimle ilgili aşağıdaki ipuçlarını sağlar:

• Aşağı doğru eğim, modelin iyileştiğini gösterir.
• Yukarı doğru eğim, modelin kötüleştiğini gösterir.
• Düz bir eğim, modelin yakınsama noktasına ulaştığını gösterir.

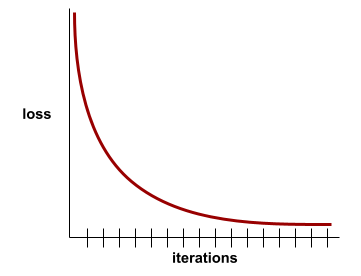
Örneğin, aşağıdaki biraz idealize edilmiş kayıp eğrisi şunları gösterir:

• İlk yinelemeler sırasında hızlı model iyileştirmesini ifade eden dik bir aşağı eğim.
• Eğitim sona erene kadar kademeli olarak düzleşen (ancak yine de aşağı doğru) bir eğim. Bu, ilk yinelemelerdeki hızdan biraz daha yavaş bir hızda modelin iyileşmeye devam ettiğini gösterir.
• Eğitimin sonuna doğru düz bir eğim, yakınsama olduğunu gösterir.

Eğitim kaybı önemli olsa da genelleme konusuna da göz atın.

doğru negatif (TN)

#fundamentals

#Metric

Modelin negatif sınıfı doğru şekilde tahmin ettiği bir örnek. Örneğin, model belirli bir e-posta iletisinin spam olmadığını çıkarır ve bu e-posta iletisi gerçekten spam değildir.

Gerçek pozitif (TP)

#fundamentals

#Metric

Modelin pozitif sınıfı doğru tahmin ettiği bir örnek. Örneğin, model belirli bir e-posta iletisinin spam olduğunu çıkarımlıyor ve bu e-posta iletisi gerçekten spam oluyor.

Gerçek pozitif oranı (TPR)

#fundamentals

#Metric

Geri çağırma ile eş anlamlıdır. Yani:

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

Gerçek pozitif oranı, ROC eğrisindeki y eksenidir.

V

doğrulama kaybı

#fundamentals

#Metric

Eğitimin belirli bir iterasyonu sırasında doğrulama kümesindeki bir modelin kaybını temsil eden bir metrik.

Ayrıca genelleştirme eğrisini de inceleyin.

değişken önemleri

#df

#Metric

Her bir özelliğin model için göreli önemini gösteren bir puan grubu.

Örneğin, ev fiyatlarını tahmin eden bir karar ağacını ele alalım. Bu karar ağacının üç özellik kullandığını varsayalım: boyut, yaş ve stil. Üç özellik için değişken önem düzeyleri kümesi {size=5.8, age=2.5, style=4.7} olarak hesaplanırsa boyut, karar ağacı için yaş veya stilden daha önemlidir.

Farklı değişken önem metrikleri vardır. Bu metrikler, makine öğrenimi uzmanlarını modellerin farklı yönleri hakkında bilgilendirebilir.

W

Wasserstein kaybı

#Metric

Üretilen verilerin dağıtımı ile gerçek veriler arasındaki toprak taşıyıcının mesafesine dayalı olarak üretken çekişmeli ağlarda yaygın olarak kullanılan kayıp işlevlerinden biridir.