مسرد تعلُّم الآلة: المقاييس

تحتوي هذه الصفحة على مصطلحات مسرد المقاييس. للاطّلاع على جميع مصطلحات المسرد، يُرجى النقر هنا.

A

الدقة

#fundamentals

#Metric

عدد التوقّعات الصحيحة للتصنيف مقسومًا على إجمالي عدد التوقّعات والمقصود:

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

على سبيل المثال، إذا قدّم نموذج 40 توقّعًا صحيحًا و10 توقّعات غير صحيحة، ستكون دقة النموذج كما يلي:

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

يقدّم التصنيف الثنائي أسماء محدّدة لمختلف فئات التوقعات الصحيحة والتوقعات غير الصحيحة. وبالتالي، تكون صيغة الدقة للتصنيف الثنائي كما يلي:

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

where:

• TP هو عدد الحالات الموجبة الصحيحة (التوقّعات الصحيحة).
• TN هو عدد الحالات السالبة الصحيحة (التوقعات الصحيحة).
• FP هو عدد الحالات الموجبة الخاطئة (التوقعات غير الصحيحة).
• FN هو عدد الحالات السالبة الخاطئة (التوقعات غير الصحيحة).

تحديد أوجه التشابه والاختلاف بين الدقة والضبط والاسترجاع

انقر على الرمز للحصول على تفاصيل حول الدقة ومجموعات البيانات غير المتوازنة بين الفئات.

على الرغم من أنّ الدقة مقياس قيّم في بعض الحالات، إلا أنّها تكون مضلّلة للغاية في حالات أخرى. يُذكر أنّ الدقة عادةً ما تكون مقياسًا غير مناسب لتقييم نماذج التصنيف التي تعالج مجموعات بيانات غير متوازنة الفئات.

على سبيل المثال، لنفترض أنّ الثلوج تتساقط في مدينة شبه استوائية معيّنة لمدة 25 يومًا فقط في القرن. بما أنّ عدد الأيام التي لم تتساقط فيها الثلوج (الفئة السلبية) يفوق بكثير عدد الأيام التي تساقطت فيها الثلوج (الفئة الإيجابية)، فإنّ مجموعة بيانات الثلوج الخاصة بهذه المدينة غير متوازنة الفئات. لنفترض أنّ هناك نموذج تصنيف ثنائي من المفترض أن يتنبأ بما إذا كان سيتساقط الثلج أم لا كل يوم، ولكنّه يتنبأ ببساطة بأنّه "لن يتساقط الثلج" كل يوم. هذا النموذج دقيق للغاية ولكن ليس لديه القدرة على التوقّع. يلخّص الجدول التالي النتائج لقرن من التوقعات:

الفئة	العدد
TP	0
تونس	36499
FP	0
FN	25

وبالتالي، تكون دقة هذا النموذج كما يلي:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

على الرغم من أنّ نسبة الدقة البالغة 99.93% تبدو نسبة مذهلة، إلا أنّ النموذج لا يتمتع في الواقع بأي قدرة على التنبؤ.

عادةً ما يكون الضبط والاسترجاع مقياسَين أكثر فائدة من الدقة لتقييم النماذج المدرَّبة على مجموعات بيانات غير متوازنة الفئات.

---

يمكنك الاطّلاع على التصنيف: الدقة والاسترجاع والضبط والمقاييس ذات الصلة في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.

المساحة تحت منحنى الدقة والاستدعاء

#Metric

اطّلِع على المساحة تحت منحنى الدقة والاسترجاع.

المساحة تحت منحنى ROC

#Metric

اطّلِع على المساحة تحت منحنى ROC‏ (AUC).

المساحة تحت منحنى ROC

#fundamentals

#Metric

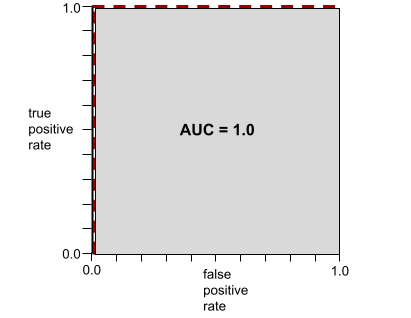
رقم يتراوح بين 0.0 و1.0 يمثّل قدرة نموذج التصنيف الثنائي على فصل الفئات الإيجابية عن الفئات السلبية. كلما اقتربت قيمة AUC من 1.0، كانت قدرة النموذج على فصل الفئات عن بعضها البعض أفضل.

على سبيل المثال، توضّح الصورة التالية نموذج تصنيف يفصل تمامًا بين الفئات الإيجابية (الدوائر الخضراء) والفئات السلبية (المستطيلات الأرجوانية). يحتوي هذا النموذج المثالي بشكل غير واقعي على قيمة AUC تبلغ 1.0:

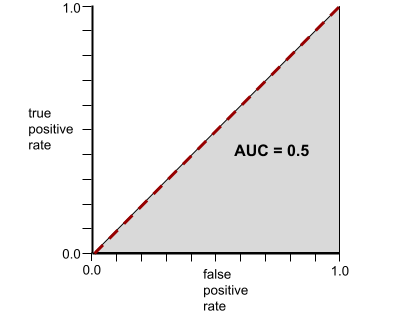
في المقابل، يوضّح الرسم التوضيحي التالي نتائج نموذج تصنيف أنشأ نتائج عشوائية. يحتوي هذا النموذج على قيمة AUC تبلغ 0.5:

نعم، النموذج السابق لديه قيمة AUC تبلغ 0.5، وليس 0.0.

وتقع معظم النماذج في مكان ما بين هذين الحدّين. على سبيل المثال، يفصل النموذج التالي بين القيم الإيجابية والسلبية إلى حد ما، وبالتالي يكون لديه قيمة AUC تتراوح بين 0.5 و1.0:

تتجاهل مقياس AUC أي قيمة تحدّدها لحدّ التصنيف. بدلاً من ذلك، تأخذ المساحة تحت منحنى ROC في الاعتبار جميع عتبات التصنيف الممكنة.

انقر على الرمز للتعرّف على العلاقة بين منحنيَي AUC وROC.

تمثّل المساحة تحت منحنى ROC المساحة تحت منحنى ROC. على سبيل المثال، يبدو منحنى ROC لنموذج يفصل الإيجابيات عن السلبيات بشكل مثالي كما يلي:

مساحة AUC هي مساحة المنطقة الرمادية في الرسم التوضيحي السابق. في هذه الحالة غير العادية، تكون المساحة ببساطة هي طول المنطقة الرمادية (1.0) مضروبًا في عرض المنطقة الرمادية (1.0). وبالتالي، فإنّ ناتج ضرب 1.0 في 1.0 يعطي قيمة AUC تساوي 1.0 بالضبط، وهي أعلى قيمة ممكنة لنتيجة AUC.

في المقابل، يكون منحنى ROC الخاص بنموذج تصنيف لا يمكنه فصل الفئات على الإطلاق على النحو التالي. مساحة هذه المنطقة الرمادية هي 0.5.

يبدو منحنى ROC الأكثر شيوعًا على النحو التالي تقريبًا:

سيكون من الصعب احتساب المساحة تحت هذا المنحنى يدويًا، ولهذا السبب يتم عادةً احتساب معظم قيم AUC باستخدام برنامج.

---

انقر على الرمز للاطّلاع على تعريف أكثر رسميةً لمصطلح "معدّل التحويل".

مساحة تحت المنحنى (AUC) هي احتمال أن يكون نموذج التصنيف أكثر ثقة في أنّ مثالاً إيجابيًا تم اختياره عشوائيًا هو إيجابي بالفعل من أن يكون مثالاً سلبيًا تم اختياره عشوائيًا هو إيجابي.

---

يمكنك الاطّلاع على التصنيف: منحنى ROC ومقياس AUC في "دورة مكثّفة عن تعلُّم الآلة" للحصول على مزيد من المعلومات.

متوسط الدقة عند k

#Metric

مقياس لتلخيص أداء نموذج بشأن طلب واحد يؤدي إلى إنشاء نتائج مرتبة، مثل قائمة مرقّمة باقتراحات كتب متوسط الدقة عند k هو، حسنًا، متوسط قيم الدقة عند k لكل نتيجة ذات صلة. وبالتالي، فإنّ صيغة متوسط الدقة عند k هي:

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

where:

• تمثّل السمة\(n\) عدد العناصر ذات الصلة في القائمة.

يختلف هذا المقياس عن الاسترجاع عند k.

ملاحظة: يقيس مقياس "متوسط الدقة عند k" الناتج الخاص بطلب واحد. استخدِم متوسط الدقة عند k لتقييم جودة نتائج النموذج في العديد من الطلبات المختلفة.

ملاحظة: يختصر بعض الأشخاص متوسط الدقة عند k إلى متوسط الدقة.

انقر على الرمز للاطّلاع على مثال

لنفترض أنّ نموذجًا لغويًا كبيرًا تلقّى طلب البحث التالي:

List the 6 funniest movies of all time in order.

ويعرض النموذج اللغوي الكبير القائمة التالية:

1. الجنرال
2. Mean Girls
3. Platoon
4. وصيفات العروس
5. المواطن كين
6. This is Spinal Tap

أربعة من الأفلام في القائمة المعروضة مضحكة جدًا (أي أنّها ذات صلة) ولكن فيلمَين دراميان (غير ذي صلة). يوضّح الجدول التالي تفاصيل النتائج:

الموضع	فيلم	هل هي ذات صلة؟	مقياس الدقة عند k
1	الجنرال	نعم	1
2	Mean Girls	نعم	1
3	Platoon	لا	غير ذي صلة
4	وصيفات العروس	نعم	0.75
5	المواطن كين	لا	غير ذي صلة
6	This is Spinal Tap	نعم	0.67

عدد النتائج ذات الصلة هو 4. وبالتالي، يمكنك حساب متوسط الدقة عند 6 على النحو التالي:

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

خط الأساس

#Metric

نموذج يُستخدَم كنقطة مرجعية لمقارنة مستوى أداء نموذج آخر (عادةً ما يكون أكثر تعقيدًا). على سبيل المثال، يمكن أن يكون نموذج الانحدار اللوجستي أساسًا جيدًا للنموذج العميق.

بالنسبة إلى مشكلة معيّنة، يساعد خط الأساس مطوّري النماذج في تحديد الحد الأدنى المتوقّع للأداء الذي يجب أن يحقّقه النموذج الجديد ليكون مفيدًا.

C

التكلفة

#Metric

مرادف لكلمة خسارة

العدالة في حالة عدم توفّر الحقائق

#responsible

#Metric

مقياس الإنصاف الذي يتحقّق مما إذا كان نموذج التصنيف يعرض النتيجة نفسها لشخص ما كما يعرضها لشخص آخر مطابق للأول، باستثناء ما يتعلق بواحدة أو أكثر من السمات الحسّاسة. يُعدّ تقييم نموذج التصنيف من حيث العدالة الواقعية الافتراضية إحدى الطرق للكشف عن المصادر المحتملة للتحيّز في النموذج.

يمكنك الاطّلاع على أيّ مما يلي لمزيد من المعلومات:

• الإنصاف: الإنصاف الافتراضي في "دورة مكثّفة حول تعلُّم الآلة"
• When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness

الإنتروبيا المتقاطعة

#Metric

تعميم فقدان السجلّ على مشاكل التصنيف المتعدد الفئات يقيس الانتروبيا المتقاطعة الفرق بين توزيعَين للاحتمالات. يمكنك الاطّلاع أيضًا على مقياس الحيرة.

دالة التوزيع التراكمي (CDF)

#Metric

دالة تحدّد عدد المرّات التي تكون فيها العيّنات أقل من قيمة مستهدَفة أو مساوية لها. على سبيل المثال، لنفترض أنّ هناك توزيعًا طبيعيًا للقيم المستمرة. يخبرك التوزيع التراكمي بأنّ% 50 تقريبًا من العيّنات يجب أن تكون أقل من أو تساوي المتوسط، وأنّ% 84 تقريبًا من العيّنات يجب أن تكون أقل من أو تساوي الانحراف المعياري الواحد فوق المتوسط.

D

التكافؤ الديمغرافي

#responsible

#Metric

مقياس العدالة الذي يتم استيفاؤه إذا كانت نتائج تصنيف النموذج لا تعتمد على سمة حساسة معيّنة.

على سبيل المثال، إذا كان كل من سكان ليليبوت وبروبدينغناغ يتقدّمون بطلبات إلى جامعة غلوبدوبدريب، يتم تحقيق التكافؤ الديموغرافي إذا كانت النسبة المئوية للطلاب المقبولين من ليليبوت هي نفسها النسبة المئوية للطلاب المقبولين من بروبدينغناغ، بغض النظر عمّا إذا كانت إحدى المجموعتين أكثر تأهيلاً من الأخرى في المتوسط.

يختلف هذا المقياس عن التكافؤ في الاحتمالات وتكافؤ الفرص، اللذين يسمحان بأن تعتمد نتائج التصنيف بشكل إجمالي على السمات الحسّاسة، ولكنّهما لا يسمحان بأن تعتمد نتائج التصنيف لبعض تصنيفات الحقيقة الأساسية المحدّدة على السمات الحسّاسة. يمكنك الاطّلاع على "مكافحة التمييز باستخدام تكنولوجيا تعلُّم الآلة الأذكى" للحصول على رسم توضيحي يستعرض المفاضلة بين الخيارات عند تحسين التكافؤ الديمغرافي.

يمكنك الاطّلاع على الإنصاف: التكافؤ الديمغرافي في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.

E

مسافة نقل التراب (EMD)

#Metric

مقياس للتشابه النسبي بين توزيعَين كلّما كانت مسافة نقل التراب أقل، تشابهت التوزيعات أكثر.

مسافة التعديل

#Metric

مقياس لمدى تشابه سلسلتَي نص مع بعضهما البعض. في التعلّم الآلي، تكون مسافة التعديل مفيدة للأسباب التالية:

• يسهل احتساب مسافة التعديل.
• يمكن أن تقارن مسافة التعديل بين سلسلتَين معروفتَين بأنّهما متشابهتَين.
• يمكن أن تحدّد مسافة التعديل درجة تشابه السلاسل المختلفة مع سلسلة معيّنة.

تتوفّر عدة تعريفات لمسافة التعديل، ويستخدم كل منها عمليات مختلفة على السلاسل. يمكنك الاطّلاع على مسافة Levenshtein للحصول على مثال.

دالة التوزيع التراكمي التجريبية (eCDF أو EDF)

#Metric

دالة التوزيع التراكمي استنادًا إلى القياسات التجريبية من مجموعة بيانات حقيقية قيمة الدالة عند أي نقطة على طول المحور س هي جزء الملاحظات في مجموعة البيانات التي تكون أقل من أو تساوي القيمة المحددة.

الإنتروبيا

#df

#Metric

في نظرية المعلومات، القصور هو وصف لمدى عدم القدرة على التنبؤ بتوزيع الاحتمالات. ويمكن تعريف القصور أيضًا بأنه مقدار المعلومات التي يحتوي عليها كل مثال. يكون التوزيع ذا أعلى إنتروبيا ممكنة عندما تكون جميع قيم المتغيّر العشوائي متساوية الاحتمالية.

إنّ إنتروبيا مجموعة تتضمّن قيمتَين محتملتَين هما "0" و "1" (على سبيل المثال، التصنيفات في مسألة تصنيف ثنائي) تخضع للصيغة التالية:

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

where:

• H هو القصور.
• p هي نسبة الأمثلة التي تكون فيها القيمة "1".
• q هي نسبة الأمثلة التي تكون فيها القيمة "0". يُرجى العِلم أنّ q = (1 - p)
• log هو بشكل عام log₂. في هذه الحالة، وحدة الإنتروبيا هي بت.

على سبيل المثال، لنفترض ما يلي:

• تحتوي 100 عينة على القيمة "1"
• تحتوي 300 عينة على القيمة "0"

وبالتالي، تكون قيمة القصور كما يلي:

• p = 0.25
• q = 0.75
• H = (-0.25)log₂(0.25) - (0.75)log₂(0.75) = 0.81 بت لكل مثال

ستكون قيمة الإنتروبيا لمجموعة متوازنة تمامًا (على سبيل المثال، 200 من القيمة "0" و200 من القيمة "1") هي 1.0 بت لكل مثال. وكلما أصبحت المجموعة أكثر عدم توازن، اقترب القصور فيها من 0.0.

في أشجار القرارات، يساعد الانتروبيا في صياغة تحصيل المعلومات لمساعدة المقسّم في اختيار الشروط أثناء نمو شجرة قرارات التصنيف.

مقارنة الإنتروبيا بما يلي:

• مقياس جيني للتفاوت
• دالة الخسارة الإنتروبيا المتداخلة

يُطلق على القصور غالبًا اسم قصور شانون.

لمزيد من المعلومات، راجِع أداة التقسيم التام للتصنيف الثنائي باستخدام الميزات الرقمية في دورة "غابات القرارات".

تكافؤ الفرص

#responsible

#Metric

مقياس الإنصاف لتقييم ما إذا كان النموذج يتوقّع النتيجة المطلوبة بشكل جيد وبالمقدار نفسه لجميع قيم السمة الحسّاسة. بعبارة أخرى، إذا كانت النتيجة المرغوبة لنموذج هي الفئة الموجبة، سيكون الهدف هو أن يكون معدّل الإيجابية الحقيقية هو نفسه لجميع المجموعات.

يرتبط تكافؤ الفرص بتكافؤ الاحتمالات، الذي يتطلّب أن يكون كلّ من معدلات الموجب الصائب ومعدلات الموجب الخاطئ متطابقًا لجميع المجموعات.

لنفترض أنّ جامعة Glubbdubdrib تقبل طلابًا من Lilliput وBrobdingnag في برنامج رياضيات صارم. تقدّم المدارس الثانوية في ليليبوت منهجًا دراسيًا قويًا في الرياضيات، ومعظم الطلاب مؤهّلون للالتحاق بالبرنامج الجامعي. لا تقدّم المدارس الثانوية في بروبدينغناغ دروسًا في الرياضيات على الإطلاق، ونتيجةً لذلك، يكون عدد الطلاب المؤهّلين أقل بكثير. تتحقّق المساواة في الفرص بالنسبة إلى التصنيف المفضّل "مقبول" فيما يتعلّق بالجنسية (ليليبوتية أو بروبدينغناغية) إذا كان الطلاب المؤهّلون متساوون في فرص القبول بغض النظر عمّا إذا كانوا ليليبوتايين أو بروبدينغناغيين.

على سبيل المثال، لنفترض أنّ 100 شخص من ليليبوت و100 شخص من بروبدينغناغ يقدّمون طلبات التحاق بجامعة غلوبدبدريب، ويتم اتخاذ قرارات القبول على النحو التالي:

الجدول 1. مقدّمو الطلبات من ليليبوت (90% منهم مؤهّلون)

	مؤهَّل	غير معرَّف
تم قبول الطلب	45	3
تم الرفض	45	7
المجموع	90	10
النسبة المئوية للطلاب المؤهّلين المقبولين: 45/90 =%50 النسبة المئوية للطلاب غير المؤهّلين المرفوضين: 7/10 =%70 النسبة المئوية الإجمالية للطلاب المقبولين من ليليبوت: (45+3)/100 = %48

 

الجدول 2. مقدّمو الطلبات من Brobdingnagian (10% مؤهَّلون):

	مؤهَّل	غير معرَّف
تم قبول الطلب	5	9
تم الرفض	5	81
المجموع	10	90
نسبة الطلاب المؤهّلين المقبولين: 5/10 =%50 نسبة الطلاب غير المؤهّلين المرفوضين: 81/90 =%90 النسبة الإجمالية للطلاب المقبولين من Brobdingnagian: (5+9)/100 = %14

تستوفي الأمثلة السابقة شرط تكافؤ الفرص لقبول الطلاب المؤهّلين، لأنّ كلّاً من سكان ليليبوت وبروبدينغناغ المؤهّلين لديهم فرصة بنسبة% 50 للقبول.

على الرغم من استيفاء شرط تكافؤ الفرص، لا يتم استيفاء مقياسَي العدالة التاليَين:

• التكافؤ الديمغرافي: يتم قبول سكان ليليبوت وبروبدينغناغ في الجامعة بمعدلات مختلفة، إذ يتم قبول% 48 من الطلاب من ليليبوت، ولكن يتم قبول% 14 فقط من الطلاب من بروبدينغناغ.
• تكافؤ الفرص: على الرغم من أنّ الطلاب المؤهَّلين من ليليبوت وبروبدينغناغ لديهم فرصة متساوية للقبول، لا يتم استيفاء الشرط الإضافي الذي ينص على أنّ الطلاب غير المؤهَّلين من ليليبوت وبروبدينغناغ لديهم فرصة متساوية للرفض. تبلغ نسبة الرفض لدى Lilliputians غير المؤهّلين% 70، بينما تبلغ نسبة الرفض لدى Brobdingnagians غير المؤهّلين% 90.

يمكنك الاطّلاع على الإنصاف: تكافؤ الفرص في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.

المعدّلات المتساوية

#responsible

#Metric

مقياس عدالة لتقييم ما إذا كان النموذج يتنبأ بالنتائج بشكل جيد وبالمثل لجميع قيم السمة الحسّاسة فيما يتعلق بكل من الفئة الموجبة والفئة السالبة، وليس فئة واحدة أو الأخرى حصريًا. بعبارة أخرى، يجب أن يكون كل من معدّل الموجب الصائب ومعدّل السالب الخاطئ متساويَين بالنسبة إلى جميع المجموعات.

تتعلّق تكافؤ الفرص بالمساواة في الفرص، التي تركّز فقط على معدّلات الخطأ لفئة واحدة (موجبة أو سالبة).

على سبيل المثال، لنفترض أنّ جامعة Glubbdubdrib تقبل الطلاب من Lilliput وBrobdingnag في برنامج رياضيات صارم. تقدّم المدارس الثانوية في ليليبوت منهجًا دراسيًا قويًا في الرياضيات، ومعظم الطلاب مؤهّلون للالتحاق بالبرنامج الجامعي. لا تقدّم المدارس الثانوية في بروبدينغناغ دروسًا في الرياضيات على الإطلاق، ونتيجةً لذلك، يكون عدد الطلاب المؤهّلين أقل بكثير. يتم استيفاء شرط تكافؤ الفرص إذا كان احتمال قبول المتقدّمين المؤهّلين في البرنامج متساويًا بغض النظر عن حجمهم، وإذا كان احتمال رفض المتقدّمين غير المؤهّلين متساويًا بغض النظر عن حجمهم.

لنفترض أنّ 100 شخص من ليليبوت و100 شخص من بروبدينغناغ يقدّمون طلبات إلى جامعة غلوبدوبدريب، ويتم اتخاذ قرارات القبول على النحو التالي:

الجدول 3. مقدّمو الطلبات من ليليبوت (90% منهم مؤهّلون)

	مؤهَّل	غير معرَّف
تم قبول الطلب	45	2
تم الرفض	45	8
المجموع	90	10
نسبة الطلاب المؤهّلين المقبولين: 45/90 =%50 نسبة الطلاب غير المؤهّلين المرفوضين: 8/10 =%80 النسبة الإجمالية للطلاب المقبولين من Lilliputian: (45+2)/100 = %47

 

الجدول 4. مقدّمو الطلبات من Brobdingnagian (10% مؤهَّلون):

	مؤهَّل	غير معرَّف
تم قبول الطلب	5	18
تم الرفض	5	72
المجموع	10	90
نسبة الطلاب المؤهّلين المقبولين: 5/10 =%50 نسبة الطلاب غير المؤهّلين المرفوضين: 72/90 =%80 النسبة الإجمالية للطلاب المقبولين من Brobdingnagian: (5+18)/100 = %23

يتم استيفاء شرط تكافؤ الفرص لأنّ الطلاب المؤهّلين من ليليبوت وبروبدينغناغ لديهم فرصة متساوية بنسبة% 50 للقبول، بينما الطلاب غير المؤهّلين من ليليبوت وبروبدينغناغ لديهم فرصة متساوية بنسبة% 80 للرفض.

ملاحظة: على الرغم من استيفاء شرط تكافؤ الفرص هنا، لا يتم استيفاء شرط التكافؤ الديمغرافي. يتم قبول الطلاب من ليليبوت وبروبدينغناغ في جامعة غلوبدوبدريب بمعدلات مختلفة، حيث يتم قبول% 47 من الطلاب من ليليبوت و% 23 من الطلاب من بروبدينغناغ.

يتم تعريف تكافؤ الفرص رسميًا في "تكافؤ الفرص في التعلّم الخاضع للإشراف" على النحو التالي: "يتوافق المتنبئ Ŷ مع تكافؤ الفرص فيما يتعلق بالسمة المحمية A والنتيجة Y إذا كان Ŷ وA مستقلين، بشرط Y".

ملاحظة: قارِن بين مقياس تكافؤ الفرص الأكثر مرونة ومقياس تكافؤ الاحتمالات.

evals

#generativeAI

#Metric

تُستخدَم في المقام الأول كاختصار لتقييمات النماذج اللغوية الكبيرة. بشكل عام، التقييمات هي اختصار لأي شكل من أشكال التقييم.

التقييم

#generativeAI

#Metric

تشير هذه العملية إلى قياس جودة نموذج أو مقارنة نماذج مختلفة ببعضها البعض.

لتقييم نموذج تعلُّم الآلة المُوجّه، يتم عادةً مقارنته بمجموعة التحقّق ومجموعة الاختبار. يتضمّن تقييم نموذج اللغة الكبير عادةً تقييمات أوسع للجودة والأمان.

F

F₁

#Metric

مقياس التصنيف الثنائي "المجمّع" الذي يعتمد على كل من الدقة والتذكّر. في ما يلي الصيغة:

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

انقر على الرمز للاطّلاع على أمثلة.

لنفترض أنّ قيمتَي الدقة واكتمال التوقعات الإيجابية هما:

• الدقة = 0.6
• recall = 0.4

يمكنك احتساب مقياس F₁ على النحو التالي:

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

عندما تكون الدقة والتذكّر متشابهَين إلى حد كبير (كما في المثال السابق)، يكون مقياس _F1 قريبًا من المتوسط. عندما يختلف مقياسا الدقة والتذكّر بشكل كبير، يكون مقياس F₁ أقرب إلى القيمة الأقل. على سبيل المثال:

• الدقة = 0.9
• recall = 0.1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

مقياس العدالة

#responsible

#Metric

تعريف رياضي لمفهوم "الإنصاف" يمكن قياسه. تشمل بعض مقاييس العدالة الشائعة الاستخدام ما يلي:

• تكافؤ الفرص
• تعادل الأداء المستند إلى التوقّعات
• العدالة القائمة على التفكير الافتراضي
• التكافؤ الديمغرافي

تتداخل العديد من مقاييس العدالة مع بعضها البعض، راجِع عدم توافق مقاييس العدالة.

سالب خاطئ (FN)

#fundamentals

#Metric

مثال يخطئ فيه النموذج في التنبؤ بالفئة السلبية. على سبيل المثال، يتوقّع النموذج أنّ رسالة إلكترونية معيّنة ليست رسالة غير مرغوب فيها (الفئة السلبية)، ولكنّ هذه الرسالة الإلكترونية هي في الواقع رسالة غير مرغوب فيها.

معدّل السالب الخاطئ

#Metric

يشير ذلك المصطلح إلى نسبة الأمثلة الإيجابية الفعلية التي توقّع النموذج بشكل خاطئ أنّها تنتمي إلى الفئة السلبية. تحتسب الصيغة التالية معدّل النتائج السلبية الخاطئة:

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

لمزيد من المعلومات، يمكنك الاطّلاع على الحدود ومصفوفة الالتباس في "دورة مكثّفة عن تعلّم الآلة".

موجب خاطئ (FP)

#fundamentals

#Metric

مثال يخطئ فيه النموذج في التنبؤ بالفئة الإيجابية. على سبيل المثال، يتوقّع النموذج أنّ رسالة إلكترونية معيّنة هي رسالة غير مرغوب فيها (الفئة الإيجابية)، ولكن ليست هذه الرسالة الإلكترونية في الواقع رسالة غير مرغوب فيها.

لمزيد من المعلومات، يمكنك الاطّلاع على الحدود ومصفوفة الالتباس في "دورة مكثّفة عن تعلّم الآلة".

معدّل الموجب الخاطئ

#fundamentals

#Metric

يشير ذلك المصطلح إلى نسبة الأمثلة السلبية الفعلية التي توقّع النموذج بشكل خاطئ أنّها تنتمي إلى الفئة الإيجابية. تحتسب الصيغة التالية معدّل الإيجابية الخاطئة:

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

معدل الموجب الخاطئ هو المحور السيني في منحنى خاصية تشغيل جهاز الاستقبال.

يمكنك الاطّلاع على التصنيف: منحنى ROC ومقياس AUC في "دورة مكثّفة عن تعلُّم الآلة" للحصول على مزيد من المعلومات.

أهمية الميزات

#df

#Metric

مرادف أهمية المتغيرات

النموذج الأساسي

#generativeAI

#Metric

نموذج مدرَّب مسبقًا كبير جدًا تم تدريبه على مجموعة تدريب هائلة ومتنوّعة. يمكن للنموذج الأساسي تنفيذ ما يلي:

• الاستجابة بشكل جيد لمجموعة كبيرة من الطلبات
• يمكن استخدامه كنموذج أساسي لإجراء المزيد من عمليات الضبط الدقيق أو التخصيص الأخرى.

بعبارة أخرى، يكون النموذج الأساسي فعّالاً جدًا بشكل عام، ولكن يمكن تخصيصه بشكل أكبر ليصبح أكثر فائدةً لمهمة معيّنة.

نسبة النجاحات

#generativeAI

#Metric

مقياس لتقييم النص الذي تم إنشاؤه بواسطة نموذج تعلُّم آلي نسبة النجاح هي عدد مخرجات النصوص التي تم إنشاؤها "بنجاح" مقسومًا على إجمالي عدد مخرجات النصوص التي تم إنشاؤها. على سبيل المثال، إذا أنشأ نموذج لغوي كبير 10 مقاطع برمجية، ونجح خمسة منها، ستكون نسبة النجاح 50%.

على الرغم من أنّ مقياس "نسبة النجاح" مفيد بشكل عام في الإحصاء، إلا أنّه في تعلُّم الآلة، يكون هذا المقياس مفيدًا بشكل أساسي لقياس المهام التي يمكن التحقّق منها، مثل إنشاء الرموز البرمجية أو حلّ المسائل الرياضية.

G

gini impurity

#df

#Metric

مقياس مشابه لإنتروبيا تستخدم أدوات التقسيم قيمًا مشتقة من عدم المساواة في جيني أو الإنتروبيا لإنشاء شروط لتصنيف أشجار القرارات. يتم استنتاج تحصيل المعلومات من قصور المعلومات. لا يوجد مصطلح مكافئ مقبول عالميًا للمقياس المستمد من عدم نقاء جيني، ولكن هذا المقياس غير المسمى لا يقل أهمية عن اكتساب المعلومات.

يُطلق على عدم نقاء جيني أيضًا اسم مؤشر جيني أو ببساطة جيني.

انقر على الرمز للاطّلاع على التفاصيل الرياضية حول مقياس عدم المساواة في توزيع الأرباح.

مقياس عدم المساواة في جيني هو احتمال تصنيف قطعة جديدة من البيانات بشكل خاطئ مأخوذة من التوزيع نفسه. يتم احتساب معامل جيني لمجموعة تتضمّن قيمتَين محتملتَين، "0" و "1" (على سبيل المثال، التصنيفات في مسألة تصنيف ثنائي)، باستخدام الصيغة التالية:

   I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

where:

• I هو مؤشر عدم المساواة في جيني.
• p هي نسبة الأمثلة التي تكون فيها القيمة "1".
• q هي نسبة الأمثلة التي تكون فيها القيمة "0". يُرجى العِلم أنّ q = 1-p

على سبيل المثال، لنفترض مجموعة البيانات التالية:

• تحتوي 100 تصنيف (0.25 من مجموعة البيانات) على القيمة "1"
• تحتوي 300 تصنيف (0.75 من مجموعة البيانات) على القيمة "0"

وبالتالي، فإنّ معامل جيني هو:

• p = 0.25
• q = 0.75
• I = 1 - (0.25² + 0.75²) = 0.375

نتيجةً لذلك، سيكون هناك احتمال بنسبة% 37.5 بأن يتم تصنيف تصنيف عشوائي من مجموعة البيانات نفسها بشكل خاطئ، واحتمال بنسبة% 62.5 بأن يتم تصنيفه بشكل صحيح.

سيحتوي التصنيف المتوازن تمامًا (على سبيل المثال، 200 من القيمة "0" و200 من القيمة "1") على معامل عدم نقاء جيني يبلغ 0.5. سيكون للتصنيف غير المتوازن بشكل كبير مؤشر جيني غير نقي قريب من 0.0.

---

H

الخسارة المفصلية

#Metric

مجموعة من دوال الخسارة الخاصة بالتصنيف والمصمّمة للعثور على حدود القرار بأكبر مسافة ممكنة من كل مثال تدريبي، وبالتالي زيادة الهامش بين الأمثلة والحدود إلى أقصى حد. تستخدِم آلات المتجهات الداعمة القائمة على النواة دالة الخسارة المفصلية (أو دالة ذات صلة، مثل دالة الخسارة المفصلية التربيعية). بالنسبة إلى التصنيف الثنائي، يتم تعريف دالة الخسارة المفصلية على النحو التالي:

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

حيث y هي التصنيف الصحيح، إما -1 أو +1، وy' هي المخرجات الأولية لنموذج التصنيف:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

نتيجةً لذلك، يبدو الرسم البياني لدالة الخسارة المفصلية مقابل (y * y') على النحو التالي:

I

عدم توافق مقاييس الإنصاف

#responsible

#Metric

تشير إلى فكرة أنّ بعض مفاهيم العدالة غير متوافقة مع بعضها البعض ولا يمكن تحقيقها في الوقت نفسه. نتيجةً لذلك، لا يوجد مقياس عالمي واحد لتحديد مدى العدل يمكن تطبيقه على جميع مشاكل تعلُّم الآلة.

على الرغم من أنّ ذلك قد يبدو محبطًا، إلا أنّ عدم التوافق بين مقاييس العدالة لا يعني أنّ الجهود المبذولة لتحقيق العدالة غير مثمرة. بدلاً من ذلك، يقترح أنّه يجب تحديد العدالة حسب السياق لمشكلة تعلّم آلي معيّنة، بهدف منع الأضرار المرتبطة بحالات الاستخدام المحدّدة.

يمكنك الاطّلاع على مقالة "حول إمكانية تحقيق العدالة" للحصول على مناقشة أكثر تفصيلاً حول عدم توافق مقاييس العدالة.

العدالة الفردية

#responsible

#Metric

مقياس عدالة يتحقّق مما إذا تم تصنيف الأفراد المتشابهين بشكل مماثل. على سبيل المثال، قد ترغب أكاديمية Brobdingnagian في تحقيق العدالة الفردية من خلال ضمان أنّ فرص قبول طالبَين متطابقَين في الدرجات ونتائج الاختبارات الموحّدة متساوية.

يُرجى العِلم أنّ العدالة الفردية تعتمد بشكل كامل على طريقة تحديد "التشابه" (في هذه الحالة، الدرجات ونتائج الاختبارات)، وقد تواجه خطر حدوث مشاكل جديدة في العدالة إذا لم يتضمّن مقياس التشابه معلومات مهمة (مثل مدى صعوبة المناهج الدراسية للطالب).

يمكنك الاطّلاع على "العدالة من خلال الوعي" للحصول على مناقشة أكثر تفصيلاً حول العدالة الفردية.

تحصيل المعلومات

#df

#Metric

في غابات القرارات، يشير إلى الفرق بين القصور في أحد الأجزاء ومجموع القصور في الأجزاء الفرعية المرجّح (حسب عدد الأمثلة). القصور في أحد الأجزاء هو القصور في الأمثلة الواردة في هذا الجزء.

على سبيل المثال، إليك قيم الإنتروبيا التالية:

• إنتروبيا العقدة الرئيسية = 0.6
• القصور في جزء ثانوي واحد مع 16 مثالاً ذا صلة = 0.2
• مقياس القصور في جزء فرعي آخر يتضمّن 24 مثالاً ذا صلة = 0.1

وبالتالي، فإنّ% 40 من الأمثلة تقع في إحدى العُقد الفرعية و% 60 في العقدة الفرعية الأخرى. ولذلك:

• مجموع القصور المرجّح للعُقد الثانوية = (0.4 * 0.2) + (0.6 * 0.1) = 0.14

إذًا، تحصيل المعلومات هو:

• تحصيل المعلومات = قصور الجزء الأصلي - مجموع القصور المرجّح للأجزاء الفرعية
• تحصيل المعلومات = 0.6 - 0.14 = 0.46

تسعى معظم أدوات التقسيم إلى إنشاء شروط تزيد من اكتساب المعلومات إلى أقصى حد.

توافق المقيّمين

#Metric

مقياس لعدد المرات التي يتفق فيها المقيمون البشريون عند تنفيذ مهمة ما. إذا لم يتّفق المقيّمون، قد يكون من الضروري تحسين تعليمات المهمة. يُعرف هذا المقياس أيضًا باسم اتفاقية بين المعلقين أو اتساق التقييم. يُرجى الاطّلاع أيضًا على معامل كابا لكوهين، وهو أحد مقاييس الاتفاق بين المقيّمين الأكثر شيوعًا.

لمزيد من المعلومات، يمكنك الاطّلاع على البيانات الفئوية: المشاكل الشائعة في "دورة تدريبية مكثّفة حول تعلُّم الآلة".

L

خسارة L₁

#fundamentals

#Metric

دالة الخسارة التي تحسب القيمة المطلقة للفرق بين قيم التصنيف الفعلية والقيم التي يتوقّعها النموذج. على سبيل المثال، إليك طريقة حساب خسارة L₁ لمجموعة من خمسة أمثلة:

القيمة الفعلية للمثال	القيمة المتوقّعة للنموذج	القيمة المطلقة للتغيير
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		‫8 = خسارة L1

يكون معدّل الخطأ في ₁ أقل حساسية للقيم الشاذة من معدّل الخطأ في ₂.

متوسط الخطأ المطلق هو متوسط خسارة ₁ لكل مثال.

انقر على الرمز للاطّلاع على الرياضيات الرسمية.

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

حيث:

• $n$ هو عدد الأمثلة.
• $y$ هي القيمة الفعلية للتصنيف.
• $\hat{y}$ هي القيمة التي يتوقّعها النموذج لـ $y$.

---

يمكنك الاطّلاع على الانحدار الخطي: الخسارة في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.

خسارة ₂

#fundamentals

#Metric

يشير ذلك المصطلح إلى دالة خسارة تحسب مربع الفرق بين قيم التصنيف الفعلية والقيم التي يتوقّعها النموذج. على سبيل المثال، إليك طريقة حساب خسارة L₂ لمجموعة من خمسة أمثلة:

القيمة الفعلية للمثال	القيمة المتوقّعة للنموذج	مربع دلتا
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		‫16 = L2 خسارة

بسبب التربيع، يؤدي فقدان L₂ إلى تضخيم تأثير القيم الشاذة. أي أنّ دالة الخسارة L₂ تتأثر بشكل أكبر بالتوقعات السيئة مقارنةً بدالة الخسارة L₁. على سبيل المثال، سيكون معدّل فقدان حزمة L₁ السابقة 8 بدلاً من 16. لاحظ أنّ قيمة متطرفة واحدة تمثّل 9 من 16.

تستخدِم نماذج الانحدار عادةً دالة الخسارة L₂.

متوسط الخطأ التربيعي هو متوسط خسارة ₂ لكل مثال. الخسارة التربيعية هي اسم آخر للخسارة من النوع L₂.

انقر على الرمز للاطّلاع على الرياضيات الرسمية.

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

حيث:

• $n$ هو عدد الأمثلة.
• $y$ هي القيمة الفعلية للتصنيف.
• $\hat{y}$ هي القيمة التي يتوقّعها النموذج لـ $y$.

---

يمكنك الاطّلاع على الانحدار اللوجستي: الخسارة والتسوية في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.

تقييمات النماذج اللغوية الكبيرة

#generativeAI

#Metric

مجموعة من المقاييس ومقاييس الأداء لتقييم أداء النماذج اللغوية الكبيرة (LLM) بشكل عام، تتضمّن عمليات تقييم النماذج اللغوية الكبيرة ما يلي:

• مساعدة الباحثين في تحديد المجالات التي تحتاج فيها النماذج اللغوية الكبيرة إلى تحسين
• وهي مفيدة في مقارنة نماذج اللغات الكبيرة المختلفة وتحديد أفضلها لتنفيذ مهمة معيّنة.
• المساعدة في ضمان أنّ استخدام النماذج اللغوية الكبيرة آمن وأخلاقي

لمزيد من المعلومات، يمكنك الاطّلاع على النماذج اللغوية الكبيرة (LLM) في "دورة مكثّفة عن تعلُّم الآلة".

خسارة

#fundamentals

#Metric

أثناء تدريب نموذج خاضع للإشراف، يتم قياس مدى بُعد توقّع النموذج عن تصنيفه.

تحسب دالة الخسارة الخسارة.

يمكنك الاطّلاع على الانحدار الخطي: الخسارة في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.

دالة الخسارة

#fundamentals

#Metric

أثناء التدريب أو الاختبار، تُستخدَم دالة رياضية لحساب الخسارة في دفعة من الأمثلة. تعرض دالة الخسارة خسارة أقل للنماذج التي تقدّم توقعات جيدة مقارنةً بالنماذج التي تقدّم توقعات سيئة.

عادةً ما يكون الهدف من التدريب هو تقليل الخسارة التي تعرضها دالة الخسارة.

تتوفّر العديد من أنواع دوال الخسارة المختلفة. اختَر دالة الخسارة المناسبة لنوع النموذج الذي تنشئه. على سبيل المثال:

• فقدان _L2 (أو متوسط الخطأ التربيعي) هو دالة الفقدان للانحدار الخطي.
• الخسارة اللوغارتمية هي دالة الخسارة في الانحدار اللوجستي.

M

متوسّط الخطأ المطلق (MAE)

#Metric

متوسط الخسارة لكل مثال عند استخدام L₁ loss احسب متوسّط الخطأ المطلق على النحو التالي:

1. احسب خسارة L₁ لمجموعة.
2. قسِّم خسارة L₁ على عدد الأمثلة في المجموعة.

انقر على الرمز للاطّلاع على الرياضيات الرسمية.

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

where:

• $n$ هو عدد الأمثلة.
• $y$ هي القيمة الفعلية للتصنيف.
• $\hat{y}$ هي القيمة التي يتوقّعها النموذج لـ $y$.

---

على سبيل المثال، لنفترض أنّنا نريد حساب خسارة L₁ على مجموعة من خمسة أمثلة كما يلي:

القيمة الفعلية للمثال	القيمة المتوقّعة للنموذج	الخسارة (الفرق بين القيمة الفعلية والقيمة المتوقّعة)
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		‫8 = خسارة L1

إذًا، قيمة L₁ هي 8 وعدد الأمثلة هو 5. وبالتالي، فإنّ متوسّط الخطأ المطلق هو:

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

قارِن بين متوسط الخطأ المطلق ومتوسط الخطأ التربيعي وجذر متوسط الخطأ التربيعي.

متوسط الدقة عند k (mAP@k)

#generativeAI

#Metric

المتوسط الإحصائي لكل نتائج متوسط الدقة عند k في مجموعة بيانات التحقّق. يُستخدم مقياس متوسط الدقة عند k لتقييم جودة المحتوى المقترح الذي يقدّمه نظام التوصية.

على الرغم من أنّ عبارة "المتوسط الحسابي" تبدو مكرّرة، فإنّ اسم المقياس مناسب. ففي النهاية، يعثر هذا المقياس على متوسط قيم متوسط الدقة عند k المتعددة.

انقر على الرمز للاطّلاع على مثال.

لنفترض أنّك تنشئ نظام اقتراحات يقدّم قائمة مخصّصة بالروايات المقترَحة لكل مستخدم. استنادًا إلى الملاحظات الواردة من المستخدمين المحدّدين، يمكنك حساب خمسة من متوسطات الدقة عند k (تقييم واحد لكل مستخدم):

• 0.73
• 0.77
• 0.67
• 0.82
• 0.76

وبالتالي، فإنّ متوسّط الدقة عند K هو:

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

متوسط الخطأ التربيعي (MSE)

#Metric

متوسط الخسارة لكل مثال عند استخدام خسارة ₂ احسب متوسط الخطأ التربيعي على النحو التالي:

1. احسب خسارة L₂ لمجموعة.
2. قسِّم خسارة L₂ على عدد الأمثلة في المجموعة.

انقر على الرمز للاطّلاع على الرياضيات الرسمية.

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ حيث:

• $n$ هو عدد الأمثلة.
• $y$ هي القيمة الفعلية للتصنيف.
• $\hat{y}$ هي القيمة التي يتوقّعها النموذج لـ $y$.

---

على سبيل المثال، لنفترض أنّك تريد حساب الخسارة في المجموعة التالية المكوّنة من خمسة أمثلة:

القيمة الفعلية	توقّعات النموذج	فقدان البيانات	الخسارة التربيعية
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			‫16 = L2 خسارة

وبالتالي، يكون متوسط الخطأ التربيعي كما يلي:

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

متوسط الخطأ التربيعي هو محسِّن شائع للتدريب، خاصةً في الانحدار الخطي.

قارِن بين "متوسط الخطأ التربيعي" و"متوسط الخطأ المطلق" و"جذر متوسط الخطأ التربيعي".

تستخدم TensorFlow Playground متوسط الخطأ التربيعي لاحتساب قيم الخسارة.

انقر على الرمز للاطّلاع على مزيد من التفاصيل حول القيم الشاذة.

تؤثر القيم الشاذة بشكل كبير في متوسط الخطأ التربيعي. على سبيل المثال، إذا كانت الخسارة 1، تكون الخسارة التربيعية 1، ولكن إذا كانت الخسارة 3، تكون الخسارة التربيعية 9. في الجدول السابق، يمثّل المثال الذي يتضمّن خسارة 3 حسابات حوالي% 56 من متوسط الخطأ التربيعي، بينما يمثّل كل مثال يتضمّن خسارة حساب واحد% 6 فقط من متوسط الخطأ التربيعي.

لا تؤثر القيم الشاذة في متوسّط الخطأ المطلق بنفس درجة تأثيرها في متوسّط الخطأ التربيعي. على سبيل المثال، يؤدي فقدان 3 حسابات إلى خطأ مطلق متوسط بنسبة% 38 تقريبًا.

القص هو إحدى الطرق لمنع القيم المتطرفة من التأثير سلبًا في قدرة النموذج على التوقّع.

---

المقياس

#TensorFlow

#Metric

إحصاء يهمّك

الهدف هو مقياس يحاول نظام تعلُّم الآلة تحسينه.

Metrics API (tf.metrics)

#Metric

واجهة برمجة تطبيقات TensorFlow لتقييم النماذج على سبيل المثال، تحدّد tf.metrics.accuracy عدد المرات التي تتطابق فيها توقّعات النموذج مع التصنيفات.

دالة الخسارة الحدّية الدنيا

#Metric

دالة خسارة لشبكات الخصومة التوليدية، استنادًا إلى الإنتروبيا المتقاطعة بين توزيع البيانات التي تم إنشاؤها والبيانات الحقيقية

يتم استخدام دالة الخسارة Minimax في الورقة البحثية الأولى لوصف الشبكات التوليدية الخصومية.

يمكنك الاطّلاع على دوال الخسارة في دورة شبكات الخصومة التوليدية للحصول على مزيد من المعلومات.

سعة النموذج

#Metric

مدى تعقيد المشاكل التي يمكن أن يتعلّمها النموذج وكلما زادت درجة تعقيد المشاكل التي يمكن أن يتعلّمها النموذج، زادت قدرته. تزداد سعة النموذج عادةً مع عدد مَعلمات النموذج. للحصول على تعريف رسمي لقدرة نموذج التصنيف، يُرجى الاطّلاع على سمة VC.

لا

فئة سالبة

#fundamentals

#Metric

في التصنيف الثنائي، يُطلق على إحدى الفئتَين اسم إيجابية ويُطلق على الأخرى اسم سلبية. الفئة الإيجابية هي الشيء أو الحدث الذي يختبره النموذج، والفئة السلبية هي الاحتمال الآخر. على سبيل المثال:

• قد تكون الفئة السلبية في اختبار طبي هي "ليس ورمًا".
• قد تكون الفئة السلبية في نموذج تصنيف الرسائل الإلكترونية هي "ليست رسالة غير مرغوب فيها".

يجب التمييز بينها وبين الفئة الموجبة.

O

هدف

#Metric

مقياس تحاول الخوارزمية تحسينه.

دالة الهدف

#Metric

الصيغة الرياضية أو المقياس الذي يهدف النموذج إلى تحسينه. على سبيل المثال، دالة الهدف في الانحدار الخطي هي عادةً متوسط الخطأ التربيعي. لذلك، عند تدريب نموذج انحدار خطي، يهدف التدريب إلى تقليل متوسط الخطأ التربيعي.

في بعض الحالات، يكون الهدف هو تحقيق الحد الأقصى لدالة الهدف. على سبيل المثال، إذا كانت دالة الهدف هي الدقة، يكون الهدف هو زيادة الدقة إلى أقصى حد.

يمكنك الاطّلاع أيضًا على الخسارة.

P

pass at k (pass@k)

#Metric

مقياس لتحديد جودة الرمز البرمجي (مثل Python) الذي ينشئه نموذج لغوي كبير وبشكل أكثر تحديدًا، يخبرك مقياس "النجاح عند k" باحتمالية اجتياز مجموعة واحدة على الأقل من مجموعات الرموز البرمجية التي تم إنشاؤها من بين k مجموعة من الرموز البرمجية لجميع اختبارات الوحدة.

غالبًا ما تواجه النماذج اللغوية الكبيرة صعوبة في إنشاء تعليمات برمجية جيدة للمشاكل البرمجية المعقّدة. يتعامل مهندسو البرمجيات مع هذه المشكلة من خلال مطالبة النموذج اللغوي الكبير بإنشاء حلول متعدّدة (k) للمشكلة نفسها. بعد ذلك، يختبر مهندسو البرامج كل حل من الحلول باستخدام اختبارات الوحدات. يعتمد احتساب نسبة النجاح عند k على نتيجة اختبارات الوحدات:

• إذا نجح واحد أو أكثر من هذه الحلول في اختبار الوحدة، يعني ذلك أنّ النموذج اللغوي الكبير اجتاز تحدّي إنشاء الرمز البرمجي.
• إذا لم ينجح أي من الحلول في اجتياز اختبار الوحدة، يعني ذلك أنّ النموذج اللغوي الكبير لم ينجح في اجتياز تحدّي إنشاء الرمز البرمجي.

صيغة "النجاح عند k" هي كما يلي:

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

بشكل عام، تؤدي القيم الأعلى k إلى تحقيق نتائج أعلى في مقياس "النجاح عند k"، ولكن تتطلّب القيم الأعلى k المزيد من موارد النماذج اللغوية الكبيرة واختبارات الوحدات.

انقر على الرمز للاطّلاع على مثال.

لنفترض أنّ مهندس برامج يطلب من نموذج لغوي كبير إنشاء k=10 حلول لـ n=50 مشكلة صعبة في البرمجة. في ما يلي النتائج:

• 30 بطاقة
• ‫20 حالة فشل

وبالتالي، فإنّ درجة النجاح عند 10 هي:

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

الأداء

#Metric

مصطلح مُحمّل بالمعاني التالية:

• المعنى العادي ضمن هندسة البرمجيات وهي: ما هي سرعة (أو كفاءة) تشغيل هذا البرنامج؟
• المعنى في سياق تعلُّم الآلة في هذه الحالة، يجيب الأداء عن السؤال التالي: ما مدى صحة هذا النموذج؟ أي ما مدى دقة توقّعات النموذج؟

أهمية المتغيرات في التبديل

#df

#Metric

أحد أنواع أهمية المتغير الذي يقيّم الزيادة في خطأ التوقّع للنموذج بعد تبديل قيم الميزة. أهمية المتغيرات المستندة إلى التبديل هي مقياس مستقل عن النموذج.

مقياس الارتباك

#Metric

مقياس لمدى نجاح النموذج في إنجاز مهمته. على سبيل المثال، لنفترض أنّ مهمتك هي قراءة الأحرف القليلة الأولى من كلمة يكتبها المستخدم على لوحة مفاتيح الهاتف، وتقديم قائمة بالكلمات المحتملة التي يمكن إكمالها. إنّ مقياس الحيرة، P، لهذه المهمة هو تقريبًا عدد التخمينات التي عليك تقديمها لكي تحتوي قائمتك على الكلمة الفعلية التي يحاول المستخدم كتابتها.

ترتبط الحيرة بالإنتروبيا المتقاطعة على النحو التالي:

$$P= 2^{-\text{cross entropy}}$$

فئة موجبة

#fundamentals

#Metric

الفئة التي تختبرها.

على سبيل المثال، قد تكون الفئة الموجبة في نموذج السرطان هي "ورم". قد تكون الفئة الإيجابية في نموذج تصنيف رسائل إلكترونية هي "رسائل غير مرغوب فيها".

يجب التمييز بينها وبين الفئة السلبية.

انقر على الرمز للاطّلاع على ملاحظات إضافية.

قد يكون مصطلح الفئة الإيجابية مربكًا لأنّ النتيجة "الإيجابية" للعديد من الاختبارات غالبًا ما تكون نتيجة غير مرغوب فيها. على سبيل المثال، تتوافق الفئة الإيجابية في العديد من الاختبارات الطبية مع الأورام أو الأمراض. بشكل عام، تريد أن يقول لك الطبيب: "تهانينا! كانت نتائج اختبارك سلبية". على أي حال، الفئة الإيجابية هي الحدث الذي يسعى الاختبار إلى العثور عليه.

صحيح أنّك تختبر في الوقت نفسه الفئتين الإيجابية والسلبية.

---

المساحة تحت منحنى الدقة والاستدعاء (PR)

#Metric

مساحة تحت منحنى الدقة والاستدعاء الذي تم الحصول عليه من خلال رسم نقاط (الاستدعاء، الدقة) لقيم مختلفة لحد التصنيف.

الدقة

#fundamentals

#Metric

مقياس لنماذج التصنيف يجيب عن السؤال التالي:

عندما توقّع النموذج الفئة الموجبة، ما هي النسبة المئوية للتوقّعات الصحيحة؟

في ما يلي الصيغة:

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

where:

• تعني النتيجة الإيجابية الصحيحة أنّ النموذج توقّع بشكلٍ صحيح الفئة الإيجابية.
• تعني النتيجة الموجبة الخاطئة أنّ النموذج توقّع بشكل خاطئ الفئة الموجبة.

على سبيل المثال، لنفترض أنّ أحد النماذج قدّم 200 توقّع إيجابي. من بين هذه التوقّعات الإيجابية البالغ عددها 200:

• كانت 150 منها نتائج موجبة صحيحة.
• كانت 50 منها حالات موجبة خاطئة.

في هذه الحالة:

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

يجب التمييز بينه وبين الدقة واكتمال التوقعات الإيجابية.

يمكنك الاطّلاع على التصنيف: الدقة والاسترجاع والضبط والمقاييس ذات الصلة في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.

الدقة عند k (precision@k)

#Metric

مقياس لتقييم قائمة مرتبة من العناصر. تحدّد مقياس الدقة عند k نسبة أول k عنصر في تلك القائمة التي تكون "ذات صلة". والمقصود:

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

يجب أن تكون قيمة k أقل من أو تساوي طول القائمة التي تم إرجاعها. يُرجى العلم أنّ طول القائمة التي يتم عرضها ليس جزءًا من عملية الاحتساب.

غالبًا ما يكون مدى الصلة بالموضوع أمرًا شخصيًا، وحتى المقيّمون البشريون الخبراء يختلفون في كثير من الأحيان بشأن العناصر ذات الصلة بالموضوع.

المقارنة بـ:

• متوسط الدقة عند k
• متوسط الدقة عند k

انقر على الرمز للاطّلاع على مثال.

لنفترض أنّ نموذجًا لغويًا كبيرًا تلقّى طلب البحث التالي:

List the 6 funniest movies of all time in order.

ويعرض النموذج اللغوي الكبير القائمة الموضّحة في العمودين الأول والثاني من الجدول التالي:

الموضع	فيلم	هل هي ذات صلة؟
1	الجنرال	نعم
2	Mean Girls	نعم
3	Platoon	لا
4	وصيفات العروس	نعم
5	المواطن كين	لا
6	This is Spinal Tap	نعم

فيلمان من الأفلام الثلاثة الأولى ذات صلة، لذا تكون الدقة عند 3 كما يلي:

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

ثلاثة من الأفلام الخمسة الأولى مضحكة جدًا، لذا فإنّ الدقة عند 5 هي:

$$\text{precision at 5} = \frac{\text{3}} {\text{5}} = 0.6$$

---

منحنى الدقة والاستدعاء

#Metric

منحنى الدقة مقابل الاسترجاع عند عتبات التصنيف المختلفة

انحياز التوقّعات

#Metric

تشير هذه القيمة إلى مدى اختلاف متوسط التوقعات عن متوسط التصنيفات في مجموعة البيانات.

يجب عدم الخلط بين هذا المصطلح ومصطلح التحيز في نماذج تعلُّم الآلة أو مع التحيز في الأخلاقيات والعدالة.

التكافؤ التوقّعي

#responsible

#Metric

مقياس الإنصاف يتحقّق مما إذا كانت معدّلات الدقة متساوية للمجموعات الفرعية قيد الدراسة في نموذج تصنيف معيّن.

على سبيل المثال، إذا كان هناك نموذج يتوقّع قبول الطلاب في الكلية، سيحقّق هذا النموذج تكافؤ التوقّعات بالنسبة إلى الجنسية إذا كان معدّل دقته متساويًا بالنسبة إلى الأشخاص من ليليبوت وبروبدينغناغ.

يُطلق على ميزة "تطابق الأسعار التوقّعية" أحيانًا اسم تطابق الأسعار التوقّعية.

يمكنك الاطّلاع على "تعريفات العدالة الموضّحة" (الفقرة 3.2.1) للحصول على مناقشة أكثر تفصيلاً حول التكافؤ التوقعي.

ميزة "تساوي الأسعار التوقّعي"

#responsible

#Metric

اسم آخر للتكافؤ التوقعي

دالة الكثافة الاحتمالية

#Metric

دالة تحدّد عدد مرات تكرار عيّنات البيانات التي تتضمّن بالضبط قيمة معيّنة. عندما تكون قيم مجموعة البيانات عبارة عن أرقام نقطة عائمة مستمرة، نادرًا ما تحدث تطابقات تامة. ومع ذلك، يؤدي تكامل دالة كثافة الاحتمال من القيمة x إلى القيمة y إلى الحصول على التكرار المتوقّع لعيّنات البيانات بين x وy.

على سبيل المثال، لنفترض أنّ لدينا توزيعًا عاديًا بمتوسط 200 وانحراف معياري يبلغ 30. لتحديد التكرار المتوقّع لعينات البيانات التي تقع ضمن النطاق من 211.4 إلى 218.7، يمكنك دمج دالة كثافة الاحتمال للتوزيع الطبيعي من 211.4 إلى 218.7.

R

تذكُّر الإعلان

#fundamentals

#Metric

مقياس لنماذج التصنيف يجيب عن السؤال التالي:

عندما كانت الحقيقة الأساسية هي الفئة الموجبة، ما هي النسبة المئوية للتوقعات التي حدّدها النموذج بشكل صحيح على أنّها الفئة الموجبة؟

في ما يلي الصيغة:

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

where:

• تعني النتيجة الإيجابية الصحيحة أنّ النموذج توقّع بشكلٍ صحيح الفئة الإيجابية.
• يعني السلبي الخاطئ أنّ النموذج توقّع بشكل خاطئ الفئة السلبية.

على سبيل المثال، لنفترض أنّ نموذجك قدّم 200 توقّع بشأن أمثلة كانت الحقيقة الأساسية فيها هي الفئة الموجبة. من بين هذه التوقعات الـ 200:

• كانت 180 منها نتائج موجبة صحيحة.
• كانت 20 منها نتائج سلبية خاطئة.

في هذه الحالة:

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

انقر على الرمز للاطّلاع على ملاحظات حول مجموعات البيانات غير المتوازنة الفئات.

تكون مقياس الاسترجاع مفيدة بشكل خاص في تحديد القدرة التنبؤية لنماذج التصنيف التي تكون فيها الفئة الإيجابية نادرة. على سبيل المثال، لنفترض أنّ لديك مجموعة بيانات غير متوازنة بين الفئات، حيث تظهر الفئة الإيجابية لمرض معيّن لدى 10 مرضى فقط من بين مليون مريض. لنفترض أنّ نموذجك قدّم خمسة ملايين توقّع أدّت إلى النتائج التالية:

• ‫30 حالة موجبة صحيحة
• 20 نتيجة سلبية خاطئة
• ‫4,999,000 نتيجة سالبة صحيحة
• ‫950 نتيجة موجبة خاطئة

وبالتالي، فإنّ معدّل استرجاع هذا النموذج هو:

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

في المقابل، دقة هذا النموذج هي:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

قد تبدو هذه القيمة العالية للدقة مثيرة للإعجاب، ولكنّها في الأساس بلا معنى. يُعدّ الاسترجاع مقياسًا أكثر فائدة لمجموعات البيانات غير المتوازنة الفئات من الدقة.

---

يمكنك الاطّلاع على التصنيف: الدقة والاسترجاع والضبط والمقاييس ذات الصلة للحصول على مزيد من المعلومات.

معدّل التذكّر عند k (recall@k)

#Metric

مقياس لتقييم الأنظمة التي تعرض قائمة مرتبة (منظَّمة) من العناصر. تحدّد مقياس الاسترجاع عند k نسبة العناصر ذات الصلة في أول k عنصر في تلك القائمة من إجمالي عدد العناصر ذات الصلة التي تم عرضها.

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

التباين مع الدقة عند k

انقر على الرمز للاطّلاع على مثال.

لنفترض أنّ نموذجًا لغويًا كبيرًا يتلقّى طلب البحث التالي:

List the 10 funniest movies of all time in order.

ويعرض النموذج اللغوي الكبير القائمة الموضّحة في العمودَين الأولَين:

الموضع	فيلم	هل هي ذات صلة؟
1	الجنرال	نعم
2	Mean Girls	نعم
3	Platoon	لا
4	وصيفات العروس	نعم
5	This is Spinal Tap	نعم
6	Airplane!	نعم
7	يوم خنزير الأرض	نعم
8	Monty Python and the Holy Grail	نعم
9	Oppenheimer‫	لا
10	جاهل	نعم

ثمانية من الأفلام في القائمة السابقة مضحكة جدًا، لذا فهي "عناصر ذات صلة في القائمة". وبالتالي، سيكون الرقم 8 هو المقام في جميع عمليات حساب مقياس التذكّر عند k. ماذا عن البسط؟ حسنًا، 3 من العناصر الأربعة الأولى ذات صلة، لذا يكون الاسترجاع عند 4 كما يلي:

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

7 من الأفلام الـ 8 الأولى مضحكة جدًا، لذا يكون معدّل التذكّر عند 8 ثوانٍ كما يلي:

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

منحنى الأمثلة الإيجابية

#fundamentals

#Metric

رسم بياني لمعدّل الموجب الصحيح مقابل معدّل الموجب الخاطئ لقيم مختلفة لحدود التصنيف في التصنيف الثنائي.

يشير شكل منحنى ROC إلى قدرة نموذج التصنيف الثنائي على فصل الفئات الإيجابية عن الفئات السلبية. لنفترض مثلاً أنّ نموذج تصنيف ثنائي يفصل تمامًا بين جميع الفئات السلبية وجميع الفئات الإيجابية:

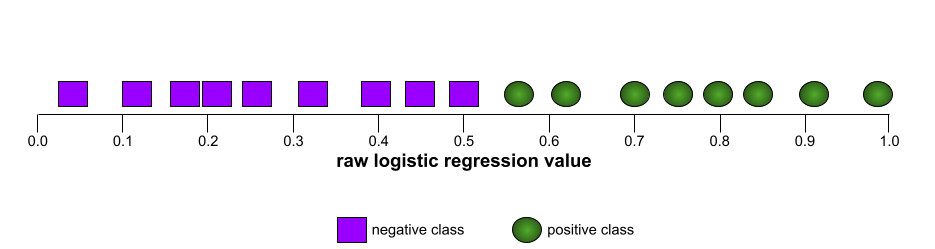
يبدو منحنى ROC للنموذج السابق على النحو التالي:

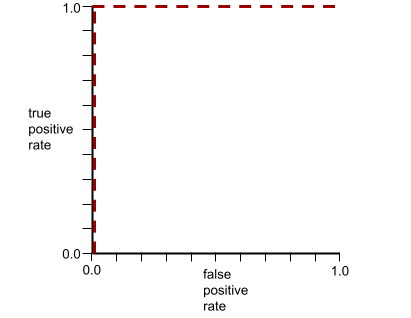
في المقابل، يوضح الرسم البياني التالي قيم الانحدار اللوجستي الأولية لنموذج سيئ لا يمكنه الفصل بين الفئات السلبية والفئات الإيجابية على الإطلاق:

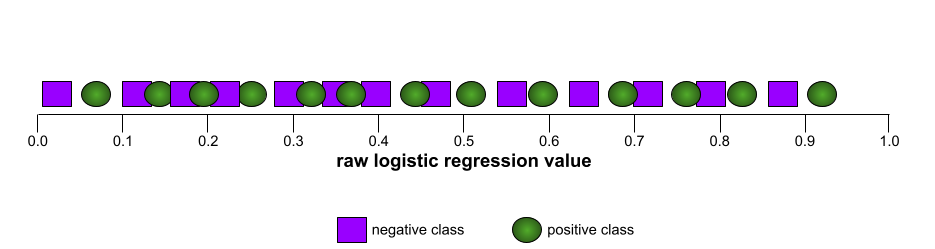
يبدو منحنى ROC لهذا النموذج على النحو التالي:

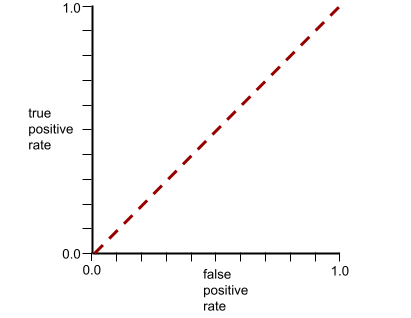
في الوقت نفسه، في العالم الحقيقي، تفصل معظم نماذج التصنيف الثنائي بين الفئات الإيجابية والسلبية إلى حد ما، ولكن ليس بشكل مثالي عادةً. لذا، يقع منحنى ROC النموذجي في مكان ما بين الحدّين الأقصى والأدنى:

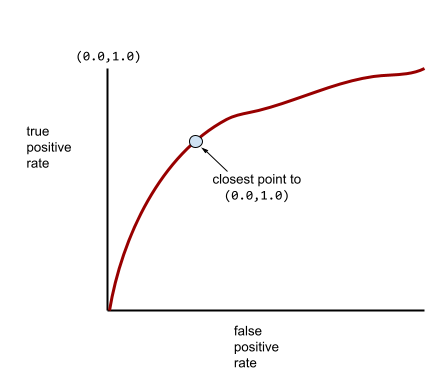
تحدّد النقطة الأقرب إلى (0.0,1.0) على منحنى ROC نظريًا عتبة التصنيف المثالية. ومع ذلك، تؤثر العديد من المشاكل الأخرى في العالم الحقيقي على اختيار الحد الأمثل للتصنيف. على سبيل المثال، قد تتسبّب النتائج السلبية الخاطئة في أضرار أكبر بكثير من النتائج الإيجابية الخاطئة.

يلخّص مقياس عددي يُسمى AUC منحنى ROC في قيمة واحدة ذات فاصلة عائمة.

جذر الخطأ التربيعي المتوسّط (RMSE)

#fundamentals

#Metric

الجذر التربيعي لمتوسط الخطأ التربيعي

ROUGE (Recall-Oriented Understudy for Gisting Evaluation)

#Metric

مجموعة من المقاييس التي تقيّم نماذج التلخيص التلقائي والترجمة الآلية. تحدّد مقاييس ROUGE مدى تداخل النص المرجعي مع النص الذي أنشأه نموذج تعلُّم الآلة. يقيس كل مقياس من مقاييس عائلة ROUGE التداخل بطريقة مختلفة. تشير نتائج ROUGE الأعلى إلى تشابه أكبر بين النص المرجعي والنص الذي تم إنشاؤه مقارنةً بنتائج ROUGE الأقل.

يُنشئ كل فرد من عائلة مقاييس ROUGE عادةً المقاييس التالية:

• الدقة
• التذكُّر
• F₁

ملاحظة: تستخدم مقاييس الدقة والاسترجاع في ROUGE بشكل مختلف قليلاً عن مقاييس الدقة والاسترجاع التقليدية.

للاطّلاع على التفاصيل والأمثلة، يُرجى مراجعة:

• ROUGE-L
• ROUGE-N
• ROUGE-S

ملاحظة: BLEU وBLEURT يركّزان على الدقة، بينما يركّز ROUGE على الاسترجاع. نتيجةً لذلك، يُعدّ مقياسا BLEU وBLEURT أفضل لتقييم الترجمة الآلية (لأنّ التركيز يكون على الدقة)، بينما يُعدّ مقياس ROUGE أفضل للتلخيص (لأنّ التركيز يكون على الاسترجاع).

ROUGE-L

#Metric

أحد مقاييس عائلة ROUGE يركّز على طول أطول تسلسل فرعي مشترك في النص المرجعي والنص الذي تم إنشاؤه. تحسب الصيغ التالية مقياسَي التذكّر والدقة لمقياس ROUGE-L:

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

يمكنك بعد ذلك استخدام F₁ لتجميع مقياسَي ROUGE-L recall وROUGE-L precision في مقياس واحد:

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

انقر على الرمز للحصول على مثال على عملية احتساب مقياس ROUGE-L.

ضَع في اعتبارك النص المرجعي والنص الذي تم إنشاؤه التاليَين.

الفئة	مَن أنتج؟	نص
النص المرجعي	مترجم بشري	أريد فهم مجموعة متنوعة من الأشياء.
النص الذي يتم إنشاؤه	نموذج تعلُّم الآلة	أريد تعلُّم الكثير من الأشياء.

وبناءً على ذلك:

• أطول تسلسل فرعي مشترك هو 5 (أريد أن أفعل بعض الأمور)
• عدد الكلمات في النص المرجعي هو 9.
• عدد الكلمات في النص الذي تم إنشاؤه هو 7.

نتيجةً لذلك:

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

تتجاهل مقياس ROUGE-L أي أسطر جديدة في النص المرجعي والنص الذي تم إنشاؤه، لذا يمكن أن يتضمّن أطول تسلسل فرعي مشترك عدة جمل. عندما يتضمّن النص المرجعي والنص الذي تم إنشاؤه جملًا متعددة، يكون مقياس ROUGE-Lsum، وهو صيغة معدّلة من مقياس ROUGE-L، أفضل بشكل عام. تحدّد مقياس ROUGE-Lsum أطول تسلسل فرعي مشترك لكل جملة في فقرة، ثم يحسب متوسط أطول التسلسلات الفرعية المشتركة.

انقر على الرمز للحصول على مثال لحساب ROUGE-Lsum.

ضَع في اعتبارك النص المرجعي والنص الذي تم إنشاؤه التاليَين.

الفئة	مَن أنتج؟	نص
النص المرجعي	مترجم بشري	سطح المريخ جاف. ويقع معظم الماء على عمق كبير تحت الأرض.
النص الذي يتم إنشاؤه	نموذج تعلُّم الآلة	سطح المريخ جاف. ومع ذلك، فإنّ الغالبية العظمى من المياه توجد تحت الأرض.

ولذلك:

	الجملة الأولى	الجملة الثانية
أطول تسلسل مشترك	‫2 (المريخ جاف)	‫3 (المياه تحت الأرض)
طول جملة النص المرجعي	6	7
طول الجملة في النص الذي تم إنشاؤه	5	8

نتيجةً لذلك:

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#Metric

مجموعة من المقاييس ضمن عائلة ROUGE تقارن بين N-grams المشتركة بحجم معيّن في النص المرجعي والنص الذي تم إنشاؤه. على سبيل المثال:

• تقيس مقياس ROUGE-1 عدد الرموز المميزة المشتركة في النص المرجعي والنص الذي تم إنشاؤه.
• يقيس مقياس ROUGE-2 عدد ثنائيات الحروف (ثنائيات الحروف) المشتركة في النص المرجعي والنص الذي تم إنشاؤه.
• يقيس مقياس ROUGE-3 عدد الثلاثيات المشتركة (3-grams) في النص المرجعي والنص الذي تم إنشاؤه.

يمكنك استخدام الصيغ التالية لاحتساب مقياسَي التذكّر والدقة في ROUGE-N لأي عنصر من عناصر عائلة ROUGE-N:

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

يمكنك بعد ذلك استخدام F₁ لتجميع مقياسَي الاسترجاع والدقة في ROUGE-N في مقياس واحد:

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

انقر على الرمز للاطّلاع على مثال.

لنفترض أنّك قرّرت استخدام مقياس ROUGE-2 لقياس فعالية ترجمة نموذج تعلُّم الآلة مقارنةً بالترجمة التي يقدّمها مترجم بشري.

الفئة	مَن أنتج؟	نص	Bigrams
النص المرجعي	مترجم بشري	أريد فهم مجموعة متنوعة من الأشياء.	أريد، أريد أن، أن أفهم، أفهم مجموعة، مجموعة واسعة، واسعة من، من الأشياء
النص الذي يتم إنشاؤه	نموذج تعلُّم الآلة	أريد تعلُّم الكثير من الأشياء.	أريد أن أتعلّم الكثير من الأشياء

وبناءً على ذلك:

• عدد الثنائيات المتطابقة هو 3 (أريد وأريد أن ومن الأشياء).
• عدد الثنائيات في النص المرجعي هو 8.
• عدد الثنائيات في النص الذي تم إنشاؤه هو 6.

نتيجةً لذلك:

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#Metric

شكل متسامح من ROUGE-N يتيح مطابقة skip-gram. أي أنّ مقياس ROUGE-N لا يحتسب سوى N-grams التي تتطابق تمامًا، ولكن مقياس ROUGE-S يحتسب أيضًا N-grams التي تفصل بينها كلمة واحدة أو أكثر. على سبيل المثال، يمكنك القيام بما يلي:

• النص المرجعي: غيوم بيضاء
• النص الذي تم إنشاؤه: سُحب بيضاء متطايرة

عند احتساب مقياس ROUGE-N، لا يتطابق المقطع الثنائي غيوم بيضاء مع غيوم بيضاء متراكمة. ومع ذلك، عند احتساب مقياس ROUGE-S، فإنّ الغيوم البيضاء تتطابق مع الغيوم البيضاء المتصاعدة.

معامل التحديد

#Metric

مقياس الانحدار الذي يشير إلى مقدار التباين في تصنيف بسبب ميزة فردية أو مجموعة ميزات قيمة R^2 هي قيمة بين 0 و1، ويمكن تفسيرها على النحو التالي:

• تشير قيمة R-squared البالغة 0 إلى أنّ أيًا من الاختلافات في التصنيف لا يعود إلى مجموعة الميزات.
• يشير معامل التحديد R-squared الذي تبلغ قيمته 1 إلى أنّ كل التباين في التصنيف يرجع إلى مجموعة الميزات.
• يشير معامل تحديد بين 0 و1 إلى مدى إمكانية توقّع التباين في التصنيف من ميزة معيّنة أو مجموعة الميزات. على سبيل المثال، يعني معامل التحديد البالغ 0.10 أنّ %10 من التباين في التصنيف يرجع إلى مجموعة الميزات، ويعني معامل التحديد البالغ 0.20 أنّ %20 من التباين يرجع إلى مجموعة الميزات، وهكذا.

معامل تحديد الارتباط هو مربع معامل ارتباط بيرسون بين القيم التي توقّعها النموذج والحقيقة الأساسية.

S

تسجيل النتائج

#Metric

جزء من نظام الاقتراحات يقدّم قيمة أو ترتيبًا لكل عنصر تم إنتاجه في مرحلة إنشاء المرشّحين.

مقياس التشابه

#clustering

#Metric

في خوارزميات التجميع، يشير ذلك المصطلح إلى المقياس المستخدَم لتحديد مدى التشابه بين أي مثالَين.

مقياس التناثر

#Metric

عدد العناصر التي تم ضبطها على صفر (أو قيمة فارغة) في متّجه أو مصفوفة مقسومًا على إجمالي عدد الإدخالات في هذا المتّجه أو المصفوفة على سبيل المثال، لنفترض أنّ لديك مصفوفة تتضمّن 100 عنصر، منها 98 خلية تحتوي على القيمة صفر. يتم احتساب مقياس التباين على النحو التالي:

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

تشير ندرة الخصائص إلى ندرة خطوط متجهة للخصائص، وتشير ندرة النماذج إلى ندرة أوزان النماذج.

تربيع الخسارة المفصلية

#Metric

مربّع الخسارة المفصلية تفرض الخسارة المفصلية التربيعية عقوبة أشد على القيم الشاذة مقارنةً بالخسارة المفصلية العادية.

الخسارة التربيعية

#fundamentals

#Metric

مرادف الخسارة_{التربيعية}

T

فقدان الاختبار

#fundamentals

#Metric

مقياس يمثّل الخسارة التي يتكبّدها النموذج مقارنةً بمجموعة الاختبار عند إنشاء نموذج، تحاول عادةً تقليل خسارة الاختبار. ويرجع ذلك إلى أنّ انخفاض مقياس القصور في مجموعة الاختبار هو إشارة جودة أقوى من انخفاض مقياس القصور في مجموعة التدريب أو انخفاض مقياس القصور في مجموعة التحقّق.

يشير الفارق الكبير بين خسارة الاختبار وخسارة التدريب أو خسارة التحقّق أحيانًا إلى ضرورة زيادة معدّل التسوية.

دقة أعلى k

#Metric

النسبة المئوية لعدد المرات التي يظهر فيها "تصنيف مستهدَف" ضمن أول k مواضع في القوائم التي تم إنشاؤها يمكن أن تكون القوائم اقتراحات مخصّصة أو قائمة بعناصر مرتّبة حسب softmax.

يُعرف مقياس "دقة أعلى k" أيضًا باسم الدقة عند k.

ملاحظة: يمكن أن تكون التصنيفات المستهدَفة أي فئة (وليس بالضرورة فئة الحقيقة الأساسية)، لذا لا تكون دقة أعلى k نتائج مطابقة مكافئة دائمًا للدقة التقليدية.

انقر على الرمز للاطّلاع على مثال.

لنفترض أنّ هناك نظامًا لتعلُّم الآلة يستخدم دالة softmax لتحديد احتمالات أنواع الأشجار استنادًا إلى صورة لأوراق الشجر. يعرض الجدول التالي قوائم النتائج التي تم إنشاؤها من خمس صور لأشجار الإدخال. يحتوي كل صف على تصنيف مستهدَف وأكثر خمسة تصنيفات احتمالية. على سبيل المثال، عندما كانت التسمية المستهدَفة هي شجرة القيقب، حدّد نموذج تعلُّم الآلة شجرة الدردار على أنّها الشجرة الأكثر احتمالاً، وشجرة البلوط على أنّها الشجرة الثانية الأكثر احتمالاً، وهكذا.

تصنيف الهدف	1	2	3	4	5
قيقب	elm	البلوط	maple	زان	حور
قرانيا	البلوط	dogwood	حور	hickory	قيقب
البلوط	oak	الزيزفون	جراد	ألدر	linden
linden	قيقب	paw-paw	البلوط	الزيزفون	حور
البلوط	جراد	linden	oak	قيقب	paw-paw

يظهر التصنيف المستهدف في الموضع الأول مرة واحدة فقط، لذا تكون دقة أعلى تصنيف كما يلي:

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

يظهر التصنيف المستهدف في أحد المراكز الثلاثة الأولى أربع مرات، وبالتالي تكون دقة المراكز الثلاثة الأولى كما يلي:

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

لغة غير لائقة

#Metric

درجة إساءة المحتوى أو تهديده أو إهانته يمكن للعديد من نماذج تعلُّم الآلة تحديد مستوى السمية وقياسه. تحدّد معظم هذه النماذج مستوى السمية وفقًا لمعايير متعدّدة، مثل مستوى اللغة المسيئة ومستوى اللغة التي تتضمّن تهديدات.

فقدان التدريب

#fundamentals

#Metric

مقياس يمثّل الخسارة التي يتكبّدها النموذج خلال عملية تدريب معيّنة. على سبيل المثال، لنفترض أنّ دالة الخسارة هي متوسط الخطأ التربيعي. لنفترض أنّ الخطأ في التدريب (متوسط الخطأ التربيعي) في التكرار العاشر هو 2.2، وأنّ الخطأ في التدريب في التكرار المئة هو 1.9.

يعرض مخطّط الخسارة الخسارة أثناء التدريب مقابل عدد التكرارات. تقدّم منحنى الخسارة التلميحات التالية حول التدريب:

• يشير الميل الهبوطي إلى أنّ النموذج يتحسّن.
• يشير الميل التصاعدي إلى أنّ النموذج يزداد سوءًا.
• يشير الميل المسطّح إلى أنّ النموذج قد بلغ حالة التقارب.

على سبيل المثال، يوضّح منحنى الخسارة المثالي إلى حد ما التالي ما يلي:

• ميل حادّ نحو الأسفل خلال التكرارات الأولية، ما يشير إلى تحسُّن سريع في النموذج
• ميل ينخفض تدريجيًا (ولكنه يظلّ متّجهًا للأسفل) إلى أن يقترب من نهاية التدريب، ما يشير إلى تحسّن مستمر في النموذج بوتيرة أبطأ بعض الشيء من التكرارات الأولية
• ميل مستوٍ في نهاية التدريب، ما يشير إلى التقارب

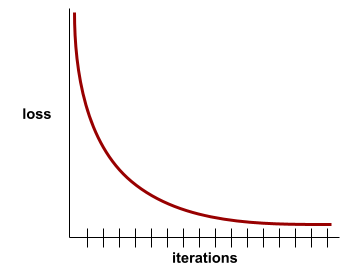
على الرغم من أهمية فقدان التدريب، يُرجى الاطّلاع أيضًا على التعميم.

سالب صحيح

#fundamentals

#Metric

مثال يوضّح كيف يتنبأ النموذج بشكل صحيح بالفئة السلبية. على سبيل المثال، يستنتج النموذج أنّ رسالة إلكترونية معيّنة ليست رسالة غير مرغوب فيها، وأنّ هذه الرسالة الإلكترونية ليست رسالة غير مرغوب فيها بالفعل.

موجب صحيح (TP)

#fundamentals

#Metric

مثال يوضح كيف يتنبأ النموذج بشكل صحيح بالفئة الإيجابية. على سبيل المثال، يستنتج النموذج أنّ رسالة إلكترونية معيّنة هي رسالة غير مرغوب فيها، وأنّ هذه الرسالة الإلكترونية هي بالفعل رسالة غير مرغوب فيها.

معدّل الموجب الصحيح (TPR)

#fundamentals

#Metric

مرادف لكلمة استدعاء والمقصود:

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

معدل الموجب الصحيح هو المحور الصادي في منحنى ROC.

V

فقدان التحقّق من الصحة

#fundamentals

#Metric

مقياس يمثّل الخسارة التي يتكبّدها النموذج على مجموعة التحقّق خلال تكرار معيّن من التدريب.

يمكنك الاطّلاع أيضًا على منحنى التعميم.

أهمية المتغيرات

#df

#Metric

مجموعة من النتائج تشير إلى الأهمية النسبية لكل سمة في النموذج.

على سبيل المثال، لنفترض أنّ لديك شجرة قرارات تقدّر أسعار المنازل. لنفترض أنّ شجرة القرار هذه تستخدم ثلاث سمات: الحجم والعمر والأسلوب. إذا تم حساب مجموعة من أهمية المتغيرات للميزات الثلاث على النحو التالي: {size=5.8, age=2.5, style=4.7}، فإنّ الحجم أكثر أهمية لشجرة القرار من العمر أو النمط.

تتوفّر مقاييس مختلفة لأهمية المتغيرات، ويمكن أن تفيد خبراء تعلُّم الآلة بشأن جوانب مختلفة من النماذج.

واط

دالة الخسارة Wasserstein

#Metric

إحدى دوال الخسارة الشائعة الاستخدام في الشبكات التوليدية الخصومية، استنادًا إلى مسافة نقل التراب بين توزيع البيانات التي تم إنشاؤها والبيانات الحقيقية.