Glosario de aprendizaje automático: Métricas

Esta página contiene términos del glosario de métricas. Para consultar todos los términos del glosario, haz clic aquí.

A

exactitud

#fundamentals

#Metric

Es la cantidad de predicciones de clasificación correctas dividida por la cantidad total de predicciones. Es decir:

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

Por ejemplo, un modelo que realizó 40 predicciones correctas y 10 incorrectas tendría una precisión de:

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

La clasificación binaria proporciona nombres específicos para las diferentes categorías de predicciones correctas y predicciones incorrectas. Por lo tanto, la fórmula de exactitud para la clasificación binaria es la siguiente:

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

Donde:

• TP es la cantidad de verdaderos positivos (predicciones correctas).
• TN es la cantidad de verdaderos negativos (predicciones correctas).
• FP es la cantidad de falsos positivos (predicciones incorrectas).
• FN es la cantidad de falsos negativos (predicciones incorrectas).

Compara y contrasta la exactitud con la precisión y la recuperación.

Haz clic en el ícono para obtener detalles sobre la precisión y los conjuntos de datos desequilibrados en cuanto a las clases.

Si bien es una métrica valiosa en algunas situaciones, la precisión es muy engañosa en otras. En particular, la exactitud suele ser una métrica deficiente para evaluar los modelos de clasificación que procesan conjuntos de datos con desequilibrio de clases.

Por ejemplo, supongamos que en una determinada ciudad subtropical nieva solo 25 días por siglo. Dado que los días sin nieve (la clase negativa) superan ampliamente a los días con nieve (la clase positiva), el conjunto de datos de nieve para esta ciudad está desequilibrado en cuanto a las clases. Imagina un modelo de clasificación binaria que debería predecir si nevará o no cada día, pero que simplemente predice "no nevará" todos los días. Este modelo es muy preciso, pero no tiene poder predictivo. En la siguiente tabla, se resumen los resultados para un siglo de predicciones:

Categoría	Número
VP	0
TN	36499
FP	0
FN	25

Por lo tanto, la precisión de este modelo es la siguiente:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

Si bien el 99.93% de exactitud parece un porcentaje muy impresionante, el modelo en realidad no tiene poder predictivo.

La precisión y la recuperación suelen ser métricas más útiles que la exactitud para evaluar modelos entrenados en conjuntos de datos con clases desequilibradas.

---

Consulta Clasificación: Precisión, recuperación, exactitud y métricas relacionadas en el Curso intensivo de aprendizaje automático para obtener más información.

Área bajo la curva de PR

#Metric

Consulta PR AUC (área bajo la curva de PR).

área bajo la curva ROC

#Metric

Consulta AUC (área bajo la curva ROC).

AUC (área bajo la curva ROC)

#fundamentals

#Metric

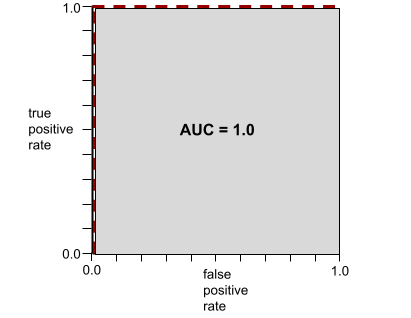
Es un número entre 0.0 y 1.0 que representa la capacidad de un modelo de clasificación binaria para separar las clases positivas de las clases negativas. Cuanto más cerca esté el AUC de 1.0, mejor será la capacidad del modelo para separar las clases entre sí.

Por ejemplo, la siguiente ilustración muestra un modelo de clasificación que separa perfectamente las clases positivas (óvalos verdes) de las clases negativas (rectángulos morados). Este modelo irrealmente perfecto tiene un AUC de 1.0:

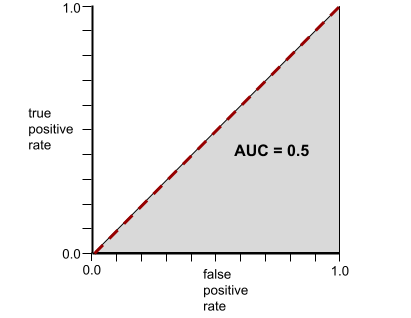
Por el contrario, la siguiente ilustración muestra los resultados de un modelo de clasificación que generó resultados aleatorios. Este modelo tiene un AUC de 0.5:

Sí, el modelo anterior tiene un AUC de 0.5, no de 0.0.

La mayoría de los modelos se encuentran en algún punto intermedio entre los dos extremos. Por ejemplo, el siguiente modelo separa los positivos de los negativos en cierta medida y, por lo tanto, tiene un AUC entre 0.5 y 1.0:

El AUC ignora cualquier valor que establezcas para el umbral de clasificación. En cambio, el AUC considera todos los umbrales de clasificación posibles.

Haz clic en el ícono para obtener información sobre la relación entre las curvas ROC y el AUC.

El AUC representa el área bajo una curva ROC. Por ejemplo, la curva ROC de un modelo que separa perfectamente los positivos de los negativos se ve de la siguiente manera:

El AUC es el área de la región gris en la ilustración anterior. En este caso inusual, el área es simplemente la longitud de la región gris (1.0) multiplicada por el ancho de la región gris (1.0). Por lo tanto, el producto de 1.0 y 1.0 genera un AUC de exactamente 1.0, que es la puntuación de AUC más alta posible.

Por el contrario, la curva ROC para un modelo de clasificación que no puede separar las clases en absoluto es la siguiente. El área de esta región gris es 0.5.

Una curva ROC más típica se ve aproximadamente de la siguiente manera:

Calcular el área bajo esta curva de forma manual sería un trabajo arduo, por lo que, por lo general, un programa calcula la mayoría de los valores del AUC.

---

Haz clic en el ícono para obtener una definición más formal del AUC.

El AUC es la probabilidad de que un modelo de clasificación tenga más certeza de que un ejemplo positivo elegido al azar sea realmente positivo que de que un ejemplo negativo elegido al azar sea positivo.

---

Para obtener más información, consulta Clasificación: ROC y AUC en el Curso intensivo de aprendizaje automático.

Precisión promedio en k

#Metric

Es una métrica para resumir el rendimiento de un modelo en una sola instrucción que genera resultados clasificados, como una lista numerada de recomendaciones de libros. La precisión promedio en k es, bueno, el promedio de los valores de precisión en k para cada resultado relevante. Por lo tanto, la fórmula para la precisión promedio en k es la siguiente:

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

Donde:

• \(n\) es la cantidad de elementos pertinentes en la lista.

Compara esto con la recuperación en k.

Nota: La precisión promedio en k evalúa el resultado para una sola instrucción. Usa la métrica precisión media en k para evaluar la calidad del resultado de un modelo en muchas instrucciones diferentes.

Nota: Algunas personas abrevian precisión media en k como precisión media.

Haz clic en el ícono para ver un ejemplo.

Supongamos que se le da la siguiente búsqueda a un modelo de lenguaje grande:

List the 6 funniest movies of all time in order.

Y el modelo de lenguaje grande devuelve la siguiente lista:

1. El general
2. Mean Girls
3. Pelotón
4. Damas en guerra
5. Citizen Kane
6. This is Spinal Tap

Cuatro de las películas de la lista devuelta son muy divertidas (es decir, son relevantes), pero dos son dramas (no son relevantes). En la siguiente tabla, se detallan los resultados:

Posición	Película	¿Es relevante?	Precisión en k
1	El general	Sí	1.0
2	Mean Girls	Sí	1.0
3	Pelotón	No	No es relevante
4	Damas en guerra	Sí	0.75
5	Citizen Kane	No	No es relevante
6	This is Spinal Tap	Sí	0.67

La cantidad de resultados relevantes es 4. Por lo tanto, puedes calcular la precisión promedio en 6 de la siguiente manera:

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

modelo de referencia

#Metric

Un modelo que se usa como punto de referencia para comparar el rendimiento de otro modelo (por lo general, uno más complejo). Por ejemplo, un modelo de regresión logística podría servir como un buen modelo de referencia para un modelo profundo.

Para un problema en particular, el modelo de referencia ayuda a los desarrolladores a cuantificar el rendimiento mínimo esperado que debe alcanzar un modelo nuevo para que sea útil.

C

costo

#Metric

Sinónimo de pérdida.

Equidad contrafáctica

#responsible

#Metric

Es una métrica de equidad que verifica si un modelo de clasificación produce el mismo resultado para una persona que para otra idéntica a la primera, excepto en lo que respecta a uno o más atributos sensibles. Evaluar un modelo de clasificación para la equidad contrafáctica es un método para identificar posibles fuentes de sesgo en un modelo.

Consulta cualquiera de los siguientes artículos para obtener más información:

• Equidad: Equidad contrafáctica en el Curso intensivo de aprendizaje automático.
• When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness (Cuando los mundos chocan: Integración de diferentes suposiciones contrafácticas en la equidad)

entropía cruzada

#Metric

Es una generalización de la pérdida de registro para problemas de clasificación de clases múltiples. La entropía cruzada cuantifica la diferencia entre dos distribuciones de probabilidad. Consulta también perplejidad.

Función de distribución acumulativa (FDA)

#Metric

Es una función que define la frecuencia de las muestras menores o iguales que un valor objetivo. Por ejemplo, considera una distribución normal de valores continuos. Una CDF te indica que, aproximadamente, el 50% de las muestras deben ser menores o iguales a la media y que, aproximadamente, el 84% de las muestras deben ser menores o iguales a una desviación estándar por encima de la media.

D

Paridad demográfica

#responsible

#Metric

Es una métrica de equidad que se cumple si los resultados de la clasificación de un modelo no dependen de un atributo sensible determinado.

Por ejemplo, si tanto los liliputienses como los brobdingnagianos postulan a la Universidad de Glubbdubdrib, se logra la paridad demográfica si el porcentaje de liliputienses admitidos es el mismo que el porcentaje de brobdingnagianos admitidos, independientemente de si un grupo está, en promedio, más calificado que el otro.

Esto contrasta con la igualdad de probabilidades y la igualdad de oportunidades, que permiten que los resultados de la clasificación en conjunto dependan de atributos sensibles, pero no permiten que los resultados de la clasificación para ciertas etiquetas de verdad fundamental especificadas dependan de atributos sensibles. Consulta "Cómo combatir la discriminación con un aprendizaje automático más inteligente" para ver una visualización que explora las compensaciones cuando se optimiza la paridad demográfica.

Consulta Equidad: paridad demográfica en el Curso intensivo de aprendizaje automático para obtener más información.

E

Distancia de Earth Mover (EMD)

#Metric

Es una medida de la similitud relativa de dos distribuciones. Cuanto menor sea la distancia de movimiento de tierra, más similares serán las distribuciones.

Distancia de edición

#Metric

Es una medición de la similitud entre dos cadenas de texto. En el aprendizaje automático, la distancia de edición es útil por los siguientes motivos:

• La distancia de edición es fácil de calcular.
• La distancia de edición puede comparar dos cadenas que se sabe que son similares entre sí.
• La distancia de edición puede determinar el grado en que diferentes cadenas son similares a una cadena determinada.

Existen varias definiciones de distancia de edición, cada una con diferentes operaciones de cadenas. Consulta Distancia de Levenshtein para ver un ejemplo.

función de distribución acumulativa empírica (eCDF o EDF)

#Metric

Una función de distribución acumulativa basada en mediciones empíricas de un conjunto de datos real. El valor de la función en cualquier punto a lo largo del eje X es la fracción de observaciones en el conjunto de datos que son menores o iguales que el valor especificado.

entropía

#df

#Metric

En la teoría de la información, es una descripción de qué tan impredecible es una distribución de probabilidad. Como alternativa, la entropía también se define como la cantidad de información que contiene cada ejemplo. Una distribución tiene la entropía más alta posible cuando todos los valores de una variable aleatoria son igualmente probables.

La entropía de un conjunto con dos valores posibles "0" y "1" (por ejemplo, las etiquetas en un problema de clasificación binaria) tiene la siguiente fórmula:

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

Donde:

• H es la entropía.
• p es la fracción de ejemplos de "1".
• q es la fracción de ejemplos "0". Ten en cuenta que q = (1 - p).
• log suele ser log₂. En este caso, la unidad de entropía es un bit.

Por ejemplo, supongamos lo siguiente:

• 100 ejemplos contienen el valor "1".
• 300 ejemplos contienen el valor "0".

Por lo tanto, el valor de la entropía es el siguiente:

• p = 0.25
• q = 0.75
• H = (-0.25)log₂(0.25) - (0.75)log₂(0.75) = 0.81 bits por ejemplo

Un conjunto perfectamente equilibrado (por ejemplo, 200 "0" y 200 "1") tendría una entropía de 1.0 bits por ejemplo. A medida que un conjunto se vuelve más desequilibrado, su entropía se acerca a 0.0.

En los árboles de decisión, la entropía ayuda a formular la ganancia de información para ayudar al divisor a seleccionar las condiciones durante el crecimiento de un árbol de decisión de clasificación.

Compara la entropía con lo siguiente:

• impureza de Gini
• Función de pérdida de entropía cruzada

A menudo, la entropía se denomina entropía de Shannon.

Consulta Divisor exacto para la clasificación binaria con características numéricas en el curso de Bosques de decisión para obtener más información.

Igualdad de oportunidades

#responsible

#Metric

Una métrica de equidad para evaluar si un modelo predice el resultado deseable con la misma precisión para todos los valores de un atributo sensible. En otras palabras, si el resultado deseable para un modelo es la clase positiva, el objetivo sería que la tasa de verdaderos positivos sea la misma para todos los grupos.

La igualdad de oportunidades se relaciona con la igualdad de probabilidades, que requiere que tanto las tasas de verdaderos positivos como las tasas de falsos positivos sean las mismas para todos los grupos.

Supongamos que la Universidad de Glubbdubdrib admite tanto a liliputienses como a brobdingnagianos en un programa riguroso de matemáticas. Las escuelas secundarias de Lilliput ofrecen un plan de estudios sólido de clases de matemáticas, y la gran mayoría de los estudiantes están calificados para el programa universitario. Las escuelas secundarias de Brobdingnag no ofrecen clases de matemáticas, por lo que muchos menos estudiantes están calificados. Se satisface la igualdad de oportunidades para la etiqueta preferida de "admitido" con respecto a la nacionalidad (liliputiense o brobdingnagiana) si los estudiantes calificados tienen la misma probabilidad de ser admitidos, independientemente de si son liliputienses o brobdingnagianos.

Por ejemplo, supongamos que 100 liliputienses y 100 brobdingnagianos solicitan ingresar a la Universidad de Glubbdubdrib, y las decisiones de admisión se toman de la siguiente manera:

Tabla 1: Solicitantes de Lilliputian (el 90% cumple con los requisitos)

	Calificado	No cumple con los requisitos
Admitida	45	3
Rechazado	45	7
Total	90	10
Porcentaje de estudiantes calificados admitidos: 45/90 = 50% Porcentaje de estudiantes no calificados rechazados: 7/10 = 70% Porcentaje total de estudiantes de Lilliput admitidos: (45 + 3)/100 = 48%

 

Tabla 2: Solicitantes brobdingnagianos (el 10% está calificado):

	Calificado	No cumple con los requisitos
Admitida	5	9
Rechazado	5	81
Total	10	90
Porcentaje de estudiantes calificados admitidos: 5/10 = 50% Porcentaje de estudiantes no calificados rechazados: 81/90 = 90% Porcentaje total de estudiantes de Brobdingnag admitidos: (5 + 9)/100 = 14%

Los ejemplos anteriores satisfacen la igualdad de oportunidades para la aceptación de estudiantes calificados, ya que tanto los liliputienses como los brobdingnagianos calificados tienen un 50% de probabilidades de ser admitidos.

Si bien se satisface la igualdad de oportunidades, no se satisfacen las siguientes dos métricas de equidad:

• Paridad demográfica: Los liliputienses y los brobdingnagianos son admitidos en la universidad en diferentes proporciones: el 48% de los estudiantes liliputienses son admitidos, pero solo el 14% de los estudiantes brobdingnagianos.
• Probabilidades ecualizadas: Si bien los estudiantes calificados de Liliput y Brobdingnag tienen la misma probabilidad de ser admitidos, no se cumple la restricción adicional de que los estudiantes no calificados de Liliput y Brobdingnag tengan la misma probabilidad de ser rechazados. Los liliputienses no calificados tienen una tasa de rechazo del 70%, mientras que los brobdingnagianos no calificados tienen una tasa de rechazo del 90%.

Consulta Equidad: Igualdad de oportunidades en el Curso intensivo de aprendizaje automático para obtener más información.

Probabilidades ecualizadas

#responsible

#Metric

Es una métrica de equidad para evaluar si un modelo predice resultados con la misma precisión para todos los valores de un atributo sensible con respecto a la clase positiva y la clase negativa, no solo una clase o la otra de forma exclusiva. En otras palabras, tanto la tasa de verdaderos positivos como la tasa de falsos negativos deben ser iguales para todos los grupos.

La métrica de probabilidades igualadas se relaciona con la igualdad de oportunidades, que solo se enfoca en las tasas de error para una sola clase (positiva o negativa).

Por ejemplo, supongamos que la Universidad de Glubbdubdrib admite tanto a liliputienses como a brobdingnagianos en un riguroso programa de matemáticas. Las escuelas secundarias de Lilliput ofrecen un plan de estudios sólido de clases de matemáticas, y la gran mayoría de los estudiantes están calificados para el programa universitario. Las escuelas secundarias de Brobdingnag no ofrecen clases de matemáticas, por lo que muchos menos estudiantes están calificados. Se satisfacen las probabilidades igualadas siempre que, sin importar si un solicitante es liliputiense o brobdingnagiano, si está calificado, es igualmente probable que sea admitido en el programa y, si no está calificado, es igualmente probable que sea rechazado.

Supongamos que 100 liliputienses y 100 brobdingnagianos solicitan ingresar a la Universidad de Glubbdubdrib, y las decisiones de admisión se toman de la siguiente manera:

Tabla 3: Solicitantes de Lilliputian (el 90% cumple con los requisitos)

	Calificado	No cumple con los requisitos
Admitida	45	2
Rechazado	45	8
Total	90	10
Porcentaje de estudiantes calificados admitidos: 45/90 = 50% Porcentaje de estudiantes no calificados rechazados: 8/10 = 80% Porcentaje total de estudiantes de Lilliput admitidos: (45 + 2)/100 = 47%

 

Tabla 4. Solicitantes brobdingnagianos (el 10% está calificado):

	Calificado	No cumple con los requisitos
Admitida	5	18
Rechazado	5	72
Total	10	90
Porcentaje de estudiantes calificados admitidos: 5/10 = 50% Porcentaje de estudiantes no calificados rechazados: 72/90 = 80% Porcentaje total de estudiantes de Brobdingnag admitidos: (5 + 18)/100 = 23%

Se cumple la igualdad de probabilidades porque los estudiantes calificados de Liliput y Brobdingnag tienen un 50% de probabilidades de ser admitidos, y los estudiantes no calificados de Liliput y Brobdingnag tienen un 80% de probabilidades de ser rechazados.

Nota: Si bien aquí se cumple la igualdad de probabilidades, no se cumple la paridad demográfica. Los estudiantes liliputienses y brobdingnagianos son admitidos en la Universidad de Glubbdubdrib en diferentes proporciones: el 47% de los estudiantes liliputienses son admitidos, y el 23% de los estudiantes brobdingnagianos son admitidos.

La igualdad de probabilidades se define formalmente en "Equality of Opportunity in Supervised Learning" de la siguiente manera: "El predictor Ŷ satisface la igualdad de probabilidades con respecto al atributo protegido A y el resultado Y si Ŷ y A son independientes, condicionales en Y".

Nota: Compara la métrica de probabilidades iguales con la métrica más flexible de igualdad de oportunidades.

evals

#generativeAI

#Metric

Se usa principalmente como abreviatura de evaluaciones de LLM. En términos más generales, evals es la abreviatura de cualquier forma de evaluación.

sin conexión

#generativeAI

#Metric

Proceso para medir la calidad de un modelo o comparar diferentes modelos entre sí.

Para evaluar un modelo de aprendizaje automático supervisado, por lo general, lo comparas con un conjunto de validación y un conjunto de prueba. Evaluar un LLM suele implicar evaluaciones más amplias de calidad y seguridad.

F

F₁

#Metric

Es una métrica de clasificación binaria "acumulada" que se basa tanto en la precisión como en la recuperación. Esta es la fórmula:

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

Haz clic en el ícono para ver ejemplos.

Supongamos que la precisión y la recuperación tienen los siguientes valores:

• precisión = 0.6
• recuperación = 0.4

Puedes calcular F₁ de la siguiente manera:

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

Cuando la precisión y la recuperación son bastante similares (como en el ejemplo anterior), la F₁ se acerca a su media. Cuando la precisión y la recuperación difieren significativamente, F₁ se acerca al valor más bajo. Por ejemplo:

• precisión = 0.9
• recuperación = 0.1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

métrica de equidad

#responsible

#Metric

Una definición matemática de "equidad" que se pueda medir Algunas métricas de equidad de uso común son las siguientes:

• Probabilidades igualadas
• Paridad predictiva
• Equidad contrafáctica
• Paridad demográfica

Muchas métricas de equidad son mutuamente excluyentes. Consulta la incompatibilidad de métricas de equidad.

falso negativo (FN)

#fundamentals

#Metric

Ejemplo en el que el modelo predice de manera incorrecta la clase negativa. Por ejemplo, el modelo predice que un mensaje de correo electrónico en particular no es spam (la clase negativa), pero ese mensaje de correo electrónico en realidad es spam.

tasa de falsos negativos

#Metric

Proporción de ejemplos positivos reales para los que el modelo predijo erróneamente la clase negativa. La siguiente fórmula calcula la tasa de falsos negativos:

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

Para obtener más información, consulta Umbrales y la matriz de confusión en el Curso intensivo de aprendizaje automático.

Falso positivo (FP)

#fundamentals

#Metric

Ejemplo en el que el modelo predice de manera incorrecta la clase positiva. Por ejemplo, el modelo predice que un mensaje de correo electrónico en particular es spam (la clase positiva), pero ese mensaje de correo electrónico en realidad no es spam.

Para obtener más información, consulta Umbrales y la matriz de confusión en el Curso intensivo de aprendizaje automático.

tasa de falsos positivos (FPR)

#fundamentals

#Metric

Proporción de ejemplos negativos reales para los que el modelo predijo erróneamente la clase positiva. La siguiente fórmula calcula la tasa de falsos positivos:

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

La tasa de falsos positivos es el eje X en una curva ROC.

Para obtener más información, consulta Clasificación: ROC y AUC en el Curso intensivo de aprendizaje automático.

Importancia de los atributos

#df

#Metric

Sinónimo de importancia de las variables.

modelo de base

#generativeAI

#Metric

Un modelo previamente entrenado muy grande entrenado con un conjunto de entrenamiento enorme y diverso. Un modelo de base puede hacer lo siguiente:

• Responder bien a una amplia variedad de solicitudes
• Sirve como un modelo base para ajustes adicionales o cualquier otra personalización.

En otras palabras, un modelo de base ya es muy capaz en un sentido general, pero se puede personalizar aún más para que sea más útil para una tarea específica.

fracción de éxitos

#generativeAI

#Metric

Es una métrica para evaluar el texto generado de un modelo de AA. La fracción de éxitos es la cantidad de resultados de texto generados "exitosos" dividida por la cantidad total de resultados de texto generados. Por ejemplo, si un modelo de lenguaje grande generó 10 bloques de código, de los cuales cinco fueron exitosos, la fracción de éxitos sería del 50%.

Si bien la fracción de éxitos es útil en general en las estadísticas, en el AA, esta métrica es principalmente útil para medir tareas verificables, como la generación de código o los problemas matemáticos.

G

Impureza de Gini

#df

#Metric

Es una métrica similar a la entropía. Los divisores usan valores derivados de la impureza de Gini o la entropía para componer condiciones para los árboles de decisión de clasificación. La ganancia de información se deriva de la entropía. No existe un término equivalente aceptado universalmente para la métrica derivada de la impureza de Gini. Sin embargo, esta métrica sin nombre es tan importante como la ganancia de información.

La impureza de Gini también se denomina índice de Gini o, simplemente, Gini.

Haz clic en el ícono para obtener detalles matemáticos sobre la impureza de Gini.

La impureza de Gini es la probabilidad de clasificar erróneamente un nuevo fragmento de datos extraído de la misma distribución. La impureza de Gini de un conjunto con dos valores posibles, "0" y "1" (por ejemplo, las etiquetas en un problema de clasificación binaria), se calcula con la siguiente fórmula:

   I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

Donde:

• I es la impureza de Gini.
• p es la fracción de ejemplos de "1".
• q es la fracción de ejemplos "0". Ten en cuenta que q = 1 - p.

Por ejemplo, considera el siguiente conjunto de datos:

• 100 etiquetas (el 0.25 del conjunto de datos) contienen el valor "1".
• 300 etiquetas (el 0.75 del conjunto de datos) contienen el valor "0".

Por lo tanto, la impureza de Gini es la siguiente:

• p = 0.25
• q = 0.75
• I = 1 - (0.25² + 0.75²) = 0.375

Por lo tanto, una etiqueta aleatoria del mismo conjunto de datos tendría un 37.5% de probabilidades de clasificarse de forma incorrecta y un 62.5% de probabilidades de clasificarse de forma correcta.

Una etiqueta perfectamente equilibrada (por ejemplo, 200 "0" y 200 "1") tendría una impureza de Gini de 0.5. Una etiqueta muy desequilibrada tendría una impureza de Gini cercana a 0.0.

---

H

Pérdida de bisagra

#Metric

Es una familia de funciones de pérdida para la clasificación diseñadas para encontrar el límite de decisión lo más distante posible de cada ejemplo de entrenamiento, para así maximizar el margen entre los ejemplos y el límite. Las KSVM usan la pérdida de bisagra (o un atributo relacionado, como la pérdida de bisagra al cuadrado). Para la clasificación binaria, la función de pérdida de bisagra se define de la siguiente manera:

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

donde y es la etiqueta verdadera, ya sea -1 o +1, y y' es el resultado sin procesar del modelo de clasificación:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

En consecuencia, un gráfico de la pérdida de bisagra en comparación con (y * y') se ve de la siguiente manera:

I

Incompatibilidad de métricas de equidad

#responsible

#Metric

La idea de que algunas nociones de equidad son mutuamente incompatibles y no se pueden satisfacer de manera simultánea. Como resultado, no existe una sola métrica universal para cuantificar la equidad que se pueda aplicar a todos los problemas de AA.

Si bien esto puede parecer desalentador, la incompatibilidad de las métricas de equidad no implica que los esfuerzos por lograr la equidad sean infructuosos. En cambio, sugiere que la equidad debe definirse de forma contextual para un problema de AA determinado, con el objetivo de evitar los daños específicos de sus casos de uso.

Consulta "On the (im)possibility of fairness" para obtener un análisis más detallado sobre la incompatibilidad de las métricas de equidad.

equidad individual

#responsible

#Metric

Es una métrica de equidad que verifica si las personas similares se clasifican de manera similar. Por ejemplo, la Academia Brobdingnagian podría querer satisfacer la equidad individual garantizando que dos estudiantes con calificaciones idénticas y resultados de pruebas estandarizadas tengan la misma probabilidad de ser admitidos.

Ten en cuenta que la equidad individual depende por completo de cómo definas la "similitud" (en este caso, las calificaciones y los resultados de las pruebas), y puedes correr el riesgo de introducir nuevos problemas de equidad si tu métrica de similitud omite información importante (como el rigor del plan de estudios de un estudiante).

Consulta "Fairness Through Awareness" para obtener un análisis más detallado de la equidad individual.

Ganancia de información

#df

#Metric

En los bosques de decisión, es la diferencia entre la entropía de un nodo y la suma ponderada (según la cantidad de ejemplos) de la entropía de sus nodos secundarios. La entropía de un nodo es la entropía de los ejemplos en ese nodo.

Por ejemplo, considera los siguientes valores de entropía:

• entropía del nodo principal = 0.6
• entropía de un nodo secundario con 16 ejemplos relevantes = 0.2
• entropía de otro nodo secundario con 24 ejemplos relevantes = 0.1

Por lo tanto, el 40% de los ejemplos se encuentran en un nodo secundario y el 60% en el otro. Por lo tanto:

• Suma de entropía ponderada de los nodos secundarios = (0.4 * 0.2) + (0.6 * 0.1) = 0.14

Por lo tanto, la ganancia de información es la siguiente:

• Ganancia de información = entropía del nodo principal - suma ponderada de la entropía de los nodos secundarios
• Ganancia de información = 0.6 - 0.14 = 0.46

La mayoría de los divisores buscan crear condiciones que maximicen la ganancia de información.

Acuerdo entre evaluadores

#Metric

Es una medición de la frecuencia con la que los evaluadores humanos coinciden cuando realizan una tarea. Si los evaluadores no están de acuerdo, es posible que deban mejorarse las instrucciones de la tarea. En algunas ocasiones, también se denomina acuerdo entre anotadores o fiabilidad entre evaluadores. Consulta también el coeficiente kappa de Cohen, que es una de las mediciones de acuerdo entre evaluadores más populares.

Consulta Datos categóricos: Problemas comunes en el Curso intensivo de aprendizaje automático para obtener más información.

L

Pérdida L₁

#fundamentals

#Metric

Una función de pérdida que calcula el valor absoluto de la diferencia entre los valores de la etiqueta real y los valores que predice un modelo. Por ejemplo, aquí se muestra el cálculo de la pérdida L₁ para un lote de cinco ejemplos:

Valor real del ejemplo	Valor predicho del modelo	Valor absoluto del delta
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = pérdida L1

La pérdida L₁ es menos sensible a los valores atípicos que la pérdida L₂.

El error absoluto medio es la pérdida promedio de L₁ por ejemplo.

Haz clic en el ícono para ver la fórmula matemática.

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

En el ejemplo anterior, se ilustra lo siguiente:

• Aquí, $n$ es la cantidad de ejemplos.
• $y$ es el valor real de la etiqueta.
• $\hat{y}$ es el valor que el modelo predice para $y$.

---

Consulta Regresión lineal: Pérdida en el Curso intensivo de aprendizaje automático para obtener más información.

Pérdida L₂

#fundamentals

#Metric

Es una función de pérdida que calcula el cuadrado de la diferencia entre los valores de la etiqueta real y los valores que predice un modelo. Por ejemplo, aquí se muestra el cálculo de la pérdida de L₂ para un lote de cinco ejemplos:

Valor real del ejemplo	Valor predicho del modelo	Cuadrado de delta
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = pérdida L2

Debido al componente cuadrático, la pérdida L₂ amplifica la influencia de los valores atípicos. Es decir, la pérdida L₂ reacciona de manera más severa a las predicciones incorrectas que la pérdida L₁. Por ejemplo, la pérdida de L₁ para el lote anterior sería de 8 en lugar de 16. Ten en cuenta que un solo valor atípico representa 9 de los 16.

Los modelos de regresión suelen usar la pérdida L₂ como función de pérdida.

El error cuadrático medio es la pérdida promedio de L₂ por ejemplo. La pérdida al cuadrado es otro nombre para la pérdida L₂.

Haz clic en el ícono para ver la fórmula matemática.

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

En el ejemplo anterior, se ilustra lo siguiente:

• Aquí, $n$ es la cantidad de ejemplos.
• $y$ es el valor real de la etiqueta.
• $\hat{y}$ es el valor que el modelo predice para $y$.

---

Para obtener más información, consulta Regresión logística: Pérdida y regularización en el Curso intensivo de aprendizaje automático.

Evaluaciones de LLM (evals)

#generativeAI

#Metric

Es un conjunto de métricas y comparativas para evaluar el rendimiento de los modelos de lenguaje grandes (LLM). A grandes rasgos, las evaluaciones de LLM son las siguientes:

• Ayudar a los investigadores a identificar áreas en las que los LLM necesitan mejorar
• Son útiles para comparar diferentes LLM y determinar cuál es el mejor para una tarea en particular.
• Ayudar a garantizar que los LLMs sean seguros y éticos para su uso

Consulta Modelos de lenguaje extenso (LLM) en el Curso intensivo de aprendizaje automático para obtener más información.

pérdida

#fundamentals

#Metric

Durante el entrenamiento de un modelo supervisado, se calcula una medida de qué tan lejos está la predicción de un modelo de su etiqueta.

Una función de pérdida calcula la pérdida.

Consulta Regresión lineal: Pérdida en el Curso intensivo de aprendizaje automático para obtener más información.

función de pérdida

#fundamentals

#Metric

Durante el entrenamiento o las pruebas, es una función matemática que calcula la pérdida en un lote de ejemplos. Una función de pérdida devuelve una pérdida menor para los modelos que realizan buenas predicciones que para los modelos que realizan predicciones deficientes.

Por lo general, el objetivo del entrenamiento es minimizar la pérdida que devuelve una función de pérdida.

Existen muchos tipos diferentes de funciones de pérdida. Elige la función de pérdida adecuada para el tipo de modelo que estás creando. Por ejemplo:

• La pérdida L₂ (o error cuadrático medio) es la función de pérdida para la regresión lineal.
• La pérdida logística es la función de pérdida para la regresión logística.

M

Error absoluto medio (MAE)

#Metric

Es la pérdida promedio por ejemplo cuando se usa la pérdida de L₁. Calcula el error absoluto medio de la siguiente manera:

1. Calcula la pérdida L₁ para un lote.
2. Divide la pérdida de L₁ por la cantidad de ejemplos del lote.

Haz clic en el ícono para ver la fórmula matemática.

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

Donde:

• Aquí, $n$ es la cantidad de ejemplos.
• $y$ es el valor real de la etiqueta.
• $\hat{y}$ es el valor que el modelo predice para $y$.

---

Por ejemplo, considera el cálculo de la pérdida de L₁ en el siguiente lote de cinco ejemplos:

Valor real del ejemplo	Valor predicho del modelo	Pérdida (diferencia entre el valor real y el valor predicho)
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = pérdida L1

Por lo tanto, la pérdida L₁ es 8 y la cantidad de ejemplos es 5. Por lo tanto, el error absoluto medio es el siguiente:

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

Compara el error absoluto medio con el error cuadrático medio y la raíz cuadrada del error cuadrático medio.

Precisión media en k (mAP@k)

#generativeAI

#Metric

Es la media estadística de todas las puntuaciones de precisión promedio en k en un conjunto de datos de validación. Un uso de la precisión media promedio en k es evaluar la calidad de las recomendaciones que genera un sistema de recomendación.

Aunque la frase "promedio medio" suena redundante, el nombre de la métrica es apropiado. Después de todo, esta métrica encuentra la media de varios valores de precisión promedio en k.

Haz clic en el ícono para ver un ejemplo.

Supongamos que creas un sistema de recomendaciones que genera una lista personalizada de novelas recomendadas para cada usuario. Según los comentarios de los usuarios seleccionados, calculas las siguientes cinco puntuaciones de precisión promedio en k (una puntuación por usuario):

• 0.73
• 0.77
• 0.67
• 0.82
• 0.76

Por lo tanto, la precisión media en K es la siguiente:

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

Error cuadrático medio (ECM)

#Metric

Es la pérdida promedio por ejemplo cuando se usa la pérdida L₂. Calcula el error cuadrático medio de la siguiente manera:

1. Calcula la pérdida L₂ para un lote.
2. Divide la pérdida L₂ por la cantidad de ejemplos del lote.

Haz clic en el ícono para ver la fórmula matemática.

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ donde:

• Aquí, $n$ es la cantidad de ejemplos.
• $y$ es el valor real de la etiqueta.
• $\hat{y}$ es la predicción del modelo para $y$.

---

Por ejemplo, considera la pérdida en el siguiente lote de cinco ejemplos:

Valor real	Predicción del modelo	Pérdida	Pérdida al cuadrado
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			16 = pérdida L2

Por lo tanto, el error cuadrático medio es el siguiente:

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

El error cuadrático medio es un optimizador de entrenamiento popular, en especial para la regresión lineal.

Compara el error cuadrático medio con el error absoluto medio y la raíz cuadrada del error cuadrático medio.

TensorFlow Playground usa el error cuadrático medio para calcular los valores de pérdida.

Haz clic en el ícono para ver más detalles sobre los valores atípicos.

Los valores atípicos influyen mucho en el error cuadrático medio. Por ejemplo, una pérdida de 1 es una pérdida al cuadrado de 1, pero una pérdida de 3 es una pérdida al cuadrado de 9. En la tabla anterior, el ejemplo con una pérdida de 3 representa aproximadamente el 56% del error cuadrático medio, mientras que cada uno de los ejemplos con una pérdida de 1 representa solo el 6% del error cuadrático medio.

Los valores atípicos no influyen en el error absoluto medio tanto como en el error cuadrático medio. Por ejemplo, una pérdida de 3 cuentas solo representa el 38% del error absoluto medio.

El recorte es una forma de evitar que los valores atípicos extremos perjudiquen la capacidad predictiva de tu modelo.

---

métrica

#TensorFlow

#Metric

Es una estadística que te interesa.

Un objetivo es una métrica que un sistema de aprendizaje automático intenta optimizar.

API de Metrics (tf.metrics)

#Metric

Es una API de TensorFlow para evaluar modelos. Por ejemplo, tf.metrics.accuracy determina con qué frecuencia las predicciones de un modelo coinciden con las etiquetas.

Pérdida de minimax

#Metric

Es una función de pérdida para las redes adversarias generativas, basada en la entropía cruzada entre la distribución de los datos generados y los datos reales.

La pérdida de Minimax se usa en el primer artículo para describir las redes adversarias generativas.

Consulta Funciones de pérdida en el curso de Redes Adversarias Generativas para obtener más información.

capacidad del modelo

#Metric

Es la complejidad de los problemas que un modelo puede aprender. Mientras más complejos sean los problemas que un modelo puede aprender, mayor será la capacidad del modelo. La capacidad de un modelo generalmente aumenta con la cantidad de parámetros del modelo. Para obtener una definición formal de la capacidad de un modelo de clasificación, consulta Dimensión VC.

N

clase negativa

#fundamentals

#Metric

En la clasificación binaria, una clase se denomina positiva y la otra, negativa. La clase positiva es el elemento o evento que el modelo está probando, y la clase negativa es la otra posibilidad. Por ejemplo:

• La clase negativa en una prueba médica puede ser "no es un tumor".
• La clase negativa en un modelo de clasificación de correos electrónicos podría ser "no es spam".

Compara esto con la clase positiva.

O

objetivo

#Metric

Es una métrica que tu algoritmo intenta optimizar.

función objetivo

#Metric

Es la fórmula matemática o la métrica que un modelo intenta optimizar. Por ejemplo, la función objetivo para la regresión lineal suele ser la pérdida cuadrática media. Por lo tanto, cuando se entrena un modelo de regresión lineal, el objetivo del entrenamiento es minimizar la pérdida cuadrática media.

En algunos casos, el objetivo es maximizar la función objetivo. Por ejemplo, si la función objetivo es la precisión, el objetivo es maximizar la precisión.

Consulta también pérdida.

P

Pase en k (pass@k)

#Metric

Es una métrica para determinar la calidad del código (por ejemplo, Python) que genera un modelo de lenguaje grande. Más específicamente, Pass at k te indica la probabilidad de que al menos un bloque de código generado de los k bloques de código generados pase todas sus pruebas de unidades.

Los modelos de lenguaje grandes suelen tener dificultades para generar código adecuado para problemas de programación complejos. Los ingenieros de software se adaptan a este problema solicitando al modelo de lenguaje grande que genere varias (k) soluciones para el mismo problema. Luego, los ingenieros de software prueban cada una de las soluciones con pruebas de unidades. El cálculo de la aprobación en k depende del resultado de las pruebas de unidades:

• Si una o más de esas soluciones pasan la prueba de unidades, el LLM aprueba ese desafío de generación de código.
• Si ninguna de las soluciones pasa la prueba de unidades, el LLM falla en ese desafío de generación de código.

La fórmula para el pase en k es la siguiente:

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

En general, los valores más altos de k producen puntuaciones más altas de aprobación en k; sin embargo, los valores más altos de k requieren más recursos de modelos grandes de lenguaje y pruebas de unidades.

Haz clic en el ícono para ver un ejemplo.

Supongamos que un ingeniero de software le pide a un modelo de lenguaje grande que genere k=10 soluciones para n=50 problemas de programación difíciles. Estos son los resultados:

• 30 pases
• 20 errores

Por lo tanto, la puntuación de aprobación en el nivel 10 es la siguiente:

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

rendimiento

#Metric

Término sobrecargado con los siguientes significados:

• El significado estándar dentro de la ingeniería de software. Es decir, ¿qué tan rápidamente (o eficazmente) se ejecuta este software?
• El significado en el aprendizaje automático. Aquí, el rendimiento responde a la siguiente pregunta: ¿Qué tan correcto es este modelo? Es decir, ¿qué tan buenas son las predicciones del modelo?

Importancia de las variables por permutación

#df

#Metric

Es un tipo de importancia de la variable que evalúa el aumento en el error de predicción de un modelo después de permutar los valores del atributo. La importancia de las variables de permutación es una métrica independiente del modelo.

perplejidad

#Metric

Medición de qué tan bien está logrando su tarea el modelo. Por ejemplo, supongamos que tu tarea es leer las primeras letras de una palabra que un usuario está escribiendo en el teclado de un teléfono y ofrecer una lista de posibles palabras para completar. La perplejidad, P, para esta tarea es aproximadamente la cantidad de suposiciones que debes ofrecer para que tu lista contenga la palabra real que el usuario intenta escribir.

La perplejidad está relacionada con la entropía cruzada de la siguiente manera:

$$P= 2^{-\text{cross entropy}}$$

clase positiva

#fundamentals

#Metric

Es la clase para la que realizas la prueba.

Por ejemplo, la clase positiva en un modelo de cáncer podría ser "tumor". La clase positiva en un modelo de clasificación de correos electrónicos puede ser "spam".

Compara esto con la clase negativa.

Haz clic en el ícono para ver notas adicionales.

El término clase positiva puede ser confuso porque el resultado "positivo" de muchas pruebas suele ser un resultado no deseado. Por ejemplo, la clase positiva en muchas pruebas médicas corresponde a tumores o enfermedades. En general, quieres que un médico te diga: "¡Felicitaciones! Los resultados de tu prueba fueron negativos". De todos modos, la clase positiva es el evento que la prueba busca encontrar.

Sin duda, estás probando simultáneamente las clases positivas y negativas.

---

PR AUC (área bajo la curva de PR)

#Metric

Es el área bajo la curva de precisión-recuperación interpolada, que se obtiene trazando los puntos (recuperación, precisión) para diferentes valores del umbral de clasificación.

precision

#fundamentals

#Metric

Es una métrica para los modelos de clasificación que responde la siguiente pregunta:

Cuando el modelo predijo la clase positiva, ¿qué porcentaje de las predicciones fueron correctas?

Esta es la fórmula:

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

Donde:

• Un verdadero positivo significa que el modelo predijo correctamente la clase positiva.
• Un falso positivo significa que el modelo predijo erróneamente la clase positiva.

Por ejemplo, supongamos que un modelo realizó 200 predicciones positivas. De estas 200 predicciones positivas, se obtuvieron los siguientes resultados:

• 150 fueron verdaderos positivos.
• 50 fueron falsos positivos.

En este caso, ocurre lo siguiente:

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

Compara esto con la exactitud y la recuperación.

Consulta Clasificación: Precisión, recuperación, exactitud y métricas relacionadas en el Curso intensivo de aprendizaje automático para obtener más información.

Precisión en k (precision@k)

#Metric

Es una métrica para evaluar una lista de elementos clasificados (ordenados). La precisión en k identifica la fracción de los primeros k elementos de esa lista que son "relevantes". Es decir:

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

El valor de k debe ser menor o igual que la longitud de la lista que se muestra. Ten en cuenta que la longitud de la lista devuelta no forma parte del cálculo.

La relevancia suele ser subjetiva. Incluso los evaluadores humanos expertos suelen no estar de acuerdo sobre qué elementos son relevantes.

Comparar con:

• Precisión promedio en k
• Precisión media en k

Haz clic en el ícono para ver un ejemplo.

Supongamos que se le da la siguiente búsqueda a un modelo de lenguaje grande:

List the 6 funniest movies of all time in order.

El modelo de lenguaje grande devuelve la lista que se muestra en las dos primeras columnas de la siguiente tabla:

Posición	Película	¿Es relevante?
1	El general	Sí
2	Mean Girls	Sí
3	Pelotón	No
4	Damas en guerra	Sí
5	Citizen Kane	No
6	This is Spinal Tap	Sí

Dos de las primeras tres películas son relevantes, por lo que la precisión en 3 es la siguiente:

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

Tres de las primeras cinco películas son muy divertidas, por lo que la precisión en 5 es la siguiente:

$$\text{precision at 5} = \frac{\text{3}} {\text{5}} = 0.6$$

---

curva de precisión-recuperación

#Metric

Curva de precisión en función de la recuperación en diferentes umbrales de clasificación.

sesgo de predicción

#Metric

Es un valor que indica qué tan lejos está el promedio de las predicciones del promedio de las etiquetas en el conjunto de datos.

No se debe confundir con el término de sesgo en los modelos de aprendizaje automático ni con el sesgo en la ética y la equidad.

Paridad predictiva

#responsible

#Metric

Es una métrica de equidad que verifica si, para un modelo de clasificación determinado, las tasas de precisión son equivalentes para los subgrupos en consideración.

Por ejemplo, un modelo que predice la aceptación en la universidad satisfaría la paridad predictiva para la nacionalidad si su tasa de precisión es la misma para los liliputienses y los brobdingnagianos.

A veces, la paridad predictiva también se denomina paridad de la tasa predictiva.

Consulta "Explicación de las definiciones de equidad" (sección 3.2.1) para obtener un análisis más detallado de la paridad predictiva.

Paridad de tarifas predictiva

#responsible

#Metric

Otro nombre para la paridad predictiva.

función de densidad de probabilidad

#Metric

Es una función que identifica la frecuencia con la que las muestras de datos tienen exactamente un valor determinado. Cuando los valores de un conjunto de datos son números de punto flotante continuos, rara vez se producen coincidencias exactas. Sin embargo, integrar una función de densidad de probabilidad desde el valor x hasta el valor y produce la frecuencia esperada de las muestras de datos entre x y y.

Por ejemplo, considera una distribución normal con una media de 200 y una desviación estándar de 30. Para determinar la frecuencia esperada de las muestras de datos que se encuentran dentro del rango de 211.4 a 218.7, puedes integrar la función de densidad de probabilidad para una distribución normal de 211.4 a 218.7.

R

recall

#fundamentals

#Metric

Es una métrica para los modelos de clasificación que responde la siguiente pregunta:

Cuando la verdad fundamental era la clase positiva, ¿qué porcentaje de predicciones identificó correctamente el modelo como la clase positiva?

Esta es la fórmula:

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

Donde:

• Un verdadero positivo significa que el modelo predijo correctamente la clase positiva.
• Un falso negativo significa que el modelo predijo erróneamente la clase negativa.

Por ejemplo, supongamos que tu modelo realizó 200 predicciones sobre ejemplos para los que la verdad fundamental era la clase positiva. De estas 200 predicciones, se cumplen las siguientes condiciones:

• 180 fueron verdaderos positivos.
• 20 fueron falsos negativos.

En este caso, ocurre lo siguiente:

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

Haz clic en el ícono de notas sobre los conjuntos de datos con desequilibrio de clases.

La recuperación es particularmente útil para determinar la capacidad predictiva de los modelos de clasificación en los que la clase positiva es poco frecuente. Por ejemplo, considera un conjunto de datos con desequilibrio de clases en el que la clase positiva para una determinada enfermedad se presenta en solo 10 pacientes de un millón. Supongamos que tu modelo realiza cinco millones de predicciones que arrojan los siguientes resultados:

• 30 verdaderos positivos
• 20 falsos negativos
• 4,999,000 verdaderos negativos
• 950 falsos positivos

Por lo tanto, la recuperación de este modelo es la siguiente:

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

En cambio, la precisión de este modelo es la siguiente:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

Ese valor alto de precisión parece impresionante, pero es esencialmente insignificante. La recuperación es una métrica mucho más útil que la precisión para los conjuntos de datos con desequilibrio de clases.

---

Consulta Clasificación: Métricas de precisión, recuperación, exactitud y relacionadas para obtener más información.

Recuperación en k (recall@k)

#Metric

Es una métrica para evaluar sistemas que generan una lista de elementos clasificados (ordenados). La recuperación en k identifica la fracción de elementos pertinentes en los primeros k elementos de esa lista en relación con la cantidad total de elementos pertinentes devueltos.

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

Compara esto con la precisión en k.

Haz clic en el ícono para ver un ejemplo.

Supongamos que se le da la siguiente búsqueda a un modelo de lenguaje grande:

List the 10 funniest movies of all time in order.

El modelo de lenguaje grande devuelve la lista que se muestra en las dos primeras columnas:

Posición	Película	¿Es relevante?
1	El general	Sí
2	Mean Girls	Sí
3	Pelotón	No
4	Damas en guerra	Sí
5	This is Spinal Tap	Sí
6	¡Un avión!	Sí
7	Groundhog Day	Sí
8	Los caballeros de la mesa cuadrada	Sí
9	Oppenheimer	No
10	Ni idea	Sí

Ocho de las películas de la lista anterior son muy divertidas, por lo que son "elementos pertinentes en la lista". Por lo tanto, 8 será el denominador en todos los cálculos de recuperación en k. ¿Qué sucede con el numerador? Bueno, 3 de los primeros 4 elementos son relevantes, por lo que la recuperación en 4 es la siguiente:

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

7 de las primeras 8 películas son muy divertidas, por lo que el recuerdo en 8 es el siguiente:

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

Curva ROC (característica operativa del receptor)

#fundamentals

#Metric

Es un gráfico de la tasa de verdaderos positivos en comparación con la tasa de falsos positivos para diferentes umbrales de clasificación en la clasificación binaria.

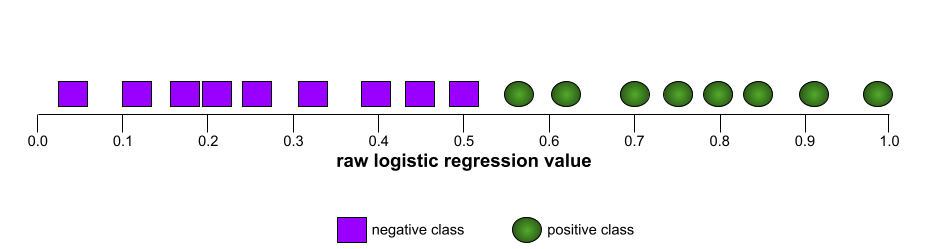
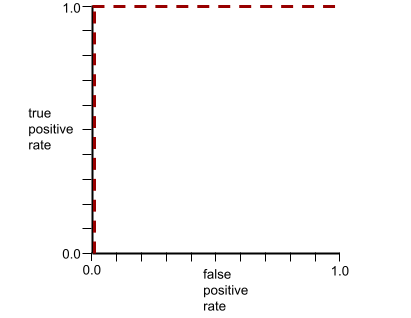
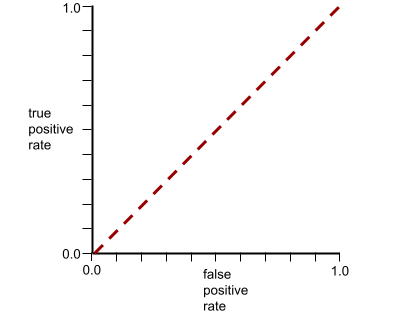
La forma de una curva ROC sugiere la capacidad de un modelo de clasificación binaria para separar las clases positivas de las negativas. Supongamos, por ejemplo, que un modelo de clasificación binaria separa perfectamente todas las clases negativas de todas las clases positivas:

La curva ROC del modelo anterior se ve de la siguiente manera:

En cambio, en la siguiente ilustración, se grafican los valores de regresión logística sin procesar para un modelo terrible que no puede separar las clases negativas de las positivas:

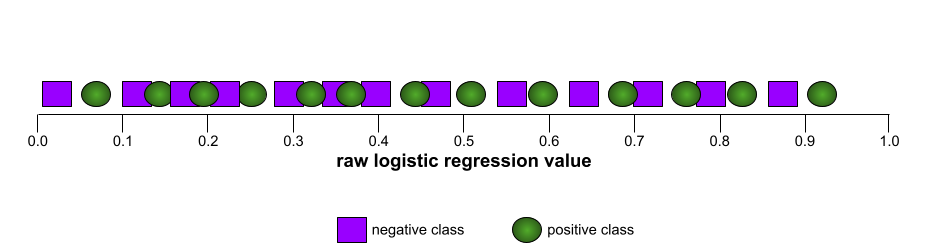
La curva ROC para este modelo se ve de la siguiente manera:

Mientras tanto, en el mundo real, la mayoría de los modelos de clasificación binaria separan las clases positivas y negativas en cierto grado, pero no de forma perfecta. Por lo tanto, una curva ROC típica se encuentra en algún punto entre los dos extremos:

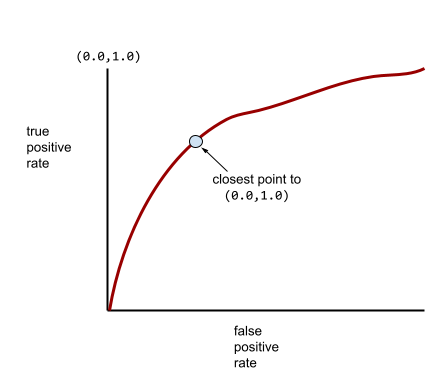
En teoría, el punto de una curva ROC más cercano a (0.0, 1.0) identifica el umbral de clasificación ideal. Sin embargo, varios otros problemas del mundo real influyen en la selección del umbral de clasificación ideal. Por ejemplo, tal vez los falsos negativos causen mucho más dolor que los falsos positivos.

Una métrica numérica llamada AUC resume la curva ROC en un solo valor de punto flotante.

Raíz cuadrada del error cuadrático medio (RMSE)

#fundamentals

#Metric

Raíz cuadrada del error cuadrático medio.

ROUGE (Recall-Oriented Understudy for Gisting Evaluation)

#Metric

Es una familia de métricas que evalúan los modelos de traducción automática y resumen automático. Las métricas de ROUGE determinan el grado en que un texto de referencia se superpone con el texto generado de un modelo de AA. Cada miembro de la familia ROUGE mide la superposición de una manera diferente. Las puntuaciones ROUGE más altas indican una mayor similitud entre el texto de referencia y el texto generado que las puntuaciones ROUGE más bajas.

Por lo general, cada miembro de la familia ROUGE genera las siguientes métricas:

• Precisión
• Recuperación
• F₁

Nota: ROUGE usa la precisión y la recuperación de forma algo diferente a la precisión y la recuperación tradicionales.

Para obtener detalles y ejemplos, consulta lo siguiente:

• ROUGE-L
• ROUGE-N
• ROUGE-S

Nota: BLEU y BLEURT se optimizan para la precisión, mientras que ROUGE se optimiza para la recuperación. Por lo tanto, BLEU y BLEURT son mejores métricas para evaluar la traducción automática (ya que el enfoque está en la precisión), mientras que ROUGE es una mejor métrica para el resumen (ya que el enfoque está en la recuperación).

ROUGE-L

#Metric

Es un miembro de la familia ROUGE que se enfoca en la longitud de la subsecuencia común más larga en el texto de referencia y el texto generado. Las siguientes fórmulas calculan la recuperación y la precisión para ROUGE-L:

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

Luego, puedes usar F₁ para combinar la recuperación de ROUGE-L y la precisión de ROUGE-L en una sola métrica:

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

Haz clic en el ícono para ver un ejemplo del cálculo de ROUGE-L.

Considera el siguiente texto de referencia y el texto generado.

Categoría	¿Quién produjo el contenido?	Texto
Texto de referencia	Traductor humano	Quiero comprender una amplia variedad de cosas.
Texto generado	Modelo de AA	Quiero aprender muchas cosas.

Por lo tanto:

• La subsecuencia común más larga es 5 (I want to of things).
• La cantidad de palabras en el texto de referencia es 9.
• La cantidad de palabras en el texto generado es 7.

Por lo tanto, sucede lo siguiente:

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

ROUGE-L ignora los saltos de línea en el texto de referencia y el texto generado, por lo que la subsecuencia común más larga podría abarcar varias oraciones. Cuando el texto de referencia y el texto generado incluyen varias oraciones, ROUGE-Lsum, una variación de ROUGE-L, suele ser una mejor métrica. ROUGE-Lsum determina la subsecuencia común más larga para cada oración de un pasaje y, luego, calcula la media de esas subsecuencias comunes más largas.

Haz clic en el ícono para ver un ejemplo del cálculo de ROUGE-Lsum.

Considera el siguiente texto de referencia y el texto generado.

Categoría	¿Quién produjo el contenido?	Texto
Texto de referencia	Traductor humano	La superficie de Marte está seca. Casi toda el agua se encuentra a gran profundidad bajo tierra.
Texto generado	Modelo de AA	Marte tiene una superficie seca. Sin embargo, la gran mayoría del agua se encuentra bajo tierra.

Por lo tanto:

	Primera oración	Segunda oración
Secuencia común más larga	2 (Marte seco)	3 (el agua está bajo tierra)
Longitud de las oraciones del texto de referencia	6	7
Longitud de las oraciones del texto generado	5	8

Por lo tanto, sucede lo siguiente:

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#Metric

Es un conjunto de métricas dentro de la familia ROUGE que compara los N-gramas compartidos de un tamaño determinado en el texto de referencia y el texto generado. Por ejemplo:

• ROUGE-1 mide la cantidad de tokens compartidos en el texto de referencia y el texto generado.
• ROUGE-2 mide la cantidad de bigramas (2-gramas) compartidos en el texto de referencia y el texto generado.
• ROUGE-3 mide la cantidad de trigramas (3-gramas) compartidos en el texto de referencia y el texto generado.

Puedes usar las siguientes fórmulas para calcular la recuperación de ROUGE-N y la precisión de ROUGE-N para cualquier miembro de la familia de ROUGE-N:

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

Luego, puedes usar F₁ para resumir la recuperación de ROUGE-N y la precisión de ROUGE-N en una sola métrica:

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

Haz clic en el ícono para ver un ejemplo.

Supongamos que decides usar ROUGE-2 para medir la eficacia de la traducción de un modelo de AA en comparación con la de un traductor humano.

Categoría	¿Quién produjo el contenido?	Texto	Bigramas
Texto de referencia	Traductor humano	Quiero comprender una amplia variedad de cosas.	Quiero, quiero, quiero entender, entender una, una amplia, amplia variedad, variedad de, de cosas.
Texto generado	Modelo de AA	Quiero aprender muchas cosas.	Quiero, quiero, aprender, aprender mucho, mucho, de cosas

Por lo tanto:

• La cantidad de bigramas coincidentes es 3 (I want, want to y of things).
• La cantidad de bigramas en el texto de referencia es 8.
• La cantidad de bigramas en el texto generado es 6.

Por lo tanto, sucede lo siguiente:

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#Metric

Es una forma flexible de ROUGE-N que permite la coincidencia de skip-gramas. Es decir, ROUGE-N solo cuenta los n-gramas que coinciden exactamente, pero ROUGE-S también cuenta los n-gramas separados por una o más palabras. Por ejemplo, considera lo siguiente:

• Texto de referencia: Nubes blancas
• Texto generado: Nubes blancas y ondulantes

Cuando se calcula ROUGE-N, el 2-grama Nubes blancas no coincide con Nubes blancas y ondulantes. Sin embargo, cuando se calcula ROUGE-S, Nubes blancas sí coincide con Nubes blancas y ondulantes.

R al cuadrado

#Metric

Es una métrica de regresión que indica qué parte de la variación en una etiqueta se debe a un atributo individual o a un conjunto de atributos. El coeficiente de determinación R² es un valor entre 0 y 1 que puedes interpretar de la siguiente manera:

• Un R al cuadrado de 0 significa que ninguna variación de la etiqueta se debe al conjunto de atributos.
• Un R al cuadrado de 1 significa que toda la variación de la etiqueta se debe al conjunto de atributos.
• Un R al cuadrado entre 0 y 1 indica en qué medida la variación de la etiqueta se puede predecir a partir de un atributo en particular o del conjunto de atributos. Por ejemplo, un R al cuadrado de 0.10 significa que el 10% de la varianza en la etiqueta se debe al conjunto de atributos, un R al cuadrado de 0.20 significa que el 20% se debe al conjunto de atributos, y así sucesivamente.

R al cuadrado es el cuadrado del coeficiente de correlación de Pearson entre los valores que predijo un modelo y la verdad fundamental.

S

puntuación

#Metric

Es la parte de un sistema de recomendación que proporciona un valor o una clasificación para cada elemento producido por la fase de generación de candidatos.

medida de similitud

#clustering

#Metric

En los algoritmos de agrupamiento en clústeres, es la métrica que se usa para determinar qué tan parecidos (cuán similares) son dos ejemplos cualesquiera.

dispersión

#Metric

Es la cantidad de elementos establecidos en cero (o nulos) en un vector o una matriz dividida por la cantidad total de entradas en ese vector o matriz. Por ejemplo, considera una matriz de 100 elementos en la que 98 celdas contienen cero. El cálculo de la dispersión es el siguiente:

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

La esparcidad de los atributos se refiere a la esparcidad de un vector de atributos, mientras que la esparcidad del modelo se refiere a la esparcidad de los pesos del modelo.

pérdida de bisagra al cuadrado

#Metric

Cuadrado de la pérdida de bisagra. La pérdida de bisagra al cuadrado penaliza los valores atípicos con mayor severidad que la pérdida de bisagra normal.

Pérdida al cuadrado

#fundamentals

#Metric

Sinónimo de pérdida L₂.

T

Pérdida de prueba

#fundamentals

#Metric

Es una métrica que representa la pérdida de un modelo en relación con el conjunto de prueba. Cuando compilas un modelo, por lo general, intentas minimizar la pérdida de la prueba. Esto se debe a que una pérdida de prueba baja es un indicador de calidad más sólido que una pérdida de entrenamiento baja o una pérdida de validación baja.

A veces, una gran brecha entre la pérdida de prueba y la pérdida de entrenamiento o la pérdida de validación sugiere que debes aumentar la tasa de regularización.

Precisión del top-k

#Metric

Es el porcentaje de veces que aparece una "etiqueta objetivo" en las primeras k posiciones de las listas generadas. Las listas pueden ser recomendaciones personalizadas o una lista de elementos ordenados por softmax.

La precisión del Top-k también se conoce como precisión en k.

Nota: La etiqueta de destino puede ser cualquier clase (no necesariamente la clase de la verdad fundamental), por lo que la precisión de los k resultados más probables no siempre es equivalente a la precisión tradicional.

Haz clic en el ícono para ver un ejemplo.

Considera un sistema de aprendizaje automático que usa softmax para identificar las probabilidades de los árboles en función de una imagen de las hojas de los árboles. En la siguiente tabla, se muestran las listas de salida generadas a partir de cinco imágenes de árboles de entrada. Cada fila contiene una etiqueta de destino y los cinco árboles más probables. Por ejemplo, cuando la etiqueta objetivo era arce, el modelo de aprendizaje automático identificó olmo como el árbol más probable, roble como el segundo árbol más probable, y así sucesivamente.

Etiqueta de destino	1	2	3	4	5
arce	olmo	roble	maple	haya	álamo
cornejo	roble	dogwood	álamo	Nogal americano	arce
roble	oak	Tilo	langosta	aliso	linden
linden	arce	paw-paw	roble	Tilo	álamo
roble	langosta	linden	oak	arce	paw-paw

La etiqueta objetivo aparece en la primera posición solo una vez, por lo que la precisión del top-1 es la siguiente:

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

La etiqueta objetivo aparece en una de las tres primeras posiciones cuatro veces, por lo que la precisión del top-3 es la siguiente:

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

tóxico

#Metric

Grado en que el contenido es abusivo, amenazante u ofensivo Muchos modelos de aprendizaje automático pueden identificar y medir la toxicidad. La mayoría de estos modelos identifican la toxicidad según varios parámetros, como el nivel de lenguaje abusivo y el nivel de lenguaje amenazante.

Pérdida de entrenamiento

#fundamentals

#Metric

Es una métrica que representa la pérdida de un modelo durante una iteración de entrenamiento en particular. Por ejemplo, supongamos que la función de pérdida es el error cuadrático medio. Quizás la pérdida de entrenamiento (el error cuadrático medio) para la décima iteración sea de 2.2, y la pérdida de entrenamiento para la iteración número 100 sea de 1.9.

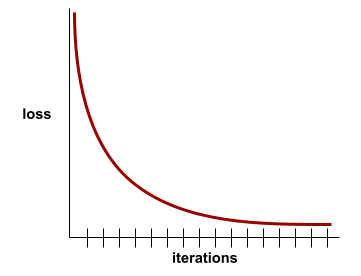
Una curva de pérdida representa la pérdida de entrenamiento en función de la cantidad de iteraciones. Una curva de pérdida proporciona las siguientes sugerencias sobre el entrenamiento:

• Una pendiente descendente implica que el modelo está mejorando.
• Una pendiente ascendente implica que el modelo está empeorando.
• Una pendiente plana implica que el modelo alcanzó la convergencia.

Por ejemplo, la siguiente curva de pérdida algo idealizada muestra lo siguiente:

• Una pendiente descendente pronunciada durante las iteraciones iniciales, lo que implica una mejora rápida del modelo
• Una pendiente que se aplana gradualmente (pero que sigue siendo descendente) hasta cerca del final del entrenamiento, lo que implica una mejora continua del modelo a un ritmo algo más lento que durante las iteraciones iniciales.
• Una pendiente plana hacia el final del entrenamiento, lo que sugiere convergencia.

Si bien la pérdida de entrenamiento es importante, también debes consultar la generalización.

verdadero negativo (VN)

#fundamentals

#Metric

Ejemplo en el que el modelo predice correctamente la clase negativa. Por ejemplo, el modelo infiere que un mensaje de correo electrónico en particular no es spam y, en efecto, ese mensaje no es spam.

verdadero positivo (VP)

#fundamentals

#Metric

Ejemplo en el que el modelo predice correctamente la clase positiva. Por ejemplo, el modelo infiere que un mensaje de correo electrónico en particular es spam y realmente lo es.

tasa de verdaderos positivos (TVP)

#fundamentals

#Metric

Sinónimo de recuperación. Es decir:

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

La tasa de verdaderos positivos es el eje Y en una curva ROC.

V

Pérdida de validación

#fundamentals

#Metric

Es una métrica que representa la pérdida de un modelo en el conjunto de validación durante una iteración particular del entrenamiento.

Consulta también curva de generalización.

Importancia de las variables

#df

#Metric

Es un conjunto de puntuaciones que indica la importancia relativa de cada atributo para el modelo.

Por ejemplo, considera un árbol de decisión que estima los precios de las casas. Supongamos que este árbol de decisión usa tres atributos: tamaño, edad y estilo. Si se calcula que un conjunto de importancias de variables para las tres características es {tamaño=5.8, edad=2.5, estilo=4.7}, entonces el tamaño es más importante para el árbol de decisión que la edad o el estilo.

Existen diferentes métricas de importancia de las variables que pueden informar a los expertos en AA sobre diferentes aspectos de los modelos.

W

Pérdida de Wasserstein

#Metric

Es una de las funciones de pérdida que se usan comúnmente en las redes adversarias generativas, basada en la distancia de movimiento de tierra entre la distribución de los datos generados y los datos reales.