Diese Seite enthält Begriffe aus dem Messwerteglossar. Hier finden Sie alle Glossarbegriffe.
A
Genauigkeit
Die Anzahl der richtigen Klassifizierungsvorhersagen, dividiert durch die Gesamtzahl der Vorhersagen. Das bedeutet:
Ein Modell, das beispielsweise 40 korrekte und 10 falsche Vorhersagen getroffen hat, hätte eine Genauigkeit von:
Bei der binären Klassifizierung werden bestimmte Namen für die verschiedenen Kategorien von richtigen Vorhersagen und falschen Vorhersagen verwendet. Die Formel für die Genauigkeit bei der binären Klassifizierung lautet also:
Dabei gilt:
- TP ist die Anzahl der richtig positiven Ergebnisse (richtige Vorhersagen).
- TN ist die Anzahl der richtig negativen Ergebnisse (richtige Vorhersagen).
- FP ist die Anzahl der falsch positiven Ergebnisse (falsche Vorhersagen).
- FN ist die Anzahl der falsch negativen Ergebnisse (falsche Vorhersagen).
Vergleichen Sie die Genauigkeit mit Trefferquote und Erinnerung.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Klassifizierung: Genauigkeit, Trefferquote, Präzision und zugehörige Messwerte.
Bereich unter der PR-Kurve
Weitere Informationen finden Sie unter PR AUC (Area under the PR Curve).
Bereich unter der ROC-Kurve
Weitere Informationen finden Sie unter AUC (Area under the ROC curve).
AUC (Area Under the ROC Curve, Bereich unter der ROC-Kurve)
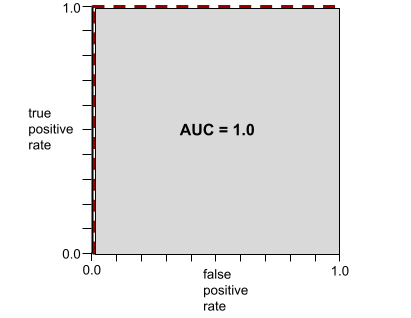
Eine Zahl zwischen 0,0 und 1,0, die angibt, wie gut ein binäres Klassifizierungsmodell positive Klassen von negativen Klassen trennen kann. Je näher die AUC an 1,0 liegt, desto besser kann das Modell Klassen voneinander trennen.
Die folgende Abbildung zeigt beispielsweise ein Klassifikationsmodell, das positive Klassen (grüne Ovale) perfekt von negativen Klassen (lila Rechtecke) trennt. Dieses unrealistisch perfekte Modell hat einen AUC-Wert von 1,0:

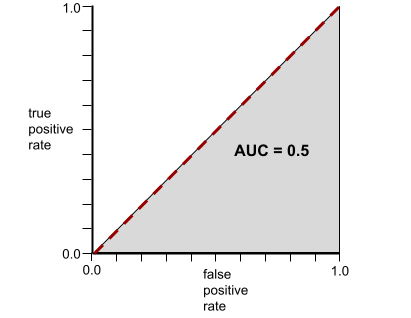
Die folgende Abbildung zeigt dagegen die Ergebnisse für ein Klassifizierungsmodell, das zufällige Ergebnisse generiert hat. Dieses Modell hat einen AUC-Wert von 0,5:

Ja, das vorherige Modell hat einen AUC-Wert von 0,5, nicht 0,0.
Die meisten Modelle liegen irgendwo zwischen den beiden Extremen. Im folgenden Modell werden beispielsweise positive und negative Ergebnisse etwas getrennt. Daher liegt die AUC zwischen 0, 5 und 1, 0:

Bei der AUC wird jeder Wert ignoriert, den Sie für Klassifizierungsschwellenwert festlegen. Stattdessen werden bei der AUC alle möglichen Klassifizierungsschwellenwerte berücksichtigt.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Klassifizierung: ROC und AUC.
Durchschnittliche Precision bei k
Ein Messwert zur Zusammenfassung der Leistung eines Modells bei einem einzelnen Prompt, der sortierte Ergebnisse generiert, z. B. eine nummerierte Liste mit Buchempfehlungen. Die durchschnittliche Precision bei k ist der Durchschnitt der Precision bei k-Werte für jedes relevante Ergebnis. Die Formel für die durchschnittliche Precision bei k lautet daher:
\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]
Dabei gilt:
- \(n\) ist die Anzahl der relevanten Elemente in der Liste.
Im Gegensatz dazu steht Recall at k.
B
baseline
Ein Modell, das als Referenzpunkt verwendet wird, um zu vergleichen, wie gut ein anderes Modell (in der Regel ein komplexeres) funktioniert. Ein logistisches Regressionsmodell kann beispielsweise als gute Baseline für ein Deep-Learning-Modell dienen.
Für ein bestimmtes Problem hilft die Baseline den Modellentwicklern, die minimale erwartete Leistung zu quantifizieren, die ein neues Modell erreichen muss, damit es nützlich ist.
Boolesche Fragen (BoolQ)
Ein Dataset zur Bewertung der Fähigkeit eines LLM, Ja-Nein-Fragen zu beantworten. Jede Aufgabe im Dataset besteht aus drei Komponenten:
- Eine Anfrage
- Ein Abschnitt, der die Antwort auf die Anfrage impliziert.
- Die richtige Antwort, die entweder Ja oder Nein lautet.
Beispiel:
- Anfrage: Gibt es in Michigan Atomkraftwerke?
- Passage: …drei Kernkraftwerke versorgen Michigan mit etwa 30% des Stroms.
- Richtige Antwort: Ja
Die Fragen wurden aus anonymisierten, aggregierten Google-Suchanfragen zusammengestellt und die Informationen wurden anhand von Wikipedia-Seiten überprüft.
Weitere Informationen finden Sie unter BoolQ: Exploring the Surprising Difficulty of Natural Yes/No Questions.
BoolQ ist eine Komponente des SuperGLUE-Ensembles.
BoolQ
Abkürzung für Boolesche Fragen.
C
CB
Abkürzung für CommitmentBank.
F-Wert für Zeichen-N-Gramme (ChrF)
Ein Messwert zur Bewertung von Modellen für die maschinelle Übersetzung. Der F-Score für Zeichen-N-Gramme gibt an, inwieweit sich N-Gramme im Referenztext mit den N-Grammen im generierten Text eines ML-Modells überschneiden.
Der F-Score für Zeichen-N-Gramme ähnelt den Messwerten in den Familien ROUGE und BLEU. Es gibt jedoch folgende Unterschiede:
- Der F-Score für Zeichen-N-Gramme wird für Zeichen-N-Gramme berechnet.
- ROUGE und BLEU basieren auf Wort-N-Grammen oder Tokens.
Auswahl plausibler Alternativen (Choice of Plausible Alternatives, COPA)
Ein Dataset zur Bewertung, wie gut ein LLM die bessere von zwei alternativen Antworten auf eine Prämisse identifizieren kann. Jede Aufgabe im Datensatz besteht aus drei Komponenten:
- Eine Prämisse, die in der Regel eine Aussage ist, gefolgt von einer Frage
- Zwei mögliche Antworten auf die in der Prämisse gestellte Frage, von denen eine richtig und die andere falsch ist
- Die richtige Antwort
Beispiel:
- Prämisse:Der Mann hat sich den Zeh gebrochen. Was war die URSACHE dafür?
- Mögliche Antworten:
- Er hat ein Loch in der Socke.
- Er hat sich einen Hammer auf den Fuß fallen lassen.
- Richtige Antwort:2
COPA ist eine Komponente des SuperGLUE-Ensembles.
CommitmentBank (CB)
Ein Datensatz zur Bewertung der Fähigkeit eines LLM, festzustellen, ob der Autor einer Passage eine Zielklausel in dieser Passage glaubt. Jeder Eintrag im Dataset enthält:
- Ein Textabschnitt
- Eine Zielklausel in diesem Abschnitt
- Ein boolescher Wert, der angibt, ob der Autor des Abschnitts die Zielklausel
Beispiel:
- Passage:Es war schön, Artemis lachen zu hören. Sie ist so ein ernstes Kind. Ich wusste nicht, dass sie Humor hat.
- Zielklausel:Sie hatte einen Sinn für Humor.
- Boolesch: „Wahr“, was bedeutet, dass der Autor die Zielklausel für wahr hält.
CommitmentBank ist eine Komponente des SuperGLUE-Ensembles.
COPA
Abkürzung für Choice of Plausible Alternatives (Auswahl plausibler Alternativen).
Kosten
Synonym für Verlust.
Kontrafaktische Fairness
Eine Fairness-Messwert, mit dem geprüft wird, ob ein Klassifizierungsmodell für eine Person dasselbe Ergebnis liefert wie für eine andere Person, die mit der ersten identisch ist, mit Ausnahme von einem oder mehreren vertraulichen Attributen. Die Bewertung eines Klassifizierungsmodells hinsichtlich kontrafaktischer Fairness ist eine Methode, um potenzielle Quellen für Bias in einem Modell aufzudecken.
Weitere Informationen finden Sie hier:
- Fairness: Kontrafaktische Fairness im Crashkurs „Maschinelles Lernen“
- When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness
Cross-Entropy
Eine Verallgemeinerung des Log-Verlusts für Klassifizierungsprobleme mit mehreren Klassen. Die Kreuzentropie quantifiziert den Unterschied zwischen zwei Wahrscheinlichkeitsverteilungen. Siehe auch Perplexity.
Verteilungsfunktion
Eine Funktion, die die Häufigkeit von Stichproben definiert, die kleiner oder gleich einem Zielwert sind. Betrachten wir beispielsweise eine Normalverteilung von kontinuierlichen Werten. Eine kumulative Verteilungsfunktion gibt an, dass etwa 50% der Stichproben kleiner oder gleich dem Mittelwert sein sollten und etwa 84% der Stichproben kleiner oder gleich einer Standardabweichung über dem Mittelwert sein sollten.
D
demografische Parität
Ein Fairness-Messwert, der erfüllt ist, wenn die Ergebnisse der Klassifizierung eines Modells nicht von einem bestimmten sensiblen Attribut abhängen.
Wenn sich beispielsweise sowohl Lilliputaner als auch Brobdingnagianer an der Glubbdubdrib University bewerben, wird demografische Parität erreicht, wenn der Prozentsatz der zugelassenen Lilliputaner dem Prozentsatz der zugelassenen Brobdingnagianer entspricht, unabhängig davon, ob eine Gruppe im Durchschnitt qualifizierter ist als die andere.
Im Gegensatz dazu erlauben ausgeglichene Chancen und Chancengleichheit, dass Klassifizierungsergebnisse insgesamt von sensiblen Attributen abhängen, aber nicht, dass Klassifizierungsergebnisse für bestimmte angegebene Ground-Truth-Labels von sensiblen Attributen abhängen. Im Google Research-Blogpost zum Thema „Diskriminierung durch intelligentes maschinelles Lernen“ finden Sie eine Visualisierung, in der die Kompromisse bei der Optimierung für demografische Parität dargestellt werden.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Fairness: demographic parity.
E
Earth Mover’s Distance (EMD)
Ein Maß für die relative Ähnlichkeit zweier Verteilungen. Je geringer die Earth Mover’s Distance, desto ähnlicher sind die Verteilungen.
Bearbeitungsdistanz
Ein Maß dafür, wie ähnlich sich zwei Textstrings sind. Im maschinellen Lernen ist die Bearbeitungsdistanz aus folgenden Gründen nützlich:
- Die Distanz lässt sich leicht berechnen.
- Mit der Edit-Distanz können zwei Strings verglichen werden, die sich ähneln.
- Mit der Edit-Distanz lässt sich ermitteln, wie ähnlich verschiedene Strings einem bestimmten String sind.
Es gibt verschiedene Definitionen von Bearbeitungsdistanz, die jeweils unterschiedliche String-Operationen verwenden. Ein Beispiel finden Sie unter Levenshtein-Distanz.
Empirische Verteilungsfunktion (eCDF oder EDF)
Eine kumulative Verteilungsfunktion basierend auf empirischen Messungen aus einem realen Dataset. Der Wert der Funktion an einem beliebigen Punkt entlang der x-Achse ist der Anteil der Beobachtungen im Dataset, die kleiner oder gleich dem angegebenen Wert sind.
Entropie
In der Informationstheorie wird die Unvorhersehbarkeit einer Wahrscheinlichkeitsverteilung beschrieben. Alternativ wird die Entropie auch als die Menge an Informationen definiert, die jedes Beispiel enthält. Eine Verteilung hat die höchstmögliche Entropie, wenn alle Werte einer Zufallsvariablen gleich wahrscheinlich sind.
Die Entropie einer Menge mit zwei möglichen Werten „0“ und „1“ (z. B. die Labels in einem binären Klassifizierungsproblem) wird mit der folgenden Formel berechnet:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
Dabei gilt:
- H ist die Entropie.
- p ist der Anteil der Beispiele mit dem Wert „1“.
- q ist der Anteil der Beispiele mit dem Wert „0“. Hinweis: q = (1 – p)
- log ist im Allgemeinen log2. In diesem Fall ist die Entropieeinheit ein Bit.
Nehmen wir beispielsweise Folgendes an:
- 100 Beispiele enthalten den Wert „1“.
- 300 Beispiele enthalten den Wert „0“
Der Entropiewert ist also:
- p = 0,25
- q = 0,75
- H = (-0,25)log2(0,25) – (0,75)log2(0,75) = 0,81 Bit pro Beispiel
Ein perfekt ausgeglichener Satz (z. B. 200 „0“ und 200 „1“) hätte eine Entropie von 1, 0 Bit pro Beispiel. Je unausgewogener ein Set wird, desto mehr nähert sich seine Entropie dem Wert 0,0 an.
In Entscheidungsbäumen wird mit Entropie der Informationsgewinn formuliert, damit der Splitter beim Erstellen eines Klassifizierungsentscheidungsbaums die Bedingungen auswählen kann.
Entropie vergleichen mit:
Entropie wird oft als Shannon-Entropie bezeichnet.
Weitere Informationen finden Sie im Kurs „Entscheidungsbäume“ unter Exact splitter for binary classification with numerical features (Genaue Aufteilung für die binäre Klassifizierung mit numerischen Features).
Chancengleichheit
Ein Fairness-Messwert, um zu bewerten, ob ein Modell das gewünschte Ergebnis für alle Werte eines sensiblen Attributs gleich gut vorhersagt. Wenn das gewünschte Ergebnis für ein Modell die positive Klasse ist, sollte die Rate der richtig positiven Ergebnisse für alle Gruppen gleich sein.
Die Chancengleichheit hängt mit ausgeglichenen Chancen zusammen, bei denen sowohl die Trefferquote als auch die Falsch-Positiv-Rate für alle Gruppen gleich sein müssen.
Angenommen, die Glubbdubdrib University nimmt sowohl Lilliputaner als auch Brobdingnagianer in ein anspruchsvolles Mathematikprogramm auf. Die weiterführenden Schulen der Lilliputaner bieten einen soliden Lehrplan für Mathematik, und die überwiegende Mehrheit der Schüler ist für das Universitätsprogramm qualifiziert. Die weiterführenden Schulen in Brobdingnag bieten überhaupt keine Mathematikunterricht an, weshalb viel weniger Schüler qualifiziert sind. Chancengleichheit für das bevorzugte Label „zugelassen“ in Bezug auf die Nationalität (Lilliputaner oder Brobdingnagianer) ist gegeben, wenn qualifizierte Schüler oder Studenten unabhängig davon, ob sie Lilliputaner oder Brobdingnagianer sind, mit gleicher Wahrscheinlichkeit zugelassen werden.
Nehmen wir beispielsweise an, dass sich 100 Lilliputaner und 100 Brobdingnagianer für die Glubbdubdrib University bewerben und die Zulassungsentscheidungen wie folgt getroffen werden:
Tabelle 1. Lilliputian-Bewerber (90% sind qualifiziert)
| Qualifiziert | Unqualifiziert | |
|---|---|---|
| Zugelassen | 45 | 3 |
| Abgelehnt | 45 | 7 |
| Gesamt | 90 | 10 |
|
Prozentsatz der zugelassenen qualifizierten Studenten: 45/90 = 50% Prozentsatz der abgelehnten nicht qualifizierten Studenten: 7/10 = 70% Gesamtprozentsatz der zugelassenen Lilliputian-Studenten: (45+3)/100 = 48% |
||
Tabelle 2 Brobdingnagian-Bewerber (10% sind qualifiziert):
| Qualifiziert | Unqualifiziert | |
|---|---|---|
| Zugelassen | 5 | 9 |
| Abgelehnt | 5 | 81 |
| Gesamt | 10 | 90 |
|
Prozentsatz der zugelassenen qualifizierten Studenten: 5/10 = 50% Prozentsatz der abgelehnten nicht qualifizierten Studenten: 81/90 = 90% Gesamtprozentsatz der zugelassenen Brobdingnagian-Studenten: (5+9)/100 = 14% |
||
Die vorherigen Beispiele erfüllen die Chancengleichheit für die Aufnahme qualifizierter Lernender, da sowohl qualifizierte Lilliputaner als auch Brobdingnagianer eine 50-prozentige Chance haben, aufgenommen zu werden.
Die Gleichheit der Chancen ist erfüllt, die folgenden beiden Fairnessmesswerte jedoch nicht:
- Demografische Parität: Lilliputaner und Brobdingnagianer werden mit unterschiedlichen Raten an der Universität zugelassen. 48% der Lilliputaner werden zugelassen, aber nur 14% der Brobdingnagianer.
- Gleiche Chancen: Obwohl qualifizierte Lilliputaner und Brobdingnagianer die gleiche Chance haben, zugelassen zu werden, wird die zusätzliche Einschränkung, dass nicht qualifizierte Lilliputaner und Brobdingnagianer die gleiche Chance haben, abgelehnt zu werden, nicht erfüllt. Bei nicht qualifizierten Lilliput-Kandidaten liegt die Ablehnungsrate bei 70 %, bei nicht qualifizierten Brobdingnag-Kandidaten bei 90 %.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Fairness: Equality of opportunity.
ausgeglichene Chancen
Ein Fairness-Messwert, mit dem bewertet wird, ob ein Modell Ergebnisse für alle Werte eines sensiblen Attributs in Bezug auf die positive Klasse und die negative Klasse gleichermaßen gut vorhersagt. Mit anderen Worten: Sowohl die Trefferquote als auch die Falsch-Negativ-Rate sollten für alle Gruppen gleich sein.
Die gleichberechtigten Chancen hängen mit der Chancengleichheit zusammen, die sich nur auf Fehlerraten für eine einzelne Klasse (positiv oder negativ) konzentriert.
Angenommen, die Glubbdubdrib University nimmt sowohl Lilliputaner als auch Brobdingnagianer in ein anspruchsvolles Mathematikprogramm auf. Die weiterführenden Schulen von Lilliput bieten einen umfassenden Lehrplan für Mathematik, und die überwiegende Mehrheit der Schüler ist für das Universitätsprogramm qualifiziert. Die weiterführenden Schulen in Brobdingnag bieten überhaupt keine Mathematikunterricht an, weshalb viel weniger Schüler qualifiziert sind. Die Bedingung „Equalized Odds“ ist erfüllt, wenn ein Bewerber unabhängig davon, ob er ein Lilliputaner oder ein Brobdingnagianer ist, bei Eignung mit gleicher Wahrscheinlichkeit für das Programm zugelassen wird und bei Nichteignung mit gleicher Wahrscheinlichkeit abgelehnt wird.
Angenommen, 100 Lilliputaner und 100 Brobdingnagianer bewerben sich an der Glubbdubdrib University und die Zulassungsentscheidungen werden so getroffen:
Tabelle 3 Lilliputian-Bewerber (90% sind qualifiziert)
| Qualifiziert | Unqualifiziert | |
|---|---|---|
| Zugelassen | 45 | 2 |
| Abgelehnt | 45 | 8 |
| Gesamt | 90 | 10 |
|
Prozentsatz der zugelassenen qualifizierten Schüler: 45/90 = 50% Prozentsatz der abgelehnten nicht qualifizierten Schüler: 8/10 = 80% Gesamtprozentsatz der zugelassenen Lilliputian-Schüler: (45+2)/100 = 47% |
||
Tabelle 4. Brobdingnagian-Bewerber (10% sind qualifiziert):
| Qualifiziert | Unqualifiziert | |
|---|---|---|
| Zugelassen | 5 | 18 |
| Abgelehnt | 5 | 72 |
| Gesamt | 10 | 90 |
|
Prozentsatz der zugelassenen qualifizierten Studenten: 5/10 = 50% Prozentsatz der abgelehnten nicht qualifizierten Studenten: 72/90 = 80% Gesamtprozentsatz der zugelassenen Brobdingnagian-Studenten: (5+18)/100 = 23% |
||
Die Bedingung „Equalized Odds“ ist erfüllt, da qualifizierte liliputanische und brobdingnagische Studenten beide eine 50-prozentige Chance haben, zugelassen zu werden, und nicht qualifizierte liliputanische und brobdingnagische Studenten eine 80-prozentige Chance haben, abgelehnt zu werden.
„Equalized Odds“ wird in „Equality of Opportunity in Supervised Learning“ formal so definiert: „Der Vorhersagewert Ŷ erfüllt die Bedingung ‚Equalized Odds‘ in Bezug auf das geschützte Attribut A und das Ergebnis Y, wenn Ŷ und A unabhängig sind, bedingt durch Y.“
evals
Wird hauptsächlich als Abkürzung für LLM-Bewertungen verwendet. Im Allgemeinen ist Evals eine Abkürzung für jede Form von Bewertung.
Agentenbewertung
Der Prozess, bei dem die Qualität eines Modells gemessen oder verschiedene Modelle miteinander verglichen werden.
Um ein Modell für beaufsichtigtes maschinelles Lernen zu bewerten, vergleichen Sie es in der Regel mit einem Validierungsset und einem Testset. Bewertung eines LLM: Hier werden in der Regel umfassendere Qualitäts- und Sicherheitsbewertungen durchgeführt.
genau passende Keywords
Ein Alles-oder-Nichts-Messwert, bei dem die Ausgabe des Modells entweder genau mit der Grundwahrheit oder dem Referenztext übereinstimmt oder nicht. Wenn die Ground Truth beispielsweise orange ist, ist die einzige Modellantwort, die die genaue Übereinstimmung erfüllt, orange.
Mit „Genau übereinstimmend“ können auch Modelle bewertet werden, deren Ausgabe eine Sequenz ist (eine sortierte Liste von Elementen). Im Allgemeinen erfordert die genaue Übereinstimmung, dass die generierte sortierte Liste genau mit der Ground Truth übereinstimmt. Das bedeutet, dass jedes Element in beiden Listen in derselben Reihenfolge sein muss. Wenn die Ground Truth mehrere korrekte Sequenzen enthält, muss die Ausgabe des Modells nur mit einer der korrekten Sequenzen übereinstimmen, um als „genaue Übereinstimmung“ zu gelten.
Extreme Summarization (xsum)
Ein Dataset zur Bewertung der Fähigkeit eines LLM, ein einzelnes Dokument zusammenzufassen. Jeder Eintrag im Dataset besteht aus:
- Ein Dokument, das von der British Broadcasting Corporation (BBC) verfasst wurde.
- Eine Zusammenfassung des Dokuments in einem Satz.
Weitere Informationen finden Sie unter Don't Give Me the Details, Just the Summary! Topic-Aware Convolutional Neural Networks for Extreme Summarization.
F
F1
Ein Messwert für die binäre Klassifizierung, der sowohl auf Precision als auch auf Recall basiert. Hier ist die Formel:
Fairnessmesswert
Eine messbare mathematische Definition von „Fairness“. Häufig verwendete Fairness-Messwerte sind:
Viele Fairnessmesswerte schließen sich gegenseitig aus. Weitere Informationen finden Sie unter Inkompatibilität von Fairnessmesswerten.
falsch negativ (FN)
Ein Beispiel, in dem das Modell fälschlicherweise die negative Klasse vorhersagt. Das Modell sagt beispielsweise voraus, dass eine bestimmte E‑Mail-Nachricht kein Spam (die negative Klasse) ist, aber diese E‑Mail-Nachricht ist tatsächlich Spam.
Rate falsch negativer Ergebnisse
Der Anteil der tatsächlich positiven Beispiele, für die das Modell fälschlicherweise die negative Klasse vorhergesagt hat. Die Falsch-Negativ-Rate wird mit der folgenden Formel berechnet:
Weitere Informationen finden Sie im Machine Learning Crash Course unter Schwellenwerte und die Konfusionsmatrix.
Falsch positiv (FP)
Ein Beispiel, in dem das Modell fälschlicherweise die positive Klasse vorhersagt. Das Modell sagt beispielsweise voraus, dass eine bestimmte E‑Mail-Nachricht Spam (die positive Klasse) ist, aber diese E‑Mail-Nachricht ist tatsächlich kein Spam.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Schwellenwerte und die Konfusionsmatrix.
Rate falsch positiver Ergebnisse (False Positive Rate, FPR)
Der Anteil der tatsächlich negativen Beispiele, für die das Modell fälschlicherweise die positive Klasse vorhergesagt hat. Die Falsch-Positiv-Rate wird mit der folgenden Formel berechnet:
Die Rate falsch positiver Ergebnisse ist die X-Achse in einer ROC-Kurve.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Klassifizierung: ROC und AUC.
Featurewichtigkeiten
Synonym für Variablenwichtigkeiten.
Foundation Model
Ein sehr großes vortrainiertes Modell, das mit einem enormen und vielfältigen Trainingsset trainiert wurde. Ein Foundation Model kann beides:
- Auf eine Vielzahl von Anfragen gut reagieren.
- Als Basismodell für zusätzliches Feinabstimmung oder andere Anpassungen dienen.
Ein Foundation Model ist also bereits sehr leistungsfähig, kann aber weiter angepasst werden, um für eine bestimmte Aufgabe noch nützlicher zu sein.
Anteil der Erfolge
Eine Messgröße zur Bewertung des generierten Texts eines ML-Modells. Der Anteil der Erfolge ist die Anzahl der „erfolgreichen“ generierten Textausgaben geteilt durch die Gesamtzahl der generierten Textausgaben. Wenn beispielsweise ein Large Language Model 10 Codeblöcke generiert hat, von denen fünf erfolgreich waren, beträgt der Anteil der Erfolge 50%.
Der Anteil der erfolgreichen Versuche ist in der Statistik allgemein nützlich. Im Bereich des maschinellen Lernens ist dieser Messwert jedoch hauptsächlich für die Messung überprüfbarer Aufgaben wie der Codegenerierung oder mathematischer Probleme nützlich.
G
Gini-Unreinheit
Ein Messwert, der der Entropie ähnelt. Splitter verwenden Werte, die entweder aus der Gini-Unreinheit oder der Entropie abgeleitet werden, um Bedingungen für die Klassifizierung Entscheidungsbäume zu erstellen. Information Gain wird aus der Entropie abgeleitet. Es gibt keinen allgemein akzeptierten Begriff für den Messwert, der aus der Gini-Unreinheit abgeleitet wird. Dieser unbenannte Messwert ist jedoch genauso wichtig wie der Informationsgewinn.
Die Gini-Unreinheit wird auch als Gini-Index oder einfach als Gini bezeichnet.
H
Hinge-Verlust
Eine Familie von Verlustfunktionen für die Klassifizierung, die darauf ausgelegt sind, die Entscheidungsgrenze so weit wie möglich von jedem Trainingsbeispiel entfernt zu finden und so den Abstand zwischen Beispielen und der Grenze zu maximieren. KSVMs verwenden den Hinge-Verlust (oder eine ähnliche Funktion wie den quadratischen Hinge-Verlust). Bei der binären Klassifizierung wird die Hinge-Verlustfunktion so definiert:
Dabei ist y das tatsächliche Label (-1 oder +1) und y' die Rohausgabe des Klassifizierungsmodells:
Daher sieht ein Diagramm des Hinge-Verlusts im Vergleich zu (y * y') so aus:

I
Inkompatibilität von Fairnessmesswerten
Die Idee, dass einige Fairnesskonzepte sich gegenseitig ausschließen und nicht gleichzeitig erfüllt werden können. Daher gibt es keinen einzelnen universellen Messwert zur Quantifizierung von Fairness, der auf alle ML-Probleme angewendet werden kann.
Das mag entmutigend klingen, aber die Inkompatibilität von Fairnessmesswerten bedeutet nicht, dass Bemühungen um Fairness vergeblich sind. Stattdessen wird vorgeschlagen, dass Fairness für ein bestimmtes ML-Problem kontextbezogen definiert werden muss, um Schäden zu vermeiden, die für die Anwendungsfälle spezifisch sind.
Eine detailliertere Erläuterung der Inkompatibilität von Fairness-Messwerten finden Sie unter On the (im)possibility of fairness.
Individuelle Fairness
Ein Fairness-Messwert, der prüft, ob ähnliche Personen ähnlich klassifiziert werden. Die Brobdingnagian Academy möchte beispielsweise die individuelle Fairness gewährleisten, indem sie dafür sorgt, dass zwei Schüler mit identischen Noten und standardisierten Testergebnissen die gleiche Wahrscheinlichkeit haben, zugelassen zu werden.
Die individuelle Fairness hängt ganz davon ab, wie Sie „Ähnlichkeit“ definieren (in diesem Fall Noten und Testergebnisse). Es besteht das Risiko, dass neue Fairnessprobleme entstehen, wenn Ihr Ähnlichkeitsmesswert wichtige Informationen (z. B. die Strenge des Lehrplans eines Schülers) nicht berücksichtigt.
Eine detailliertere Erläuterung von individueller Fairness finden Sie unter Fairness Through Awareness.
Informationsgewinn
In Entscheidungsbäumen ist das die Differenz zwischen der Entropie eines Knotens und der gewichteten (nach Anzahl der Beispiele) Summe der Entropie seiner untergeordneten Knoten. Die Entropie eines Knotens ist die Entropie der Beispiele in diesem Knoten.
Sehen wir uns zum Beispiel die folgenden Entropiewerte an:
- Entropie des übergeordneten Knotens = 0,6
- Entropie eines untergeordneten Knotens mit 16 relevanten Beispielen = 0,2
- Entropie eines anderen untergeordneten Knotens mit 24 relevanten Beispielen = 0,1
40% der Beispiele befinden sich also in einem untergeordneten Knoten und 60% im anderen. Beispiele:
- Gewichtete Entropiesumme der untergeordneten Knoten = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Der Informationsgewinn ist also:
- Information Gain = Entropie des übergeordneten Knotens – gewichtete Entropiesumme der untergeordneten Knoten
- Information Gain = 0,6 – 0,14 = 0,46
Die meisten Splitter versuchen, Bedingungen zu erstellen, die den Informationsgewinn maximieren.
Übereinstimmung zwischen Ratern
Ein Maß dafür, wie oft menschliche Bewerter bei der Erledigung einer Aufgabe übereinstimmen. Wenn sich die Rater nicht einig sind, müssen die Aufgabenanweisungen möglicherweise verbessert werden. Wird manchmal auch als Übereinstimmung zwischen Annotatoren oder Interrater-Reliabilität bezeichnet. Siehe auch Cohens Kappa, eine der beliebtesten Messungen der Interrater-Übereinstimmung.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Kategorische Daten: Häufige Probleme.
L
L1-Verlust
Eine Verlustfunktion, die den absoluten Wert der Differenz zwischen den tatsächlichen Label-Werten und den Werten berechnet, die ein Modell vorhersagt. Hier ist beispielsweise die Berechnung des L1-Verlusts für einen Batch mit fünf Beispielen:
| Tatsächlicher Wert des Beispiels | Vom Modell prognostizierter Wert | Absoluter Wert des Deltas |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1-Verlust | ||
Der L1-Verlust reagiert weniger empfindlich auf Ausreißer als der L2-Verlust.
Der mittlere absolute Fehler ist der durchschnittliche L1-Verlust pro Beispiel.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Verlust.
L2-Verlust
Eine Verlustfunktion, die das Quadrat der Differenz zwischen den tatsächlichen Label-Werten und den Werten berechnet, die ein Modell vorhersagt. Hier ist beispielsweise die Berechnung des L2-Verlusts für einen Batch mit fünf Beispielen:
| Tatsächlicher Wert des Beispiels | Vom Modell prognostizierter Wert | Quadrat von Delta |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2-Verlust | ||
Durch die Quadrierung verstärkt der L2-Verlust den Einfluss von Ausreißern. Das bedeutet, dass der L2-Verlust stärker auf schlechte Vorhersagen reagiert als der L1-Verlust. Der L1-Verlust für den vorherigen Batch wäre beispielsweise 8 statt 16. Ein einzelner Ausreißer macht 9 der 16 aus.
In Regressionsmodellen wird in der Regel der L2-Verlust als Verlustfunktion verwendet.
Der mittlere quadratische Fehler ist der durchschnittliche L2-Verlust pro Beispiel. Squared Loss ist ein anderer Name für den L2-Verlust.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Logistische Regression: Verlust und Regularisierung.
LLM-Bewertungen
Eine Reihe von Messwerten und Benchmarks zur Bewertung der Leistung von Large Language Models (LLMs). Auf hoher Ebene:
- Forschern helfen, Bereiche zu identifizieren, in denen LLMs verbessert werden müssen.
- Sie sind nützlich, um verschiedene LLMs zu vergleichen und das beste LLM für eine bestimmte Aufgabe zu ermitteln.
- Dazu beitragen, dass LLMs sicher und ethisch vertretbar sind.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Large Language Models (LLMs).
Niederlage
Beim Training eines überwachten Modells wird gemessen, wie weit die Vorhersage eines Modells von seinem Label entfernt ist.
Mit einer Verlustfunktion wird der Verlust berechnet.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Lineare Regression: Verlust.
Verlustfunktion
Während des Trainings oder Tests wird eine mathematische Funktion verwendet, mit der der Verlust für einen Batch von Beispielen berechnet wird. Eine Verlustfunktion gibt einen niedrigeren Verlust für Modelle zurück, die gute Vorhersagen treffen, als für Modelle, die schlechte Vorhersagen treffen.
Das Ziel des Trainings besteht in der Regel darin, den Verlust zu minimieren, der von einer Verlustfunktion zurückgegeben wird.
Es gibt viele verschiedene Arten von Verlustfunktionen. Wählen Sie die geeignete Verlustfunktion für den Typ des Modells aus, das Sie erstellen. Beispiel:
- L2-Verlust (oder mittlerer quadratischer Fehler) ist die Verlustfunktion für die lineare Regression.
- Logarithmischer Verlust ist die Verlustfunktion für die logistische Regression.
M
Matrixfaktorisierung
In der Mathematik ein Mechanismus zum Ermitteln der Matrizen, deren Punktprodukt eine Zielmatrix annähert.
In Empfehlungssystemen enthält die Zielmatrix häufig die Bewertungen der Nutzer für Elemente. Die Zielmatrix für ein Filmempfehlungssystem könnte beispielsweise so aussehen. Die positiven Ganzzahlen sind Nutzerbewertungen und 0 bedeutet, dass der Nutzer den Film nicht bewertet hat:
| Casablanca | Die Philadelphia Story | Black Panther | Wonder Woman | Pulp Fiction | |
|---|---|---|---|---|---|
| Nutzer 1 | 5 | 3 | 0,0 | 2.0 | 0,0 |
| Nutzer 2 | 4.0 | 0,0 | 0,0 | 1.0 | 5 |
| Nutzer 3 | 3 | 1.0 | 4.0 | 5,0 | 0,0 |
Das Filmempfehlungssystem soll Nutzereinstufungen für Filme vorhersagen, die noch nicht bewertet wurden. Wird Nutzer 1 beispielsweise Black Panther mögen?
Ein Ansatz für Empfehlungssysteme besteht darin, mithilfe der Matrixfaktorisierung die folgenden beiden Matrizen zu generieren:
- Eine Nutzermatrix mit der Form „Anzahl der Nutzer × Anzahl der Einbettungsdimensionen“.
- Eine Artikelmatrix mit der Form „Anzahl der Einbettungsdimensionen × Anzahl der Artikel“.
Wenn wir beispielsweise die Matrixfaktorisierung auf unsere drei Nutzer und fünf Elemente anwenden, erhalten wir möglicherweise die folgenden Nutzer- und Elementmatrizen:
User Matrix Item Matrix 1.1 2.3 0.9 0.2 1.4 2.0 1.2 0.6 2.0 1.7 1.2 1.2 -0.1 2.1 2.5 0.5
Das Punktprodukt der Nutzermatrix und der Artikelmatrix ergibt eine Empfehlungsmatrix, die nicht nur die ursprünglichen Nutzerbewertungen, sondern auch Vorhersagen für die Filme enthält, die jeder Nutzer noch nicht gesehen hat. Die Bewertung von Casablanca durch Nutzer 1 war beispielsweise 5,0. Das Punktprodukt, das dieser Zelle in der Empfehlungsmatrix entspricht, sollte idealerweise etwa 5,0 betragen.Das ist auch der Fall:
(1.1 * 0.9) + (2.3 * 1.7) = 4.9Und noch wichtiger: Wird Nutzer 1 Black Panther mögen? Wenn Sie das Skalarprodukt aus der ersten Zeile und der dritten Spalte bilden, erhalten Sie eine Vorhersage von 4,3:
(1.1 * 1.4) + (2.3 * 1.2) = 4.3Bei der Matrixfaktorisierung werden in der Regel eine Nutzermatrix und eine Elementmatrix erstellt, die zusammen deutlich kompakter sind als die Zielmatrix.
MBPP
Abkürzung für Mostly Basic Python Problems (meist grundlegende Python-Probleme).
Mittlerer absoluter Fehler (MAE)
Der durchschnittliche Verlust pro Beispiel, wenn der L1-Verlust verwendet wird. So berechnen Sie den mittleren absoluten Fehler:
- Berechnet den L1-Verlust für einen Batch.
- Teilen Sie den L1-Verlust durch die Anzahl der Beispiele im Batch.
Betrachten Sie beispielsweise die Berechnung des L1-Verlusts für den folgenden Batch mit fünf Beispielen:
| Tatsächlicher Wert des Beispiels | Vom Modell prognostizierter Wert | Verlust (Differenz zwischen tatsächlichem und vorhergesagtem Wert) |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1-Verlust | ||
Der L1-Verlust beträgt also 8 und die Anzahl der Beispiele ist 5. Der mittlere absolute Fehler ist also:
Mean Absolute Error = L1 loss / Number of Examples Mean Absolute Error = 8/5 = 1.6
Stellen Sie den mittleren absoluten Fehler dem mittleren quadratischen Fehler und dem Wurzel der mittleren Fehlerquadratsumme gegenüber.
Mittlere durchschnittliche Precision bei k (mAP@k)
Der statistische Mittelwert aller durchschnittlichen Precision bei k-Werte in einem Validierungs-Dataset. Mit der mittleren durchschnittlichen Präzision bei k lässt sich die Qualität von Empfehlungen beurteilen, die von einem Empfehlungssystem generiert werden.
Auch wenn die Formulierung „durchschnittlicher Mittelwert“ redundant klingt, ist der Name des Messwerts angemessen. Dieser Messwert ist schließlich der Mittelwert mehrerer durchschnittliche Precision bei k-Werte.
Mittlere quadratische Abweichung (MSE)
Der durchschnittliche Verlust pro Beispiel, wenn der L2-Verlust verwendet wird. So berechnen Sie die mittlere quadratische Abweichung:
- Berechnet den L2-Verlust für einen Batch.
- Teilen Sie den L2-Verlust durch die Anzahl der Beispiele im Batch.
Betrachten Sie beispielsweise den Verlust für den folgenden Batch mit fünf Beispielen:
| Tatsächlicher Wert | Vorhersage des Modells | Verlust | Quadratischer Verlust |
|---|---|---|---|
| 7 | 6 | 1 | 1 |
| 5 | 4 | 1 | 1 |
| 8 | 11 | 3 | 9 |
| 4 | 6 | 2 | 4 |
| 9 | 8 | 1 | 1 |
| 16 = L2-Verlust | |||
Die mittlere quadratische Abweichung ist also:
Mean Squared Error = L2 loss / Number of Examples Mean Squared Error = 16/5 = 3.2
Die mittlere quadratische Abweichung ist ein beliebter Optimizer für das Training, insbesondere für die lineare Regression.
Vergleichen Sie die mittlere quadratische Abweichung mit dem mittleren absoluten Fehler und der Wurzel der mittleren Fehlerquadratsumme.
Im TensorFlow Playground wird der mittlere quadratische Fehler verwendet, um Verlustwerte zu berechnen.
Messwert
Eine Statistik, die Ihnen wichtig ist.
Ein Ziel ist ein Messwert, den ein System für maschinelles Lernen zu optimieren versucht.
Metrics API (tf.metrics)
Eine TensorFlow-API zum Bewerten von Modellen. Mit tf.metrics.accuracy wird beispielsweise festgelegt, wie oft die Vorhersagen eines Modells mit Labels übereinstimmen.
Minimax-Verlust
Eine Verlustfunktion für generative kontradiktorische Netzwerke, die auf der Kreuzentropie zwischen der Verteilung der generierten Daten und der tatsächlichen Daten basiert.
Der Minimax-Verlust wird im ersten Paper zur Beschreibung generativer kontradiktorischer Netzwerke verwendet.
Weitere Informationen finden Sie im Kurs zu generativen kontradiktorischen Netzwerken unter Verlustfunktionen.
Modellkapazität
Die Komplexität der Probleme, die ein Modell lernen kann. Je komplexer die Probleme sind, die ein Modell lernen kann, desto höher ist die Kapazität des Modells. Die Kapazität eines Modells steigt in der Regel mit der Anzahl der Modellparameter. Eine formale Definition der Kapazität von Klassifikationsmodellen finden Sie unter VC-Dimension.
Erfolge
Ein ausgefeilter Gradientenabstiegsalgorithmus, bei dem ein Lernschritt nicht nur vom Derivat im aktuellen Schritt, sondern auch von den Derivaten der unmittelbar vorangegangenen Schritte abhängt. Beim Momentum wird ein exponentiell gewichteter gleitender Durchschnitt der Gradienten im Zeitverlauf berechnet, analog zum Impuls in der Physik. Momentum kann verhindern, dass das Lernen in lokalen Minima stecken bleibt.
Mostly Basic Python Problems (MBPP)
Ein Dataset zur Bewertung der Fähigkeit eines LLM, Python-Code zu generieren. Mostly Basic Python Problems enthält etwa 1.000 von der Community erstellte Programmieraufgaben. Jedes Problem im Dataset enthält:
- Eine Aufgabenbeschreibung
- Lösungscode
- Drei automatisierte Testläufe
N
negative Klasse
Bei der binären Klassifizierung wird eine Klasse als positiv und die andere als negativ bezeichnet. Die positive Klasse ist das Ding oder Ereignis, auf das das Modell testet, und die negative Klasse ist die andere Möglichkeit. Beispiel:
- Die negative Klasse in einem medizinischen Test könnte „kein Tumor“ sein.
- Die negative Klasse in einem Klassifizierungsmodell für E‑Mails könnte „Kein Spam“ sein.
Kontrast zur positiven Klasse.
O
Ziel
Ein Messwert, den Ihr Algorithmus optimieren soll.
Zielfunktion
Die mathematische Formel oder der Messwert, die bzw. den ein Modell optimieren soll. Die Zielfunktion für die lineare Regression ist in der Regel der mittlere quadratische Verlust. Beim Trainieren eines linearen Regressionsmodells wird daher versucht, den mittleren quadratischen Verlust zu minimieren.
In einigen Fällen ist das Ziel, die Zielfunktion zu maximieren. Wenn die Zielfunktion beispielsweise die Genauigkeit ist, besteht das Ziel darin, die Genauigkeit zu maximieren.
Siehe auch Verlust.
P
Bestanden bei k (pass@k)
Ein Messwert zur Bestimmung der Qualität von Code (z. B. Python), der von einem Large Language Model generiert wird. Genauer gesagt gibt „Bestanden bei k“ an, wie wahrscheinlich es ist, dass mindestens ein generierter Codeblock von k generierten Codeblöcken alle zugehörigen Unittests besteht.
Große Sprachmodelle haben oft Schwierigkeiten, guten Code für komplexe Programmierprobleme zu generieren. Softwareentwickler begegnen diesem Problem, indem sie das große Sprachmodell auffordern, mehrere (k) Lösungen für dasselbe Problem zu generieren. Anschließend testen Softwareentwickler jede der Lösungen mit Unittests. Die Berechnung von „Bestanden“ bei k hängt vom Ergebnis der Unit-Tests ab:
- Wenn eine oder mehrere dieser Lösungen den Unittest bestehen, besteht das LLM diese Aufgabe zur Codeerstellung.
- Wenn keine der Lösungen den Unittest besteht, besteht das LLM diese Aufgabe zur Codegenerierung nicht.
Die Formel für „Bestanden“ bei k lautet so:
\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]
Im Allgemeinen führen höhere Werte von k zu höheren „Pass at k“-Ergebnissen. Allerdings erfordern höhere Werte von k mehr Ressourcen für Large Language Models und Einheitentests.
Leistung
Überladener Begriff mit den folgenden Bedeutungen:
- Die Standardbedeutung in der Softwareentwicklung. Konkret: Wie schnell (oder effizient) läuft diese Software?
- Die Bedeutung im Zusammenhang mit maschinellem Lernen. Die Leistung beantwortet die folgende Frage: Wie korrekt ist dieses Modell? Wie gut sind die Vorhersagen des Modells?
Bewertung von Variablen durch Permutation
Eine Art von Variablenwichtigkeit, die die Zunahme des Vorhersagefehlers eines Modells nach Permutation der Werte des Features bewertet. Die Permutationsvariablenwichtigkeit ist ein modellunabhängiger Messwert.
Perplexity
Ein Maß dafür, wie gut ein Modell seine Aufgabe erfüllt. Angenommen, Ihre Aufgabe besteht darin, die ersten Buchstaben eines Worts zu lesen, das ein Nutzer auf einer Smartphone-Tastatur eingibt, und eine Liste mit möglichen Vervollständigungswörtern anzubieten. Die Perplexität P für diese Aufgabe entspricht ungefähr der Anzahl der Vermutungen, die Sie anbieten müssen, damit Ihre Liste das tatsächliche Wort enthält, das der Nutzer eingeben möchte.
Die Perplexität hängt so mit der Kreuzentropie zusammen:
positive Klasse
Die Klasse, die Sie testen.
Die positive Klasse in einem Krebsmodell könnte beispielsweise „Tumor“ sein. Die positive Klasse in einem E-Mail-Klassifizierungsmodell kann beispielsweise „Spam“ sein.
Im Gegensatz zur negativen Klasse.
PR AUC (Bereich unter der PR-Kurve)
Die Fläche unter der interpolierten Genauigkeits-/Trefferquotenkurve, die durch das Darstellen von (Recall, Precision)-Punkten für verschiedene Werte des Klassifizierungsschwellenwerts ermittelt wird.
Precision
Ein Messwert für Klassifizierungsmodelle, der die folgende Frage beantwortet:
Wenn das Modell die positive Klasse vorhergesagt hat, wie viel Prozent der Vorhersagen waren richtig?
Hier ist die Formel:
Dabei gilt:
- „Richtig positiv“ bedeutet, dass das Modell die positive Klasse richtig vorhergesagt hat.
- „Falsch positiv“ bedeutet, dass das Modell die positive Klasse fälschlicherweise vorhergesagt hat.
Angenommen, ein Modell hat 200 positive Vorhersagen getroffen. Von diesen 200 positiven Vorhersagen:
- 150 Ergebnisse waren richtig positiv.
- 50 davon waren Fehlalarme.
In diesem Fall gilt:
Genauigkeit und Trefferquote im Vergleich.
Weitere Informationen finden Sie im Machine Learning Crash Course unter Klassifizierung: Genauigkeit, Trefferquote, Präzision und zugehörige Messwerte.
Precision bei k (precision@k)
Ein Messwert zur Bewertung einer sortierten Liste von Elementen. Die Genauigkeit bei k gibt den Anteil der ersten k Elemente in dieser Liste an, die „relevant“ sind. Das bedeutet:
\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]
Der Wert von k muss kleiner oder gleich der Länge der zurückgegebenen Liste sein. Die Länge der zurückgegebenen Liste ist nicht Teil der Berechnung.
Die Relevanz ist oft subjektiv. Selbst menschliche Prüfer, die Experten auf diesem Gebiet sind, sind sich oft nicht einig, welche Elemente relevant sind.
Vergleichen mit:
Precision-/Recall-Kurve
Eine Kurve mit Genauigkeit im Vergleich zur Trefferquote bei verschiedenen Klassifizierungsschwellenwerten.
Vorhersage-Bias
Ein Wert, der angibt, wie weit der Durchschnitt der Vorhersagen vom Durchschnitt der Labels im Datensatz entfernt ist.
Nicht zu verwechseln mit dem Bias-Term in Modellen für maschinelles Lernen oder mit Bias in Ethik und Fairness.
Prognoseparität
Ein Fairness-Messwert, mit dem geprüft wird, ob die Precision-Raten für die betrachteten Untergruppen für ein bestimmtes Klassifizierungsmodell gleich sind.
Ein Modell, das die Zulassung zum College vorhersagt, würde beispielsweise die Vorhersageparität für die Nationalität erfüllen, wenn die Precision-Rate für Lilliputaner und Brobdingnagianer gleich ist.
Die Vorhersageparität wird manchmal auch als Parität der Vorhersagerate bezeichnet.
Eine detailliertere Erläuterung der Vorhersageparität finden Sie im Abschnitt 3.2.1 von Fairness Definitions Explained.
Prognostizierte Ratenparität
Ein anderer Name für Vorhersageparität.
Wahrscheinlichkeitsdichtefunktion
Eine Funktion, mit der die Häufigkeit von Datenstichproben mit genau einem bestimmten Wert ermittelt wird. Wenn die Werte eines Datensatzes kontinuierliche Gleitkommazahlen sind, kommt es selten zu genauen Übereinstimmungen. Wenn Sie eine Wahrscheinlichkeitsdichtefunktion vom Wert x bis zum Wert y integrieren, erhalten Sie die erwartete Häufigkeit von Datenstichproben zwischen x und y.
Angenommen, Sie haben eine Normalverteilung mit einem Mittelwert von 200 und einer Standardabweichung von 30. Um die erwartete Häufigkeit von Datenstichproben im Bereich von 211,4 bis 218,7 zu ermitteln, können Sie die Wahrscheinlichkeitsdichtefunktion für eine Normalverteilung von 211,4 bis 218,7 integrieren.
R
Reading Comprehension with Commonsense Reasoning Dataset (ReCoRD)
Ein Dataset zur Bewertung der Fähigkeit eines LLM, Common Sense-Schlussfolgerungen zu ziehen. Jedes Beispiel im Dataset enthält drei Komponenten:
- Ein oder zwei Absätze aus einem Nachrichtenartikel
- Eine Anfrage, in der eine der in der Passage explizit oder implizit identifizierten Entitäten maskiert ist.
- Die Antwort (der Name der Entität, die in die Maske gehört)
Eine ausführliche Liste mit Beispielen finden Sie unter ReCoRD.
ReCoRD ist eine Komponente des SuperGLUE-Ensembles.
RealToxicityPrompts
Ein Dataset, das eine Reihe von Satzanfängen enthält, die möglicherweise schädliche Inhalte enthalten. Mit diesem Dataset können Sie die Fähigkeit eines LLM bewerten, nicht toxischen Text zu generieren, um den Satz zu vervollständigen. Normalerweise verwenden Sie die Perspective API, um zu ermitteln, wie gut das LLM diese Aufgabe ausgeführt hat.
Weitere Informationen finden Sie unter RealToxicityPrompts: Evaluating Neural Toxic Degeneration in Language Models.
Rückruf
Ein Messwert für Klassifizierungsmodelle, der die folgende Frage beantwortet:
Wenn die Ground Truth die positive Klasse war, bei wie viel Prozent der Vorhersagen hat das Modell die positive Klasse richtig erkannt?
Hier ist die Formel:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
Dabei gilt:
- „Richtig positiv“ bedeutet, dass das Modell die positive Klasse richtig vorhergesagt hat.
- „Falsch negativ“ bedeutet, dass das Modell fälschlicherweise die negative Klasse vorhergesagt hat.
Angenommen, Ihr Modell hat 200 Vorhersagen für Beispiele getroffen, für die die Grundwahrheit die positive Klasse war. Von diesen 200 Vorhersagen:
- 180 Ergebnisse waren richtig positiv.
- 20 Ergebnisse waren falsch negativ.
In diesem Fall gilt:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
Recall bei k (recall@k)
Eine Metrik zur Bewertung von Systemen, die eine sortierte Liste von Elementen ausgeben. Der Recall bei k gibt den Anteil der relevanten Elemente in den ersten k Elementen in dieser Liste im Verhältnis zur Gesamtzahl der zurückgegebenen relevanten Elemente an.
\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]
Kontrast zu Precision at k.
Erkennen von Textual Entailment (RTE)
Ein Dataset zur Bewertung der Fähigkeit eines LLM, festzustellen, ob eine Hypothese aus einem Textabschnitt abgeleitet werden kann. Jedes Beispiel in einer RTE-Bewertung besteht aus drei Teilen:
- Eine Passage, in der Regel aus Nachrichten- oder Wikipedia-Artikeln
- Eine Hypothese
- Die richtige Antwort ist entweder:
- Wahr: Die Hypothese kann aus dem Abschnitt abgeleitet werden.
- Falsch. Die Hypothese kann nicht aus dem Abschnitt abgeleitet werden.
Beispiel:
- Ausschnitt:Der Euro ist die Währung der Europäischen Union.
- Hypothese:In Frankreich wird der Euro als Währung verwendet.
- Implikation:Richtig, da Frankreich Teil der Europäischen Union ist.
RTE ist eine Komponente des SuperGLUE-Ensembles.
ReCoRD
Abkürzung für Reading Comprehension with Commonsense Reasoning Dataset (Dataset zum Leseverständnis mit vernünftigem Abwägen).
ROC-Kurve (Receiver Operating Characteristic)
Ein Diagramm der Richtig-Positiv-Rate im Vergleich zur Falsch-Positiv-Rate für verschiedene Klassifizierungsschwellenwerte bei der binären Klassifizierung.
Die Form einer ROC-Kurve gibt Aufschluss darüber, wie gut ein binäres Klassifikationsmodell positive von negativen Klassen trennen kann. Angenommen, ein binäres Klassifizierungsmodell trennt alle negativen Klassen perfekt von allen positiven Klassen:
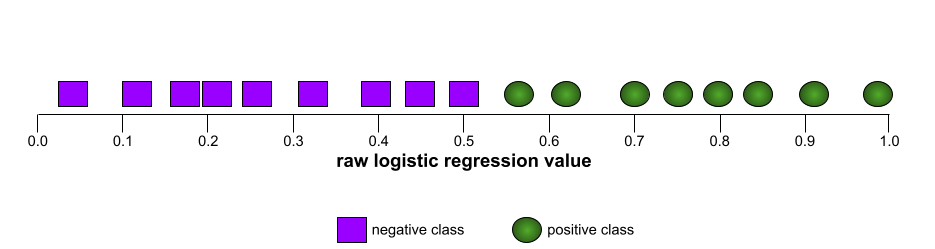
Die ROC-Kurve für das vorherige Modell sieht so aus:
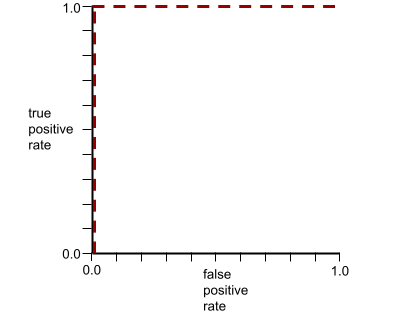
Im Gegensatz dazu zeigt die folgende Abbildung die Rohwerte der logistischen Regression für ein schlechtes Modell, das negative Klassen überhaupt nicht von positiven Klassen trennen kann:
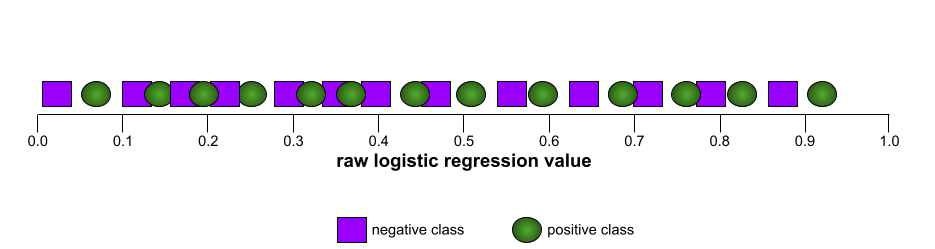
Die ROC-Kurve für dieses Modell sieht so aus:
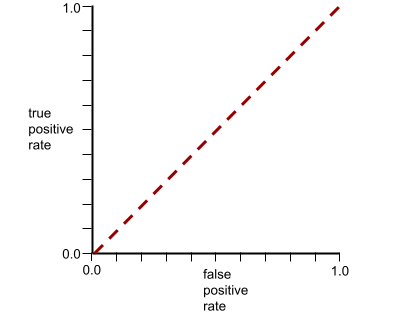
In der realen Welt trennen die meisten binären Klassifizierungsmodelle positive und negative Klassen bis zu einem gewissen Grad, aber in der Regel nicht perfekt. Eine typische ROC-Kurve liegt also irgendwo zwischen den beiden Extremen:
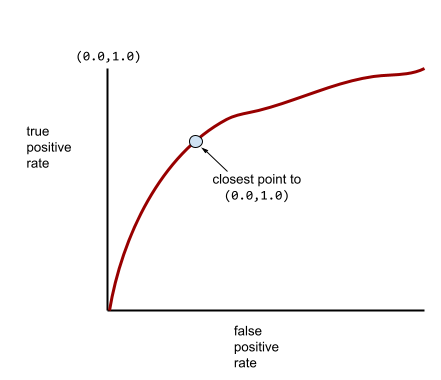
Der Punkt auf einer ROC-Kurve, der theoretisch am nächsten an (0,0,1,0) liegt, gibt den idealen Klassifizierungsschwellenwert an. Die Auswahl des idealen Klassifizierungsschwellenwerts wird jedoch von mehreren anderen realen Problemen beeinflusst. Falsch negative Ergebnisse verursachen beispielsweise möglicherweise viel mehr Probleme als falsch positive Ergebnisse.
Ein numerischer Messwert namens AUC fasst die ROC-Kurve in einem einzelnen Gleitkommawert zusammen.
Wurzel der mittleren Fehlerquadratsumme (RMSE)
Die Quadratwurzel der mittleren quadratischen Abweichung.
ROUGE (Recall-Oriented Understudy for Gisting Evaluation)
Eine Familie von Messwerten zur Bewertung von Modellen für die automatische Zusammenfassung und maschinelle Übersetzung. ROUGE-Messwerte geben an, inwieweit sich ein Referenztext mit dem generierten Text eines ML-Modells überschneidet. Jedes Mitglied der ROUGE-Familie misst die Überschneidung auf unterschiedliche Weise. Höhere ROUGE-Werte weisen auf eine größere Ähnlichkeit zwischen dem Referenztext und dem generierten Text hin als niedrigere ROUGE-Werte.
Für jedes Mitglied der ROUGE-Familie werden in der Regel die folgenden Messwerte generiert:
- Precision
- Recall
- F1
Weitere Informationen und Beispiele finden Sie unter:
ROUGE-L
Ein Mitglied der ROUGE-Familie, das sich auf die Länge der längsten gemeinsamen Untersequenz im Referenztext und generierten Text konzentriert. Mit den folgenden Formeln werden Recall und Precision für ROUGE-L berechnet:
Anschließend können Sie F1 verwenden, um die ROUGE-L-Trefferquote und die ROUGE-L-Genauigkeit in einem einzigen Messwert zusammenzufassen:
Bei ROUGE-L werden alle Zeilenumbrüche im Referenztext und im generierten Text ignoriert. Die längste gemeinsame Untersequenz kann sich also über mehrere Sätze erstrecken. Wenn der Referenztext und der generierte Text mehrere Sätze umfassen, ist in der Regel eine Variante von ROUGE-L namens ROUGE-Lsum ein besserer Messwert. ROUGE-Lsum ermittelt die längste gemeinsame Teilsequenz für jeden Satz in einem Abschnitt und berechnet dann den Mittelwert dieser längsten gemeinsamen Teilsequenzen.
ROUGE-N
Eine Reihe von Messwerten aus der ROUGE-Familie, mit denen die gemeinsamen N-Gramme einer bestimmten Größe im Referenztext und im generierten Text verglichen werden. Beispiel:
- Mit ROUGE-1 wird die Anzahl der gemeinsamen Tokens im Referenztext und im generierten Text gemessen.
- Mit ROUGE-2 wird die Anzahl der gemeinsamen Bigramme (2-Gramme) im Referenztext und im generierten Text gemessen.
- Mit ROUGE-3 wird die Anzahl der gemeinsamen Trigramme (3-Gramme) im Referenztext und im generierten Text gemessen.
Mit den folgenden Formeln können Sie den ROUGE-N-Recall und die ROUGE-N-Präzision für jedes Mitglied der ROUGE-N-Familie berechnen:
Anschließend können Sie mit F1 den ROUGE-N-Recall und die ROUGE-N-Präzision in einem einzigen Messwert zusammenfassen:
ROUGE-S
Eine tolerantere Form von ROUGE-N, die den Abgleich von Skip-Grammen ermöglicht. ROUGE-N zählt nur N-Gramme, die genau übereinstimmen. ROUGE-S zählt auch N-Gramme, die durch ein oder mehrere Wörter getrennt sind. Sie könnten beispielsweise Folgendes versuchen:
- Referenztext: Weiße Wolken
- Generierter Text: Weiße, bauschige Wolken
Bei der Berechnung von ROUGE-N stimmt das 2-Gramm White clouds nicht mit White billowing clouds überein. Bei der Berechnung von ROUGE-S wird Weiße Wolken jedoch mit Weiße, sich auftürmende Wolken abgeglichen.
R-Quadrat
Ein Regressionsmesswert, der angibt, wie viel Variation in einem Label auf ein einzelnes Feature oder eine Gruppe von Features zurückzuführen ist. R-Quadrat ist ein Wert zwischen 0 und 1, den Sie so interpretieren können:
- Ein R-Quadrat von 0 bedeutet, dass keine der Variationen eines Labels auf den Funktionssatz zurückzuführen ist.
- Ein R-Quadrat von 1 bedeutet, dass die gesamte Variation eines Labels auf die Gruppe von Features zurückzuführen ist.
- Ein R-Quadrat zwischen 0 und 1 gibt an, inwieweit die Variation des Labels anhand eines bestimmten Merkmals oder der Merkmalsgruppe vorhergesagt werden kann. Ein R-Quadrat von 0,10 bedeutet beispielsweise, dass 10 % der Varianz des Labels auf die Feature-Gruppe zurückzuführen sind. Ein R-Quadrat von 0,20 bedeutet, dass 20 % auf die Feature-Gruppe zurückzuführen sind usw.
Das Bestimmtheitsmaß (R-Quadrat) ist das Quadrat des Pearson-Korrelationskoeffizienten zwischen den von einem Modell vorhergesagten Werten und der Ground Truth.
RTE
Abkürzung für Recognizing Textual Entailment (Erkennen von Textimplikationen).
S
Bewertung
Der Teil eines Empfehlungssystems, der einen Wert oder ein Ranking für jedes Element liefert, das in der Phase der Kandidatengenerierung erstellt wird.
Ähnlichkeitsmaß
In Clustering-Algorithmen wird mit diesem Messwert bestimmt, wie ähnlich sich zwei Beispiele sind.
dünne Besetzung
Die Anzahl der Elemente, die in einem Vektor oder einer Matrix auf null gesetzt wurden, geteilt durch die Gesamtzahl der Einträge in diesem Vektor oder dieser Matrix. Betrachten Sie beispielsweise eine Matrix mit 100 Elementen, in der 98 Zellen den Wert 0 enthalten. Die Berechnung der Sparsity erfolgt so:
Feature-Sparsity bezieht sich auf die Sparsity eines Feature-Vektors, Modell-Sparsity auf die Sparsity der Modellgewichte.
SQuAD
Akronym für Stanford Question Answering Dataset (Stanford-Dataset für die Beantwortung von Fragen), das im Paper SQuAD: 100,000+ Questions for Machine Comprehension of Text (SQuAD: Über 100.000 Fragen zum maschinellen Verstehen von Text) vorgestellt wurde. Die Fragen in diesem Dataset stammen von Personen, die Fragen zu Wikipedia-Artikeln gestellt haben. Einige der Fragen in SQuAD haben Antworten, andere absichtlich nicht. Daher können Sie SQuAD verwenden, um die Fähigkeit eines LLM zu bewerten, Folgendes zu tun:
- Beantworten Sie Fragen, die beantwortet werden können.
- Fragen identifizieren, die nicht beantwortet werden können.
Genau passend in Kombination mit F sind die gängigsten Messwerte für die Bewertung von LLMs anhand von SQuAD.
Quadratischer Hinge-Verlust
Das Quadrat des Hinge-Verlusts. Der quadratische Hinge-Verlust bestraft Ausreißer stärker als der reguläre Hinge-Verlust.
Quadratischer Verlust
Synonym für L2-Verlust.
SuperGLUE
Eine Gruppe von Datasets zur Bewertung der allgemeinen Fähigkeit eines LLM, Text zu verstehen und zu generieren. Das Ensemble besteht aus den folgenden Datasets:
- Boolesche Fragen (BoolQ)
- CommitmentBank (CB)
- Choice of Plausible Alternatives (COPA)
- Leseverständnis für mehrere Sätze (MultiRC)
- ReCoRD-Dataset (Reading Comprehension with Commonsense Reasoning Dataset)
- Erkennen von Textual Entailment (RTE)
- Words in Context (WiC)
- Winograd Schema Challenge (WSC)
Weitere Informationen finden Sie unter SuperGLUE: A Stickier Benchmark for General-Purpose Language Understanding Systems.
T
Testverlust
Ein Messwert, der den Verlust eines Modells im Vergleich zum Test-Dataset darstellt. Beim Erstellen eines Modells versuchen Sie in der Regel, den Testverlust zu minimieren. Das liegt daran, dass ein geringer Testverlust ein stärkeres Qualitätssignal ist als ein geringer Trainingsverlust oder ein geringer Validierungsverlust.
Eine große Lücke zwischen Testverlust und Trainings- oder Validierungsverlust deutet manchmal darauf hin, dass Sie die Regularisierungsrate erhöhen müssen.
Top-K-Genauigkeit
Der Prozentsatz der Fälle, in denen ein „Ziellabel“ innerhalb der ersten k Positionen der generierten Listen erscheint. Die Listen können personalisierte Empfehlungen oder eine Liste von Elementen sein, die nach softmax sortiert sind.
Die Top‑k-Genauigkeit wird auch als Genauigkeit bei k bezeichnet.
Toxizität
Inwieweit Inhalte beleidigend, bedrohlich oder anstößig sind. Viele Modelle für maschinelles Lernen können schädliche Inhalte erkennen, messen und klassifizieren. Die meisten dieser Modelle erkennen toxische Inhalte anhand mehrerer Parameter, z. B. des Ausmaßes an beleidigender und bedrohlicher Sprache.
Trainingsverlust
Ein Messwert, der den Verlust eines Modells während eines bestimmten Trainingsdurchlaufs darstellt. Angenommen, die Verlustfunktion ist Mean Squared Error. Vielleicht beträgt der Trainingsverlust (der mittlere quadratische Fehler) für die 10.Iteration 2,2 und der Trainingsverlust für die 100.Iteration 1,9.
In einer Verlustkurve wird der Trainingsverlust im Verhältnis zur Anzahl der Iterationen dargestellt. Eine Verlustkurve kann folgende Hinweise zum Training geben:
- Ein abwärts gerichteter Verlauf deutet darauf hin, dass sich das Modell verbessert.
- Ein Aufwärtstrend bedeutet, dass das Modell schlechter wird.
- Eine flache Steigung bedeutet, dass das Modell konvergiert ist.
Das folgende etwas idealisierte Verlustkurvenbeispiel zeigt:
- Ein steiler Abwärtstrend in den ersten Iterationen, der auf eine schnelle Verbesserung des Modells hindeutet.
- Ein allmählich abflachender (aber immer noch abwärts gerichteter) Verlauf bis kurz vor dem Ende des Trainings, was auf eine kontinuierliche Verbesserung des Modells hinweist, wenn auch etwas langsamer als in den ersten Iterationen.
- Ein flacher Abfall gegen Ende des Trainings, der auf Konvergenz hindeutet.
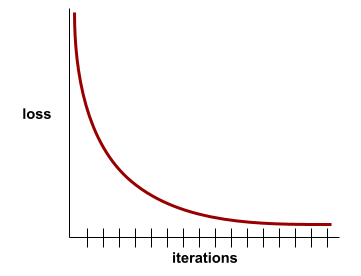
Der Trainingsverlust ist zwar wichtig, aber sehen Sie sich auch die Generalisierung an.
Beantwortung von Quizfragen
Datasets zur Bewertung der Fähigkeit eines LLM, Quizfragen zu beantworten. Jedes Dataset enthält Frage-Antwort-Paare, die von Trivia-Fans erstellt wurden. Verschiedene Datasets basieren auf unterschiedlichen Quellen, darunter:
- Websuche (TriviaQA)
- Wikipedia (TriviaQA_wiki)
Weitere Informationen finden Sie unter TriviaQA: A Large Scale Distantly Supervised Challenge Dataset for Reading Comprehension.
richtig negativ (RN)
Ein Beispiel, in dem das Modell die negative Klasse richtig vorhersagt. Das Modell leitet beispielsweise ab, dass eine bestimmte E‑Mail-Nachricht kein Spam ist, und diese E‑Mail-Nachricht ist tatsächlich kein Spam.
Richtig positiv (TP)
Ein Beispiel, in dem das Modell die positive Klasse richtig vorhersagt. Das Modell leitet beispielsweise ab, dass eine bestimmte E‑Mail-Nachricht Spam ist, und diese E‑Mail-Nachricht ist tatsächlich Spam.
Rate richtig positiver Ergebnisse (True Positive Rate, TPR)
Synonym für Rückruf. Das bedeutet:
Die Rate richtig positiver Ergebnisse ist die Y-Achse in einer ROC-Kurve.
Typologically Diverse Question Answering (TyDi QA)
Ein großer Datensatz zur Bewertung der Fähigkeit eines LLM, Fragen zu beantworten. Das Dataset enthält Frage- und Antwortpaare in vielen Sprachen.
Weitere Informationen finden Sie unter TyDi QA: A Benchmark for Information-Seeking Question Answering in Typologically Diverse Languages.
V
Validierungsverlust
Eine Messwert, die den Verlust eines Modells im Validierungs-Dataset während eines bestimmten Trainingsdurchlaufs darstellt.
Siehe auch Verallgemeinerungskurve.
Variablenwichtigkeiten
Eine Reihe von Werten, die die relative Wichtigkeit der einzelnen Features für das Modell angibt.
Betrachten Sie beispielsweise einen Entscheidungsbaum, der Hauspreise schätzt. Angenommen, in diesem Entscheidungsbaum werden drei Attribute verwendet: Größe, Alter und Stil. Wenn die Wichtigkeit der drei Variablen {size=5.8, age=2.5, style=4.7} ist, ist die Größe für den Entscheidungsbaum wichtiger als das Alter oder der Stil.
Es gibt verschiedene Messwerte für die Wichtigkeit von Variablen, die ML-Experten über unterschiedliche Aspekte von Modellen informieren können.
W
Wasserstein-Verlust
Eine der Verlustfunktionen, die häufig in generativen kontradiktorischen Netzwerken verwendet werden, basierend auf der Earth Mover's Distance zwischen der Verteilung der generierten Daten und der realen Daten.
WiC
Abkürzung für Wörter im Kontext.
WikiLingua (wiki_lingua)
Ein Dataset zur Bewertung der Fähigkeit eines LLM, kurze Artikel zusammenzufassen. WikiHow, eine Enzyklopädie mit Artikeln, in denen erklärt wird, wie verschiedene Aufgaben ausgeführt werden, ist die von Menschen verfasste Quelle für die Artikel und die Zusammenfassungen. Jeder Eintrag im Dataset besteht aus:
- Ein Artikel, der erstellt wird, indem jeder Schritt der Prosaversion (Absatz) der nummerierten Liste angehängt wird, mit Ausnahme des Eröffnungssatzes jedes Schritts.
- Eine Zusammenfassung des Artikels, bestehend aus dem ersten Satz jedes Schritts in der nummerierten Liste.
Weitere Informationen finden Sie unter WikiLingua: A New Benchmark Dataset for Cross-Lingual Abstractive Summarization.
Winograd Schema Challenge (WSC)
Ein Format (oder ein Dataset, das diesem Format entspricht) zur Bewertung der Fähigkeit eines LLM, die Wortgruppe zu bestimmen, auf die sich ein Pronomen bezieht.
Jeder Eintrag in einer Winograd Schema Challenge besteht aus:
- Eine kurze Passage, die ein Zielpronomen enthält
- Ein Zielpronomen
- Kandidaten für Nomenphrasen, gefolgt von der richtigen Antwort (ein boolescher Wert). Wenn sich das Zielpronomen auf diesen Kandidaten bezieht, ist die Antwort „True“. Wenn sich das Zielpronomen nicht auf diesen Kandidaten bezieht, ist die Antwort „False“.
Beispiel:
- Passage: Mark erzählte Pete viele Lügen über sich selbst, die Pete in sein Buch aufnahm. Er hätte ehrlicher sein sollen.
- Zielpronomen: Er
- Mögliche Nomenphrasen:
- Mark: „True“, da sich das Zielpronomen auf Mark bezieht.
- Pete: Falsch, weil sich das Zielpronomen nicht auf Peter bezieht.
Die Winograd Schema Challenge ist eine Komponente des SuperGLUE-Ensembles.
Words in Context (WiC)
Ein Datensatz zur Bewertung, wie gut ein LLM Kontext verwendet, um Wörter mit mehreren Bedeutungen zu verstehen. Jeder Eintrag im Dataset enthält:
- Zwei Sätze, die jeweils das Zielwort enthalten
- Das Zielwort
- Die richtige Antwort (ein boolescher Wert), wobei:
- „True“ bedeutet, dass das Zielwort in den beiden Sätzen dieselbe Bedeutung hat.
- „Falsch“ bedeutet, dass das Zielwort in den beiden Sätzen eine andere Bedeutung hat.
Beispiel:
- Zwei Sätze:
- Im Flussbett liegt viel Müll.
- Ich habe beim Schlafen immer ein Glas Wasser neben meinem Bett stehen.
- Das Zielwort:Bett
- Richtige Antwort: Falsch, weil das Zielwort in den beiden Sätzen eine unterschiedliche Bedeutung hat.
Weitere Informationen finden Sie unter WiC: the Word-in-Context Dataset for Evaluating Context-Sensitive Meaning Representations.
„Words in Context“ ist eine Komponente des SuperGLUE-Ensembles.
WSC
Abkürzung für Winograd Schema Challenge.
X
XL-Summe (xlsum)
Ein Dataset zum Bewerten der Fähigkeit eines LLM, Text zusammenzufassen. XL-Sum bietet Einträge in vielen Sprachen. Jeder Eintrag im Dataset enthält:
- Ein Artikel der British Broadcasting Company (BBC).
- Eine Zusammenfassung des Artikels, die vom Autor des Artikels verfasst wurde. Beachten Sie, dass diese Zusammenfassung Wörter oder Wortgruppen enthalten kann, die nicht im Artikel vorkommen.
Weitere Informationen finden Sie unter XL-Sum: Large-Scale Multilingual Abstractive Summarization for 44 Languages.