本页包含指标术语表中的术语。如需查看所有术语,请点击此处。
A
准确性
正确的分类预测数量除以预测总数。具体来说:
例如,如果某个模型做出了 40 次正确预测和 10 次错误预测,那么其准确率为:
二元分类为不同类别的正确预测和错误预测提供了具体名称。因此,二元分类的准确率公式如下:
其中:
如需了解详情,请参阅机器学习速成课程中的分类:准确率、召回率、精确率和相关指标。
PR 曲线下的面积
请参阅 PR AUC(PR 曲线下面积)。
ROC 曲线下面积
请参阅 AUC(ROC 曲线下面积)。
AUC(ROC 曲线下面积)
一个介于 0.0 和 1.0 之间的数字,表示二元分类模型区分正类别和负类别的能力。 AUC 越接近 1.0,模型区分不同类别的能力就越好。
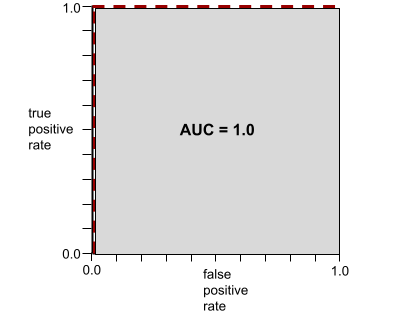
例如,下图显示了一个完美区分正类别(绿色椭圆)和负类别(紫色矩形)的分类模型。这个不切实际的完美模型的 AUC 为 1.0:

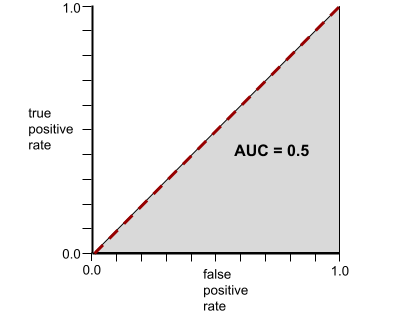
相反,下图显示了生成随机结果的分类模型的结果。此模型的 AUC 为 0.5:

是的,上述模型的 AUC 为 0.5,而不是 0.0。
大多数模型都介于这两个极端之间。例如,以下模型在一定程度上区分了正例和负例,因此其 AUC 介于 0.5 和 1.0 之间:

AUC 会忽略您为分类阈值设置的任何值。相反,AUC 会考虑所有可能的分类阈值。
如需了解详情,请参阅机器学习速成课程中的分类:ROC 和 AUC。
前 k 名的平均精确率
一种用于总结模型在生成排名结果(例如图书推荐的编号列表)的单个提示上的表现的指标。k 处的平均精确率是指每个相关结果的 k 处的精确率的平均值。 因此,前 k 个结果的平均精确率的公式为:
\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]
其中:
- \(n\) 是列表中的相关商品数量。
与 k 处的召回率相对。
B
baseline
一种用作参考点的模型,用于比较另一模型(通常是更复杂的模型)的效果。例如,逻辑回归模型可以作为深度模型的良好基准。
对于特定问题,基准有助于模型开发者量化新模型必须达到的最低预期性能,以便新模型发挥作用。
布尔值问题 (BoolQ)
用于评估 LLM 在回答是/否问题方面的熟练程度的数据集。 数据集中的每个挑战都包含三个组成部分:
- 查询
- 暗示查询答案的段落。
- 正确答案,即是或否。
例如:
- 问题:密歇根州有核电站吗?
- 原文:...three nuclear power plants supply Michigan with about 30% of its electricity.
- 正确答案:是
研究人员从匿名化的汇总 Google 搜索查询中收集问题,然后使用维基百科页面来确定信息。
如需了解详情,请参阅 BoolQ:探索自然语言是/否问题的惊人难度。
BoolQ 是 SuperGLUE 集成模型的一个组成部分。
BoolQ
布尔值问题的缩写。
C
CB
CommitmentBank 的缩写。
字符 N-gram F 得分 (ChrF)
用于评估机器翻译模型的指标。 字符 N 元语法 F 分数用于确定参考文本中的 N 元语法与机器学习模型生成的文本中的 N 元语法的重叠程度。
字符 N 元语法 F 分数与 ROUGE 和 BLEU 系列中的指标类似,但有以下区别:
- 字符 N 元语法 F 分数基于字符 N 元语法。
- ROUGE 和 BLEU 基于字词 N 元语法或标记进行操作。
选择合理的替代方案 (COPA)
一个用于评估 LLM 在识别前提的两个备选答案中哪个更优方面的能力的数据集。数据集中的每个挑战都包含三个组成部分:
- 前提,通常是陈述后跟问题
- 前提中提出的问题的两种可能答案,其中一种正确,另一种不正确
- 正确答案
例如:
- 前提:该男子弄伤了脚趾。导致这种情况的原因是什么?
- 可能的回答:
- 他的袜子破了个洞。
- 他把锤子掉在了脚上。
- 正确答案:2
COPA 是 SuperGLUE 集成模型的一个组成部分。
承诺银行 (CB)
一个用于评估 LLM 在确定段落作者是否相信该段落中的目标子句方面的熟练程度的数据集。数据集中的每个条目都包含:
- 一段文字
- 相应段落中的目标子句
- 一个布尔值,用于指示相应段落的作者是否认为目标子句
例如:
- 原文:听到阿耳特弥斯大笑,真是开心。她是个很严肃的孩子。 我不知道她还挺幽默的。
- 目标子句:她很有幽默感
- 布尔值:True,表示作者认为目标子句
CommitmentBank 是 SuperGLUE 集成模型的一个组成部分。
COPA
选择合理替代方案的缩写。
费用
与损失的含义相同。
反事实公平性
一种公平性指标,用于检查分类模型是否会针对以下两种个体生成相同的结果:一种个体与另一种个体完全相同,只是在一种或多种敏感属性方面有所不同。评估分类模型的反事实公平性是发现模型中潜在偏差来源的一种方法。
如需了解详情,请参阅以下任一内容:
- 公平性:反事实公平性,机器学习速成课程。
- 当世界相撞时:在公平性中整合不同的反事实假设
交叉熵
将对数损失推广到多类别分类问题。交叉熵可以量化两种概率分布之间的差异。另请参阅困惑度。
累积分布函数 (CDF)
一种用于定义小于或等于目标值的样本频率的函数。例如,假设存在一个连续值的正态分布。CDF 会告诉您,大约 50% 的样本应小于或等于平均值,大约 84% 的样本应小于或等于平均值加一个标准差。
D
人口统计均等
一种公平性指标,如果模型分类的结果不依赖于给定的敏感属性,则满足该指标。
例如,如果小人国人和巨人国人都申请了 Glubbdubdrib 大学,那么如果录取的小人国人百分比与录取的大人国人百分比相同,则实现了人口统计学上的平等,无论一个群体是否比另一个群体平均而言更符合条件。
与均衡赔率和机会均等形成对比,后者允许分类结果总体上取决于敏感属性,但不允许某些指定标准答案标签的分类结果取决于敏感属性。如需查看直观图表,了解在优化人口统计学均等性时需要做出的权衡,请参阅“通过更智能的机器学习避免歧视”。
如需了解详情,请参阅机器学习速成课程中的公平性:人口统计学奇偶性。
E
推土机距离 (EMD)
一种衡量两种分布相对相似度的指标。 推土机距离越小,分布越相似。
修改距离
衡量两个文本字符串彼此之间的相似程度。 在机器学习中,编辑距离非常有用,原因如下:
- 编辑距离很容易计算。
- 编辑距离可以比较已知彼此相似的两个字符串。
- 编辑距离可以确定不同字符串与给定字符串的相似程度。
编辑距离有多种定义,每种定义都使用不同的字符串操作。如需查看示例,请参阅 Levenshtein 距离。
经验累积分布函数(eCDF 或 EDF)
基于真实数据集的实证测量结果的累积分布函数。函数在 x 轴上任意点的值是数据集中小于或等于指定值的观测值的比例。
熵
在 信息论中,用于描述概率分布的不可预测程度。或者,熵也可以定义为每个示例包含的信息量。当随机变量的所有值具有相同的可能性时,分布的熵最大。
具有两个可能值“0”和“1”(例如,二元分类问题中的标签)的集合的熵具有以下公式:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
其中:
- H 是熵。
- p 是“1”示例的比例。
- q 是“0”示例的比例。请注意,q = (1 - p)
- 对数通常为以 2 为底的对数。在本例中,熵单位为比特。
例如,假设情况如下:
- 100 个示例包含值“1”
- 300 个示例包含值“0”
因此,熵值为:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 每个示例 0.81 位
完全平衡的集合(例如,200 个“0”和 200 个“1”)的每个示例的熵为 1.0 位。随着集合变得越来越不平衡,其熵会趋向于 0.0。
在决策树中,熵有助于制定信息增益,从而帮助分裂器在分类决策树的增长过程中选择条件。
将熵与以下对象进行比较:
熵通常称为香农熵。
如需了解详情,请参阅决策森林课程中的使用数值特征进行二元分类的精确分裂器。
机会均等
一种公平性指标,用于评估模型是否能针对敏感属性的所有值同样准确地预测出理想结果。换句话说,如果模型的理想结果是正类别,那么目标就是让所有组的真正例率保持一致。
机会平等与赔率均衡有关,后者要求所有群组的真正例率和假正例率都相同。
假设 Glubbdubdrib 大学允许小人国人和巨人国人参加严格的数学课程。Lilliputians 的中学提供完善的数学课程,绝大多数学生都符合大学课程的入学条件。Brobdingnagians 的中学根本不提供数学课程,因此,他们的学生中只有极少数人符合条件。如果合格学生被录取的机会均等,无论他们是小人国人还是巨人国人,那么对于“已录取”这一首选标签,就满足了在国籍(小人国或巨人国)方面的机会均等。
例如,假设有 100 名小人国人和 100 名巨人国人申请了 Glubbdubdrib 大学,录取决定如下:
表 1. Lilliputian 申请者(90% 符合条件)
| 符合资格 | 不合格 | |
|---|---|---|
| 已录取 | 45 | 3 |
| 已拒绝 | 45 | 7 |
| 总计 | 90 | 10 |
|
被录取的合格学生所占百分比:45/90 = 50% 被拒的不合格学生所占百分比:7/10 = 70% 被录取的小人国学生所占总百分比:(45+3)/100 = 48% |
||
表 2. Brobdingnagian 申请者(10% 符合条件):
| 符合资格 | 不合格 | |
|---|---|---|
| 已录取 | 5 | 9 |
| 已拒绝 | 5 | 81 |
| 总计 | 10 | 90 |
|
符合条件的学生录取百分比:5/10 = 50% 不符合条件的学生拒绝百分比:81/90 = 90% Brobdingnagian 学生总录取百分比:(5+9)/100 = 14% |
||
上述示例满足了合格学生在入学方面的机会平等,因为合格的利立浦特人和布罗卜丁奈格人都只有 50% 的入学机会。
虽然满足了机会均等,但未满足以下两个公平性指标:
- 人口统计均等:小人国人和巨人国人被大学录取的比例不同;48% 的小人国学生被录取,但只有 14% 的巨人国学生被录取。
- 机会均等:虽然符合条件的小人国学生和巨人国学生被录取的几率相同,但不符合条件的小人国学生和巨人国学生被拒的几率相同这一额外限制条件并未得到满足。不合格的 Lilliputian 的拒绝率为 70%,而不合格的 Brobdingnagian 的拒绝率为 90%。
如需了解详情,请参阅机器学习速成课程中的公平性:机会平等。
均衡赔率
一种公平性指标,用于评估模型是否能针对敏感属性的所有值,同样准确地预测正类别和负类别的结果,而不仅仅是其中一个类别。换句话说,所有组的真正例率和假负例率都应相同。
均衡赔率与机会均等相关,后者仅关注单个类别(正类别或负类别)的错误率。
例如,假设 Glubbdubdrib 大学允许小人国人和巨人国人同时参加一项严格的数学课程。Lilliputians 的中学提供完善的数学课程,绝大多数学生都符合大学课程的入学条件。Brobdingnagians 的中学根本不提供数学课程,因此,他们的学生中只有极少数人符合条件。只要满足以下条件,即可实现均衡赔率:无论申请者是小人国人还是巨人国人,如果他们符合条件,被该计划录取的可能性都相同;如果他们不符合条件,被拒绝的可能性也相同。
假设有 100 名小人国人和 100 名巨人国人申请了 Glubbdubdrib 大学,并且录取决定如下:
表 3. Lilliputian 申请者(90% 符合条件)
| 符合资格 | 不合格 | |
|---|---|---|
| 已录取 | 45 | 2 |
| 已拒绝 | 45 | 8 |
| 总计 | 90 | 10 |
|
被录取的合格学生所占百分比:45/90 = 50% 被拒绝的不合格学生所占百分比:8/10 = 80% 被录取的 Lilliputian 学生总数所占百分比:(45+2)/100 = 47% |
||
表 4. Brobdingnagian 申请者(10% 符合条件):
| 符合资格 | 不合格 | |
|---|---|---|
| 已录取 | 5 | 18 |
| 已拒绝 | 5 | 72 |
| 总计 | 10 | 90 |
|
符合条件的学生被录取百分比:5/10 = 50% 不符合条件的学生被拒绝百分比:72/90 = 80% Brobdingnagian 学生被录取总百分比:(5+18)/100 = 23% |
||
由于符合条件的小人国学生和巨人国学生被录取的概率均为 50%,而不符合条件的小人国学生和巨人国学生被拒绝的概率均为 80%,因此满足了赔率均等条件。
“监督学习中的机会平等”中对均衡赔率的正式定义如下:“如果预测变量 Ŷ 和受保护属性 A 在以结果 Y 为条件的情况下相互独立,则预测变量 Ŷ 满足关于受保护属性 A 和结果 Y 的均衡赔率。”
evals
主要用作 LLM 评估的缩写。 更广泛地说,evals 是任何形式的评估的缩写。
评估
衡量模型质量或比较不同模型的过程。
若要评估监督式机器学习模型,您通常需要根据验证集和测试集来判断模型的效果。评估 LLM 通常涉及更广泛的质量和安全性评估。
完全匹配
一种非此即彼的指标,即模型的输出要么与标准答案或参考文本完全一致,要么完全不一致。例如,如果标准答案是 orange,则只有模型输出 orange 满足完全匹配条件。
完全匹配还可以评估输出为序列(已排名商品列表)的模型。一般来说,完全匹配要求生成的排名列表与实际情况完全一致;也就是说,两个列表中的每个项目都必须按相同的顺序排列。不过,如果评估依据包含多个正确序列,那么完全匹配仅要求模型的输出与一个正确序列匹配。
极简摘要 (xsum)
用于评估 LLM 总结单个文档的能力的数据集。数据集中的每个条目都包含以下内容:
- 由英国广播公司 (BBC) 撰写的一份文档。
- 相应文档的单句摘要。
如需了解详情,请参阅不要给我详细信息,只要摘要!Topic-Aware Convolutional Neural Networks for Extreme Summarization。
F
F1
一种“汇总”二元分类指标,同时依赖于精确率和召回率。公式如下:
公平性指标
可衡量的“公平性”的数学定义。 一些常用的公平性指标包括:
许多公平性指标是互斥的;请参阅公平性指标互不相容。
假负例 (FN)
被模型错误地预测为负类别的样本。例如,模型预测某封电子邮件不是垃圾邮件(负类别),但该电子邮件实际上是垃圾邮件。
假负例率
模型错误地将实际正例预测为负例的比例。以下公式用于计算假负率:
如需了解详情,请参阅机器学习速成课程中的阈值和混淆矩阵。
假正例 (FP)
被模型错误地预测为正类别的样本。例如,模型预测某封电子邮件是垃圾邮件(正类别),但该电子邮件实际上不是垃圾邮件。
如需了解详情,请参阅机器学习速成课程中的阈值和混淆矩阵。
假正例率 (FPR)
模型错误地将实际负例预测为正例的比例。以下公式用于计算假正例率:
假正例率是 ROC 曲线的 x 轴。
如需了解详情,请参阅机器学习速成课程中的分类:ROC 和 AUC。
特征重要性
与变量重要性的含义相同。
基础模型
一种非常大的预训练模型,使用庞大而多样的训练集进行训练。基础模型可以执行以下两项操作:
换句话说,基础模型在一般意义上已经非常强大,但可以进一步自定义,以便在特定任务中发挥更大的作用。
成功次数所占的比例
用于评估机器学习模型生成的文本的指标。 成功率是指“成功”生成的文本输出数量除以生成的文本输出总数量。例如,如果某个大型语言模型生成了 10 个代码块,其中 5 个成功生成,那么成功率就是 50%。
虽然成功率在整个统计学中都非常有用,但在机器学习中,此指标主要用于衡量可验证的任务,例如代码生成或数学问题。
G
Gini 不纯度
与 entropy 类似的指标。拆分器使用从 Gini 不纯度或熵派生的值来为分类决策树组成条件。 信息增益源自熵。没有普遍接受的源自 Gini 不纯度的指标等效术语;不过,此未命名的指标与信息增益同样重要。
Gini 不纯度也称为 Gini 指数,或简称为 Gini。
H
合页损失函数
一类用于分类的损失函数,旨在找到尽可能远离每个训练示例的决策边界,从而使示例和边界之间的边距最大化。核支持向量机使用合页损失函数(或相关函数,例如平方合页损失函数)。对于二元分类,铰链损失函数的定义如下:
其中,y 是真实标签(-1 或 +1),y' 是分类模型的原始输出:
因此,铰链损失与 (y * y') 的对比图如下所示:

I
公平性指标互不相容
某些公平性概念互不相容,无法同时满足。因此,没有一种通用的指标可用于量化公平性,并适用于所有机器学习问题。
虽然这可能令人沮丧,但公平性指标互不相容并不意味着公平性方面的努力是徒劳的。相反,它表明必须根据特定机器学习问题的具体情况来定义公平性,目的是防止出现特定于其应用场景的危害。
如需更详细地了解公平性指标的不兼容性,请参阅“公平性的(不)可能性”。
个体公平性
一种公平性指标,用于检查相似的个体是否被归为相似的类别。例如,Brobdingnagian Academy 可能希望通过确保成绩和标准化考试分数完全相同的两名学生获得入学的可能性相同,来满足个人公平性。
请注意,个体公平性完全取决于您如何定义“相似性”(在本例中为成绩和考试分数),如果相似性指标遗漏了重要信息(例如学生课程的严格程度),您可能会引入新的公平性问题。
如需详细了解个体公平性,请参阅“通过感知实现公平”。
信息增益
在决策森林中,节点熵与其子节点熵的加权(按示例数量)和之间的差。节点的熵是指该节点中示例的熵。
例如,请考虑以下熵值:
- 父节点的熵 = 0.6
- 一个子节点的熵(包含 16 个相关示例)= 0.2
- 另一个子节点的熵(有 24 个相关示例)= 0.1
因此,40% 的示例位于一个子节点中,而 60% 的示例位于另一个子节点中。因此:
- 子节点的加权熵之和 = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
因此,信息增益为:
- 信息增益 = 父节点的熵 - 子节点的加权熵之和
- 信息增益 = 0.6 - 0.14 = 0.46
评分者间一致性信度
衡量人工标注者在执行任务时达成一致的频率。 如果评分者意见不一致,可能需要改进任务说明。 有时也称为注释者间一致性信度或评分者间可靠性信度。另请参阅 Cohen's kappa(最热门的评分者间一致性信度衡量指标之一)。
如需了解详情,请参阅机器学习速成课程中的类别数据:常见问题。
L
L1 损失
一种损失函数,用于计算实际标签值与模型预测的值之间的差的绝对值。例如,以下是针对包含 5 个示例的批次计算 L1 损失的示例:
| 示例的实际值 | 模型的预测值 | 增量的绝对值 |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1 损失 | ||
平均绝对误差是每个样本的平均 L1 损失。
如需了解详情,请参阅机器学习速成课程中的线性回归:损失。
L2 损失
一种损失函数,用于计算实际标签值与模型预测的值之间的平方差。例如,以下是针对包含 5 个示例的批次计算 L2 损失的示例:
| 示例的实际值 | 模型的预测值 | 增量的平方 |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 损失 | ||
由于取平方值,因此 L2 损失会放大离群值的影响。也就是说,与 L1 损失相比,L2 损失对不良预测的反应更强烈。例如,前一个批次的 L1 损失将为 8 而不是 16。请注意,一个离群值就占了 16 个中的 9 个。
回归模型通常使用 L2 损失作为损失函数。
均方误差是指每个样本的平均 L2 损失。 平方损失是 L2 损失的另一种叫法。
如需了解详情,请参阅机器学习速成课程中的逻辑回归:损失和正规化。
大语言模型评估
用于评估大型语言模型 (LLM) 性能的一组指标和基准。概括来讲,大语言模型评估:
- 帮助研究人员确定 LLM 需要改进的方面。
- 有助于比较不同的 LLM,并确定最适合特定任务的 LLM。
- 帮助确保 LLM 的使用安全且合乎道德。
如需了解详情,请参阅机器学习速成课程中的大型语言模型 (LLM)。
损失
在监督式模型的训练期间,用于衡量模型的预测与标签之间的差距。
损失函数用于计算损失。
如需了解详情,请参阅机器学习速成课程中的线性回归:损失。
损失函数
在训练或测试期间,用于计算一批示例的损失的数学函数。对于做出良好预测的模型,损失函数会返回较低的损失;对于做出不良预测的模型,损失函数会返回较高的损失。
训练的目标通常是尽量减少损失函数返回的损失。
损失函数有很多不同的种类。根据您要构建的模型类型选择合适的损失函数。例如:
M
矩阵分解
在数学中,矩阵分解是一种寻找其点积近似目标矩阵的矩阵的机制。
在推荐系统中,目标矩阵通常包含用户对商品的评分。例如,电影推荐系统的目标矩阵可能如下所示,其中正整数表示用户评分,0 表示用户未对该电影进行评分:
| 卡萨布兰卡 | 《费城故事》 | Black Panther | 神奇女侠 | 《低俗小说》 | |
|---|---|---|---|---|---|
| 用户 1 | 5.0 | 3.0 | 0.0 | 2.0 | 0.0 |
| 用户 2 | 4.0 | 0.0 | 0.0 | 1.0 | 5.0 |
| 用户 3 | 3.0 | 1.0 | 4.0 | 5.0 | 0.0 |
电影推荐系统旨在预测无评分电影的用户评分。例如,用户 1 会喜欢《黑豹》吗?
推荐系统采用的一种方法是,使用矩阵分解生成以下两个矩阵:
例如,对我们的三名用户和五个推荐项进行矩阵分解,会得到以下用户矩阵和项矩阵:
User Matrix Item Matrix 1.1 2.3 0.9 0.2 1.4 2.0 1.2 0.6 2.0 1.7 1.2 1.2 -0.1 2.1 2.5 0.5
用户矩阵和项矩阵的点积会得到一个推荐矩阵,其中不仅包含原始用户评分,还包含对每位用户未观看影片的预测。 例如,假设用户 1 对《卡萨布兰卡》的评分为 5.0。对应于推荐矩阵中该单元格的点积应该在 5.0 左右,计算方式如下:
(1.1 * 0.9) + (2.3 * 1.7) = 4.9更重要的是,用户 1 会喜欢《黑豹》吗?计算第一行和第三列所对应的点积,得到的预测评分为 4.3:
(1.1 * 1.4) + (2.3 * 1.2) = 4.3矩阵分解通常会生成用户矩阵和项矩阵,这两个矩阵合在一起明显比目标矩阵更为紧凑。
MBPP
Mostly Basic Python Problems 的缩写。
平均绝对误差 (MAE)
使用 L1 损失时,每个样本的平均损失。按如下方式计算平均绝对误差:
- 计算批次的 L1 损失。
- 将 L1 损失除以批次中的样本数。
例如,假设有以下一批包含 5 个示例的数据,请考虑计算 L1 损失:
| 示例的实际值 | 模型的预测值 | 损失(实际值与预测值之间的差值) |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1 损失 | ||
因此,L1 损失为 8,示例数量为 5。因此,平均绝对误差为:
Mean Absolute Error = L1 loss / Number of Examples Mean Absolute Error = 8/5 = 1.6
前 k 名的平均精确率均值 (mAP@k)
验证数据集中所有 k 处的平均精确率得分的统计平均值。平均精确率(取前 k 个结果)的一个用途是判断推荐系统生成的推荐的质量。
虽然“平均平均值”一词听起来有些冗余,但该指标的名称是合适的。毕竟,此指标会计算多个 k 值处的平均精确率的平均值。
均方误差 (MSE)
使用 L2 损失时,每个样本的平均损失。按如下方式计算均方误差:
- 计算批次的 L2 损失。
- 将 L2 损失除以批次中的样本数。
例如,假设以下一批包含 5 个示例,损失如下:
| 实际值 | 模型预测 | 损失 | 平方损失 |
|---|---|---|---|
| 7 | 6 | 1 | 1 |
| 5 | 4 | 1 | 1 |
| 8 | 11 | 3 | 9 |
| 4 | 6 | 2 | 4 |
| 9 | 8 | 1 | 1 |
| 16 = L2 损失 | |||
因此,均方误差为:
Mean Squared Error = L2 loss / Number of Examples Mean Squared Error = 16/5 = 3.2
TensorFlow Playground 使用均方差来计算损失值。
指标
您关心的一项统计数据。
目标是机器学习系统尝试优化的指标。
Metrics API (tf.metrics)
用于评估模型的 TensorFlow API。例如,tf.metrics.accuracy 用于确定模型的预测与标签的匹配频率。
minimax 损失
一种基于生成数据与真实数据分布之间的交叉熵的生成对抗网络的损失函数。
第一篇论文中使用了 minimax 损失来描述生成对抗网络。
如需了解详情,请参阅生成对抗网络课程中的损失函数。
模型容量
模型可以学习的问题的复杂性。模型可以学习的问题越复杂,模型的能力就越高。模型能力通常会随着模型参数数量的增加而增强。如需了解分类模型容量的正式定义,请参阅 VC 维度。
造势
一种复杂的梯度下降算法,其中学习步长不仅取决于当前步长的导数,还取决于紧邻的前一步长(或多个步长)的导数。动量涉及计算梯度随时间的指数加权移动平均值,类似于物理学中的动量。动量有时可以防止学习陷入局部最小值。
Mostly Basic Python Problems (MBPP)
一个用于评估 LLM 在生成 Python 代码方面的熟练程度的数据集。 Mostly Basic Python Problems 提供了大约 1,000 个众包编程问题。 数据集中的每个问题都包含:
- 任务说明
- 解决方案代码
- 三个自动化测试用例
否
负类别
在二元分类中,一种类别称为正类别,另一种类别称为负类别。正类别是模型正在测试的事物或事件,负类别则是另一种可能性。例如:
- 在医学检查中,负类别可以是“非肿瘤”。
- 在电子邮件分类模型中,负类别可以是“非垃圾邮件”。
与正类别相对。
O
目标
算法尝试优化的指标。
目标函数
模型旨在优化的数学公式或指标。 例如,线性回归的目标函数通常是均方损失。因此,在训练线性回归模型时,训练旨在尽量减少均方损失。
在某些情况下,目标是最大化目标函数。 例如,如果目标函数是准确率,则目标是最大限度地提高准确率。
另请参阅损失。
P
前 k 名中的通过率 (pass@k)
一种用于确定大语言模型生成的代码(例如 Python)质量的指标。 更具体地说,pass@k 表示在生成的 k 个代码块中,至少有一个代码块通过所有单元测试的可能性。
大语言模型通常难以针对复杂的编程问题生成优质代码。软件工程师通过提示大语言模型为同一问题生成多个 (k) 解决方案来应对这一问题。然后,软件工程师会针对单元测试对每个解决方案进行测试。通过率(在 k 处)的计算取决于单元测试的结果:
- 如果这些解决方案中的一个或多个通过了单元测试,则 LLM 通过了该代码生成挑战。
- 如果没有任何解决方案通过单元测试,则 LLM 未能通过该代码生成挑战。
通过率(在 k 处)的公式如下:
\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]
一般来说,k 值越高,pass@k 得分就越高;不过,k 值越高,所需的大型语言模型和单元测试资源就越多。
性能
一个多含义术语,具有以下含义:
- 在软件工程中的标准含义。即:软件的运行速度有多快(或有多高效)?
- 在机器学习中的含义。在机器学习领域,性能旨在回答以下问题:模型的准确度有多高?即模型在预测方面的表现有多好?
排列变量重要性
一种变量重要性,用于评估在对特征值进行置换后模型预测误差的增加情况。排列变量重要性是一种与模型无关的指标。
困惑度
一种衡量指标,用于衡量模型能够多好地完成任务。 例如,假设您的任务是读取用户在手机键盘上输入的前几个字母,并提供可能的补全字词列表。此任务的困惑度 P 大致是指您需要提供多少个猜测,才能使您的列表包含用户尝试输入的实际字词。
困惑度与交叉熵的关系如下:
正类别
您要测试的类。
例如,在癌症模型中,正类别可以是“肿瘤”。 在电子邮件分类模型中,正类别可以是“垃圾邮件”。
与负类别相对。
PR AUC(PR 曲线下的面积)
通过绘制不同分类阈值的(召回率、精确率)点而获得的插值精确率-召回率曲线下的面积。
精确度
一种分类模型指标,可为您提供以下信息:
当模型预测为正类别时,预测正确的百分比是多少?
公式如下:
其中:
- 真正例是指模型正确预测了正类别。
- 假正例是指模型错误地预测了正类别。
例如,假设某个模型做出了 200 次正预测。在这 200 个正例预测中:
- 其中 150 个是真正例。
- 其中 50 个是假正例。
在此示例中:
如需了解详情,请参阅机器学习速成课程中的分类:准确率、召回率、精确率和相关指标。
前 k 名的精确率(precision@k)
用于评估排名(有序)商品列表的指标。 前 k 项的精确率是指该列表中的前 k 项中“相关”项所占的比例。具体来说:
\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]
k 的值必须小于或等于返回列表的长度。 请注意,返回列表的长度不属于计算的一部分。
相关性通常是主观的;即使是专业的人工评估员也经常在哪些内容相关的问题上意见不一。
比较对象:
精确率与召回率曲线
预测偏差
预测性平价
一种公平性指标,用于检查对于给定的分类模型,所考虑的子群组的精确率是否相等。
例如,如果一个预测大学录取情况的模型对小人国人和巨人国人的精确率相同,那么该模型就满足了民族预测均等性。
预测性均等有时也称为预测率均等。
如需更详细地了解预测对等性,请参阅“公平性定义说明”(第 3.2.1 部分)。
预测性价格一致性
预测奇偶性的另一个名称。
概率密度函数
一种用于确定具有确切特定值的数据样本的频次的函数。如果数据集的值是连续的浮点数,则很少会出现完全匹配的情况。不过,对概率密度函数从值 x 到值 y 进行积分,可得出介于 x 和 y 之间的数据样本的预期频次。
例如,假设有一个平均值为 200、标准差为 30 的正态分布。若要确定落在 211.4 到 218.7 范围内的数据样本的预期频次,您可以对正态分布的概率密度函数从 211.4 到 218.7 进行积分。
R
ReCoRD 数据集上的阅读理解与常识推理
一个用于评估 LLM 常识推理能力的数据集。数据集中的每个示例都包含三个组成部分:
- 新闻报道中的一两个段落
- 一种查询,其中段落中明确或隐式标识的某个实体被遮盖。
- 答案(属于掩码的实体的名称)
如需查看大量示例,请参阅 ReCoRD。
ReCoRD 是 SuperGLUE 集成模型的一个组成部分。
RealToxicityPrompts
包含一组可能包含有害内容的句子开头的数据集。使用此数据集评估 LLM 生成无毒文本以完成句子的能力。通常,您可以使用 Perspective API 来确定 LLM 在此任务中的表现。
如需了解详情,请参阅RealToxicityPrompts:评估语言模型中的神经毒性退化。
召回
一种分类模型指标,可为您提供以下信息:
公式如下:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
其中:
- 真正例是指模型正确预测了正类别。
- 假负例是指模型错误地预测了负类别。
例如,假设您的模型对评估依据为正类别的样本进行了 200 次预测。在这 200 个预测中:
- 其中 180 个是真正例。
- 20 个为假负例。
在此示例中:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
如需了解详情,请参阅分类:准确率、召回率、精确率和相关指标。
前 k 名召回率 (recall@k)
一种用于评估输出排名(有序)商品列表的系统的指标。 “前 k 项的召回率”是指在返回的相关项总数中,相应列表的前 k 项中相关项所占的比例。
\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]
与 k 处的精确率相对。
识别文本蕴涵关系 (RTE)
一个用于评估 LLM 是否能够确定假设是否可以从文本段落中得出(逻辑上)的数据集。RTE 评估中的每个示例都包含三个部分:
- 一段文字,通常来自新闻或维基百科文章
- 假设
- 正确答案(以下任一选项):
- True,表示假设可以从段落中得出
- False,表示假设无法从段落中得出
例如:
- 原文:欧元是欧盟的货币。
- 假设:法国使用欧元作为货币。
- 蕴涵:为 True,因为法国是欧盟的一部分。
RTE 是 SuperGLUE 集成模型的一个组成部分。
ReCoRD
Reading Comprehension with Commonsense Reasoning Dataset 的缩写。
ROC(接收者操作特征)曲线
在二元分类中,针对不同的分类阈值,绘制真正例率与假正例率的对比图。
ROC 曲线的形状表明了二元分类模型区分正类别和负类别的能力。例如,假设某个二元分类模型能够完美区分所有负类别和所有正类别:
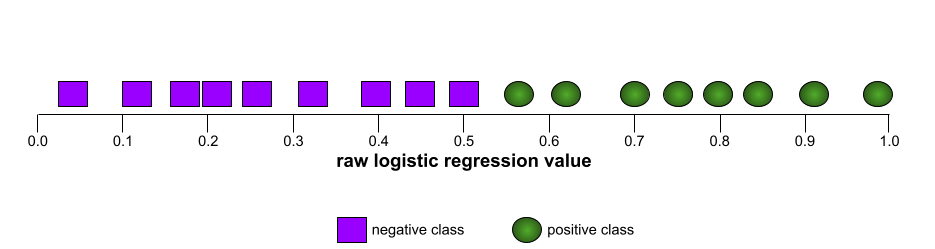
上述模型的 ROC 曲线如下所示:
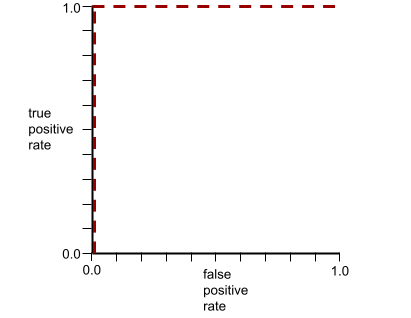
相比之下,下图绘制了一个糟糕模型的原始逻辑回归值,该模型根本无法区分负类和正类:
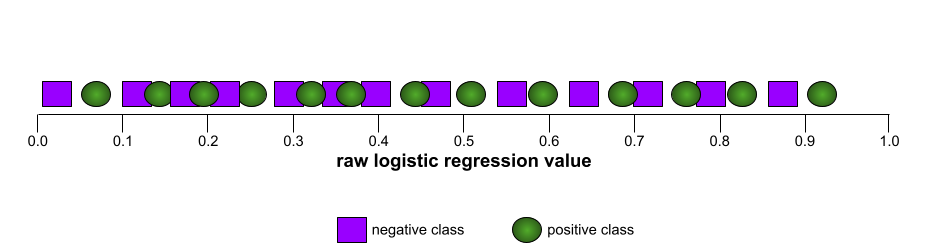
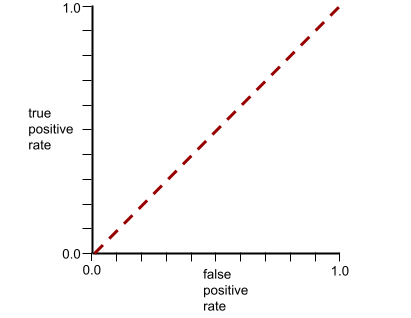
相应模型的 ROC 曲线如下所示:
与此同时,在现实世界中,大多数二元分类模型都会在一定程度上区分正类别和负类别,但通常不会完全区分。因此,典型的 ROC 曲线介于这两个极端之间:
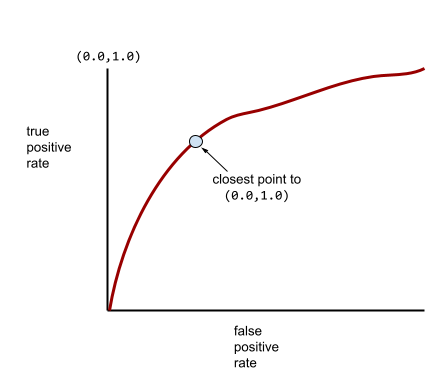
从理论上讲,ROC 曲线上最接近 (0.0,1.0) 的点可确定理想的分类阈值。不过,还有一些现实世界中的问题会影响理想分类阈值的选择。例如,假负例造成的损失可能远高于假正例。
一种名为 AUC 的数值指标可将 ROC 曲线汇总为单个浮点值。
均方根误差 (RMSE)
均方误差的平方根。
ROUGE(以召回率为导向的摘要评估研究)
用于评估自动摘要和机器翻译模型的一系列指标。 ROUGE 指标用于确定参考文本与机器学习模型生成的文本之间的重叠程度。ROUGE 系列中的每个成员都以不同的方式衡量重叠程度。ROUGE 得分越高,表示参考文本与生成的文本之间的相似度越高;ROUGE 得分越低,表示参考文本与生成的文本之间的相似度越低。
每个 ROUGE 系列成员通常会生成以下指标:
- 精确率
- 召回率
- F1
如需了解详情和示例,请参阅:
ROUGE-L
ROUGE 系列的成员,侧重于参考文本和生成文本中最长公共子序列的长度。以下公式用于计算 ROUGE-L 的召回率和精确率:
然后,您可以使用 F1 将 ROUGE-L 召回率和 ROUGE-L 精确率汇总为一个指标:
ROUGE-L 会忽略参考文本和生成的文本中的所有换行符,因此最长公共子序列可能会跨越多个句子。如果参考文本和生成的文本包含多个句子,那么通常最好使用 ROUGE-L 的一种变体,即 ROUGE-Lsum。ROUGE-Lsum 会确定段落中每个句子的最长公共子序列,然后计算这些最长公共子序列的平均值。
ROUGE-N
ROUGE 系列中的一组指标,用于比较参考文本和生成文本中特定大小的共享 N-gram。例如:
- ROUGE-1 用于衡量参考文本和生成文本中共享的 token 数量。
- ROUGE-2 用于衡量参考文本和生成的文本中共享的二元语法(2-gram)数量。
- ROUGE-3 用于衡量参考文本和生成的文本中共享的三元语法(3-gram)数量。
您可以使用以下公式计算任何 ROUGE-N 成员的 ROUGE-N 召回率和 ROUGE-N 精确率:
然后,您可以使用 F1 将 ROUGE-N 召回率和 ROUGE-N 精确率汇总为一个指标:
ROUGE-S
一种宽松形式的 ROUGE-N,可实现 skip-gram 匹配。也就是说,ROUGE-N 只会统计完全匹配的 N 元语法,而 ROUGE-S 还会统计被一个或多个字词分隔的 N 元语法。例如,应该考虑以下事项:
计算 ROUGE-N 时,二元语法“白云”与“白色滚滚的云”不匹配。不过,在计算 ROUGE-S 时,白云与白色的滚滚云海相匹配。
R 平方
一种回归指标,用于指示标签的变异中有多少是由单个特征或一组特征造成的。R 平方是介于 0 和 1 之间的值,您可以按如下方式解读:
- R 平方值为 0 表示标签的任何变异都不是由特征集造成的。
- R 平方值为 1 表示标签的所有变异都归因于特征集。
- 介于 0 和 1 之间的 R 平方值表示标签的变异在多大程度上可以通过特定特征或特征集来预测。例如,R 平方值为 0.10 表示标签中 10% 的方差是由特征集造成的;R 平方值为 0.20 表示 20% 的方差是由特征集造成的,依此类推。
RTE
识别文本蕴涵的缩写。
S
评分
推荐系统的一部分,用于为候选生成阶段生成的每个商品提供价值或排名。
相似度度量
在聚类算法中,用于确定任何两种样本相似程度的指标。
稀疏性
向量或矩阵中设置为零(或 null)的元素数量除以该向量或矩阵中的条目总数。例如,假设有一个包含 100 个元素的矩阵,其中 98 个单元格包含零。稀疏度的计算方式如下:
特征稀疏度是指特征向量的稀疏度;模型稀疏度是指模型权重的稀疏度。
SQuAD
斯坦福问答数据集的英文缩写,该数据集在论文《SQuAD:用于机器理解文本的 10 万多个问题》中首次提出。此数据集中的问题来自针对维基百科文章提出问题的用户。SQuAD 中的某些问题有答案,但其他问题故意没有答案。因此,您可以使用 SQuAD 来评估 LLM 在以下两方面的能力:
- 回答可以回答的问题。
- 确定无法回答的问题。
完全匹配与 F1 相结合,是根据 SQuAD 评估 LLM 的最常用指标。
平方合页损失函数
合页损失函数的平方。与常规合页损失相比,平方合页损失对离群值的惩罚更严厉。
平方损失函数
与 L2 损失的含义相同。
SuperGLUE
用于评估 LLM 理解和生成文本的整体能力的数据集集成。集成包含以下数据集:
- 布尔值问题 (BoolQ)
- CommitmentBank (CB)
- 合理替代方案选择 (COPA)
- 多句子阅读理解 (MultiRC)
- ReCoRD:基于常识推理的阅读理解数据集
- 识别文本蕴涵关系 (RTE)
- 上下文中的字词 (WiC)
- Winograd Schema Challenge (WSC)
如需了解详情,请参阅SuperGLUE:通用语言理解系统更具粘性的基准。
T
测试损失
一种表示模型针对测试集的损失的指标。在构建模型时,您通常会尝试最大限度地减少测试损失。这是因为,与较低的训练损失或较低的验证损失相比,较低的测试损失是更强的质量信号。
测试损失与训练损失或验证损失之间的差距过大有时表明您需要提高正则化率。
前 k 名准确率
“目标标签”在生成的列表的前 k 个位置中出现的次数所占的百分比。这些列表可以是个性化推荐,也可以是按 softmax 排序的商品列表。
前 k 名准确率也称为前 k 名准确率。
恶意
内容具有侮辱性、威胁性或冒犯性的程度。许多机器学习模型都可以识别、衡量和分类有害内容。这些模型大多会根据多个参数(例如滥用性语言的程度和威胁性语言的程度)来识别有害内容。
训练损失
一种指标,表示模型在特定训练迭代期间的损失。例如,假设损失函数为均方误差。例如,第 10 次迭代的训练损失(均方误差)为 2.2,第 100 次迭代的训练损失为 1.9。
损失曲线绘制的是训练损失与迭代次数的关系图。损失曲线可提供以下有关训练的提示:
- 下降斜率表示模型正在改进。
- 向上倾斜表示模型效果越来越差。
- 平坦的斜率表示模型已达到收敛。
例如,以下有些理想化的损失曲线显示:
- 初始迭代期间的陡峭下降斜率,表示模型改进速度很快。
- 斜率逐渐变平(但仍向下),直到接近训练结束时,这表示模型仍在不断改进,但速度比初始迭代期间略慢。
- 训练结束时斜率趋于平缓,表明模型已收敛。
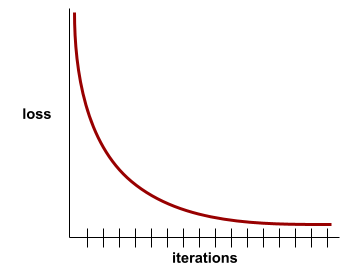
虽然训练损失很重要,但另请参阅泛化。
冷知识问答
用于评估 LLM 回答冷知识问题的能力的数据集。 每个数据集都包含由知识问答爱好者创作的问答对。不同的数据集基于不同的来源,包括:
- 网页搜索 (TriviaQA)
- 维基百科 (TriviaQA_wiki)
如需了解详情,请参阅 TriviaQA:一个大规模的远程监督型阅读理解挑战数据集。
真负例 (TN)
模型正确预测负类别的示例。例如,模型推断出某封电子邮件不是垃圾邮件,而该电子邮件确实不是垃圾邮件。
真正例 (TP)
模型正确预测正类别的示例。例如,模型推断出某封电子邮件是垃圾邮件,而该电子邮件确实是垃圾邮件。
真正例率 (TPR)
与召回率的含义相同。具体来说:
真正例率是 ROC 曲线的 y 轴。
Typologically Diverse Question Answering (TyDi QA)
一个大型数据集,用于评估 LLM 在回答问题方面的熟练程度。 该数据集包含多种语言的问题和答案对。
如需了解详情,请参阅 TyDi QA:一个用于在类型多样的语言中进行信息搜索问答的基准。
V
验证损失
另请参阅泛化曲线。
变量重要性
一组分数,用于指示每个特征对模型的相对重要性。
例如,假设有一个用于估算房价的决策树。假设此决策树使用三个特征:尺寸、年龄和款式。如果计算出的三个特征的一组变量重要性为 {size=5.8, age=2.5, style=4.7},则对于决策树而言,size 比 age 或 style 更重要。
存在不同的变量重要性指标,可让机器学习专家了解模型的不同方面。
W
Wasserstein 损失
一种常用于生成对抗网络的损失函数,基于生成数据分布与真实数据分布之间的推土机距离。
WiC
上下文中的字词的缩写。
WikiLingua (wiki_lingua)
一个用于评估 LLM 总结短篇文章能力的数据集。 WikiHow 是一个包含各种任务操作指南的文章百科全书,是文章和摘要的人工撰写来源。数据集中的每个条目都包含以下内容:
- 通过附加编号列表的散文(段落)版本中的每个步骤(不包括每个步骤的开头句子)来创建文章。
- 该文章的摘要,由编号列表中的每个步骤的开头一句组成。
如需了解详情,请参阅 WikiLingua:一种用于跨语言摘要生成的新基准数据集。
Winograd Schema Challenge (WSC)
一种用于评估 LLM 确定代词所指名词短语的能力的格式(或符合该格式的数据集)。
Winograd 架构挑战中的每个条目都包含:
- 包含目标代词的简短段落
- 目标人称代词
- 候选名词短语,后跟正确答案(布尔值)。 如果目标代词指代的是此候选人,则答案为 True。 如果目标代词未指代此候选对象,则答案为 False。
例如:
- 段落:Mark 向 Pete 谎报了很多关于自己的事情,Pete 将这些谎报的内容写进了他的书中。他本应更诚实。
- 目标代词:他
- 候选名词短语:
- Mark: True,因为目标代词指的是 Mark
- Pete:错误,因为目标代词指的不是 Peter
Winograd Schema Challenge 是 SuperGLUE 集成的一部分。
Words in Context (WiC)
一个用于评估 LLM 在多义词理解方面对上下文的利用程度的数据集。数据集中的每个条目都包含:
- 两个句子,每个句子都包含目标字词
- 目标字词
- 正确答案(布尔值),其中:
- True 表示目标字词在两个句子中的含义相同
- False 表示目标字词在两个句子中的含义不同
例如:
- 两句话:
- 河床上有很多垃圾。
- 睡觉时,我会在床边放一杯水。
- 目标字词:床
- 正确答案:错误,因为目标字词在两个句子中的含义不同。
如需了解详情,请参阅 WiC:用于评估上下文相关语义表示的上下文词语数据集。
Words in Context 是 SuperGLUE 集成模型的一个组成部分。
WSC
Winograd 架构挑战赛的缩写。
X
XL-Sum (xlsum)
用于评估 LLM 总结文本的熟练程度的数据集。 XL-Sum 提供多种语言的条目。数据集中的每个条目都包含:
- 一篇文章,摘自英国广播公司 (BBC)。
- 文章作者撰写的文章摘要。请注意,该摘要可能包含文章中没有的字词或短语。
如需了解详情,请参阅XL-Sum:面向 44 种语言的大规模多语言抽取式摘要。