Bảng thuật ngữ về học máy: Chỉ số

Trang này chứa các thuật ngữ trong Bảng thuật ngữ về chỉ số. Để xem tất cả các thuật ngữ trong bảng chú giải, hãy nhấp vào đây.

A

độ chính xác

#fundamentals

#Chỉ số

Số lượng dự đoán phân loại chính xác chia cho tổng số dự đoán. Đó là:

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

Ví dụ: một mô hình đưa ra 40 dự đoán chính xác và 10 dự đoán không chính xác sẽ có độ chính xác là:

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

Phân loại nhị phân cung cấp tên cụ thể cho các danh mục khác nhau của dự đoán chính xác và dự đoán không chính xác. Vì vậy, công thức tính độ chính xác cho phân loại nhị phân như sau:

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

trong đó:

• TP là số lượng dương tính thật (dự đoán chính xác).
• TN là số lượng âm tính thật (dự đoán chính xác).
• FP là số lượng kết quả dương tính giả (dự đoán không chính xác).
• FN là số lượng âm tính giả (dự đoán không chính xác).

So sánh và đối chiếu độ chính xác với độ đo lường chính xác và khả năng thu hồi.

Nhấp vào biểu tượng để biết thông tin chi tiết về độ chính xác và tập dữ liệu không cân bằng theo lớp.

Mặc dù là một chỉ số có giá trị trong một số trường hợp, nhưng độ chính xác lại rất dễ gây hiểu lầm trong những trường hợp khác. Đáng chú ý là độ chính xác thường là một chỉ số kém để đánh giá các mô hình phân loại xử lý các tập dữ liệu mất cân bằng lớp.

Ví dụ: giả sử tuyết chỉ rơi 25 ngày mỗi thế kỷ ở một thành phố cận nhiệt đới nào đó. Vì số ngày không có tuyết (lớp âm) nhiều hơn hẳn số ngày có tuyết (lớp dương), nên tập dữ liệu về tuyết của thành phố này là tập dữ liệu bất cân đối về loại. Hãy tưởng tượng một mô hình phân loại nhị phân được cho là dự đoán có tuyết hay không có tuyết mỗi ngày nhưng chỉ dự đoán "không có tuyết" mỗi ngày. Mô hình này có độ chính xác cao nhưng không có khả năng dự đoán. Bảng sau đây tóm tắt kết quả của một thế kỷ dự đoán:

Danh mục	Số
TP	0
TN (Tunisia)	36499
FP	0
FN	25

Do đó, độ chính xác của mô hình này là:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

Mặc dù độ chính xác 99,93% có vẻ là một tỷ lệ rất ấn tượng, nhưng mô hình này thực sự không có khả năng dự đoán.

Độ chính xác và khả năng thu hồi thường là những chỉ số hữu ích hơn so với độ chính xác để đánh giá các mô hình được huấn luyện trên tập dữ liệu không cân bằng theo lớp.

---

Hãy xem phần Phân loại: Độ chính xác, khả năng thu hồi, độ đo và các chỉ số liên quan trong Khoá học cấp tốc về học máy để biết thêm thông tin.

diện tích dưới đường cong PR

#Chỉ số

Xem PR AUC (Diện tích dưới đường cong PR).

diện tích dưới đường cong ROC

#Chỉ số

Xem AUC (Diện tích dưới đường cong ROC).

AUC (Diện tích dưới đường cong ROC)

#fundamentals

#Chỉ số

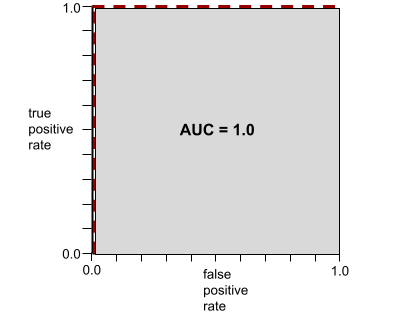
Một số từ 0,0 đến 1,0 biểu thị khả năng của mô hình phân loại nhị phân trong việc tách các lớp dương khỏi các lớp âm. AUC càng gần 1.0 thì khả năng tách các lớp của mô hình càng tốt.

Ví dụ: hình minh hoạ sau đây cho thấy một mô hình phân loại tách biệt hoàn toàn các lớp dương (hình bầu dục màu xanh lục) với các lớp âm (hình chữ nhật màu tím). Mô hình hoàn hảo một cách phi thực tế này có AUC là 1.0:

Ngược lại, hình minh hoạ sau đây cho thấy kết quả của một mô hình phân loại đã tạo ra kết quả ngẫu nhiên. Mô hình này có AUC là 0,5:

Có, mô hình trước đó có AUC là 0, 5 chứ không phải 0.

Hầu hết các mô hình đều nằm ở khoảng giữa hai thái cực này. Ví dụ: mô hình sau đây tách biệt phần nào các giá trị dương với giá trị âm, do đó có AUC nằm trong khoảng từ 0, 5 đến 1.0:

AUC bỏ qua mọi giá trị mà bạn đặt cho ngưỡng phân loại. Thay vào đó, AUC sẽ xem xét tất cả các ngưỡng phân loại có thể có.

Nhấp vào biểu tượng này để tìm hiểu về mối quan hệ giữa đường cong AUC và ROC.

AUC biểu thị diện tích dưới đường cong ROC. Ví dụ: đường cong ROC cho một mô hình phân tách hoàn hảo các giá trị dương với các giá trị âm sẽ có dạng như sau:

AUC là diện tích của vùng màu xám trong hình minh hoạ trước đó. Trong trường hợp bất thường này, diện tích chỉ đơn giản là chiều dài của vùng màu xám (1.0) nhân với chiều rộng của vùng màu xám (1.0). Vì vậy, tích của 1.0 và 1.0 sẽ cho ra AUC chính xác là 1.0, đây là điểm AUC cao nhất có thể.

Ngược lại, đường cong ROC cho một mô hình phân loại hoàn toàn không thể tách các lớp như sau. Diện tích của vùng màu xám này là 0,5.

Đường cong ROC điển hình hơn sẽ có dạng gần như sau:

Việc tính toán diện tích dưới đường cong này theo cách thủ công sẽ rất khó khăn. Đó là lý do tại sao một chương trình thường tính toán hầu hết các giá trị AUC.

---

Nhấp vào biểu tượng để xem định nghĩa chính thức hơn về AUC.

AUC là xác suất mà mô hình phân loại sẽ tin tưởng hơn rằng một ví dụ dương được chọn ngẫu nhiên thực sự là dương so với một ví dụ âm được chọn ngẫu nhiên là dương.

---

Hãy xem phần Phân loại: ROC và AUC trong Khoá học học máy ứng dụng để biết thêm thông tin.

độ chính xác trung bình tại k

#Chỉ số

Một chỉ số để tóm tắt hiệu suất của mô hình trên một câu lệnh duy nhất tạo ra kết quả được xếp hạng, chẳng hạn như danh sách đề xuất sách có đánh số. Độ chính xác trung bình tại k là giá trị trung bình của các giá trị độ chính xác tại k cho mỗi kết quả có liên quan. Do đó, công thức tính độ chính xác trung bình tại k là:

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

trong đó:

• \(n\) là số lượng mặt hàng có liên quan trong danh sách.

Tương phản với khả năng nhớ lại ở k.

Lưu ý: Độ chính xác trung bình tại k đánh giá đầu ra cho một câu lệnh duy nhất. Sử dụng độ chính xác trung bình tại k để đánh giá chất lượng đầu ra của một mô hình trên nhiều câu lệnh khác nhau.

Lưu ý: Một số người viết tắt độ chính xác trung bình tại k thành độ chính xác trung bình.

Nhấp vào biểu tượng để xem ví dụ

Giả sử một mô hình ngôn ngữ lớn được đưa ra truy vấn sau:

List the 6 funniest movies of all time in order.

Và mô hình ngôn ngữ lớn sẽ trả về danh sách sau:

1. The General
2. Mean Girls
3. Platoon
4. Phù dâu
5. Công dân Kane
6. This is Spinal Tap

Bốn trong số các bộ phim trong danh sách được trả về rất hài hước (tức là có liên quan) nhưng hai bộ phim là phim chính kịch (không liên quan). Bảng sau đây trình bày chi tiết kết quả:

Vị trí	Phim	Có liên quan không?	Độ chính xác tại k
1	The General	Có	1.0
2	Mean Girls	Có	1.0
3	Platoon	Không	không phù hợp
4	Phù dâu	Có	0,75
5	Công dân Kane	Không	không phù hợp
6	This is Spinal Tap	Có	0,67

Số lượng kết quả có liên quan là 4. Do đó, bạn có thể tính độ chính xác trung bình tại 6 như sau:

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

đường cơ sở

#Chỉ số

Một mô hình được dùng làm điểm tham chiếu để so sánh hiệu suất của một mô hình khác (thường là mô hình phức tạp hơn). Ví dụ: mô hình hồi quy logistic có thể đóng vai trò là một đường cơ sở tốt cho mô hình sâu.

Đối với một vấn đề cụ thể, đường cơ sở giúp các nhà phát triển mô hình định lượng hiệu suất tối thiểu dự kiến mà một mô hình mới phải đạt được để mô hình mới đó hữu ích.

C

chi phí

#Chỉ số

Từ đồng nghĩa với thua.

tính công bằng phản thực tế

#responsible

#Chỉ số

Chỉ số công bằng kiểm tra xem mô hình phân loại có tạo ra cùng một kết quả cho một cá nhân như kết quả của một cá nhân khác giống với cá nhân đầu tiên hay không, ngoại trừ một hoặc nhiều thuộc tính nhạy cảm. Đánh giá mô hình phân loại để đảm bảo tính công bằng phản thực tế là một phương pháp để xác định các nguồn thiên vị tiềm ẩn trong một mô hình.

Hãy xem một trong hai phần sau để biết thêm thông tin:

• Tính công bằng: Tính công bằng phản thực tế trong Khoá học học máy ứng dụng.
• Khi các thế giới xung đột: Tích hợp các giả định phản thực tế khác nhau về tính công bằng

cross-entropy

#Chỉ số

Một khái quát hoá của Log Loss thành các vấn đề phân loại đa mục tiêu. Entropy chéo định lượng sự khác biệt giữa hai hàm phân phối xác suất. Xem thêm độ phức tạp.

hàm phân phối tích luỹ (CDF)

#Chỉ số

Một hàm xác định tần suất của các mẫu nhỏ hơn hoặc bằng một giá trị mục tiêu. Ví dụ: hãy xem xét hàm phân phối chuẩn của các giá trị liên tục. CDF cho biết khoảng 50% mẫu phải nhỏ hơn hoặc bằng giá trị trung bình và khoảng 84% mẫu phải nhỏ hơn hoặc bằng một độ lệch chuẩn so với giá trị trung bình.

D

tương đương về nhân khẩu học

#responsible

#Chỉ số

Một chỉ số công bằng được đáp ứng nếu kết quả phân loại của một mô hình không phụ thuộc vào một thuộc tính nhạy cảm nhất định.

Ví dụ: nếu cả người Lilliput và người Brobdingnag đều đăng ký vào Đại học Glubbdubdrib, thì sự bình đẳng về nhân khẩu học sẽ đạt được nếu tỷ lệ phần trăm người Lilliput được nhận vào học bằng với tỷ lệ phần trăm người Brobdingnag được nhận vào học, bất kể một nhóm có trình độ chuyên môn cao hơn nhóm còn lại hay không.

Tương phản với xác suất cân bằng và cơ hội bình đẳng, cho phép kết quả phân loại tổng hợp phụ thuộc vào các thuộc tính nhạy cảm, nhưng không cho phép kết quả phân loại cho một số nhãn dữ liệu thực tế được chỉ định phụ thuộc vào các thuộc tính nhạy cảm. Xem bài viết "Chống phân biệt đối xử bằng công nghệ học máy thông minh hơn" để xem hình ảnh minh hoạ khám phá các điểm đánh đổi khi tối ưu hoá để đạt được sự bình đẳng về nhân khẩu học.

Hãy xem phần Tính công bằng: sự bình đẳng về nhân khẩu học trong Khoá học học máy ứng dụng để biết thêm thông tin.

E

khoảng cách di chuyển của đất (EMD)

#Chỉ số

Thước đo mức độ tương đồng tương đối của hai phân phối. Khoảng cách di chuyển của máy xúc càng thấp thì các bản phân phối càng giống nhau.

khoảng cách chỉnh sửa

#Chỉ số

Một chỉ số đo lường mức độ tương đồng giữa hai chuỗi văn bản. Trong học máy, khoảng cách chỉnh sửa rất hữu ích vì những lý do sau:

• Khoảng cách chỉnh sửa rất dễ tính toán.
• Khoảng cách chỉnh sửa có thể so sánh hai chuỗi được biết là tương tự nhau.
• Khoảng cách chỉnh sửa có thể xác định mức độ tương tự của các chuỗi khác nhau với một chuỗi nhất định.

Có một số định nghĩa về khoảng cách chỉnh sửa, mỗi định nghĩa sử dụng các thao tác khác nhau trên chuỗi. Hãy xem Khoảng cách Levenshtein để biết ví dụ.

hàm phân phối tích luỹ thực nghiệm (eCDF hoặc EDF)

#Chỉ số

Một hàm phân phối tích luỹ dựa trên các phép đo thực nghiệm từ một tập dữ liệu thực. Giá trị của hàm tại bất kỳ điểm nào dọc theo trục x là phần nhỏ của các quan sát trong tập dữ liệu nhỏ hơn hoặc bằng giá trị đã chỉ định.

entropy

#df

#Chỉ số

Trong lý thuyết thông tin, nội dung mô tả mức độ khó dự đoán của một phân phối xác suất. Ngoài ra, entropy cũng được xác định là lượng thông tin mà mỗi ví dụ chứa. Phân phối có entropy cao nhất có thể khi tất cả các giá trị của một biến ngẫu nhiên đều có khả năng xảy ra như nhau.

Độ đo hỗn loạn của một tập hợp có 2 giá trị có thể là "0" và "1" (ví dụ: nhãn trong bài toán phân loại nhị phân) có công thức sau:

  H = -p log p – q log q = -p log p – (1-p) * log (1-p)

trong đó:

• H là entropy.
• p là phân số của "1" ví dụ.
• q là tỷ lệ của các ví dụ "0". Lưu ý rằng q = (1 – p)
• log thường là log₂. Trong trường hợp này, đơn vị entropy là một bit.

Ví dụ: giả sử những điều sau đây:

• 100 ví dụ chứa giá trị "1"
• 300 ví dụ chứa giá trị "0"

Do đó, giá trị entropy là:

• p = 0,25
• q = 0,75
• H = (-0,25)log₂(0,25) – (0,75)log₂(0,75) = 0,81 bit cho mỗi ví dụ

Một tập hợp cân bằng hoàn hảo (ví dụ: 200 "0" và 200 "1") sẽ có độ đo entropy là 1 bit cho mỗi ví dụ. Khi một tập hợp trở nên mất cân bằng, entropy của tập hợp đó sẽ tiến về 0.0.

Trong cây quyết định, entropy giúp xây dựng mức tăng thông tin để giúp bộ phân tách chọn điều kiện trong quá trình phát triển cây quyết định phân loại.

So sánh entropy với:

• độ tinh khiết gini
• Hàm mất mát cross-entropy

Độ đo hỗn loạn thường được gọi là độ đo hỗn loạn của Shannon.

Hãy xem phần Bộ phân tách chính xác để phân loại nhị phân bằng các đặc điểm số trong khoá học Rừng quyết định để biết thêm thông tin.

bình đẳng về cơ hội

#responsible

#Chỉ số

Một chỉ số công bằng để đánh giá xem một mô hình có dự đoán kết quả mong muốn một cách công bằng cho tất cả các giá trị của một thuộc tính nhạy cảm hay không. Nói cách khác, nếu kết quả mong muốn cho một mô hình là lớp dương tính, thì mục tiêu là phải có tỷ lệ dương tính thực giống nhau cho tất cả các nhóm.

Bình đẳng về cơ hội có liên quan đến tỷ lệ cược cân bằng, theo đó cả tỷ lệ dương tính thực và tỷ lệ dương tính giả đều phải giống nhau đối với tất cả các nhóm.

Giả sử Đại học Glubbdubdrib nhận cả người Lilliput và người Brobdingnag vào một chương trình toán học nghiêm ngặt. Các trường trung học của người Lilliput cung cấp một chương trình học vững chắc về các lớp toán và phần lớn học sinh đủ điều kiện tham gia chương trình đại học. Các trường trung học của người Brobdingnag không có lớp học toán, và do đó, số lượng học sinh đủ tiêu chuẩn của họ ít hơn nhiều. Cơ hội bình đẳng được đáp ứng cho nhãn ưu tiên "được nhận" đối với quốc tịch (Lilliput hoặc Brobdingnag) nếu sinh viên đủ tiêu chuẩn có khả năng được nhận như nhau bất kể họ là người Lilliput hay người Brobdingnag.

Ví dụ: giả sử có 100 người Lilliput và 100 người Brobdingnag đăng ký vào Đại học Glubbdubdrib, và quyết định nhập học được đưa ra như sau:

Bảng 1. Người đăng ký Lilliputian (90% đủ điều kiện)

	Đủ tiêu chuẩn	Không đủ tiêu chuẩn
Được chấp nhận	45	3
Bị từ chối	45	7
Tổng	90	10
Tỷ lệ phần trăm học viên đủ điều kiện được nhận: 45/90 = 50% Tỷ lệ phần trăm học viên không đủ điều kiện bị từ chối: 7/10 = 70% Tổng tỷ lệ phần trăm học viên Lilliputian được nhận: (45+3)/100 = 48%

 

Bảng 2. Ứng viên khổng lồ (10% đủ tiêu chuẩn):

	Đủ tiêu chuẩn	Không đủ tiêu chuẩn
Được chấp nhận	5	9
Bị từ chối	5	81
Tổng	10	90
Tỷ lệ phần trăm sinh viên đủ điều kiện được nhận: 5/10 = 50% Tỷ lệ phần trăm sinh viên không đủ điều kiện bị từ chối: 81/90 = 90% Tổng tỷ lệ phần trăm sinh viên Brobdingnagian được nhận: (5+9)/100 = 14%

Các ví dụ trước đó đáp ứng sự bình đẳng về cơ hội chấp nhận sinh viên đủ tiêu chuẩn vì cả người Lilliput và người Brobdingnag đều có 50% cơ hội được nhận.

Mặc dù đã đáp ứng được sự bình đẳng về cơ hội, nhưng 2 chỉ số công bằng sau đây chưa được đáp ứng:

• tính bình đẳng về nhân khẩu học: Người Lilliput và người Brobdingnag được nhận vào trường đại học với tỷ lệ khác nhau; 48% sinh viên Lilliput được nhận, nhưng chỉ có 14% sinh viên Brobdingnag được nhận.
• cơ hội ngang nhau: Mặc dù cả học viên Lilliputian và Brobdingnagian đủ tiêu chuẩn đều có cơ hội được nhận như nhau, nhưng ràng buộc bổ sung là cả học viên Lilliputian và Brobdingnagian không đủ tiêu chuẩn đều có cơ hội bị từ chối như nhau lại không được đáp ứng. Người Lilliput không đủ tiêu chuẩn có tỷ lệ bị từ chối là 70%, trong khi người Brobdingnag không đủ tiêu chuẩn có tỷ lệ bị từ chối là 90%.

Hãy xem bài viết Tính công bằng: Cơ hội bình đẳng trong Khoá học cấp tốc về học máy để biết thêm thông tin.

tỷ lệ cược cân bằng

#responsible

#Chỉ số

Một chỉ số công bằng để đánh giá xem một mô hình có dự đoán kết quả tốt như nhau cho tất cả các giá trị của một thuộc tính nhạy cảm hay không, liên quan đến cả lớp dương và lớp âm – không chỉ một lớp hoặc lớp kia một cách riêng biệt. Nói cách khác, cả tỷ lệ dương tính thực và tỷ lệ âm tính giả đều phải giống nhau đối với tất cả các nhóm.

Cơ hội bình đẳng liên quan đến sự bình đẳng về cơ hội, chỉ tập trung vào tỷ lệ lỗi cho một lớp duy nhất (dương hoặc âm).

Ví dụ: giả sử Đại học Glubbdubdrib nhận cả người Lilliput và người Brobdingnag vào một chương trình toán học nghiêm ngặt. Các trường trung học của người Lilliput cung cấp một chương trình học tập toàn diện về các lớp toán và phần lớn học sinh đủ điều kiện tham gia chương trình đại học. Các trường trung học của người Brobdingnag không có lớp học toán nào, và do đó, số lượng học sinh đủ điều kiện của họ ít hơn nhiều. Điều kiện về xác suất ngang bằng được đáp ứng miễn là bất kể người đăng ký là người Lilliput hay người Brobdingnag, nếu họ đủ tiêu chuẩn, thì họ đều có khả năng được nhận vào chương trình như nhau, và nếu họ không đủ tiêu chuẩn, thì họ đều có khả năng bị từ chối như nhau.

Giả sử có 100 người Lilliput và 100 người Brobdingnag đăng ký vào Đại học Glubbdubdrib, và quyết định nhập học được đưa ra như sau:

Bảng 3. Người đăng ký Lilliputian (90% đủ điều kiện)

	Đủ tiêu chuẩn	Không đủ tiêu chuẩn
Được chấp nhận	45	2
Bị từ chối	45	8
Tổng	90	10
Tỷ lệ phần trăm học sinh đủ điều kiện được nhận: 45/90 = 50% Tỷ lệ phần trăm học sinh không đủ điều kiện bị từ chối: 8/10 = 80% Tổng tỷ lệ phần trăm học sinh Lilliputian được nhận: (45+2)/100 = 47%

 

Bảng 4. Ứng viên khổng lồ (10% đủ tiêu chuẩn):

	Đủ tiêu chuẩn	Không đủ tiêu chuẩn
Được chấp nhận	5	18
Bị từ chối	5	72
Tổng	10	90
Tỷ lệ phần trăm sinh viên đủ điều kiện được nhận: 5/10 = 50% Tỷ lệ phần trăm sinh viên không đủ điều kiện bị từ chối: 72/90 = 80% Tổng tỷ lệ phần trăm sinh viên Brobdingnagian được nhận: (5+18)/100 = 23%

Điều kiện về xác suất ngang bằng được đáp ứng vì cả sinh viên đủ tiêu chuẩn ở Lilliput và Brobdingnag đều có 50% cơ hội được nhận, còn sinh viên không đủ tiêu chuẩn ở Lilliput và Brobdingnag có 80% cơ hội bị từ chối.

Lưu ý: Mặc dù đã đáp ứng được điều kiện về xác suất ngang nhau, nhưng tính bình đẳng về nhân khẩu học chưa được đáp ứng. Sinh viên Lilliputian và Brobdingnagian được nhận vào Đại học Glubbdubdrib với tỷ lệ khác nhau; 47% sinh viên Lilliputian được nhận và 23% sinh viên Brobdingnagian được nhận.

Tỷ lệ cược cân bằng được xác định chính thức trong "Cơ hội bình đẳng trong học có giám sát" như sau: "hàm dự đoán Ŷ đáp ứng tỷ lệ cược cân bằng đối với thuộc tính được bảo vệ A và kết quả Y nếu Ŷ và A độc lập, có điều kiện trên Y."

Lưu ý: So sánh xác suất cân bằng với chỉ số cơ hội bình đẳng thoải mái hơn.

evals

#generativeAI

#Chỉ số

Chủ yếu được dùng làm từ viết tắt cho các hoạt động đánh giá mô hình ngôn ngữ lớn (LLM). Nói chung, evals là từ viết tắt của mọi hình thức đánh giá.

đánh giá

#generativeAI

#Chỉ số

Quy trình đo lường chất lượng của một mô hình hoặc so sánh các mô hình khác nhau với nhau.

Để đánh giá một mô hình học máy có giám sát, bạn thường đánh giá mô hình đó dựa trên một tập hợp xác thực và một tập hợp kiểm thử. Đánh giá một LLM thường bao gồm các đánh giá rộng hơn về chất lượng và độ an toàn.

F

F₁

#Chỉ số

Một chỉ số "tổng hợp" phân loại nhị phân dựa trên cả độ chính xác và khả năng thu hồi. Sau đây là công thức:

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

Nhấp vào biểu tượng để xem ví dụ.

Giả sử độ chính xác và độ thu hồi có các giá trị sau:

• độ chính xác = 0,6
• recall = 0,4

Bạn tính F₁ như sau:

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

Khi độ chính xác và độ thu hồi khá tương tự nhau (như trong ví dụ trước), F₁ gần với giá trị trung bình của chúng. Khi độ chính xác và độ thu hồi khác nhau đáng kể, F₁ sẽ gần với giá trị thấp hơn. Ví dụ:

• độ chính xác = 0,9
• mức độ ghi nhớ = 0,1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

chỉ số công bằng

#responsible

#Chỉ số

Định nghĩa toán học về "sự công bằng" có thể đo lường được. Sau đây là một số chỉ số công bằng thường dùng:

• xác suất cân bằng
• tính tương đương dự đoán
• tính công bằng phản thực tế
• tính tương đồng về nhân khẩu học

Nhiều chỉ số công bằng loại trừ lẫn nhau; hãy xem sự không tương thích của các chỉ số công bằng.

âm tính giả (FN)

#fundamentals

#Chỉ số

Ví dụ về trường hợp mô hình dự đoán nhầm lớp âm tính. Ví dụ: mô hình dự đoán rằng một thư email cụ thể không phải là thư rác (lớp âm tính), nhưng thư email đó thực sự là thư rác.

tỷ lệ âm tính giả

#Chỉ số

Tỷ lệ ví dụ dương tính thực tế mà mô hình dự đoán nhầm là lớp âm tính. Công thức sau đây dùng để tính tỷ lệ âm tính giả:

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

Hãy xem phần Ngưỡng và ma trận nhầm lẫn trong Khoá học học máy ứng dụng để biết thêm thông tin.

dương tính giả (FP)

#fundamentals

#Chỉ số

Ví dụ trong đó mô hình dự đoán nhầm lớp dương tính. Ví dụ: mô hình dự đoán rằng một thư email cụ thể là thư rác (lớp dương tính), nhưng thư email đó thực sự không phải là thư rác.

Hãy xem phần Ngưỡng và ma trận nhầm lẫn trong Khoá học học máy ứng dụng để biết thêm thông tin.

tỷ lệ dương tính giả (FPR)

#fundamentals

#Chỉ số

Tỷ lệ ví dụ thực tế có kết quả âm tính mà mô hình dự đoán nhầm thành lớp dương tính. Công thức sau đây dùng để tính tỷ lệ dương tính giả:

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

Tỷ lệ dương tính giả là trục x trong đường cong ROC.

Hãy xem phần Phân loại: ROC và AUC trong Khoá học học máy ứng dụng để biết thêm thông tin.

tầm quan trọng của các đặc điểm

#df

#Chỉ số

Từ đồng nghĩa với mức độ quan trọng của biến.

mô hình nền tảng

#generativeAI

#Chỉ số

Một mô hình được huấn luyện trước có quy mô rất lớn, được huấn luyện trên một tập huấn luyện khổng lồ và đa dạng. Một mô hình cơ sở có thể làm cả hai việc sau:

• Đáp ứng tốt nhiều loại yêu cầu.
• Đóng vai trò là một mô hình cơ sở để điều chỉnh hoặc tuỳ chỉnh thêm.

Nói cách khác, mô hình cơ sở đã có khả năng rất cao theo nghĩa chung nhưng có thể được tuỳ chỉnh thêm để trở nên hữu ích hơn nữa cho một nhiệm vụ cụ thể.

phân số thành công

#generativeAI

#Chỉ số

Một chỉ số để đánh giá văn bản do AI tạo của một mô hình học máy. Phân số thành công là số lượng đầu ra văn bản được tạo "thành công" chia cho tổng số đầu ra văn bản được tạo. Ví dụ: nếu mô hình ngôn ngữ lớn tạo ra 10 khối mã, trong đó có 5 khối thành công, thì tỷ lệ thành công sẽ là 50%.

Mặc dù tỷ lệ thành công thường hữu ích trong thống kê, nhưng trong học máy, chỉ số này chủ yếu hữu ích để đo lường các tác vụ có thể xác minh như tạo mã hoặc giải toán.

G

độ tinh khiết Gini

#df

#Chỉ số

Một chỉ số tương tự như entropy. Trình phân tách sử dụng các giá trị bắt nguồn từ độ tinh khiết gini hoặc entropy để tạo điều kiện cho cây quyết định phân loại. Mức tăng thông tin được suy ra từ entropy. Không có thuật ngữ tương đương được chấp nhận rộng rãi cho chỉ số bắt nguồn từ độ tinh khiết Gini; tuy nhiên, chỉ số chưa được đặt tên này cũng quan trọng như mức tăng thông tin.

Độ tinh khiết Gini còn được gọi là chỉ số Gini hoặc đơn giản là Gini.

Nhấp vào biểu tượng để biết thông tin chi tiết về toán học liên quan đến độ tinh khiết Gini.

Độ tinh khiết Gini là xác suất phân loại sai một phần dữ liệu mới được lấy từ cùng một hàm phân phối. Độ tinh khiết Gini của một tập hợp có 2 giá trị có thể là "0" và "1" (ví dụ: nhãn trong vấn đề phân loại nhị phân) được tính theo công thức sau:

   I = 1 – (p² + q²) = 1 – (p² + (1 – p)²)

trong đó:

• I là độ tinh khiết gini.
• p là phân số của "1" ví dụ.
• q là tỷ lệ của các ví dụ "0". Lưu ý rằng q = 1 – p

Ví dụ: hãy xem xét tập dữ liệu sau:

• 100 nhãn (0,25 tập dữ liệu) chứa giá trị "1"
• 300 nhãn (0,75 tập dữ liệu) chứa giá trị "0"

Do đó, độ tinh khiết Gini là:

• p = 0,25
• q = 0,75
• I = 1 – (0,25² + 0,75²) = 0,375

Do đó, một nhãn ngẫu nhiên trong cùng tập dữ liệu sẽ có 37,5% khả năng bị phân loại sai và 62,5% khả năng được phân loại đúng.

Một nhãn cân bằng hoàn hảo (ví dụ: 200 "0" và 200 "1") sẽ có độ tinh khiết Gini là 0, 5. Nhãn mất cân bằng cao sẽ có độ tinh khiết Gini gần bằng 0.0.

---

Cao

tổn thất khớp nối

#Chỉ số

Một nhóm các hàm mất mát cho phân loại được thiết kế để tìm ranh giới quyết định càng xa càng tốt so với mỗi ví dụ huấn luyện, do đó tối đa hoá khoảng cách giữa các ví dụ và ranh giới. KSVM sử dụng tổn thất bản lề (hoặc một hàm liên quan, chẳng hạn như tổn thất bản lề bình phương). Đối với phân loại nhị phân, hàm mất mát lề được xác định như sau:

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

trong đó y là nhãn thực, có thể là -1 hoặc +1, còn y' là đầu ra thô của mô hình phân loại:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

Do đó, biểu đồ về tổn thất bản lề so với (y * y') có dạng như sau:

I

sự không tương thích của các chỉ số công bằng

#responsible

#Chỉ số

Ý tưởng cho rằng một số khái niệm về sự công bằng không tương thích với nhau và không thể đáp ứng đồng thời. Do đó, không có một chỉ số chung duy nhất để định lượng tính công bằng có thể áp dụng cho tất cả các vấn đề về học máy.

Mặc dù điều này có vẻ đáng thất vọng, nhưng sự không tương thích của các chỉ số công bằng không có nghĩa là những nỗ lực hướng đến sự công bằng là vô ích. Thay vào đó, nó đề xuất rằng sự công bằng phải được xác định theo ngữ cảnh cho một vấn đề cụ thể về học máy, với mục tiêu là ngăn chặn những tác hại cụ thể đối với các trường hợp sử dụng của vấn đề đó.

Hãy xem bài viết "Về (sự) bất khả thi của tính công bằng" để biết thêm thông tin chi tiết về sự không tương thích của các chỉ số công bằng.

tính công bằng cho từng cá nhân

#responsible

#Chỉ số

Một chỉ số công bằng kiểm tra xem những cá nhân tương tự có được phân loại tương tự hay không. Ví dụ: Brobdingnagian Academy có thể muốn đáp ứng sự công bằng cho từng cá nhân bằng cách đảm bảo rằng 2 học viên có điểm số và điểm kiểm tra tiêu chuẩn giống hệt nhau có khả năng được nhận vào học như nhau.

Xin lưu ý rằng tính công bằng cho từng cá nhân hoàn toàn phụ thuộc vào cách bạn xác định "mức độ tương đồng" (trong trường hợp này là điểm số và điểm kiểm tra), đồng thời bạn có thể gặp phải nguy cơ xuất hiện các vấn đề mới về tính công bằng nếu chỉ số về mức độ tương đồng của bạn bỏ lỡ thông tin quan trọng (chẳng hạn như mức độ nghiêm ngặt của chương trình học của học viên).

Hãy xem bài viết "Công bằng thông qua nhận thức" để biết thêm thông tin chi tiết về sự công bằng cho từng cá nhân.

mức tăng thông tin

#df

#Chỉ số

Trong rừng quyết định, sự khác biệt giữa entropy của một nút và tổng entropy có trọng số (theo số lượng ví dụ) của các nút con. Độ đo entropy của một nút là độ đo entropy của các ví dụ trong nút đó.

Ví dụ: hãy xem xét các giá trị entropy sau:

• entropy của nút mẹ = 0,6
• entropy của một nút con có 16 ví dụ liên quan = 0,2
• entropy của một nút con khác với 24 ví dụ có liên quan = 0,1

Vì vậy, 40% ví dụ nằm trong một nút con và 60% nằm trong nút con còn lại. Vì thế:

• tổng entropy có trọng số của các nút con = (0,4 * 0,2) + (0,6 * 0,1) = 0,14

Vậy mức tăng thông tin là:

• mức tăng thông tin = entropy của nút mẹ – tổng entropy có trọng số của các nút con
• mức tăng thông tin = 0,6 – 0,14 = 0,46

Hầu hết bộ phân tách đều tìm cách tạo ra các điều kiện giúp tối đa hoá mức tăng thông tin.

mức độ đồng thuận

#Chỉ số

Chỉ số đo lường tần suất mà người đánh giá đồng ý với nhau khi thực hiện một nhiệm vụ. Nếu người đánh giá không đồng ý, thì có thể bạn cần cải thiện hướng dẫn cho nhiệm vụ. Đôi khi còn được gọi là mức độ nhất trí giữa các chú thích viên hoặc độ tin cậy giữa các chuyên gia đánh giá. Xem thêm Kappa của Cohen, đây là một trong những chỉ số phổ biến nhất về mức độ nhất quán giữa các chuyên gia đánh giá.

Hãy xem bài viết Dữ liệu phân loại: Các vấn đề thường gặp trong Khoá học cấp tốc về học máy để biết thêm thông tin.

L

Tổn thất L₁

#fundamentals

#Chỉ số

Một hàm tổn thất tính toán giá trị tuyệt đối của mức chênh lệch giữa các giá trị nhãn thực tế và các giá trị mà một mô hình dự đoán. Ví dụ: sau đây là cách tính tổn thất L₁ cho một lô gồm 5 ví dụ:

Giá trị thực tế của ví dụ	Giá trị dự đoán của mô hình	Giá trị tuyệt đối của delta
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = tổn thất L1

Mất mát L₁ ít nhạy cảm với giá trị ngoại lệ hơn mất mát L₂.

Sai số tuyệt đối trung bình là mức tổn thất L₁ trung bình trên mỗi ví dụ.

Nhấp vào biểu tượng để xem công thức toán học chính thức.

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

trong đó:

• $n$ là số lượng ví dụ.
• $y$ là giá trị thực tế của nhãn.
• $\hat{y}$ là giá trị mà mô hình dự đoán cho $y$.

---

Hãy xem phần Hồi quy tuyến tính: Mất mát trong Khoá học cấp tốc về học máy để biết thêm thông tin.

Tổn thất L₂

#fundamentals

#Chỉ số

Một hàm tổn thất tính bình phương của sự khác biệt giữa các giá trị nhãn thực tế và các giá trị mà một mô hình dự đoán. Ví dụ: sau đây là cách tính tổn thất L₂ cho một lô gồm 5 ví dụ:

Giá trị thực tế của ví dụ	Giá trị dự đoán của mô hình	Bình phương của delta
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = tổn thất L2

Do bình phương, tổn thất L₂ sẽ khuếch đại ảnh hưởng của các giá trị ngoại lai. Tức là tổn thất L₂ phản ứng mạnh hơn với các dự đoán không chính xác so với tổn thất L₁. Ví dụ: tổn thất L₁ cho lô trước đó sẽ là 8 thay vì 16. Xin lưu ý rằng một giá trị ngoại lệ duy nhất chiếm 9 trong số 16 giá trị.

Mô hình hồi quy thường sử dụng tổn thất L₂ làm hàm tổn thất.

Sai số bình phương trung bình là tổn thất L₂ trung bình trên mỗi ví dụ. Tổn thất bình phương là một tên khác của tổn thất L₂.

Nhấp vào biểu tượng để xem công thức toán học chính thức.

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

trong đó:

• $n$ là số lượng ví dụ.
• $y$ là giá trị thực tế của nhãn.
• $\hat{y}$ là giá trị mà mô hình dự đoán cho $y$.

---

Hãy xem phần Hồi quy logistic: Hàm mất mát và điều chuẩn trong Khoá học cấp tốc về học máy để biết thêm thông tin.

Đánh giá LLM

#generativeAI

#Chỉ số

Một bộ chỉ số và điểm chuẩn để đánh giá hiệu suất của các mô hình ngôn ngữ lớn (LLM). Ở cấp độ cao, các hoạt động đánh giá LLM:

• Giúp các nhà nghiên cứu xác định những khía cạnh mà LLM cần cải thiện.
• Hữu ích trong việc so sánh các LLM khác nhau và xác định LLM phù hợp nhất cho một nhiệm vụ cụ thể.
• Giúp đảm bảo rằng các LLM an toàn và có đạo đức khi sử dụng.

Hãy xem Mô hình ngôn ngữ lớn (LLM) trong Khoá học học máy ứng dụng để biết thêm thông tin.

thua

#fundamentals

#Chỉ số

Trong quá trình huấn luyện một mô hình có giám sát, một thước đo cho biết dự đoán của mô hình cách xa nhãn của mô hình bao nhiêu.

Hàm tổn thất tính toán tổn thất.

Hãy xem phần Hồi quy tuyến tính: Mất mát trong Khoá học cấp tốc về học máy để biết thêm thông tin.

hàm tổn thất

#fundamentals

#Chỉ số

Trong quá trình huấn luyện hoặc kiểm thử, một hàm toán học sẽ tính toán mức tổn thất trên một lô ví dụ. Hàm tổn thất trả về mức tổn thất thấp hơn cho những mô hình đưa ra dự đoán chính xác so với những mô hình đưa ra dự đoán không chính xác.

Mục tiêu của việc huấn luyện thường là giảm thiểu mức tổn thất mà một hàm tổn thất trả về.

Có nhiều loại hàm tổn thất. Chọn hàm tổn thất phù hợp cho loại mô hình mà bạn đang xây dựng. Ví dụ:

• Mất mát L₂ (hoặc Sai số bình phương trung bình) là hàm mất mát cho hồi quy tuyến tính.
• Log Loss là hàm tổn thất cho hồi quy logistic.

M

Sai số tuyệt đối trung bình (MAE)

#Chỉ số

Mức tổn thất trung bình trên mỗi ví dụ khi sử dụng tổn thất L₁. Tính Sai số tuyệt đối trung bình như sau:

1. Tính toán tổn thất L₁ cho một lô.
2. Chia tổn thất L₁ cho số lượng ví dụ trong lô.

Nhấp vào biểu tượng để xem công thức toán học chính thức.

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

trong đó:

• $n$ là số lượng ví dụ.
• $y$ là giá trị thực tế của nhãn.
• $\hat{y}$ là giá trị mà mô hình dự đoán cho $y$.

---

Ví dụ: hãy xem xét việc tính toán tổn thất L₁ trên lô gồm 5 ví dụ sau:

Giá trị thực tế của ví dụ	Giá trị dự đoán của mô hình	Mất mát (chênh lệch giữa giá trị thực tế và giá trị dự đoán)
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = tổn thất L1

Vậy, tổn thất L₁ là 8 và số lượng ví dụ là 5. Do đó, Sai số tuyệt đối trung bình là:

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

Tương phản Sai số tuyệt đối trung bình với Sai số bình phương trung bình và Sai số trung bình bình phương.

độ chính xác trung bình tại k (mAP@k)

#generativeAI

#Chỉ số

Giá trị trung bình thống kê của tất cả các điểm độ chính xác trung bình tại k trên một tập dữ liệu xác thực. Một cách sử dụng độ chính xác trung bình tại k là đánh giá chất lượng của các đề xuất do hệ thống đề xuất tạo ra.

Mặc dù cụm từ "giá trị trung bình" nghe có vẻ dư thừa, nhưng tên của chỉ số này là phù hợp. Sau tất cả, chỉ số này tìm ra giá trị trung bình của nhiều giá trị độ chính xác trung bình tại k.

Nhấp vào biểu tượng để xem ví dụ.

Giả sử bạn tạo một hệ thống đề xuất tạo ra danh sách tiểu thuyết được đề xuất riêng cho từng người dùng. Dựa trên ý kiến phản hồi của một số người dùng được chọn, bạn tính 5 điểm độ chính xác trung bình tại k (mỗi người dùng một điểm):

• 0,73
• 0,77
• 0,67
• 0,82
• 0,76

Do đó, Độ chính xác trung bình tại K trung bình là:

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

Sai số bình phương trung bình (MSE)

#Chỉ số

Mức tổn thất trung bình trên mỗi ví dụ khi sử dụng tổn thất L₂. Tính Sai số bình phương trung bình như sau:

1. Tính tổn thất L₂ cho một lô.
2. Chia tổn thất L₂ cho số lượng ví dụ trong lô.

Nhấp vào biểu tượng để xem công thức toán học chính thức.

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ where:

• $n$ là số lượng ví dụ.
• $y$ là giá trị thực tế của nhãn.
• $\hat{y}$ là giá trị dự đoán của mô hình cho $y$.

---

Ví dụ: hãy xem xét tổn thất trên lô gồm 5 ví dụ sau:

Giá trị thực tế	Dự đoán của mô hình	Thua	Tổn thất bình phương
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			16 = tổn thất L2

Do đó, Sai số bình phương trung bình là:

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

Sai số bình phương trung bình là một trình tối ưu hoá huấn luyện phổ biến, đặc biệt là đối với hồi quy tuyến tính.

So sánh Sai số bình phương trung bình với Sai số tuyệt đối trung bình và Sai số trung bình bình phương.

TensorFlow Playground sử dụng Sai số bình phương trung bình để tính giá trị tổn thất.

Nhấp vào biểu tượng để xem thêm thông tin chi tiết về giá trị ngoại lệ.

Giá trị ngoại lai ảnh hưởng lớn đến Sai số bình phương trung bình. Ví dụ: tổn thất 1 là tổn thất bình phương 1, nhưng tổn thất 3 là tổn thất bình phương 9. Trong bảng trên, ví dụ có mức tổn thất là 3 tài khoản chiếm khoảng 56% Sai số bình phương trung bình, trong khi mỗi ví dụ có mức tổn thất là 1 tài khoản chỉ chiếm 6% Sai số bình phương trung bình.

Các giá trị ngoại lệ không ảnh hưởng đến Sai số tuyệt đối trung bình nhiều như Sai số bình phương trung bình. Ví dụ: việc mất 3 tài khoản chỉ chiếm khoảng 38% Sai số tuyệt đối trung bình.

Cắt bớt là một cách để ngăn chặn các giá trị ngoại lệ cực đoan làm tổn hại đến khả năng dự đoán của mô hình.

---

chỉ số

#TensorFlow

#Chỉ số

Một số liệu thống kê mà bạn quan tâm.

Mục tiêu là một chỉ số mà hệ thống học máy cố gắng tối ưu hoá.

Metrics API (tf.metrics)

#Chỉ số

Một API TensorFlow để đánh giá các mô hình. Ví dụ: tf.metrics.accuracy xác định tần suất dự đoán của một mô hình khớp với nhãn.

mất mát minimax

#Chỉ số

Một hàm tổn thất cho mạng đối kháng sinh tạo, dựa trên cross-entropy giữa phân phối dữ liệu được tạo và dữ liệu thực.

Mất mát tối thiểu tối đa được sử dụng trong bài viết đầu tiên để mô tả mạng đối nghịch tạo sinh.

Hãy xem Hàm tổn thất trong khoá học Mạng sinh đối kháng để biết thêm thông tin.

dung lượng mô hình

#Chỉ số

Độ phức tạp của các vấn đề mà một mô hình có thể học được. Mô hình càng có thể học được nhiều vấn đề phức tạp thì năng lực của mô hình càng cao. Dung lượng của mô hình thường tăng lên theo số lượng tham số mô hình. Để biết định nghĩa chính thức về năng lực của mô hình phân loại, hãy xem phương diện VC.

Không

lớp âm

#fundamentals

#Chỉ số

Trong phân loại nhị phân, một lớp được gọi là dương tính và lớp còn lại được gọi là âm tính. Lớp dương là đối tượng hoặc sự kiện mà mô hình đang kiểm thử và lớp âm là khả năng khác. Ví dụ:

• Lớp âm tính trong một xét nghiệm y tế có thể là "không phải khối u".
• Lớp âm trong mô hình phân loại email có thể là "không phải thư rác".

Tương phản với lớp dương.

O

mục tiêu

#Chỉ số

Một chỉ số mà thuật toán của bạn đang cố gắng tối ưu hoá.

hàm mục tiêu

#Chỉ số

Công thức toán học hoặc chỉ số mà một mô hình hướng đến việc tối ưu hoá. Ví dụ: hàm mục tiêu cho hồi quy tuyến tính thường là Mất mát bình phương trung bình. Do đó, khi huấn luyện mô hình hồi quy tuyến tính, quá trình huấn luyện nhằm mục đích giảm thiểu Mất mát bình phương trung bình.

Trong một số trường hợp, mục tiêu là tối đa hoá hàm mục tiêu. Ví dụ: nếu hàm mục tiêu là độ chính xác, thì mục tiêu là tối đa hoá độ chính xác.

Xem thêm tổn thất.

Điểm

pass at k (pass@k)

#Chỉ số

Một chỉ số để xác định chất lượng mã (ví dụ: Python) mà mô hình ngôn ngữ lớn tạo ra. Cụ thể hơn, pass ở k cho biết khả năng ít nhất một khối mã được tạo trong số k khối mã được tạo sẽ vượt qua tất cả các kiểm thử đơn vị.

Các mô hình ngôn ngữ lớn thường gặp khó khăn trong việc tạo mã tốt cho các vấn đề lập trình phức tạp. Các kỹ sư phần mềm thích ứng với vấn đề này bằng cách nhắc mô hình ngôn ngữ lớn tạo ra nhiều (k) giải pháp cho cùng một vấn đề. Sau đó, các kỹ sư phần mềm sẽ kiểm thử từng giải pháp dựa trên các kiểm thử đơn vị. Việc tính toán số lượt vượt qua ở k phụ thuộc vào kết quả của các kiểm thử đơn vị:

• Nếu một hoặc nhiều giải pháp trong số đó vượt qua kiểm thử đơn vị, thì LLM sẽ Vượt qua thử thách tạo mã đó.
• Nếu không có giải pháp nào vượt qua được quy trình kiểm thử đơn vị, thì LLM sẽ Không thành công trong thử thách tạo mã đó.

Công thức cho lượt chuyền ở k như sau:

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

Nhìn chung, các giá trị k cao hơn sẽ tạo ra điểm vượt qua k cao hơn; tuy nhiên, các giá trị k cao hơn đòi hỏi nhiều mô hình ngôn ngữ lớn và tài nguyên kiểm thử đơn vị hơn.

Nhấp vào biểu tượng để xem ví dụ.

Giả sử một kỹ sư phần mềm yêu cầu mô hình ngôn ngữ lớn tạo ra k=10 giải pháp cho n=50 vấn đề khó về lập trình. Sau đây là kết quả:

• 30 thẻ/vé
• 20 lần không thành công

Do đó, điểm vượt qua ở mức 10 là:

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

hiệu quả hoạt động

#Chỉ số

Thuật ngữ bị nạp chồng với các ý nghĩa sau:

• Ý nghĩa tiêu chuẩn trong kỹ thuật phần mềm. Cụ thể: Phần mềm này chạy nhanh (hoặc hiệu quả) như thế nào?
• Ý nghĩa trong công nghệ học máy. Ở đây, hiệu suất trả lời câu hỏi sau: Mô hình này chính xác đến mức nào? Tức là mức độ chính xác của thông tin dự đoán do mô hình đưa ra.

mức độ quan trọng của biến hoán vị

#df

#Chỉ số

Một loại mức độ quan trọng của biến đánh giá mức tăng lỗi dự đoán của một mô hình sau khi hoán vị các giá trị của đối tượng. Mức độ quan trọng của biến hoán vị là một chỉ số độc lập với mô hình.

độ hỗn loạn

#Chỉ số

Một chỉ số đo lường mức độ hoàn thành nhiệm vụ của mô hình. Ví dụ: giả sử nhiệm vụ của bạn là đọc một vài chữ cái đầu tiên của một từ mà người dùng đang nhập trên bàn phím điện thoại và đưa ra danh sách các từ có thể hoàn thành. Độ phức tạp (P) cho tác vụ này xấp xỉ số lượng các từ bạn cần đoán để danh sách của bạn chứa từ thực tế mà người dùng đang cố gắng nhập.

Độ phức tạp có liên quan đến cross-entropy như sau:

$$P= 2^{-\text{cross entropy}}$$

lớp dương

#fundamentals

#Chỉ số

Lớp học mà bạn đang kiểm thử.

Ví dụ: lớp dương tính trong mô hình ung thư có thể là "khối u". Lớp dương tính trong mô hình phân loại email có thể là "thư rác".

Tương phản với lớp âm.

Nhấp vào biểu tượng để xem thêm ghi chú.

Thuật ngữ lớp dương tính có thể gây nhầm lẫn vì kết quả "dương tính" của nhiều xét nghiệm thường là kết quả không mong muốn. Ví dụ: lớp dương tính trong nhiều xét nghiệm y tế tương ứng với các khối u hoặc bệnh tật. Nói chung, bạn muốn bác sĩ nói với bạn rằng: "Chúc mừng! Kết quả xét nghiệm của bạn là âm tính". Bất kể điều gì, lớp dương tính là sự kiện mà kiểm thử đang tìm kiếm.

Thừa nhận rằng bạn đang đồng thời kiểm thử cho cả các lớp dương tính và âm tính.

---

AUC PR (diện tích dưới đường cong PR)

#Chỉ số

Diện tích dưới đường cong độ chính xác-khả năng thu hồi được nội suy, thu được bằng cách vẽ các điểm (khả năng thu hồi, độ chính xác) cho các giá trị khác nhau của ngưỡng phân loại.

độ chính xác

#fundamentals

#Chỉ số

Một chỉ số cho các mô hình phân loại giúp trả lời câu hỏi sau:

Khi mô hình dự đoán lớp dương tính, tỷ lệ phần trăm dự đoán chính xác là bao nhiêu?

Sau đây là công thức:

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

trong đó:

• dương tính thật có nghĩa là mô hình đã dự đoán chính xác lớp dương tính.
• dương tính giả có nghĩa là mô hình đã nhầm lẫn dự đoán hạng mục dương.

Ví dụ: giả sử một mô hình đưa ra 200 dự đoán dương tính. Trong số 200 dự đoán tích cực này:

• 150 trường hợp là dương tính thật.
• 50 trường hợp là dương tính giả.

Trong trường hợp này:

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

Tương phản với độ chính xác và khả năng thu hồi.

Hãy xem phần Phân loại: Độ chính xác, khả năng thu hồi, độ đo và các chỉ số liên quan trong Khoá học cấp tốc về học máy để biết thêm thông tin.

độ chính xác tại k (precision@k)

#Chỉ số

Một chỉ số để đánh giá danh sách các mục được xếp hạng (theo thứ tự). Độ chính xác tại k xác định tỷ lệ của k mục đầu tiên trong danh sách đó là "phù hợp". Đó là:

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

Giá trị của k phải nhỏ hơn hoặc bằng độ dài của danh sách được trả về. Xin lưu ý rằng độ dài của danh sách được trả về không thuộc phạm vi tính toán.

Mức độ phù hợp thường mang tính chủ quan; ngay cả người đánh giá là chuyên gia cũng thường không đồng ý về những mục nào là phù hợp.

So với:

• độ chính xác trung bình tại k
• độ chính xác trung bình tại k

Nhấp vào biểu tượng để xem ví dụ.

Giả sử một mô hình ngôn ngữ lớn được đưa ra truy vấn sau:

List the 6 funniest movies of all time in order.

Và mô hình ngôn ngữ lớn sẽ trả về danh sách xuất hiện trong hai cột đầu tiên của bảng sau:

Vị trí	Phim	Có liên quan không?
1	The General	Có
2	Mean Girls	Có
3	Platoon	Không
4	Phù dâu	Có
5	Công dân Kane	Không
6	This is Spinal Tap	Có

Hai trong số 3 bộ phim đầu tiên có liên quan, vì vậy, độ chính xác ở 3 là:

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

3 trong số 5 bộ phim đầu tiên rất hài hước, nên độ chính xác ở mức 5 là:

$$\text{precision at 5} = \frac{\text{3}} {\text{5}} = 0.6$$

---

đường cong độ chính xác-độ thu hồi

#Chỉ số

Đường cong độ chính xác so với khả năng thu hồi ở các ngưỡng phân loại khác nhau.

độ lệch của dự đoán

#Chỉ số

Giá trị cho biết mức độ khác biệt giữa giá trị trung bình của các dự đoán và giá trị trung bình của nhãn trong tập dữ liệu.

Không nhầm lẫn với thuật ngữ thiên kiến trong các mô hình học máy hoặc với thiên kiến trong đạo đức và sự công bằng.

tính tương đương dự đoán

#responsible

#Chỉ số

Một chỉ số công bằng kiểm tra xem đối với một mô hình phân loại nhất định, tỷ lệ độ chính xác có tương đương với các nhóm phụ đang được xem xét hay không.

Ví dụ: một mô hình dự đoán việc được nhận vào trường đại học sẽ đáp ứng tính tương đồng dự đoán về quốc tịch nếu tỷ lệ chính xác của mô hình này là như nhau đối với người Lilliput và người Brobdingnag.

Đôi khi, tính tương đương dự đoán còn được gọi là tính tương đương dự đoán về giá.

Hãy xem phần "Giải thích định nghĩa về tính công bằng" (mục 3.2.1) để biết thông tin chi tiết hơn về tính tương đồng dự đoán.

tỷ lệ ngang bằng dự đoán

#responsible

#Chỉ số

Một tên khác của tính chẵn lẻ dự đoán.

hàm mật độ xác suất

#Chỉ số

Một hàm xác định tần suất của các mẫu dữ liệu có chính xác một giá trị cụ thể. Khi các giá trị của một tập dữ liệu là các số dấu phẩy động liên tục, thì hiếm khi xảy ra trường hợp khớp chính xác. Tuy nhiên, việc tích hợp hàm mật độ xác suất từ giá trị x đến giá trị y sẽ cho ra tần suất dự kiến của các mẫu dữ liệu trong khoảng từ x đến y.

Ví dụ: hãy xem xét một phân phối chuẩn có giá trị trung bình là 200 và độ lệch chuẩn là 30. Để xác định tần suất dự kiến của các mẫu dữ liệu nằm trong phạm vi từ 211,4 đến 218,7, bạn có thể tích hợp hàm mật độ xác suất cho một phân phối chuẩn từ 211,4 đến 218,7.

Điểm

mức độ ghi nhớ

#fundamentals

#Chỉ số

Một chỉ số cho các mô hình phân loại giúp trả lời câu hỏi sau:

Khi dữ liệu thực tế là lớp dương tính, mô hình đã xác định chính xác bao nhiêu phần trăm dự đoán là lớp dương tính?

Sau đây là công thức:

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

trong đó:

• dương tính thật có nghĩa là mô hình đã dự đoán chính xác lớp dương tính.
• âm tính giả nghĩa là mô hình nhầm lẫn dự đoán lớp âm tính.

Ví dụ: giả sử mô hình của bạn đưa ra 200 dự đoán về các ví dụ mà chân lý cơ bản là lớp dương tính. Trong số 200 dự đoán này:

• 180 trường hợp là dương tính thật.
• 20 trường hợp là âm tính giả.

Trong trường hợp này:

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

Nhấp vào biểu tượng để xem ghi chú về tập dữ liệu bất cân đối về loại.

Độ đo này đặc biệt hữu ích để xác định khả năng dự đoán của các mô hình phân loại trong đó lớp dương hiếm khi xuất hiện. Ví dụ: hãy xem xét tập dữ liệu mất cân bằng lớp trong đó lớp dương tính của một bệnh cụ thể chỉ xảy ra ở 10 bệnh nhân trong số một triệu. Giả sử mô hình của bạn đưa ra 5 triệu dự đoán và mang lại những kết quả sau:

• 30 kết quả dương tính thật
• 20 kết quả âm tính giả
• 4.999.000 kết quả âm tính thật
• 950 Dương tính giả

Do đó, độ đo recall của mô hình này là:

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

Ngược lại, độ chính xác của mô hình này là:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

Giá trị độ chính xác cao đó trông có vẻ ấn tượng nhưng về cơ bản là vô nghĩa. Độ thu hồi là một chỉ số hữu ích hơn nhiều so với độ chính xác đối với các tập dữ liệu bất cân đối về loại.

---

Hãy xem bài viết Phân loại: Độ chính xác, khả năng thu hồi, độ đo lường và các chỉ số liên quan để biết thêm thông tin.

tỷ lệ ghi nhớ ở k (recall@k)

#Chỉ số

Một chỉ số để đánh giá các hệ thống xuất ra danh sách các mục được xếp hạng (theo thứ tự). Độ thu hồi tại k xác định tỷ lệ các mục có liên quan trong k mục đầu tiên trong danh sách đó so với tổng số mục có liên quan được trả về.

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

Độ tương phản với độ chính xác tại k.

Nhấp vào biểu tượng để xem ví dụ.

Giả sử một mô hình ngôn ngữ lớn được đưa ra truy vấn sau:

List the 10 funniest movies of all time in order.

Và mô hình ngôn ngữ lớn sẽ trả về danh sách xuất hiện trong 2 cột đầu tiên:

Vị trí	Phim	Có liên quan không?
1	The General	Có
2	Mean Girls	Có
3	Platoon	Không
4	Phù dâu	Có
5	This is Spinal Tap	Có
6	Airplane!	Có
7	Ngày chuột chũi	Có
8	Monty Python và Chén Thánh	Có
9	Oppenheimer	Không
10	Clueless	Có

8 bộ phim trong danh sách trước đó rất hài hước, nên chúng là "các mục có liên quan trong danh sách". Do đó, 8 sẽ là mẫu số trong tất cả các phép tính về độ thu hồi tại k. Còn tử số thì sao? Vậy là 3 trong số 4 mục đầu tiên có liên quan, nên độ chính xác ở 4 là:

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

7 trong số 8 bộ phim đầu tiên rất hài hước, vì vậy, hãy nhớ lại ở mức 8:

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

Đường cong ROC (đường cong đặc tính hoạt động của máy thu)

#fundamentals

#Chỉ số

Biểu đồ về tỷ lệ dương tính thực so với tỷ lệ dương tính giả cho các ngưỡng phân loại khác nhau trong phân loại nhị phân.

Hình dạng của đường cong ROC cho thấy khả năng của mô hình phân loại nhị phân trong việc tách các lớp dương tính khỏi các lớp âm tính. Ví dụ: giả sử một mô hình phân loại nhị phân tách biệt hoàn toàn tất cả các lớp âm tính với tất cả các lớp dương tính:

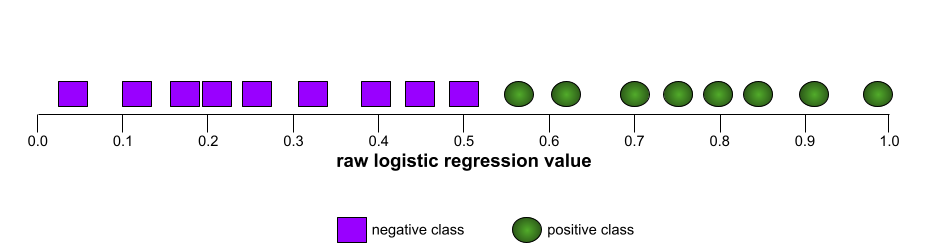
Đường cong ROC cho mô hình trước đó có dạng như sau:

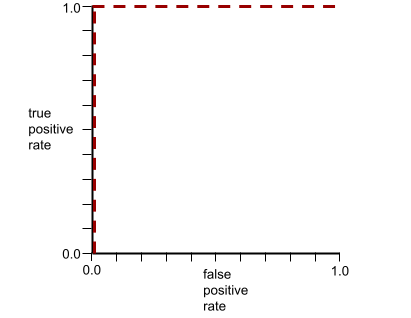
Ngược lại, hình minh hoạ sau đây vẽ đồ thị các giá trị hồi quy logistic thô cho một mô hình kém không thể tách các lớp âm tính khỏi các lớp dương tính:

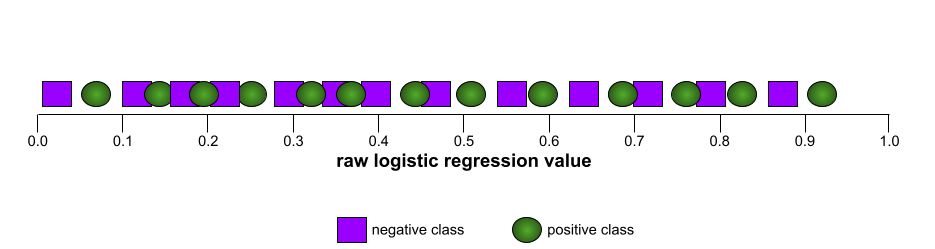
Đường cong ROC cho mô hình này có dạng như sau:

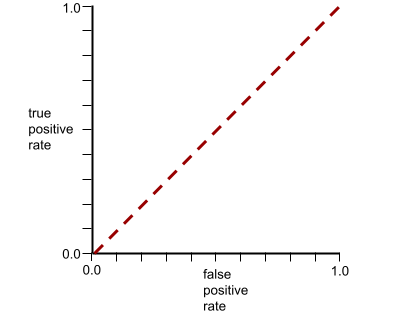
Trong khi đó, trong thế giới thực, hầu hết các mô hình phân loại nhị phân đều tách biệt các lớp dương và âm ở một mức độ nào đó, nhưng thường không hoàn hảo. Vì vậy, đường cong ROC điển hình sẽ nằm ở đâu đó giữa hai cực đoan này:

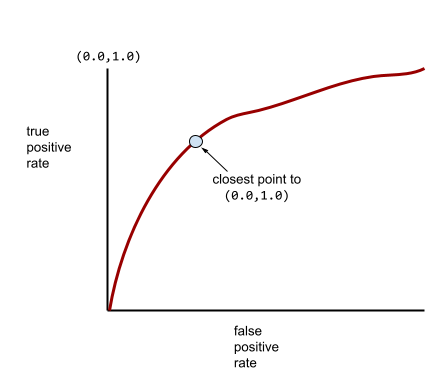
Điểm trên đường cong ROC gần với (0.0,1.0) nhất về mặt lý thuyết sẽ xác định ngưỡng phân loại lý tưởng. Tuy nhiên, một số vấn đề khác ngoài đời thực ảnh hưởng đến việc lựa chọn ngưỡng phân loại lý tưởng. Ví dụ: có lẽ kết quả âm tính giả gây ra nhiều phiền toái hơn kết quả dương tính giả.

Một chỉ số bằng số có tên là AUC tóm tắt đường cong ROC thành một giá trị dấu phẩy động duy nhất.

Sai số trung bình bình phương (RMSE)

#fundamentals

#Chỉ số

Căn bậc hai của Sai số bình phương trung bình.

ROUGE (Recall-Oriented Understudy for Gisting Evaluation)

#Chỉ số

Một nhóm các chỉ số đánh giá mô hình tóm tắt tự động và dịch máy. Các chỉ số ROUGE xác định mức độ mà văn bản tham chiếu trùng lặp với văn bản do mô hình ML tạo. Mỗi thành phần trong họ ROUGE đo lường mức độ trùng lặp theo một cách khác nhau. Điểm ROUGE càng cao thì văn bản tham chiếu và văn bản được tạo càng giống nhau hơn so với điểm ROUGE thấp hơn.

Mỗi thành viên trong họ ROUGE thường tạo ra các chỉ số sau:

• Chính xác
• Nhớ lại
• F₁

Lưu ý: ROUGE sử dụng độ chính xác và khả năng thu hồi hơi khác so với độ chính xác và khả năng thu hồi truyền thống.

Để biết thông tin chi tiết và ví dụ, hãy xem:

• ROUGE-L
• ROUGE-N
• ROUGE-S

Lưu ý: BLEU và BLEURT tối ưu hoá cho độ chính xác trong khi ROUGE tối ưu hoá cho khả năng thu hồi. Do đó, BLEU và BLEURT là những chỉ số phù hợp hơn để đánh giá bản dịch của máy (vì trọng tâm là độ chính xác) trong khi ROUGE là chỉ số phù hợp hơn cho việc tóm tắt (vì trọng tâm là khả năng thu hồi).

ROUGE-L

#Chỉ số

Một thành viên của họ ROUGE tập trung vào độ dài của chuỗi con chung dài nhất trong văn bản tham chiếu và văn bản được tạo. Các công thức sau đây tính toán độ thu hồi và độ chính xác cho ROUGE-L:

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

Sau đó, bạn có thể sử dụng F₁ để tổng hợp độ thu hồi ROUGE-L và độ chính xác ROUGE-L thành một chỉ số duy nhất:

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

Nhấp vào biểu tượng để xem ví dụ về cách tính ROUGE-L.

Hãy xem xét văn bản tham khảo và văn bản được tạo sau đây.

Danh mục	Ai sản xuất?	Văn bản
Văn bản tham khảo	Biên dịch viên	Tôi muốn hiểu biết nhiều điều.
Văn bản được tạo	Mô hình học máy	Tôi muốn học hỏi nhiều điều.

Do đó:

• Dãy con chung dài nhất là 5 (I want to of things)
• Số từ trong văn bản tham chiếu là 9.
• Số từ trong văn bản được tạo là 7.

Do đó:

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

ROUGE-L bỏ qua mọi dấu xuống dòng trong văn bản tham chiếu và văn bản được tạo, vì vậy, chuỗi con chung dài nhất có thể trải dài trên nhiều câu. Khi văn bản tham chiếu và văn bản được tạo có nhiều câu, thì một biến thể của ROUGE-L có tên là ROUGE-Lsum thường là chỉ số phù hợp hơn. ROUGE-Lsum xác định chuỗi con chung dài nhất cho mỗi câu trong một đoạn văn, sau đó tính giá trị trung bình của những chuỗi con chung dài nhất đó.

Nhấp vào biểu tượng để xem ví dụ về cách tính ROUGE-Lsum.

Hãy xem xét văn bản tham khảo và văn bản được tạo sau đây.

Danh mục	Ai sản xuất?	Văn bản
Văn bản tham khảo	Biên dịch viên	Bề mặt của Sao Hoả khô cằn. Gần như toàn bộ nước đều nằm sâu dưới lòng đất.
Văn bản được tạo	Mô hình học máy	Sao Hoả có bề mặt khô cằn. Tuy nhiên, phần lớn nước nằm dưới lòng đất.

Vì thế:

	Câu đầu tiên	Câu thứ hai
Chuỗi con chung dài nhất	2 (Sao Hoả khô)	3 (nước ở dưới lòng đất)
Độ dài câu của văn bản tham chiếu	6	7
Độ dài câu của văn bản được tạo	5	8

Do đó:

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#Chỉ số

Một nhóm chỉ số trong họ ROUGE so sánh các N-gram dùng chung có kích thước nhất định trong văn bản tham chiếu và văn bản được tạo. Ví dụ:

• ROUGE-1 đo lường số lượng mã thông báo được chia sẻ trong văn bản tham chiếu và văn bản được tạo.
• ROUGE-2 đo lường số lượng bigram (2-gram) được chia sẻ trong văn bản tham chiếu và văn bản được tạo.
• ROUGE-3 đo số lượng trigram (3-gram) dùng chung trong văn bản tham chiếu và văn bản được tạo.

Bạn có thể sử dụng các công thức sau để tính độ thu hồi ROUGE-N và độ chính xác ROUGE-N cho bất kỳ thành viên nào trong họ ROUGE-N:

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

Sau đó, bạn có thể sử dụng F₁ để tổng hợp độ thu hồi ROUGE-N và độ chính xác ROUGE-N thành một chỉ số duy nhất:

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

Nhấp vào biểu tượng để xem ví dụ.

Giả sử bạn quyết định sử dụng ROUGE-2 để đo lường mức độ hiệu quả của bản dịch do một mô hình học máy tạo ra so với bản dịch của một người dịch.

Danh mục	Ai sản xuất?	Văn bản	Bigram
Văn bản tham khảo	Biên dịch viên	Tôi muốn hiểu biết nhiều điều.	Tôi muốn, muốn hiểu, hiểu rõ, rõ nhiều, nhiều thứ, thứ
Văn bản được tạo	Mô hình học máy	Tôi muốn học hỏi nhiều điều.	Tôi muốn, muốn học, học thật nhiều, thật nhiều điều

Do đó:

• Số lượng 2-gram trùng khớp là 3 (I want, want to và of things).
• Số lượng 2-gram trong văn bản tham chiếu là 8.
• Số lượng 2-gram trong văn bản được tạo là 6.

Do đó:

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#Chỉ số

Một dạng ROUGE-N linh hoạt cho phép so khớp skip-gram. Tức là ROUGE-N chỉ tính N-gram khớp chính xác, nhưng ROUGE-S cũng tính N-gram được phân tách bằng một hoặc nhiều từ. Ví dụ: hãy cân nhắc những điều sau đây:

• văn bản tham chiếu: Mây trắng
• văn bản được tạo: Những đám mây trắng bồng bềnh

Khi tính toán ROUGE-N, 2-gram White clouds (Mây trắng) không khớp với White billowing clouds (Mây trắng cuồn cuộn). Tuy nhiên, khi tính toán ROUGE-S, White clouds (Mây trắng) sẽ khớp với White billowing clouds (Mây trắng cuồn cuộn).

R bình phương

#Chỉ số

Một chỉ số hồi quy cho biết mức độ biến thiên của một nhãn là do một tính năng riêng lẻ hoặc do một tập hợp tính năng. R bình phương là một giá trị nằm trong khoảng từ 0 đến 1, bạn có thể diễn giải như sau:

• R bình phương bằng 0 có nghĩa là không có biến thể nào của nhãn là do bộ tính năng.
• R bình phương bằng 1 có nghĩa là tất cả các biến thể của nhãn đều là do tập hợp đối tượng.
• R bình phương từ 0 đến 1 cho biết mức độ mà sự biến thiên của nhãn có thể được dự đoán từ một đặc điểm cụ thể hoặc bộ đặc điểm. Ví dụ: R bình phương bằng 0,10 có nghĩa là 10% phương sai trong nhãn là do tập hợp đối tượng, R bình phương bằng 0,20 có nghĩa là 20% là do tập hợp đối tượng, v.v.

R bình phương là bình phương của hệ số tương quan Pearson giữa các giá trị mà một mô hình dự đoán và sự thật cơ bản.

S

tính điểm

#Chỉ số

Phần của hệ thống đề xuất cung cấp giá trị hoặc thứ hạng cho từng mục do giai đoạn tạo đề xuất tạo ra.

đo lường mức độ tương đồng

#clustering

#Chỉ số

Trong thuật toán phân cụm, chỉ số được dùng để xác định mức độ giống nhau (mức độ tương tự) giữa hai ví dụ bất kỳ.

độ thưa

#Chỉ số

Số lượng phần tử được đặt thành 0 (hoặc rỗng) trong một vectơ hoặc ma trận chia cho tổng số mục trong vectơ hoặc ma trận đó. Ví dụ: hãy xem xét một ma trận gồm 100 phần tử, trong đó 98 ô chứa số 0. Cách tính độ thưa thớt như sau:

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

Độ thưa thớt của đối tượng đề cập đến độ thưa thớt của một vectơ đối tượng; độ thưa thớt của mô hình đề cập đến độ thưa thớt của trọng số mô hình.

tổn thất khớp nối bình phương

#Chỉ số

Bình phương của tổn thất khớp nối. Bình phương tổn thất khớp nối phạt các giá trị ngoại lệ nghiêm khắc hơn so với tổn thất khớp nối thông thường.

tổn thất bình phương

#fundamentals

#Chỉ số

Từ đồng nghĩa với tổn thất _L2.

T

mất mát trong kiểm thử

#fundamentals

#Chỉ số

Một chỉ số biểu thị mức tổn thất của một mô hình so với tập dữ liệu kiểm thử. Khi tạo một mô hình, bạn thường cố gắng giảm thiểu tổn thất trong quá trình kiểm thử. Đó là vì tổn thất thấp trong quá trình kiểm thử là một tín hiệu chất lượng mạnh hơn so với tổn thất thấp trong quá trình huấn luyện hoặc tổn thất thấp trong quá trình xác thực.

Đôi khi, khoảng cách lớn giữa tổn thất trong quá trình kiểm thử và tổn thất trong quá trình huấn luyện hoặc tổn thất trong quá trình xác thực cho thấy bạn cần tăng tỷ lệ điều chỉnh.

độ chính xác top-k

#Chỉ số

Tỷ lệ phần trăm số lần "nhãn mục tiêu" xuất hiện trong k vị trí đầu tiên của danh sách được tạo. Các danh sách này có thể là đề xuất được cá nhân hoá hoặc danh sách các mục được sắp xếp theo softmax.

Độ chính xác của k mục hàng đầu còn được gọi là độ chính xác tại k.

Lưu ý: Nhãn mục tiêu có thể là bất kỳ lớp nào (không nhất thiết phải là lớp sự thật cơ bản), vì vậy, độ chính xác k hàng đầu không phải lúc nào cũng tương đương với độ chính xác truyền thống.

Nhấp vào biểu tượng để xem ví dụ.

Hãy cân nhắc một hệ thống học máy sử dụng hàm softmax để xác định xác suất của cây dựa trên hình ảnh lá cây. Bảng sau đây cho thấy các danh sách đầu ra được tạo từ 5 hình ảnh cây đầu vào. Mỗi hàng chứa một nhãn mục tiêu và 5 cây có khả năng cao nhất. Ví dụ: khi nhãn mục tiêu là maple, mô hình học máy đã xác định elm là cây có khả năng cao nhất, oak là cây có khả năng cao thứ hai, v.v.

Nhãn mục tiêu	1	2	3	4	5
cây phong	elm	gỗ sồi	maple	cây dẻ gai	cây dương
cây sơn thù du	gỗ sồi	dogwood	cây dương	hickory	cây phong
gỗ sồi	oak	gỗ đoan	châu chấu	cây dương tía	linden
linden	cây phong	paw-paw	gỗ sồi	gỗ đoan	cây dương
gỗ sồi	châu chấu	linden	oak	cây phong	paw-paw

Nhãn mục tiêu chỉ xuất hiện ở vị trí đầu tiên một lần, vì vậy, độ chính xác top-1 là:

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

Nhãn mục tiêu xuất hiện ở một trong 3 vị trí hàng đầu 4 lần, vì vậy, độ chính xác của 3 vị trí hàng đầu là:

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

nội dung độc hại

#Chỉ số

Mức độ nội dung mang tính lạm dụng, đe doạ hoặc phản cảm. Nhiều mô hình học máy có thể xác định và đo lường mức độ độc hại. Hầu hết các mô hình này đều xác định nội dung độc hại dựa trên nhiều thông số, chẳng hạn như mức độ ngôn từ xúc phạm và mức độ ngôn từ đe doạ.

tổn thất trong quá trình huấn luyện

#fundamentals

#Chỉ số

Một chỉ số biểu thị mức tổn thất của mô hình trong một lần lặp lại huấn luyện cụ thể. Ví dụ: giả sử hàm tổn thất là Sai số bình phương trung bình. Có thể tổn thất huấn luyện (Lỗi bình phương trung bình) cho lần lặp thứ 10 là 2,2 và tổn thất huấn luyện cho lần lặp thứ 100 là 1,9.

Đường cong tổn thất vẽ tổn thất trong quá trình huấn luyện so với số lần lặp lại. Đường cong tổn thất cung cấp các gợi ý sau về quá trình huấn luyện:

• Độ dốc giảm cho thấy mô hình đang cải thiện.
• Đường dốc lên cho thấy mô hình đang trở nên kém hiệu quả hơn.
• Độ dốc bằng phẳng cho thấy mô hình đã đạt đến sự hội tụ.

Ví dụ: đường cong tổn thất (khá lý tưởng) sau đây cho thấy:

• Đường dốc xuống dốc trong các lần lặp lại ban đầu, cho thấy mô hình được cải thiện nhanh chóng.
• Độ dốc giảm dần (nhưng vẫn đi xuống) cho đến gần cuối quá trình huấn luyện, điều này ngụ ý rằng mô hình tiếp tục cải thiện với tốc độ chậm hơn so với các lần lặp lại ban đầu.
• Đường dốc bằng phẳng về cuối quá trình huấn luyện, cho thấy sự hội tụ.

Mặc dù tổn thất khi huấn luyện là rất quan trọng, nhưng bạn cũng nên xem khả năng khái quát hoá.

âm tính thật (TN)

#fundamentals

#Chỉ số

Ví dụ trong đó mô hình dự đoán chính xác lớp âm. Ví dụ: mô hình suy luận rằng một thư email cụ thể không phải là thư rác và thư email đó thực sự không phải là thư rác.

dương tính thật (TP)

#fundamentals

#Chỉ số

Ví dụ trong đó mô hình dự đoán chính xác lớp dương tính. Ví dụ: mô hình suy luận rằng một thư email cụ thể là thư rác và thư email đó thực sự là thư rác.

tỷ lệ dương tính thật (TPR)

#fundamentals

#Chỉ số

Từ đồng nghĩa với mức độ ghi nhớ. Đó là:

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

Tỷ lệ dương tính thật là trục y trong đường cong ROC.

V

mất mát xác thực

#fundamentals

#Chỉ số

Một chỉ số biểu thị mất mát của mô hình trên tập hợp xác thực trong một lần lặp lại cụ thể của quá trình huấn luyện.

Xem thêm đường cong khái quát hoá.

mức độ quan trọng của biến

#df

#Chỉ số

Một tập hợp các điểm số cho biết tầm quan trọng tương đối của từng đặc điểm đối với mô hình.

Ví dụ: hãy xem xét một cây quyết định ước tính giá nhà. Giả sử cây quyết định này sử dụng 3 đặc điểm: kích thước, độ tuổi và kiểu dáng. Nếu một tập hợp các mức độ quan trọng của biến cho 3 đặc điểm được tính là {size=5.8, age=2.5, style=4.7}, thì kích thước quan trọng hơn đối với cây quyết định so với độ tuổi hoặc kiểu dáng.

Có nhiều chỉ số về tầm quan trọng của biến, có thể cung cấp thông tin cho các chuyên gia về học máy về nhiều khía cạnh của mô hình.

W

Tổn thất Wasserstein

#Chỉ số

Một trong những hàm tổn thất thường được dùng trong mạng đối nghịch sinh, dựa trên khoảng cách của hàm di chuyển trên mặt đất giữa phân phối dữ liệu được tạo và dữ liệu thực.