Trampas de análisis

"Todos los modelos son incorrectos, pero algunos son útiles". — George Box, 1978

Si bien son potentes, las técnicas estadísticas tienen sus limitaciones. Comprender estas limitaciones puede ayudar a un investigador a evitar errores y afirmaciones imprecisas, como la afirmación de BF Skinner de que Shakespeare no usó la aliteración más de lo que predeciría la aleatoriedad. (el estudio de Skinner no tenía suficiente potencia.¹).

Incertidumbre y barras de error

Es importante especificar la incertidumbre en tu análisis. Es igual de importante cuantificar la incertidumbre en los análisis de otras personas. Es posible que los datos que parecen trazar una tendencia en un gráfico, pero que tienen barras de error superpuestas, no indiquen ningún patrón. La incertidumbre también puede ser demasiado alta para sacar conclusiones útiles de un estudio o una prueba estadística en particular. Si un estudio de investigación requiere precisión a nivel del lote, un conjunto de datos geoespaciales con una incertidumbre de +/- 500 m tiene demasiada incertidumbre para poder usarse.

Como alternativa, los niveles de incertidumbre pueden ser útiles durante los procesos de toma de decisiones. Los datos que respaldan un tratamiento de agua en particular con un 20% de incertidumbre en los resultados pueden generar una recomendación para implementar ese tratamiento de agua con un monitoreo continuo del programa para abordar esa incertidumbre.

Las redes neuronales Bayesianas pueden cuantificar la incertidumbre prediciendo distribuciones de valores en lugar de valores únicos.

Irrelevancia

Como se mencionó en la introducción, siempre hay al menos una pequeña brecha entre los datos y la realidad. El profesional de AA astuto debe establecer si el conjunto de datos es relevante para la pregunta que se hace.

Huff describe un estudio temprano de opinión pública que descubrió que las respuestas de los estadounidenses blancos a la pregunta de qué tan fácil era para los estadounidenses negros ganarse la vida se relacionaban de forma directa e inversa con su nivel de simpatía hacia los estadounidenses negros. A medida que aumentaba el animosidad racial, las respuestas sobre las oportunidades económicas esperadas se volvían cada vez más optimistas. Esto podría haberse malinterpretado como un signo de progreso. Sin embargo, el estudio no pudo mostrar nada sobre las oportunidades económicas reales disponibles para los estadounidenses negros en ese momento y no era adecuado para sacar conclusiones sobre la realidad del mercado laboral, solo las opiniones de las personas que respondieron la encuesta. Los datos recopilados, de hecho, eran irrelevantes para el estado del mercado laboral.²

Podrías entrenar un modelo con datos de encuestas como el que se describió anteriormente, en el que el resultado mide el optimismo en lugar de la oportunidad. Sin embargo, como las oportunidades predicadas son irrelevantes para las oportunidades reales, si afirmaras que el modelo predice oportunidades reales, estarías tergiversando lo que predice.

Confusión

Una variable de confusión, confusión o cofactor es una variable que no se está estudiando y que influye en las variables que sí se están estudiando y puede distorsionar los resultados. Por ejemplo, considera un modelo de AA que predice las tasas de mortalidad de un país de entrada según los atributos de la política de salud pública. Supongamos que la mediana de edad no es una función. Supongamos además que algunos países tienen una población más antigua que otros. Si se ignora la variable de confusión de la edad media, este modelo podría predecir tasas de mortalidad defectuosas.

En Estados Unidos, el origen étnico suele estar fuertemente correlacionado con la clase socioeconómica, aunque solo el origen étnico, y no la clase, se registra con los datos de mortalidad. Los factores de confusión relacionados con la clase, como el acceso a la atención médica, la nutrición, el trabajo peligroso y la vivienda segura, pueden tener una influencia más fuerte en las tasas de mortalidad que el origen étnico, pero se descuidan porque no se incluyen en los conjuntos de datos.³ Identificar y controlar estos factores de confusión es fundamental para crear modelos útiles y sacar conclusiones significativas y precisas.

Si un modelo se entrena con datos de mortalidad existentes, que incluyen el origen étnico, pero no la clase, es posible que prediga la mortalidad en función del origen étnico, incluso si la clase es un predictor más sólido de la mortalidad. Esto podría generar suposiciones imprecisas sobre la causalidad y predicciones imprecisas sobre la mortalidad de los pacientes. Los profesionales del AA deberían preguntar si existen factores de confusión en sus datos, así como qué variables significativas podrían faltar en su conjunto de datos.

En 1985, el Estudio de Salud de las Enfermeras, un estudio de cohorte observacional de la Escuela de Medicina de Harvard y la Escuela de Salud Pública de Harvard, descubrió que las personas de la cohorte que tomaban terapia de reemplazo de estrógeno tenían una menor incidencia de ataques cardíacos en comparación con las personas de la cohorte que nunca tomaron estrógeno. Como resultado, los médicos recetaron estrógeno a sus pacientes menopáusicas y posmenopáusicas durante décadas, hasta que un estudio clínico en 2002 identificó los riesgos para la salud que generaba la terapia de estrógeno a largo plazo. Se detuvo la práctica de recetar estrógeno a mujeres postmenopáusicas, pero no antes de causar unas decenas de miles de muertes prematuras.

Varios factores de confusión podrían haber causado la asociación. Los epidemiólogos descubrieron que las mujeres que toman terapia de reemplazo hormonal, en comparación con las que no lo hacen, suelen ser más delgadas, más educadas, más ricas, más conscientes de su salud y más propensas a hacer ejercicio. En diferentes estudios, se descubrió que la educación y la riqueza reducen el riesgo de enfermedades cardíacas. Esos efectos habrían confundido la aparente correlación entre la terapia con estrógenos y los ataques cardíacos.⁴

Porcentajes con números negativos

Evita usar porcentajes cuando haya números negativos,⁵ ya que se pueden ocultar todo tipo de ganancias y pérdidas significativas. Supongamos, para simplificar las matemáticas, que la industria de restaurantes tiene 2 millones de empleos. Si la industria pierde 1 millón de esos puestos a fines de marzo de 2020, no experimenta ningún cambio neto durante diez meses y recupera 900,000 puestos a principios de febrero de 2021, una comparación interanual a principios de marzo de 2021 sugeriría solo una pérdida del 5% de los puestos de trabajo en restaurantes. Si no hubiera otros cambios, una comparación interanual a fines de abril de 2021 sugeriría un aumento del 90% en los empleos de restaurantes, lo que es un panorama muy diferente de la realidad.

Se prefieren los números reales, normalizados según corresponda. Consulta Cómo trabajar con datos numéricos para obtener más información.

Falacia post hoc y correlaciones inutilizables

La falacia post hoc es la suposición de que, como el evento B siguió al evento A, el evento A causó el evento B. En términos más simples, supone una relación de causa y efecto donde no existe una. De forma más simple: las correlaciones no prueban la causalidad.

Además de una relación clara de causa y efecto, las correlaciones también pueden provenir de lo siguiente:

• La casualidad pura (consulta Correlaciones espurias de Tyler Vigen para ver ejemplos, incluida una fuerte correlación entre el porcentaje de divorcios en Maine y el consumo de margarina).
• Una relación real entre dos variables, aunque no está claro cuál es la variable causal y cuál es la afectada.
• Una tercera causa independiente que influye en ambas variables, aunque las variables correlacionadas no están relacionadas entre sí. Por ejemplo, la inflación global puede aumentar los precios de los yates y del apio.⁶

También es riesgoso extrapolar una correlación más allá de los datos existentes. Huff señala que una pequeña cantidad de lluvia mejorará los cultivos, pero una cantidad excesiva los dañará; la relación entre la lluvia y los resultados de los cultivos no es lineal.⁷ (Consulta las siguientes dos secciones para obtener más información sobre las relaciones no lineales). Jones señala que el mundo está lleno de eventos impredecibles, como la guerra y el hambre, que someten los pronósticos futuros de los datos de series temporales a una gran cantidad de incertidumbre.⁸

Además, incluso una correlación genuina basada en la causa y el efecto puede no ser útil para tomar decisiones. Como ejemplo, Huff menciona la correlación entre la capacidad de casarse y la educación universitaria en la década de 1950. Las mujeres que fueron a la universidad tenían menos probabilidades de casarse, pero podría haber sido el caso de que las mujeres que fueron a la universidad tenían menos inclinación a casarse en primer lugar. Si ese fuera el caso, una educación universitaria no cambiaría las probabilidades de casarse.⁹

Si un análisis detecta una correlación entre dos variables de un conjunto de datos, haz las siguientes preguntas:

• ¿Qué tipo de correlación es: causa y efecto, espuria, relación desconocida o causada por una tercera variable?
• ¿Qué tan riesgosa es la extrapolación de los datos? Cada predicción del modelo sobre los datos que no están en el conjunto de datos de entrenamiento es, en efecto, una interpolación o extrapolación de los datos.
• ¿Se puede usar la correlación para tomar decisiones útiles? Por ejemplo, el optimismo podría estar fuertemente correlacionado con el aumento de los salarios, pero el análisis de sentimiento de un gran corpus de datos de texto, como las publicaciones en redes sociales de los usuarios de un país en particular, no sería útil para predecir aumentos de salarios en ese país.

Cuando entrenan un modelo, quienes practican el AA suelen buscar atributos que tengan una correlación significativa con la etiqueta. Si no se comprende bien la relación entre los atributos y la etiqueta, esto podría generar los problemas que se describen en esta sección, incluidos los modelos basados en correlaciones falsas y los que suponen que las tendencias históricas continuarán en el futuro, cuando en realidad no es así.

El sesgo lineal

En “Pensamiento lineal en un mundo no lineal”, Bart de Langhe, Stefano Puntoni y Richard Larrick describen el sesgo lineal como la tendencia del cerebro humano a esperar y buscar relaciones lineales, aunque muchos fenómenos no son lineales. La relación entre las actitudes y el comportamiento humanos, por ejemplo, es una curva convexa y no una línea. En un artículo de 2007 del Journal of Consumer Policy citado por de Langhe et al., Jenny van Doorn et al. modelaron la relación entre la preocupación de los encuestados por el medio ambiente y las compras de productos orgánicos. Las personas con las preocupaciones más extremas sobre el medioambiente compraron más productos orgánicos, pero hubo muy poca diferencia entre todos los demás encuestados.

Gráfico de compras de productos orgánicos en comparación con la puntuación de preocupación ambiental simplificado y adaptado del artículo de van Doorn et al.

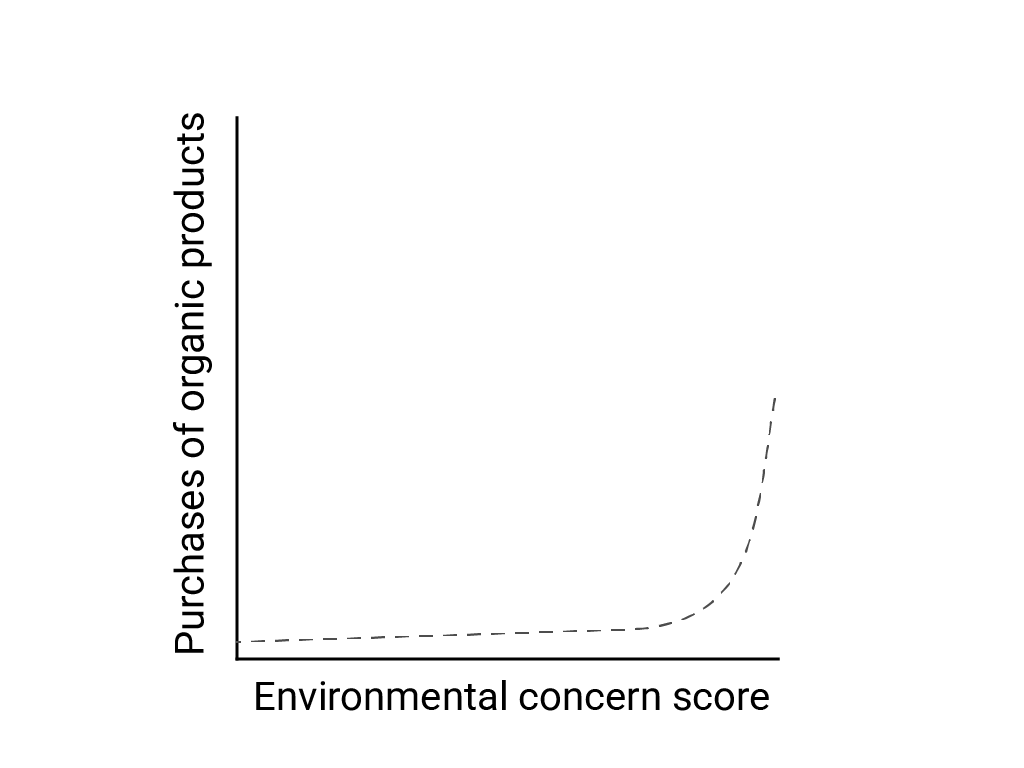
Cuando diseñes modelos o estudios, ten en cuenta la posibilidad de relaciones no lineales. Debido a que las pruebas A/B pueden pasar por alto las relaciones no lineales, considera también probar una tercera condición intermedia, C. También considera si el comportamiento inicial que parece ser lineal seguirá siendo lineal o si los datos futuros podrían mostrar un comportamiento más logarítmico o algún otro comportamiento no lineal.

Ejemplo de un ajuste lineal deficiente a datos logarítmicos

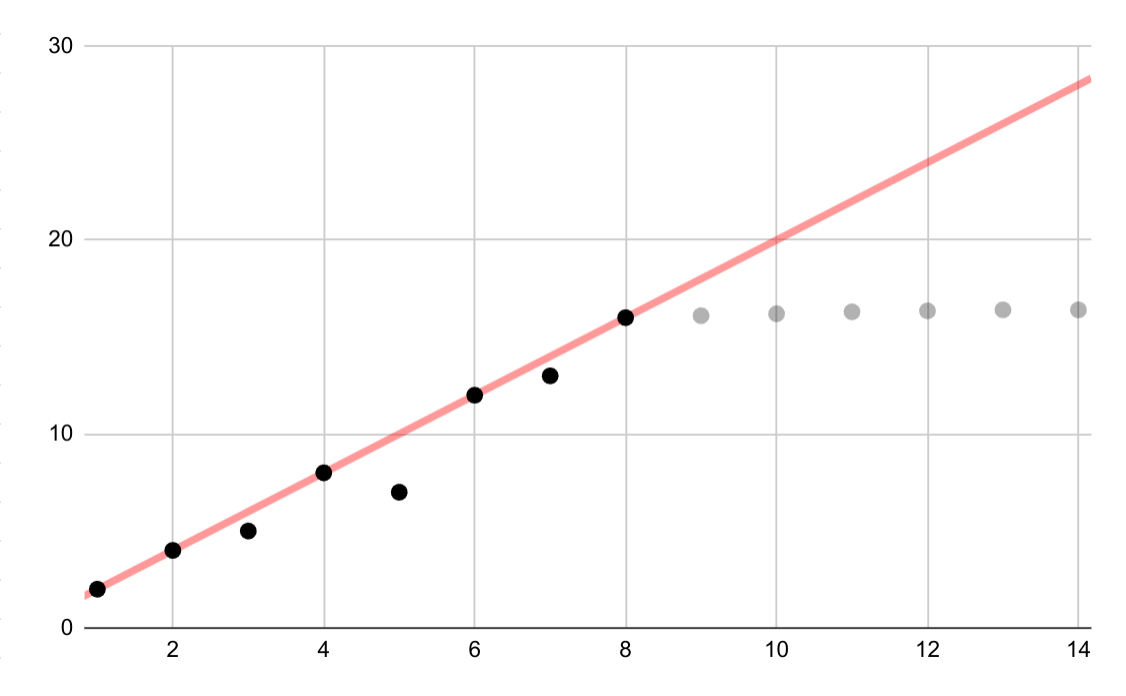
En este ejemplo hipotético, se muestra una aproximación lineal errónea para los datos logarítmicos. Si solo estuvieran disponibles los primeros datos, sería tentador y, a la vez, incorrecto, suponer una relación lineal continua entre las variables.

Interpolación lineal

Examina cualquier interpolación entre los datos, ya que la interpolación introduce puntos ficticios, y los intervalos entre las mediciones reales pueden contener fluctuaciones significativas. Como ejemplo, considera la siguiente visualización de cuatro datos conectados con interpolaciones lineales:

Ejemplo de interpolación lineal.

Luego, considera este ejemplo de fluctuaciones entre datos que se borran con una interpolación lineal:

Ejemplo de fluctuación significativa (un terremoto) entre los datos.

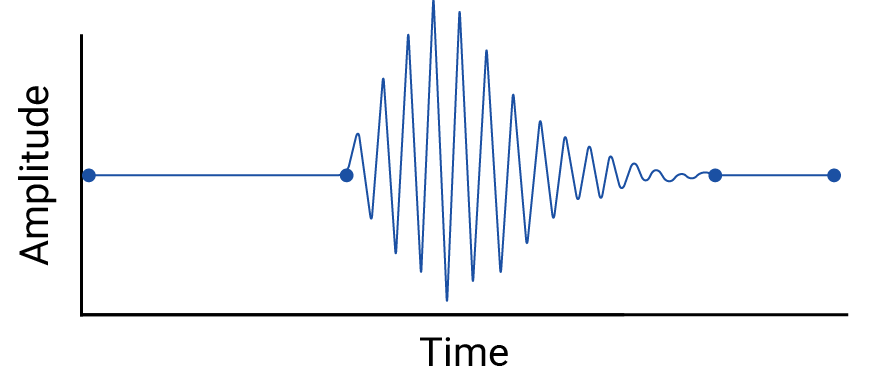
El ejemplo es artificial porque los sismógrafos recopilan datos continuos, por lo que no se perdería este terremoto. Sin embargo, es útil para ilustrar las suposiciones que hacen las interpolaciones y los fenómenos reales que los profesionales de los datos podrían pasar por alto.

Fenómeno de Runge

El fenómeno de Runge, también conocido como "oscilación polinómica", es un problema en el extremo opuesto del espectro de la interpolación lineal y el sesgo lineal. Cuando se ajusta una interpolación de polinomios a los datos, es posible usar un polinomio con un grado demasiado alto (el grado o orden es el exponente más alto en la ecuación polinómica). Esto produce oscilaciones extrañas en los bordes. Por ejemplo, aplicar una interpolación polinómica de grado 11, lo que significa que el término de orden más alto en la ecuación polinómica tiene \(x^{11}\), a datos aproximadamente lineales, genera predicciones notablemente malas al principio y al final del rango de datos:

Ejemplo del movimiento polinómico

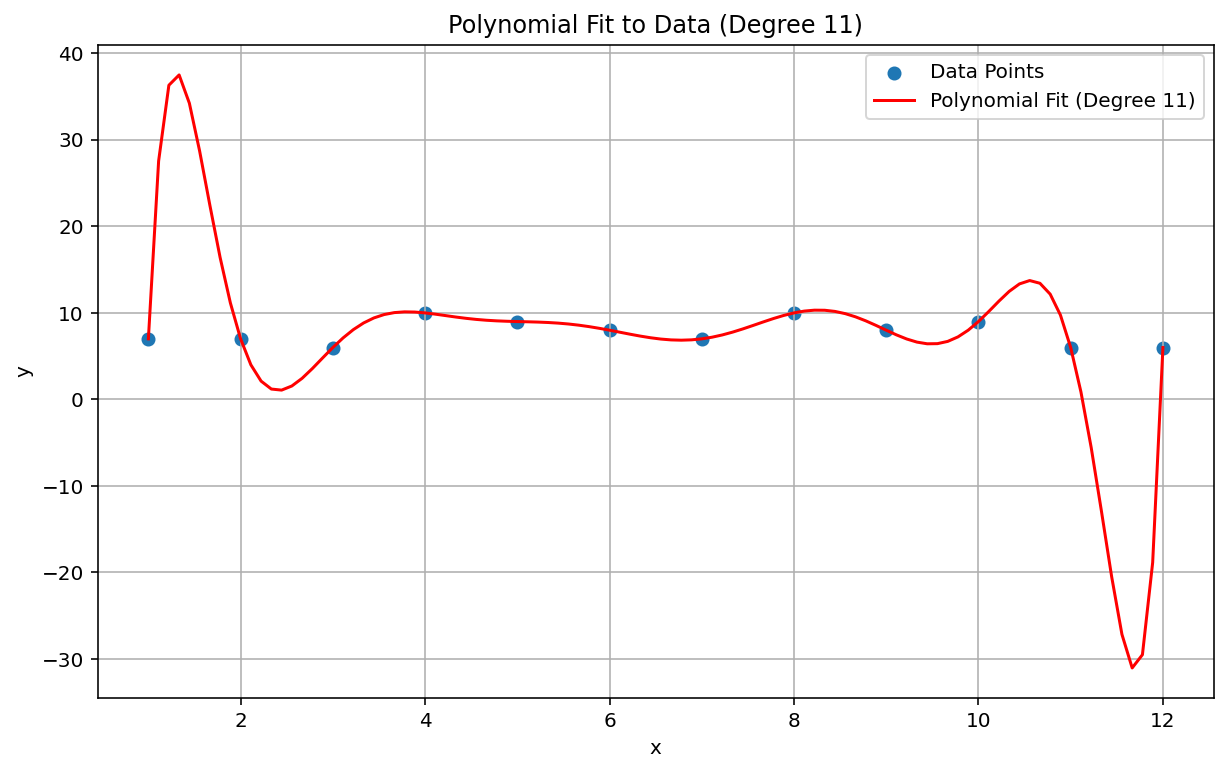
En el contexto del AA, un fenómeno análogo es el ajuste excesivo.

Errores estadísticos que no se detectan

A veces, una prueba estadística puede ser demasiado débil para detectar un efecto pequeño. La baja potencia en el análisis estadístico implica una baja probabilidad de identificar correctamente los eventos verdaderos y, por lo tanto, una alta probabilidad de falsos negativos. Katherine Button y otros escribieron en Nature: “Cuando los estudios en un campo determinado se diseñan con una potencia del 20%, significa que, si hay 100 efectos genuinos no nulos que se deben descubrir en ese campo, se espera que estos estudios descubran solo 20 de ellos”. A veces, aumentar el tamaño de la muestra puede ser útil, al igual que un diseño del estudio cuidadoso.

Una situación análoga en el AA es el problema de la clasificación y la elección de un umbral de clasificación. Elegir un umbral más alto genera menos falsos positivos y más falsos negativos, mientras que un umbral más bajo genera más falsos positivos y menos falsos negativos.

Además de los problemas con la potencia estadística, como la correlación está diseñada para detectar relaciones lineales, se pueden pasar por alto las correlaciones no lineales entre las variables. Del mismo modo, las variables pueden estar relacionadas entre sí, pero no estar correlacionadas estadísticamente. Las variables también pueden tener una correlación negativa, pero no estar relacionadas en absoluto, en lo que se conoce como paradoja de Berkson o falacia de Berkson. El ejemplo clásico de la falacia de Berkson es la correlación negativa espuria entre cualquier factor de riesgo y una enfermedad grave cuando se observa una población de pacientes hospitalizados (en comparación con la población general), que surge del proceso de selección (una condición lo suficientemente grave como para requerir hospitalización).

Considera si alguna de estas situaciones se aplica.

Modelos desactualizados y suposiciones no válidas

Incluso los modelos buenos pueden degradarse con el tiempo porque el comportamiento (y el mundo, en lo que a eso respecta) puede cambiar. Los primeros modelos predictivos de Netflix tuvieron que retirarse a medida que su base de clientes cambió de usuarios jóvenes y expertos en tecnología a la población general.¹⁰

Los modelos también pueden contener suposiciones silenciosas e inexactas que pueden permanecer ocultas hasta que se produce la falla catastrófica del modelo, como en la crisis del mercado de 2008. Los modelos de valor en riesgo (VaR) de la industria financiera afirmaban estimar con precisión la pérdida máxima de la cartera de cualquier operador, por ejemplo, una pérdida máxima de USD 100,000 esperada el 99% de las veces. Sin embargo, en las condiciones anormales del accidente, una cartera con una pérdida máxima esperada de USD 100,000 a veces perdía USD 1,000,000 o más.

Los modelos de VaR se basaban en suposiciones erróneas, incluidas las siguientes:

• Los cambios en el mercado anteriores son predictivos de los cambios futuros.
• Los rendimientos previstos se basaban en una distribución normal (con colas finas y, por lo tanto, predecible).

Gráfico de la distribución de von Mises, que tiene colas delgadas en K alto y colas gruesas en K bajo.

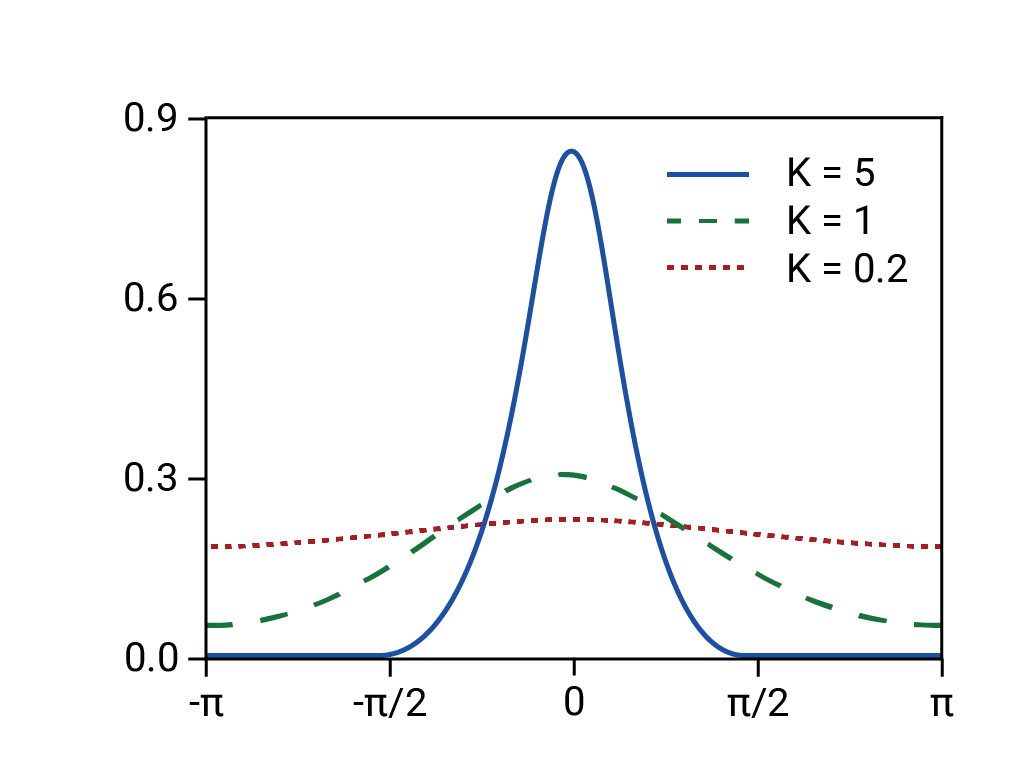
De hecho, la distribución subyacente era de cola larga, "salvaje" o fractal, lo que significa que había un riesgo mucho mayor de eventos extremos, supuestamente raros y de cola larga de lo que predeciría una distribución normal. La naturaleza de colas gruesas de la distribución real era bien conocida, pero no se tomaron medidas al respecto. Lo que se sabía menos era lo complejos y estrechamente vinculados que eran varios fenómenos, incluidos los intercambios basados en computadoras con liquidaciones automáticas.¹¹

Problemas de agregación

Los datos agregados, que incluyen la mayoría de los datos demográficos y epidemiológicos, están sujetos a un conjunto particular de trampas. La paradoja de Simpson, o paradoja de agregación, ocurre en los datos agregados, en los que las tendencias aparentes desaparecen o se revierten cuando los datos se agregan en un nivel diferente, debido a factores de confusión y relaciones causales malinterpretadas.

La falacia ecológica implica extrapolar erróneamente la información sobre una población en un nivel de agregación a otro nivel de agregación, en el que la afirmación puede no ser válida. Es posible que una enfermedad que afecta al 40% de los trabajadores agrícolas de una provincia no esté presente con la misma prevalencia en la población general. También es muy probable que haya granjas o pueblos agrícolas aislados en esa provincia que no experimenten una prevalencia tan alta de esa enfermedad. Suponer una prevalencia del 40% en esos lugares menos afectados también sería falaz.

El problema de las unidades de área modificable (MAUP) es un problema conocido en los datos geoespaciales que Stan Openshaw describió en 1984 en CATMOG 38. Según las formas y los tamaños de las áreas que se usan para agregar datos, un profesional de datos geoespaciales puede establecer casi cualquier correlación entre las variables de los datos. Dibujar distritos electorales que favorezcan a un partido o a otro es un ejemplo de MAUP.

Todas estas situaciones implican una extrapolación inadecuada de un nivel de agregación a otro. Los diferentes niveles de análisis pueden requerir diferentes agregaciones o incluso conjuntos de datos completamente diferentes.¹²

Ten en cuenta que los datos censales, demográficos y epidemiológicos suelen agruparse por zonas por motivos de privacidad y que estas zonas suelen ser arbitrarias, es decir, no se basan en límites significativos del mundo real. Cuando se trabaja con estos tipos de datos, los profesionales del AA deben verificar si el rendimiento y las predicciones del modelo cambian según el tamaño y la forma de las zonas seleccionadas o el nivel de agregación y, de ser así, si las predicciones del modelo se ven afectadas por uno de estos problemas de agregación.

Referencias

Button, Katharine et al. "Power failure: why small sample size undermines the reliability of neuroscience." Nature Reviews Neuroscience, vol. 14 (2013), 365–376. DOI: https://doi.org/10.1038/nrn3475

Cairo, Alberto. How Charts Lie: Getting Smarter about Visual Information. NY: W.W. Norton, 2019.

Davenport, Thomas H. "A Predictive Analytics Primer". En HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), págs. 81-86.

De Langhe, Bart, Stefano Puntoni y Richard Larrick. “Pensamiento lineal en un mundo no lineal”. En HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), pp. 131-154.

Ellenberg, Jordan. How Not to Be Wrong: The Power of Mathematical Thinking. Nueva York: Penguin, 2014.

Huff, Darrell. Cómo mentir con estadísticas. Nueva York: W.W. Norton, 1954.

Jones, Ben. Evitar errores de datos Hoboken, NJ: Wiley, 2020.

Openshaw, Stan. “The Modifiable Areal Unit Problem”, CATMOG 38 (Norwich, Inglaterra: Geo Books 1984) 37.

The Risks of Financial Modeling: VaR and the Economic Meltdown, 111º Congreso (2009) (testimonios de Nassim N. Taleb y Richard Bookstaber).

Ritter, David. "Cuándo actuar en función de una correlación y cuándo no hacerlo". En HBR Guide to Data Analytics Basics for Managers (Boston: HBR Press, 2018), pp. 103-109.

Tulchinsky, Theodore H. y Elena A. Varavikova. “Capítulo 3: Medir, supervisar y evaluar la salud de una población” en The New Public Health, 3ª ed. San Diego: Academic Press, 2014, pp. 91-147. DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.

Van Doorn, Jenny, Peter C. Verhoef, y Tammo H. A. Bijmolt. “La importancia de las relaciones no lineales entre la actitud y el comportamiento en la investigación sobre políticas”. Journal of Consumer Policy 30 (2007) 75–90. DOI: https://doi.org/10.1007/s10603-007-9028-3

Referencia de la imagen

Basado en la "Distribución de Von Mises". Rainald62, 2018. Origen

---

1. Ellenberg 125. ↩

2. Huff 77-79. Huff cita la Oficina de Investigación de la Opinión Pública de Princeton, pero es posible que esté pensando en el informe de abril de 1944 del National Opinion Research Center de la Universidad de Denver. ↩

3. Tulchinsky y Varavikova. ↩

4. Gary Taubes, Do We Really Know What Makes Us Healthy?" en The New York Times Magazine, 16 de septiembre de 2007. ↩

5. Ellenberg 78. ↩

6. Huff 91-92. ↩

7. Huff 93. ↩

8. Jones 157-167. ↩

9. Huff 95. ↩

10. Davenport 84. ↩

11. Consulta el testimonio ante el Congreso de Nassim N. Taleb y Richard Bookstaber en The Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) 11-67. ↩

12. Cairo 155, 162. ↩