Comment déboguer et atténuer les échecs d'optimisation ?
Résumé : Si le modèle rencontre des difficultés d'optimisation, il est important de les résoudre avant d'essayer d'autres solutions. Le diagnostic et la correction des échecs d'entraînement sont un domaine de recherche actif.
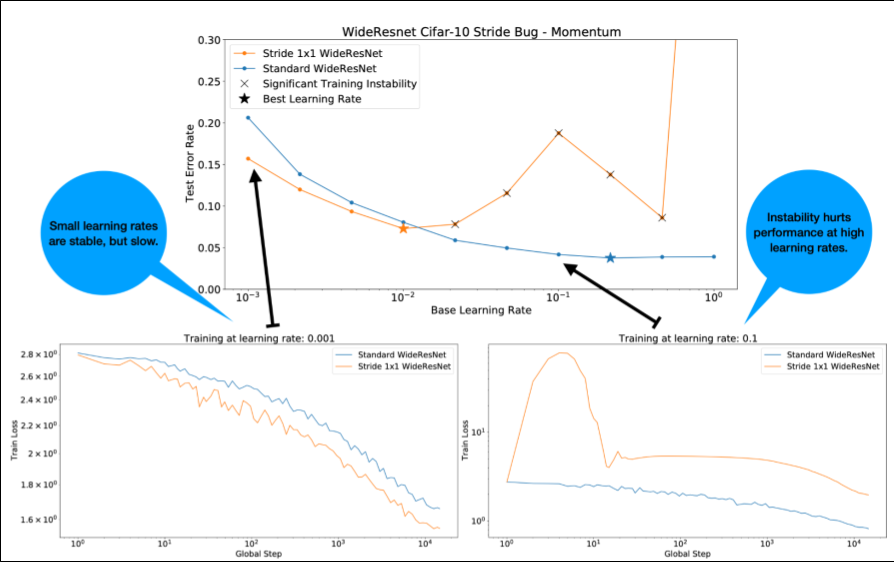
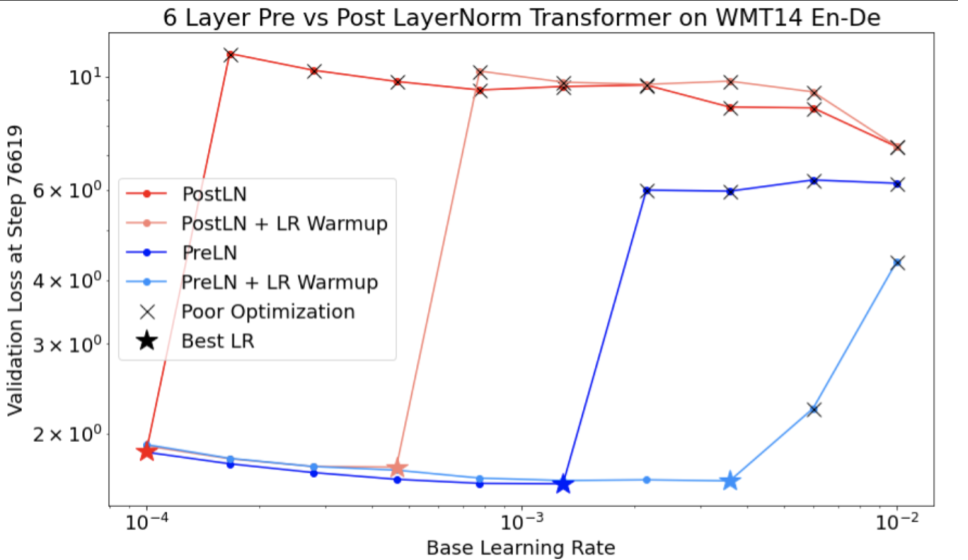
Notez les points suivants concernant la figure 4 :
- La modification des foulées ne dégrade pas les performances à des taux d'apprentissage faibles.
- En raison de l'instabilité, les taux d'apprentissage élevés ne permettent plus d'entraîner correctement les modèles.
- L'application de 1 000 étapes d'échauffement du taux d'apprentissage résout cette instance particulière d'instabilité, ce qui permet un entraînement stable avec un taux d'apprentissage maximal de 0,1.
Identifier les charges de travail instables
Toute charge de travail devient instable si le taux d'apprentissage est trop élevé. L'instabilité ne pose problème que lorsqu'elle vous oblige à utiliser un taux d'apprentissage trop faible. Il convient de distinguer au moins deux types d'instabilité de l'entraînement :
- Instabilité lors de l'initialisation ou au début de l'entraînement.
- Instabilité soudaine en cours d'entraînement.
Vous pouvez adopter une approche systématique pour identifier les problèmes de stabilité dans votre charge de travail en procédant comme suit :
- Effectuez un balayage du taux d'apprentissage et trouvez le meilleur taux d'apprentissage lr*.
- Tracez les courbes de perte d'entraînement pour les taux d'apprentissage juste au-dessus de lr*.
- Si les taux d'apprentissage > lr* présentent une instabilité de perte (la perte augmente et ne diminue pas pendant les périodes d'entraînement), la correction de l'instabilité améliore généralement l'entraînement.
Enregistrez la norme L2 du gradient de perte complet pendant l'entraînement, car les valeurs aberrantes peuvent entraîner une instabilité factice au milieu de l'entraînement. Cela peut vous aider à déterminer l'agressivité avec laquelle vous devez écrêter les gradients ou les mises à jour des poids.
REMARQUE : Certains modèles présentent une instabilité très précoce, suivie d'une reprise qui entraîne un entraînement lent, mais stable. Les plannings d'évaluation courants peuvent passer à côté de ces problèmes en n'évaluant pas les modèles assez souvent.
Pour vérifier cela, vous pouvez effectuer un entraînement abrégé d'environ 500 étapes à l'aide de lr = 2 * current best, mais évaluer chaque étape.
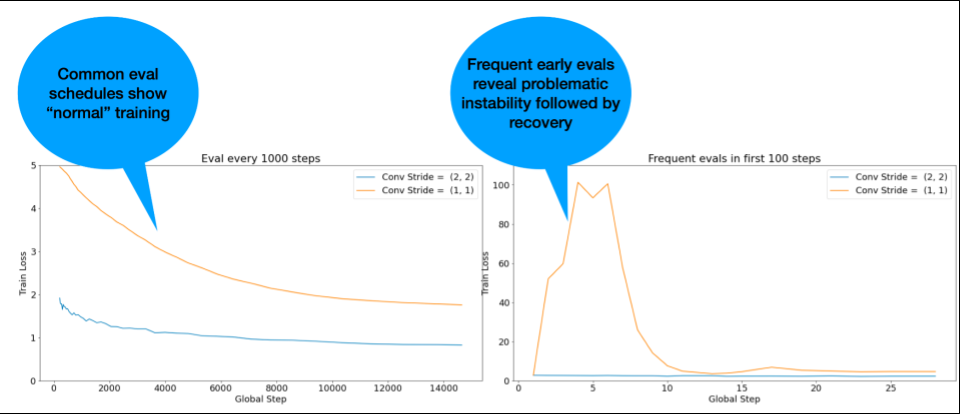
Solutions potentielles pour les problèmes d'instabilité courants
Voici quelques solutions possibles pour les problèmes d'instabilité courants :
- Appliquez l'échauffement du taux d'apprentissage. Cette option est idéale en cas d'instabilité précoce de l'entraînement.
- Appliquez le bornement de la norme du gradient. Cela est utile pour l'instabilité en début et en milieu d'entraînement, et peut corriger certaines mauvaises initialisations que l'échauffement ne peut pas résoudre.
- Essayez un autre optimiseur. Parfois, Adam peut gérer des instabilités que Momentum ne peut pas gérer. Il s'agit d'un domaine de recherche actif.
- Assurez-vous d'utiliser les bonnes pratiques et les meilleures initialisations pour l'architecture de votre modèle (des exemples suivront). Ajoutez des connexions résiduelles et une normalisation si le modèle n'en contient pas déjà.
- Normalisez comme dernière opération avant le résidu. Exemple :
x + Norm(f(x)). Notez queNorm(x + f(x))peut entraîner des problèmes. - Essayez d'initialiser les branches résiduelles à 0. (Voir ReZero is All You Need: Fast Convergence at Large Depth.)
- Diminuez le taux d'apprentissage. Il s'agit d'un dernier recours.
Échauffement du taux d'apprentissage
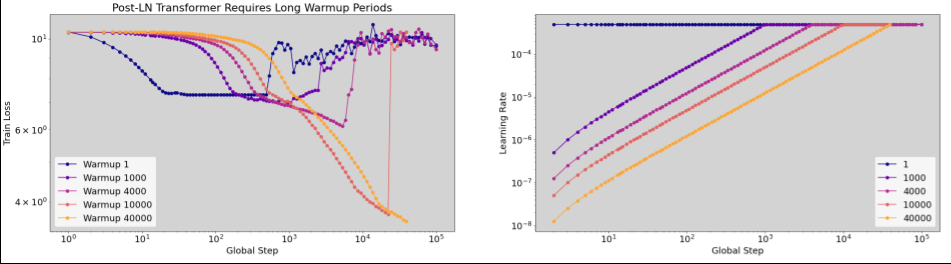
Quand appliquer l'échauffement du taux d'apprentissage ?
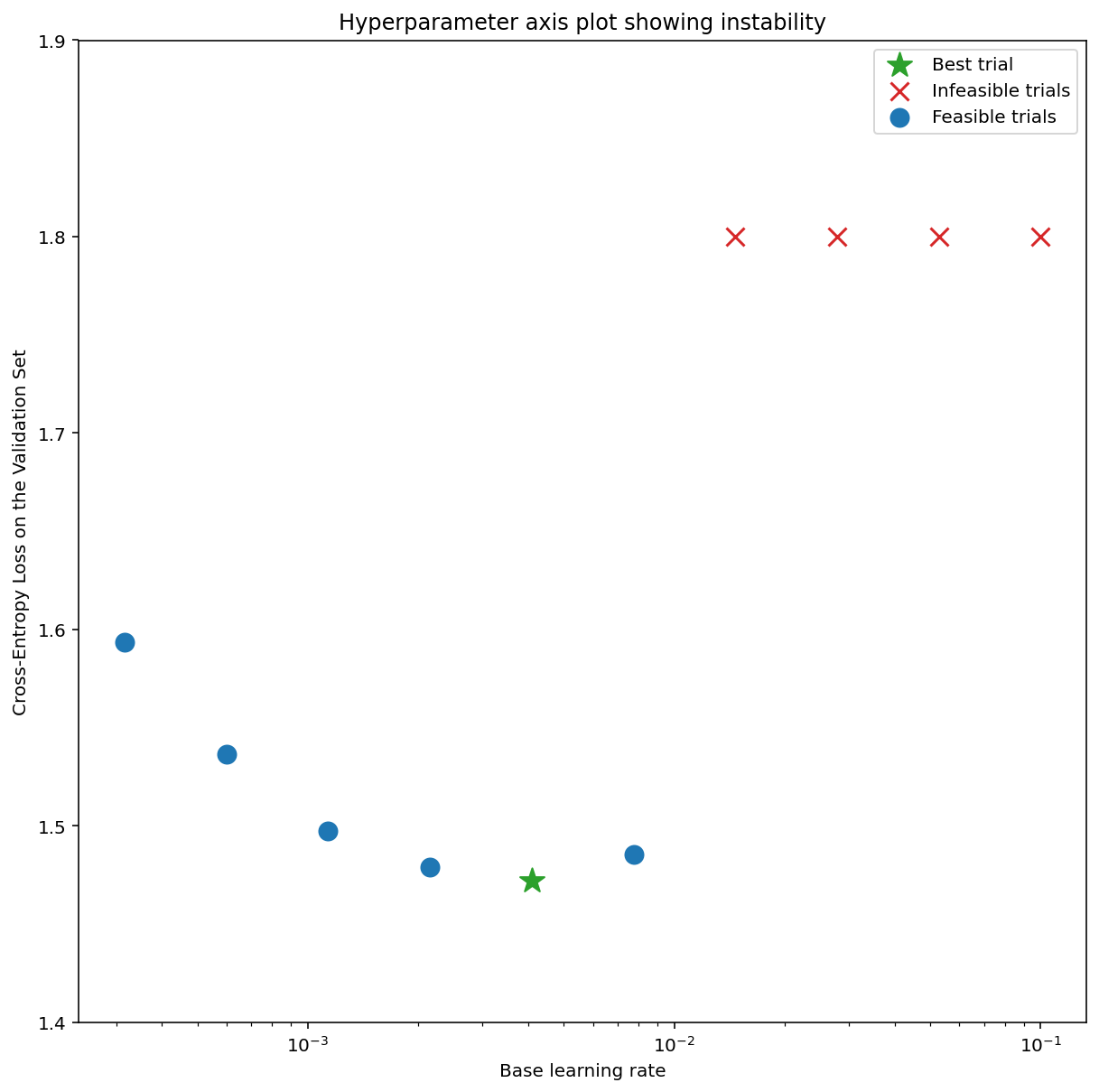
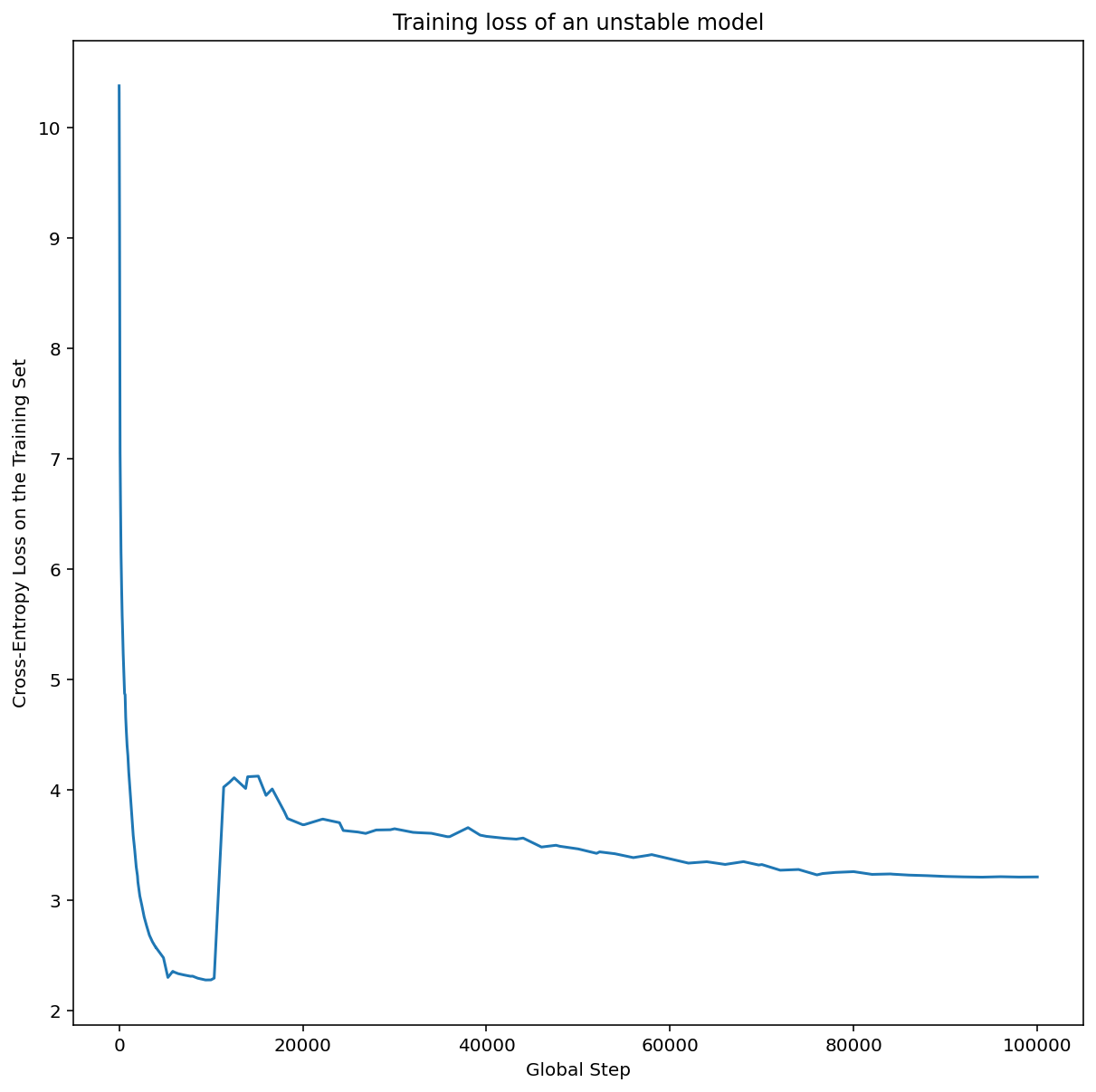
La figure 7a montre un graphique d'axe d'hyperparamètres qui indique qu'un modèle présente des instabilités d'optimisation, car le meilleur taux d'apprentissage se trouve juste à la limite de l'instabilité.
La figure 7b montre comment vérifier cela en examinant la perte d'entraînement d'un modèle entraîné avec un taux d'apprentissage 5 ou 10 fois supérieur à ce pic. Si ce graphique montre une augmentation soudaine de la perte après une baisse constante (par exemple, à l'étape 10 000 dans la figure ci-dessus), le modèle souffre probablement d'une instabilité d'optimisation.
Appliquer un échauffement du taux d'apprentissage
Soit unstable_base_learning_rate le taux d'apprentissage auquel le modèle devient instable, en utilisant la procédure précédente.
L'échauffement consiste à ajouter un calendrier du taux d'apprentissage qui augmente le taux d'apprentissage de 0 à une valeur stable base_learning_rate qui est au moins un ordre de grandeur supérieur à unstable_base_learning_rate.
Par défaut, nous vous recommandons d'essayer un base_learning_rate qui est 10 fois unstable_base_learning_rate. Notez toutefois qu'il serait possible d'exécuter à nouveau toute cette procédure pour, par exemple, 100 unstable_base_learning_rate. Voici le calendrier spécifique :
- Augmentez de 0 à base_learning_rate au cours de warmup_steps.
- Entraînez-vous à un taux constant pour post_warmup_steps.
Votre objectif est de trouver le nombre de warmup_steps le plus petit possible qui vous permet d'accéder à des taux d'apprentissage maximaux beaucoup plus élevés que unstable_base_learning_rate.
Pour chaque base_learning_rate, vous devez donc ajuster warmup_steps et post_warmup_steps. Il est généralement acceptable de définir post_warmup_steps sur 2*warmup_steps.
L'échauffement peut être ajusté indépendamment d'un calendrier de diminution existant. warmup_steps doit être balayé à quelques ordres de grandeur différents. Par exemple, une étude pourrait essayer [10, 1000, 10,000, 100,000]. Le point le plus élevé possible ne doit pas dépasser 10 % de max_train_steps.
Une fois qu'un warmup_steps qui ne fait pas exploser l'entraînement à base_learning_rate a été établi, il doit être appliqué au modèle de référence.
En substance, ajoutez cette programmation à la programmation existante et utilisez la sélection optimale des points de contrôle décrite ci-dessus pour comparer cette expérience à la référence. Par exemple, si nous avions initialement 10 000 max_train_steps et que nous avons effectué warmup_steps pendant 1 000 étapes, la nouvelle procédure d'entraînement devrait s'exécuter pendant 11 000 étapes au total.
Si de longues warmup_steps sont nécessaires pour un entraînement stable (> 5 % de max_train_steps), vous devrez peut-être augmenter max_train_steps pour en tenir compte.
Il n'existe pas vraiment de valeur "typique" pour l'ensemble des charges de travail. Certains modèles n'ont besoin que de 100 étapes, tandis que d'autres (en particulier les transformateurs) peuvent en nécessiter plus de 40 000.
Bornement du gradient
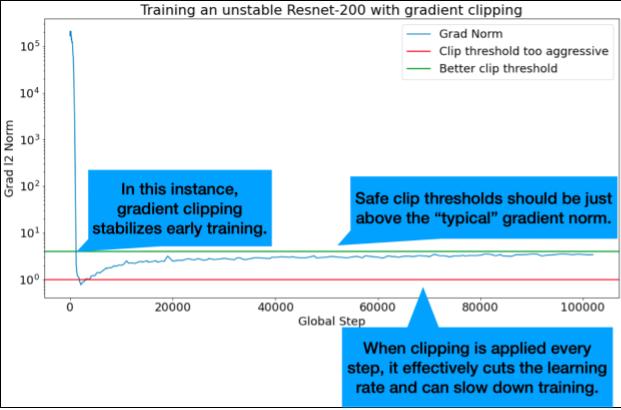
Le clipping de gradient est particulièrement utile en cas de problèmes de gradient importants ou aberrants. L'écrêtement du gradient peut résoudre l'un des problèmes suivants :
- Instabilité précoce de l'entraînement (norme de gradient élevée au début)
- Instabilités en cours d'entraînement (pics de gradient soudains en cours d'entraînement).
Des périodes d'échauffement plus longues peuvent parfois corriger les instabilités que le clipping ne corrige pas. Pour en savoir plus, consultez Échauffement du taux d'apprentissage.
🤖 Qu'en est-il de l'écrêtage pendant l'échauffement ?
Les seuils de clipping idéaux sont légèrement supérieurs à la norme de gradient "typique".
Voici un exemple de la façon dont l'écrêtage du gradient pourrait être effectué :
- Si la norme du gradient $\left | g \right |$ est supérieure au seuil de clipping du gradient $\lambda$, alors ${g}'= \lambda \times \frac{g}{\left | g \right |}$, où ${g}'$ est le nouveau gradient.
Enregistrez la norme de gradient non écrêtée pendant l'entraînement. Par défaut, générer :
- Graphique de la norme du gradient en fonction de l'étape
- Histogramme des normes de gradient agrégées sur toutes les étapes
Choisissez un seuil de clipping du gradient en fonction du 90e centile des normes de gradient. Le seuil dépend de la charge de travail, mais 90 % est un bon point de départ. Si 90 % ne fonctionne pas, vous pouvez ajuster ce seuil.
🤖 Pourquoi ne pas mettre en place une sorte de stratégie adaptative ?
Si vous essayez le clipping de gradient et que les problèmes d'instabilité persistent, vous pouvez essayer de le renforcer, c'est-à-dire de réduire le seuil.
Un bornement de la norme du gradient extrêmement agressif (c'est-à-dire que plus de 50 % des mises à jour sont bornées) est, en substance, une étrange façon de réduire le taux d'apprentissage. Si vous utilisez un écrêtement extrêmement agressif, vous devriez probablement simplement réduire le taux d'apprentissage.
Pourquoi appelez-vous le taux d'apprentissage et les autres paramètres d'optimisation des hyperparamètres ? Ils ne sont pas des paramètres d'une distribution a priori.
Le terme "hyperparamètre" a une signification précise dans le machine learning bayésien. Par conséquent, le fait de désigner le taux d'apprentissage et la plupart des autres paramètres de deep learning réglables comme des "hyperparamètres" est sans doute un abus de langage. Nous préférons utiliser le terme "métaparamètre" pour les taux d'apprentissage, les paramètres architecturaux et tous les autres éléments réglables de l'apprentissage profond. En effet, le terme "métaparamètre" permet d'éviter toute confusion liée à une mauvaise utilisation du mot "hyperparamètre". Cette confusion est particulièrement probable lorsque l'on parle d'optimisation bayésienne, où les modèles de surface de réponse probabilistes ont leurs propres vrais hyperparamètres.
Malheureusement, bien que le terme "hyperparamètre" puisse être source de confusion, il est devenu extrêmement courant dans la communauté du deep learning. Par conséquent, pour ce document, destiné à un large public qui comprend de nombreuses personnes qui ne sont probablement pas au courant de cette technicité, nous avons choisi de contribuer à une source de confusion dans le domaine dans l'espoir d'en éviter une autre. Cela dit, nous pourrions faire un choix différent lors de la publication d'un article de recherche, et nous encourageons les autres à utiliser "méta-paramètre" à la place dans la plupart des contextes.
Pourquoi la taille de lot ne doit-elle pas être ajustée pour améliorer directement les performances de l'ensemble de validation ?
Modifier la taille du lot sans changer d'autres détails du pipeline d'entraînement affecte souvent les performances de l'ensemble de validation. Toutefois, la différence de performances de l'ensemble de validation entre deux tailles de lot disparaît généralement si le pipeline d'entraînement est optimisé indépendamment pour chaque taille de lot.
Les hyperparamètres qui interagissent le plus fortement avec la taille de lot et qui sont donc les plus importants à régler séparément pour chaque taille de lot sont les hyperparamètres de l'optimiseur (par exemple, le taux d'apprentissage, le moment) et les hyperparamètres de régularisation. Les tailles de lot plus petites introduisent plus de bruit dans l'algorithme d'entraînement en raison de la variance de l'échantillon. Ce bruit peut avoir un effet régularisant. Ainsi, les tailles de lot plus importantes peuvent être plus sujettes au surapprentissage et peuvent nécessiter une régularisation plus forte et/ou des techniques de régularisation supplémentaires. De plus, vous devrez peut-être ajuster le nombre de pas d'entraînement lorsque vous modifierez la taille du lot.
Une fois tous ces effets pris en compte, il n'existe aucune preuve convaincante que la taille du lot affecte les performances de validation maximales réalisables. Pour en savoir plus, consultez Shallue et al. 2018.
Quelles sont les règles de mise à jour pour tous les algorithmes d'optimisation populaires ?
Cette section fournit des règles de mise à jour pour plusieurs algorithmes d'optimisation populaires.
Descente de gradient stochastique (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Où $\eta_t$ est le taux d'apprentissage à l'étape $t$.
Momentum
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Où $\eta_t$ est le taux d'apprentissage à l'étape $t$, et $\gamma$ est le coefficient de momentum.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Où $\eta_t$ est le taux d'apprentissage à l'étape $t$, et $\gamma$ est le coefficient de momentum.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
