Jak debugować i ograniczać niepowodzenia optymalizacji?
Podsumowanie: jeśli model ma problemy z optymalizacją, przed wypróbowaniem innych rozwiązań należy je rozwiązać. Diagnozowanie i korygowanie błędów trenowania to obszar aktywnych badań.
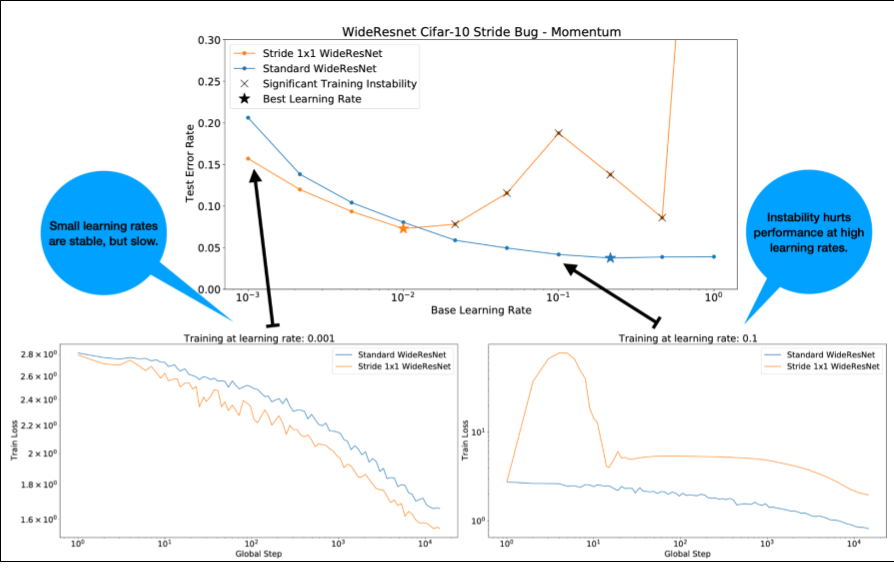
Zwróć uwagę na te kwestie dotyczące rysunku 4:
- Zmiana kroków nie pogarsza skuteczności przy niskich współczynnikach uczenia się.
- Wysokie współczynniki uczenia nie zapewniają już dobrego trenowania ze względu na niestabilność.
- Zastosowanie 1000 kroków rozgrzewki współczynnika uczenia rozwiązuje ten konkretny przypadek niestabilności, umożliwiając stabilne trenowanie przy maksymalnym współczynniku uczenia wynoszącym 0,1.
Rozpoznawanie niestabilnych zadań
Każde zadanie staje się niestabilne, jeśli współczynnik uczenia jest zbyt duży. Niestabilność jest problemem tylko wtedy, gdy zmusza Cię do używania zbyt małej szybkości uczenia się. Warto wyróżnić co najmniej 2 rodzaje niestabilności trenowania:
- niestabilność na etapie inicjowania lub na początku trenowania;
- Nagła niestabilność w trakcie trenowania.
Aby systematycznie identyfikować problemy ze stabilnością w obciążeniu, wykonaj te czynności:
- Przeprowadź test szybkości uczenia się i znajdź najlepszą szybkość uczenia się lr*.
- Wykreśl krzywe utraty trenowania dla szybkości uczenia się tuż powyżej lr*.
- Jeśli współczynniki uczenia > lr* wykazują niestabilność straty (strata rośnie, a nie maleje w okresach trenowania), wyeliminowanie tej niestabilności zwykle poprawia trenowanie.
Podczas trenowania rejestruj normę L2 pełnego gradientu straty, ponieważ wartości odstające mogą powodować fałszywą niestabilność w środku trenowania. Może to wpływać na to, jak agresywnie przycinać gradienty lub aktualizacje wag.
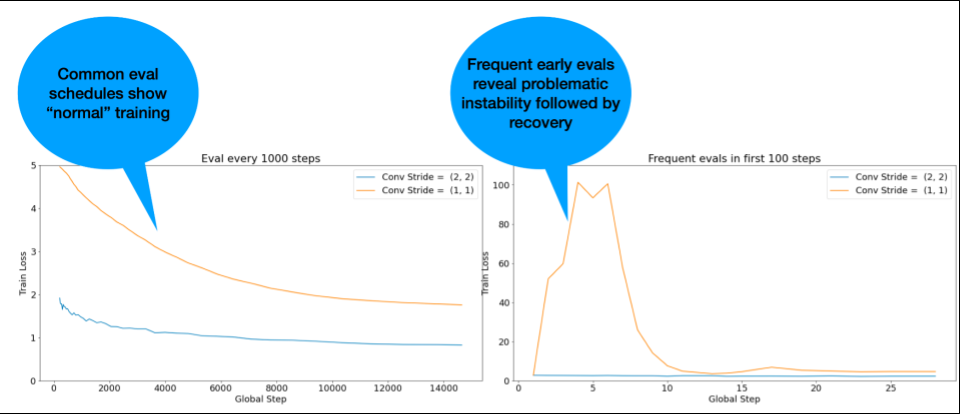
UWAGA: w przypadku niektórych modeli na początku występuje niestabilność, po której następuje poprawa, co skutkuje powolnym, ale stabilnym trenowaniem. Typowe harmonogramy oceny mogą nie wykryć tych problemów, ponieważ nie są wystarczająco częste.
Aby to sprawdzić, możesz przeprowadzić skrócone trenowanie obejmujące tylko około 500 kroków za pomocą lr = 2 * current best, ale oceniać każdy krok.
Potencjalne rozwiązania typowych problemów z niestabilnością
Wypróbuj te rozwiązania typowych problemów z niestabilnością:
- Zastosuj rozgrzewkę tempa uczenia się. Ta opcja jest najlepsza w przypadku niestabilności na początku trenowania.
- Zastosuj przycinanie gradientu. Jest to korzystne w przypadku niestabilności na początku i w środku procesu uczenia, a także może rozwiązać problemy z nieprawidłową inicjacją, których nie można rozwiązać za pomocą rozgrzewki.
- Wypróbuj nowy optymalizator. Czasami Adam radzi sobie z niestabilnościami, z którymi Momentum nie może sobie poradzić. To obszar aktywnych badań.
- Upewnij się, że w architekturze modelu stosujesz sprawdzone metody i najlepsze inicjalizacje (przykłady poniżej). Dodaj połączenia resztkowe i normalizację, jeśli model ich jeszcze nie zawiera.
- Normalizuj jako ostatnią operację przed wartością resztową. Na przykład:
x + Norm(f(x)). Pamiętaj, że znakNorm(x + f(x))może powodować problemy. - Spróbuj zainicjować gałęzie resztkowe wartością 0. (Zobacz ReZero is All You Need: Fast Convergence at Large Depth).
- Obniż szybkość uczenia się. To ostateczność.
Rozgrzewka tempa uczenia się
Kiedy stosować rozgrzewkę tempa uczenia się
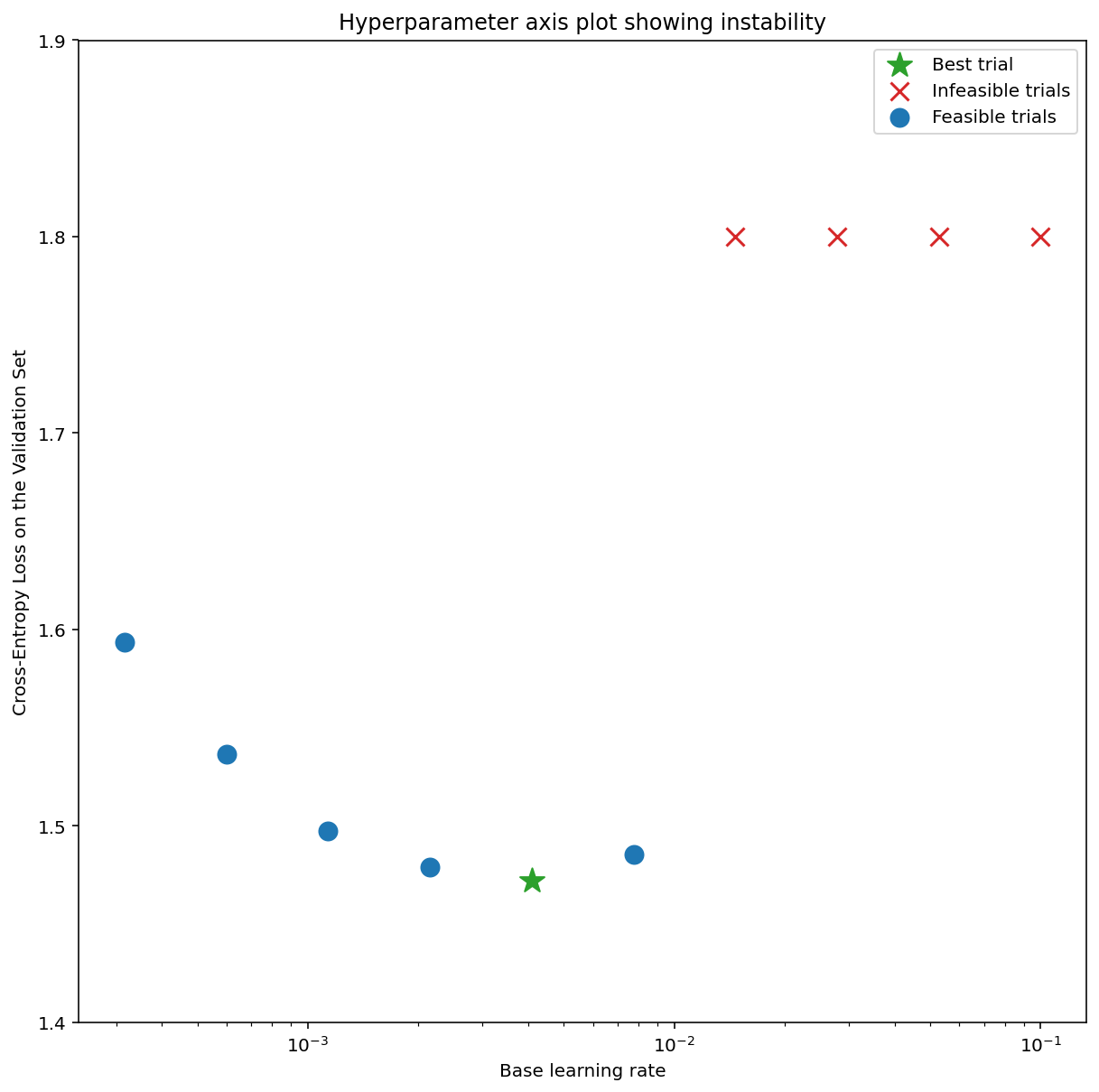
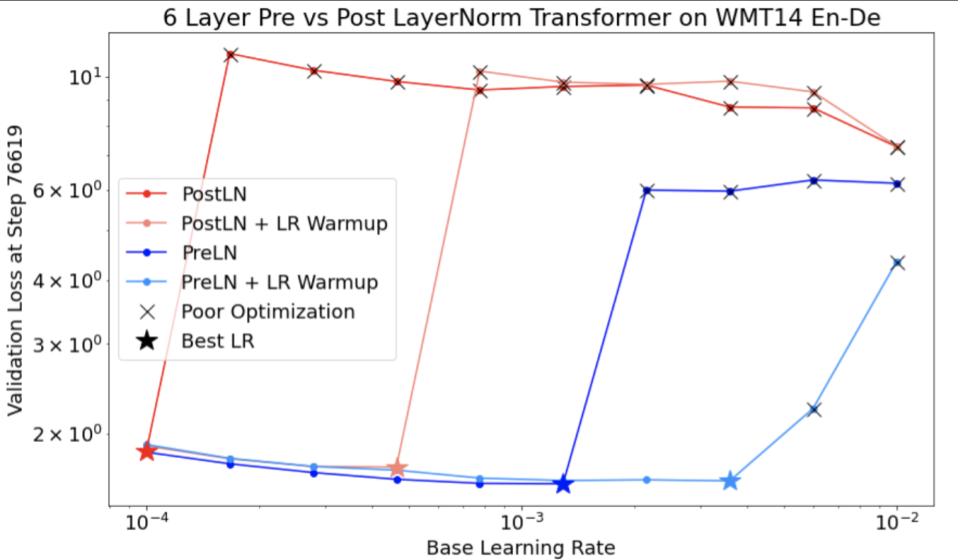
Ilustracja 7a przedstawia wykres osi hiperparametrów, który wskazuje, że model wykazuje niestabilność optymalizacji, ponieważ najlepsza szybkość uczenia się znajduje się na granicy niestabilności.
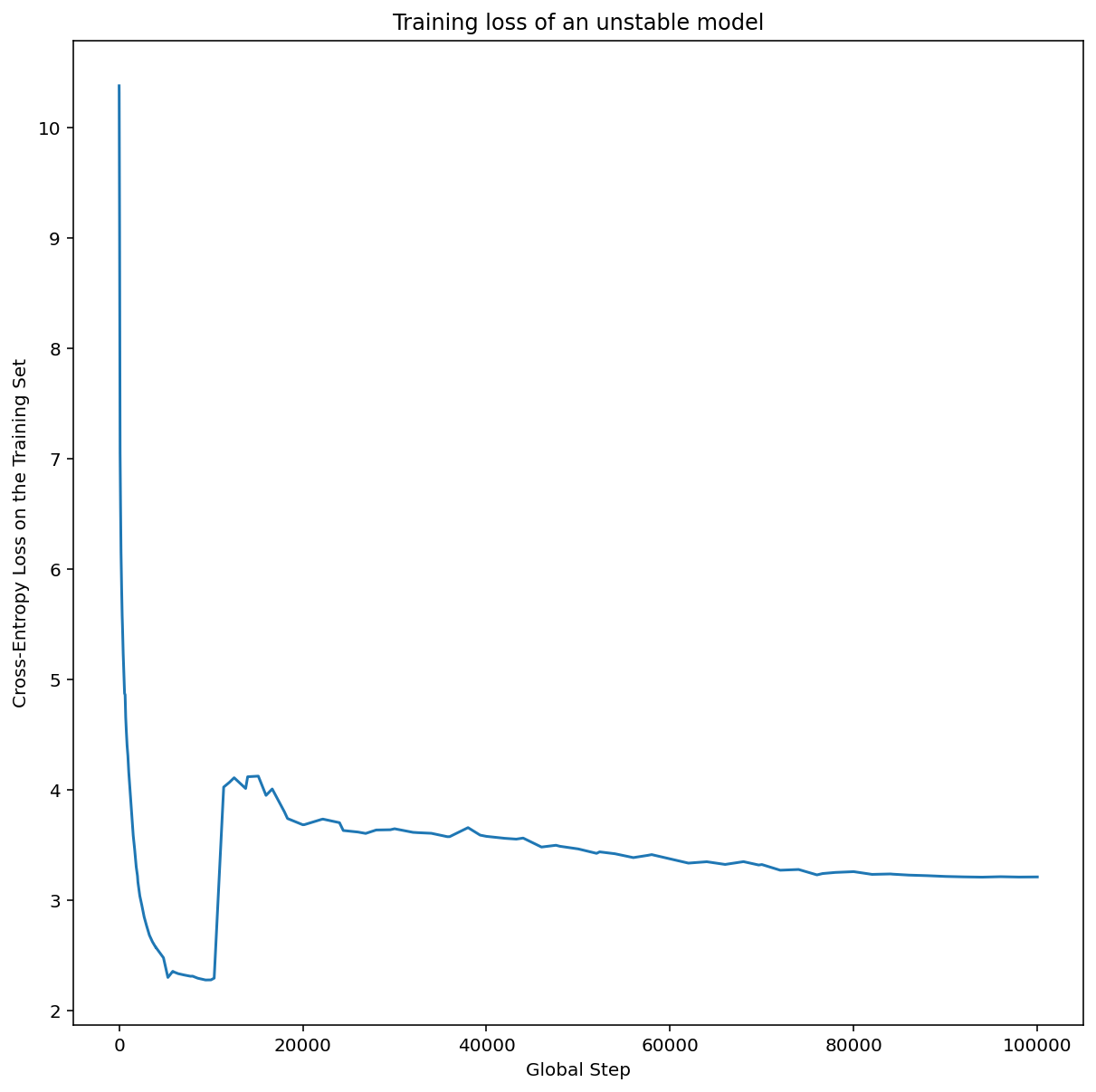
Na rysunku 7b pokazano, jak można to sprawdzić, analizując stratę trenowania modelu wytrenowanego ze współczynnikiem uczenia 5 lub 10 razy większym niż ten szczyt. Jeśli na wykresie widać nagły wzrost wartości funkcji straty po okresie stabilnego spadku (np.na kroku ~10 tys. na powyższym rysunku), model prawdopodobnie ma problemy ze stabilnością optymalizacji.
Jak zastosować rozgrzewkę tempa uczenia się
Niech unstable_base_learning_rate będzie tempem uczenia się, przy którym model staje się niestabilny, zgodnie z powyższą procedurą.
Rozgrzewka polega na dodaniu na początku harmonogramu tempa uczenia się, który zwiększa tempo uczenia się od 0 do pewnej stabilnej wartości base_learning_rate, która jest co najmniej o rząd wielkości większa niż unstable_base_learning_rate.
Domyślnie będzie to base_learning_rate o wartości 10xunstable_base_learning_rate. Pamiętaj jednak, że całą procedurę można powtórzyć np. 100 razyunstable_base_learning_rate. Harmonogram jest następujący:
- Wzrost od 0 do base_learning_rate w ciągu warmup_steps.
- Trenuj ze stałą szybkością przez post_warmup_steps.
Twoim celem jest znalezienie najmniejszej liczby warmup_steps, która pozwoli Ci uzyskać najwyższe współczynniki uczenia się, znacznie wyższe niż unstable_base_learning_rate.
Dlatego w przypadku każdego elementu base_learning_rate musisz dostroić parametry warmup_steps i post_warmup_steps. Zwykle można ustawić post_warmup_steps na 2*warmup_steps.
Rozgrzewkę można dostosowywać niezależnie od istniejącego harmonogramu spadku. warmup_steps
należy zmieniać w kilku różnych rzędach wielkości. Na przykład w badaniu można sprawdzić [10, 1000, 10,000, 100,000]. Największy możliwy punkt nie powinien przekraczać 10% max_train_steps.
Gdy zostanie ustalona wartość warmup_steps, która nie powoduje gwałtownego wzrostu trenowania przy wartości base_learning_rate, należy ją zastosować w modelu podstawowym.
Zasadniczo dodaj ten harmonogram do istniejącego harmonogramu i użyj optymalnego wyboru punktów kontrolnych omówionego powyżej, aby porównać ten eksperyment z wartością bazową. Jeśli np. pierwotnie mieliśmy 10 000 max_train_steps i wykonaliśmy warmup_steps kroków, nowa procedura trenowania powinna trwać łącznie 11 000 kroków.
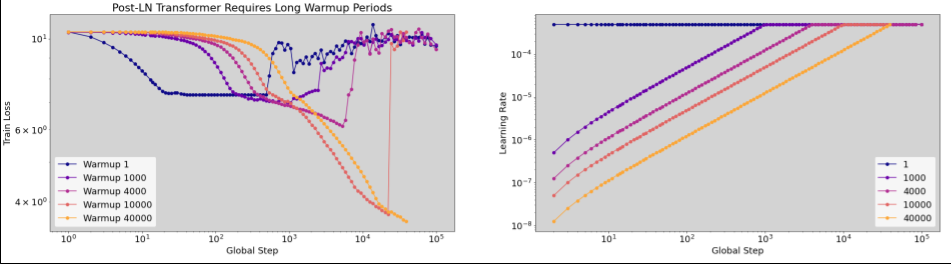
Jeśli do stabilnego trenowania wymagane są długie warmup_steps (>5% max_train_steps), może być konieczne zwiększenie max_train_steps.
W przypadku pełnego zakresu obciążeń nie ma „typowych” wartości. Niektóre modele wymagają tylko 100 kroków, a inne (zwłaszcza transformatory) mogą potrzebować ponad 40 tys.
Obcinanie gradientu
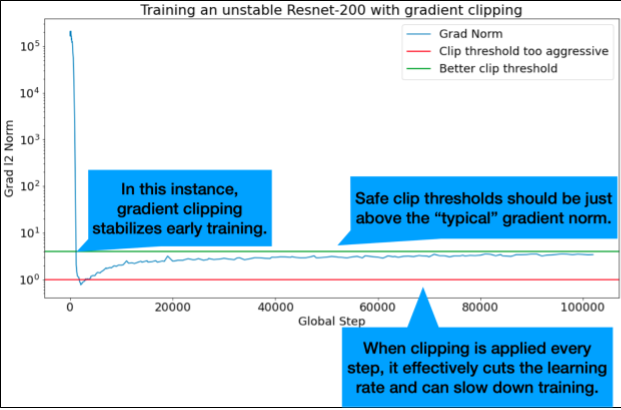
Obcinanie gradientu jest najbardziej przydatne, gdy występują duże lub odstające problemy z gradientem. Obcinanie gradientu może rozwiązać te problemy:
- niestabilność na początku trenowania (duża norma gradientu na początku);
- niestabilność w trakcie trenowania (nagłe skoki gradientu w trakcie trenowania);
Czasami dłuższe okresy rozgrzewki mogą korygować niestabilności, których nie koryguje przycinanie; więcej informacji znajdziesz w sekcji Rozgrzewka współczynnika uczenia się.
🤖 A co z przycinaniem podczas rozgrzewki?
Idealne progi przycinania znajdują się tuż powyżej „typowej” normy gradientu.
Oto przykład, jak można to zrobić:
- Jeśli norma gradientu $\left | g \right |$ jest większa niż próg przycinania gradientu $\lambda$, wykonaj działanie ${g}'= \lambda \times \frac{g}{\left | g \right |}$, gdzie ${g}'$ to nowy gradient.
Rejestruj nieobcięte normy gradientu podczas trenowania. Domyślnie generuj:
- Wykres normy gradientu w zależności od kroku
- Histogram norm gradientów zebranych ze wszystkich kroków
Wybierz próg przycinania gradientu na podstawie 90 percentyla norm gradientu. Próg zależy od obciążenia, ale 90% to dobry punkt wyjścia. Jeśli 90% nie działa, możesz dostosować ten próg.
🤖 A co z jakąś strategią adaptacyjną?
Jeśli po zastosowaniu przycinania gradientu problemy z niestabilnością nadal występują, możesz spróbować jeszcze bardziej ograniczyć gradient, czyli zmniejszyć próg.
Bardzo agresywne przycinanie gradientu (czyli przycinanie >50% aktualizacji) jest w zasadzie dziwnym sposobem na zmniejszenie współczynnika uczenia. Jeśli używasz bardzo agresywnego przycinania, prawdopodobnie lepiej będzie po prostu zmniejszyć współczynnik uczenia się.
Dlaczego tempo uczenia się i inne parametry optymalizacji nazywasz hiperparametrami? Nie są one parametrami żadnego rozkładu a priori.
Termin „hiperparametr” ma w kontekście bayesowskiego uczenia maszynowego precyzyjne znaczenie, więc określanie szybkości uczenia i większości innych parametrów głębokiego uczenia, które można dostrajać, jako „hiperparametrów” jest prawdopodobnie nadużyciem terminologii. Wolelibyśmy używać terminu „metaparametr” w odniesieniu do współczynników uczenia, parametrów architektury i wszystkich innych elementów, które można dostrajać w uczeniu głębokim. Dzieje się tak, ponieważ metaparametr pozwala uniknąć potencjalnych nieporozumień wynikających z niewłaściwego użycia słowa „hiperparametr”. To zamieszanie jest szczególnie prawdopodobne w przypadku optymalizacji bayesowskiej, w której probabilistyczne modele powierzchni odpowiedzi mają własne prawdziwe hiperparametry.
Chociaż termin „hiperparametr” może być mylący, stał się bardzo popularny w społeczności zajmującej się uczeniem głębokim. Dlatego w tym dokumencie, przeznaczonym dla szerokiego grona odbiorców, w tym wielu osób, które prawdopodobnie nie są świadome tego technicznego aspektu, zdecydowaliśmy się przyczynić do jednego źródła zamieszania w tej dziedzinie, aby uniknąć innego. Możemy jednak podjąć inną decyzję podczas publikowania artykułu naukowego i zachęcamy innych do używania w większości kontekstów terminu „metaparametr”.
Dlaczego rozmiaru partii nie należy dostosowywać w celu bezpośredniego zwiększenia skuteczności zbioru weryfikacyjnego?
Zmiana rozmiaru partii bez zmiany innych szczegółów potoku trenowania często wpływa na skuteczność zbioru weryfikacyjnego. Różnica w skuteczności zbioru weryfikacyjnego między dwoma rozmiarami partii zwykle znika, jeśli potok trenowania jest optymalizowany niezależnie dla każdego rozmiaru partii.
Hiperparametry, które najsilniej oddziałują na rozmiar pakietu, a tym samym są najważniejsze do osobnego dostrajania dla każdego rozmiaru pakietu, to hiperparametry optymalizatora (np. tempo uczenia się, momentum) i hiperparametry regularyzacji. Mniejsze rozmiary partii wprowadzają więcej szumu do algorytmu trenowania ze względu na wariancję próbki. Ten szum może mieć efekt regulujący. W związku z tym większe rozmiary partii mogą być bardziej podatne na przetrenowanie i wymagać silniejszej regularyzacji lub dodatkowych technik regularyzacji. Dodatkowo podczas zmiany rozmiaru partii może być konieczne dostosowanie liczby kroków trenowania.
Po uwzględnieniu wszystkich tych efektów nie ma przekonujących dowodów na to, że rozmiar partii wpływa na maksymalną osiągalną skuteczność walidacji. Więcej informacji znajdziesz w artykule Shallue i in. 2018.
Jakie są reguły aktualizacji wszystkich popularnych algorytmów optymalizacji?
W tej sekcji znajdziesz reguły aktualizacji kilku popularnych algorytmów optymalizacji.
Stochastyczny spadek wzdłuż gradientu (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
gdzie $\eta_t$ to tempo uczenia się w kroku $t$.
Wykorzystanie chwili
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
gdzie $\eta_t$ to tempo uczenia się na etapie $t$, a $\gamma$ to współczynnik momentu.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
gdzie $\eta_t$ to tempo uczenia się na etapie $t$, a $\gamma$ to współczynnik momentu.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
