¿Cómo se pueden depurar y mitigar los errores de optimización?
Resumen: Si el modelo tiene dificultades de optimización, es importante que las corrijas antes de probar otras cosas. El diagnóstico y la corrección de los fracasos en el entrenamiento son áreas activas de investigación.
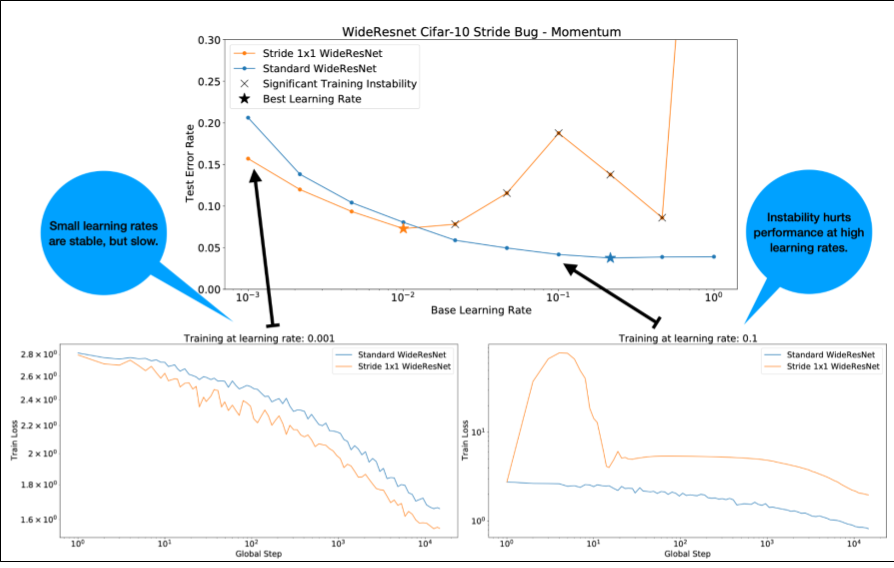
Ten en cuenta lo siguiente con respecto a la Figura 4:
- Cambiar los avances no degrada el rendimiento con tasas de aprendizaje bajas.
- Las tasas de aprendizaje altas ya no se entrenan bien debido a la inestabilidad.
- La aplicación de 1,000 pasos de preparación de la tasa de aprendizaje resuelve esta instancia particular de inestabilidad, lo que permite un entrenamiento estable a una tasa de aprendizaje máxima de 0.1.
Identifica cargas de trabajo inestables
Cualquier carga de trabajo se vuelve inestable si la tasa de aprendizaje es demasiado grande. La inestabilidad es solo un problema cuando te obliga a usar una tasa de aprendizaje demasiado pequeña. Vale la pena distinguir al menos dos tipos de inestabilidad de entrenamiento:
- Inestabilidad en la inicialización o al principio del entrenamiento.
- Inestabilidad repentina en medio del entrenamiento
Puedes adoptar un enfoque sistemático para identificar problemas de estabilidad en tu carga de trabajo de la siguiente manera:
- Haz una barrer la tasa de aprendizaje y encuentra la mejor tasa de aprendizaje lr*.
- Trazar las curvas de pérdida de entrenamiento para las tasas de aprendizaje un poco superiores a lr*
- Si las tasas de aprendizaje > lr* muestran inestabilidad de pérdida (la pérdida sube y no baja durante los períodos de entrenamiento), corregir la inestabilidad suele mejorar el entrenamiento.
Registra la norma L2 del gradiente de pérdida completa durante el entrenamiento, ya que los valores atípicos pueden causar inestabilidad falsa en medio del entrenamiento. Esto puede informar qué tan agresivamente debes recortar gradientes o actualizaciones de peso.
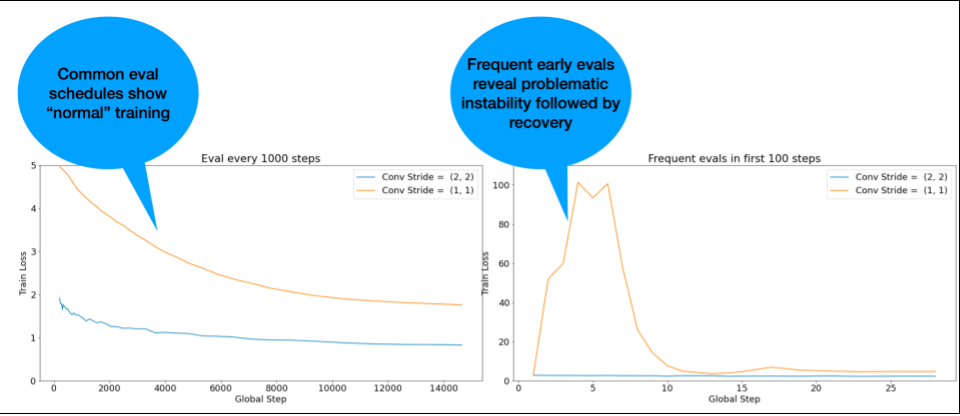
NOTA: Algunos modelos muestran una inestabilidad muy temprana seguida de una recuperación que da como resultado un entrenamiento lento pero estable. Los programas de evaluación comunes pueden pasar por alto estos problemas, ya que no se evalúan con suficiente frecuencia.
A fin de verificar esto, puedes entrenar para una ejecución abreviada de solo 500 pasos con lr = 2 * current best, pero evalúa cada paso.
Posibles soluciones para los patrones de inestabilidad comunes
Considera las siguientes soluciones posibles para los patrones de inestabilidad comunes:
- Aplicar preparación de la tasa de aprendizaje Esto es mejor para la inestabilidad en los primeros entrenamientos.
- Aplica el recorte de gradientes. Esto es bueno para la inestabilidad en la etapa inicial y media del entrenamiento, y puede corregir algunas inicializaciones incorrectas que no se pueden realizar con la preparación.
- Prueba un optimizador nuevo. A veces, Adam puede manejar inestabilidades que Momentum no puede. Esta es un área de investigación activa.
- Asegúrate de usar las prácticas recomendadas y las inicializaciones recomendadas para la arquitectura de tu modelo (ejemplos a continuación). Agrega conexiones residuales y normalización si el modelo aún no las contiene.
- Normalizar como la última operación antes del residual. Por ejemplo:
x + Norm(f(x))Ten en cuenta queNorm(x + f(x))puede causar problemas. - Intenta inicializar las ramas residuales en 0. (consulta ReZero es todo lo que necesitas: convergencia rápida a gran escala).
- Reducir la tasa de aprendizaje Este es el último recurso.
Preparación de la tasa de aprendizaje
Cuándo aplicar la preparación de la tasa de aprendizaje
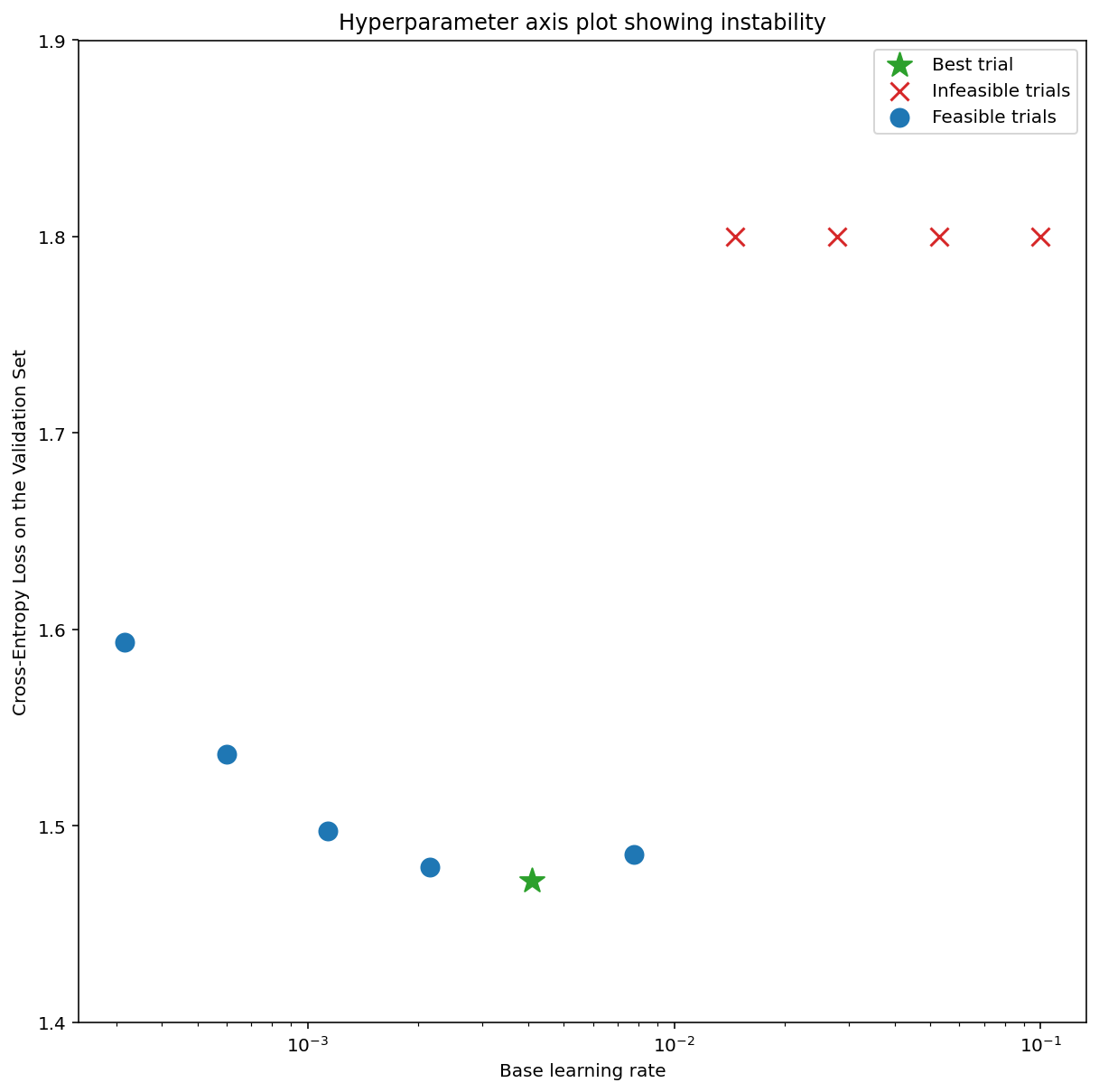
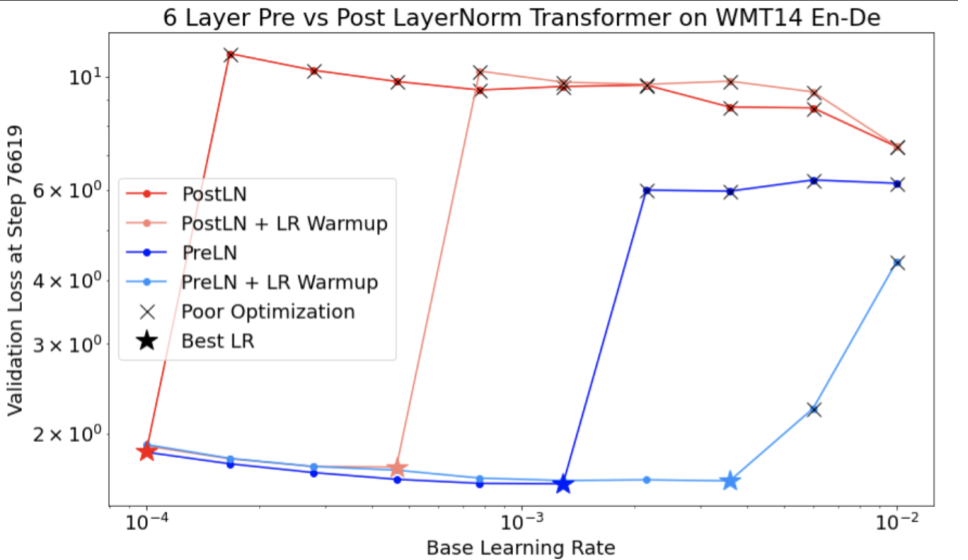
En la Figura 7a, se muestra un gráfico del eje de hiperparámetros que indica que un modelo tiene inestabilidades de optimización, ya que la mejor tasa de aprendizaje está justo en el límite de la inestabilidad.
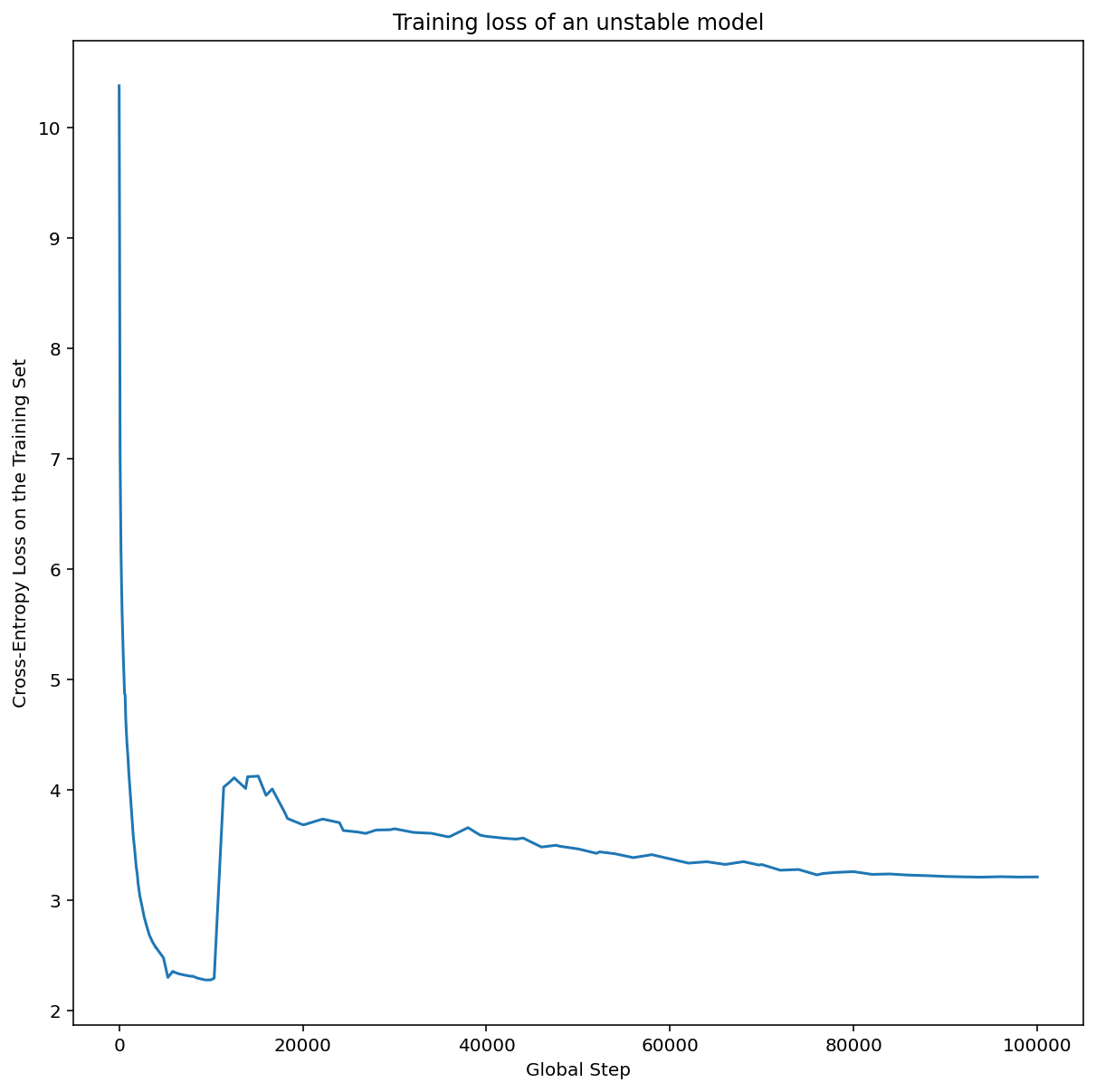
En la Figura 7b, se muestra cómo esto se puede verificar dos veces si se examina la pérdida de entrenamiento de un modelo entrenado con una tasa de aprendizaje que es 5 o 10 veces mayor que este máximo. Si ese gráfico muestra un aumento repentino de la pérdida después de una disminución constante (p.ej., en el paso ~10,000 en la figura anterior), es probable que el modelo sufra inestabilidad de optimización.
Cómo aplicar la preparación de la tasa de aprendizaje
Usa el procedimiento anterior para que unstable_base_learning_rate sea la tasa de aprendizaje en la que el modelo se vuelve inestable.
La preparación implica anteponer un programa de tasa de aprendizaje que aumente la tasa de aprendizaje de 0 a una base_learning_rate estable que sea al menos un orden de magnitud mayor que unstable_base_learning_rate.
La opción predeterminada sería probar un base_learning_rate con un valor de 10x unstable_base_learning_rate. Sin embargo, ten en cuenta que sería posible volver a ejecutar todo este procedimiento para algo como 100x unstable_base_learning_rate. El cronograma específico es el siguiente:
- Aumenta el valor de 0 a base_learning_rate a través de hotup_steps.
- Entrena a una frecuencia constante para post_warmup_steps.
Tu objetivo es encontrar el menor número de warmup_steps que te permita acceder a las tasas de aprendizaje máximas mucho más altas que unstable_base_learning_rate.
Por lo tanto, para cada base_learning_rate, debes ajustar warmup_steps y post_warmup_steps. Por lo general, es correcto configurar post_warmup_steps como 2*warmup_steps.
La preparación se puede ajustar independientemente de un programa de decaimiento existente. warmup_steps debe barrerse de diferentes órdenes de magnitud. Por ejemplo, un estudio de ejemplo podría probar [10, 1000, 10,000, 100,000]. El punto máximo posible no debe ser superior al 10% de max_train_steps.
Una vez que se establece un warmup_steps que no infla el entrenamiento en base_learning_rate, se debe aplicar al modelo de referencia.
Básicamente, antepone este programa al programa existente y usa
la selección del punto de control óptima que se describió anteriormente para comparar este experimento
con el modelo de referencia. Por ejemplo, si originalmente teníamos 10,000 max_train_steps y realizamos warmup_steps en 1,000 pasos, el procedimiento de entrenamiento nuevo debería ejecutarse en 11,000 pasos en total.
Si se requieren warmup_steps largos para el entrenamiento estable (más del 5% de max_train_steps), es posible que debas aumentar max_train_steps para dar cuenta de esto.
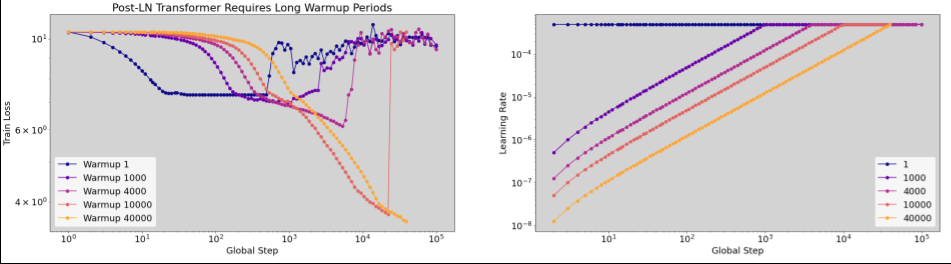
Realmente no hay un valor “típico” en todo el rango de cargas de trabajo. Algunos modelos solo necesitan 100 pasos, mientras que otros (en particular, los transformadores) pueden necesitar más de 40,000.
Recorte de gradiente
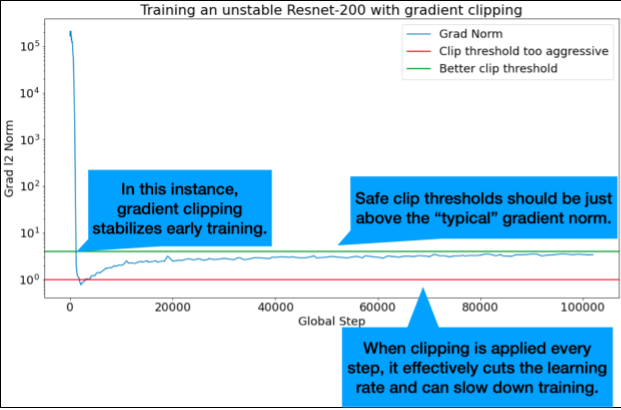
El recorte de gradientes es más útil cuando se producen problemas de gradiente grandes o con valores atípicos. El recorte de gradientes puede solucionar cualquiera de los siguientes problemas:
- Inestabilidad en el entrenamiento temprano (norma del gradiente grande temprana)
- Inestabilidades en la mitad del entrenamiento (aumento repentino del gradiente en la mitad del entrenamiento)
A veces, los períodos de preparación más largos pueden corregir las inestabilidades que el recorte no lo hace. Para obtener más información, consulta Preparación de la tasa de aprendizaje.
📊 ¿Qué ocurre con el recorte durante el calentamiento?
Los umbrales de recorte ideales están justo por encima de la norma de gradiente “típico”.
Este es un ejemplo de cómo se puede realizar el recorte de gradientes:
- Si la norma del gradiente $\left | g \right |$ es mayor que el umbral de recorte de gradientes $\lambda$, entonces ${g}'= \lambda \times \frac{g}{\left | g \right |}$, donde ${g}'$ es el nuevo gradiente.
Registra la norma del gradiente sin recortar durante el entrenamiento. De forma predeterminada, genera lo siguiente:
- Un gráfico de la norma del gradiente frente al paso
- Un histograma de las normas de gradiente agregadas en todos los pasos
Elige un umbral de recorte de gradientes basado en el percentil 90 de las normas de gradiente. El umbral depende de la carga de trabajo, pero el 90% es un buen punto de partida. Si el 90% no funciona, puedes ajustar este umbral.
📊 ¿Qué ocurre con algún tipo de estrategia adaptativa?
Si intentas el recorte de gradientes y los problemas de inestabilidad persisten, puedes esforzarte más. Es decir, puedes reducir el umbral.
El recorte de gradientes extremadamente agresivo (es decir, más del 50% de las actualizaciones se recortan) es, en esencia, una forma extraña de reducir la tasa de aprendizaje. Si notas que usas recortes extremadamente agresivos, probablemente debas reducir la tasa de aprendizaje.
¿Por qué se llaman hiperparámetros de la tasa de aprendizaje y otros parámetros de optimización? No son parámetros de ninguna distribución anterior.
El término “hiperparámetro” tiene un significado preciso en el aprendizaje automático bayesiano, por lo que se podría decir que hacer referencia a la tasa de aprendizaje y a la mayoría de los otros parámetros ajustables del aprendizaje profundo como “hiperparámetros” es un abuso de terminología. Preferimos usar el término “metaparámetro” para las tasas de aprendizaje, los parámetros arquitectónicos y todos los demás aspectos del aprendizaje profundo que se pueden ajustar. Esto se debe a que el metaparámetro evita la potencial de confusión que proviene del uso inadecuado de la palabra “hiperparámetro”. Esta confusión es muy probable cuando se habla de la optimización bayesiana, en la que los modelos de superficie de respuesta probabilísticos tienen sus propios hiperparámetros verdaderos.
Lamentablemente, aunque puede ser confuso, el término “hiperparámetro” se volvió muy común en la comunidad del aprendizaje profundo. Por lo tanto, en este documento, dirigido a un público amplio que incluye a muchas personas que tienen pocas probabilidades de conocer este aspecto técnico, tomamos la decisión de contribuir a una fuente de confusión en el campo para evitar otra. Dicho esto, podríamos tomar una decisión diferente cuando publiquemos un artículo de investigación y recomendamos a otros que usen un “metaparámetro” en su lugar en la mayoría de los contextos.
¿Por qué el tamaño del lote no debería ajustarse para mejorar directamente el rendimiento del conjunto de validación?
Cambiar el tamaño del lote sin cambiar ningún otro detalle de la canalización de entrenamiento suele afectar el rendimiento del conjunto de validación. Sin embargo, la diferencia en el rendimiento del conjunto de validación entre dos tamaños de lote suele desaparecer si la canalización de entrenamiento se optimiza de forma independiente para cada tamaño de lote.
Los hiperparámetros que interactúan más con el tamaño del lote y, por lo tanto, que son más importantes de ajustar por separado para cada tamaño del lote son los hiperparámetros del optimizador (por ejemplo, la tasa de aprendizaje, el impulso) y los de regularización. Los tamaños de lotes más pequeños introducen más ruido en el algoritmo de entrenamiento debido a la variación de la muestra. Este ruido puede tener un efecto de regularización. Por lo tanto, los tamaños de lote más grandes pueden ser más propensos al sobreajuste y pueden requerir una regularización más fuerte o técnicas de regularización adicionales. Además, es posible que debas ajustar la cantidad de pasos de entrenamiento cuando cambies el tamaño del lote.
Una vez que se tienen en cuenta todos estos efectos, no hay evidencia convincente de que el tamaño del lote afecte el rendimiento máximo de la validación que se puede alcanzar. Para obtener más información, consulta Shallue et al. 2018.
¿Cuáles son las reglas de actualización de todos los algoritmos de optimización populares?
En esta sección, se proporcionan reglas de actualización para varios algoritmos de optimización populares.
Descenso de gradientes estocástico (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Donde $\eta_t$ es la tasa de aprendizaje en el paso $t$.
Momentum
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Donde $\eta_t$ es la tasa de aprendizaje en el paso $t$ y $\gamma$ es el coeficiente de impulso.
Nesteróv
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Donde $\eta_t$ es la tasa de aprendizaje en el paso $t$ y $\gamma$ es el coeficiente de impulso.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]