Wie lassen sich Optimierungsfehler beheben und vermeiden?
Zusammenfassung: Wenn das Modell Optimierungsprobleme hat, müssen diese behoben werden, bevor Sie andere Maßnahmen ergreifen. Die Diagnose und Korrektur von Trainingsfehlern ist ein aktives Forschungsgebiet.
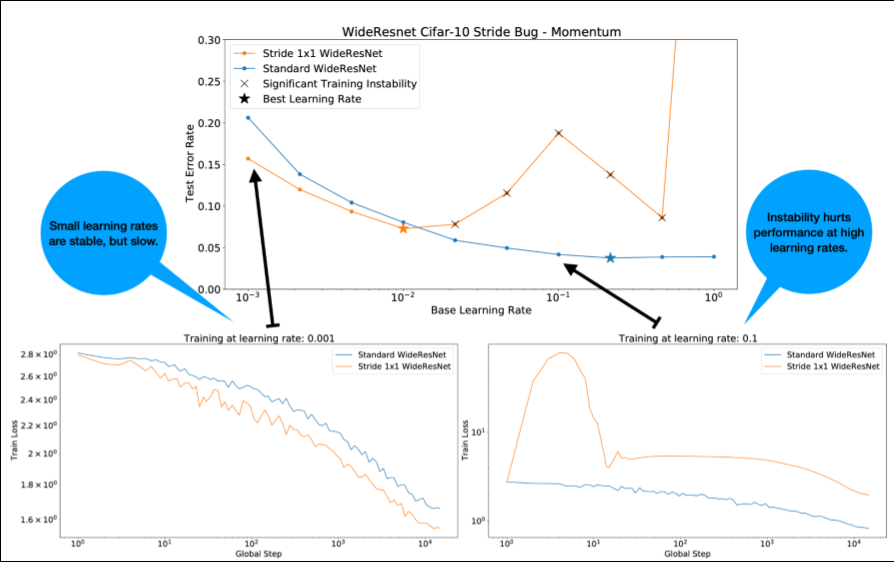
Beachten Sie bei Abbildung 4 Folgendes:
- Das Ändern der Schritte führt nicht zu einer Leistungsminderung bei niedrigen Lernraten.
- Aufgrund der Instabilität ist das Training mit hohen Lernraten nicht mehr effektiv.
- Durch die Anwendung von 1.000 Schritten für das Aufwärmen der Lernrate wird diese spezielle Instabilität behoben und ein stabiles Training mit einer maximalen Lernrate von 0, 1 ermöglicht.
Instabile Arbeitslasten identifizieren
Jede Arbeitslast wird instabil, wenn die Lernrate zu hoch ist. Instabilität ist nur dann ein Problem, wenn sie Sie zwingt, eine zu kleine Lernrate zu verwenden. Es gibt mindestens zwei Arten von Trainingsinstabilität:
- Instabilität bei der Initialisierung oder zu Beginn des Trainings.
- Plötzliche Instabilität während des Trainings.
Sie können Stabilitätsprobleme in Ihrer Arbeitslast systematisch identifizieren, indem Sie Folgendes tun:
- Führen Sie einen Lernratensweep durch und ermitteln Sie die beste Lernrate lr*.
- Trainingsverlustkurven für Lernraten knapp über lr* darstellen.
- Wenn bei Lernraten > lr* die Verlustinstabilität auftritt (der Verlust steigt während des Trainings anstatt zu sinken), kann das Training durch Beheben der Instabilität in der Regel verbessert werden.
Protokollieren Sie die L2-Norm des vollständigen Verlustgradienten während des Trainings, da Ausreißerwerte in der Mitte des Trainings zu einer falschen Instabilität führen können. Dies kann Aufschluss darüber geben, wie aggressiv Gradienten oder Gewichtsaktualisierungen begrenzt werden sollten.
HINWEIS: Bei einigen Modellen tritt sehr früh eine Instabilität auf, gefolgt von einer Erholung, die zu einem langsamen, aber stabilen Training führt. Bei gängigen Bewertungszeitplänen werden diese Probleme möglicherweise nicht erkannt, da die Bewertung nicht häufig genug erfolgt.
Um dies zu prüfen, können Sie mit lr = 2 * current best nur etwa 500 Schritte trainieren, aber jeden Schritt auswerten.
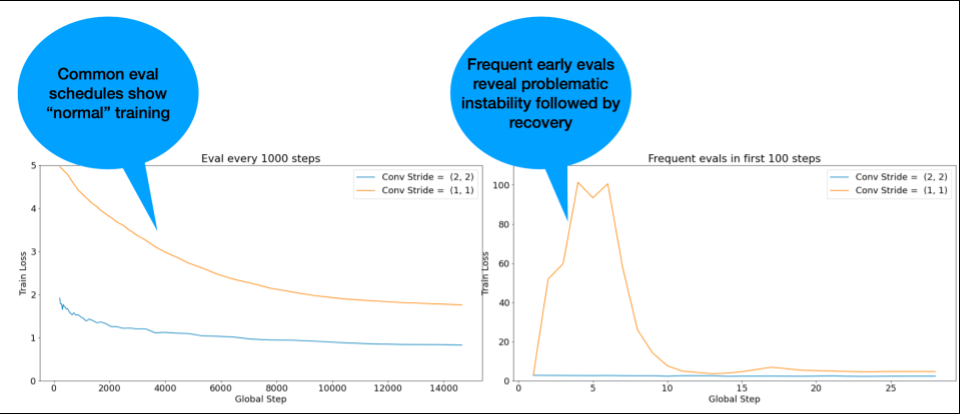
Mögliche Lösungen für häufige Instabilitätsmuster
Hier sind einige mögliche Lösungen für häufige Instabilitätsmuster:
- Lernraten-Warmup anwenden. Diese Option eignet sich am besten für eine instabile Trainingsphase.
- Gradient Clipping anwenden Das ist sowohl für Instabilität in der frühen als auch in der mittleren Trainingsphase gut und kann einige schlechte Initialisierungen beheben, die durch Warmup nicht behoben werden können.
- Probieren Sie einen neuen Optimierer aus. Manchmal kann Adam Instabilitäten bewältigen, die Momentum nicht bewältigen kann. Dies ist ein aktives Forschungsgebiet.
- Achten Sie darauf, dass Sie Best Practices und optimale Initialisierungen für Ihre Modellarchitektur verwenden (Beispiele folgen). Fügen Sie Residual Connections und Normalisierung hinzu, falls das Modell diese noch nicht enthält.
- Normalisieren Sie als letzten Vorgang vor dem Residual. Beispiel:
x + Norm(f(x)).Norm(x + f(x))kann zu Problemen führen. - Initialisieren Sie die Residual-Branches mit 0. Weitere Informationen finden Sie unter ReZero is All You Need: Fast Convergence at Large Depth.
- Verringern Sie die Lernrate. Dies ist das letzte Mittel.
Warm-up der Lernrate
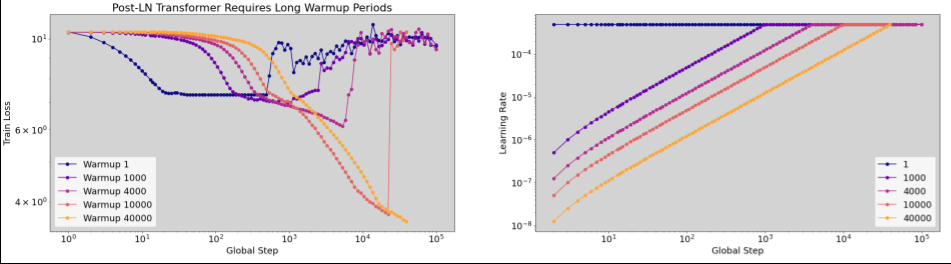
Wann sollte das Aufwärmen der Lernrate angewendet werden?
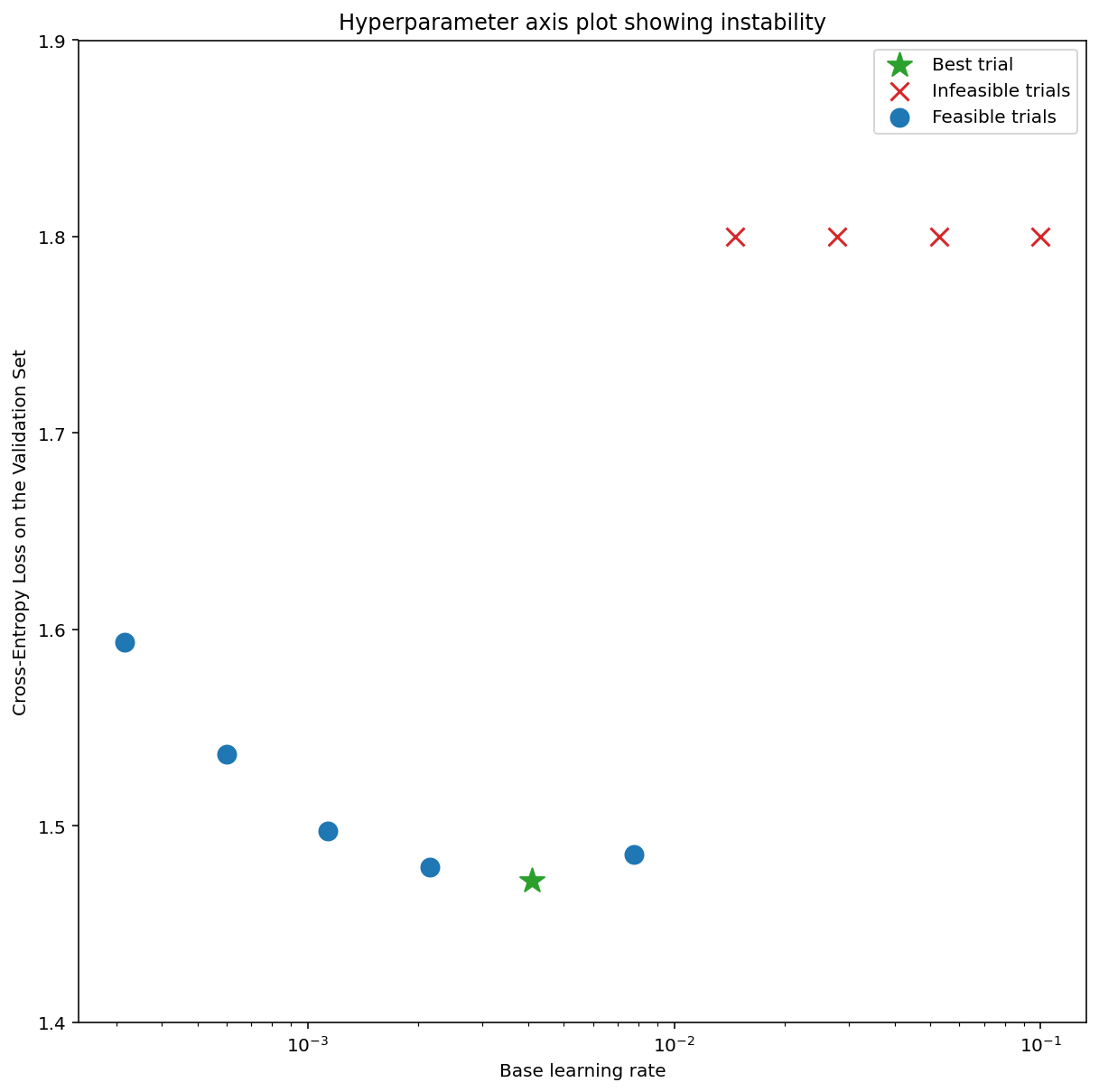
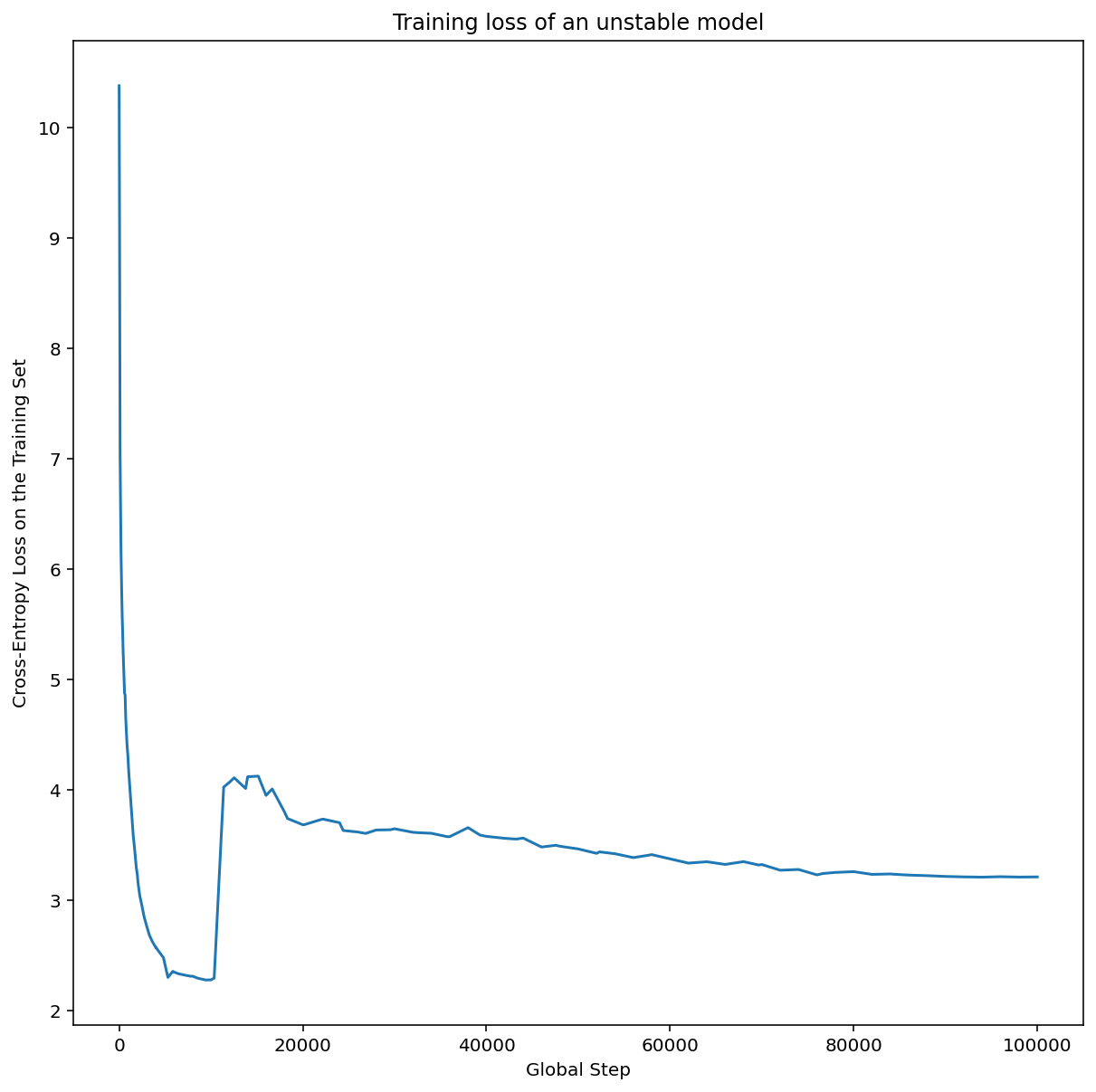
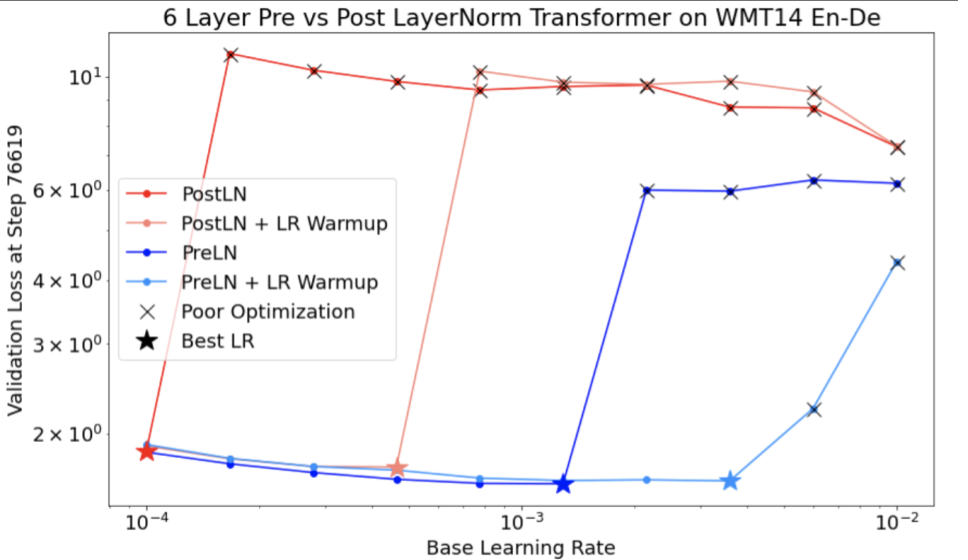
Abbildung 7a zeigt ein Diagramm mit Hyperparameterachsen, das auf Optimierungsinstabilitäten in einem Modell hinweist, da die beste Lernrate direkt an der Grenze zur Instabilität liegt.
In Abbildung 7b sehen Sie, wie Sie das überprüfen können, indem Sie den Trainingsverlust eines Modells untersuchen, das mit einer Lernrate trainiert wurde, die entweder 5- oder 10-mal höher als dieser Spitzenwert ist. Wenn in diesem Diagramm nach einem stetigen Rückgang ein plötzlicher Anstieg des Verlusts zu sehen ist (z. B. bei Schritt ~10.000 in der Abbildung oben), leidet das Modell wahrscheinlich unter Optimierungsinstabilität.
Lernrate-Warmup anwenden
Sei unstable_base_learning_rate die Lernrate, bei der das Modell mit dem vorherigen Verfahren instabil wird.
Beim Warm-up wird ein Lernratenschema vorangestellt, bei dem die Lernrate von 0 auf einen stabilen Wert base_learning_rate erhöht wird, der mindestens eine Größenordnung größer als unstable_base_learning_rate ist.
Standardmäßig wird ein base_learning_rate mit dem 10-Fachen von unstable_base_learning_rate verwendet. Es wäre jedoch möglich, diesen gesamten Vorgang noch einmal für etwa 100 unstable_base_learning_rate durchzuführen. Der genaue Zeitplan ist:
- Steigern Sie den Wert von 0 auf base_learning_rate über warmup_steps.
- Trainieren Sie mit einer konstanten Rate für „post_warmup_steps“.
Ihr Ziel ist es, die kleinste Anzahl von warmup_steps zu finden, mit der Sie auf Spitzen-Lernraten zugreifen können, die viel höher als unstable_base_learning_rate sind.
Für jede base_learning_rate müssen Sie also warmup_steps und post_warmup_steps optimieren. Normalerweise ist es in Ordnung, post_warmup_steps auf 2*warmup_steps festzulegen.
Die Aufwärmphase kann unabhängig von einem vorhandenen Verfallszeitplan optimiert werden. warmup_steps
sollte über einige Größenordnungen hinweg variiert werden. In einer Beispielstudie könnte beispielsweise [10, 1000, 10,000, 100,000] getestet werden. Der größte zulässige Punkt darf nicht mehr als 10% von max_train_steps betragen.
Sobald ein warmup_steps festgelegt wurde, das das Training bei base_learning_rate nicht beeinträchtigt, sollte es auf das Basismodell angewendet werden.
Hängen Sie dieses Programm im Grunde an das vorhandene Programm an und vergleichen Sie dieses Experiment mit der Baseline. Verwenden Sie dazu die oben beschriebene optimale Prüfpunktauswahl. Wenn wir beispielsweise ursprünglich 10.000 max_train_steps hatten und warmup_steps für 1.000 Schritte durchgeführt haben, sollte das neue Trainingsverfahren insgesamt 11.000 Schritte umfassen.
Wenn lange warmup_steps für ein stabiles Training erforderlich sind (>5% von max_train_steps), müssen Sie möglicherweise max_train_steps erhöhen, um dies zu berücksichtigen.
Es gibt keinen „typischen“ Wert für alle Arbeitslasten. Für einige Modelle sind nur 100 Schritte erforderlich, während für andere (insbesondere Transformer) möglicherweise mehr als 40.000 Schritte erforderlich sind.
Gradientenbeschneidung
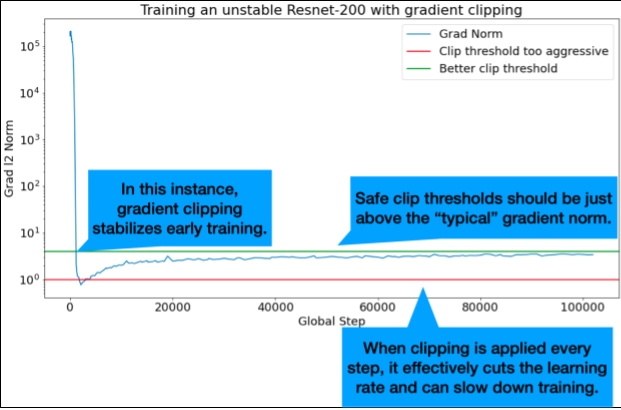
Das Beschneiden von Gradienten ist am nützlichsten, wenn große oder Ausreißer-Gradienten auftreten. Mit Gradient Clipping können Sie eines der folgenden Probleme beheben:
- Instabilität des Trainings in der Anfangsphase (große Gradientennorm in der Anfangsphase)
- Instabilitäten während des Trainings (plötzliche Gradientenspitzen während des Trainings).
Manchmal können längere Warm-up-Phasen Instabilitäten korrigieren, die durch Clipping nicht behoben werden. Weitere Informationen finden Sie unter Learning Rate Warmup.
🤖 Was ist mit Clipping während des Aufwärmens?
Die idealen Clip-Schwellenwerte liegen knapp über der „typischen“ Gradientennorm.
Hier ist ein Beispiel dafür, wie das Clipping von Gradienten erfolgen kann:
- Wenn die Norm des Gradienten $\left | g \right |$ größer als der Grenzwert für das Beschneiden des Gradienten $\lambda$ ist, gilt Folgendes: ${g}'= \lambda \times \frac{g}{\left | g \right |}$, wobei ${g}'$ der neue Gradient ist.
Die nicht beschnittene Gradientennorm während des Trainings protokollieren. Standardmäßig generieren:
- Diagramm der Gradientennorm im Vergleich zum Schritt
- Ein Histogramm der Gradientennormen, die über alle Schritte hinweg aggregiert werden
Wählen Sie einen Grenzwert für das Gradienten-Clipping basierend auf dem 90. Perzentil der Gradientennormen aus. Der Grenzwert ist arbeitslastabhängig, aber 90% sind ein guter Ausgangspunkt. Wenn 90% nicht funktionieren, können Sie diesen Schwellenwert anpassen.
🤖 Was ist mit einer Art adaptiver Strategie?
Wenn Sie Gradient Clipping ausprobieren und die Instabilitätsprobleme weiterhin bestehen, können Sie es noch einmal versuchen, indem Sie den Schwellenwert verkleinern.
Extrem aggressives Gradienten-Clipping (d. h. > 50% der Updates werden geclippt) ist im Grunde eine ungewöhnliche Methode, um die Lernrate zu reduzieren. Wenn Sie sehr aggressives Clipping verwenden, sollten Sie die Lernrate wahrscheinlich einfach reduzieren.
Warum werden die Lernrate und andere Optimierungsparameter als Hyperparameter bezeichnet? Sie sind keine Parameter einer Prior-Verteilung.
Der Begriff „Hyperparameter“ hat im bayesschen maschinellen Lernen eine genaue Bedeutung. Die Lernrate und die meisten anderen abstimmbaren Deep-Learning-Parameter als „Hyperparameter“ zu bezeichnen, ist daher wohl ein Missbrauch der Terminologie. Wir würden den Begriff „Metaparameter“ lieber für Lernraten, Architekturparameter und alle anderen abstimmbaren Aspekte des Deep Learnings verwenden. So wird die Verwirrung vermieden, die durch die falsche Verwendung des Wortes „Hyperparameter“ entstehen kann. Diese Verwechslung ist besonders wahrscheinlich, wenn es um die Bayes'sche Optimierung geht, bei der die probabilistischen Reaktionsflächenmodelle eigene echte Hyperparameter haben.
Leider ist der Begriff „Hyperparameter“ in der Deep-Learning-Community sehr verbreitet, obwohl er verwirrend sein kann. Daher haben wir uns in diesem Dokument, das für ein breites Publikum bestimmt ist, zu dem viele Menschen gehören, die sich dieser technischen Details wahrscheinlich nicht bewusst sind, entschieden, zu einer Quelle der Verwirrung in diesem Bereich beizutragen, um eine andere zu vermeiden. Bei der Veröffentlichung eines Forschungsberichts würden wir uns jedoch möglicherweise anders entscheiden und empfehlen, in den meisten Kontexten stattdessen „Metaparameter“ zu verwenden.
Warum sollte die Batchgröße nicht so angepasst werden, dass die Leistung des Validierungssatzes direkt verbessert wird?
Wenn Sie die Batchgröße ändern, ohne andere Details der Trainingspipeline zu ändern, wirkt sich das häufig auf die Leistung des Validierungssets aus. Der Unterschied in der Leistung des Validierungssatzes zwischen zwei Batchgrößen verschwindet jedoch in der Regel, wenn die Trainingspipeline unabhängig für jede Batchgröße optimiert wird.
Die Hyperparameter, die am stärksten mit der Batch-Größe interagieren und daher für jede Batch-Größe separat optimiert werden müssen, sind die Optimierer-Hyperparameter (z. B. Lernrate, Momentum) und die Regularisierungs-Hyperparameter. Bei kleineren Batchgrößen wird aufgrund der Stichprobenvarianz mehr Rauschen in den Trainingsalgorithmus eingeführt. Dieses Rauschen kann eine regularisierende Wirkung haben. Größere Batchgrößen sind daher anfälliger für Overfitting und erfordern möglicherweise eine stärkere Regularisierung und/oder zusätzliche Regularisierungstechniken. Außerdem müssen Sie möglicherweise die Anzahl der Trainingsschritte anpassen, wenn Sie die Batchgröße ändern.
Wenn alle diese Effekte berücksichtigt werden, gibt es keine überzeugenden Beweise dafür, dass die Batchgröße die maximal erreichbare Validierungsleistung beeinflusst. Weitere Informationen finden Sie unter Shallue et al. 2018.
Welche Aktualisierungsregeln gelten für die gängigen Optimierungsalgorithmen?
In diesem Abschnitt finden Sie Aktualisierungsregeln für einige beliebte Optimierungsalgorithmen.
Stochastic Gradient Descent (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Dabei ist $\eta_t$ die Lernrate im Schritt $t$.
Erfolge
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Dabei ist $\eta_t$ die Lernrate im Schritt $t$ und $\gamma$ der Momentum-Koeffizient.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Dabei ist $\eta_t$ die Lernrate im Schritt $t$ und $\gamma$ der Momentum-Koeffizient.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
