كيف يمكن تصحيح أخطاء التحسين والحدّ منها؟
الملخّص: إذا كان النموذج يواجه صعوبات في التحسين، من المهم حلّها قبل تجربة إجراءات أخرى. ويشكّل تشخيص حالات تعذُّر التدريب وتصحيحها مجالاً نشطًا للبحث.
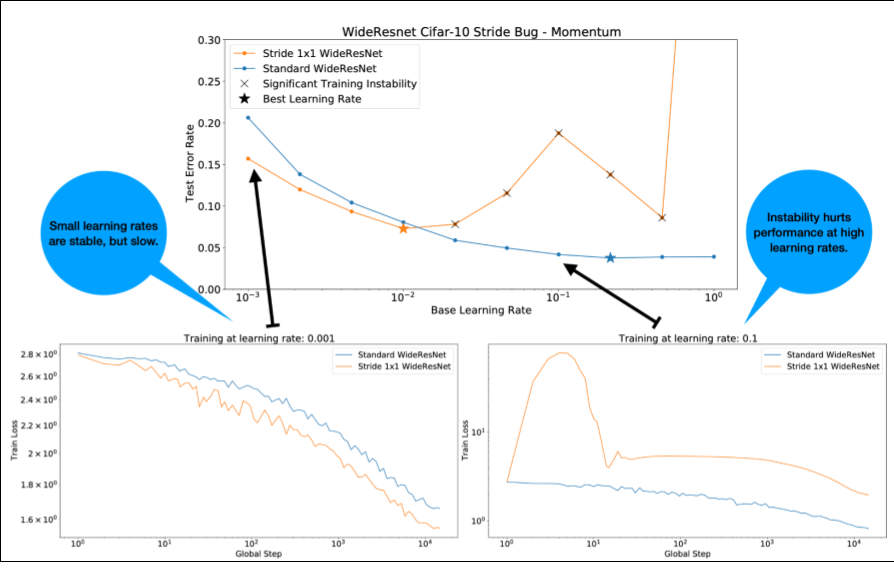
يُرجى ملاحظة ما يلي بشأن الشكل 4:
- لا يؤدي تغيير الخطوات إلى تدهور الأداء عند معدّلات التعلّم المنخفضة.
- لم تعُد معدّلات التعلّم المرتفعة تتدرب بشكل جيد بسبب عدم الاستقرار.
- يؤدي تطبيق 1, 000 خطوة من عملية الإحماء لمعدّل التعلّم إلى حلّ حالة عدم الاستقرار هذه، ما يتيح التدريب المستقر بمعدّل تعلّم أقصى يبلغ 0.1.
تحديد أعباء العمل غير المستقرة
تصبح أيّ عبء عمل غير مستقر إذا كان معدّل التعلّم كبيرًا جدًا. لا تشكّل حالة عدم الاستقرار مشكلة إلا عندما تجبرك على استخدام معدّل تعلّم صغير جدًا. هناك نوعان على الأقل من عدم استقرار التدريب يستحقان التمييز:
- عدم الاستقرار عند التهيئة أو في المراحل المبكرة من التدريب
- عدم استقرار مفاجئ في منتصف التدريب
يمكنك اتّباع نهج منظَّم لتحديد مشاكل الثبات في عبء العمل من خلال تنفيذ ما يلي:
- نفِّذ عملية بحث عن معدّل التعلّم lr* الأفضل.
- رسم منحنيات فقدان التدريب لمعدّلات التعلّم أعلى من lr* مباشرةً
- إذا كانت معدّلات التعلّم > lr* تعرض عدم استقرار في الخسارة (تزداد الخسارة بدلاً من أن تنخفض خلال فترات التدريب)، سيؤدي حلّ مشكلة عدم الاستقرار عادةً إلى تحسين التدريب.
سجِّل معيار L2 لتدرّج الخسارة الكامل أثناء التدريب، لأنّ القيم الشاذة يمكن أن تتسبّب في عدم استقرار زائف في منتصف التدريب. ويمكن أن يحدّد ذلك مدى فعالية عملية قص التدرّجات أو تعديل الأوزان.
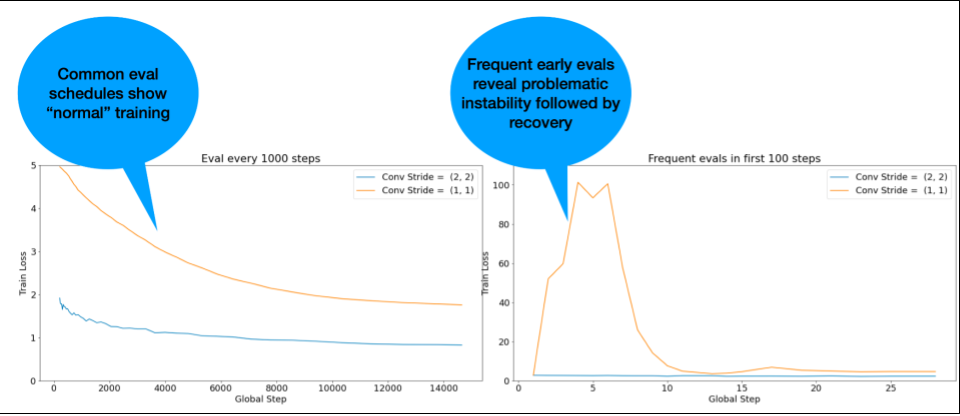
ملاحظة: تُظهر بعض النماذج عدم استقرار مبكرًا جدًا يتبعه تحسّن يؤدي إلى تدريب بطيء ولكن مستقر. قد لا ترصد جداول التقييم الشائعة هذه المشاكل لأنّها لا تُجري التقييم بشكل متكرر بما يكفي.
للتحقّق من ذلك، يمكنك التدريب على تشغيل مختصر يتضمّن 500 خطوة فقط باستخدام lr = 2 * current best، ولكن عليك تقييم كل خطوة.
الحلول المحتملة لأنماط عدم الاستقرار الشائعة
في ما يلي بعض الحلول المحتملة لأنماط عدم الاستقرار الشائعة:
- تطبيق عملية الإحماء لمعدّل التعلّم هذا الخيار هو الأفضل في حال عدم استقرار التدريب في مراحله الأولى.
- طبِّق اقتصاص التدرّج. ويفيد ذلك في معالجة حالات عدم الاستقرار في المراحل المبكرة والمتوسطة من التدريب، وقد يحلّ بعض المشاكل في عمليات التهيئة الأولية التي لا يمكن حلّها باستخدام عملية الإحماء.
- جرِّب أداة تحسين جديدة. في بعض الأحيان، يمكن لـ Adam التعامل مع حالات عدم الاستقرار التي لا يمكن لـ Momentum التعامل معها. وهذا مجال نشط للبحث.
- تأكَّد من استخدام أفضل الممارسات وأفضل عمليات التهيئة الأولية لبنية النموذج (سترد أمثلة لاحقًا). أضِف عمليات ربط متبقية وعمليات تسوية إذا لم يكن النموذج يتضمّنها.
- يجب إجراء عملية التسوية كآخر عملية قبل حساب الرصيد المتبقي. على سبيل المثال:
x + Norm(f(x)). يُرجى العِلم أنّ استخدامNorm(x + f(x))يمكن أن يتسبّب في حدوث مشاكل. - حاوِل ضبط الفروع المتبقية على 0. (يمكنك الاطّلاع على ReZero is All You Need: Fast Convergence at Large Depth.)
- خفض معدّل التعلّم هذا هو الحلّ الأخير.
زيادة معدّل التعلّم تدريجيًا
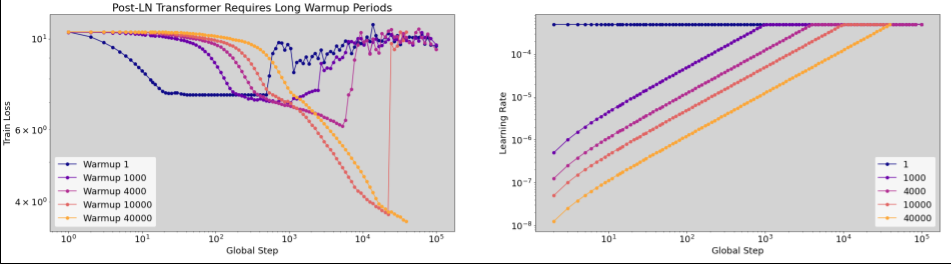
حالات تطبيق عملية الإحماء لمعدّل التعلّم
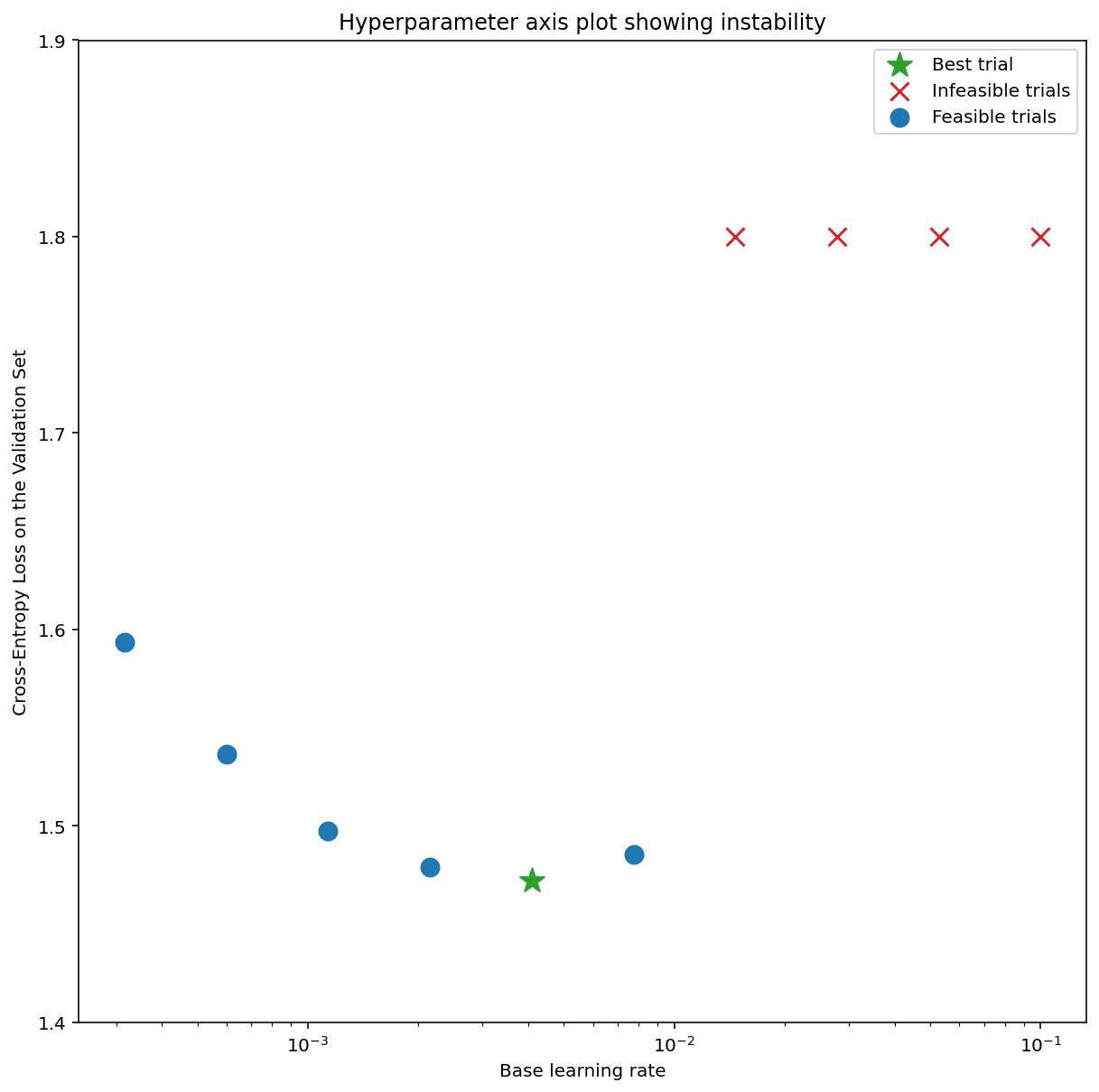
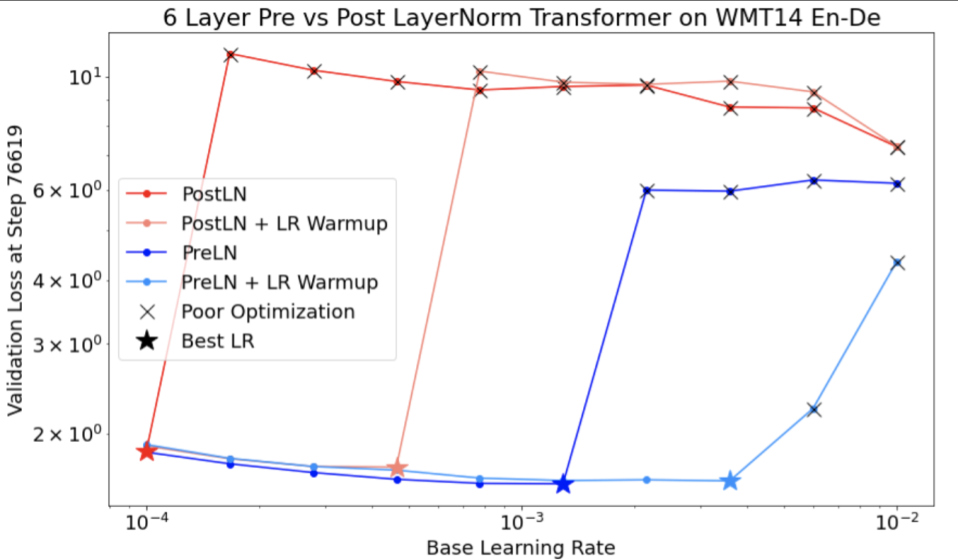
يعرض الشكل 7 (أ) رسمًا بيانيًا لمحور المعلمات الفائقة يشير إلى نموذج يعاني من حالات عدم استقرار في التحسين، لأنّ أفضل معدّل تعلّم يقع على حافة عدم الاستقرار.
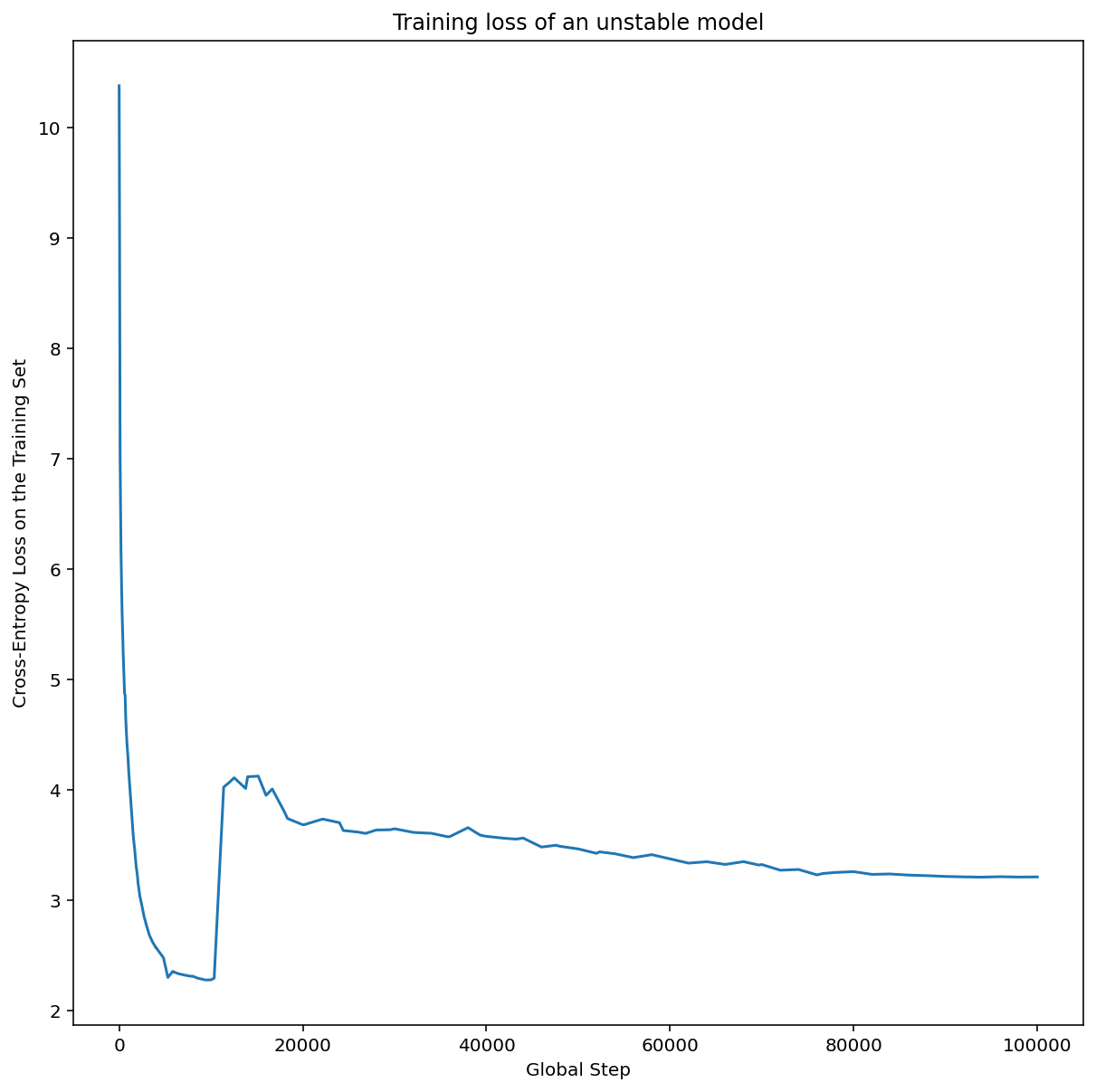
يوضّح الشكل 7 (ب) كيف يمكن التحقّق من ذلك بشكل مضاعف من خلال فحص خسارة التدريب لنموذج تم تدريبه بمعدّل تعلّم أكبر بمقدار 5 أو 10 مرات من هذا الحد الأقصى. إذا أظهر هذا الرسم البياني ارتفاعًا مفاجئًا في الخسارة بعد انخفاض ثابت (على سبيل المثال، عند الخطوة 10,000 تقريبًا في الشكل أعلاه)، من المحتمل أن يعاني النموذج من عدم استقرار التحسين.
كيفية تطبيق عملية الإحماء لمعدّل التعلّم
لنفترض أنّ unstable_base_learning_rate هو معدّل التعلّم الذي يصبح النموذج عنده غير مستقر، وذلك باستخدام الإجراء السابق.
يتضمّن الإحماء إضافة جدول معدّل التعلّم الذي يزيد معدّل التعلّم من 0 إلى قيمة ثابتة base_learning_rate تكون أكبر بمقدار واحد على الأقل من unstable_base_learning_rate.
سيكون الإعداد التلقائي هو تجربة base_learning_rate أكبر بـ 10 مرات من unstable_base_learning_rate. مع ذلك، من الممكن إعادة تنفيذ هذه العملية بأكملها، مثلاً، 100 مرة
unstable_base_learning_rate. الجدول الزمني المحدّد هو:
- زيادة تدريجية من 0 إلى base_learning_rate على مدار warmup_steps
- التدريب بمعدّل ثابت لعدد post_warmup_steps
هدفك هو العثور على أقل عدد من warmup_steps يتيح لك الوصول إلى معدلات تعلّم قصوى أعلى بكثير من unstable_base_learning_rate.
لذا، يجب ضبط warmup_steps وpost_warmup_steps لكل base_learning_rate. عادةً ما يكون من المناسب ضبط post_warmup_steps على
2*warmup_steps.
يمكن ضبط فترة الإحماء بشكل مستقل عن جدول التراجع الحالي. يجب أن يتم مسح warmup_steps
ببعض القيم المختلفة من حيث الحجم. على سبيل المثال، يمكن أن تحاول دراسة نموذجية استخدام [10, 1000, 10,000, 100,000]. يجب ألا تزيد أكبر نقطة ممكنة عن% 10 من max_train_steps.
بعد إنشاء warmup_steps لا يؤدي إلى تفجير التدريب عند base_learning_rate،
يجب تطبيقه على النموذج الأساسي.
بشكل أساسي، أضِف هذه الجدولة إلى الجدولة الحالية، واستخدِم أفضل خيار لنقطة التحقّق الذي تمت مناقشته أعلاه لمقارنة هذه التجربة بالقيمة الأساسية. على سبيل المثال، إذا كان لدينا في الأصل 10,000 max_train_steps
وأجرينا warmup_steps لمدة 1,000 خطوة، يجب أن يستمر إجراء التدريب الجديد
لمدة 11,000 خطوة إجمالاً.
إذا كانت warmup_steps الطويلة مطلوبة للتدريب المستقر (أكثر من% 5 من max_train_steps)، قد تحتاج إلى زيادة max_train_steps لتفسير ذلك.
ليس هناك قيمة "نموذجية" في النطاق الكامل لأحمال العمل. تحتاج بعض النماذج إلى 100 خطوة فقط، بينما قد تحتاج نماذج أخرى (خاصةً المحوّلات) إلى 40 ألف خطوة أو أكثر.
اقتصاص التدرّج
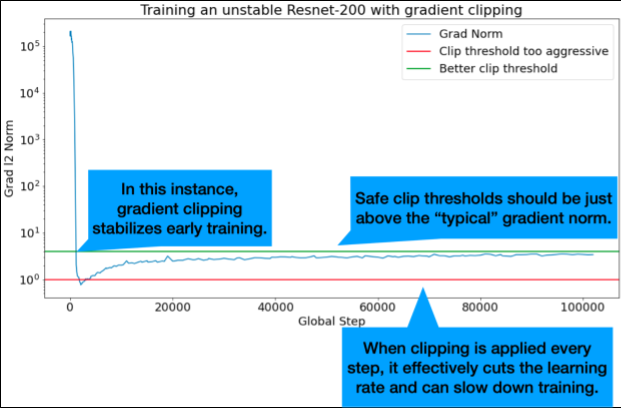
يكون اقتصاص التدرّج مفيدًا في الحالات التي تحدث فيها مشاكل كبيرة أو استثنائية في التدرّج. يمكن أن يحلّ Gradient Clipping إحدى المشكلتين التاليتين:
- عدم استقرار التدريب المبكر (معيار تدرّج كبير في المراحل المبكرة)
- حالات عدم استقرار في منتصف عملية التدريب (ارتفاعات مفاجئة في التدرّج في منتصف عملية التدريب)
في بعض الأحيان، يمكن أن تؤدي فترات الإحماء الأطول إلى تصحيح حالات عدم الاستقرار التي لا يمكن تصحيحها باستخدام ميزة "اقتصاص التدرّج". لمزيد من التفاصيل، راجِع مقالة الإحماء بمعدّل التعلّم.
🤖 ماذا عن القص أثناء فترة الإحماء؟
تكون الحدود المثالية لقص القيم أعلى بقليل من معيار التدرّج "العادي".
في ما يلي مثال على كيفية تنفيذ عملية الحدّ من التدرّج:
- إذا كان معيار التدرّج $\left | g \right |$ أكبر من الحد الأدنى لقطع التدرّج $\lambda$، نفّذ ما يلي: ${g}'= \lambda \times \frac{g}{\left | g \right |}$ حيث ${g}'$ هو التدرّج الجديد.
تسجيل معيار التدرج غير المقطوع أثناء التدريب تلقائيًا، يتم إنشاء:
- رسم بياني لمعيار التدرّج مقابل الخطوة
- مدرّج تكراري لمعايير التدرّج مجمّعة على جميع الخطوات
اختَر حدًا لقص التدرّج استنادًا إلى الشريحة المئوية التسعين لمعايير التدرّج. يختلف الحدّ الأدنى حسب عبء العمل، ولكن% 90 هي نقطة بداية جيدة. إذا لم تنجح نسبة% 90، يمكنك تعديل هذا الحدّ.
🤖 ماذا عن نوع من الاستراتيجية التكيّفية؟
إذا جرّبت ميزة "اقتصاص التدرّج" واستمرت مشاكل عدم الثبات، يمكنك تجربة تطبيقها بشكل أكثر صرامة، أي يمكنك تقليل الحدّ.
إنّ الحدّ من التدرّج بشكل مفرط (أي، الحدّ من أكثر من% 50 من التعديلات) هو في الأساس طريقة غريبة لخفض معدّل التعلّم. إذا كنت تستخدم عملية قص شديدة، من الأفضل أن تخفّض معدّل التعلّم بدلاً من ذلك.
لماذا تُطلق على معدّل التعلّم ومعلمات التحسين الأخرى اسم "مُدخلات ضبط"؟ وهي ليست مَعلمات لأي توزيع سابق.
للمصطلح "المَعلم الفائق" معنى دقيق في تعلُّم الآلة المستند إلى الإحصاء البايزي، لذا فإنّ الإشارة إلى معدّل التعلّم ومعظم مَعلمات التعلّم العميق الأخرى القابلة للضبط على أنّها "مَعلمات فائقة" هو استخدام غير صحيح للمصطلح. نفضّل استخدام مصطلح "المَعلمة الفوقية" للإشارة إلى معدّلات التعلّم ومَعلمات التصميم وجميع العناصر الأخرى القابلة للضبط في التعلّم العميق. ويرجع ذلك إلى أنّ المَعلمة الفوقية تتجنّب أي التباس محتمل قد ينشأ عن إساءة استخدام كلمة "المَعلمة الفائقة". ويزداد احتمال حدوث هذا الالتباس عند مناقشة التحسين البايزي، حيث تتضمّن نماذج سطح الاستجابة الاحتمالية معلَمات فائقة حقيقية خاصة بها.
على الرغم من أنّ مصطلح "المَعلمات الفائقة" قد يكون مربكًا، إلا أنّه أصبح شائعًا جدًا في مجال التعلّم العميق. لذلك، بالنسبة إلى هذا المستند المخصّص لجمهور واسع يتضمّن العديد من الأشخاص الذين من غير المرجّح أن يكونوا على دراية بهذه التفاصيل الفنية، اخترنا المساهمة في مصدر واحد للالتباس في هذا المجال على أمل تجنُّب مصدر آخر. مع ذلك، قد نتّخذ قرارًا مختلفًا عند نشر ورقة بحثية، وننصح الآخرين باستخدام "المعلَمة الفوقية" بدلاً من ذلك في معظم السياقات.
لماذا لا يتم ضبط حجم الدفعة لتحسين أداء مجموعة التحقّق مباشرةً؟
يؤثر تغيير حجم الدفعة بدون تغيير أي تفاصيل أخرى في مسار التدريب غالبًا في أداء مجموعة التحقّق. ومع ذلك، يختفي الفرق في أداء مجموعة التحقّق بين حجمَي الدُفعات عادةً إذا تم تحسين مسار التدريب بشكل مستقل لكل حجم دفعة.
إنّ المعلَمات الفائقة التي تتفاعل بشكل كبير مع حجم الدفعة، وبالتالي، الأكثر أهمية لضبطها بشكل منفصل لكل حجم دفعة، هي المعلَمات الفائقة للمحسِّن (على سبيل المثال، معدّل التعلّم، والزخم) والمعلَمات الفائقة للتسوية. تؤدي أحجام الدُفعات الأصغر إلى إدخال المزيد من الضوضاء إلى خوارزمية التدريب بسبب تباين العيّنات. ويمكن أن يكون لهذا التشويش تأثير منتظم. وبالتالي، قد تكون أحجام الدُفعات الأكبر أكثر عرضةً للزيادة في التوافق مع البيانات التدريبية، وقد تتطلّب تسوية أقوى و/أو تقنيات تسوية إضافية. بالإضافة إلى ذلك، قد تحتاج إلى تعديل عدد خطوات التدريب عند تغيير حجم الدفعة.
بعد أخذ كل هذه التأثيرات في الاعتبار، لا يتوفّر أي دليل مقنع على أنّ حجم الدفعة يؤثر في الحد الأقصى للأداء الذي يمكن تحقيقه في عملية التحقّق من الصحة. للحصول على التفاصيل، يُرجى الاطّلاع على Shallue et al. 2018.
ما هي قواعد التعديل لجميع خوارزميات التحسين الشائعة؟
يقدّم هذا القسم قواعد تعديل للعديد من خوارزميات التحسين الرائجة.
النزول المتدرّج العشوائي (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
حيث $\eta_t$ هو معدل التعلّم في الخطوة $t$.
الزخم
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
حيث $\eta_t$ هو معدّل التعلّم في الخطوة $t$، و $\gamma$ هو معامل الزخم.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
حيث $\eta_t$ هو معدّل التعلّم في الخطوة $t$، و $\gamma$ هو معامل الزخم.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
