Bagaimana cara men-debug dan mengurangi kegagalan pengoptimalan?
Ringkasan: Jika model mengalami kesulitan pengoptimalan, Anda harus memperbaikinya sebelum mencoba hal lain. Mendiagnosis dan memperbaiki kegagalan pelatihan adalah bidang riset yang terus berkembang.
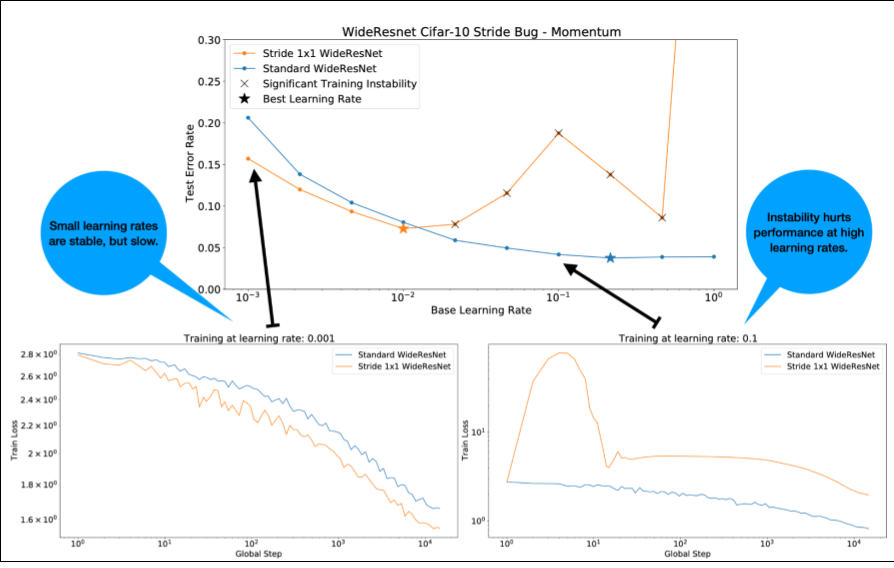
Perhatikan hal berikut tentang Gambar 4:
- Mengubah langkah tidak menurunkan performa pada kecepatan pembelajaran yang rendah.
- Kecepatan pembelajaran yang tinggi tidak lagi berfungsi dengan baik karena ketidakstabilan.
- Menerapkan 1.000 langkah pemanasan kecepatan pembelajaran menyelesaikan instance ketidakstabilan ini, sehingga memungkinkan pelatihan yang stabil pada kecepatan pembelajaran maksimum 0,1.
Mengidentifikasi workload yang tidak stabil
Beban kerja apa pun akan menjadi tidak stabil jika kecepatan pembelajaran terlalu besar. Ketidakstabilan hanya menjadi masalah jika memaksa Anda menggunakan laju pembelajaran yang terlalu kecil. Setidaknya ada dua jenis ketidakstabilan pelatihan yang perlu dibedakan:
- Ketidakstabilan saat inisialisasi atau di awal pelatihan.
- Ketidakstabilan mendadak di tengah pelatihan.
Anda dapat mengambil pendekatan sistematis untuk mengidentifikasi masalah stabilitas dalam workload Anda dengan melakukan hal berikut:
- Lakukan penyapuan kecepatan pembelajaran dan temukan kecepatan pembelajaran terbaik lr*.
- Plot kurva kerugian pelatihan untuk kecepatan pembelajaran tepat di atas lr*.
- Jika laju pembelajaran > lr* menunjukkan ketidakstabilan kerugian (kerugian meningkat, bukan menurun selama periode pelatihan), maka memperbaiki ketidakstabilan biasanya akan meningkatkan pelatihan.
Mencatat norma L2 dari gradien kerugian penuh selama pelatihan, karena nilai pencilan dapat menyebabkan ketidakstabilan palsu di tengah pelatihan. Hal ini dapat menginformasikan seberapa agresif gradien atau pembaruan bobot dipangkas.
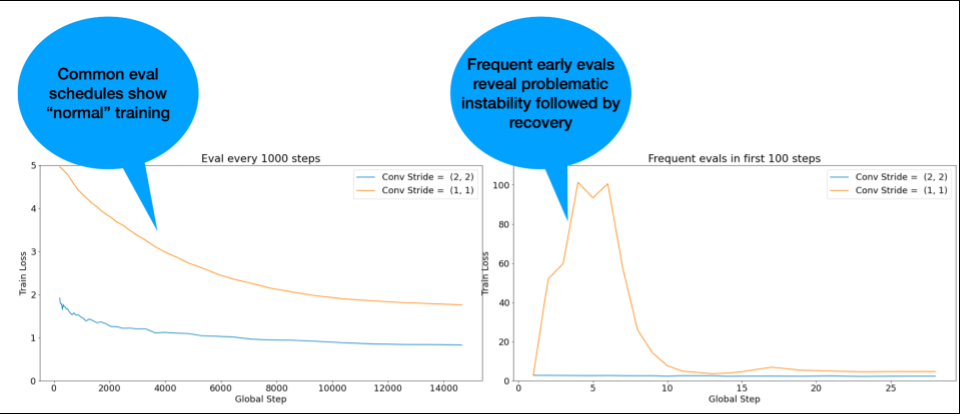
CATATAN: Beberapa model menunjukkan ketidakstabilan yang sangat awal, diikuti dengan pemulihan yang menghasilkan pelatihan yang lambat tetapi stabil. Jadwal evaluasi umum dapat melewatkan masalah ini karena tidak cukup sering melakukan evaluasi.
Untuk memeriksanya, Anda dapat melatih untuk menjalankan versi singkat hanya ~500 langkah
menggunakan lr = 2 * current best, tetapi mengevaluasi setiap langkah.
Perbaikan potensial untuk pola ketidakstabilan umum
Pertimbangkan kemungkinan perbaikan berikut untuk pola ketidakstabilan umum:
- Terapkan pemanasan kecepatan pembelajaran. Cara ini paling cocok untuk ketidakstabilan pelatihan awal.
- Menerapkan pemotongan gradien. Hal ini baik untuk ketidakstabilan awal dan pertengahan pelatihan, dan dapat memperbaiki beberapa inisialisasi buruk yang tidak dapat dilakukan oleh pemanasan.
- Coba pengoptimal baru. Terkadang Adam dapat menangani ketidakstabilan yang tidak dapat ditangani Momentum. Ini adalah area riset yang aktif.
- Pastikan Anda menggunakan praktik terbaik dan inisialisasi terbaik untuk arsitektur model Anda (contoh akan diberikan). Tambahkan koneksi residual dan normalisasi jika model belum memilikinya.
- Lakukan normalisasi sebagai operasi terakhir sebelum residu. Contoh:
x + Norm(f(x))Perhatikan bahwaNorm(x + f(x))dapat menyebabkan masalah. - Coba inisialisasi cabang residual ke 0. (Lihat ReZero is All You Need: Fast Convergence at Large Depth.)
- Turunkan kecepatan pembelajaran. Ini adalah upaya terakhir.
Pemanasan kecepatan pembelajaran
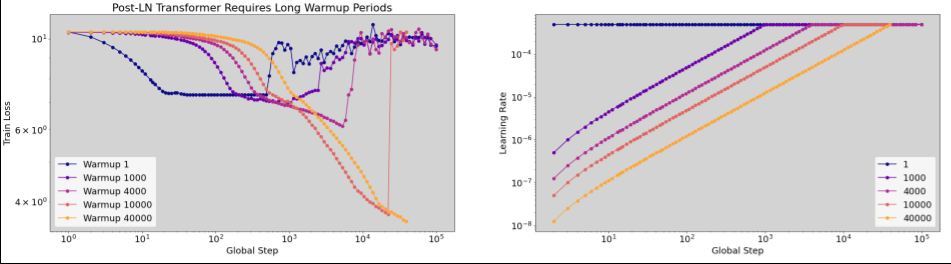
Waktu untuk menerapkan pemanasan kecepatan pembelajaran
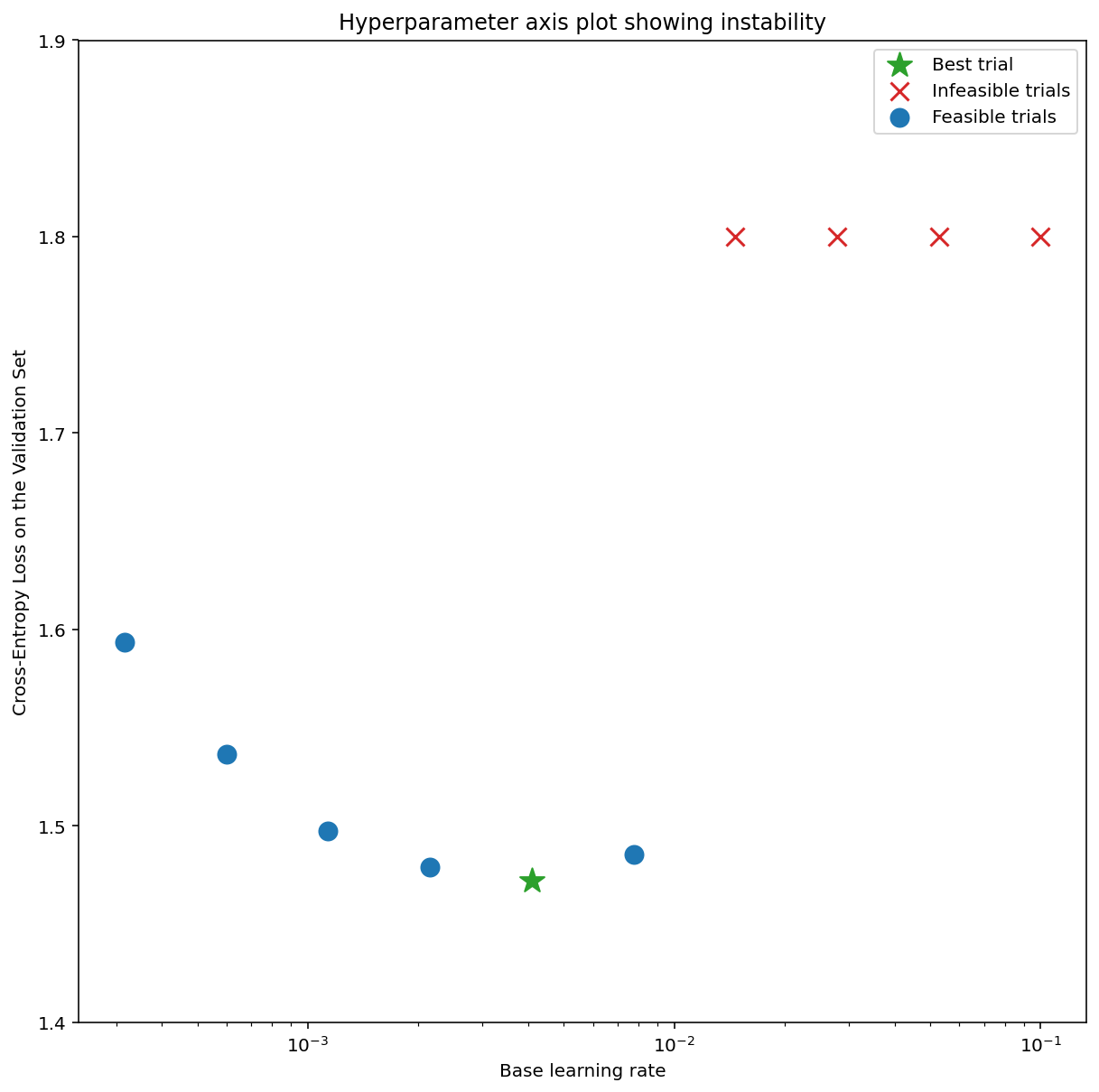
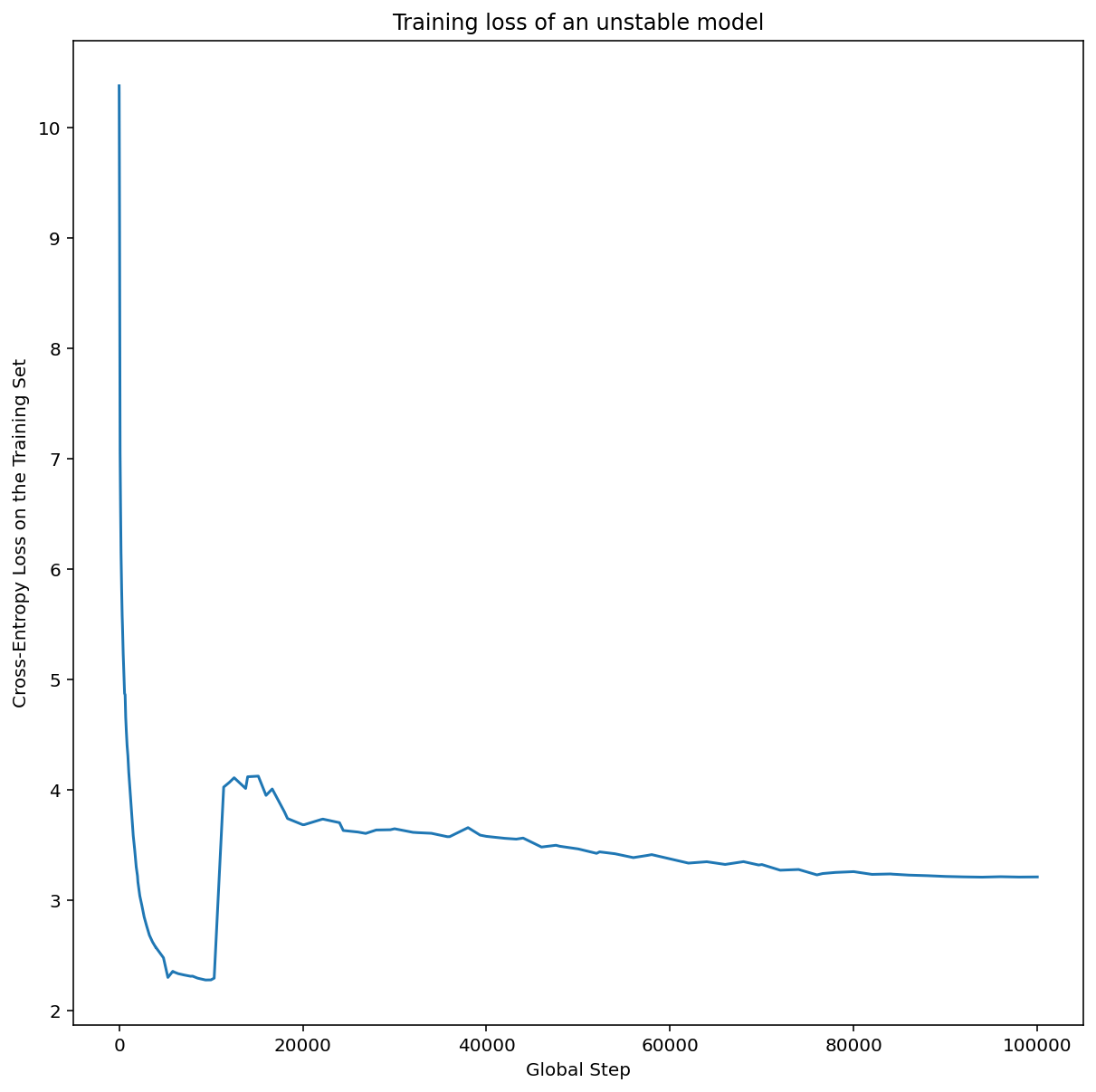
Gambar 7a menunjukkan plot sumbu hyperparameter yang mengindikasikan model mengalami ketidakstabilan pengoptimalan, karena laju pembelajaran terbaik berada tepat di tepi ketidakstabilan.
Gambar 7b menunjukkan cara memverifikasi hal ini dengan memeriksa kerugian pelatihan model yang dilatih dengan laju pembelajaran 5x atau 10x lebih besar daripada puncak ini. Jika plot tersebut menunjukkan peningkatan kerugian secara tiba-tiba setelah penurunan yang stabil (misalnya, pada langkah ~10 ribu pada gambar di atas), berarti model kemungkinan mengalami ketidakstabilan pengoptimalan.
Cara menerapkan pemanasan kecepatan pembelajaran
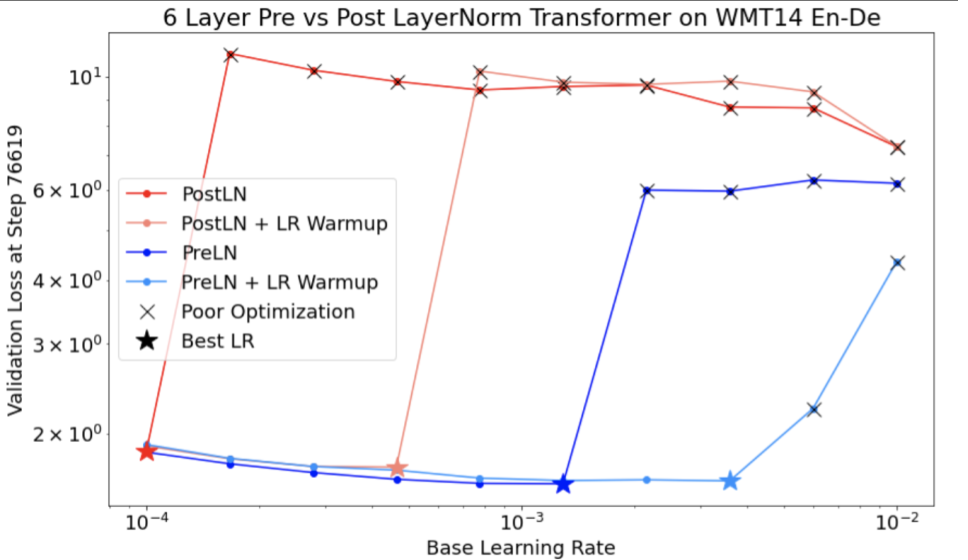
Misalkan unstable_base_learning_rate adalah kecepatan pembelajaran saat model
menjadi tidak stabil, menggunakan prosedur sebelumnya.
Pemanasan melibatkan penambahan jadwal kecepatan pembelajaran yang meningkatkan kecepatan pembelajaran dari 0 ke base_learning_rate yang stabil dan setidaknya satu kali lebih besar dari unstable_base_learning_rate.
Defaultnya adalah mencoba base_learning_rate yang 10x
unstable_base_learning_rate. Namun, perlu diperhatikan bahwa Anda dapat menjalankan seluruh prosedur ini lagi untuk sesuatu seperti 100x unstable_base_learning_rate. Jadwal spesifiknya adalah:
- Tingkatkan dari 0 ke base_learning_rate selama warmup_steps.
- Latih dengan kecepatan konstan untuk post_warmup_steps.
Tujuan Anda adalah menemukan jumlah warmup_steps terpendek yang memungkinkan Anda mengakses kecepatan pembelajaran puncak yang jauh lebih tinggi daripada unstable_base_learning_rate.
Jadi, untuk setiap base_learning_rate, Anda perlu menyesuaikan warmup_steps dan
post_warmup_steps. Biasanya tidak masalah untuk menyetel post_warmup_steps menjadi
2*warmup_steps.
Pemanasan dapat disesuaikan secara terpisah dari jadwal peluruhan yang ada. warmup_steps
harus disapu pada beberapa urutan besarnya yang berbeda. Misalnya, studi contoh dapat mencoba [10, 1000, 10,000, 100,000]. Titik yang paling besar dan layak tidak boleh lebih dari 10% dari max_train_steps.
Setelah warmup_steps yang tidak mengacaukan pelatihan pada base_learning_rate
ditetapkan, warmup_steps tersebut harus diterapkan ke model dasar.
Pada dasarnya, tambahkan jadwal ini ke jadwal yang ada, dan gunakan
pemilihan checkpoint optimal yang dibahas di atas untuk membandingkan eksperimen
ini dengan dasar. Misalnya, jika awalnya kita memiliki 10.000 max_train_steps
dan melakukan warmup_steps selama 1.000 langkah, prosedur pelatihan baru harus
berjalan selama total 11.000 langkah.
Jika warmup_steps yang panjang diperlukan untuk pelatihan yang stabil (>5% dari
max_train_steps), Anda mungkin perlu meningkatkan max_train_steps untuk memperhitungkan hal ini.
Sebenarnya tidak ada nilai "umum" di seluruh rentang workload. Beberapa model hanya memerlukan 100 langkah, sementara model lainnya (terutama transformer) mungkin memerlukan 40 ribu langkah atau lebih.
Pemotongan gradien
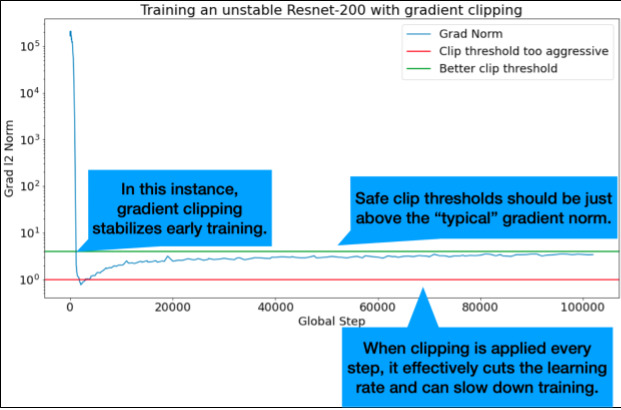
Pemangkasan gradien paling berguna saat masalah gradien besar atau pencilan terjadi. Pemangkasan Gradien dapat memperbaiki salah satu masalah berikut:
- Ketidakstabilan pelatihan awal (norma gradien besar di awal)
- Ketidakstabilan selama pelatihan (lonjakan gradien tiba-tiba di tengah pelatihan).
Terkadang periode pemanasan yang lebih lama dapat memperbaiki ketidakstabilan yang tidak dapat diperbaiki oleh pemangkasan; untuk mengetahui detailnya, lihat Pemanasan laju pembelajaran.
🤖 Bagaimana dengan pemangkasan selama pemanasan?
Nilai minimum klip yang ideal berada tepat di atas norma gradien "khas".
Berikut contoh cara melakukan kliping gradien:
- Jika norma gradien $\left | g \right |$ lebih besar daripada nilai minimum kliping gradien $\lambda$, maka lakukan ${g}'= \lambda \times \frac{g}{\left | g \right |}$ dengan ${g}'$ adalah gradien baru.
Mencatat norma gradien yang tidak diklip selama pelatihan. Secara default, buat:
- Plot norma gradien vs. langkah
- Histogram norma gradien yang digabungkan di semua langkah
Pilih nilai clipping gradien berdasarkan persentil ke-90 dari norma gradien. Nilai minimum bergantung pada beban kerja, tetapi 90% adalah titik awal yang baik. Jika 90% tidak berhasil, Anda dapat menyesuaikan nilai minimum ini.
🤖 Bagaimana dengan strategi adaptif?
Jika Anda mencoba pemangkasan gradien dan masalah ketidakstabilan tetap ada, Anda dapat mencobanya lebih keras; yaitu, Anda dapat membuat nilai minimum lebih kecil.
Pemangkasan gradien yang sangat agresif (yaitu, >50% pembaruan dipangkas), pada dasarnya, adalah cara aneh untuk mengurangi kecepatan pembelajaran. Jika Anda menggunakan pemangkasan yang sangat agresif, sebaiknya Anda cukup mengurangi kecepatan pembelajaran.
Mengapa Anda menyebut kecepatan pembelajaran dan parameter pengoptimalan lainnya sebagai hyperparameter? Nilai tersebut bukan parameter distribusi sebelumnya.
Istilah "hyperparameter" memiliki makna yang tepat dalam machine learning Bayesian, sehingga menyebut kecepatan pembelajaran dan sebagian besar parameter deep learning lain yang dapat disesuaikan sebagai "hyperparameter" dapat dikatakan sebagai penyalahgunaan terminologi. Kami lebih memilih menggunakan istilah "metaparameter" untuk kecepatan pembelajaran, parameter arsitektur, dan semua hal lain yang dapat disesuaikan dalam deep learning. Hal ini karena metaparameter menghindari potensi kebingungan yang berasal dari penyalahgunaan kata "hyperparameter". Kebingungan ini terutama mungkin terjadi saat membahas pengoptimalan Bayesian, di mana model permukaan respons probabilistik memiliki hyperparameter sebenarnya sendiri.
Sayangnya, meskipun berpotensi membingungkan, istilah "hyperparameter" telah menjadi sangat umum dalam komunitas deep learning. Oleh karena itu, untuk dokumen ini, yang ditujukan bagi audiens luas yang mencakup banyak orang yang kemungkinan tidak menyadari teknisitas ini, kami memilih untuk berkontribusi pada satu sumber kebingungan di bidang ini dengan harapan menghindari sumber kebingungan lainnya. Namun, kami mungkin membuat pilihan yang berbeda saat menerbitkan makalah penelitian, dan kami akan mendorong orang lain untuk menggunakan "metaparameter" dalam sebagian besar konteks.
Mengapa ukuran batch tidak boleh disesuaikan untuk meningkatkan performa set validasi secara langsung?
Mengubah ukuran batch tanpa mengubah detail lain dari pipeline pelatihan sering kali memengaruhi performa set validasi. Namun, perbedaan performa set validasi antara dua ukuran batch biasanya akan hilang jika pipeline pelatihan dioptimalkan secara terpisah untuk setiap ukuran batch.
Hyperparameter yang berinteraksi paling kuat dengan ukuran batch, dan oleh karena itu paling penting untuk disesuaikan secara terpisah untuk setiap ukuran batch, adalah hyperparameter pengoptimal (misalnya, kecepatan pembelajaran, momentum) dan hyperparameter regularisasi. Ukuran batch yang lebih kecil akan menimbulkan lebih banyak noise ke dalam algoritma pelatihan karena varians sampel. Derau ini dapat memiliki efek regularisasi. Oleh karena itu, ukuran batch yang lebih besar lebih rentan terhadap overfitting dan mungkin memerlukan regularisasi yang lebih kuat dan/atau teknik regularisasi tambahan. Selain itu, Anda mungkin perlu menyesuaikan jumlah langkah pelatihan saat mengubah ukuran batch.
Setelah semua efek ini dipertimbangkan, tidak ada bukti meyakinkan bahwa ukuran batch memengaruhi performa validasi maksimum yang dapat dicapai. Untuk mengetahui detailnya, lihat Shallue et al. 2018.
Apa aturan pembaruan untuk semua algoritma pengoptimalan populer?
Bagian ini memberikan aturan pembaruan untuk beberapa algoritma pengoptimalan populer.
Penurunan gradien stokastik (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Dengan $\eta_t$ adalah kecepatan pemelajaran pada langkah $t$.
Momentum
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Dengan $\eta_t$ adalah kecepatan pembelajaran pada langkah $t$, dan $\gamma$ adalah koefisien momentum.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Dengan $\eta_t$ adalah kecepatan pembelajaran pada langkah $t$, dan $\gamma$ adalah koefisien momentum.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
