কিভাবে অপ্টিমাইজেশান ব্যর্থতা ডিবাগ এবং প্রশমিত করা যেতে পারে?
সারাংশ: মডেলটি যদি অপ্টিমাইজেশান সমস্যার সম্মুখীন হয়, তবে অন্যান্য জিনিস চেষ্টা করার আগে সেগুলি ঠিক করা গুরুত্বপূর্ণ৷ প্রশিক্ষণের ব্যর্থতা নির্ণয় এবং সংশোধন করা গবেষণার একটি সক্রিয় ক্ষেত্র।
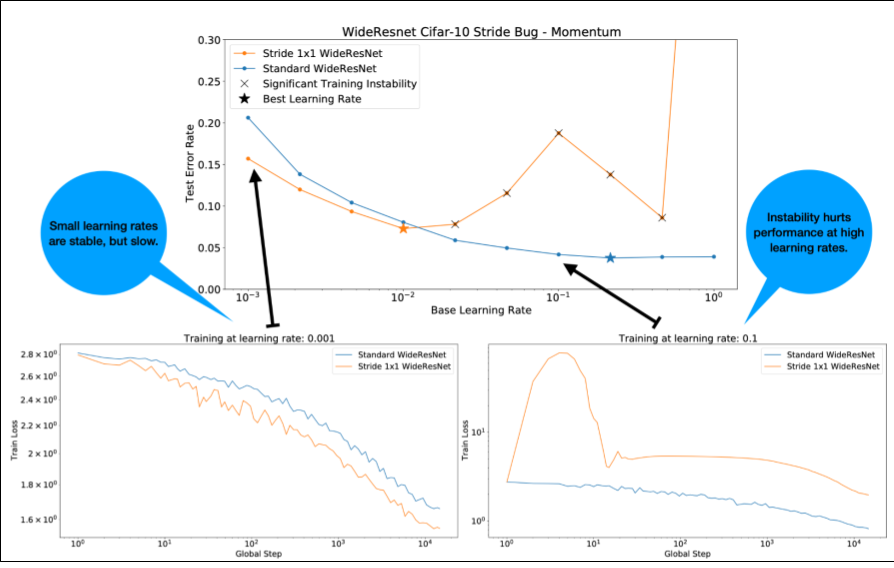
চিত্র 4 সম্পর্কে নিম্নলিখিত লক্ষ্য করুন:
- অগ্রগতির পরিবর্তন কম শেখার হারে কর্মক্ষমতা হ্রাস করে না ।
- অস্থিরতার কারণে উচ্চ শিক্ষার হার আর ভালভাবে প্রশিক্ষিত হয় না।
- লার্নিং রেট ওয়ার্মআপের 1000টি ধাপ প্রয়োগ করা অস্থিরতার এই বিশেষ দৃষ্টান্তের সমাধান করে, সর্বোচ্চ 0.1 শেখার হারে স্থিতিশীল প্রশিক্ষণের অনুমতি দেয়।
অস্থির কাজের চাপ সনাক্ত করা
শেখার হার খুব বেশি হলে যেকোনো কাজের চাপ অস্থির হয়ে যায়। অস্থিরতা শুধুমাত্র একটি সমস্যা যখন এটি আপনাকে একটি শেখার হার ব্যবহার করতে বাধ্য করে যা খুব ছোট। অন্তত দুই ধরনের প্রশিক্ষণের অস্থিরতা আলাদা করার মতো:
- শুরুতে বা প্রশিক্ষণের প্রথম দিকে অস্থিরতা।
- প্রশিক্ষণের মাঝখানে হঠাৎ অস্থিরতা।
আপনি নিম্নলিখিতগুলি করে আপনার কাজের চাপে স্থিতিশীলতার সমস্যাগুলি সনাক্ত করার জন্য একটি পদ্ধতিগত পদ্ধতি নিতে পারেন:
- শেখার হার সুইপ করুন এবং সেরা শেখার হার lr* খুঁজুন।
- শেখার হারের জন্য প্লট প্রশিক্ষণ ক্ষতি বক্ররেখা lr* এর ঠিক উপরে।
- যদি শেখার হার > lr* ক্ষতির অস্থিরতা দেখায় (প্রশিক্ষণের সময় ক্ষতি কম হয় না), তাহলে অস্থিরতা ঠিক করা সাধারণত প্রশিক্ষণের উন্নতি করে।
প্রশিক্ষণের সময় সম্পূর্ণ ক্ষতি গ্রেডিয়েন্টের L2 আদর্শ লগ করুন, যেহেতু বাইরের মান প্রশিক্ষণের মাঝখানে অস্থিরতা সৃষ্টি করতে পারে। এটি কতটা আক্রমনাত্মকভাবে গ্রেডিয়েন্ট বা ওজন আপডেট করতে পারে তা জানাতে পারে।
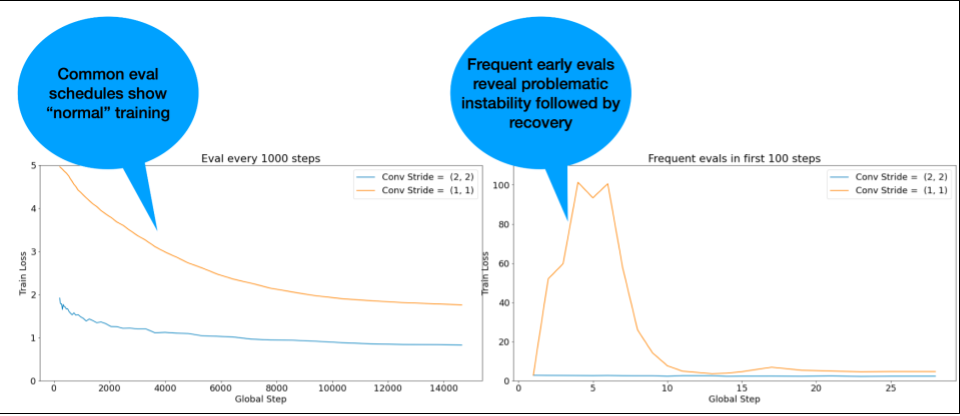
দ্রষ্টব্য: কিছু মডেল খুব তাড়াতাড়ি অস্থিরতা দেখায় এবং তারপরে পুনরুদ্ধার হয় যার ফলে ধীর কিন্তু স্থিতিশীল প্রশিক্ষণ হয়। সাধারণ মূল্যায়ন সময়সূচী ঘন ঘন যথেষ্ট মূল্যায়ন না করে এই সমস্যাগুলি মিস করতে পারে!
এটি পরীক্ষা করার জন্য, আপনি lr = 2 * current best ব্যবহার করে মাত্র ~500 ধাপের একটি সংক্ষিপ্ত দৌড়ের জন্য প্রশিক্ষণ নিতে পারেন, তবে প্রতিটি পদক্ষেপের মূল্যায়ন করুন।
সাধারণ অস্থিরতার নিদর্শনগুলির জন্য সম্ভাব্য সংশোধন
সাধারণ অস্থিরতার নিদর্শনগুলির জন্য নিম্নলিখিত সম্ভাব্য সমাধানগুলি বিবেচনা করুন:
- লার্নিং রেট ওয়ার্মআপ প্রয়োগ করুন। এটি প্রাথমিক প্রশিক্ষণের অস্থিরতার জন্য সেরা।
- গ্রেডিয়েন্ট ক্লিপিং প্রয়োগ করুন। এটি প্রাথমিক এবং মধ্য-প্রশিক্ষণের অস্থিরতা উভয়ের জন্যই ভাল, এবং এটি কিছু খারাপ শুরুর সমাধান করতে পারে যা ওয়ার্মআপ করতে পারে না।
- একটি নতুন অপ্টিমাইজার চেষ্টা করুন. কখনও কখনও অ্যাডাম অস্থিরতা পরিচালনা করতে পারে যা মোমেন্টাম পারে না। এটি গবেষণার একটি সক্রিয় ক্ষেত্র।
- নিশ্চিত করুন যে আপনি আপনার মডেল আর্কিটেকচারের জন্য সর্বোত্তম অনুশীলন এবং সর্বোত্তম সূচনা ব্যবহার করছেন (অনুসরণ করার উদাহরণ)। অবশিষ্ট সংযোগ এবং স্বাভাবিককরণ যোগ করুন যদি মডেলটিতে ইতিমধ্যে সেগুলি না থাকে।
- অবশিষ্টাংশের আগে শেষ অপারেশন হিসাবে স্বাভাবিক করুন। যেমন:
x + Norm(f(x))। মনে রাখবেন যেNorm(x + f(x))সমস্যা সৃষ্টি করতে পারে। - অবশিষ্ট শাখাগুলিকে 0-তে আরম্ভ করার চেষ্টা করুন। (দেখুন ReZeroই আপনার প্রয়োজন: বড় গভীরতায় দ্রুত কনভারজেন্স। )
- শেখার হার কম করুন। এটি একটি শেষ অবলম্বন।
শেখার হার ওয়ার্মআপ
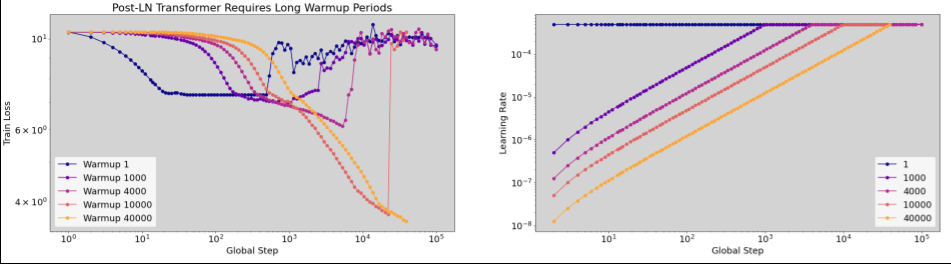
কখন লার্নিং রেট ওয়ার্মআপ প্রয়োগ করতে হবে
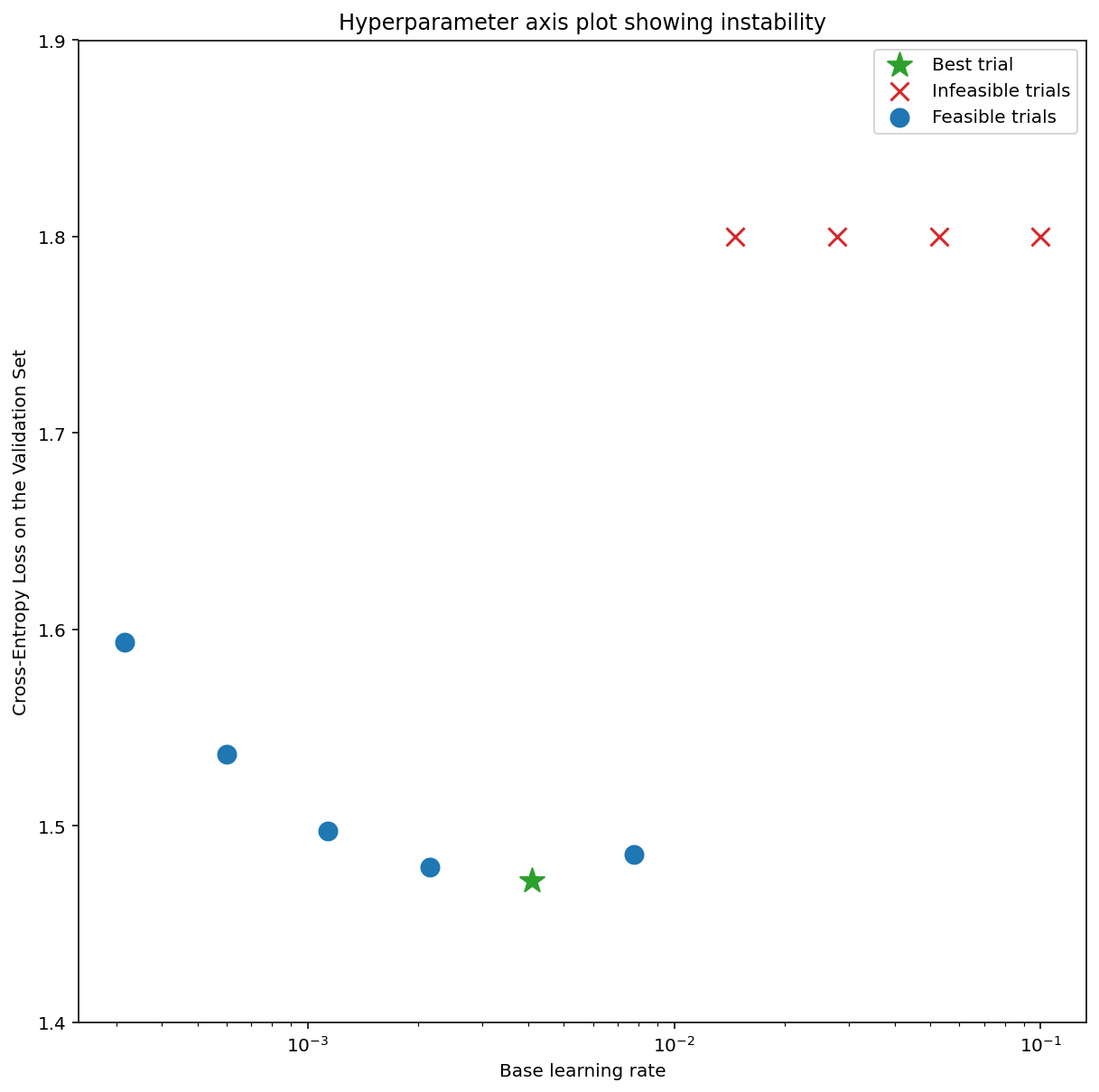
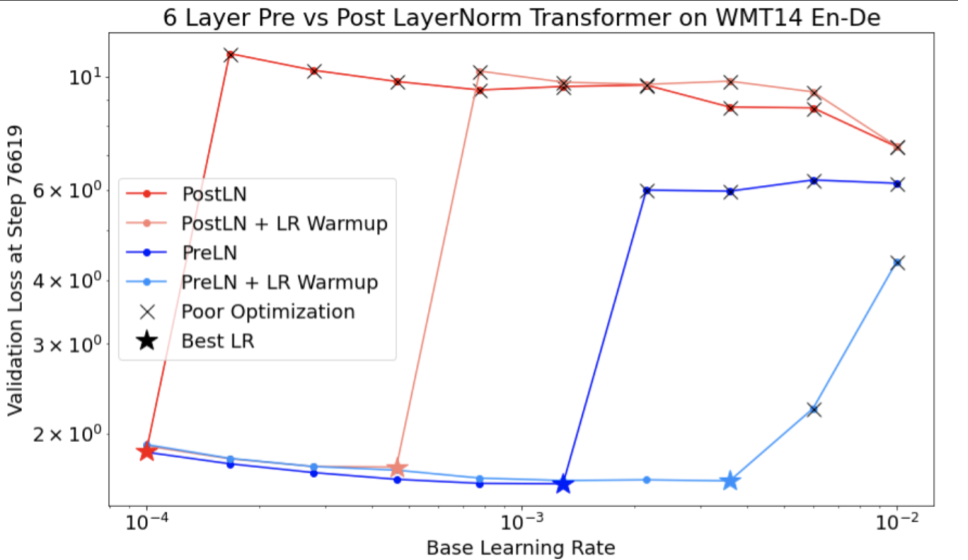
চিত্র 7a একটি হাইপারপ্যারামিটার অক্ষ প্লট দেখায় যা অপ্টিমাইজেশান অস্থিরতার সম্মুখীন একটি মডেলকে নির্দেশ করে, কারণ সেরা শেখার হারটি অস্থিরতার প্রান্তে।
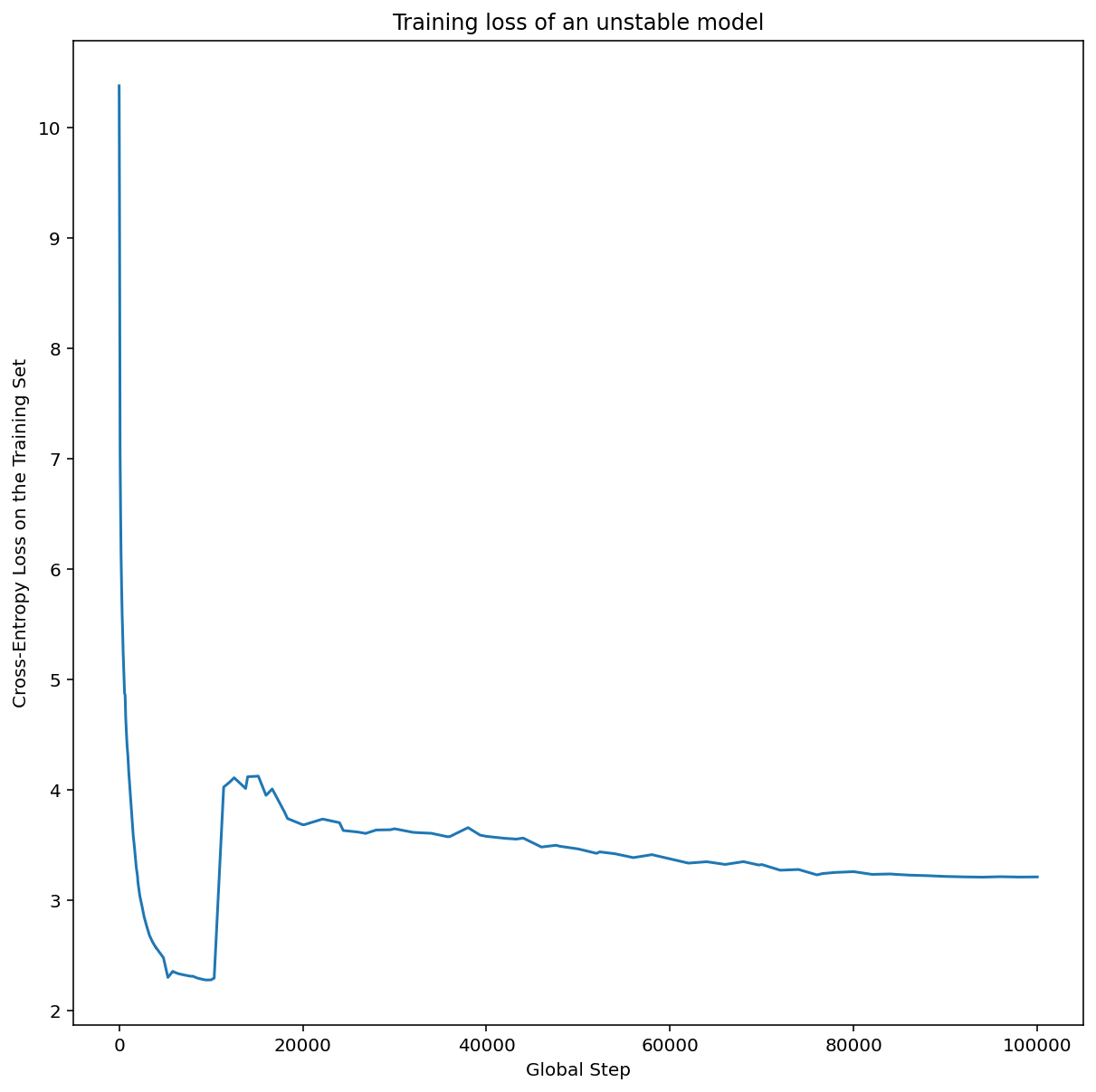
চিত্র 7b দেখায় কিভাবে এই শিখর থেকে 5x বা 10x বড় শেখার হার সহ প্রশিক্ষিত একটি মডেলের প্রশিক্ষণ ক্ষতি পরীক্ষা করে এটিকে দুবার চেক করা যেতে পারে। যদি সেই প্লটটি একটি অবিচ্ছিন্ন পতনের পর ক্ষতির আকস্মিক বৃদ্ধি দেখায় (উদাহরণস্বরূপ উপরের চিত্রে ~10k ধাপে), তাহলে মডেলটি সম্ভবত অপ্টিমাইজেশান অস্থিরতায় ভুগবে।
লার্নিং রেট ওয়ার্মআপ কীভাবে প্রয়োগ করবেন
unstable_base_learning_rate শেখার হার হতে দিন যেখানে মডেলটি পূর্ববর্তী পদ্ধতি ব্যবহার করে অস্থির হয়ে যায়।
ওয়ার্মআপের মধ্যে একটি শেখার হারের সময়সূচী প্রিপেন্ড করা জড়িত যা শেখার হারকে 0 থেকে কিছু স্থিতিশীল base_learning_rate পর্যন্ত বৃদ্ধি করে যা unstable_base_learning_rate চেয়ে অন্তত একটি ক্রম বড়। ডিফল্ট হবে একটি base_learning_rate চেষ্টা করা যা 10x unstable_base_learning_rate । যদিও মনে রাখবেন যে 100x unstable_base_learning_rate মত কিছুর জন্য এই সম্পূর্ণ পদ্ধতিটি আবার চালানো সম্ভব হবে। নির্দিষ্ট সময়সূচী হল:
- ওয়ার্মআপ_স্টেপগুলিতে 0 থেকে বেস_লার্নিং_রেট পর্যন্ত র্যাম্প করুন।
- পোস্ট_ওয়ার্মআপ_পদক্ষেপের জন্য একটি ধ্রুবক হারে ট্রেন করুন।
আপনার লক্ষ্য হল সংক্ষিপ্ততম সংখ্যক warmup_steps খুঁজে বের করা যা আপনাকে শিখর শিখর হার অ্যাক্সেস করতে দেয় যা unstable_base_learning_rate থেকে অনেক বেশি। তাই প্রতিটি base_learning_rate জন্য, আপনাকে warmup_steps এবং post_warmup_steps টিউন করতে হবে। সাধারণত post_warmup_steps 2*warmup_steps এ সেট করা ভালো।
ওয়ার্মআপ একটি বিদ্যমান ক্ষয় সময়সূচী থেকে স্বাধীনভাবে টিউন করা যেতে পারে। warmup_steps কয়েকটি ভিন্ন মাত্রার ক্রমানুসারে সুইপ করা উচিত। উদাহরণস্বরূপ, একটি উদাহরণ অধ্যয়ন চেষ্টা করতে পারে [10, 1000, 10,000, 100,000] । সবচেয়ে বড় সম্ভাব্য বিন্দু max_train_steps এর 10% এর বেশি হওয়া উচিত নয়।
একবার একটি warmup_steps যা base_learning_rate প্রশিক্ষণকে উড়িয়ে দেয় না তা প্রতিষ্ঠিত হয়ে গেলে, এটি বেসলাইন মডেলে প্রয়োগ করা উচিত। মূলত, এই সময়সূচীটিকে বিদ্যমান সময়সূচীতে প্রিপেন্ড করুন এবং এই পরীক্ষাটিকে বেসলাইনের সাথে তুলনা করতে উপরে আলোচিত সর্বোত্তম চেকপয়েন্ট নির্বাচন ব্যবহার করুন। উদাহরণ স্বরূপ, যদি আমাদের প্রাথমিকভাবে 10,000টি max_train_steps থাকে এবং 1000টি ধাপের জন্য warmup_steps করে থাকি, তাহলে নতুন প্রশিক্ষণ পদ্ধতিটি মোট 11,000টি ধাপের জন্য চালানো উচিত।
যদি স্থিতিশীল প্রশিক্ষণের জন্য দীর্ঘ warmup_steps প্রয়োজন হয় (> 5% max_train_steps ), তাহলে এর জন্য আপনাকে max_train_steps বাড়াতে হবে।
ওয়ার্কলোডের সম্পূর্ণ পরিসীমা জুড়ে সত্যিই একটি "সাধারণ" মান নেই। কিছু মডেলের জন্য শুধুমাত্র 100 ধাপ প্রয়োজন, অন্যদের (বিশেষ করে ট্রান্সফরমার) 40k+ প্রয়োজন হতে পারে।
গ্রেডিয়েন্ট ক্লিপিং
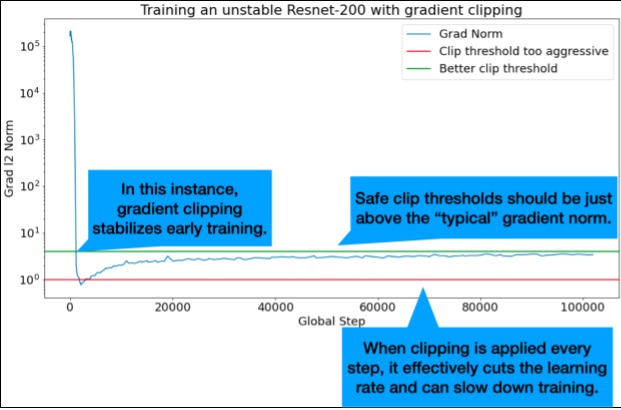
গ্রেডিয়েন্ট ক্লিপিং সবচেয়ে দরকারী যখন বড় বা বাইরের গ্রেডিয়েন্ট সমস্যা দেখা দেয়। গ্রেডিয়েন্ট ক্লিপিং নিম্নলিখিত সমস্যার যেকোনো একটি সমাধান করতে পারে:
- প্রাথমিক প্রশিক্ষণের অস্থিরতা (বড় গ্রেডিয়েন্ট আদর্শ প্রথম দিকে)
- মধ্য-প্রশিক্ষণের অস্থিরতা (হঠাৎ গ্রেডিয়েন্ট স্পাইক মধ্য প্রশিক্ষণ)।
কখনও কখনও দীর্ঘ ওয়ার্মআপ পিরিয়ড অস্থিরতা সংশোধন করতে পারে যা ক্লিপিং করে না; বিস্তারিত জানার জন্য, শেখার হার ওয়ার্মআপ দেখুন।
🤖 ওয়ার্মআপের সময় ক্লিপিং সম্পর্কে কী?
আদর্শ ক্লিপ থ্রেশহোল্ডগুলি "সাধারণ" গ্রেডিয়েন্ট আদর্শের ঠিক উপরে।
গ্রেডিয়েন্ট ক্লিপিং কীভাবে করা যেতে পারে তার একটি উদাহরণ এখানে রয়েছে:
- যদি গ্রেডিয়েন্টের আদর্শ $\left | g \right |$ গ্রেডিয়েন্ট ক্লিপিং থ্রেশহোল্ডের চেয়ে বড় $\lambda$, তারপর করুন ${g}'= \lambda \times \frac{g}{\left | g \right |}$ যেখানে ${g}'$ হল নতুন গ্রেডিয়েন্ট।
প্রশিক্ষণের সময় আনক্লিপড গ্রেডিয়েন্ট আদর্শ লগ করুন। ডিফল্টরূপে, তৈরি করুন:
- গ্রেডিয়েন্ট নর্ম বনাম ধাপের একটি প্লট
- সমস্ত ধাপে একত্রিত গ্রেডিয়েন্ট নিয়মের একটি হিস্টোগ্রাম
গ্রেডিয়েন্ট নিয়মের 90 তম শতাংশের উপর ভিত্তি করে একটি গ্রেডিয়েন্ট ক্লিপিং থ্রেশহোল্ড চয়ন করুন। থ্রেশহোল্ড কাজের চাপ নির্ভর, কিন্তু 90% একটি ভাল সূচনা পয়েন্ট। যদি 90% কাজ না করে, আপনি এই থ্রেশহোল্ড টিউন করতে পারেন।
🤖 কিছু অভিযোজিত কৌশল সম্পর্কে কি?
আপনি যদি গ্রেডিয়েন্ট ক্লিপিং চেষ্টা করেন এবং অস্থিরতার সমস্যাগুলি থেকে যায়, আপনি এটি আরও চেষ্টা করতে পারেন; যে, আপনি থ্রেশহোল্ড ছোট করতে পারেন.
অত্যন্ত আক্রমনাত্মক গ্রেডিয়েন্ট ক্লিপিং (অর্থাৎ, 50% আপডেটগুলি ক্লিপ করা হচ্ছে), মূলত, শেখার হার হ্রাস করার একটি অদ্ভুত উপায়। আপনি যদি নিজেকে অত্যন্ত আক্রমনাত্মক ক্লিপিং ব্যবহার করে দেখেন, তাহলে আপনার সম্ভবত শেখার হার কমানো উচিত।
কেন আপনি শেখার হার এবং অন্যান্য অপ্টিমাইজেশান পরামিতিগুলিকে হাইপারপ্যারামিটার বলছেন? তারা কোনো পূর্ব বন্টন পরামিতি নয়.
বায়েসিয়ান মেশিন লার্নিং-এ "হাইপারপ্যারামিটার" শব্দটির একটি সুনির্দিষ্ট অর্থ রয়েছে, তাই শেখার হার এবং অন্যান্য টিউনযোগ্য গভীর শিক্ষার প্যারামিটারগুলির বেশিরভাগকে "হাইপারপ্যারামিটার" হিসাবে উল্লেখ করা যুক্তিযুক্তভাবে পরিভাষার অপব্যবহার। আমরা শেখার হার, আর্কিটেকচারাল প্যারামিটার এবং গভীর শিক্ষার অন্যান্য সমস্ত টিউনযোগ্য জিনিসগুলির জন্য "মেটাপ্যারামিটার" শব্দটি ব্যবহার করতে পছন্দ করব। কারণ মেটাপ্যারামিটার "হাইপারপ্যারামিটার" শব্দটি অপব্যবহারের ফলে বিভ্রান্তির সম্ভাবনা এড়ায়। এই বিভ্রান্তি বিশেষত সম্ভবত যখন বায়েসিয়ান অপ্টিমাইজেশান নিয়ে আলোচনা করা হয়, যেখানে সম্ভাব্য প্রতিক্রিয়া পৃষ্ঠের মডেলগুলির নিজস্ব সত্য হাইপারপ্যারামিটার রয়েছে।
দুর্ভাগ্যবশত, সম্ভাব্য বিভ্রান্তিকর হলেও, গভীর শিক্ষার সম্প্রদায়ে "হাইপারপ্যারামিটার" শব্দটি অত্যন্ত সাধারণ হয়ে উঠেছে। অতএব, এই নথির জন্য, একটি বিস্তৃত শ্রোতাদের উদ্দেশ্যে যার মধ্যে এমন অনেক লোক রয়েছে যারা এই প্রযুক্তিগততা সম্পর্কে সচেতন হওয়ার সম্ভাবনা কম, আমরা অন্যটি এড়ানোর আশায় ক্ষেত্রের বিভ্রান্তির একটি উত্সে অবদান রাখার পছন্দ করেছি৷ এটি বলেছিল, আমরা একটি গবেষণাপত্র প্রকাশ করার সময় একটি ভিন্ন পছন্দ করতে পারি এবং আমরা বেশিরভাগ প্রসঙ্গে অন্যদের "মেটাপ্যারামিটার" ব্যবহার করতে উত্সাহিত করব৷
কেন সরাসরি বৈধতা সেট কর্মক্ষমতা উন্নত করতে ব্যাচের আকার টিউন করা উচিত নয়?
প্রশিক্ষণ পাইপলাইনের অন্য কোন বিবরণ পরিবর্তন না করে ব্যাচের আকার পরিবর্তন করা প্রায়ই বৈধতা সেটের কার্যকারিতাকে প্রভাবিত করে। যাইহোক, প্রতিটি ব্যাচের আকারের জন্য প্রশিক্ষণ পাইপলাইন স্বাধীনভাবে অপ্টিমাইজ করা হলে দুটি ব্যাচের আকারের মধ্যে বৈধতা সেটের কার্যক্ষমতার পার্থক্য সাধারণত চলে যায়।
যে হাইপারপ্যারামিটারগুলি ব্যাচের আকারের সাথে সবচেয়ে দৃঢ়ভাবে ইন্টারঅ্যাক্ট করে এবং তাই প্রতিটি ব্যাচের আকারের জন্য আলাদাভাবে সুর করা সবচেয়ে গুরুত্বপূর্ণ, সেগুলি হল অপ্টিমাইজার হাইপারপ্যারামিটার (উদাহরণস্বরূপ, শেখার হার, ভরবেগ) এবং নিয়মিতকরণের হাইপারপ্যারামিটার৷ নমুনা ভিন্নতার কারণে ছোট ব্যাচের মাপ প্রশিক্ষণের অ্যালগরিদমে আরও বেশি শব্দ করে। এই গোলমাল একটি নিয়মিত প্রভাব থাকতে পারে. সুতরাং, বৃহত্তর ব্যাচের আকারগুলি অতিরিক্ত ফিট করার প্রবণতা হতে পারে এবং আরও শক্তিশালী নিয়মিতকরণ এবং/অথবা অতিরিক্ত নিয়মিতকরণ কৌশলগুলির প্রয়োজন হতে পারে। উপরন্তু, ব্যাচের আকার পরিবর্তন করার সময় আপনাকে প্রশিক্ষণের ধাপগুলির সংখ্যা সামঞ্জস্য করতে হতে পারে।
একবার এই সমস্ত প্রভাবগুলি বিবেচনায় নেওয়া হলে, ব্যাচের আকার সর্বাধিক অর্জনযোগ্য বৈধতা কার্যকারিতাকে প্রভাবিত করে এমন কোনও বিশ্বাসযোগ্য প্রমাণ নেই। বিস্তারিত জানার জন্য, Shallue et al দেখুন। 2018
সমস্ত জনপ্রিয় অপ্টিমাইজেশান অ্যালগরিদমগুলির জন্য আপডেটের নিয়মগুলি কী কী?
এই বিভাগটি বেশ কয়েকটি জনপ্রিয় অপ্টিমাইজেশান অ্যালগরিদমের জন্য আপডেটের নিয়ম প্রদান করে।
স্টোকাস্টিক গ্রেডিয়েন্ট ডিসেন্ট (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
যেখানে $\eta_t$ হল $t$ ধাপে শেখার হার।
গতিবেগ
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
যেখানে $\eta_t$ হল $t$ ধাপে শেখার হার, এবং $\gamma$ হল ভরবেগ সহগ।
নেস্টেরভ
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
যেখানে $\eta_t$ হল $t$ ধাপে শেখার হার, এবং $\gamma$ হল ভরবেগ সহগ।
আরএমএসপ্রপ
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
অ্যাডাম
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
নাদাম
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
,কিভাবে অপ্টিমাইজেশান ব্যর্থতা ডিবাগ এবং প্রশমিত করা যেতে পারে?
সারাংশ: মডেলটি যদি অপ্টিমাইজেশান সমস্যার সম্মুখীন হয়, তবে অন্যান্য জিনিস চেষ্টা করার আগে সেগুলি ঠিক করা গুরুত্বপূর্ণ৷ প্রশিক্ষণের ব্যর্থতা নির্ণয় এবং সংশোধন করা গবেষণার একটি সক্রিয় ক্ষেত্র।

চিত্র 4 সম্পর্কে নিম্নলিখিত লক্ষ্য করুন:
- অগ্রগতির পরিবর্তন কম শেখার হারে কর্মক্ষমতা হ্রাস করে না ।
- অস্থিরতার কারণে উচ্চ শিক্ষার হার আর ভালভাবে প্রশিক্ষিত হয় না।
- লার্নিং রেট ওয়ার্মআপের 1000টি ধাপ প্রয়োগ করা অস্থিরতার এই বিশেষ দৃষ্টান্তের সমাধান করে, সর্বোচ্চ 0.1 শেখার হারে স্থিতিশীল প্রশিক্ষণের অনুমতি দেয়।
অস্থির কাজের চাপ সনাক্ত করা
শেখার হার খুব বেশি হলে যেকোনো কাজের চাপ অস্থির হয়ে যায়। অস্থিরতা শুধুমাত্র একটি সমস্যা যখন এটি আপনাকে একটি শেখার হার ব্যবহার করতে বাধ্য করে যা খুব ছোট। অন্তত দুই ধরনের প্রশিক্ষণের অস্থিরতা আলাদা করার মতো:
- শুরুতে বা প্রশিক্ষণের প্রথম দিকে অস্থিরতা।
- প্রশিক্ষণের মাঝখানে হঠাৎ অস্থিরতা।
আপনি নিম্নলিখিতগুলি করে আপনার কাজের চাপে স্থিতিশীলতার সমস্যাগুলি সনাক্ত করার জন্য একটি পদ্ধতিগত পদ্ধতি নিতে পারেন:
- শেখার হার সুইপ করুন এবং সেরা শেখার হার lr* খুঁজুন।
- শেখার হারের জন্য প্লট প্রশিক্ষণ ক্ষতি বক্ররেখা lr* এর ঠিক উপরে।
- যদি শেখার হার > lr* ক্ষতির অস্থিরতা দেখায় (প্রশিক্ষণের সময় ক্ষতি কম হয় না), তাহলে অস্থিরতা ঠিক করা সাধারণত প্রশিক্ষণের উন্নতি করে।
প্রশিক্ষণের সময় সম্পূর্ণ ক্ষতি গ্রেডিয়েন্টের L2 আদর্শ লগ করুন, যেহেতু বাইরের মান প্রশিক্ষণের মাঝখানে অস্থিরতা সৃষ্টি করতে পারে। এটি কতটা আক্রমনাত্মকভাবে গ্রেডিয়েন্ট বা ওজন আপডেট করতে পারে তা জানাতে পারে।
দ্রষ্টব্য: কিছু মডেল খুব তাড়াতাড়ি অস্থিরতা দেখায় এবং তারপরে পুনরুদ্ধার হয় যার ফলে ধীর কিন্তু স্থিতিশীল প্রশিক্ষণ হয়। সাধারণ মূল্যায়ন সময়সূচী ঘন ঘন যথেষ্ট মূল্যায়ন না করে এই সমস্যাগুলি মিস করতে পারে!
এটি পরীক্ষা করার জন্য, আপনি lr = 2 * current best ব্যবহার করে মাত্র ~500 ধাপের একটি সংক্ষিপ্ত দৌড়ের জন্য প্রশিক্ষণ নিতে পারেন, তবে প্রতিটি পদক্ষেপের মূল্যায়ন করুন।

সাধারণ অস্থিরতার নিদর্শনগুলির জন্য সম্ভাব্য সংশোধন
সাধারণ অস্থিরতার নিদর্শনগুলির জন্য নিম্নলিখিত সম্ভাব্য সমাধানগুলি বিবেচনা করুন:
- লার্নিং রেট ওয়ার্মআপ প্রয়োগ করুন। এটি প্রাথমিক প্রশিক্ষণের অস্থিরতার জন্য সেরা।
- গ্রেডিয়েন্ট ক্লিপিং প্রয়োগ করুন। এটি প্রাথমিক এবং মধ্য-প্রশিক্ষণের অস্থিরতা উভয়ের জন্যই ভাল, এবং এটি কিছু খারাপ শুরুর সমাধান করতে পারে যা ওয়ার্মআপ করতে পারে না।
- একটি নতুন অপ্টিমাইজার চেষ্টা করুন. কখনও কখনও অ্যাডাম অস্থিরতা পরিচালনা করতে পারে যা মোমেন্টাম পারে না। এটি গবেষণার একটি সক্রিয় ক্ষেত্র।
- নিশ্চিত করুন যে আপনি আপনার মডেল আর্কিটেকচারের জন্য সর্বোত্তম অনুশীলন এবং সর্বোত্তম সূচনা ব্যবহার করছেন (অনুসরণ করার উদাহরণ)। অবশিষ্ট সংযোগ এবং স্বাভাবিককরণ যোগ করুন যদি মডেলটিতে ইতিমধ্যে সেগুলি না থাকে।
- অবশিষ্টাংশের আগে শেষ অপারেশন হিসাবে স্বাভাবিক করুন। যেমন:
x + Norm(f(x))। মনে রাখবেন যেNorm(x + f(x))সমস্যা সৃষ্টি করতে পারে। - অবশিষ্ট শাখাগুলিকে 0-তে শুরু করার চেষ্টা করুন। (দেখুন ReZero হল আপনার যা প্রয়োজন: বড় গভীরতায় দ্রুত কনভারজেন্স। )
- শেখার হার কম করুন। এটি একটি শেষ অবলম্বন।
শেখার হার ওয়ার্মআপ

কখন লার্নিং রেট ওয়ার্মআপ প্রয়োগ করতে হবে


চিত্র 7a একটি হাইপারপ্যারামিটার অক্ষ প্লট দেখায় যা অপ্টিমাইজেশান অস্থিরতার সম্মুখীন একটি মডেলকে নির্দেশ করে, কারণ সেরা শেখার হারটি অস্থিরতার প্রান্তে।
চিত্র 7b দেখায় কিভাবে এই শিখর থেকে 5x বা 10x বড় শেখার হার সহ প্রশিক্ষিত একটি মডেলের প্রশিক্ষণ ক্ষতি পরীক্ষা করে এটিকে দুবার চেক করা যেতে পারে। যদি সেই প্লটটি একটি অবিচ্ছিন্ন পতনের পর ক্ষতির আকস্মিক বৃদ্ধি দেখায় (উদাহরণস্বরূপ উপরের চিত্রে ~10k ধাপে), তাহলে মডেলটি সম্ভবত অপ্টিমাইজেশান অস্থিরতায় ভুগবে।
লার্নিং রেট ওয়ার্মআপ কীভাবে প্রয়োগ করবেন

unstable_base_learning_rate শেখার হার হতে দিন যেখানে মডেলটি পূর্ববর্তী পদ্ধতি ব্যবহার করে অস্থির হয়ে যায়।
ওয়ার্মআপের মধ্যে একটি শেখার হারের সময়সূচী প্রিপেন্ড করা জড়িত যা শেখার হারকে 0 থেকে কিছু স্থিতিশীল base_learning_rate পর্যন্ত বৃদ্ধি করে যা unstable_base_learning_rate চেয়ে অন্তত একটি ক্রম বড়। ডিফল্ট হবে একটি base_learning_rate চেষ্টা করা যা 10x unstable_base_learning_rate । যদিও মনে রাখবেন যে 100x unstable_base_learning_rate মত কিছুর জন্য এই সম্পূর্ণ পদ্ধতিটি আবার চালানো সম্ভব হবে। নির্দিষ্ট সময়সূচী হল:
- ওয়ার্মআপ_স্টেপগুলিতে 0 থেকে বেস_লার্নিং_রেট পর্যন্ত র্যাম্প করুন।
- পোস্ট_ওয়ার্মআপ_পদক্ষেপের জন্য একটি ধ্রুবক হারে ট্রেন করুন।
আপনার লক্ষ্য হল সংক্ষিপ্ততম সংখ্যক warmup_steps খুঁজে বের করা যা আপনাকে শিখর শিখর হার অ্যাক্সেস করতে দেয় যা unstable_base_learning_rate থেকে অনেক বেশি। তাই প্রতিটি base_learning_rate জন্য, আপনাকে warmup_steps এবং post_warmup_steps টিউন করতে হবে। সাধারণত post_warmup_steps 2*warmup_steps এ সেট করা ভালো।
ওয়ার্মআপ একটি বিদ্যমান ক্ষয় সময়সূচী থেকে স্বাধীনভাবে টিউন করা যেতে পারে। warmup_steps কয়েকটি ভিন্ন মাত্রার ক্রমানুসারে সুইপ করা উচিত। উদাহরণস্বরূপ, একটি উদাহরণ অধ্যয়ন চেষ্টা করতে পারে [10, 1000, 10,000, 100,000] । সবচেয়ে বড় সম্ভাব্য বিন্দু max_train_steps এর 10% এর বেশি হওয়া উচিত নয়।
একবার একটি warmup_steps যা base_learning_rate প্রশিক্ষণকে উড়িয়ে দেয় না তা প্রতিষ্ঠিত হয়ে গেলে, এটি বেসলাইন মডেলে প্রয়োগ করা উচিত। মূলত, এই সময়সূচীটিকে বিদ্যমান সময়সূচীতে প্রিপেন্ড করুন এবং এই পরীক্ষাটিকে বেসলাইনের সাথে তুলনা করতে উপরে আলোচিত সর্বোত্তম চেকপয়েন্ট নির্বাচন ব্যবহার করুন। উদাহরণ স্বরূপ, যদি আমাদের প্রাথমিকভাবে 10,000টি max_train_steps থাকে এবং 1000টি ধাপের জন্য warmup_steps করে থাকি, তাহলে নতুন প্রশিক্ষণ পদ্ধতিটি মোট 11,000টি ধাপের জন্য চালানো উচিত।
যদি স্থিতিশীল প্রশিক্ষণের জন্য দীর্ঘ warmup_steps প্রয়োজন হয় (> 5% max_train_steps ), তাহলে এর জন্য আপনাকে max_train_steps বাড়াতে হবে।
ওয়ার্কলোডের সম্পূর্ণ পরিসীমা জুড়ে সত্যিই একটি "সাধারণ" মান নেই। কিছু মডেলের জন্য শুধুমাত্র 100 ধাপ প্রয়োজন, অন্যদের (বিশেষ করে ট্রান্সফরমার) 40k+ প্রয়োজন হতে পারে।
গ্রেডিয়েন্ট ক্লিপিং

গ্রেডিয়েন্ট ক্লিপিং সবচেয়ে দরকারী যখন বড় বা বাইরের গ্রেডিয়েন্ট সমস্যা দেখা দেয়। গ্রেডিয়েন্ট ক্লিপিং নিম্নলিখিত সমস্যার যেকোনো একটি সমাধান করতে পারে:
- প্রাথমিক প্রশিক্ষণের অস্থিরতা (বড় গ্রেডিয়েন্ট আদর্শ প্রথম দিকে)
- মধ্য-প্রশিক্ষণের অস্থিরতা (হঠাৎ গ্রেডিয়েন্ট স্পাইক মধ্য প্রশিক্ষণ)।
কখনও কখনও দীর্ঘ ওয়ার্মআপ পিরিয়ড অস্থিরতা সংশোধন করতে পারে যা ক্লিপিং করে না; বিস্তারিত জানার জন্য, শেখার হার ওয়ার্মআপ দেখুন।
🤖 ওয়ার্মআপের সময় ক্লিপিং সম্পর্কে কী?
আদর্শ ক্লিপ থ্রেশহোল্ডগুলি "সাধারণ" গ্রেডিয়েন্ট আদর্শের ঠিক উপরে।
গ্রেডিয়েন্ট ক্লিপিং কীভাবে করা যেতে পারে তার একটি উদাহরণ এখানে রয়েছে:
- যদি গ্রেডিয়েন্টের আদর্শ $\left | g \right |$ গ্রেডিয়েন্ট ক্লিপিং থ্রেশহোল্ডের চেয়ে বড় $\lambda$, তারপর করুন ${g}'= \lambda \times \frac{g}{\left | g \right |}$ যেখানে ${g}'$ হল নতুন গ্রেডিয়েন্ট।
প্রশিক্ষণের সময় আনক্লিপড গ্রেডিয়েন্ট আদর্শ লগ করুন। ডিফল্টরূপে, তৈরি করুন:
- গ্রেডিয়েন্ট নর্ম বনাম ধাপের একটি প্লট
- সমস্ত ধাপে একত্রিত গ্রেডিয়েন্ট নিয়মের একটি হিস্টোগ্রাম
গ্রেডিয়েন্ট নিয়মের 90 তম শতাংশের উপর ভিত্তি করে একটি গ্রেডিয়েন্ট ক্লিপিং থ্রেশহোল্ড চয়ন করুন। থ্রেশহোল্ড কাজের চাপ নির্ভর, কিন্তু 90% একটি ভাল সূচনা পয়েন্ট। যদি 90% কাজ না করে, আপনি এই থ্রেশহোল্ড টিউন করতে পারেন।
🤖 কিছু অভিযোজিত কৌশল সম্পর্কে কি?
আপনি যদি গ্রেডিয়েন্ট ক্লিপিং চেষ্টা করেন এবং অস্থিরতার সমস্যাগুলি থেকে যায়, আপনি এটি আরও চেষ্টা করতে পারেন; যে, আপনি থ্রেশহোল্ড ছোট করতে পারেন.
অত্যন্ত আক্রমনাত্মক গ্রেডিয়েন্ট ক্লিপিং (অর্থাৎ, 50% আপডেটগুলি ক্লিপ করা হচ্ছে), মূলত, শেখার হার হ্রাস করার একটি অদ্ভুত উপায়। আপনি যদি নিজেকে অত্যন্ত আক্রমনাত্মক ক্লিপিং ব্যবহার করে দেখেন, তাহলে আপনার সম্ভবত শেখার হার কমানো উচিত।
কেন আপনি শেখার হার এবং অন্যান্য অপ্টিমাইজেশান পরামিতিগুলিকে হাইপারপ্যারামিটার বলছেন? তারা কোনো পূর্ব বন্টন পরামিতি নয়.
বায়েসিয়ান মেশিন লার্নিং-এ "হাইপারপ্যারামিটার" শব্দটির একটি সুনির্দিষ্ট অর্থ রয়েছে, তাই শেখার হার এবং অন্যান্য টিউনযোগ্য গভীর শিক্ষার প্যারামিটারগুলির বেশিরভাগকে "হাইপারপ্যারামিটার" হিসাবে উল্লেখ করা যুক্তিযুক্তভাবে পরিভাষার অপব্যবহার। আমরা শেখার হার, আর্কিটেকচারাল প্যারামিটার এবং গভীর শিক্ষার অন্যান্য সমস্ত টিউনযোগ্য জিনিসগুলির জন্য "মেটাপ্যারামিটার" শব্দটি ব্যবহার করতে পছন্দ করব। কারণ মেটাপ্যারামিটার "হাইপারপ্যারামিটার" শব্দটি অপব্যবহারের ফলে বিভ্রান্তির সম্ভাবনা এড়ায়। এই বিভ্রান্তি বিশেষত সম্ভবত যখন বায়েসিয়ান অপ্টিমাইজেশান নিয়ে আলোচনা করা হয়, যেখানে সম্ভাব্য প্রতিক্রিয়া পৃষ্ঠের মডেলগুলির নিজস্ব সত্য হাইপারপ্যারামিটার রয়েছে।
দুর্ভাগ্যবশত, সম্ভাব্য বিভ্রান্তিকর হলেও, গভীর শিক্ষার সম্প্রদায়ে "হাইপারপ্যারামিটার" শব্দটি অত্যন্ত সাধারণ হয়ে উঠেছে। অতএব, এই নথির জন্য, একটি বিস্তৃত শ্রোতাদের উদ্দেশ্যে যার মধ্যে এমন অনেক লোক রয়েছে যারা এই প্রযুক্তিগততা সম্পর্কে সচেতন হওয়ার সম্ভাবনা কম, আমরা অন্যটি এড়ানোর আশায় ক্ষেত্রের বিভ্রান্তির একটি উত্সে অবদান রাখার পছন্দ করেছি৷ এটি বলেছিল, আমরা একটি গবেষণাপত্র প্রকাশ করার সময় একটি ভিন্ন পছন্দ করতে পারি এবং আমরা বেশিরভাগ প্রসঙ্গে অন্যদের "মেটাপ্যারামিটার" ব্যবহার করতে উত্সাহিত করব৷
কেন সরাসরি বৈধতা সেট কর্মক্ষমতা উন্নত করতে ব্যাচের আকার টিউন করা উচিত নয়?
প্রশিক্ষণ পাইপলাইনের অন্য কোন বিবরণ পরিবর্তন না করে ব্যাচের আকার পরিবর্তন করা প্রায়ই বৈধতা সেটের কার্যকারিতাকে প্রভাবিত করে। যাইহোক, প্রতিটি ব্যাচের আকারের জন্য প্রশিক্ষণ পাইপলাইন স্বাধীনভাবে অপ্টিমাইজ করা হলে দুটি ব্যাচের আকারের মধ্যে বৈধতা সেটের কার্যক্ষমতার পার্থক্য সাধারণত চলে যায়।
যে হাইপারপ্যারামিটারগুলি ব্যাচের আকারের সাথে সবচেয়ে দৃঢ়ভাবে ইন্টারঅ্যাক্ট করে এবং তাই প্রতিটি ব্যাচের আকারের জন্য আলাদাভাবে সুর করা সবচেয়ে গুরুত্বপূর্ণ, সেগুলি হল অপ্টিমাইজার হাইপারপ্যারামিটার (উদাহরণস্বরূপ, শেখার হার, ভরবেগ) এবং নিয়মিতকরণের হাইপারপ্যারামিটার৷ নমুনা ভিন্নতার কারণে ছোট ব্যাচের মাপ প্রশিক্ষণের অ্যালগরিদমে আরও বেশি শব্দ করে। এই গোলমাল একটি নিয়মিত প্রভাব থাকতে পারে. সুতরাং, বৃহত্তর ব্যাচের আকারগুলি অতিরিক্ত ফিট করার প্রবণতা হতে পারে এবং আরও শক্তিশালী নিয়মিতকরণ এবং/অথবা অতিরিক্ত নিয়মিতকরণ কৌশলগুলির প্রয়োজন হতে পারে। উপরন্তু, ব্যাচের আকার পরিবর্তন করার সময় আপনাকে প্রশিক্ষণের ধাপগুলির সংখ্যা সামঞ্জস্য করতে হতে পারে।
একবার এই সমস্ত প্রভাবগুলি বিবেচনায় নেওয়া হলে, ব্যাচের আকার সর্বাধিক অর্জনযোগ্য বৈধতা কার্যকারিতাকে প্রভাবিত করে এমন কোনও বিশ্বাসযোগ্য প্রমাণ নেই। বিস্তারিত জানার জন্য, Shallue et al দেখুন। 2018
সমস্ত জনপ্রিয় অপ্টিমাইজেশান অ্যালগরিদমগুলির জন্য আপডেটের নিয়মগুলি কী কী?
এই বিভাগটি বেশ কয়েকটি জনপ্রিয় অপ্টিমাইজেশান অ্যালগরিদমের জন্য আপডেটের নিয়ম প্রদান করে।
স্টোকাস্টিক গ্রেডিয়েন্ট ডিসেন্ট (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
যেখানে $\eta_t$ হল $t$ ধাপে শেখার হার।
গতিবেগ
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
যেখানে $\eta_t$ হল $t$ ধাপে শেখার হার, এবং $\gamma$ হল ভরবেগ সহগ।
নেস্টেরভ
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
যেখানে $\eta_t$ হল $t$ ধাপে শেখার হার, এবং $\gamma$ হল ভরবেগ সহগ।
আরএমএসপ্রপ
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
অ্যাডাম
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
নাদাম
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
