איך אפשר לנפות באגים בבעיות באופטימיזציה ולצמצם את ההשפעה שלהן?
סיכום: אם המודל נתקל בקשיים באופטימיזציה, חשוב לפתור אותם לפני שמנסים דברים אחרים. אנחנו עדיין עורכים מחקרים בנושא אבחון של כשלים באימון ותיקון שלהם.
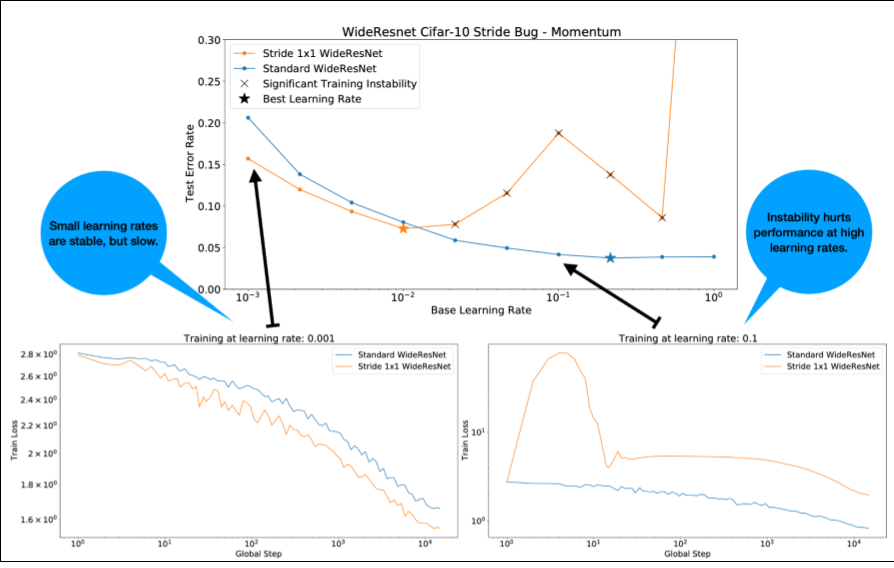
שימו לב לנקודות הבאות לגבי איור 4:
- שינוי הצעדים לא פוגע בביצועים בשיעורי למידה נמוכים.
- שיעורי למידה גבוהים כבר לא מאפשרים אימון טוב בגלל חוסר היציבות.
- החלת 1,000 שלבים של חימום קצב הלמידה פותרת את המקרה הספציפי הזה של חוסר יציבות, ומאפשרת אימון יציב בקצב למידה מקסימלי של 0.1.
זיהוי עומסי עבודה לא יציבים
כל עומס עבודה הופך ללא יציב אם קצב הלמידה גדול מדי. חוסר יציבות הוא בעיה רק אם הוא מחייב שימוש בקצב למידה קטן מדי. יש לפחות שני סוגים של חוסר יציבות באימון שכדאי להבחין ביניהם:
- חוסר יציבות בתחילת האימון או בשלב מוקדם שלו.
- חוסר יציבות פתאומי באמצע האימון.
כדי לזהות בעיות ביציבות של עומס העבודה, אפשר לפעול באופן שיטתי:
- מבצעים סריקה של קצב הלמידה ומוצאים את קצב הלמידה הטוב ביותר lr*.
- משרטטים עקומות של הפסדי אימון לשיעורי למידה שגבוהים רק מעט מ-lr*.
- אם שיעורי הלמידה > lr* מראים חוסר יציבות בהפסד (ההפסד עולה ולא יורד במהלך תקופות האימון), בדרך כלל תיקון חוסר היציבות משפר את האימון.
מתעדים את נורמת L2 של שיפוע ההפסד המלא במהלך האימון, כי ערכים חריגים יכולים לגרום לחוסר יציבות מזויף באמצע האימון. המידע הזה יכול לעזור להבין עד כמה כדאי להגביל את הגרדיאנטים או את עדכוני המשקלים.
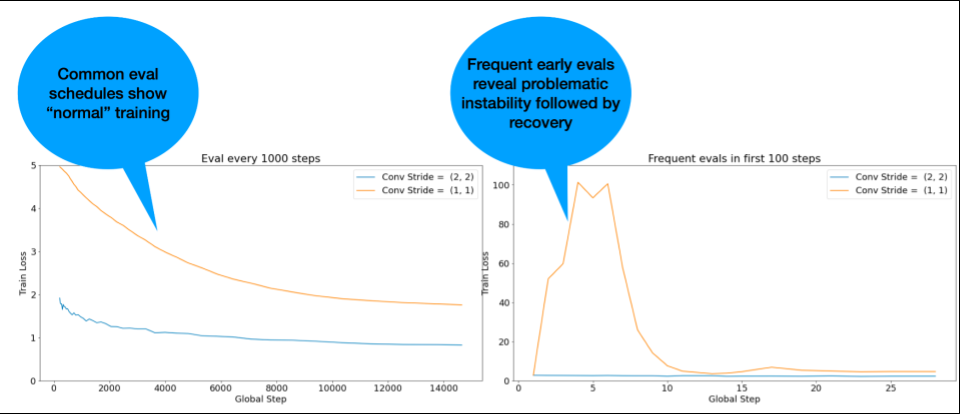
הערה: בדגמים מסוימים נצפית חוסר יציבות בשלב מוקדם מאוד, ואחריו מתרחש שיפור שמוביל לאימון איטי אבל יציב. בדרך כלל, לוחות זמנים נפוצים להערכה לא מצליחים לזהות את הבעיות האלה כי הם לא מתבצעים בתדירות גבוהה מספיק.
כדי לבדוק את זה, אפשר להריץ אימון מקוצר של כ-500 שלבים בלבד באמצעות lr = 2 * current best, אבל להעריך כל שלב.
תיקונים אפשריים לדפוסי חוסר יציבות נפוצים
הנה כמה פתרונות אפשריים לדפוסי חוסר יציבות נפוצים:
- החלה של תקופת הכנה לשיעור הלמידה. האפשרות הזו מתאימה במיוחד לחוסר יציבות בשלב מוקדם של האימון.
- החלת חיתוך של צבע מדורג. השיטה הזו טובה לחוסר יציבות בשלבים מוקדמים ובשלבי אמצע של האימון, והיא עשויה לתקן אתחולים שגויים שחימום לא יכול לתקן.
- כדאי לנסות כלי אופטימיזציה חדש. לפעמים Adam יכול להתמודד עם חוסר יציבות ש-Momentum לא יכול. זהו תחום מחקר פעיל.
- חשוב לוודא שאתם משתמשים בשיטות מומלצות ובאתחולים הטובים ביותר לארכיטקטורת המודל (דוגמאות בהמשך). מוסיפים חיבורים שיוריים ונורמליזציה אם המודל לא מכיל אותם.
- מבצעים נורמליזציה כפעולה האחרונה לפני השארית. לדוגמה:
x + Norm(f(x)). שימו לב ששימוש ב-Norm(x + f(x))עלול לגרום לבעיות. - כדאי לנסות לאתחל ענפים שיוריים ל-0. (ראו ReZero is All You Need: Fast Convergence at Large Depth.)
- להקטין את קצב הלמידה. זו האפשרות האחרונה.
חימום קצב הלמידה
מתי כדאי להשתמש בחימום של קצב הלמידה
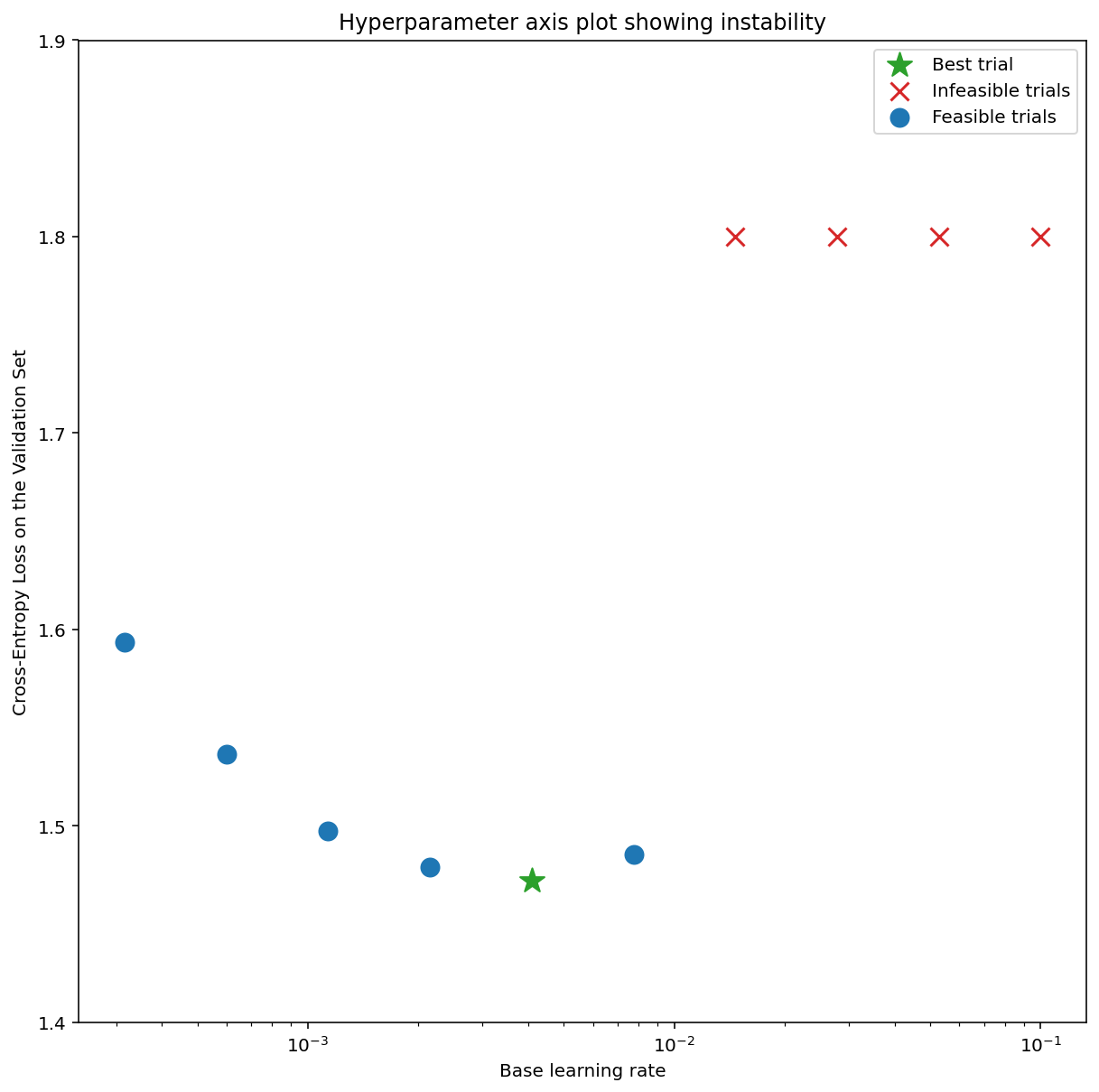
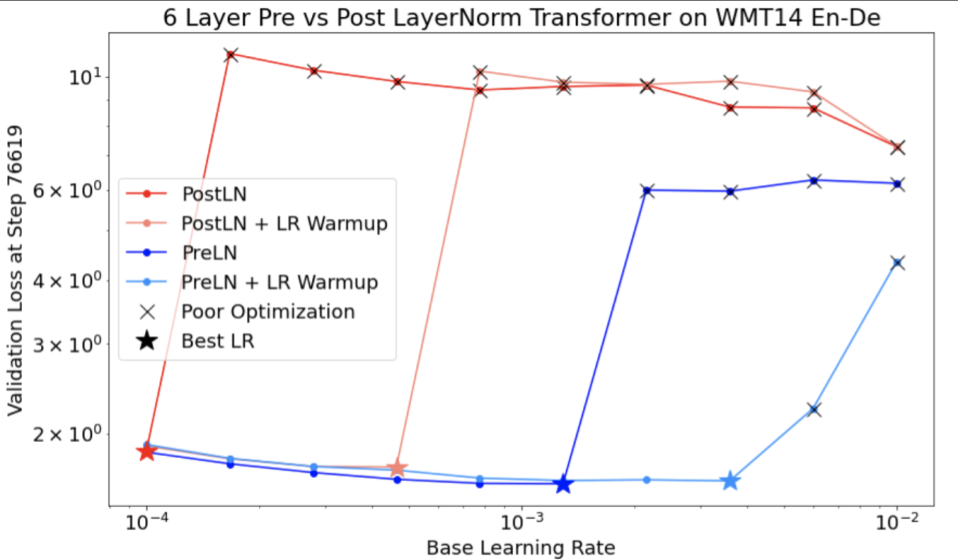
איור 7א מציג תרשים של ציר היפרפרמטרים שמצביע על מודל שחווה חוסר יציבות באופטימיזציה, כי קצב הלמידה הטוב ביותר נמצא ממש בקצה של חוסר היציבות.
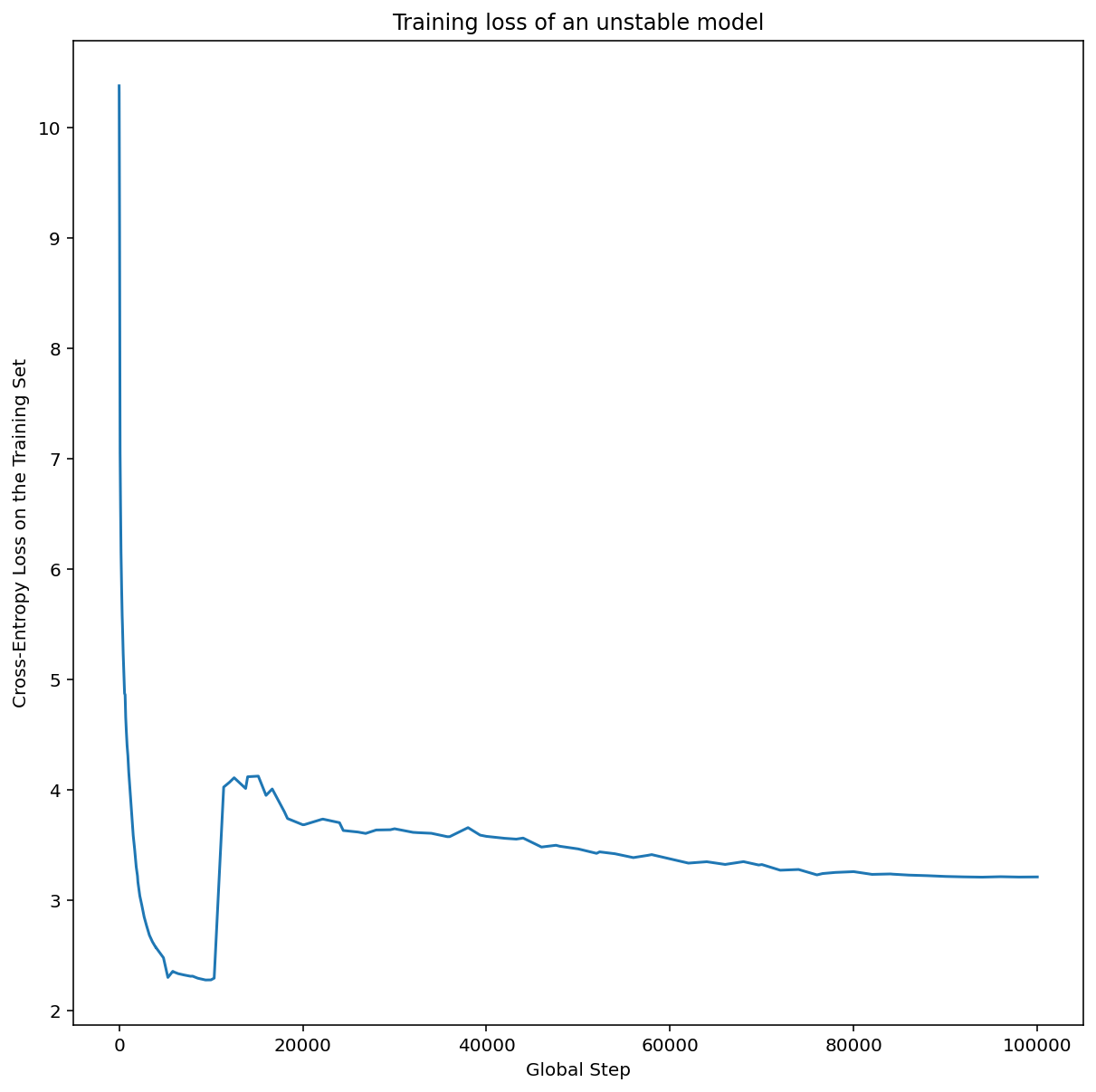
באיור 7ב מוצג איך אפשר לבדוק את זה באמצעות בחינת הפסד האימון של מודל שאומן עם קצב למידה שגדול פי 5 או פי 10 מהשיא הזה. אם בתרשים הזה רואים עלייה פתאומית בערך ה-loss אחרי ירידה יציבה (לדוגמה, בשלב ~10k בתרשים שלמעלה), סביר להניח שהמודל סובל מחוסר יציבות באופטימיזציה.
איך משתמשים בחימום של קצב הלמידה
נסמן ב-unstable_base_learning_rate את קצב הלמידה שבו המודל הופך ללא יציב, באמצעות התהליך הקודם.
חימום כולל הוספה של תזמון קצב למידה שמגדיל את קצב הלמידה מ-0 לערך יציב base_learning_rate שהוא לפחות בסדר גודל אחד גדול יותר מ-unstable_base_learning_rate.
ברירת המחדל תהיה לנסות base_learning_rate שהוא פי 10 מ-unstable_base_learning_rate. אבל אפשר לחזור על התהליך הזה לגבי משהו כמו 100xunstable_base_learning_rate. לוח הזמנים הספציפי הוא:
- תקופת הרצה מ-0 עד base_learning_rate על פני warmup_steps.
- אימון בקצב קבוע למשך post_warmup_steps.
המטרה היא למצוא את מספר ה-warmup_steps הקצר ביותר שיאפשר לכם לגשת לשיעורי למידה גבוהים בהרבה מ-unstable_base_learning_rate.
לכן, לכל base_learning_rate צריך לשנות את warmup_steps ואת post_warmup_steps. בדרך כלל אפשר להגדיר את post_warmup_steps כ-2*warmup_steps.
אפשר לשנות את ההגדרות של תקופת ההרצה בנפרד מלוח זמנים קיים של דעיכה. warmup_steps
צריך להשתמש בכמה סדרי גודל שונים. לדוגמה, מחקר יכול לנסות [10, 1000, 10,000, 100,000]. הנקודה הכי גדולה האפשרית לא יכולה להיות יותר מ-10% מ-max_train_steps.
אחרי שמגדירים warmup_steps שלא גורם לאימון להתפוצץ ב-base_learning_rate
צריך להחיל אותו על מודל הבסיס.
בעצם, מוסיפים את לוח הזמנים הזה לפני לוח הזמנים הקיים, ומשתמשים בבחירת נקודות הבדיקה האופטימלית שצוינה למעלה כדי להשוות את הניסוי הזה לערך הבסיס. לדוגמה, אם במקור היו 10,000 max_train_steps
ועשינו warmup_steps ל-1,000 שלבים, הליך האימון החדש צריך
לרוץ ל-11,000 שלבים בסך הכול.
אם נדרשים warmup_steps ארוכים לאימון יציב (יותר מ-5% מ-max_train_steps), יכול להיות שתצטרכו להגדיל את max_train_steps כדי להתחשב בכך.
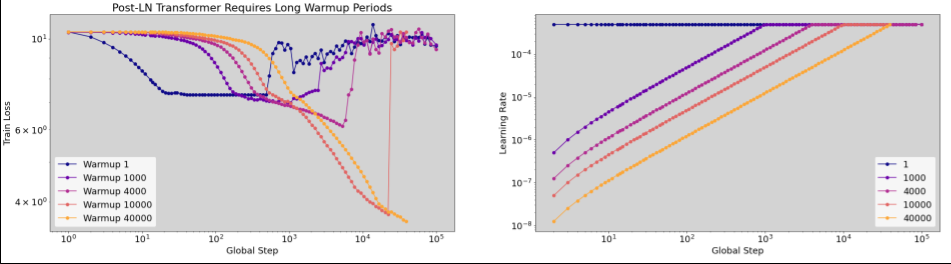
אין באמת ערך 'טיפוסי' בכל טווח העומסים. יש מודלים שנדרשים להם רק 100 שלבים, ויש מודלים (במיוחד טרנספורמטורים) שנדרשים להם 40,000 שלבים ויותר.
חיתוך הדרגתי
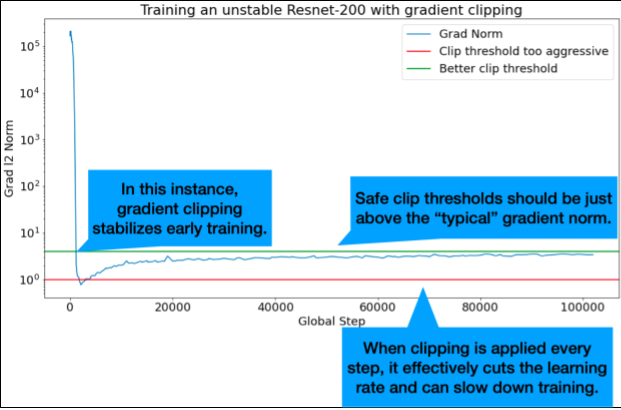
חיתוך שיפועים שימושי במיוחד כשמתרחשות בעיות גדולות או חריגות בשיפועים. התכונה 'חיתוך הדרגתי' יכולה לפתור את הבעיות הבאות:
- חוסר יציבות מוקדם באימון (נורמת גרדיאנט גדולה בשלב מוקדם)
- חוסר יציבות במהלך האימון (עליות פתאומיות בשיפוע במהלך האימון).
לפעמים תקופות חימום ארוכות יותר יכולות לתקן חוסר יציבות שלא ניתן לתקן באמצעות חיתוך. לפרטים נוספים, אפשר לעיין במאמר בנושא חימום קצב הלמידה.
🤖 מה לגבי חיתוך במהלך החימום?
הסף האידיאלי לקליפים הוא קצת מעל הנורמה של השיפוע ה'טיפוסי'.
דוגמה לאופן שבו אפשר לבצע חיתוך של מעברי צבע:
- אם הנורמה של הגרדיאנט $\left | g \right |$ גדולה מסף חיתוך הגרדיאנט $\lambda$, אז מתבצעת הפעולה ${g}'= \lambda \times \frac{g}{\left | g \right |}$ כאשר ${g}'$ הוא הגרדיאנט החדש.
תיעוד הנורמה של הגרדיאנט שלא נחתך במהלך האימון. כברירת מחדל, המערכת יוצרת:
- תרשים של נורמת הגרדיאנט לעומת השלב
- היסטוגרמה של נורמות הגרדיאנטים שנצברות על פני כל השלבים
בוחרים סף לחיתוך הדרגתי על סמך האחוזון ה-90 של נורמות הדרגתיות. הסף תלוי בעומס העבודה, אבל 90% הם נקודת התחלה טובה. אם 90% לא עובד, אפשר לשנות את ערך הסף הזה.
🤖 מה לגבי שיטה אדפטיבית כלשהי?
אם מנסים לגזור את הגרדיאנט ובעיות חוסר היציבות נמשכות, אפשר לנסות לגזור אותו בצורה חזקה יותר, כלומר להקטין את ערך הסף.
חיתוך גרדיאנט אגרסיבי במיוחד (כלומר, חיתוך של יותר מ-50% מהעדכונים) הוא למעשה דרך מוזרה להפחית את קצב הלמידה. אם אתם משתמשים בחיתוך אגרסיבי במיוחד, כדאי פשוט להקטין את קצב הלמידה.
למה קצב הלמידה ופרמטרים אחרים של אופטימיזציה נקראים היפר-פרמטרים? הם לא פרמטרים של אף התפלגות קודמת.
למונח 'היפר-פרמטר' יש משמעות מדויקת בלמידת מכונה בייסיאנית, ולכן השימוש במונח הזה לתיאור קצב הלמידה ורוב הפרמטרים האחרים של למידה עמוקה שניתנים לכוונון הוא שימוש לא מדויק במינוח. אנחנו מעדיפים להשתמש במונח 'מטא-פרמטר' לתיאור של שיעורי למידה, פרמטרים ארכיטקטוניים וכל שאר הדברים שניתנים להתאמה אישית בלמידה עמוקה. הסיבה לכך היא שהמטא-פרמטר מונע בלבול פוטנציאלי שנובע משימוש לא נכון במילה 'היפר-פרמטר'. הבלבול הזה סביר במיוחד כשמדובר באופטימיזציה בייסיאנית, שבה למודלים של משטחי תגובה הסתברותיים יש היפרפרמטרים משלהם.
למרות שהמונח 'היפר-פרמטר' עלול להיות מבלבל, הוא נפוץ מאוד בקהילת הלמידה העמוקה. לכן, במסמך הזה, שמיועד לקהל רחב שכולל הרבה אנשים שלא סביר שיכירו את הפרט הטכני הזה, בחרנו לתרום למקור אחד של בלבול בתחום בתקווה להימנע ממקור אחר. עם זאת, יכול להיות שנשתמש במונח אחר כשנפרסם מאמר מחקר, ונמליץ לאחרים להשתמש במונח 'מטא-פרמטר' ברוב ההקשרים.
למה לא כדאי לשנות את גודל האצווה כדי לשפר ישירות את הביצועים של קבוצת האימות?
שינוי גודל האצווה בלי לשנות פרטים אחרים בצינור ההכשרה משפיע לעיתים קרובות על הביצועים של קבוצת האימות. עם זאת, ההבדל בביצועים של קבוצת האימות בין שני גדלים של אצווה בדרך כלל נעלם אם צינור ההדרכה עובר אופטימיזציה באופן עצמאי לכל גודל אצווה.
ההיפרפרמטרים שמקיימים את האינטראקציה הכי חזקה עם גודל האצווה, ולכן הכי חשוב לכוונן אותם בנפרד לכל גודל אצווה, הם ההיפרפרמטרים של האופטימיזציה (לדוגמה, קצב הלמידה, המומנטום) וההיפרפרמטרים של הרגולריזציה. גודלי אצווה קטנים יותר מוסיפים יותר רעשי רקע לאלגוריתם האימון בגלל השונות במדגם. הרעש הזה יכול להשפיע על הרגולריזציה. לכן, גדלים גדולים יותר של אצווה יכולים להיות מועדים יותר להתאמת יתר, ועשויים לדרוש רגולריזציה חזקה יותר ו/או טכניקות רגולריזציה נוספות. בנוסף, יכול להיות שתצטרכו לשנות את מספר שלבי האימון כשמשנים את גודל האצווה.
אחרי שמביאים בחשבון את כל ההשפעות האלה, אין ראיות משכנעות לכך שגודל האצווה משפיע על ביצועי האימות המקסימליים שאפשר להשיג. פרטים נוספים זמינים במאמר Shallue et al. 2018.
מהם כללי העדכון של כל אלגוריתמי האופטימיזציה הפופולריים?
בקטע הזה מפורטים כללי עדכון לכמה אלגוריתמים פופולריים של אופטימיזציה.
ירידה סטוכסטית של גרדיאנט (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
כאשר $\eta_t$ הוא קצב הלמידה בשלב $t$.
מומנטום
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
כאשר $\eta_t$ הוא קצב הלמידה בשלב $t$, ו-$\gamma$ הוא מקדם המומנטום.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
כאשר $\eta_t$ הוא קצב הלמידה בשלב $t$, ו-$\gamma$ הוא מקדם המומנטום.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
