Como as falhas de otimização podem ser depuradas e mitigadas?
Resumo: se o modelo estiver enfrentando dificuldades de otimização, é importante corrigi-las antes de tentar outras coisas. Diagnosticar e corrigir falhas de treinamento é uma área ativa de pesquisa.
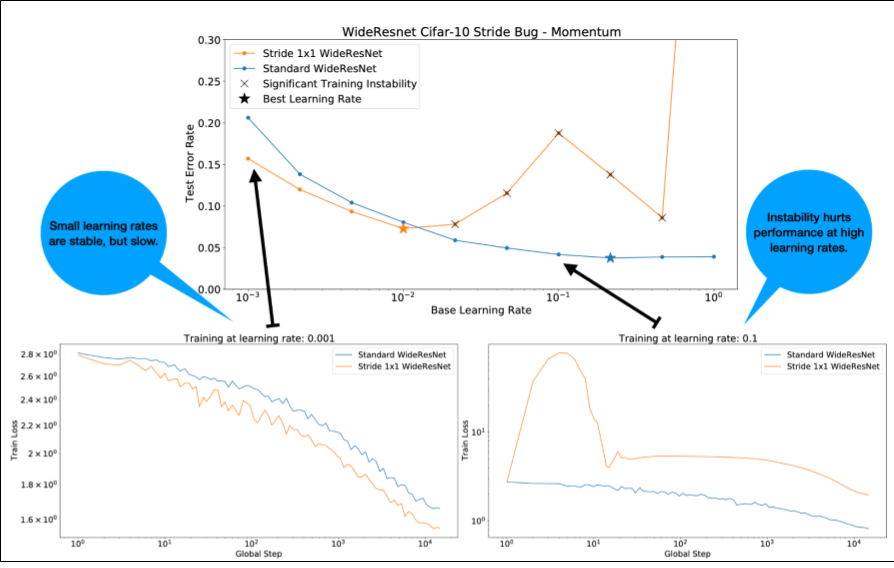
Observe o seguinte sobre a Figura 4:
- Mudar os passos não prejudica o desempenho em taxas de aprendizado baixas.
- As altas taxas de aprendizado não treinam mais bem devido à instabilidade.
- Aplicar 1.000 etapas de aquecimento da taxa de aprendizado resolve essa instância específica de instabilidade, permitindo um treinamento estável com taxa de aprendizado máxima de 0,1.
Como identificar cargas de trabalho instáveis
Qualquer carga de trabalho ficará instável se a taxa de aprendizado for muito grande. A instabilidade só é um problema quando força você a usar uma taxa de aprendizado muito pequena. É preciso distinguir pelo menos dois tipos de instabilidade de treinamento:
- Instabilidade na inicialização ou no início do treinamento.
- Instabilidade súbita no meio do treinamento.
Você pode adotar uma abordagem sistemática para identificar problemas de estabilidade na carga de trabalho fazendo o seguinte:
- Fazer uma varredura de taxa de aprendizado e encontrar a melhor taxa de aprendizado lr*.
- Traçar curvas de perda de treinamento para taxas de aprendizado logo acima de lr*.
- Se as taxas de aprendizado > lr* mostrarem instabilidade de perda (a perda não diminui durante os períodos de treinamento), corrigir a instabilidade geralmente melhora o treinamento.
Registre a norma L2 do gradiente de perda total durante o treinamento, já que valores atípicos podem causar instabilidade falsa no meio do treinamento. Isso pode informar a agressividade para recortar gradientes ou atualizações de peso.
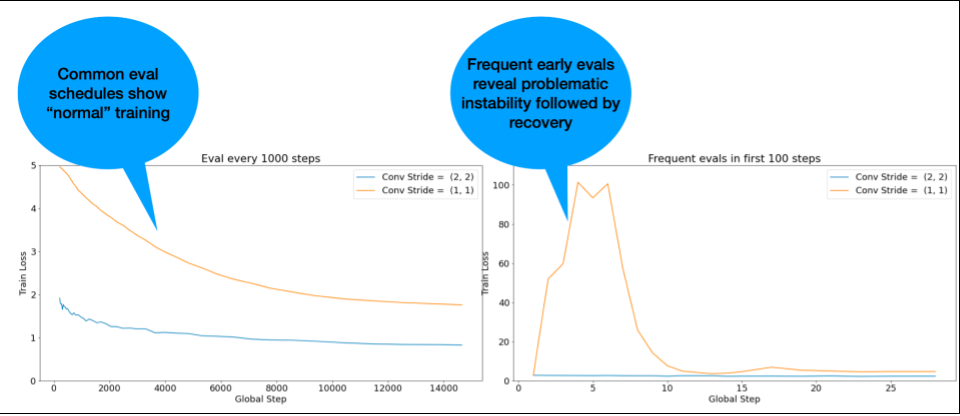
OBSERVAÇÃO: alguns modelos mostram instabilidade muito precoce, seguida por uma recuperação que resulta em um treinamento lento, mas estável. Programações de avaliação comuns podem acabar perdendo esses problemas se não avaliarem com frequência suficiente!
Para verificar isso, treine para uma sequência abreviada de apenas 500 etapas
usando lr = 2 * current best, mas avalie todas as etapas.
Possíveis correções para padrões de instabilidade comuns
Considere estas possíveis correções para padrões de instabilidade comuns:
- Aplique o aquecimento da taxa de aprendizado. Essa opção é melhor para instabilidade no início do treinamento.
- Aplique truncamento de gradiente. Isso é bom para a instabilidade inicial e durante o treinamento, além de corrigir algumas inicializações incorretas que o aquecimento não consegue.
- Experimente um novo otimizador. Às vezes, Adam pode lidar com instabilidades que a Momentum não consegue. Essa é uma área de pesquisa ativa.
- Verifique se você está usando as práticas recomendadas e as melhores inicializações para a arquitetura do seu modelo (exemplos a seguir). Adicione conexões residuais e normalização caso elas ainda não estejam no modelo.
- Normalizar como a última operação antes do residual. Por exemplo:
x + Norm(f(x)). Observe queNorm(x + f(x))pode causar problemas. - Tente inicializar as ramificações residuais para 0. Consulte ReZero is All You Need: rápida convergência em grande profundidade.
- Diminua a taxa de aprendizado. Esse é um último recurso.
Aquecimento da taxa de aprendizado
Quando aplicar o aquecimento da taxa de aprendizado
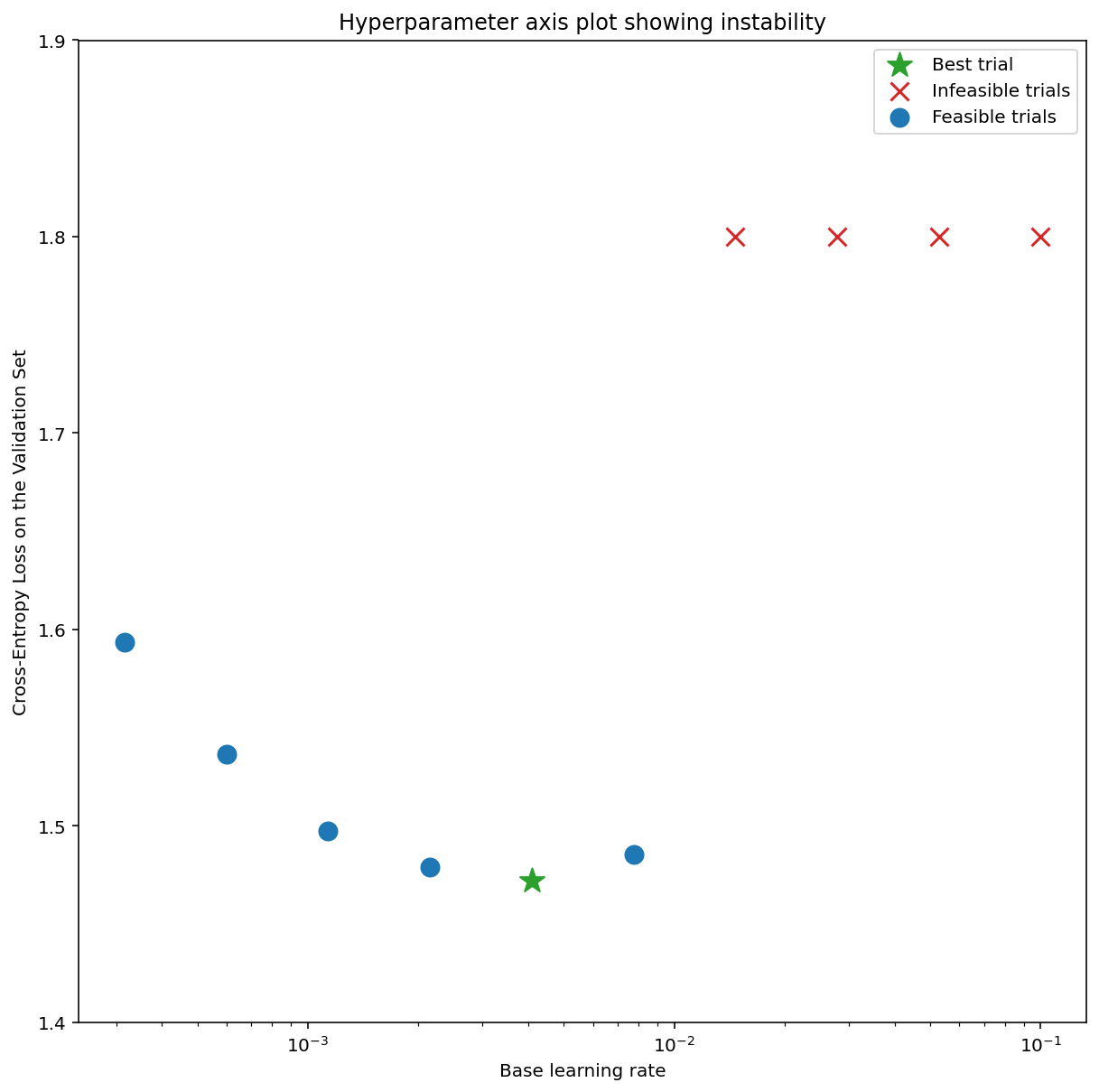
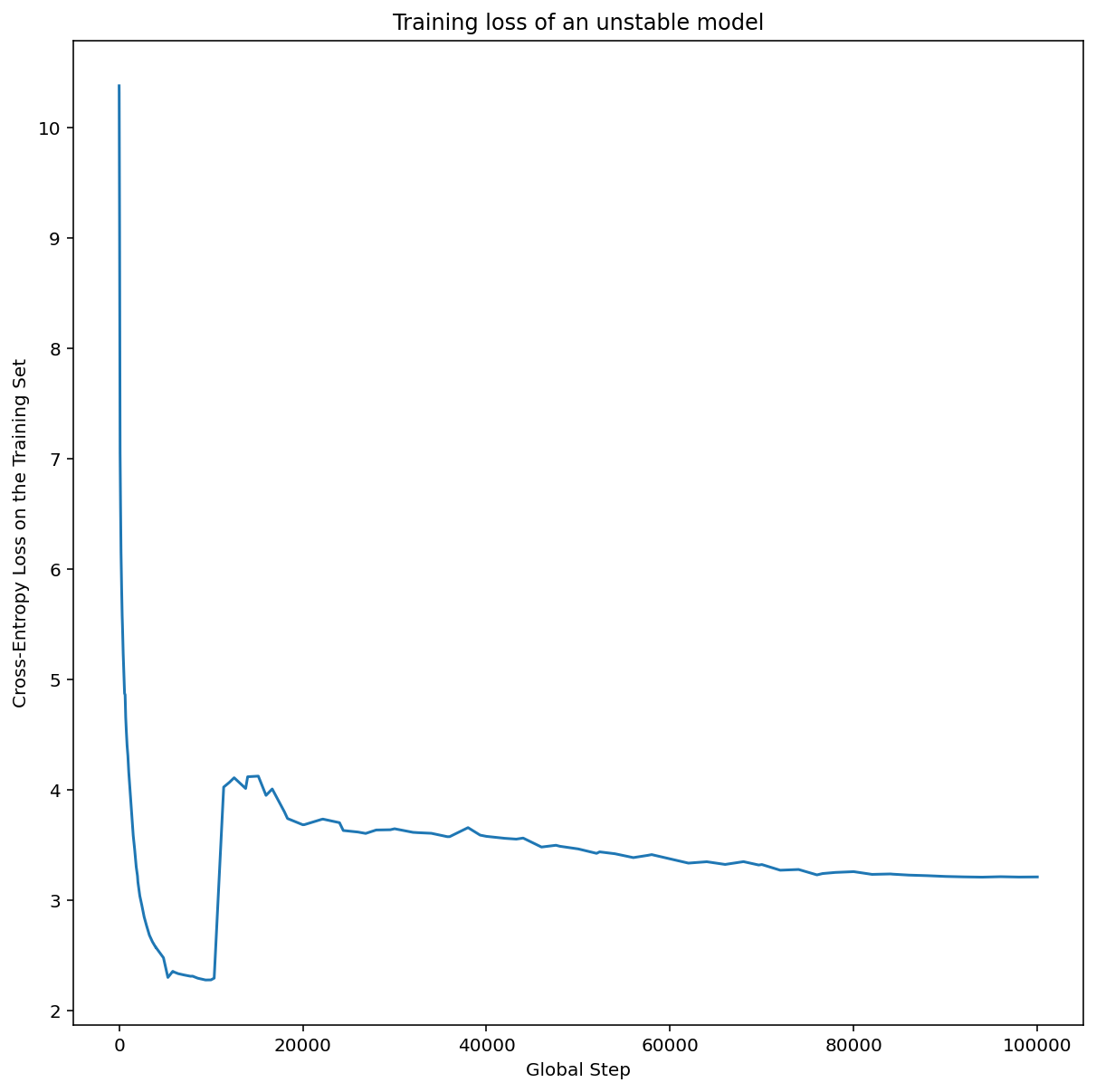
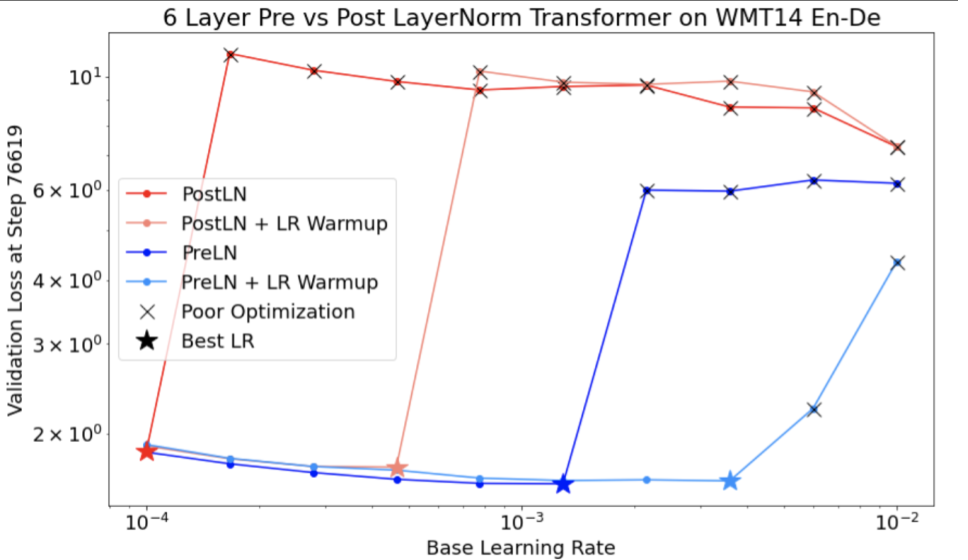
A Figura 7a mostra um gráfico de eixo de hiperparâmetro que indica um modelo com instabilidades de otimização, porque a melhor taxa de aprendizado está no limite da instabilidade.
A Figura 7b mostra como isso pode ser verificado novamente examinando a perda de treinamento de um modelo treinado com uma taxa de aprendizado 5 ou 10 vezes maior do que esse pico. Se esse gráfico mostrar um aumento repentino na perda após uma queda constante (por exemplo, na etapa ~10 mil na figura acima), é provável que o modelo sofra com a instabilidade da otimização.
Como aplicar o aquecimento da taxa de aprendizado
Permita que unstable_base_learning_rate seja a taxa de aprendizado em que o modelo
fica instável, usando o procedimento anterior.
O aquecimento envolve anexar uma programação de taxa de aprendizado que aumenta a
taxa de aprendizado de 0 para um base_learning_rate estável que seja pelo menos
uma ordem de magnitude maior que unstable_base_learning_rate.
O padrão seria tentar um base_learning_rate que fosse 10x
unstable_base_learning_rate. No entanto, é possível
executar todo esse procedimento novamente para algo como 100x
unstable_base_learning_rate. O cronograma específico é:
- Aumento de 0 para base_learning_rate em SCHEDULE_steps.
- Treine a uma taxa constante para post_aquecimento_steps.
Seu objetivo é encontrar o menor número de warmup_steps que permita
acessar taxas de aprendizado de pico muito maiores do que
unstable_base_learning_rate.
Portanto, para cada base_learning_rate, você precisa ajustar warmup_steps e
post_warmup_steps. Não há problema em definir post_warmup_steps como
2*warmup_steps.
O aquecimento pode ser ajustado independentemente de uma programação de iminência da conversão existente. warmup_steps
precisa ser varredo em algumas ordens de magnitude diferentes. Por exemplo, um
exemplo de estudo pode testar [10, 1000, 10,000, 100,000]. O maior ponto viável não pode ser maior que 10% de max_train_steps.
Depois que um warmup_steps que não explode o treinamento em base_learning_rate
for estabelecido, ele precisará ser aplicado ao modelo de referência.
Basicamente, anexe essa programação à programação atual e use a seleção ideal de ponto de verificação discutida acima para comparar esse experimento com o valor de referência. Por exemplo, se originalmente tivéssemos 10.000 max_train_steps
e executamos warmup_steps em 1.000 etapas, o novo procedimento de treinamento será
executado em um total de 11.000 etapas.
Se warmup_steps longos forem necessários para um treinamento estável (>5% de
max_train_steps), talvez seja necessário aumentar max_train_steps para considerar
isso.
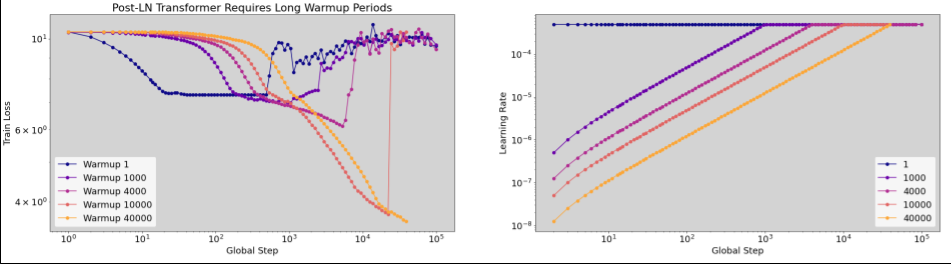
Não há um valor "típico" em toda a gama de cargas de trabalho. Alguns modelos só precisam de 100 etapas, enquanto outros (especialmente transformadores) podem precisar de mais de 40.000.
Clipe de gradiente
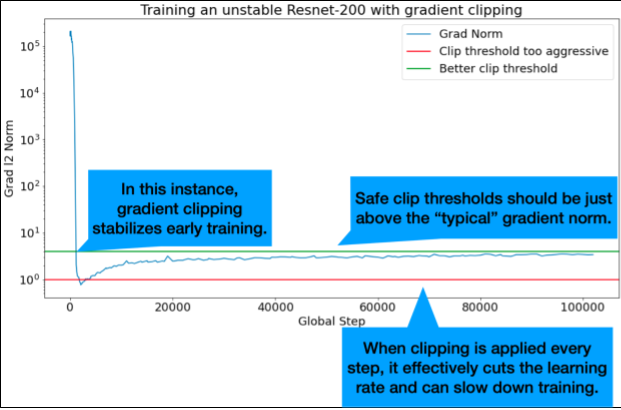
O recorte de gradiente é mais útil quando ocorrem problemas de gradientes grandes ou atípicos. O recorte de gradiente pode corrigir um dos seguintes problemas:
- Instabilidade no treinamento inicial (norma de gradiente grande antecipadamente)
- Instabilidades no meio do treinamento (picos repentinos do gradiente durante o treinamento)
Às vezes, períodos de aquecimento mais longos podem corrigir instabilidades que o recorte não corre. Para detalhes, consulte Aquecimento da taxa de aprendizado.
🤖 E quanto a clippings durante o aquecimento?
Os limites de clipe ideais estão logo acima da norma de gradiente "típica".
Veja um exemplo de como o recorte de gradiente pode ser feito:
- Se a norma do gradiente $\left | g \right |$ for maior que o limite de recorte do gradiente $\lambda$, faça ${g}'= \lambda \times \frac{g}{\left | g \right |}$, em que ${g}'$ é o novo gradiente.
Registre a norma de gradiente sem corte durante o treinamento. Por padrão, gere:
- Diagrama da norma do gradiente vs. passo
- Um histograma de normas de gradiente agregadas em todas as etapas
Escolha um limite de recorte de gradiente com base no 90o percentil das normas de gradiente. O limite depende da carga de trabalho, mas 90% é um bom ponto de partida. Se 90% não funcionar, ajuste esse limite.
🤖 E quanto a algum tipo de estratégia adaptativa?
Se você tentar o truncamento de gradiente e os problemas de instabilidade persistirem, você poderá tentar mais difícil, ou seja, diminuir o limite.
O recorte de gradiente extremamente agressivo (ou seja, mais de 50% das atualizações que são cortadas) é, essencialmente, uma maneira estranha de reduzir a taxa de aprendizado. Se você perceber que está usando um recorte extremamente agressivo, é recomendável cortar a taxa de aprendizado.
Por que a taxa de aprendizado e outros parâmetros de otimização são chamados de hiperparâmetros? Eles não são parâmetros de nenhuma distribuição anterior.
O termo "hiperparâmetro" tem um significado preciso no machine learning bayesiano. Portanto, se referir à taxa de aprendizado e à maioria dos outros parâmetros de aprendizado profundo ajustáveis como "hiperparâmetros" é um abuso da terminologia. Preferimos usar o termo "metaparâmetro" para taxas de aprendizado, parâmetros de arquitetura e todas as outras coisas ajustáveis de aprendizado profundo. Isso porque o metaparâmetro evita o potencial de confusão que ocorre do uso indevido da palavra "hiperparâmetro". Essa confusão é especialmente provável ao discutir a otimização bayesiana, em que os modelos de superfície de resposta probabilística têm os próprios hiperparâmetros verdadeiros.
Infelizmente, embora seja potencialmente confuso, o termo "hiperparâmetro" se tornou extremamente comum na comunidade de aprendizado profundo. Portanto, para este documento, destinado a um amplo público que inclui muitas pessoas que provavelmente não estão cientes desse aspecto técnico, decidimos contribuir para uma fonte de confusão no campo na esperança de evitar outra. Dito isso, podemos fazer uma escolha diferente ao publicar um artigo de pesquisa e incentivar outras pessoas a usar "metaparameter" na maioria dos contextos.
Por que o tamanho do lote não pode ser ajustado para melhorar diretamente o desempenho do conjunto de validação?
Em geral, alterar o tamanho do lote sem alterar outros detalhes do pipeline de treinamento afeta o desempenho do conjunto de validação. No entanto, a diferença no desempenho do conjunto de validação entre dois tamanhos de lote normalmente diminui se o pipeline de treinamento é otimizado de maneira independente para cada tamanho de lote.
Os hiperparâmetros que interagem mais fortemente com o tamanho do lote e, portanto, são mais importantes para serem ajustados separadamente para cada tamanho de lote são os hiperparâmetros do otimizador (por exemplo, taxa de aprendizado, momentum) e os hiperparâmetros de regularização. Tamanhos de lote menores introduzem mais ruído no algoritmo de treinamento devido à variância da amostra. Esse ruído pode ter um efeito de regularização. Assim, tamanhos de lote maiores podem ser mais propensos a overfitting e exigir regularização mais forte e/ou outras técnicas de regularização. Além disso, talvez seja necessário ajustar o número de etapas de treinamento ao alterar o tamanho do lote.
Depois que todos esses efeitos são considerados, não há evidências convincentes de que o tamanho do lote afeta o desempenho máximo de validação alcançável. Para mais detalhes, consulte Shallue et al., 2018.
Quais são as regras de atualização para todos os algoritmos de otimização mais conhecidos?
Nesta seção, fornecemos regras de atualização para vários algoritmos de otimização conhecidos.
Gradiente descendente estocástico (GDE)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Onde $\eta_t$ é a taxa de aprendizado na etapa $t$.
Momentum
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Onde $\eta_t$ é a taxa de aprendizado na etapa $t$ e $\gamma$ é o coeficiente do momentum.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Onde $\eta_t$ é a taxa de aprendizado na etapa $t$ e $\gamma$ é o coeficiente do momentum.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]