Как можно отладить и смягчить ошибки оптимизации?
Резюме: Если модель испытывает трудности с оптимизацией, важно исправить их, прежде чем пытаться что-то делать. Диагностика и исправление ошибок в обучении является активной областью исследований.
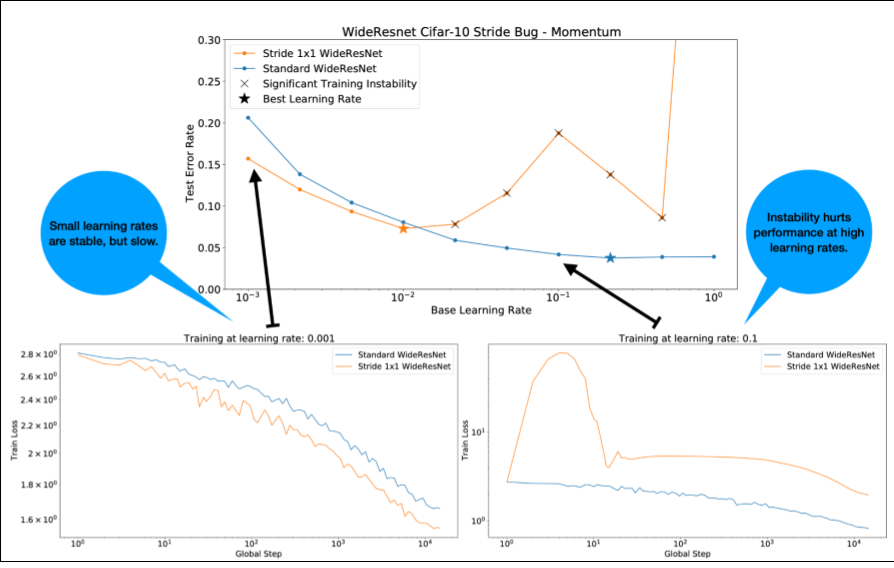
Обратите внимание на следующее относительно рисунка 4:
- Изменение темпа не ухудшает производительность при низкой скорости обучения.
- Высокие темпы обучения больше не подходят для тренировок из-за нестабильности.
- Применение 1000 шагов прогрева скорости обучения устраняет этот конкретный случай нестабильности, обеспечивая стабильное обучение с максимальной скоростью обучения 0,1.
Выявление нестабильных рабочих нагрузок
Любая рабочая нагрузка становится нестабильной, если скорость обучения слишком велика. Нестабильность является проблемой только тогда, когда она вынуждает вас использовать слишком маленькую скорость обучения. Стоит различать как минимум два типа нестабильности тренировки:
- Нестабильность при инициализации или на ранних этапах обучения.
- Внезапная нестабильность в середине тренировки.
Вы можете применить систематический подход к выявлению проблем стабильности в вашей рабочей нагрузке, выполнив следующие действия:
- Выполните анализ скорости обучения и найдите лучшую скорость обучения lr*.
- Постройте кривые потерь при обучении для скоростей обучения чуть выше lr*.
- Если скорость обучения > lr* показывает нестабильность потерь (потери растут, а не уменьшаются в периоды обучения), то исправление нестабильности обычно улучшает обучение.
Зарегистрируйте норму L2 полного градиента потерь во время обучения, поскольку выбросы могут вызвать ложную нестабильность в середине обучения. Это может указать, насколько агрессивно обрезать градиенты или обновления веса.
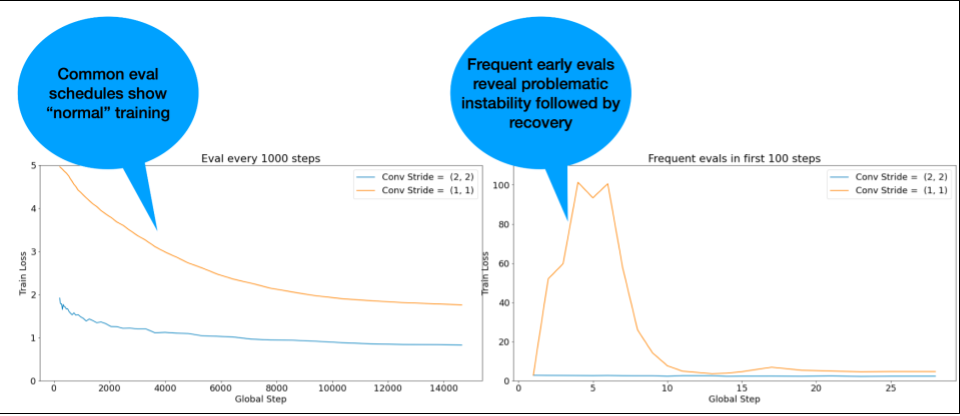
ПРИМЕЧАНИЕ. Некоторые модели демонстрируют очень раннюю нестабильность, за которой следует восстановление, что приводит к медленному, но стабильному обучению. В обычных графиках оценки эти проблемы могут быть упущены из-за недостаточно частой оценки!
Чтобы проверить это, вы можете тренироваться для сокращенного пробега всего на ~500 шагов, используя lr = 2 * current best , но оценивая каждый шаг.
Возможные исправления распространенных моделей нестабильности
Рассмотрите следующие возможные исправления распространенных закономерностей нестабильности:
- Примените разминку скорости обучения. Это лучше всего подходит для ранней нестабильности тренировок.
- Примените обрезку градиента. Это полезно как для ранней, так и для средней нестабильности тренировки, а также может исправить некоторые плохие инициализации, которые не могут быть исправлены при разминке.
- Попробуйте новый оптимизатор. Иногда Адам может справиться с нестабильностью, чего не может сделать Momentum. Это активная область исследований.
- Убедитесь, что вы используете лучшие практики и лучшие инициализации для архитектуры вашей модели (примеры приведены ниже). Добавьте остаточные связи и нормализацию, если модель их еще не содержит.
- Нормализовать как последнюю операцию перед остатком. Например:
x + Norm(f(x)). Обратите внимание, чтоNorm(x + f(x))может вызвать проблемы. - Попробуйте инициализировать остаточные ветки до 0. (См. ReZero — это все, что вам нужно: быстрая сходимость на большой глубине. )
- Снизьте скорость обучения. Это последнее средство.
Разминка скорости обучения
Когда применять разминку скорости обучения
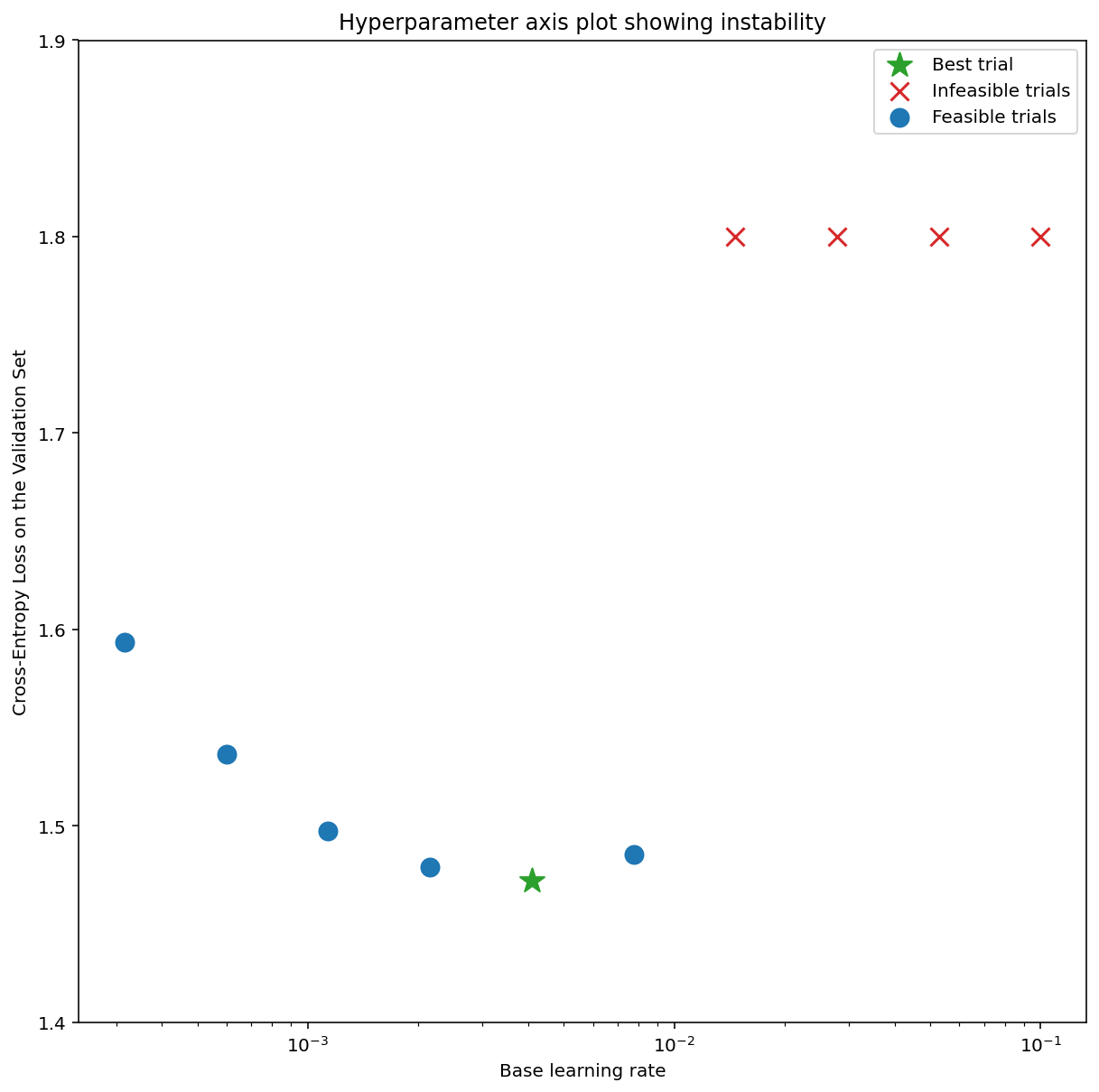
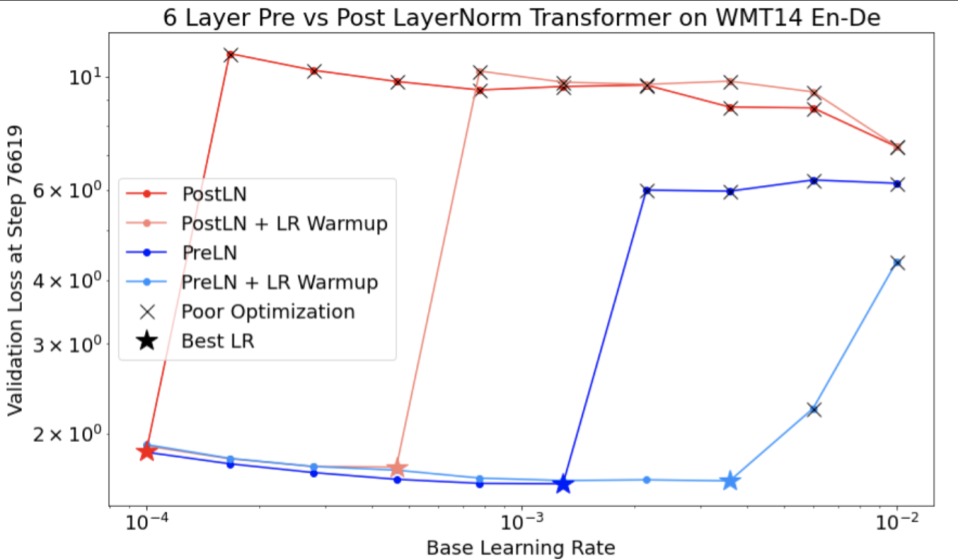
На рисунке 7a показан график оси гиперпараметров, который указывает на модель, испытывающую нестабильность оптимизации, поскольку лучшая скорость обучения находится прямо на грани нестабильности.
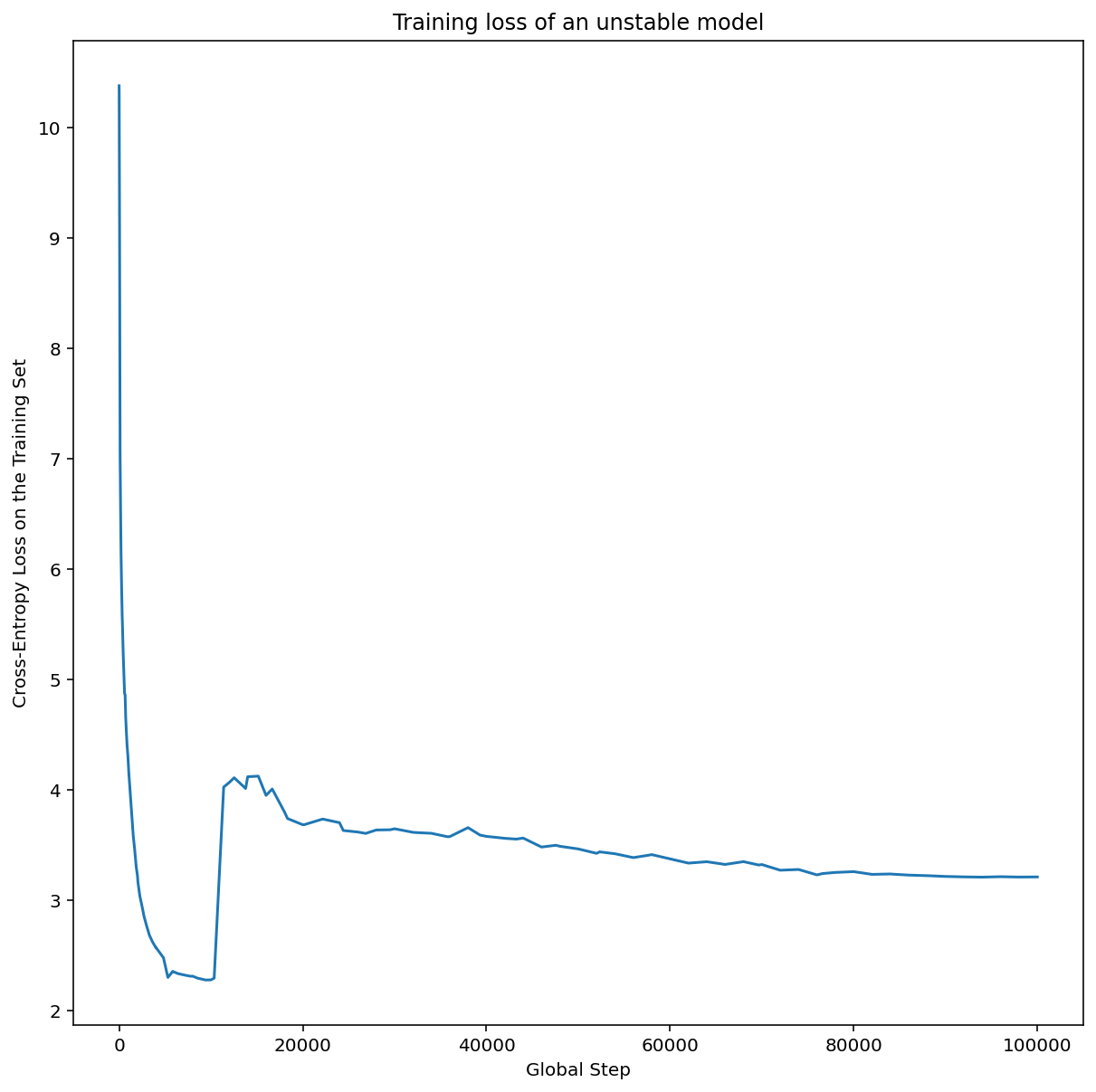
На рисунке 7b показано, как это можно перепроверить, изучив потери при обучении модели, обученной со скоростью обучения, в 5 или 10 раз превышающей этот пик. Если этот график показывает внезапный рост потерь после устойчивого снижения (например, на шаге ~ 10k на рисунке выше), то модель, вероятно, страдает от нестабильности оптимизации.
Как применить разминку скорости обучения
Пусть unstable_base_learning_rate будет скоростью обучения, при которой модель становится нестабильной, используя предыдущую процедуру.
Разминка включает в себя подготовку графика скорости обучения, который увеличивает скорость обучения от 0 до некоторого стабильного base_learning_rate , который как минимум на один порядок превышает unstable_base_learning_rate . По умолчанию будет выбрано base_learning_rate , равное 10x unstable_base_learning_rate . Однако учтите, что можно было бы запустить всю эту процедуру еще раз примерно для 100x unstable_base_learning_rate . Конкретный график:
- Увеличивайте от 0 до base_learning_rate в течение разминочных_шагов.
- Тренируйтесь с постоянной скоростью в течение post_warmup_steps.
Ваша цель — найти кратчайшее количество warmup_steps , которое позволит вам получить доступ к пиковой скорости обучения, которая намного выше, чем unstable_base_learning_rate . Таким образом, для каждого base_learning_rate вам необходимо настроить warmup_steps и post_warmup_steps . Обычно можно установить post_warmup_steps равным 2*warmup_steps .
Разминку можно настроить независимо от существующего графика затухания. warmup_steps следует изменять на несколько порядков. Например, в качестве примера исследования можно попробовать [10, 1000, 10,000, 100,000] . Самая большая возможная точка не должна превышать 10 % от max_train_steps .
После того, как установлен параметр warmup_steps , который не приводит к резкому увеличению скорости обучения при base_learning_rate , его следует применить к базовой модели. По сути, добавьте этот график к существующему графику и используйте оптимальный выбор контрольных точек, описанный выше, чтобы сравнить этот эксперимент с базовым уровнем. Например, если изначально у нас было 10 000 max_train_steps и мы выполнили warmup_steps для 1 000 шагов, новая процедура обучения должна выполнить всего 11 000 шагов.
Если для стабильной тренировки требуются длинные warmup_steps (>5% от max_train_steps ), вам может потребоваться увеличить max_train_steps , чтобы учесть это.
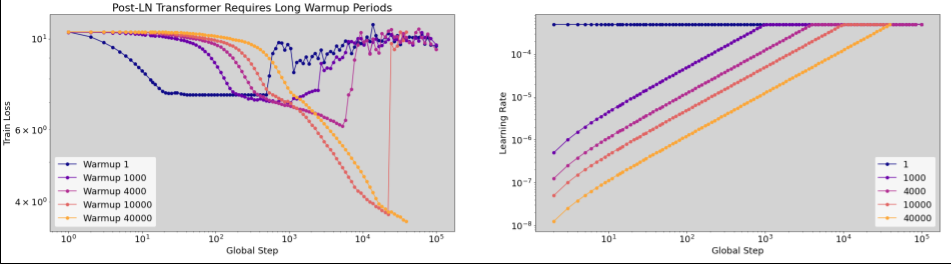
На самом деле не существует «типичного» значения для всего спектра рабочих нагрузок. Некоторым моделям требуется всего 100 шагов, а другим (особенно трансформаторам) может потребоваться более 40 тыс. шагов.
Градиентное отсечение
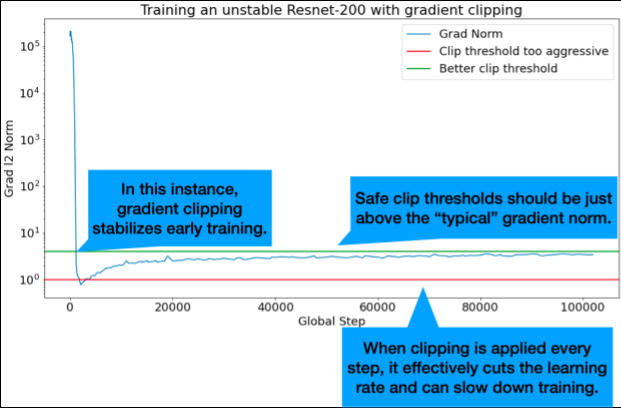
Отсечение градиента наиболее полезно при возникновении больших или резких проблем с градиентом. Градиентная обрезка может решить любую из следующих проблем:
- Ранняя тренировочная нестабильность (большая норма градиента рано)
- Нестабильность в середине тренировки (внезапные скачки градиента в середине тренировки).
Иногда более длительные периоды прогрева могут исправить нестабильность, чего не может сделать ограничение; Подробности см. в разделе «Прогрев скорости обучения» .
🤖 А как насчет обрезки во время разминки?
Идеальные пороги клиппирования чуть выше «типичной» нормы градиента.
Вот пример того, как можно сделать обрезку градиента:
- Если норма градиента $\left | g \right |$ превышает порог отсечения градиента $\lambda$, то выполните ${g}'= \lambda \times \frac{g}{\left | g \right |}$ где ${g}'$ — новый градиент.
Зарегистрируйте необрезанную норму градиента во время тренировки. По умолчанию генерируется:
- График зависимости нормы градиента от шага
- Гистограмма норм градиента, агрегированных по всем шагам
Выберите порог отсечения градиента на основе 90-го процентиля норм градиента. Порог зависит от рабочей нагрузки, но 90 % — хорошая отправная точка. Если 90% не работает, вы можете настроить этот порог.
🤖 А как насчет какой-нибудь адаптивной стратегии?
Если вы попробуете отсечение градиента, но проблемы с нестабильностью останутся, вы можете попробовать еще сильнее; то есть вы можете уменьшить порог.
Чрезвычайно агрессивное отсечение градиента (то есть обрезается> 50% обновлений) — это, по сути, странный способ снижения скорости обучения. Если вы обнаружите, что используете чрезвычайно агрессивное ограничение, вам, вероятно, следует вместо этого просто снизить скорость обучения.
Почему вы называете скорость обучения и другие параметры оптимизации гиперпараметрами? Они не являются параметрами какого-либо предшествующего распределения.
Термин «гиперпараметр» имеет точное значение в байесовском машинном обучении, поэтому называть скорость обучения и большинство других настраиваемых параметров глубокого обучения «гиперпараметрами», возможно, является злоупотреблением терминологией. Мы бы предпочли использовать термин «метапараметр» для обозначения скорости обучения, архитектурных параметров и всех других настраиваемых вещей глубокого обучения. Это связано с тем, что метапараметр позволяет избежать путаницы, возникающей из-за неправильного использования слова «гиперпараметр». Эта путаница особенно вероятна при обсуждении байесовской оптимизации, где вероятностные модели поверхности отклика имеют свои собственные истинные гиперпараметры.
К сожалению, хотя термин «гиперпараметр» может сбивать с толку, он стал чрезвычайно распространенным в сообществе специалистов по глубокому обучению. Поэтому в этом документе, предназначенном для широкой аудитории, в которую входит множество людей, которые вряд ли знают об этой формальности, мы решили внести свой вклад в один источник путаницы в этой области в надежде избежать другого. Тем не менее, мы можем сделать другой выбор при публикации исследовательской работы, и мы призываем других использовать вместо этого «метапараметр» в большинстве контекстов.
Почему бы не настроить размер пакета так, чтобы напрямую улучшить производительность проверочного набора?
Изменение размера пакета без изменения каких-либо других деталей конвейера обучения часто влияет на производительность набора проверки. Однако разница в производительности набора проверки между двумя размерами пакетов обычно исчезает, если конвейер обучения оптимизируется независимо для каждого размера пакета.
Гиперпараметры, которые наиболее сильно взаимодействуют с размером пакета и, следовательно, их наиболее важно настраивать отдельно для каждого размера пакета, — это гиперпараметры оптимизатора (например, скорость обучения, импульс) и гиперпараметры регуляризации. Меньшие размеры пакетов вносят больше шума в алгоритм обучения из-за дисперсии выборки. Этот шум может иметь регуляризирующий эффект. Таким образом, партии большего размера могут быть более склонны к переоснащению и могут потребовать более сильной регуляризации и/или дополнительных методов регуляризации. Кроме того, вам может потребоваться настроить количество шагов обучения при изменении размера пакета.
После того, как все эти эффекты приняты во внимание, не существует убедительных доказательств того, что размер партии влияет на максимально достижимую производительность проверки. Подробности см. в Shallue et al. 2018 .
Каковы правила обновления для всех популярных алгоритмов оптимизации?
В этом разделе представлены правила обновления для нескольких популярных алгоритмов оптимизации.
Стохастический градиентный спуск (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Где $\eta_t$ — скорость обучения на шаге $t$.
Импульс
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Где $\eta_t$ — скорость обучения на шаге $t$, а $\gamma$ — коэффициент импульса.
Нестеров
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Где $\eta_t$ — скорость обучения на шаге $t$, а $\gamma$ — коэффициент импульса.
РМСПроп
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
АДАМ
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
НАДАМ
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
,Как можно отладить и смягчить ошибки оптимизации?
Резюме: Если модель испытывает трудности с оптимизацией, важно исправить их, прежде чем пытаться что-то делать. Диагностика и исправление ошибок в обучении является активной областью исследований.

Обратите внимание на следующее относительно рисунка 4:
- Изменение темпа не ухудшает производительность при низкой скорости обучения.
- Высокие темпы обучения больше не подходят для тренировок из-за нестабильности.
- Применение 1000 шагов прогрева скорости обучения устраняет этот конкретный случай нестабильности, обеспечивая стабильное обучение с максимальной скоростью обучения 0,1.
Выявление нестабильных рабочих нагрузок
Любая рабочая нагрузка становится нестабильной, если скорость обучения слишком велика. Нестабильность является проблемой только тогда, когда она вынуждает вас использовать слишком маленькую скорость обучения. Стоит различать как минимум два типа нестабильности тренировки:
- Нестабильность при инициализации или на ранних этапах обучения.
- Внезапная нестабильность в середине тренировки.
Вы можете применить систематический подход к выявлению проблем стабильности в вашей рабочей нагрузке, выполнив следующие действия:
- Выполните анализ скорости обучения и найдите лучшую скорость обучения lr*.
- Постройте кривые потерь при обучении для скоростей обучения чуть выше lr*.
- Если скорость обучения > lr* показывает нестабильность потерь (потери растут, а не уменьшаются в периоды обучения), то исправление нестабильности обычно улучшает обучение.
Зарегистрируйте норму L2 полного градиента потерь во время обучения, поскольку выбросы могут вызвать ложную нестабильность в середине обучения. Это может указать, насколько агрессивно обрезать градиенты или обновления веса.
ПРИМЕЧАНИЕ. Некоторые модели демонстрируют очень раннюю нестабильность, за которой следует восстановление, что приводит к медленному, но стабильному обучению. В обычных графиках оценки эти проблемы могут быть упущены из-за недостаточно частой оценки!
Чтобы проверить это, вы можете тренироваться для сокращенного пробега всего на ~500 шагов, используя lr = 2 * current best , но оценивая каждый шаг.

Возможные исправления распространенных моделей нестабильности
Рассмотрите следующие возможные исправления распространенных закономерностей нестабильности:
- Примените разминку скорости обучения. Это лучше всего подходит для ранней нестабильности тренировок.
- Примените обрезку градиента. Это полезно как для ранней, так и для средней нестабильности тренировки, а также может исправить некоторые плохие инициализации, которые не могут быть исправлены при разминке.
- Попробуйте новый оптимизатор. Иногда Адам может справиться с нестабильностью, чего не может сделать Momentum. Это активная область исследований.
- Убедитесь, что вы используете лучшие практики и лучшие инициализации для архитектуры вашей модели (примеры приведены ниже). Добавьте остаточные связи и нормализацию, если модель их еще не содержит.
- Нормализовать как последнюю операцию перед остатком. Например:
x + Norm(f(x)). Обратите внимание, чтоNorm(x + f(x))может вызвать проблемы. - Попробуйте инициализировать остаточные ветки до 0. (См. ReZero — это все, что вам нужно: быстрая сходимость на большой глубине. )
- Снизьте скорость обучения. Это последнее средство.
Разминка скорости обучения

Когда применять разминку скорости обучения


На рисунке 7a показан график оси гиперпараметров, который указывает на модель, испытывающую нестабильность оптимизации, поскольку лучшая скорость обучения находится прямо на грани нестабильности.
На рисунке 7b показано, как это можно перепроверить, изучив потери при обучении модели, обученной со скоростью обучения, в 5 или 10 раз превышающей этот пик. Если этот график показывает внезапный рост потерь после устойчивого снижения (например, на шаге ~ 10k на рисунке выше), то модель, вероятно, страдает от нестабильности оптимизации.
Как применить разминку скорости обучения

Пусть unstable_base_learning_rate будет скоростью обучения, при которой модель становится нестабильной, используя предыдущую процедуру.
Разминка включает в себя подготовку графика скорости обучения, который увеличивает скорость обучения от 0 до некоторого стабильного base_learning_rate , который как минимум на один порядок превышает unstable_base_learning_rate . По умолчанию будет выбрано base_learning_rate , равное 10x unstable_base_learning_rate . Однако учтите, что можно было бы запустить всю эту процедуру еще раз примерно для 100x unstable_base_learning_rate . Конкретный график:
- Увеличивайте от 0 до base_learning_rate в течение разминочных_шагов.
- Тренируйтесь с постоянной скоростью в течение post_warmup_steps.
Ваша цель — найти кратчайшее количество warmup_steps , которое позволит вам получить доступ к пиковой скорости обучения, которая намного выше, чем unstable_base_learning_rate . Таким образом, для каждого base_learning_rate вам необходимо настроить warmup_steps и post_warmup_steps . Обычно можно установить post_warmup_steps равным 2*warmup_steps .
Разминку можно настроить независимо от существующего графика затухания. warmup_steps следует изменять на несколько порядков. Например, в качестве примера исследования можно попробовать [10, 1000, 10,000, 100,000] . Самая большая возможная точка не должна превышать 10 % от max_train_steps .
После того, как установлен параметр warmup_steps , который не приводит к резкому увеличению скорости обучения при base_learning_rate , его следует применить к базовой модели. По сути, добавьте этот график к существующему графику и используйте оптимальный выбор контрольных точек, описанный выше, чтобы сравнить этот эксперимент с базовым уровнем. Например, если у нас изначально было 10 000 max_train_steps и мы выполнили warmup_steps для 1 000 шагов, новая процедура обучения должна выполнить всего 11 000 шагов.
Если для стабильной тренировки требуются длинные warmup_steps (>5% от max_train_steps ), вам может потребоваться увеличить max_train_steps , чтобы учесть это.
На самом деле не существует «типичного» значения для всего спектра рабочих нагрузок. Некоторым моделям требуется всего 100 шагов, а другим (особенно трансформаторам) может потребоваться более 40 тыс. шагов.
Градиентное отсечение

Отсечение градиента наиболее полезно при возникновении больших или резких проблем с градиентом. Градиентная обрезка может решить любую из следующих проблем:
- Ранняя тренировочная нестабильность (большая норма градиента рано)
- Нестабильность в середине тренировки (внезапные скачки градиента в середине тренировки).
Иногда более длительные периоды прогрева могут исправить нестабильность, чего не может сделать ограничение; Подробности см. в разделе «Прогрев скорости обучения» .
🤖 А как насчет обрезки во время разминки?
Идеальные пороги клиппирования чуть выше «типичной» нормы градиента.
Вот пример того, как можно сделать обрезку градиента:
- Если норма градиента $\left | g \right |$ превышает порог отсечения градиента $\lambda$, то выполните ${g}'= \lambda \times \frac{g}{\left | g \right |}$ где ${g}'$ — новый градиент.
Зарегистрируйте необрезанную норму градиента во время тренировки. По умолчанию генерируется:
- График зависимости нормы градиента от шага
- Гистограмма норм градиента, агрегированных по всем шагам
Выберите порог отсечения градиента на основе 90-го процентиля норм градиента. Порог зависит от рабочей нагрузки, но 90 % — хорошая отправная точка. Если 90% не работает, вы можете настроить этот порог.
🤖 А как насчет какой-нибудь адаптивной стратегии?
Если вы попробуете отсечение градиента, но проблемы с нестабильностью останутся, вы можете попробовать еще сильнее; то есть вы можете уменьшить порог.
Чрезвычайно агрессивное отсечение градиента (то есть обрезается >50% обновлений) по сути является странным способом снижения скорости обучения. Если вы обнаружите, что используете чрезвычайно агрессивное ограничение, вам, вероятно, следует вместо этого просто снизить скорость обучения.
Почему вы называете скорость обучения и другие параметры оптимизации гиперпараметрами? Они не являются параметрами какого-либо предшествующего распределения.
Термин «гиперпараметр» имеет точное значение в байесовском машинном обучении, поэтому называть скорость обучения и большинство других настраиваемых параметров глубокого обучения «гиперпараметрами», возможно, является злоупотреблением терминологией. Мы бы предпочли использовать термин «метапараметр» для обозначения скорости обучения, архитектурных параметров и всех других настраиваемых вещей глубокого обучения. Это связано с тем, что метапараметр позволяет избежать путаницы, возникающей из-за неправильного использования слова «гиперпараметр». Эта путаница особенно вероятна при обсуждении байесовской оптимизации, где вероятностные модели поверхности отклика имеют свои собственные истинные гиперпараметры.
К сожалению, хотя термин «гиперпараметр» может сбивать с толку, он стал чрезвычайно распространенным в сообществе специалистов по глубокому обучению. Поэтому в этом документе, предназначенном для широкой аудитории, в которую входит множество людей, которые вряд ли знают об этой формальности, мы решили внести свой вклад в один источник путаницы в этой области в надежде избежать другого. Тем не менее, мы можем сделать другой выбор при публикации исследовательской работы, и мы призываем других использовать вместо этого «метапараметр» в большинстве контекстов.
Почему бы не настроить размер пакета так, чтобы напрямую улучшить производительность проверочного набора?
Изменение размера пакета без изменения каких-либо других деталей конвейера обучения часто влияет на производительность набора проверки. Однако разница в производительности набора проверки между двумя размерами пакетов обычно исчезает, если конвейер обучения оптимизируется независимо для каждого размера пакета.
Гиперпараметры, которые наиболее сильно взаимодействуют с размером пакета и, следовательно, их наиболее важно настраивать отдельно для каждого размера пакета, — это гиперпараметры оптимизатора (например, скорость обучения, импульс) и гиперпараметры регуляризации. Меньшие размеры пакетов вносят больше шума в алгоритм обучения из-за дисперсии выборки. Этот шум может иметь регуляризирующий эффект. Таким образом, партии большего размера могут быть более склонны к переоснащению и могут потребовать более сильной регуляризации и/или дополнительных методов регуляризации. Кроме того, вам может потребоваться настроить количество шагов обучения при изменении размера пакета.
После того, как все эти эффекты приняты во внимание, не существует убедительных доказательств того, что размер партии влияет на максимально достижимую производительность проверки. Подробности см. в Shallue et al. 2018 .
Каковы правила обновления для всех популярных алгоритмов оптимизации?
В этом разделе представлены правила обновления для нескольких популярных алгоритмов оптимизации.
Стохастический градиентный спуск (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Где $\eta_t$ — скорость обучения на шаге $t$.
Импульс
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Где $\eta_t$ — скорость обучения на шаге $t$, а $\gamma$ — коэффициент импульса.
Нестеров
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Где $\eta_t$ — скорость обучения на шаге $t$, а $\gamma$ — коэффициент импульса.
РМСПроп
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
АДАМ
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
НАДАМ
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
