Optimizasyon hataları nasıl ayıklanabilir ve azaltılabilir?
Özet: Model optimizasyon zorlukları yaşıyorsa başka şeyler denemeden önce bunları düzeltmek önemlidir. Eğitim hatalarını teşhis edip düzeltmek, aktif olarak devam eden bir araştırma alanıdır.

Şekil 4 ile ilgili olarak aşağıdakilere dikkat edin:
- Adımların değiştirilmesi, düşük öğrenme hızlarında performansı düşürmez.
- Yüksek öğrenme hızları, kararsızlık nedeniyle artık iyi bir şekilde eğitilmiyor.
- Öğrenme hızı ısınma işleminin 1.000 adım boyunca uygulanması, bu kararsızlık örneğini çözerek 0,1'lik maksimum öğrenme hızıyla kararlı bir eğitim sağlar.
Kararsız iş yüklerini belirleme
Öğrenme hızı çok yüksekse iş yükü dengesizleşir. Kararsızlık yalnızca çok küçük bir öğrenme hızı kullanmanıza neden olduğunda sorun yaratır. En az iki tür eğitim kararsızlığı ayırt edilmeye değerdir:
- Başlatma sırasında veya eğitimin başlarında kararsızlık.
- Eğitimin ortasında ani dengesizlik.
Aşağıdaki adımları uygulayarak iş yükünüzdeki kararlılık sorunlarını belirlemek için sistematik bir yaklaşım benimseyebilirsiniz:
- Öğrenme hızı taraması yapın ve en iyi öğrenme hızını (lr*) bulun.
- Öğrenme oranları için eğitim kaybı eğrilerini lr* değerinin hemen üzerinde çizin.
- Öğrenme hızları > lr* olduğunda kayıp kararsızlığı (eğitim dönemlerinde kayıp azalmaz, artar) görülürse kararsızlığı düzeltmek genellikle eğitimi iyileştirir.
Aykırı değerler eğitim sırasında sahte dengesizliğe neden olabileceğinden, eğitim sırasında tam kayıp gradyanının L2 normunu kaydedin. Bu, gradyanların ne kadar agresif bir şekilde kırpılacağını veya ağırlık güncellemelerinin nasıl yapılacağını belirleyebilir.
NOT: Bazı modellerde, çok erken bir aşamada kararsızlık görülür. Ardından, yavaş ancak kararlı bir eğitime yol açan bir iyileşme yaşanır. Sık değerlendirme yapılmadığı için yaygın değerlendirme planlarında bu sorunlar gözden kaçabilir.
Bunu kontrol etmek için lr = 2 * current best kullanarak yalnızca ~500 adımlık kısaltılmış bir çalıştırma için eğitim verebilirsiniz ancak her adımı değerlendirebilirsiniz.

Sık karşılaşılan kararsızlık kalıpları için olası düzeltmeler
Yaygın kararsızlık durumları için aşağıdaki olası düzeltmeleri deneyin:
- Öğrenme oranı ısınmasını uygulayın. Bu, eğitimin ilk aşamalarındaki dengesizlik için en iyi çözümdür.
- Gradyan kırpma uygulayın. Bu, hem eğitimin başlarında hem de ortalarında yaşanan kararsızlıklar için iyi bir çözümdür ve ısınma işleminin düzeltemediği bazı kötü başlatma işlemlerini düzeltebilir.
- Yeni bir optimize edici deneyin. Bazen Adam, Momentum'un ele alamadığı dengesizlikleri giderebilir. Bu, aktif bir araştırma alanıdır.
- Model mimariniz için en iyi uygulamaları ve en iyi ilk kullanımları kullandığınızdan emin olun (örnekler aşağıda verilmiştir). Modelde yoksa artık bağlantılar ve normalleştirme ekleyin.
- Kalıntıdan önceki son işlem olarak normalleştirin. Örneğin:
x + Norm(f(x)).Norm(x + f(x))karakterinin sorunlara neden olabileceğini unutmayın. - Kalan dalları 0 olarak başlatmayı deneyin. (Bkz. ReZero is All You Need: Fast Convergence at Large Depth.)
- Öğrenme hızını düşürün. Bu son çaredir.
Öğrenme oranı ısınması

Öğrenme oranı ısınması ne zaman uygulanır?


Şekil 7a'da, en iyi öğrenme oranı kararsızlığın hemen sınırında olduğundan, optimizasyon kararsızlıkları yaşayan bir modeli gösteren bir hiperparametre ekseni grafiği yer alıyor.
Şekil 7b'de, bu durumun, öğrenme hızı bu zirveden 5 veya 10 kat daha büyük olan bir modelin eğitim kaybı incelenerek nasıl iki kez kontrol edilebileceği gösterilmektedir. Bu grafik, sabit bir düşüşün ardından kayıpta ani bir artış gösteriyorsa (ör. yukarıdaki şekilde ~10 bininci adımda) model muhtemelen optimizasyon kararsızlığından etkileniyordur.
Öğrenme hızı ısınması nasıl uygulanır?

Önceki prosedür kullanılarak modelin kararsız hale geldiği öğrenme hızı unstable_base_learning_rate olsun.
Isınma, öğrenme oranını 0'dan unstable_base_learning_rate değerinden en az bir kat daha büyük olan sabit bir base_learning_rate değerine yükselten bir öğrenme oranı planının eklenmesini içerir.
Varsayılan olarak 10x base_learning_rate denenecektir
unstable_base_learning_rate. Ancak bu prosedürün tamamının 100x gibi bir değer için tekrar çalıştırılabileceğini unutmayın
unstable_base_learning_rate. Belirli program:
- Isınma adımları boyunca 0'dan base_learning_rate'e (temel öğrenme oranı) yükselir.
- post_warmup_steps için sabit bir hızda eğitim yapın.
Amacınız, warmup_steps'dan çok daha yüksek olan en yüksek öğrenme oranlarına erişmenizi sağlayan en kısa warmup_steps süresini bulmaktır.unstable_base_learning_rate
Bu nedenle, her base_learning_rate için warmup_steps ve post_warmup_steps değerlerini ayarlamanız gerekir. post_warmup_steps değerini 2*warmup_steps olarak ayarlamak genellikle sorun yaratmaz.
Isınma, mevcut bir azalma programından bağımsız olarak ayarlanabilir. warmup_steps
birkaç farklı büyüklük sırasına göre süpürülmelidir. Örneğin, örnek bir çalışmada [10, 1000, 10,000, 100,000] denenebilir. En büyük olası nokta, max_train_steps değerinin% 10'undan fazla olmamalıdır.
Eğitimi base_learning_rate'da patlatmayan bir warmup_steps oluşturulduktan sonra temel modele uygulanmalıdır.
Temel olarak, bu programı mevcut programın önüne ekleyin ve bu denemeyi temel değerle karşılaştırmak için yukarıda bahsedilen optimum kontrol noktası seçimini kullanın. Örneğin, başlangıçta 10.000 max_train_steps varsa ve 1.000 adım boyunca warmup_steps işlemi yapıldıysa yeni eğitim prosedürü toplam 11.000 adım boyunca çalıştırılmalıdır.
Kararlı eğitim için uzun warmup_steps gerekiyorsa (>%5 max_train_steps) bunu hesaba katmak için max_train_steps değerini artırmanız gerekebilir.
İş yüklerinin tüm aralığında gerçekten "tipik" bir değer yoktur. Bazı modeller yalnızca 100 adım gerektirirken diğerleri (özellikle dönüştürücüler) 40.000'den fazla adım gerektirebilir.
Gradyan kırpma
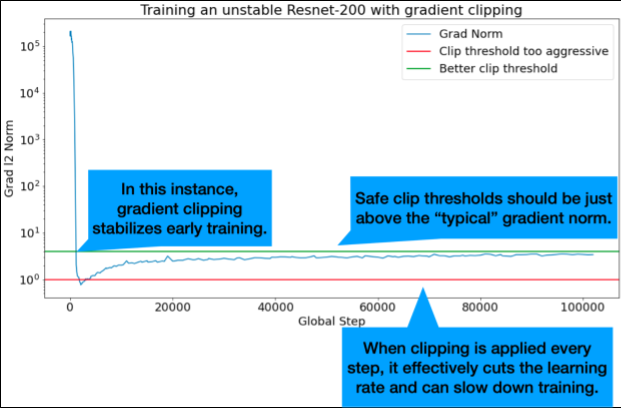
Gradyan kırpma, en çok büyük veya aykırı gradyan sorunları oluştuğunda kullanışlıdır. Gradyan kırpma, aşağıdaki sorunlardan birini düzeltebilir:
- Erken eğitimde kararsızlık (büyük gradyan normu)
- Eğitim sırasında dengesizlikler (eğitim sırasında gradyanda ani artışlar).
Bazen daha uzun ısınma süreleri, kırpmanın düzeltemediği dengesizlikleri düzeltebilir. Ayrıntılar için Öğrenme hızı ısınması bölümüne bakın.
🤖 Isınma sırasında kırpma işlemi nasıl yapılır?
İdeal kırpma eşikleri, "tipik" gradyan normunun hemen üzerindedir.
Aşağıda, gradyan kırpmanın nasıl yapılabileceğine dair bir örnek verilmiştir:
- Gradyanın normu $\left | g \right |$ gradyan kırpma eşiği $\lambda$ değerinden büyükse ${g}'= \lambda \times \frac{g}{\left | g \right |}$ işlemini yapın. Burada ${g}'$ yeni gradyanı ifade eder.
Eğitim sırasında kırpılmamış gradyan normunu günlüğe kaydeder. Varsayılan olarak oluşturulacaklar:
- Gradyan normu ile adım arasındaki ilişkiyi gösteren bir grafik
- Tüm adımlar genelinde toplanan gradyan normlarının histogramı
Gradyan normlarının 90. yüzdelik dilimine göre bir gradyan kırpma eşiği seçin. Eşik, iş yüküne bağlıdır ancak% 90 iyi bir başlangıç noktasıdır. %90 işe yaramazsa bu eşiği ayarlayabilirsiniz.
🤖 Uyarlanabilir bir strateji kullanabilir miyim?
Eğim kırpmayı denediğiniz halde kararsızlık sorunları devam ederse eşiği daha da küçülterek daha fazla kırpmayı deneyebilirsiniz.
Son derece agresif gradyan kırpma (yani güncellemelerin% 50'den fazlasının kırpılması), esasında öğrenme hızını azaltmanın tuhaf bir yoludur. Çok agresif bir kırpma kullandığınızı fark ederseniz öğrenme hızını düşürmeniz daha iyi olur.
Neden öğrenme hızına ve diğer optimizasyon parametrelerine hiperparametre diyorsunuz? Bunlar, önceki dağılımların parametreleri değildir.
"Hiperparametre" terimi, Bayesçi makine öğreniminde kesin bir anlama sahiptir. Bu nedenle, öğrenme hızına ve ayarlanabilir derin öğrenme parametrelerinin çoğuna "hiperparametre" olarak atıfta bulunmak, terminolojinin kötüye kullanılması olarak değerlendirilebilir. Öğrenme hızları, mimari parametreler ve derin öğrenmede ayarlanabilir diğer tüm öğeler için "metaparametre" terimini kullanmayı tercih ederiz. Bunun nedeni, metaparametrenin "hiperparametre" kelimesinin yanlış kullanılmasından kaynaklanan kafa karışıklığı olasılığını önlemesidir. Bu karışıklık, özellikle olasılıksal yanıt yüzeyi modellerinin kendi gerçek hiperparametrelerine sahip olduğu Bayes optimizasyonu tartışılırken ortaya çıkar.
Maalesef, kafa karıştırıcı olsa da "hiperparametre" terimi, derin öğrenme topluluğunda son derece yaygın hale geldi. Bu nedenle, bu teknik ayrıntının farkında olması muhtemel olmayan birçok kişiyi içeren geniş bir kitleye yönelik bu belgede, başka bir kafa karışıklığına yol açmamak için alandaki bir kafa karışıklığına katkıda bulunmayı tercih ettik. Bununla birlikte, bir araştırma makalesi yayınlarken farklı bir seçim yapabiliriz ve çoğu bağlamda diğer kullanıcıları "metaparametre"yi kullanmaya teşvik ederiz.
Neden toplu iş boyutu, doğrulama kümesi performansını doğrudan iyileştirecek şekilde ayarlanmamalıdır?
Toplu iş boyutunu eğitim hattının diğer ayrıntılarını değiştirmeden değiştirmek genellikle doğrulama kümesi performansını etkiler. Ancak eğitim ardışık düzeni her toplu iş boyutu için bağımsız olarak optimize edilirse iki toplu iş boyutu arasındaki doğrulama kümesi performansındaki fark genellikle ortadan kalkar.
Toplu iş boyutuyla en güçlü şekilde etkileşime giren ve bu nedenle her toplu iş boyutu için ayrı ayrı ayarlanması en önemli olan hiperparametreler, optimize edici hiperparametreler (örneğin, öğrenme hızı, momentum) ve düzenleme hiperparametreleridir. Daha küçük toplu iş boyutları, örnek varyansı nedeniyle eğitim algoritmasına daha fazla gürültü ekler. Bu gürültü, düzenleyici bir etkiye sahip olabilir. Bu nedenle, daha büyük toplu iş boyutları aşırı uyuma daha yatkın olabilir ve daha güçlü düzenlileştirme ve/veya ek düzenlileştirme teknikleri gerektirebilir. Ayrıca, toplu iş boyutunu değiştirirken eğitim adımı sayısını da ayarlamanız gerekebilir.
Tüm bu etkiler dikkate alındığında, toplu iş boyutunun ulaşılabilen maksimum doğrulama performansını etkilediğine dair ikna edici bir kanıt yoktur. Ayrıntılar için Shallue et al. 2018 başlıklı makaleyi inceleyin.
Tüm popüler optimizasyon algoritmaları için güncelleme kuralları nelerdir?
Bu bölümde, sık kullanılan çeşitli optimizasyon algoritmaları için güncelleme kuralları verilmektedir.
Stokastik gradyan inişi (SGD)
\[\theta_{t+1} = \theta_{t} - \eta_t \nabla \mathcal{l}(\theta_t)\]
Burada $\eta_t$, $t$ adımındaki öğrenme hızıdır.
İlgiyi Artırma
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t v_{t+1}\]
Burada $\eta_t$, $t$ adımındaki öğrenme oranı ve $\gamma$ ise momentum katsayısıdır.
Nesterov
\[v_0 = 0\]
\[v_{t+1} = \gamma v_{t} + \nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - \eta_t ( \gamma v_{t+1} + \nabla \mathcal{l}(\theta_{t}) )\]
Burada $\eta_t$, $t$ adımındaki öğrenme oranı ve $\gamma$ ise momentum katsayısıdır.
RMSProp
\[v_0 = 1 \text{, } m_0 = 0\]
\[v_{t+1} = \rho v_{t} + (1 - \rho) \nabla \mathcal{l}(\theta_t)^2\]
\[m_{t+1} = \gamma m_{t} + \frac{\eta_t}{\sqrt{v_{t+1} + \epsilon}}\nabla \mathcal{l}(\theta_t)\]
\[\theta_{t+1} = \theta_{t} - m_{t+1}\]
ADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l}(\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{m_{t+1}}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]
NADAM
\[m_0 = 0 \text{, } v_0 = 0\]
\[m_{t+1} = \beta_1 m_{t} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)\]
\[v_{t+1} = \beta_2 v_{t} + (1 - \beta_2) \nabla \mathcal{l} (\theta_t)^2\]
\[b_{t+1} = \frac{\sqrt{1 - \beta_2^{t+1}}}{1 - \beta_1^{t+1}}\]
\[\theta_{t+1} = \theta_{t} - \alpha_t \frac{\beta_1 m_{t+1} + (1 - \beta_1) \nabla \mathcal{l} (\theta_t)}{\sqrt{v_{t+1}} + \epsilon} b_{t+1}\]