Esta unidade se concentra na pesquisa quase aleatória.
Por que usar a pesquisa quase aleatória?
A pesquisa quase aleatória (com base em sequências de baixa discrepância) é nossa preferência em vez de ferramentas de otimização de caixa preta mais sofisticadas quando usada como parte de um processo de ajuste iterativo destinado a maximizar o insight sobre o problema de ajuste (o que chamamos de "fase de exploração"). A otimização bayesiana e ferramentas semelhantes são mais adequadas para a fase de exploração. A pesquisa quase aleatória baseada em sequências de discrepância baixa deslocadas aleatoriamente pode ser considerada "pesquisa de grade misturada e com jitter", já que ela explora um determinado espaço de pesquisa de maneira uniforme, mas aleatória, e distribui os pontos de pesquisa mais do que a pesquisa aleatória.
As vantagens da pesquisa quase aleatória em relação a ferramentas de otimização de caixa preta mais sofisticadas (por exemplo, otimização bayesiana, algoritmos evolutivos) incluem:
- A amostragem não adaptativa do espaço de pesquisa permite mudar o objetivo de ajuste na análise post hoc sem executar novamente os experimentos. Por exemplo, geralmente queremos encontrar o melhor teste em termos de erro de validação alcançado em qualquer ponto do treinamento. No entanto, a natureza não adaptativa da pesquisa quase aleatória permite encontrar o melhor teste com base no erro de validação final, no erro de treinamento ou em alguma métrica de avaliação alternativa sem repetir os experimentos.
- A pesquisa quase aleatória se comporta de maneira consistente e estatísticamente reproduzível. Deve ser possível reproduzir um estudo de seis meses atrás, mesmo se a implementação do algoritmo de pesquisa mudar, desde que ele mantenha as mesmas propriedades de uniformidade. Se você usar um software sofisticado de otimização Bayesiana, a implementação poderá mudar de maneira importante entre as versões, o que torna muito mais difícil reproduzir uma pesquisa antiga. Nem sempre é possível reverter para uma implementação antiga (por exemplo, se a ferramenta de otimização for executada como um serviço).
- A exploração uniforme do espaço de pesquisa facilita a compreensão dos resultados e do que eles podem sugerir sobre o espaço de pesquisa. Por exemplo, se o melhor ponto na travessia de pesquisa quase aleatória estiver no limite do espaço de pesquisa, esse é um bom (mas não infalível) sinal de que os limites do espaço de pesquisa precisam ser alterados. No entanto, um algoritmo de otimização de caixa-preta adaptável pode ter negligenciado o meio do espaço de pesquisa devido a alguns testes iniciais infelizmente, mesmo que contenha pontos igualmente bons, já que é exatamente esse tipo de não uniformidade que um bom algoritmo de otimização precisa empregar para acelerar a pesquisa.
- A execução de diferentes números de testes em paralelo em vez de sequencialmente não produz resultados estatisticamente diferentes ao usar a pesquisa quase aleatória (ou outros algoritmos de pesquisa não adaptáveis), ao contrário dos algoritmos adaptáveis.
- Algoritmos de pesquisa mais sofisticados nem sempre processam pontos inviáveis corretamente, especialmente se não forem projetados com o ajuste de hiperparâmetros de rede neural em mente.
- A pesquisa quase aleatória é simples e funciona muito bem quando muitos testes de ajuste são executados em paralelo. De acordo com a pesquisa1, é muito difícil para um algoritmo adaptativo superar uma pesquisa quase aleatória com o dobro do orçamento, especialmente quando muitos testes precisam ser executados em paralelo (e, portanto, há poucas chances de usar os resultados de testes anteriores ao lançar novos testes). Sem experiência em otimização bayesiana e outros métodos avançados de otimização de caixa-preta, você pode não conseguir os benefícios que eles são, em princípio, capazes de oferecer. É difícil comparar algoritmos avançados de otimização de caixa-preta em condições realistas de ajuste de aprendizado profundo. Eles são uma área muito ativa de pesquisa atual, e os algoritmos mais sofisticados têm armadilhas próprias para usuários inexperientes. Especialistas nesses métodos conseguem bons resultados, mas, em condições de alto paralelismo, o espaço de pesquisa e o orçamento tendem a ser muito mais importantes.
Dito isso, se seus recursos computacionais permitirem apenas um pequeno número de testes em paralelo e você puder executar muitos testes em sequência, a otimização bayesiana se torna muito mais atraente, apesar de tornar os resultados de ajuste mais difíceis de interpretar.
Onde posso encontrar uma implementação de pesquisa quase aleatória?
O Vizier de código aberto tem
uma implementação de pesquisa quase
aleatória.
Defina algorithm="QUASI_RANDOM_SEARCH" neste exemplo de uso do Vizier.
Há uma implementação alternativa neste exemplo de varreduras de hiperparâmetros.
Ambas as implementações geram uma sequência de Halton para um determinado espaço de
pesquisa (com a intenção de implementar uma sequência de Halton deslocada e embaralhada, conforme
recomendado em
Hyper-Parameters críticos: sem aleatório, sem
choro).
Se um algoritmo de pesquisa quase aleatória com base em uma sequência de baixa discrepância não estiver disponível, será possível substituir a pesquisa uniforme pseudoaleatória, embora isso seja provavelmente um pouco menos eficiente. Em uma ou duas dimensões, a pesquisa de grade também é aceitável, mas não em dimensões mais altas. Consulte Bergstra & Bengio, 2012.
Quantos testes são necessários para conseguir bons resultados com a pesquisa quase aleatória?
Não há como determinar quantos testes são necessários para conseguir resultados com a pesquisa quase aleatória em geral, mas você pode conferir exemplos específicos. Como mostra a Figura 3, o número de testes em um estudo pode ter um impacto significativo nos resultados:
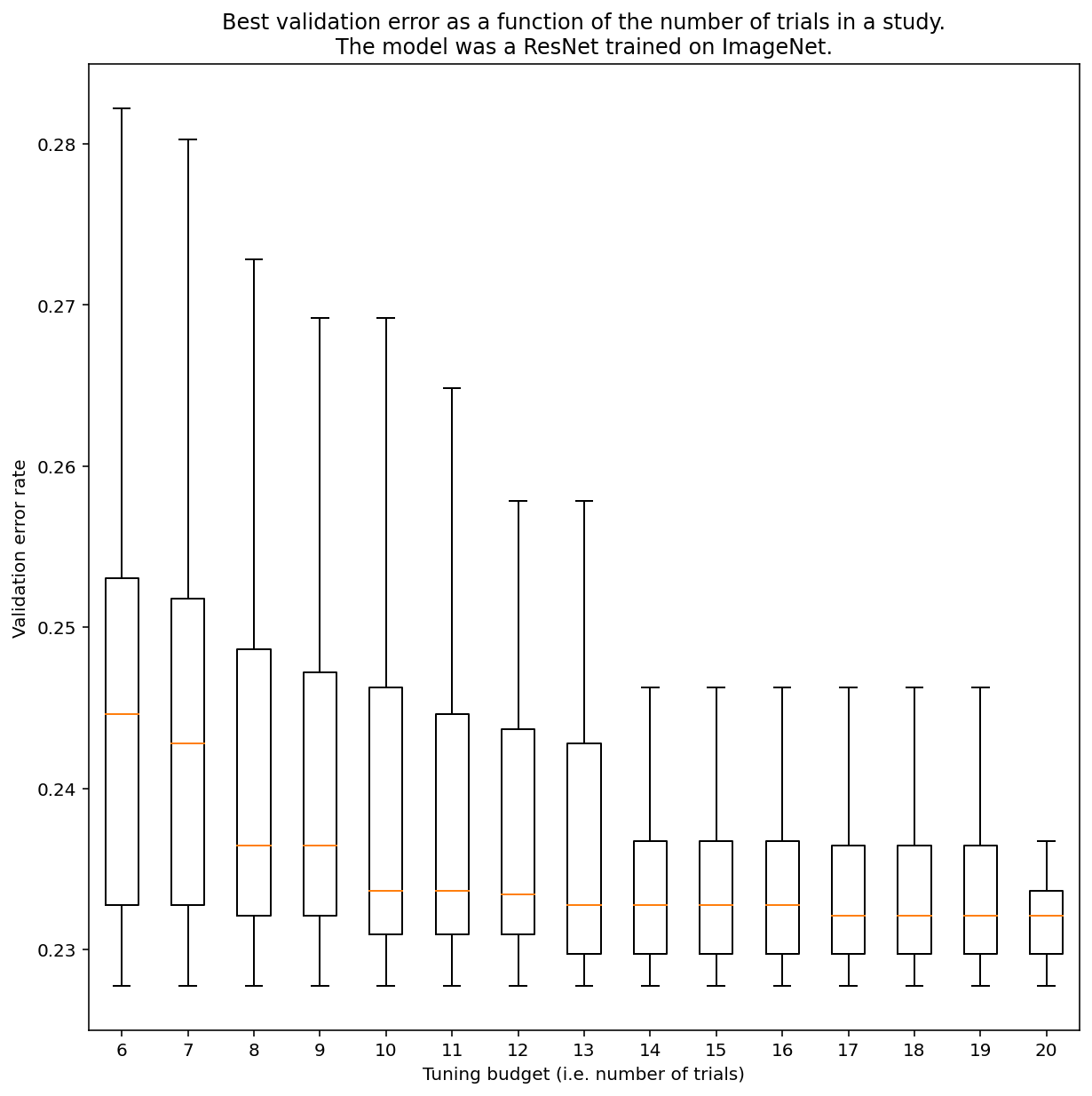
Figura 3:ResNet-50 ajustada no ImageNet com 100 testes. Usando o bootstrapping, diferentes valores de orçamento de ajuste foram simulados. Os diagramas de caixa das melhores performances de cada orçamento de teste são plotados.
Observe o seguinte sobre a Figura 3:
- Os intervalos interquartisil quando 6 testes foram amostrados são muito maiores do que quando 20 testes foram amostrados.
- Mesmo com 20 testes, a diferença entre estudos com sorte e azar provavelmente é maior do que a variação típica entre revisões do modelo em diferentes sementes aleatórias, com hiperparâmetros fixos, que para essa carga de trabalho pode ser de +/- 0,1% em uma taxa de erro de validação de aproximadamente 23%.
-
Ben Recht e Kevin Jamieson apontaram que a pesquisa aleatória com orçamento duplo é uma boa referência (o artigo da Hyperband faz argumentos semelhantes), mas é possível encontrar espaços de pesquisa e problemas em que as técnicas de otimização bayesianas mais avançadas superam a pesquisa aleatória com o dobro do orçamento. No entanto, na nossa experiência, superar a pesquisa aleatória com orçamento 2X fica muito mais difícil no regime de alto paralelismo, já que a otimização bayesiana não tem oportunidade de observar os resultados de testes anteriores. ↩
