חיפוש מעשי אקראי
קל לארגן דפים בעזרת אוספים
אפשר לשמור ולסווג תוכן על סמך ההעדפות שלך.
היחידה הזו מתמקדת בחיפוש כמעט אקראי.
למה כדאי להשתמש בחיפוש כמעט אקראי?
אנחנו מעדיפים חיפוש כמעט אקראי (על סמך רצפים עם אי-התאמה נמוכה) על פני כלים מתוחכמים יותר לאופטימיזציה של תיבת שחורה, כשמשתמשים בהם כחלק מתהליך כוונון איטרטיבי שנועד למקסם את התובנות לגבי בעיית הכוונון (מה שאנחנו מכנים 'שלב החקירה'). אופטימיזציה לפי מודלים בייסיאניים וכלים דומים מתאימים יותר לשלב הניצול.
חיפוש כמעט אקראי שמבוסס על רצפים עם פערים נמוכים שנדחו באופן אקראי יכול להיחשב כ'חיפוש רשת עם רעשי גליץ', כי הוא בודק באופן אחיד אבל אקראי מרחב חיפוש נתון ומפיץ את נקודות החיפוש יותר מאשר חיפוש אקראי.
היתרונות של חיפוש כמעט אקראי על פני כלים מתוחכמים יותר לאופטימיזציה של תיבת שחורה (למשל, אופטימיזציה בייסינית, אלגוריתמים אבולוציוניים) כוללים:
- דגימה לא אדפטיבית של מרחב החיפוש מאפשרת לשנות את יעד ההתאמה בניתוח 'אחרי מעשה' בלי להריץ מחדש את הניסויים.
לדוגמה, בדרך כלל אנחנו רוצים למצוא את הניסוי הטוב ביותר מבחינת שגיאת האימות שהתקבלה בכל שלב באימון. עם זאת, המאפיין הלא אדפטיבי של חיפוש כמעט אקראי מאפשר למצוא את הניסוי הטוב ביותר על סמך שגיאת האימות הסופית, שגיאת האימון או מדד הערכה חלופי כלשהו, בלי להריץ מחדש את הניסויים.
- חיפוש כמעט אקראי מתנהג באופן עקבי וניתנת לשחזור באופן סטטיסטי. אמורה להיות אפשרות לשחזר מחקר מלפני שישה חודשים גם אם ההטמעה של אלגוריתם החיפוש משתנה, כל עוד הוא שומר על אותם מאפייני אחידות. אם משתמשים בתוכנת אופטימיזציה מתוחכמת מבוססת-בייסיאן, יכול להיות שההטמעה תשתנה באופן משמעותי בין גרסאות, וכך יהיה קשה יותר לשחזר חיפוש ישן.
לא תמיד אפשר לחזור לגרסה קודמת של הטמעה (למשל, אם כלי האופטימיזציה פועל כשירות).
- הבדיקה הרגילה של מרחב החיפוש מאפשרת להסיק מסקנות לגבי התוצאות ולגבי מה שהן עשויות להצביע עליו לגבי מרחב החיפוש.
לדוגמה, אם הנקודה הטובה ביותר בסריקה של חיפוש כמעט אקראי נמצאת בגבול של מרחב החיפוש, זה סימן טוב (אבל לא ודאי) שצריך לשנות את גבולות מרחב החיפוש.
עם זאת, אלגוריתם אופטימיזציה אדפטיבי של תיבת שחורה עשוי להתעלם מחלק ממרחב החיפוש בגלל ניסויים מוקדמים לא מוצלחים, גם אם הוא מכיל נקודות טובות באותה מידה. הסיבה לכך היא שזהו בדיוק סוג אי-העקביות שצריך להשתמש בו באלגוריתם אופטימיזציה טוב כדי לזרז את החיפוש.
- כשמשתמשים בחיפוש כמעט אקראי (או באלגוריתמים אחרים של חיפוש לא אדפטיבי), אין הבדל סטטיסטי בין הפעלת מספרים שונים של ניסויים במקביל לבין הפעלת מספרים שונים של ניסויים ברצף, בניגוד לאלגוריתמים אדפטיביים.
- אלגוריתמים מתוחכמים יותר של חיפוש לא תמיד מטפלים נכון בנקודות לא ריאליות, במיוחד אם הם לא תוכננו תוך התחשבות בהתאמה של פרמטרים היפר-מרחביים של רשתות נוירונליות.
- חיפוש כמעט אקראי הוא פשוט ופועל במיוחד טוב כשמפעילים בו-זמנית הרבה ניסויים לכוונון.
לפי נתונים אנקדוטיים1, קשה מאוד לאלגוריתם אדפטיבי לנצח חיפוש כמעט אקראי עם תקציב כפול, במיוחד כשצריך להריץ הרבה ניסויים במקביל (ולכן יש מעט מאוד הזדמנויות להשתמש בתוצאות של ניסויים קודמים כשמפעילים ניסויים חדשים).
ללא מומחיות באופטימיזציה לפי מודלים בייסיאניים ובשיטות מתקדמות אחרות של אופטימיזציה בקופסה שחורה, יכול להיות שלא תשיגו את היתרונות שהן יכולות לספק, באופן עקרוני. קשה להשוות בין אלגוריתמים מתקדמים של אופטימיזציה בקופסה שחורה בתנאים ריאליסטיים של כוונון למידה עמוקה. זהו תחום פעיל מאוד של מחקר, ולכל אלגוריתם מתוחכם יש מלכודות משלו למשתמשים חסרי ניסיון. מומחים בשיטות האלה יכולים להשיג תוצאות טובות, אבל בתנאים של מקביליות גבוהה, מרחב החיפוש והתקציב נוטים להיות חשובים הרבה יותר.
עם זאת, אם משאבי המחשוב שלכם מאפשרים להריץ רק מספר קטן של ניסויים במקביל, ואתם יכולים להרשות לעצמכם להריץ הרבה ניסויים ברצף, אופטימיזציה בייסינית הופכת לאטרקטיבית הרבה יותר, למרות שקשה יותר לפרש את תוצאות ההתאמה.
איפה אפשר למצוא הטמעה של חיפוש כמעט אקראי?
ב-Vizir בקוד פתוח יש הטמעה של חיפוש כמעט אקראי.
מגדירים את algorithm="QUASI_RANDOM_SEARCH" בדוגמה הזו לשימוש ב-Vizier.
אפשר למצוא הטמעה חלופית בדוגמה הזו של סריקות של פרמטרים היפר-מרחביים.
שתי הטמעות האלה יוצרות רצף Halton למרחב חיפוש נתון (המטרה היא להטמיע רצף Halton שעבר דחיפה וערבוב, כפי שמומלץ במאמר פרמטרים היפר-קריטיים: ללא אקראיות, ללא קריאה).
אם לא זמין אלגוריתם חיפוש כמעט אקראי שמבוסס על רצף עם אי-התאמה נמוכה, אפשר להחליף אותו בחיפוש אחיד פסאודו-אקראי, אבל סביר להניח שהיעילות שלו תהיה מעט נמוכה יותר. כשמשתמשים ב-1-2 מאפיינים, אפשר גם לבצע חיפוש ברשימה, אבל לא במאפיינים רבים יותר. (ראו Bergstra & Bengio, 2012).
כמה ניסיונות נדרשים כדי לקבל תוצאות טובות בחיפוש כמעט אקראי?
אין דרך לקבוע כמה ניסיונות נדרשים כדי לקבל תוצאות בחיפוש כמעט אקראי באופן כללי, אבל אפשר להיעזר בדוגמאות ספציפיות. כפי שמוצג באיור 3, למספר הניסויים במחקר יכולה להיות השפעה משמעותית על התוצאות:
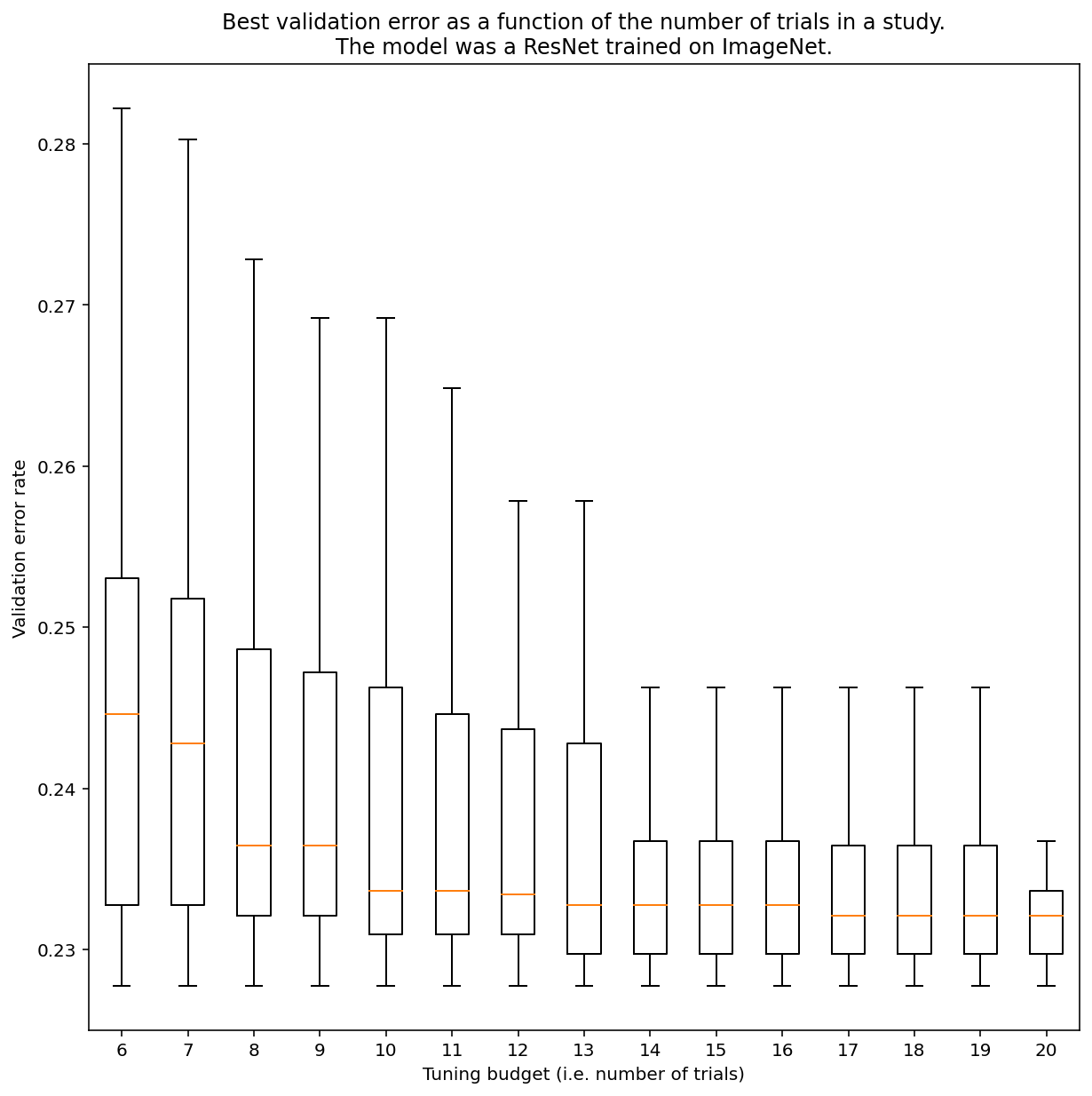
איור 3: ResNet-50 שהותאמה ב-ImageNet עם 100 ניסיונות.
באמצעות טעינה ראשונית (bootstrapping), בוצעה סימולציה של סכומים שונים של תקציב לכוונון.
מוצגים תרשימים של תיבות עם הביצועים הטובים ביותר לכל תקציב ניסיוני.
שימו לב לפרטים הבאים לגבי איור 3:
- טווחי הרבעונים כשנלקחו 6 ניסויים לדגימה גדולים בהרבה מאשר כשנלקחו 20 ניסויים לדגימה.
- גם עם 20 ניסיונות, סביר להניח שההבדל בין ניסויים עם מזל טוב במיוחד לבין ניסויים עם מזל רע במיוחד גדול מהשונות הרגילה בין אימון מחדש של המודל הזה עם זרעים אקראיים שונים, עם פרמטרים היפר-מוגדרים קבועים. עבור עומס העבודה הזה, השונות יכולה להיות בערך +/- 0.1% בשיעור שגיאות האימות של כ-23%.
אלא אם צוין אחרת, התוכן של דף זה הוא ברישיון Creative Commons Attribution 4.0 ודוגמאות הקוד הן ברישיון Apache 2.0. לפרטים, ניתן לעיין במדיניות האתר Google Developers. Java הוא סימן מסחרי רשום של חברת Oracle ו/או של השותפים העצמאיים שלה.
עדכון אחרון: 2025-07-27 (שעון UTC).
[null,null,["עדכון אחרון: 2025-07-27 (שעון UTC)."],[[["\u003cp\u003eQuasi-random search, akin to "jittered, shuffled grid search," offers consistent exploration of hyperparameter search spaces, aiding in insightful analysis and reproducibility.\u003c/p\u003e\n"],["\u003cp\u003eIts non-adaptive nature enables flexible post hoc analysis without rerunning experiments, unlike adaptive methods like Bayesian optimization.\u003c/p\u003e\n"],["\u003cp\u003eWhile Bayesian optimization excels with sequential trials, quasi-random search shines in high-parallelism scenarios, often outperforming adaptive methods with double its budget.\u003c/p\u003e\n"],["\u003cp\u003eQuasi-random search facilitates easier interpretation of results and identification of potential search space boundary issues.\u003c/p\u003e\n"],["\u003cp\u003eAlthough the required number of trials varies depending on the problem, studies show significant impact on results, highlighting the importance of adequate budget allocation.\u003c/p\u003e\n"]]],[],null,["# Quasi-random search\n\nThis unit focuses on quasi-random search.\n\nWhy use quasi-random search?\n----------------------------\n\nQuasi-random search (based on low-discrepancy sequences) is our preference\nover fancier blackbox optimization tools when used as part of an iterative\ntuning process intended to maximize insight into the tuning problem (what\nwe refer to as the \"exploration phase\"). Bayesian optimization and similar\ntools are more appropriate for the exploitation phase.\nQuasi-random search based on randomly shifted low-discrepancy sequences can\nbe thought of as \"jittered, shuffled grid search\", since it uniformly, but\nrandomly, explores a given search space and spreads out the search points\nmore than random search.\n\nThe advantages of quasi-random search over more sophisticated blackbox\noptimization tools (e.g. Bayesian optimization, evolutionary algorithms)\ninclude:\n\n- Sampling the search space non-adaptively makes it possible to change the tuning objective in post hoc analysis without rerunning experiments. For example, we usually want to find the best trial in terms of validation error achieved at any point in training. However, the non-adaptive nature of quasi-random search makes it possible to find the best trial based on final validation error, training error, or some alternative evaluation metric without rerunning any experiments.\n- Quasi-random search behaves in a consistent and statistically reproducible way. It should be possible to reproduce a study from six months ago even if the implementation of the search algorithm changes, as long as it maintains the same uniformity properties. If using sophisticated Bayesian optimization software, the implementation might change in an important way between versions, making it much harder to reproduce an old search. It isn't always possible to roll back to an old implementation (e.g. if the optimization tool is run as a service).\n- Its uniform exploration of the search space makes it easier to reason about the results and what they might suggest about the search space. For example, if the best point in the traversal of quasi-random search is at the boundary of the search space, this is a good (but not foolproof) signal that the search space bounds should be changed. However, an adaptive blackbox optimization algorithm might have neglected the middle of the search space because of some unlucky early trials even if it happens to contain equally good points, since it is this exact sort of non-uniformity that a good optimization algorithm needs to employ to speed up the search.\n- Running different numbers of trials in parallel versus sequentially does not produce statistically different results when using quasi-random search (or other non-adaptive search algorithms), unlike with adaptive algorithms.\n- More sophisticated search algorithms may not always handle infeasible points correctly, especially if they aren't designed with neural network hyperparameter tuning in mind.\n- Quasi-random search is simple and works especially well when many tuning trials are running in parallel. Anecdotally^[1](#fn1)^, it is very hard for an adaptive algorithm to beat a quasi-random search that has 2X its budget, especially when many trials need to be run in parallel (and thus there are very few chances to make use of previous trial results when launching new trials). Without expertise in Bayesian optimization and other advanced blackbox optimization methods, you might not achieve the benefits they are, in principle, capable of providing. It is hard to benchmark advanced blackbox optimization algorithms in realistic deep learning tuning conditions. They are a very active area of current research, and the more sophisticated algorithms come with their own pitfalls for inexperienced users. Experts in these methods are able to get good results, but in high-parallelism conditions the search space and budget tend to matter a lot more.\n\nThat said, if your computational resources only allow a small number of\ntrials to run in parallel and you can afford to run many trials in sequence,\nBayesian optimization becomes much more attractive despite making your\ntuning results harder to interpret.\n\nWhere can I find an implementation of quasi-random search?\n----------------------------------------------------------\n\n[Open-Source Vizier](https://github.com/google/vizier) has\n[an implementation of quasi-random\nsearch](https://github.com/google/vizier/blob/main/vizier/_src/algorithms/designers/quasi_random.py).\nSet `algorithm=\"QUASI_RANDOM_SEARCH\"` in [this Vizier usage\nexample](https://oss-vizier.readthedocs.io/en/latest/guides/user/running_vizier.html).\nAn alternative implementation exists [in this hyperparameter sweeps\nexample](https://github.com/mlcommons/algorithmic-efficiency/blob/main/algorithmic_efficiency/halton.py).\nBoth of these implementations generate a Halton sequence for a given search\nspace (intended to implement a shifted, scrambled Halton sequence as\nrecommended in\n[Critical Hyper-Parameters: No Random, No\nCry](https://arxiv.org/abs/1706.03200).\n\nIf a quasi-random search algorithm based on a low-discrepancy sequence is not\navailable, it is possible to substitute pseudo random uniform search instead,\nalthough this is likely to be slightly less efficient. In 1-2 dimensions,\ngrid search is also acceptable, although not in higher dimensions. (See\n[Bergstra \\& Bengio, 2012](https://www.jmlr.org/papers/v13/bergstra12a.html)).\n\nHow many trials are needed to get good results with quasi-random search?\n------------------------------------------------------------------------\n\nThere is no way to determine how many trials are needed to get\nresults with quasi-random search in general, but you can look at\nspecific examples. As Figure 3 shows, the number of trials in a study can\nhave a substantial impact on the results:\n\n**Figure 3:** ResNet-50 tuned on ImageNet with 100 trials.\nUsing bootstrapping, different amounts of tuning budget were simulated.\nBox plots of the best performances for each trial budget are plotted.\n\n\u003cbr /\u003e\n\nNotice the following about Figure 3:\n\n- The interquartile ranges when 6 trials were sampled are much larger than when 20 trials were sampled.\n- Even with 20 trials, the difference between especially lucky and unlucky studies are likely larger than the typical variation between retrains of this model on different random seeds, with fixed hyperparameters, which for this workload might be around +/- 0.1% on a validation error rate of \\~23%.\n\n*** ** * ** ***\n\n1. Ben Recht and Kevin Jamieson\n [pointed out](http://www.argmin.net/2016/06/20/hypertuning/) how strong\n 2X-budget random search is as a baseline (the\n [Hyperband paper](https://jmlr.org/papers/volume18/16-558/16-558.pdf)\n makes similar arguments), but it is certainly possible to find search\n spaces and problems where state-of-the-art Bayesian optimization\n techniques crush random search that has 2X the budget. However, in our\n experience beating 2X-budget random search gets much harder in the\n high-parallelism regime since Bayesian optimization has no opportunity to\n observe the results of previous trials. [↩](#fnref1)"]]

