本單元著重於準隨機搜尋。
為何要使用準隨機搜尋?
我們偏好使用近似隨機搜尋 (以低差異序列為基礎),而非更精緻的黑盒最佳化工具,做為迭代式調整程序的一部分,以便盡可能深入瞭解調整問題 (我們稱之為「探索階段」)。貝葉斯最佳化和類似工具更適合用於開發階段。以隨機偏移的低差異序列為基礎的準隨機搜尋,可視為「抖動式、隨機排列的格線搜尋」,因為它會以隨機方式探索特定搜尋空間,並將搜尋點分散開來,比隨機搜尋更為廣泛。
相較於更複雜的黑箱最佳化工具 (例如貝式最佳化、演化演算法),準隨機搜尋的優點包括:
- 非自適應方式取樣搜尋空間,可在事後分析中變更調整目標,而無須重新執行實驗。舉例來說,我們通常會想找出在訓練過程中任何時間點,驗證錯誤率達到最佳值的最佳試驗。不過,由於準隨機搜尋的非自適應特性,您可以根據最終驗證錯誤、訓練錯誤或其他評估指標,找出最佳試驗,而無需重新執行任何實驗。
- 準隨機搜尋的行為是一致且可重現的統計資料。即使搜尋演算法的實作方式有所變更,只要維持相同的一致性屬性,您應該還是可以重現六個月前的實驗。如果使用複雜的貝葉斯最佳化軟體,實作方式可能會在不同版本之間發生重大變更,因此要重現舊搜尋結果就更加困難。您不一定能回溯至舊版實作 (例如,如果最佳化工具是以服務形式執行)。
- 它對搜尋空間的探索方式一致,因此更容易推論結果,以及這些結果對搜尋空間的建議。舉例來說,如果在 quasi-random 搜尋的遍歷中,最佳點位於搜尋空間的邊界,這就是一個良好 (但不保證正確) 的信號,表示應變更搜尋空間邊界。不過,由於早期測試不幸,即使其中含有同樣優異的點,自適應黑盒最佳化演算法可能會忽略搜尋空間的中間部分,因為優良的最佳化演算法需要採用這種不一致性,才能加快搜尋速度。
- 使用準隨機搜尋 (或其他非自適應搜尋演算法) 時,如果以平行方式執行不同數量的試驗,與依序執行相比,不會產生統計上不同的結果,這與自適應演算法不同。
- 較複雜的搜尋演算法不一定能正確處理不可行點,尤其是在沒有以神經網路超參數調整為設計考量時。
- 準隨機搜尋相當簡單,在同時執行許多調整測試時,特別適合使用。據說1,自適應演算法很難勝過預算是其 2 倍的近似隨機搜尋,尤其是需要同時執行許多試驗時 (因此在推出新試驗時,很少機會能利用先前的試驗結果)。如果您不具備貝葉斯最佳化和其他進階黑箱最佳化方法的專業知識,可能無法獲得這些方法原則上可提供的優點。在實際的深度學習調整條件下,很難對進階黑箱最佳化演算法進行基準測試。目前研究人員積極投入這項領域,但更精密的演算法對經驗不足的使用者而言,可能會帶來一些陷阱。這些方法的專家可以取得良好的結果,但在高並行度情況下,搜尋空間和預算往往更為重要。
不過,如果您的運算資源只允許少量試驗同時執行,且您可以依序執行許多試驗,那麼貝葉斯最佳化就會變得更有吸引力,即使這會讓調校結果更難解讀。
哪裡可以找到準隨機搜尋的實作方式?
開放原始碼 Vizier 提供準隨機搜尋的實作方式。請在這個 Vizier 用法範例中設定 algorithm="QUASI_RANDOM_SEARCH"。這個超參數掃描範例提供了另一種實作方式。這兩種實作方式都會為特定搜尋空間產生 Halton 序列 (目的是實作經過偏移且經過雜湊處理的 Halton 序列,如重要超參數:不隨機,不哭泣所述)。
如果無法使用以低差異序列為基礎的準隨機搜尋演算法,則可以改用偽隨機均勻搜尋,但效率可能會稍微降低。在 1 到 2 個維度中,也可以使用格線搜尋,但在較高維度中則不行。(請參閱 Bergstra 和 Bengio,2012)。
要進行多少次試驗,才能透過準隨機搜尋取得良好結果?
一般來說,您無法判斷需要多少次測試才能透過近似隨機搜尋取得結果,但您可以查看具體範例。如圖 3 所示,研究中的試驗次數可能會對結果產生重大影響:
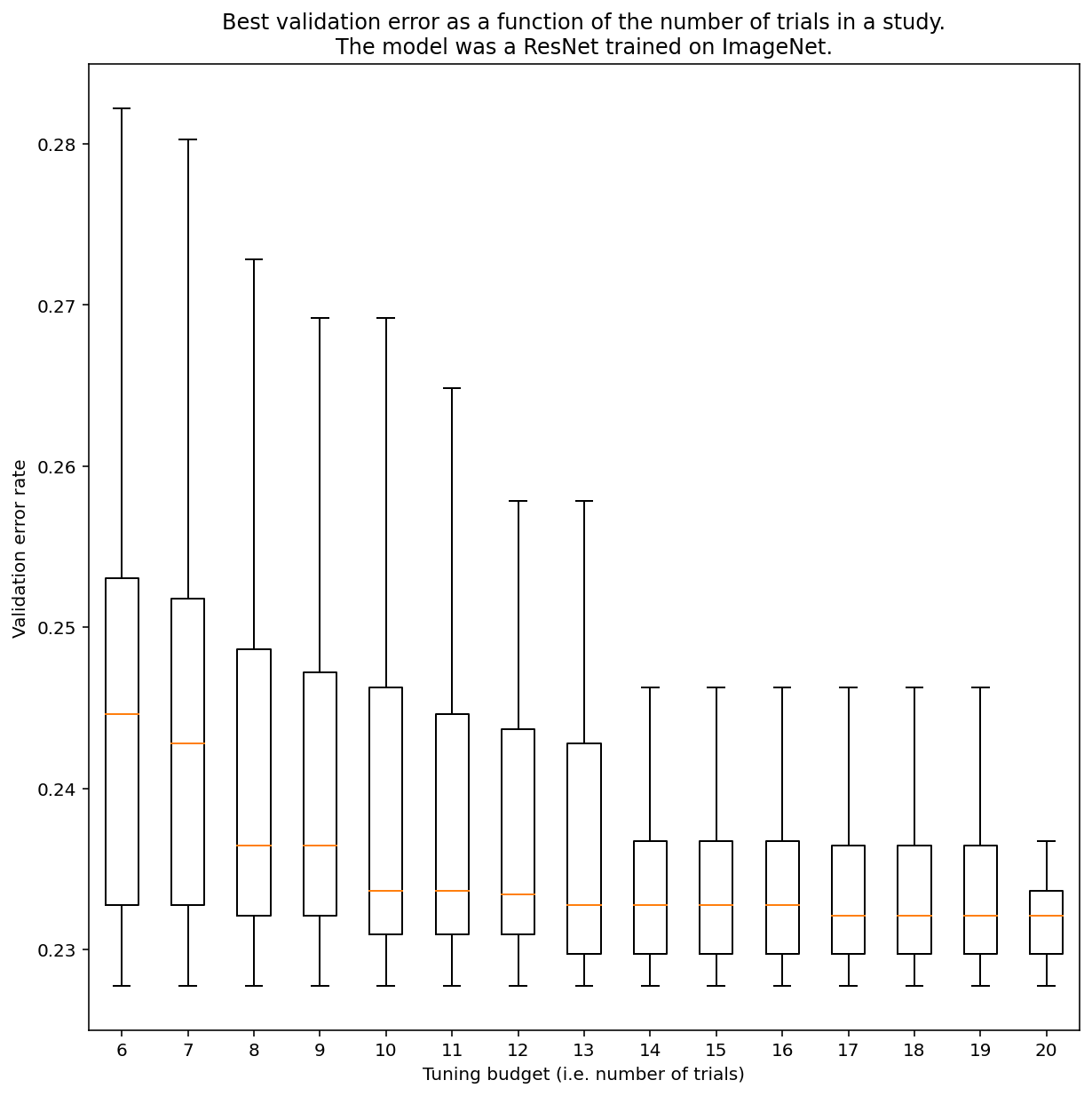
圖 3:ResNet-50 在 ImageNet 上經過 100 次嘗試後進行調整。使用 Bootstrapping 模擬不同調整預算金額。繪製每個試驗預算最佳成效的箱形圖。
請注意下列圖 3 的事項:
- 以 6 次試驗為樣本的四分位數範圍,比以 20 次試驗為樣本的範圍大得多。
- 即使進行 20 次試驗,特別幸運和不幸的試驗之間的差異,可能會比這個模型在不同隨機種子上以固定超參數重訓練時的差異還要大,在這個工作負載中,驗證錯誤率約為 23%,差異約為 +/- 0.1%。
-
Ben Recht 和 Kevin Jamieson 指出,以 2 倍預算的隨機搜尋做為基準,其強大程度 (Hyperband 論文提出類似論點),但確實有可能找到搜尋空間和問題,讓最先進的貝葉斯最佳化技術壓倒預算 2 倍的隨機搜尋。不過,在我們的實驗中,高並行度系統中要超越 2 倍預算的隨機搜尋結果,難度會大幅提高,因為貝葉斯最佳化演算法無法觀察先前試驗的結果。 ↩
