Esta unidad se enfoca en la búsqueda cuasialeatoria.
¿Por qué usar la búsqueda cuasialeatoria?
La búsqueda cuasialeatoria (basada en secuencias de baja discrepancia) es nuestra preferencia sobre las herramientas de optimización de caja negra más sofisticadas cuando se usan como parte de un proceso de ajuste iterativo destinado a maximizar la información sobre el problema de ajuste (lo que llamamos "fase de exploración"). La optimización bayesiana y herramientas similares son más apropiadas para la fase de explotación. La búsqueda cuasialeatoria basada en secuencias de baja discrepancia desplazadas de forma aleatoria se puede considerar como una "búsqueda de cuadrícula desordenada y con jitter", ya que explora de forma uniforme, pero aleatoria, un espacio de búsqueda determinado y distribuye los puntos de búsqueda más que la búsqueda aleatoria.
Las ventajas de la búsqueda cuasialeatoria sobre las herramientas de optimización de caja negra más sofisticadas (p.ej., optimización bayesiana, algoritmos evolutivos) incluyen las siguientes:
- El muestreo del espacio de búsqueda de forma no adaptativa permite cambiar el objetivo de ajuste en el análisis post hoc sin volver a ejecutar los experimentos. Por ejemplo, por lo general, queremos encontrar la mejor prueba en términos del error de validación logrado en cualquier punto del entrenamiento. Sin embargo, la naturaleza no adaptativa de la búsqueda cuasialeatoria permite encontrar la mejor prueba en función del error de validación final, el error de entrenamiento o alguna métrica de evaluación alternativa sin volver a ejecutar ningún experimento.
- La búsqueda cuasialeatoria se comporta de manera coherente y reproducible de manera estadística. Debería ser posible reproducir un estudio de hace seis meses, incluso si cambia la implementación del algoritmo de búsqueda, siempre que mantenga las mismas propiedades de uniformidad. Si usas software de optimización bayesiana sofisticado, la implementación podría cambiar de manera importante entre versiones, lo que dificultaría mucho la reproducción de una búsqueda anterior. No siempre es posible revertir a una implementación anterior (p.ej., si la herramienta de optimización se ejecuta como un servicio).
- Su exploración uniforme del espacio de búsqueda facilita el razonamiento sobre los resultados y lo que podrían sugerir sobre el espacio de búsqueda. Por ejemplo, si el mejor punto en la búsqueda cuasi-aleatoria está en el límite del espacio de búsqueda, es una buena señal (pero no infalible) de que se deben cambiar los límites del espacio de búsqueda. Sin embargo, un algoritmo de optimización de caja negra adaptativo podría haber descuidado el medio del espacio de búsqueda debido a algunas pruebas iniciales desafortunadas, incluso si contiene puntos igualmente buenos, ya que es este tipo exacto de no uniformidad que un buen algoritmo de optimización debe emplear para acelerar la búsqueda.
- Ejecutar diferentes cantidades de pruebas en paralelo en lugar de de forma secuencial no genera resultados estadísticamente diferentes cuando se usa la búsqueda cuasialeatoria (o algún otro algoritmo de búsqueda no adaptativo), a diferencia de lo que sucede con los algoritmos adaptativos.
- Es posible que los algoritmos de búsqueda más sofisticados no siempre manejen correctamente los puntos inviables, en especial si no están diseñados teniendo en cuenta el ajuste de hiperparámetros de la red neuronal.
- La búsqueda cuasialeatoria es simple y funciona especialmente bien cuando se ejecutan muchos ensayos de ajuste en paralelo. De manera anecdótica1, es muy difícil para un algoritmo adaptativo superar una búsqueda cuasi-aleatoria que tiene el doble de su presupuesto, en especial cuando se deben ejecutar muchos ensayos en paralelo (por lo que hay muy pocas posibilidades de usar los resultados de ensayos anteriores cuando se inician nuevos ensayos). Sin experiencia en la optimización bayesiana y otros métodos avanzados de optimización de caja negra, es posible que no logres los beneficios que, en principio, pueden proporcionar. Es difícil comparar algoritmos avanzados de optimización de caja negra en condiciones de ajuste de aprendizaje profundo realistas. Son un área muy activa de la investigación actual, y los algoritmos más sofisticados tienen sus propias dificultades para los usuarios sin experiencia. Los expertos en estos métodos pueden obtener buenos resultados, pero, en condiciones de alto paralelismo, el espacio de búsqueda y el presupuesto suelen ser mucho más importantes.
Dicho esto, si tus recursos de procesamiento solo permiten que se ejecute una pequeña cantidad de ensayos en paralelo y puedes permitirte ejecutar muchos ensayos en secuencia, la optimización bayesiana se vuelve mucho más atractiva a pesar de que hace que los resultados de tu ajuste sean más difíciles de interpretar.
¿Dónde puedo encontrar una implementación de la búsqueda cuasialeatoria?
Vizier de código abierto tiene una implementación de búsqueda cuasialeatoria.
Configura algorithm="QUASI_RANDOM_SEARCH" en este ejemplo de uso de Vizier.
Existe una implementación alternativa en este ejemplo de barridos de hiperparámetros.
Ambas implementaciones generan una secuencia de Halton para un espacio de búsqueda determinado (con la intención de implementar una secuencia de Halton desplazada y desordenada, como se recomienda en Hiperparámetros críticos: No aleatorio, No Cry).
Si no está disponible un algoritmo de búsqueda cuasi-aleatorio basado en una secuencia de discrepancia baja, es posible sustituir la búsqueda pseudoaleatoria uniforme, aunque es probable que sea un poco menos eficiente. En 1 o 2 dimensiones, también se acepta la búsqueda de cuadrícula, aunque no en dimensiones superiores. (consulta Bergstra y Bengio, 2012).
¿Cuántas pruebas se necesitan para obtener buenos resultados con la búsqueda cuasialeatoria?
No hay forma de determinar cuántas pruebas se necesitan para obtener resultados con la búsqueda cuasialeatoria en general, pero puedes observar ejemplos específicos. Como se muestra en la Figura 3, la cantidad de pruebas en un estudio puede tener un impacto sustancial en los resultados:
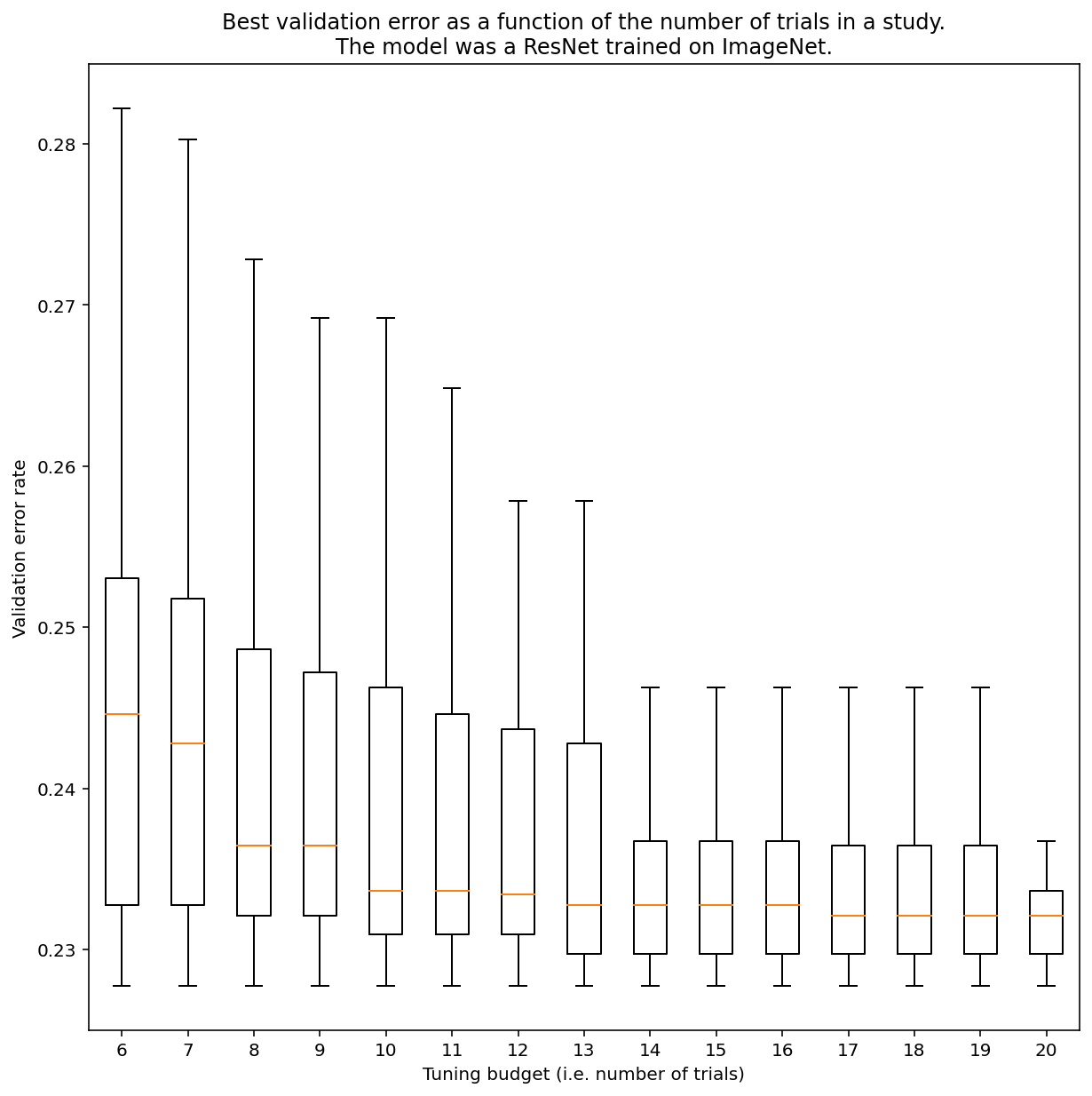
Figura 3: ResNet-50 ajustado en ImageNet con 100 pruebas. Con el arranque automático, se simularon diferentes cantidades de presupuesto de ajuste. Se trazan diagramas de caja de los mejores rendimientos para cada presupuesto de prueba.
Ten en cuenta lo siguiente sobre la Figura 3:
- Los rangos intercuartiles cuando se tomaron muestras de 6 ensayos son mucho más grandes que cuando se tomaron muestras de 20 ensayos.
- Incluso con 20 pruebas, es probable que la diferencia entre los estudios con suerte y sin suerte sea mayor que la variación típica entre los entrenamientos nuevos de este modelo en diferentes valores iniciales aleatorios, con hiperparámetros fijos, que para esta carga de trabajo podría ser de alrededor de +/- 0.1% en una tasa de error de validación de alrededor del 23%.
-
Ben Recht y Kevin Jamieson señalaron lo sólida que es la búsqueda aleatoria con un presupuesto 2 veces mayor como línea de base (el artículo de Hyperband hace argumentos similares), pero es posible encontrar espacios de búsqueda y problemas en los que las técnicas de optimización bayesiana de vanguardia superan a la búsqueda aleatoria que tiene el doble de presupuesto. Sin embargo, en nuestra experiencia, superar la búsqueda aleatoria de 2 veces el presupuesto se vuelve mucho más difícil en el régimen de alto paralelismo, ya que la optimización bayesiana no tiene la oportunidad de observar los resultados de las pruebas anteriores. ↩
