تركّز هذه الوحدة على البحث شبه العشوائي.
ما هي أهمية استخدام البحث شبه العشوائي؟
يُفضّل استخدام البحث شبه العشوائي (استنادًا إلى تسلسلات ذات اختلاف منخفض) بدلاً من أدوات التحسين الأكثر تعقيدًا في العلبة السوداء عند استخدامه كجزء من عملية تحسين متكرّرة تهدف إلى زيادة الإحصاءات إلى أقصى حدّ في ما يتعلّق بمشكلة التحسين (ما يُشار إليه باسم "مرحلة الاستكشاف"). إنّ التحسين باستخدام نظرية بايزي والأدوات المشابهة هي أكثر ملاءمةً لمرحلة الاستغلال. يمكن اعتبار البحث شبه العشوائي المستنِد إلى تسلسلات ذات اختلاف منخفض تم نقلها عشوائيًا "بحثًا متقطّعًا للشبكة بترتيب عشوائي"، لأنّه يستكشف بشكل موحّد، ولكنه عشوائي، مساحة بحث معيّنة وينشر نقاط البحث أكثر من البحث العشوائي.
تشمل مزايا البحث شبه العشوائي مقارنةً بأدوات تحسين الأداء الأكثر تعقيدًا في علب سوداء (مثل التحسين باستخدام نظرية بايزي والخوارزميات التطورية) ما يلي:
- إنّ أخذ عيّنات من مساحة البحث بشكل غير تكيُّفي يجعل من الممكن تغيير هدف الضبط في التحليل البعدي بدون إعادة إجراء التجارب. على سبيل المثال، نريد عادةً العثور على أفضل تجربة من حيث خطأ التحقّق الذي تم تحقيقه في أيّ مرحلة من مراحل التدريب. ومع ذلك، فإنّ طبيعة البحث شبه العشوائي غير التكيُّفية تجعل من الممكن العثور على أفضل تجربة استنادًا إلى خطأ التحقّق النهائي أو خطأ التدريب أو أي مقياس تقييمبديل بدون إعادة تشغيل أي تجارب.
- يتصرّف البحث شبه العشوائي بطريقة متّسقة وقابلة للتكرار إحصائيًا. من المفترض أن يكون من الممكن إعادة إنتاج دراسة من ستة أشهر حتى إذا تغيّر تنفيذ خوارزمية البحث، ما دام يحافظ على خصائص التوحيد نفسها. في حال استخدام برامج تحسين متقدمة مستندة إلى نظرية بايزي، قد يتغيّر التنفيذ بطريقة مهمة بين الإصدارات، ما يجعل من الصعب جدًا إعادة إجراء عملية بحث قديمة. لا يمكن دائمًا الرجوع إلى عملية تنفيذ قديمة (على سبيل المثال، إذا كانت أداة التحسين تعمل كخدمة).
- إنّ استكشافه الموحّد لمساحة البحث يسهّل عملية التفكير في النتائج وما قد تشير إليه عن مساحة البحث. على سبيل المثال، إذا كانت أفضل نقطة في مسار البحث شبه العشوائي تقع على حدود مساحة البحث، فهذا إشارة جيدة (ولكن ليست أكيدة) تشير إلى أنّه يجب تغيير حدود مساحة البحث. ومع ذلك، قد تكون خوارزمية التحسين التكيُّفية للصندوق الأسود قد تجاهلت وسط مساحة البحث بسبب بعض التجارب المبكرة غير المحظوظة، حتى لو كانت تحتوي على نقاط جيدة بالقدر نفسه، لأنّه هو هذا النوع تحديدًا من عدم التناسق الذي تحتاج خوارزمية التحسين الجيدة إلى استخدامه لتسريع عملية البحث.
- إنّ إجراء أعداد مختلفة من التجارب بشكل موازٍ بدلاً من إجراءها بشكل تسلسلي لا يؤدي إلى نتائج مختلفة إحصائيًا عند استخدام البحث شبه العشوائي (أو خوارزميات البحث غير التكيُّفية الأخرى)، على عكس الخوارزميات التكيُّفية.
- قد لا تتعامل خوارزميات البحث الأكثر تعقيدًا دائمًا مع نقاط التحسين غير القابلة للتنفيذ بشكل صحيح، خاصةً إذا لم يتم تصميمها مع وضع تعديل المَعلمات الفائقة لشبكة عصبية في الاعتبار.
- إنّ البحث شبه العشوائي بسيط ويعمل بشكلٍ جيد بشكلٍ خاص عند تنفيذ العديد من تجارب الضبط بالتوازي. وفقًا لإحدى القصص1، من الصعب جدًا أن تتفوّق الخوارزمية التكيُّفية على أسلوب البحث شبه العشوائي الذي يمتلك ميزانية تبلغ ضعف ميزانيتها، خاصةً عندما يكون من الضروري تنفيذ العديد من التجارب بالتوازي (وبالتالي، تكون هناك فرص قليلة جدًا لاستخدام نتائج التجارب السابقة عند إطلاق تجارب جديدة). بدون خبرة في التحسين باستخدام نظرية بايزي وطرق التحسين المتقدّمة الأخرى للصندوق الأسود، قد لا تحقّق المزايا التي يمكن أن تقدّمها، بوجهٍ عام. من الصعب تقييم أداء خوارزميات التحسين المتقدّمة التي تعمل في علب سوداء في شروط ضبط تعلُّم الآلة الواقعية. وهي مجال نشط جدًا من الأبحاث الحالية، وتشكل الالتقاطات المعقدة بعض المخاطر التي تواجه المستخدمين غير المتمرّسين. يمكن للخبراء في هذه الطرق الحصول على نتائج جيدة، ولكن في حالات التوازي العالي، تميل مساحة البحث والميزانية إلى أن تكون أكثر أهمية.
ومع ذلك، إذا كانت موارد الحوسبة تتيح فقط إجراء عدد صغير من التجارب بالتوازي وكان بإمكانك إجراء العديد من التجارب بالتسلسل، يصبح التحسين الباييزي أكثر جاذبية على الرغم من أنّه يجعل من الصعب تفسير نتائج الضبط.
أين يمكنني العثور على تطبيق للبحث شبه العشوائي؟
يحتوي برنامج Vizier المفتوح المصدر على
تنفيذ للبحث شبه العشوائي.
اضبط algorithm="QUASI_RANDOM_SEARCH" في مثال استخدام Vizier هذا.
يتوفّر تنفيذ بديل في مثال عمليات مسح المَعلمات الفائقة هذا.
تُنشئ كلتا طريقتَي التنفيذ تسلسل Halton لمساحة بحث معيّنة (يُقصد بها تنفيذ تسلسل Halton مُعدَّل ومُشَفَّر كما هو مُقترَح في المَعلمات الفائقة المهمة: لا عشوائي، لا
Cry).
إذا لم تكن خوارزمية البحث شبه العشوائي المستندة إلى تسلسل منخفض التباين متوفرة، يمكن استبدال البحث الموحّد شبه العشوائي بدلاً من ذلك، على الرغم من أنّ هذا من المرجّح أن يكون أقل فعالية قليلاً. في حالة استخدام سمة واحدة أو سمتَين، يُعدّ البحث في الشبكة مقبولًا أيضًا، ولكن ليس في السمات الأعلى. (راجِع Bergstra & Bengio, 2012).
كم عدد التجارب المطلوبة للحصول على نتائج جيدة باستخدام البحث شبه العشوائي؟
لا تتوفّر طريقة لتحديد عدد التجارب اللازمة للحصول على نتائج باستخدام البحث شبه العشوائي بشكل عام، ولكن يمكنك الاطّلاع على أمثلة محدّدة. كما يوضّح الشكل 3، يمكن أن يؤدي عدد التجارب في الدراسة إلى التأثير بشكل كبير في النتائج:
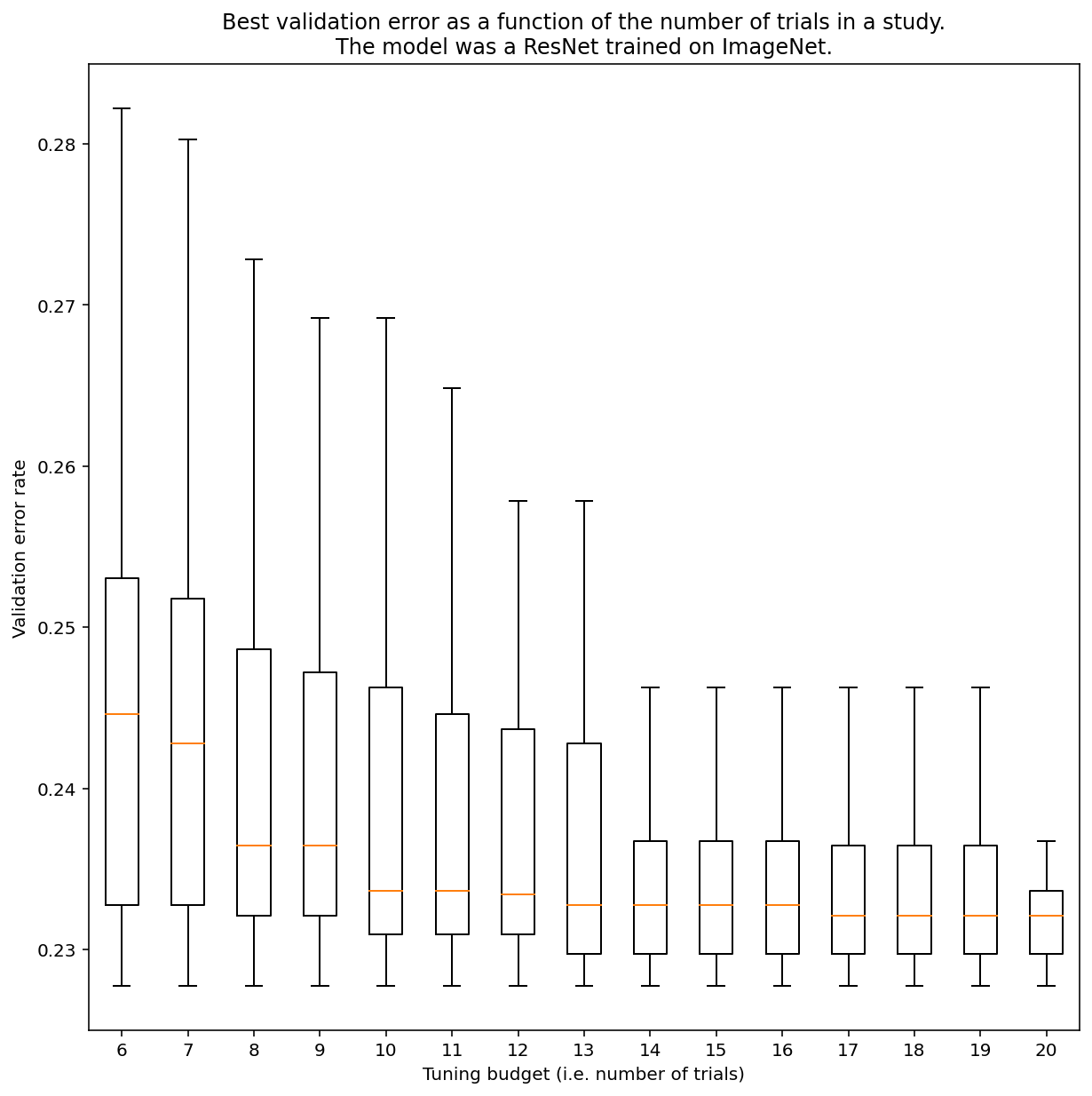
الشكل 3: ResNet-50 تم ضبطه على ImageNet من خلال 100 تجربة. باستخدام ميزة "بدء التشغيل السريع"، تمّت محاكاة مبالغ مختلفة من ميزانية الضبط. يتمّ رسم الرسوم البيانية المربّعة لأفضل الأداء لكلّ ميزانية تجريبية.
يُرجى ملاحظة ما يلي بشأن الشكل 3:
- تكون نطاقات الشريحة الربعية أكبر بكثير عند تحليل عيّنات من 6 تجارب مقارنةً بتحليل عيّنات من 20 تجربة.
- حتى مع إجراء 20 تجربة، من المرجّح أن يكون الفرق بين دراسات الحظ السعيد والحظ السيئ أكبر من التباين المعتاد بين عمليات إعادة التدريب لهذا النموذج على بذور عشوائية مختلفة، باستخدام مَعلمات متغيرة ثابتة، التي قد تبلغ هذه المعالجة حوالي 0.1% +/- عند معدل خطأ التحقق من الصحة الذي يبلغ حوالي 23%.
-
أشار كلّ من "بن ريتش" و"كيفن جاميسون" إلى مدى فعالية البحث العشوائي الذي يستخدم ميزانية مضاعفة كخط أساس (يقدّم مقال Hyperband حججًا مشابهة)، ولكن من الممكن بالتأكيد العثور على مساحات بحث ومشاكل تتفوق فيها تقنيات التحسين الباييزي الحديث على البحث العشوائي الذي يستخدم ميزانية مضاعفة. ومع ذلك، في تجربتنا، يصبح من الصعب جدًا التفوق على البحث العشوائي بميزانية مضاعفة في وضع التوازُن العالي، لأنّ تحسين "البيزيانية" لا يملك فرصة لمراقبة نتائج التجارب السابقة. ↩
