היחידה הזו מתמקדת בחיפוש כמעט אקראי.
למה כדאי להשתמש בחיפוש כמעט אקראי?
אנחנו מעדיפים חיפוש כמעט אקראי (על סמך רצפים עם אי-התאמה נמוכה) על פני כלים מתוחכמים יותר לאופטימיזציה של תיבת שחורה, כשמשתמשים בהם כחלק מתהליך כוונון איטרטיבי שנועד למקסם את התובנות לגבי בעיית הכוונון (מה שאנחנו מכנים 'שלב החקירה'). אופטימיזציה לפי מודלים בייסיאניים וכלים דומים מתאימים יותר לשלב הניצול. חיפוש כמעט אקראי שמבוסס על רצפים עם פערים נמוכים שנדחו באופן אקראי יכול להיחשב כ'חיפוש רשת עם רעשי גליץ', כי הוא בודק באופן אחיד אבל אקראי מרחב חיפוש נתון ומפיץ את נקודות החיפוש יותר מאשר חיפוש אקראי.
היתרונות של חיפוש כמעט אקראי על פני כלים מתוחכמים יותר לאופטימיזציה של תיבת שחורה (למשל, אופטימיזציה בייסינית, אלגוריתמים אבולוציוניים) כוללים:
- דגימה לא אדפטיבית של מרחב החיפוש מאפשרת לשנות את יעד ההתאמה בניתוח 'אחרי מעשה' בלי להריץ מחדש את הניסויים. לדוגמה, בדרך כלל אנחנו רוצים למצוא את הניסוי הטוב ביותר מבחינת שגיאת האימות שהתקבלה בכל שלב באימון. עם זאת, המאפיין הלא אדפטיבי של חיפוש כמעט אקראי מאפשר למצוא את הניסוי הטוב ביותר על סמך שגיאת האימות הסופית, שגיאת האימון או מדד הערכה חלופי כלשהו, בלי להריץ מחדש את הניסויים.
- חיפוש כמעט אקראי מתנהג באופן עקבי וניתנת לשחזור באופן סטטיסטי. אמורה להיות אפשרות לשחזר מחקר מלפני שישה חודשים גם אם ההטמעה של אלגוריתם החיפוש משתנה, כל עוד הוא שומר על אותם מאפייני אחידות. אם משתמשים בתוכנת אופטימיזציה מתוחכמת מבוססת-בייסיאן, יכול להיות שההטמעה תשתנה באופן משמעותי בין גרסאות, וכך יהיה קשה יותר לשחזר חיפוש ישן. לא תמיד אפשר לחזור לגרסה קודמת של הטמעה (למשל, אם כלי האופטימיזציה פועל כשירות).
- הבדיקה הרגילה של מרחב החיפוש מאפשרת להסיק מסקנות לגבי התוצאות ולגבי מה שהן עשויות להצביע עליו לגבי מרחב החיפוש. לדוגמה, אם הנקודה הטובה ביותר בסריקה של חיפוש כמעט אקראי נמצאת בגבול של מרחב החיפוש, זה סימן טוב (אבל לא ודאי) שצריך לשנות את גבולות מרחב החיפוש. עם זאת, אלגוריתם אופטימיזציה אדפטיבי של תיבת שחורה עשוי להתעלם מחלק ממרחב החיפוש בגלל ניסויים מוקדמים לא מוצלחים, גם אם הוא מכיל נקודות טובות באותה מידה. הסיבה לכך היא שזהו בדיוק סוג אי-העקביות שצריך להשתמש בו באלגוריתם אופטימיזציה טוב כדי לזרז את החיפוש.
- כשמשתמשים בחיפוש כמעט אקראי (או באלגוריתמים אחרים של חיפוש לא אדפטיבי), אין הבדל סטטיסטי בין הפעלת מספרים שונים של ניסויים במקביל לבין הפעלת מספרים שונים של ניסויים ברצף, בניגוד לאלגוריתמים אדפטיביים.
- אלגוריתמים מתוחכמים יותר של חיפוש לא תמיד מטפלים נכון בנקודות לא ריאליות, במיוחד אם הם לא תוכננו תוך התחשבות בהתאמה של פרמטרים היפר-מרחביים של רשתות נוירונליות.
- חיפוש כמעט אקראי הוא פשוט ופועל במיוחד טוב כשמפעילים בו-זמנית הרבה ניסויים לכוונון. לפי נתונים אנקדוטיים1, קשה מאוד לאלגוריתם אדפטיבי לנצח חיפוש כמעט אקראי עם תקציב כפול, במיוחד כשצריך להריץ הרבה ניסויים במקביל (ולכן יש מעט מאוד הזדמנויות להשתמש בתוצאות של ניסויים קודמים כשמפעילים ניסויים חדשים). ללא מומחיות באופטימיזציה לפי מודלים בייסיאניים ובשיטות מתקדמות אחרות של אופטימיזציה בקופסה שחורה, יכול להיות שלא תשיגו את היתרונות שהן יכולות לספק, באופן עקרוני. קשה להשוות בין אלגוריתמים מתקדמים של אופטימיזציה בקופסה שחורה בתנאים ריאליסטיים של כוונון למידה עמוקה. זהו תחום פעיל מאוד של מחקר, ולכל אלגוריתם מתוחכם יש מלכודות משלו למשתמשים חסרי ניסיון. מומחים בשיטות האלה יכולים להשיג תוצאות טובות, אבל בתנאים של מקביליות גבוהה, מרחב החיפוש והתקציב נוטים להיות חשובים הרבה יותר.
עם זאת, אם משאבי המחשוב שלכם מאפשרים להריץ רק מספר קטן של ניסויים במקביל, ואתם יכולים להרשות לעצמכם להריץ הרבה ניסויים ברצף, אופטימיזציה בייסינית הופכת לאטרקטיבית הרבה יותר, למרות שקשה יותר לפרש את תוצאות ההתאמה.
איפה אפשר למצוא הטמעה של חיפוש כמעט אקראי?
ב-Vizir בקוד פתוח יש הטמעה של חיפוש כמעט אקראי.
מגדירים את algorithm="QUASI_RANDOM_SEARCH" בדוגמה הזו לשימוש ב-Vizier.
אפשר למצוא הטמעה חלופית בדוגמה הזו של סריקות של פרמטרים היפר-מרחביים.
שתי הטמעות האלה יוצרות רצף Halton למרחב חיפוש נתון (המטרה היא להטמיע רצף Halton שעבר דחיפה וערבוב, כפי שמומלץ במאמר פרמטרים היפר-קריטיים: ללא אקראיות, ללא קריאה).
אם לא זמין אלגוריתם חיפוש כמעט אקראי שמבוסס על רצף עם אי-התאמה נמוכה, אפשר להחליף אותו בחיפוש אחיד פסאודו-אקראי, אבל סביר להניח שהיעילות שלו תהיה מעט נמוכה יותר. כשמשתמשים ב-1-2 מאפיינים, אפשר גם לבצע חיפוש ברשימה, אבל לא במאפיינים רבים יותר. (ראו Bergstra & Bengio, 2012).
כמה ניסיונות נדרשים כדי לקבל תוצאות טובות בחיפוש כמעט אקראי?
אין דרך לקבוע כמה ניסיונות נדרשים כדי לקבל תוצאות בחיפוש כמעט אקראי באופן כללי, אבל אפשר להיעזר בדוגמאות ספציפיות. כפי שמוצג באיור 3, למספר הניסויים במחקר יכולה להיות השפעה משמעותית על התוצאות:
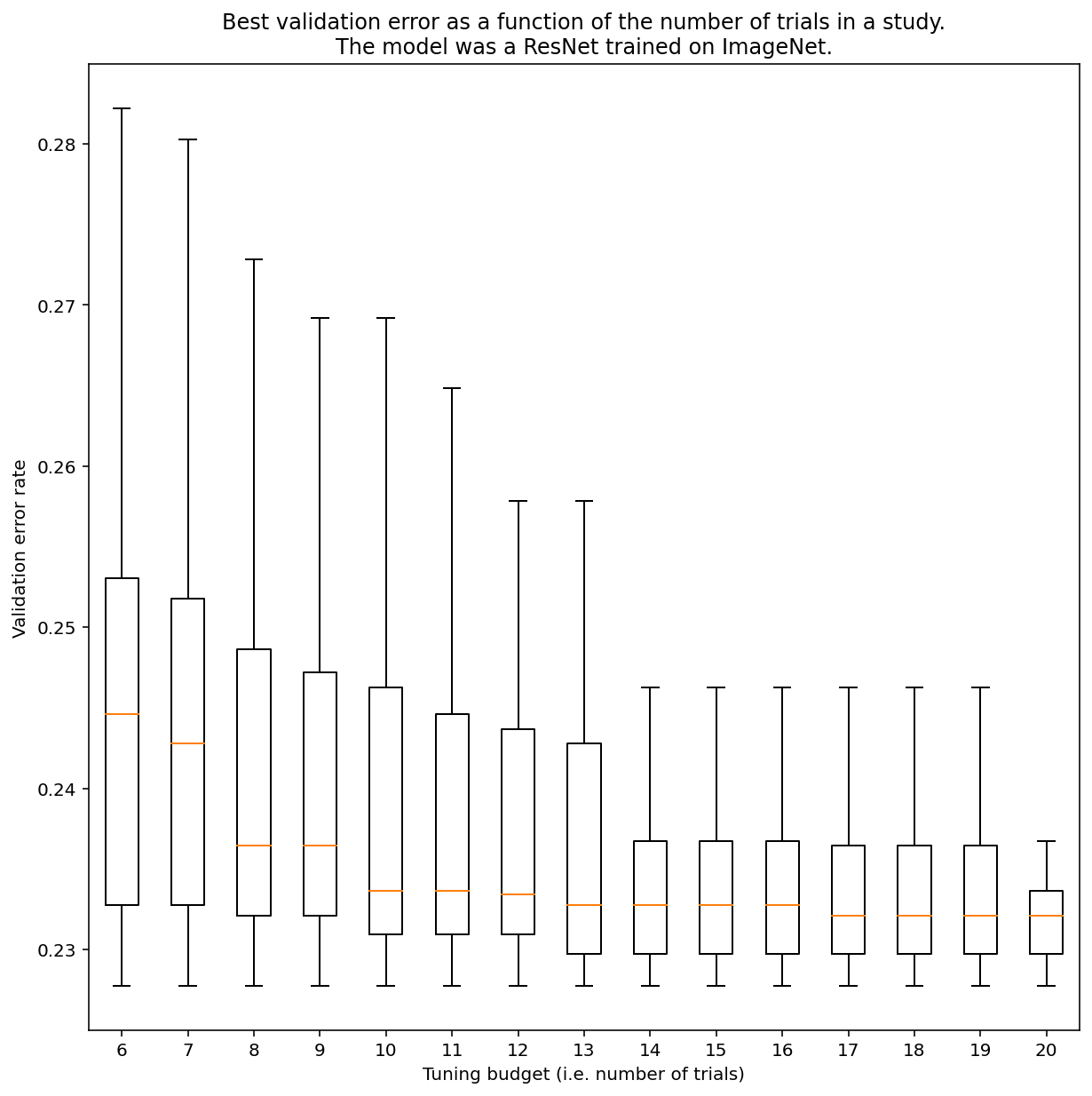
איור 3: ResNet-50 שהותאמה ב-ImageNet עם 100 ניסיונות. באמצעות טעינה ראשונית (bootstrapping), בוצעה סימולציה של סכומים שונים של תקציב לכוונון. מוצגים תרשימים של תיבות עם הביצועים הטובים ביותר לכל תקציב ניסיוני.
שימו לב לפרטים הבאים לגבי איור 3:
- טווחי הרבעונים כשנלקחו 6 ניסויים לדגימה גדולים בהרבה מאשר כשנלקחו 20 ניסויים לדגימה.
- גם עם 20 ניסיונות, סביר להניח שההבדל בין ניסויים עם מזל טוב במיוחד לבין ניסויים עם מזל רע במיוחד גדול מהשונות הרגילה בין אימון מחדש של המודל הזה עם זרעים אקראיים שונים, עם פרמטרים היפר-מוגדרים קבועים. עבור עומס העבודה הזה, השונות יכולה להיות בערך +/- 0.1% בשיעור שגיאות האימות של כ-23%.
-
בן רייט (Ben Recht) וקווין ג'יימיסון (Kevin Jamieson) ציינו עד כמה חיפוש אקראי עם תקציב כפול חזק כבסיס (במאמר על Hyperband מופיעים טיעונים דומים), אבל אפשר בהחלט למצוא מרחבי חיפוש ובעיות שבהם שיטות אופטימיזציה בייסיניות מתקדמות משיקות חיפוש אקראי עם תקציב כפול. עם זאת, לדעתנו קשה יותר להשיג תוצאות טובות יותר מחיפוש אקראי עם תקציב כפול במצב של מקביליות גבוהה, כי לאופטימיזציה הבאיאנית אין הזדמנות לצפות בתוצאות של ניסויים קודמים. ↩
