준무작위 검색

이 단원에서는 준무작위 검색에 중점을 둡니다.

준무작위 검색을 사용하는 이유

튜닝 문제에 대한 통계를 극대화하기 위한 반복적인 튜닝 프로세스('탐색 단계'라고 함)의 일부로 사용할 때는 더 정교한 블랙박스 최적화 도구보다 근사 무작위 탐색 (불일치가 적은 시퀀스를 기반으로 함)을 사용하는 것이 좋습니다. 베이즈 최적화 및 유사한 도구는 악용 단계에 더 적합합니다. 무작위로 전환된 불일치가 적은 시퀀스를 기반으로 하는 준무작위 검색은 '시점 분산 그리드 검색'으로 간주할 수 있습니다. 이는 주어진 검색 공간을 균일하지만 무작위로 탐색하고 무작위 검색보다 검색 지점을 더 넓게 펼치기 때문입니다.

더 정교한 블랙박스 최적화 도구 (예: 베이즈 최적화, 진화 알고리즘)에 비해 준무작위 검색의 이점은 다음과 같습니다.

• 검색 공간을 비적응적으로 샘플링하면 실험을 다시 실행하지 않고도 사후 분석에서 조정 목표를 변경할 수 있습니다. 예를 들어 일반적으로 학습 중 어느 시점에서든 달성된 검증 오류 측면에서 가장 좋은 실험을 찾고자 합니다. 그러나 준무작위 탐색의 비적응적 특성 덕분에 실험을 다시 실행하지 않고도 최종 검증 오류, 학습 오류 또는 대체 평가 측정항목을 기반으로 최적의 실험을 찾을 수 있습니다.
• 준무작위 검색은 일관되고 통계적으로 재현 가능한 방식으로 작동합니다. 동일한 균일성 속성을 유지하는 한 검색 알고리즘 구현이 변경되더라도 6개월 전의 연구를 재현할 수 있어야 합니다. 정교한 Bayesian 최적화 소프트웨어를 사용하는 경우 버전 간에 구현이 중요한 방식으로 변경될 수 있으므로 이전 검색을 재현하기가 훨씬 더 어려워집니다. 이전 구현으로 롤백할 수 없는 경우도 있습니다 (예: 최적화 도구가 서비스로 실행되는 경우).
• 검색 공간을 균일하게 탐색하면 결과와 검색 공간에 관해 제안할 수 있는 사항에 관해 더 쉽게 추론할 수 있습니다. 예를 들어 준무작위 검색을 통과할 때 가장 좋은 지점이 검색 공간의 경계에 있다면 검색 공간 경계를 변경해야 한다는 신호가 됩니다 (완벽하지는 않음). 그러나 적응형 블랙박스 최적화 알고리즘은 동등하게 좋은 점이 포함되어 있더라도 불운한 초기 실험으로 인해 검색 공간의 중앙을 소홀히 했을 수 있습니다. 이는 우수한 최적화 알고리즘이 검색 속도를 높이기 위해 사용해야 하는 바로 이러한 불균등성 때문입니다.
• 적응형 알고리즘과 달리 준무작위 검색 (또는 기타 비적응형 검색 알고리즘)을 사용할 때는 실험 횟수를 병렬로 실행하는 것과 순차적으로 실행하는 것 간에 통계적으로 다른 결과가 나오지 않습니다.
• 더 정교한 검색 알고리즘은 특히 신경망 초매개변수 조정을 염두에 두고 설계되지 않은 경우 실행 불가능한 지점을 올바르게 처리하지 못할 수 있습니다.
• 준무작위 탐색은 간단하며 여러 개의 튜닝 실험이 동시에 실행되는 경우에 특히 효과적입니다. 예를 들어¹, 적응형 알고리즘이 예산이 2배인 준무작위 검색을 능가하기는 매우 어렵습니다. 특히 여러 실험을 동시에 실행해야 하는 경우 (따라서 새 실험을 시작할 때 이전 실험 결과를 활용할 기회가 거의 없음) 더욱 그렇습니다. 베이즈 최적화 및 기타 고급 블랙박스 최적화 방법에 대한 전문 지식이 없으면 원칙적으로 제공할 수 있는 이점을 얻지 못할 수 있습니다. 현실적인 딥 러닝 조정 조건에서 고급 블랙박스 최적화 알고리즘을 벤치마킹하기는 어렵습니다. 현재 연구가 활발하게 진행되고 있는 분야이며, 보다 정교한 알고리즘은 경험이 없는 사용자에게도 함정이 있습니다. 이러한 방법의 전문가는 우수한 결과를 얻을 수 있지만, 높은 병렬 처리 환경에서는 검색 공간과 예산이 훨씬 더 중요합니다.

하지만 계산 리소스로 소수의 실험만 동시에 실행할 수 있고 여러 실험을 순차적으로 실행할 수 있는 경우, 조정 결과를 해석하기가 더 어려워지지만 베이즈 최적화가 훨씬 더 매력적입니다.

준무작위 탐색 구현은 어디에서 찾을 수 있나요?

오픈소스 Vizier에는 준임의적 탐색 구현이 있습니다. 이 Vizier 사용 예에서 algorithm="QUASI_RANDOM_SEARCH"를 설정합니다. 이 초매개변수 스윕 예에 대체 구현이 있습니다. 두 구현 모두 지정된 검색 공간에 대해 Halton 시퀀스를 생성합니다 (Critical Hyper-Parameters: No Random, No Cry에서 권장하는 대로 이동 및 스크램블된 Halton 시퀀스를 구현하기 위한 목적).

불일치가 적은 시퀀스를 기반으로 하는 준무작위 검색 알고리즘을 사용할 수 없는 경우, 약간 효율성이 떨어지지만 가상 무작위 균일 검색을 대신 사용할 수 있습니다. 1~2차원에서는 그리드 검색도 허용되지만 그 이상에서는 허용되지 않습니다. (Bergstra & Bengio, 2012 참고)

준무작위 검색으로 좋은 결과를 얻으려면 몇 번의 시도가 필요한가요?

일반적으로 준무작위 검색으로 결과를 얻는 데 필요한 시도 수를 결정할 방법은 없지만 특정 예시를 살펴볼 수 있습니다. 그림 3에서 볼 수 있듯이 연구의 실험 횟수는 결과에 상당한 영향을 미칠 수 있습니다.

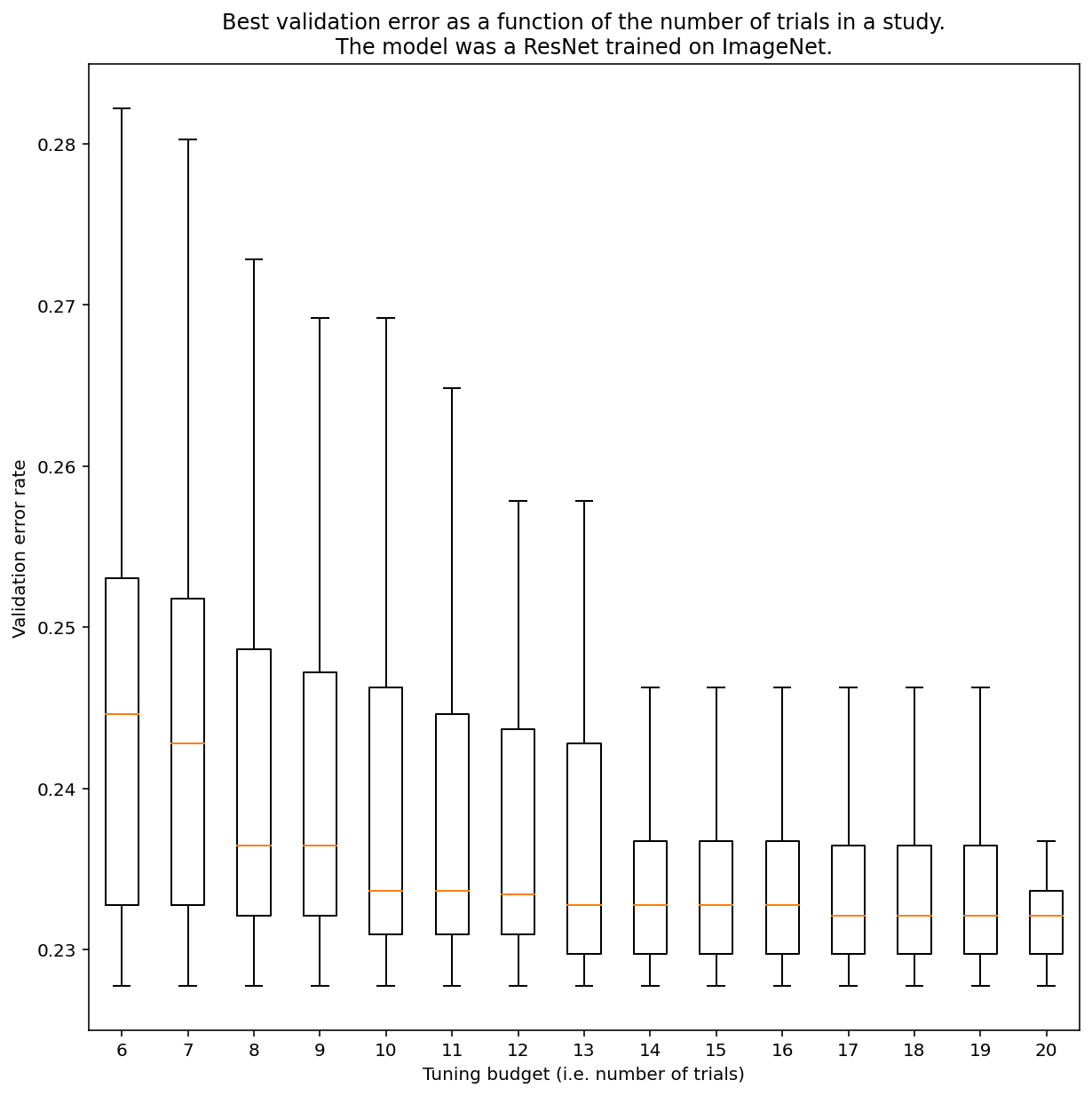
그림 3: 100회의 실험으로 ImageNet에서 조정된 ResNet-50 부트스트래핑을 사용하여 다양한 조정 예산을 시뮬레이션했습니다. 각 시험 예산의 최고 실적에 대한 박스 플롯이 표시됩니다.

 

그림 3에 관해 다음 사항에 유의하세요.

• 실험 6개를 샘플링했을 때의 사분위수 간격은 실험 20개를 샘플링했을 때보다 훨씬 큽니다.
• 실험 횟수가 20회이더라도 특히 운이 좋은 실험과 운이 나쁜 실험 간의 차이는 고정된 초매개변수를 사용하여 다양한 무작위 시드에서 이 모델을 재학습할 때의 일반적인 변동보다 클 수 있습니다. 이 워크로드의 경우 유효성 검사 오류율이 약 23% 일 때 약 +/- 0.1%일 수 있습니다.

---

1. 벤 레히트와 케빈 제이미슨은 예산이 2배인 무작위 검색이 기준으로서 얼마나 강력한지 주장했습니다 (Hyperband 논문에서도 유사한 주장을 함). 하지만 최신 베이즈 최적화 기법이 예산이 2배인 무작위 검색을 압도하는 검색 공간과 문제를 찾을 수 있습니다. 그러나 베이즈 최적화는 이전 실험의 결과를 관찰할 기회가 없으므로 경험에 비추어 볼 때 높은 병렬 처리 환경에서는 예산의 2배를 사용하는 무작위 검색을 능가하는 것이 훨씬 더 어려워집니다. ↩