本单元重点介绍了近似随机搜索。
为何使用近似随机搜索?
在迭代式调优流程中,我们更倾向于使用基于低差异序列的近似随机搜索,而不是更复杂的黑盒优化工具,以便最大限度地深入了解调优问题(我们称之为“探索阶段”)。贝叶斯优化和类似工具更适合在利用阶段使用。基于随机移位的低差异序列的近似随机搜索可以被视为“抖动式打乱的网格搜索”,因为它会均匀地(但随机地)探索给定的搜索空间,并且与随机搜索相比,搜索点分布更广。
与更复杂的黑盒优化工具(例如贝叶斯优化、进化算法)相比,近似随机搜索的优势包括:
- 通过非自适应方式对搜索空间进行抽样,您可以在后续分析中更改调整目标,而无需重新运行实验。例如,我们通常希望找到在训练的任何时间点都达到最佳验证误差的试验。不过,由于近似随机搜索的非自适应特性,我们可以根据最终验证误差、训练误差或某些替代评估指标来找到最佳试验,而无需重新运行任何实验。
- 近似随机搜索的行为方式是一致且可重现的。即使搜索算法的实现发生变化,只要它保持相同的一致性属性,您应该也能重现六个月前的实验结果。如果使用复杂的贝叶斯优化软件,不同版本之间的实现可能会发生重大变化,这会使重现旧搜索变得更加困难。并非始终可以回滚到旧实现(例如,如果优化工具以服务的形式运行)。
- 它对搜索空间的统一探索有助于更轻松地推理结果以及它们可能对搜索空间的启示。例如,如果在对准确随机搜索进行遍历时,最佳点位于搜索空间的边界,则这是一个很好的信号(但并非万无一失),表明应更改搜索空间边界。但是,自适应黑盒优化算法可能会因为一些不幸的早期试验而忽略搜索空间的中间部分,即使该部分恰好包含同样出色的点也是如此,因为正是这种非均匀性,优秀的优化算法需要利用它来加快搜索速度。
- 与自适应算法不同,使用近似随机搜索(或其他非自适应搜索算法)时,并行运行不同数量的试验与顺序运行不会产生统计上不同的结果。
- 更复杂的搜索算法并不总能正确处理不可行点,尤其是在这些算法并非专为神经网络超参数调节而设计的情况下。
- 近似随机搜索方法很简单,在并行运行许多调优试验时效果尤为出色。经验之谈1:自适应算法很难战胜预算是其 2 倍的近似随机搜索,尤其是在需要并行运行许多试验时(因此,在启动新试验时,很少有机会利用之前的试验结果)。如果您不精通贝叶斯优化和其他高级黑盒优化方法,就可能无法获得这些方法原则上能够提供的好处。在现实的深度学习调优条件下,很难对先进的黑盒优化算法进行基准测试。它们是当前研究的热门领域,但对于缺乏经验的用户来说,越复杂的算法就越容易出错。精通这些方法的专家能够获得理想的结果,但在高并行性条件下,搜索空间和预算往往更重要。
不过,如果您的计算资源仅允许并行运行少量试验,而您可以依次运行许多试验,那么贝叶斯优化会变得更具吸引力,尽管这会使调优结果更难解读。
在哪里可以找到准随机搜索的实现?
开源 Vizier 提供了近似随机搜索的实现。在此 Vizier 使用示例中设置 algorithm="QUASI_RANDOM_SEARCH"。此超参数扫描示例中提供了一种替代实现。这两种实现都会为给定的搜索空间生成 Halton 序列(旨在实现经过移位和打乱的 Halton 序列,如 Critical Hyper-Parameters: No Random, No Cry 中所建议)。
如果基于低差异序列的准随机搜索算法不可用,则可以改用伪随机均匀搜索,但效率可能会略低。在 1-2 个维度中,也可以使用网格搜索,但在更高维度中则不适用。(请参阅 Bergstra & Bengio, 2012)。
使用近似随机搜索需要进行多少次试验才能获得理想结果?
一般来说,无法确定需要进行多少次试验才能通过近似随机搜索获得结果,但您可以查看具体示例。如图 3 所示,研究中的试验次数可能会对结果产生重大影响:
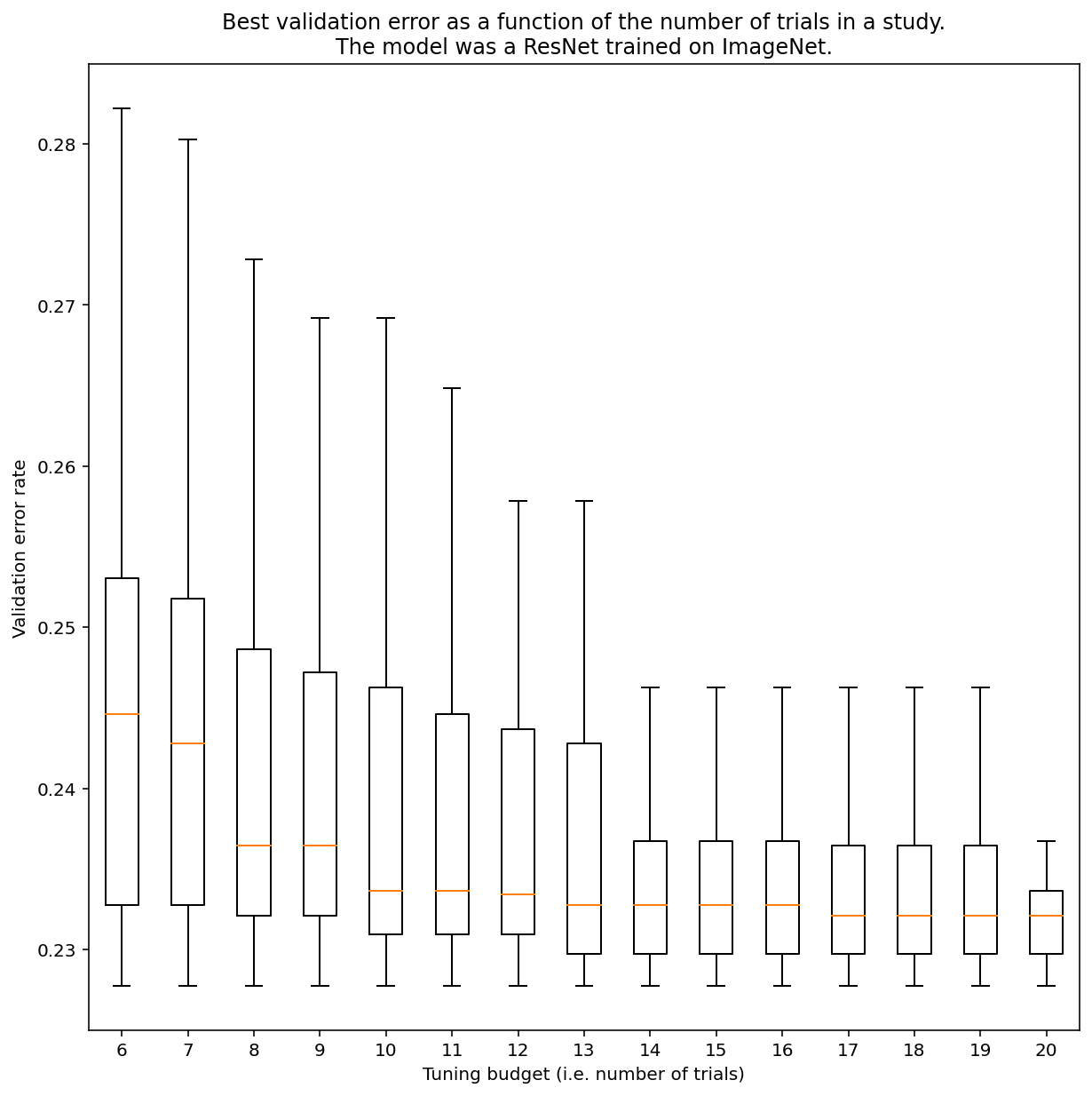
图 3:在 ImageNet 上进行了 100 次试验的 ResNet-50 调优结果。使用自举例,我们模拟了不同数量的调整预算。系统会绘制每个试验预算的最佳效果的箱形图。
请注意图 3 中的以下事项:
- 抽样 6 次的四分位范围比抽样 20 次的四分位范围大得多。
- 即使进行 20 次试验,特别幸运和特别不幸的实验之间的差异也可能大于使用固定超参数对此模型在不同随机种子上重新训练之间的典型差异,对于此工作负载,验证误差率大约为 23%,差异可能在 +/- 0.1% 左右。
-
Ben Recht 和 Kevin Jamieson 指出,作为基准,预算翻倍的随机搜索有多强大(“Hyperband”论文也提出了类似的论点),但我们肯定可以找到搜索空间和问题,在这些搜索空间和问题中,最先进的贝叶斯优化技术可以完胜预算翻倍的随机搜索。不过,根据我们的经验,在高并行模式下,要想超越预算翻倍的随机搜索,难度会大大增加,因为贝叶斯优化算法没有机会观察之前的试验结果。 ↩
