Model performansını iyileştirmek için bilimsel bir yaklaşım

Bu belgenin amaçları doğrultusunda:

Makine öğrenimi geliştirmenin nihai amacı, dağıtılan modelin faydasını en üst düzeye çıkarmaktır.

Bu bölümdeki temel adımları ve ilkeleri genellikle herhangi bir makine öğrenimi probleminde kullanabilirsiniz.

Bu bölümde aşağıdaki varsayımlar ele alınmaktadır:

• Makul bir sonuç elde eden bir yapılandırmanın yanı sıra tam olarak çalışan bir eğitim işlem hattınız zaten var.
• Anlamlı ayarlama denemeleri yapmak ve en az birkaç eğitim işini paralel olarak çalıştırmak için yeterli işlem kaynağına sahipsiniz.

Artımlı ayarlama stratejisi

Öneri: Basit bir yapılandırmayla başlayın. Ardından, soruna ilişkin bilgi edinirken kademeli olarak iyileştirmeler yapın. İyileştirmelerin güçlü kanıtlara dayandığından emin olun.

Amacınızın, modelinizin performansını en üst düzeye çıkaracak bir yapılandırma bulmak olduğunu varsayıyoruz. Bazen hedefiniz, belirli bir son tarihe kadar model iyileştirmesini en üst düzeye çıkarmaktır. Diğer durumlarda, modeli süresiz olarak iyileştirmeye devam edebilirsiniz. Örneğin, üretimde kullanılan bir modeli sürekli olarak iyileştirebilirsiniz.

Prensip olarak, olası yapılandırmaların tamamını otomatik olarak aramak için bir algoritma kullanarak performansı en üst düzeye çıkarabilirsiniz ancak bu pratik bir seçenek değildir. Olası yapılandırmaların alanı son derece büyüktür ve bu alanı insan rehberliği olmadan verimli bir şekilde arayabilecek kadar gelişmiş algoritmalar henüz yoktur. Çoğu otomatik arama algoritması, aranacak yapılandırma kümesini tanımlayan, elle tasarlanmış bir arama alanına dayanır ve bu arama alanları oldukça önemlidir.

Performansı en üst düzeye çıkarmanın en etkili yolu, basit bir yapılandırmayla başlamak ve soruna ilişkin bilgi edinirken özellikleri kademeli olarak ekleyip iyileştirmeler yapmaktır.

Her ayarlama turunda otomatik arama algoritmalarını kullanmanızı ve anlayışınız arttıkça arama alanlarını sürekli olarak güncellemenizi öneririz. Keşif yaptıkça doğal olarak daha iyi ve daha iyi yapılandırmalar bulacak, bu nedenle "en iyi" modeliniz sürekli olarak iyileşecektir.

"Lansman" terimi, en iyi yapılandırmamızda yapılan bir güncellemeyi ifade eder (bu güncelleme, bir üretim modelinin gerçek lansmanına karşılık gelebilir veya gelmeyebilir). Her "lansman" için, değişikliğin güçlü kanıtlara dayandığından (yalnızca şanslı bir yapılandırmaya dayalı rastgele bir olasılığa değil) emin olmanız gerekir. Böylece eğitim işlem hattına gereksiz karmaşıklık eklememiş olursunuz.

Genel olarak, artımlı ayarlama stratejimiz aşağıdaki dört adımı tekrarlamayı içerir:

1. Bir sonraki deneme turu için hedef seçin. Hedefin uygun şekilde kapsamlandığından emin olun.
2. Bir sonraki deneme grubunu tasarlayın. Bu hedefe doğru ilerleyen bir dizi deneme tasarlayıp uygulayın.
3. Deneysel sonuçlardan ders çıkarın. Denemeyi bir kontrol listesine göre değerlendirin.
4. Aday değişikliği kabul edip etmeyeceğinize karar verin.

Bu bölümün geri kalanında bu strateji ayrıntılı olarak açıklanmaktadır.

Bir sonraki deneme turu için bir hedef seçin

Aynı anda birden fazla özellik eklemeye veya birden fazla soruyu yanıtlamaya çalışırsanız sonuçlar üzerindeki ayrı etkileri ayıramayabilirsiniz. Örnek hedefler:

• İşlem hattında olası bir iyileştirme (ör. yeni bir düzenleyici, ön işleme seçeneği vb.) deneyin.
• Belirli bir model hiperparametresinin (örneğin, etkinleştirme işlevi) etkisini anlama
• Doğrulama hatasını en aza indirin.

Kısa vadeli doğrulama hatası iyileştirmeleri yerine uzun vadeli ilerlemeye öncelik verin

Özet: Çoğu zaman birincil hedefiniz, ayarlama sorunu hakkında bilgi edinmektir.

Zamanınızın çoğunu sorunu anlamaya, nispeten az bir kısmını ise doğrulama kümesindeki performansı en üst düzeye çıkarmaya odaklanarak geçirmenizi öneririz. Diğer bir deyişle, zamanınızın çoğunu "keşif" için, yalnızca küçük bir kısmını ise "fırsatları değerlendirme" için harcayın. Nihai performansı en üst düzeye çıkarmak için sorunu anlamak çok önemlidir. Kısa vadeli kazançlar yerine içgörülere öncelik vermek:

• Yalnızca geçmişteki bir tesadüf nedeniyle iyi performans gösteren çalıştırmalarda bulunan gereksiz değişiklikleri başlatmaktan kaçının.
• Doğrulama hatasının en hassas olduğu hiperparametreleri, en çok etkileşimde bulunan ve bu nedenle birlikte yeniden ayarlanması gereken hiperparametreleri ve diğer değişikliklere göre nispeten daha az hassas olan, dolayısıyla gelecekteki denemelerde düzeltilebilecek hiperparametreleri belirleyin.
• Aşırı uyum sorunu yaşandığında yeni düzenleyiciler gibi denenebilecek potansiyel yeni özellikler önerir.
• Gereksiz olan ve bu nedenle kaldırılabilecek özellikleri belirleyerek gelecekteki deneylerin karmaşıklığını azaltın.
• Hiperparametre ayarından elde edilen iyileştirmelerin doygunluğa ulaştığını anlama
• Ayarlama verimliliğini artırmak için arama alanlarımızı optimum değer etrafında daraltın.

Sonunda sorunu anlayacaksınız. Ardından, denemeler ayarlama sorununun yapısı hakkında en fazla bilgiyi vermese bile tamamen doğrulama hatasına odaklanabilirsiniz.

Sonraki deneme turunu tasarlama

Özet: Deneysel hedef için hangi hiperparametrelerin bilimsel, gereksiz ve sabit hiperparametreler olduğunu belirleyin. Rahatsız edici hiperparametreler üzerinde optimizasyon yaparken bilimsel hiperparametrelerin farklı değerlerini karşılaştırmak için bir çalışma dizisi oluşturun. Kaynak maliyetlerini bilimsel değerle dengelemek için rahatsız edici hiperparametrelerin arama alanını seçin.

Bilimsel, rahatsız edici ve sabit hiperparametreleri belirleme

Belirli bir hedef için tüm hiperparametreler aşağıdaki kategorilerden birine girer:

• Bilimsel hiperparametreler, modelin performansı üzerindeki etkisi ölçülmeye çalışılan parametrelerdir.
• Rahatsız edici hiperparametreler, bilimsel hiperparametrelerin farklı değerlerini adil bir şekilde karşılaştırmak için optimize edilmesi gerekenlerdir. Rahatsız edici hiperparametreler, istatistikteki rahatsız edici parametrelere benzer.
• Sabit hiperparametreler, mevcut deney turunda sabit değerlere sahiptir. Sabit hiperparametrelerin değerleri, bilimsel hiperparametrelerin farklı değerlerini karşılaştırdığınızda değişmemelidir. Bir dizi deneme için belirli hiperparametreleri düzelterek, denemelerden elde edilen sonuçların sabit hiperparametrelerin diğer ayarları için geçerli olmayabileceğini kabul etmeniz gerekir. Diğer bir deyişle, sabit hiperparametreler, denemelerden çıkardığınız tüm sonuçlar için uyarılar oluşturur.

Örneğin, hedefinizin aşağıdaki gibi olduğunu varsayalım:

Daha fazla gizli katmana sahip bir modelin doğrulama hatasının daha düşük olup olmadığını belirleyin.

Bu durumda:

• Öğrenme hızı, yalnızca her bir gizli katman sayısı için ayrı ayrı ayarlandığında farklı sayıda gizli katmana sahip modelleri adil bir şekilde karşılaştırabileceğiniz için can sıkıcı bir hiperparametredir. (Optimum öğrenme hızı genellikle model mimarisine bağlıdır.)
• Önceki denemelerde en iyi etkinleştirme işlevinin model derinliğine duyarlı olmadığını belirlediyseniz etkinleştirme işlevi sabit bir hiperparametre olabilir. Alternatif olarak, bu etkinleştirme işlevini kapsamak için gizli katmanların sayısı hakkındaki sonuçlarınızı sınırlamayı kabul edebilirsiniz. Alternatif olarak, her gizli katman sayısı için ayrı ayrı ayarlamaya hazırsanız bu bir rahatsız edici hiperparametre olabilir.

Belirli bir hiperparametre bilimsel hiperparametre, rahatsız edici hiperparametre veya sabit hiperparametre olabilir. Hiperparametrenin tanımı, deneysel hedefe bağlı olarak değişir. Örneğin, etkinleştirme işlevi aşağıdakilerden herhangi biri olabilir:

• Bilimsel hiperparametre: Sorunumuz için ReLU mu yoksa tanh mı daha iyi bir seçimdir?
• Rahatsız edici hiperparametre: Birkaç farklı olası etkinleştirme işlevine izin verdiğinizde en iyi beş katmanlı model, en iyi altı katmanlı modelden daha mı iyi?
• Sabit hiperparametre: ReLU ağlarında belirli bir konuma toplu normalleştirme eklemek yardımcı olur mu?

Yeni bir deneme grubu tasarlarken:

1. Deneysel hedef için bilimsel hiperparametreleri belirleyin. (Bu aşamada, diğer tüm hiperparametreleri rahatsız edici hiperparametreler olarak düşünebilirsiniz.)
2. Bazı rahatsız edici hiperparametreleri sabit hiperparametrelere dönüştürün.

Sınırsız kaynaklarla, bilimsel olmayan tüm hiperparametreleri rahatsız edici hiperparametreler olarak bırakırsınız. Böylece, denemelerinizden elde ettiğiniz sonuçlar, sabit hiperparametre değerleriyle ilgili uyarılar içermez. Ancak, ayarlamaya çalıştığınız rahatsız edici hiperparametre sayısı arttıkça bilimsel hiperparametrelerin her ayarı için bunları yeterince iyi ayarlayamama ve denemelerinizden yanlış sonuçlara ulaşma riskiniz de artar. Sonraki bir bölümde açıklandığı gibi, hesaplama bütçesini artırarak bu riski bertaraf edebilirsiniz. Ancak, maksimum kaynak bütçeniz genellikle bilimsel olmayan tüm hiperparametreleri ayarlamak için gerekenden daha azdır.

Sabit bir hiperparametre olarak dahil etmenin getirdiği sakıncalar, rahatsız edici bir hiperparametre olarak dahil etmenin maliyetinden daha az külfetli olduğunda rahatsız edici bir hiperparametreyi sabit bir hiperparametreye dönüştürmenizi öneririz. Bir rahatsız edici hiperparametre bilimsel hiperparametrelerle ne kadar çok etkileşim kurarsa değerini düzeltmek o kadar zararlı olur. Örneğin, ağırlık azaltma gücünün en iyi değeri genellikle model boyutuna bağlıdır. Bu nedenle, ağırlık azaltma için tek bir değer varsayarak farklı model boyutlarını karşılaştırmak çok bilgilendirici olmaz.

Bazı optimize edici parametreleri

Genel bir kural olarak, bazı optimize edici hiperparametreler (ör. öğrenme oranı, momentum, öğrenme oranı planı parametreleri, Adam beta'ları vb.) diğer değişikliklerle en çok etkileşime girme eğiliminde oldukları için rahatsız edici hiperparametrelerdir. "Mevcut işlem hattı için en iyi öğrenme oranı nedir?" gibi bir hedef çok fazla bilgi sağlamadığından bu optimize edici hiperparametreler nadiren bilimsel hiperparametrelerdir. En iyi ayar, bir sonraki işlem hattı değişikliğiyle değişebilir.

Kaynak kısıtlamaları veya bilimsel parametrelerle etkileşime girmediklerine dair özellikle güçlü kanıtlar nedeniyle bazı optimize edici hiperparametreleri zaman zaman düzeltebilirsiniz. Ancak, bilimsel hiperparametrelerin farklı ayarları arasında adil karşılaştırmalar yapmak için genellikle optimize edici hiperparametreleri ayrı ayrı ayarlamanız gerektiğini ve bu nedenle sabitlenmemesi gerektiğini varsaymalısınız. Ayrıca, bir optimize edici hiperparametre değerini diğerine tercih etmek için önsel bir neden yoktur. Örneğin, optimize edici hiperparametre değerleri genellikle ileri geçişlerin veya gradyanların hesaplama maliyetini hiçbir şekilde etkilemez.

Optimizasyon aracı seçimi

Optimizasyon uzmanı seçimi genellikle şunlardan biri olur:

• bilimsel bir hiperparametre
• sabit bir hiperparametre

Deneysel hedefiniz iki veya daha fazla farklı optimize edici arasında adil karşılaştırmalar yapmayı içeriyorsa optimize edici, bilimsel bir hiperparametredir. Örneğin:

Belirli sayıda adımda en düşük doğrulama hatasını hangi optimizasyon aracının ürettiğini belirleyin.

Alternatif olarak, aşağıdakiler dahil olmak üzere çeşitli nedenlerle optimize ediciyi sabit bir hiperparametre yapabilirsiniz:

• Önceki denemeler, ayarlama sorununuz için en iyi optimizasyon aracının mevcut bilimsel hiperparametrelerden etkilenmediğini gösteriyor.
• Eğitim eğrileri hakkında akıl yürütmek daha kolay olduğundan, bilimsel hiperparametrelerin değerlerini bu optimize ediciyi kullanarak karşılaştırmayı tercih ediyorsunuz.
• Alternatiflere kıyasla daha az bellek kullandığı için bu optimize ediciyi kullanmayı tercih ediyorsunuz.

Düzenleme hiperparametreleri

Bir düzenlileştirme tekniğiyle sunulan hiperparametreler genellikle rahatsız edici hiperparametrelerdir. Ancak düzenlileştirme tekniğinin dahil edilip edilmeyeceği bilimsel veya sabit bir hiperparametredir.

Örneğin, bırakma düzenlileştirme, kod karmaşıklığını artırır. Bu nedenle, dropout düzenlileştirmenin dahil edilip edilmeyeceğine karar verirken "dropout yok" ile "dropout"u bilimsel bir hiperparametre, dropout oranını ise rahatsız edici bir hiperparametre olarak belirleyebilirsiniz. Bu denemeye dayanarak kanalizasyona bırakma düzenlileştirme eklemeye karar verirseniz bırakma oranı, gelecekteki denemelerde rahatsız edici bir hiperparametre olur.

Mimari hiperparametreler

Mimari hiperparametreler genellikle bilimsel veya sabit hiperparametrelerdir. Çünkü mimari değişiklikler, yayın ve eğitim maliyetlerini, gecikmeyi ve bellek gereksinimlerini etkileyebilir. Örneğin, katman sayısı genellikle bilimsel veya sabit bir hiperparametredir. Bunun nedeni, katman sayısının eğitim hızı ve bellek kullanımı üzerinde önemli sonuçlar doğurma eğiliminde olmasıdır.

Bilimsel hiperparametrelerle ilgili bağımlılıklar

Bazı durumlarda, rahatsız edici ve sabit hiperparametreler kümeleri, bilimsel hiperparametrelerin değerlerine bağlıdır. Örneğin, Nesterov momentum ve Adam'daki hangi optimizasyon aracının en düşük doğrulama hatasını ürettiğini belirlemeye çalıştığınızı varsayalım. Bu durumda:

• Bilimsel hiperparametre, değerleri alan optimizasyon aracıdır. {"Nesterov_momentum", "Adam"}
• optimizer="Nesterov_momentum" değeri, can sıkıcı veya sabit hiperparametreler olabilen {learning_rate, momentum} hiperparametrelerini tanıtır.
• optimizer="Adam" değeri, {learning_rate, beta1, beta2, epsilon} hiperparametrelerini tanıtır. Bu hiperparametreler, rahatsız edici veya sabit hiperparametreler olabilir.

Yalnızca bilimsel hiperparametrelerin belirli değerleri için mevcut olan hiperparametrelere koşullu hiperparametreler denir. Aynı ada sahip olmaları nedeniyle iki koşullu hiperparametrenin aynı olduğunu varsaymayın. Önceki örnekte, learning_rate adlı koşullu hiperparametre, optimizer="Adam" için optimizer="Nesterov_momentum" için olduğundan farklı bir hiperparametredir. İki algoritmadaki rolü benzerdir (aynı olmasa da) ancak her bir optimize edicide iyi sonuç veren değer aralığı genellikle birkaç kat farklıdır.

Çalışma grubu oluşturma

Bilimsel ve rahatsız edici hiperparametreleri belirledikten sonra, deneysel hedefe ulaşmak için bir çalışma veya bir dizi çalışma tasarlamanız gerekir. Çalışma, sonraki analiz için çalıştırılacak bir dizi hiperparametre yapılandırmasını belirtir. Her yapılandırmaya deneme adı verilir. Çalışma oluşturmak için genellikle aşağıdakileri seçmeniz gerekir:

• Denemeler arasında değişen hiperparametreler.
• Bu hiperparametrelerin alabileceği değerler (arama alanı).
• Deneme sayısı.
• Arama alanından bu kadar çok deneme örneği almak için otomatik bir arama algoritması.

Alternatif olarak, hiperparametre yapılandırmaları kümesini manuel olarak belirterek de bir çalışma oluşturabilirsiniz.

Çalışmaların amacı aynı anda şunları yapmaktır:

• İşlem hattını bilimsel hiperparametrelerin farklı değerleriyle çalıştırın.
• Bilimsel hiperparametrelerin farklı değerleri arasındaki karşılaştırmaların mümkün olduğunca adil olması için rahatsız edici hiperparametreleri "optimize ederek ortadan kaldırma" (veya "optimize ederek aşma").

En basit durumda, bilimsel parametrelerin her yapılandırması için ayrı bir çalışma yaparsınız. Bu çalışmalarda, her bir çalışma, rahatsız edici hiperparametreler üzerinde ince ayar yapar. Örneğin, hedefiniz Nesterov momentum ve Adam arasından en iyi optimize ediciyi seçmekse iki çalışma oluşturabilirsiniz:

• optimizer="Nesterov_momentum" ve rahatsız edici hiperparametrelerin {learning_rate, momentum} olduğu bir çalışma
• optimizer="Adam" ve rahatsız edici hiperparametrelerin {learning_rate, beta1, beta2, epsilon} olduğu başka bir çalışma.

Her çalışmadan en iyi performansı gösteren denemeyi seçerek iki optimize ediciyi karşılaştırırsınız.

Bayes optimizasyonu veya evrimsel algoritmalar gibi yöntemler de dahil olmak üzere, rahatsız edici hiperparametreler üzerinde optimizasyon yapmak için herhangi bir gradyan içermeyen optimizasyon algoritmasını kullanabilirsiniz. Ancak, bu ayarda sağladığı çeşitli avantajlar nedeniyle ayarlama işleminin keşif aşamasında yarı rastgele aramayı tercih ederiz. Keşif tamamlandıktan sonra, varsa en yeni Bayesian optimizasyon yazılımını kullanmanızı öneririz.

Bilimsel hiperparametrelerin çok sayıda değerini karşılaştırmak istediğiniz ancak bu kadar çok bağımsız çalışma yapmanın pratik olmadığı daha karmaşık bir durumu ele alalım. Bu durumda şunları yapabilirsiniz:

• Bilimsel parametreleri, rahatsız edici hiperparametrelerle aynı arama alanına dahil edin.
• Tek bir çalışmada hem bilimsel hem de rahatsız edici hiperparametrelerin değerlerini örneklemek için bir arama algoritması kullanın.

Bu yaklaşımı kullanırken koşullu hiperparametreler sorunlara neden olabilir. Sonuçta, rahatsız edici hiperparametreler kümesi bilimsel hiperparametrelerin tüm değerleri için aynı olmadığı sürece arama alanı belirtmek zordur. Bu durumda, bilimsel hiperparametrelerin farklı değerlerinin eşit şekilde örneklenmesini sağladığı için, daha gelişmiş kara kutu optimizasyon araçları yerine yarı rastgele arama kullanmayı daha çok tercih ederiz. Arama algoritmasından bağımsız olarak, bilimsel parametrelerin eşit şekilde arandığından emin olun.

Bilgilendirici ve uygun maliyetli denemeler arasında denge kurun

Bir çalışma veya çalışma dizisi tasarlarken aşağıdaki üç hedefi yeterli düzeyde gerçekleştirmek için sınırlı bir bütçe ayırın:

• Bilimsel hiperparametrelerin yeterince farklı değerlerini karşılaştırma
• Yeterince büyük bir arama alanında rahatsız edici hiperparametreleri ayarlama
• Gereksiz hiperparametrelerin arama alanını yeterince yoğun bir şekilde örnekleme.

Bu üç hedefi ne kadar iyi gerçekleştirebilirseniz denemeden o kadar fazla analiz elde edebilirsiniz. Bilimsel hiperparametrelerin mümkün olduğunca çok değerini karşılaştırmak, denemeden elde ettiğiniz analizlerin kapsamını genişletir.

Mümkün olduğunca çok sayıda rahatsız edici hiperparametre eklemek ve her bir rahatsız edici hiperparametrenin mümkün olduğunca geniş bir aralıkta değişmesine izin vermek, bilimsel hiperparametrelerin her yapılandırması için arama alanında rahatsız edici hiperparametrelerin "iyi" bir değerinin bulunduğuna dair güveni artırır. Aksi takdirde, bilimsel parametrelerin bazı değerleri için daha iyi değerlerin bulunabileceği, rahatsız edici hiperparametre alanının olası bölgelerini aramayarak bilimsel hiperparametrelerin değerleri arasında haksız karşılaştırmalar yapabilirsiniz.

Rahatsız edici hiperparametrelerin arama alanını mümkün olduğunca yoğun bir şekilde örnekleyin. Bu işlem, arama prosedürünün arama alanınızda bulunan rahatsız edici hiperparametreler için iyi ayarlar bulacağına dair güveni artırır. Aksi takdirde, bazı değerler rahatsız edici hiperparametrelerin örneklenmesi konusunda daha şanslı olacağından bilimsel parametrelerin değerleri arasında adil olmayan karşılaştırmalar yapabilirsiniz.

Maalesef bu üç boyuttan herhangi birinde iyileştirme yapmak için aşağıdakilerden biri gerekir:

• Deneme sayısını artırarak kaynak maliyetini artırabilirsiniz.
• Diğer boyutlardan birinde kaynak tasarrufu yapmanın bir yolunu bulma

Her sorunun kendine özgü özellikleri ve hesaplama kısıtlamaları vardır. Bu nedenle, kaynakları bu üç hedef arasında paylaştırmak için belirli bir düzeyde alan bilgisi gerekir. Bir çalışma yürüttükten sonra, her zaman çalışmanın rahatsız edici hiperparametreleri yeterince iyi ayarlayıp ayarlamadığına dair bir fikir edinmeye çalışın. Yani çalışmada, bilimsel hiperparametreleri adil bir şekilde karşılaştırmak için yeterince büyük bir alan yeterince kapsamlı bir şekilde aranmıştır (sonraki bölümde daha ayrıntılı olarak açıklanmıştır).

Deneysel sonuçlardan öğrenme

Öneri: Her bir deney grubunun orijinal bilimsel hedefine ulaşmaya çalışmanın yanı sıra ek soruların yer aldığı bir kontrol listesini de inceleyin. Sorunlarla karşılaşırsanız denemeleri gözden geçirip yeniden çalıştırın.

Sonuç olarak, her deney grubu belirli bir hedefe sahiptir. Denemelerin bu hedefe yönelik sağladığı kanıtları değerlendirmeniz gerekir. Ancak doğru soruları sorarsanız belirli bir dizi denemenin orijinal hedefine ulaşmadan önce düzeltilmesi gereken sorunları genellikle bulabilirsiniz. Bu soruları sormazsanız yanlış sonuçlara varabilirsiniz.

Deneme çalıştırmak maliyetli olabileceğinden, bu bilgiler mevcut hedefle hemen alakalı olmasa bile her deneme grubundan diğer faydalı bilgileri de çıkarmanız gerekir.

Belirli bir deneme grubunu analiz ederek orijinal hedeflerine ulaşma yolunda ilerlemeden önce kendinize aşağıdaki ek soruları sorun:

• Arama alanı yeterince büyük mü? Bir çalışmadaki optimum nokta, bir veya daha fazla boyutta arama alanının sınırına yakınsa arama muhtemelen yeterince geniş değildir. Bu durumda, genişletilmiş bir arama alanıyla başka bir çalışma yapın.
• Arama alanından yeterli sayıda nokta örneklediniz mi? Aksi takdirde, daha fazla nokta çalıştırın veya ayarlama hedeflerinde daha az iddialı olun.
• Her çalışmadaki denemelerin ne kadarı uygulanamaz? Yani hangi denemeler farklılaşıyor, çok kötü kayıp değerleri alıyor veya bazı örtülü kısıtlamaları ihlal ettikleri için hiç çalışmıyor? Bir çalışmadaki puanların çok büyük bir kısmı uygulanamaz olduğunda, bu tür puanların örneklenmesini önlemek için arama alanını ayarlayın. Bu işlem bazen arama alanının yeniden parametrelendirilmesini gerektirir. Bazı durumlarda, çok sayıda uygun olmayan nokta, eğitim kodunda bir hata olduğunu gösterebilir.
• Modelde optimizasyon sorunları var mı?
• En iyi denemelerin eğitim eğrilerinden neler öğrenebilirsiniz? Örneğin, en iyi denemelerde, sorunlu aşırı uyumla tutarlı eğitim eğrileri var mı?

Gerekirse önceki soruların yanıtlarına göre arama alanını iyileştirmek ve/veya daha fazla deneme örneği almak için en son çalışmayı ya da çalışma grubunu hassaslaştırın veya başka bir düzeltici işlem yapın.

Önceki soruları yanıtladıktan sonra, denemelerin orijinal hedefinizle ilgili sağladığı kanıtları değerlendirebilirsiniz. Örneğin, bir değişikliğin yararlı olup olmadığını değerlendirebilirsiniz.

Kötü arama alanı sınırlarını belirleme

Bir arama alanından örneklenen en iyi nokta sınırına yakınsa bu alan şüpheli kabul edilir. Arama aralığını bu yönde genişletirseniz daha da iyi bir nokta bulabilirsiniz.

Arama alanı sınırlarını kontrol etmek için tamamlanan denemeleri temel hiperparametre ekseni grafikleri olarak adlandırdığımız grafiklerde çizmenizi öneririz. Bu grafiklerde, doğrulama hedefi değerini hiperparametrelerden birine (ör. öğrenme oranı) karşı çizeriz. Grafikteki her nokta tek bir denemeye karşılık gelir.

Her denemenin doğrulama hedefi değeri genellikle eğitim süresince elde ettiği en iyi değer olmalıdır.

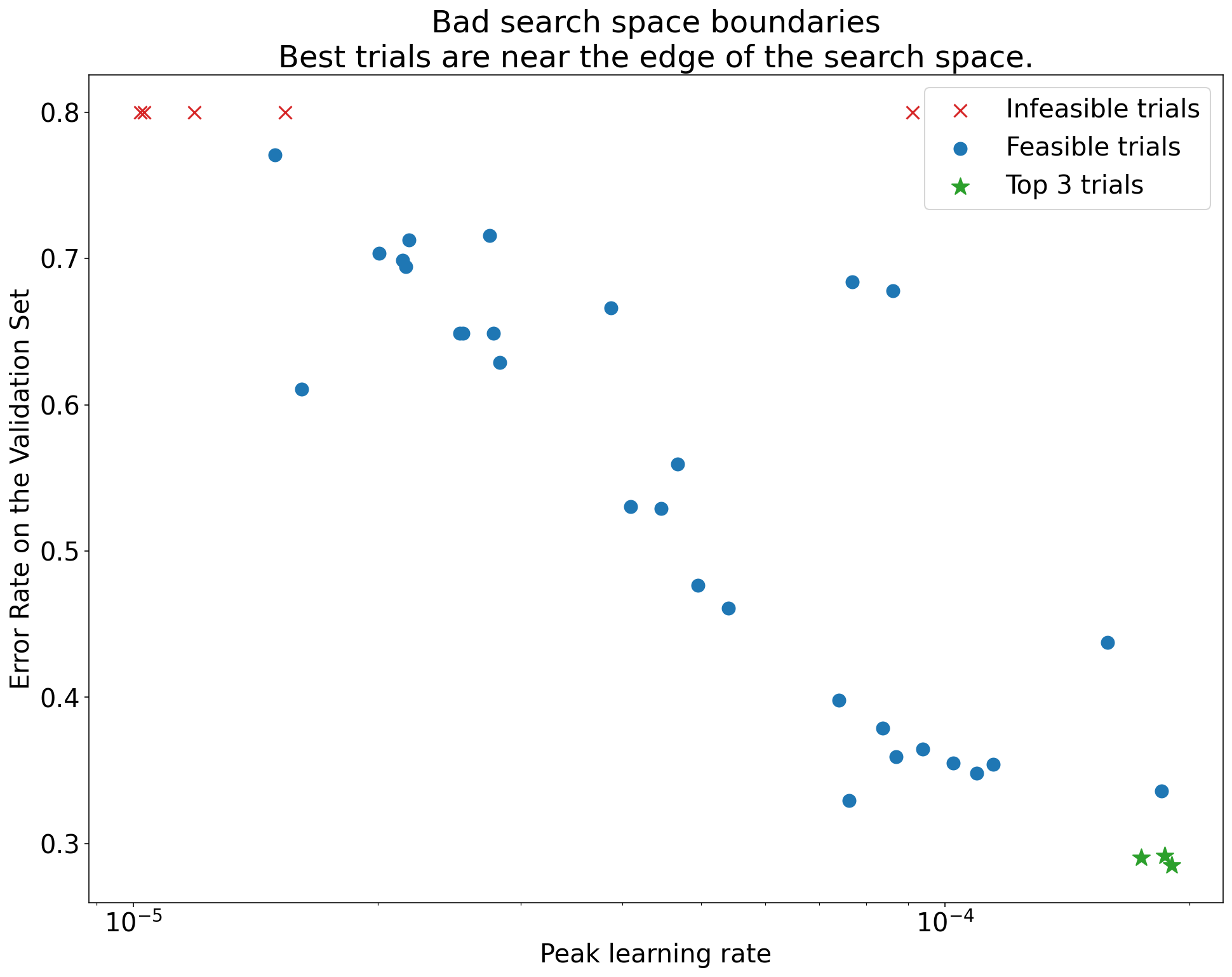
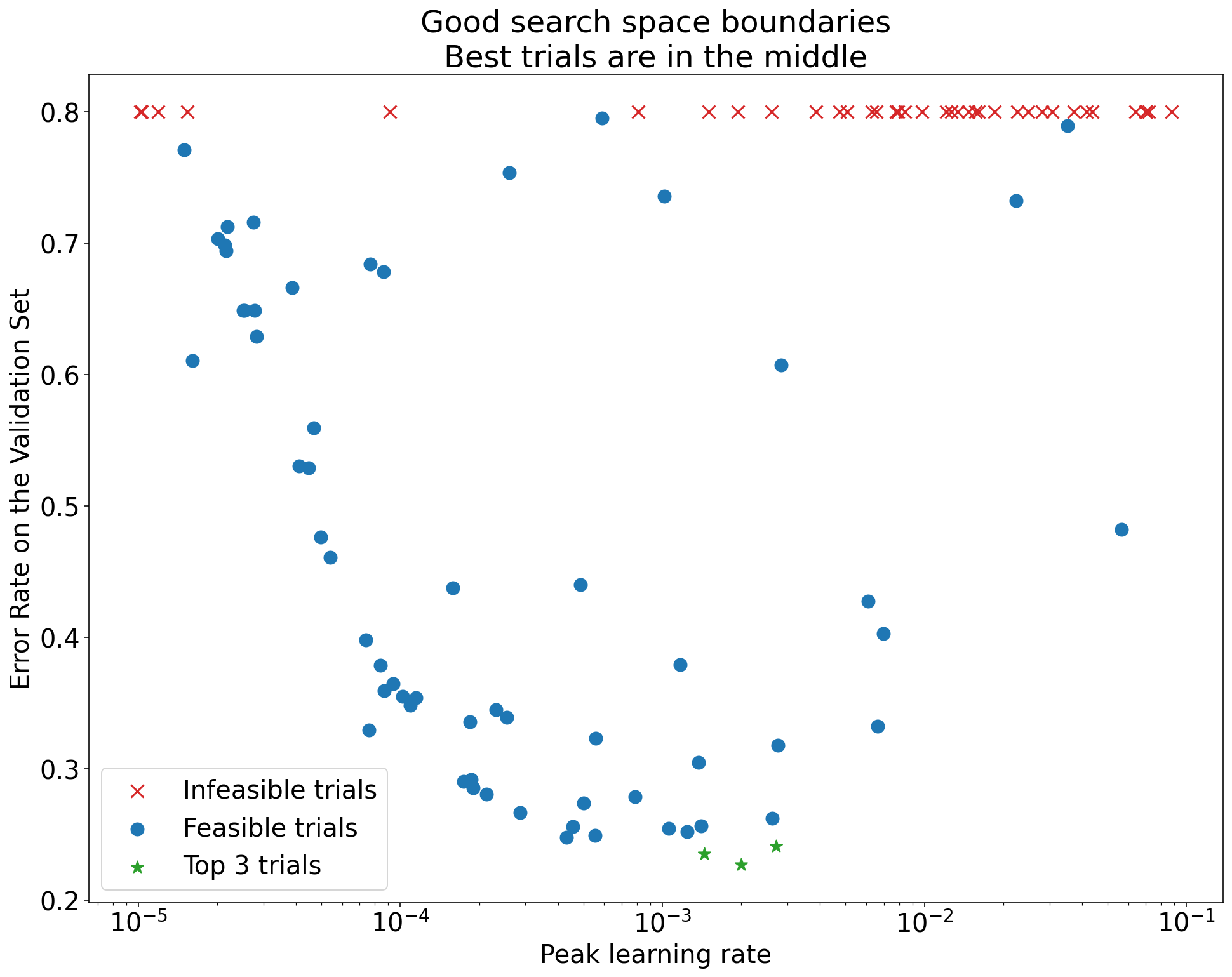
Şekil 1: Kötü arama alanı sınırları ve kabul edilebilir arama alanı sınırları örnekleri.

Şekil 1'deki grafiklerde, ilk öğrenme hızına karşı hata oranı (daha düşük değer daha iyidir) gösterilmektedir. En iyi noktalar bir arama alanının kenarına doğru kümeleniyorsa (bazı boyutlarda), gözlemlenen en iyi nokta artık sınıra yakın olmayana kadar arama alanı sınırlarını genişletmeniz gerekebilir.

Çalışmalarda genellikle farklılaşan veya çok kötü sonuçlar veren "uygulanamaz" denemeler yer alır (Şekil 1'de kırmızı X'lerle işaretlenmiştir). Tüm denemeler, belirli bir eşik değerden daha yüksek öğrenme hızları için uygun değilse ve en iyi performansı gösteren denemelerin öğrenme hızları bu bölgenin sınırında yer alıyorsa model, daha yüksek öğrenme hızlarına erişmesini engelleyen kararlılık sorunları yaşayabilir.

Arama alanında yeterli nokta örneklenmiyor

Genel olarak, arama alanının yeterince yoğun bir şekilde örneklenip örneklenmediğini bilmek çok zor olabilir. 🤖 Daha fazla deneme çalıştırmak daha az deneme çalıştırmaktan iyidir ancak daha fazla deneme çalıştırmak ek maliyet oluşturur.

Yeterli örnekleme yaptığınızı bilmek çok zor olduğundan şunları yapmanızı öneririz:

• Bütçenize uygun ürünleri deneme
• Çeşitli hiperparametre ekseni grafiklerine tekrar tekrar bakarak ve arama alanının "iyi" bölgesinde kaç nokta olduğunu anlamaya çalışarak sezgisel güveninizi kalibre etme.

Eğitim eğrilerini inceleyin

Özet: Kayıp eğrilerini incelemek, yaygın hata modlarını belirlemenin kolay bir yoludur ve olası sonraki işlemlere öncelik vermenize yardımcı olabilir.

Çoğu durumda, denemelerinizin birincil hedefi yalnızca her denemenin doğrulama hatasının dikkate alınmasını gerektirir. Ancak her denemeyi tek bir sayıya indirirken dikkatli olun. Bu odaklanma, yüzeyin altında neler olduğuna dair önemli ayrıntıları gizleyebilir. Her çalışma için en azından en iyi birkaç denemenin kayıp eğrilerine bakmanızı önemle öneririz. Birincil deneysel hedefi ele almak için gerekli olmasa bile kayıp eğrilerini (hem eğitim kaybı hem de doğrulama kaybı dahil) incelemek, yaygın hata modlarını belirlemenin iyi bir yoludur ve sonraki adımlarda hangi işlemlere öncelik vereceğinizi belirlemenize yardımcı olabilir.

Kayıp eğrilerini incelerken aşağıdaki sorulara odaklanın:

• Denemelerden herhangi birinde sorunlu aşırı uyum var mı? Sorunlu aşırı uyum, doğrulama hatası eğitim sırasında artmaya başladığında ortaya çıkar. Bilimsel hiperparametrelerin her ayarı için "en iyi" denemeyi seçerek rahatsız edici hiperparametreleri optimize ettiğiniz deneysel ayarlarda, karşılaştırdığınız bilimsel hiperparametrelerin ayarlarına karşılık gelen en iyi denemelerin her birinde sorunlu aşırı uyum olup olmadığını kontrol edin. En iyi denemelerden herhangi birinde sorunlu aşırı uyum varsa aşağıdakilerden birini veya her ikisini de yapın:

  • Denemeyi ek düzenlileştirme teknikleriyle yeniden çalıştırma
  • Bilimsel hiperparametrelerin değerlerini karşılaştırmadan önce mevcut düzenlileştirme parametrelerini yeniden ayarlayın. Bilimsel hiperparametreler düzenlileştirme parametreleri içeriyorsa bu durum geçerli olmayabilir. Bu durumda, düzenlileştirme parametrelerinin düşük güçlü ayarlarının sorunlu aşırı uyuma neden olması şaşırtıcı olmaz.

  Aşırı uyumu azaltmak için genellikle minimum kod karmaşıklığı veya ek hesaplama (ör. bırakma düzenlileştirme, etiket düzeltme, ağırlık azaltma) ekleyen yaygın düzenlileştirme teknikleri kullanılır. Bu nedenle, genellikle bir veya daha fazlasını sonraki deneme turuna eklemek kolaydır. Örneğin, bilimsel hiperparametre "gizli katman sayısı" ise ve en fazla sayıda gizli katman kullanan en iyi deneme sorunlu aşırı uyum gösteriyorsa daha az sayıda gizli katmanı hemen seçmek yerine ek düzenlileştirme ile yeniden denemenizi öneririz.

  "En iyi" denemelerin hiçbirinde sorunlu aşırı uyum olmasa bile, denemelerin herhangi birinde aşırı uyum varsa sorun olabilir. En iyi denemeyi seçmek, sorunlu aşırı uyum gösteren yapılandırmaları bastırır ve bu tür yapılandırmaları tercih etmez. Diğer bir deyişle, en iyi denemeyi seçmek daha fazla düzenlileştirme içeren yapılandırmaları tercih eder. Ancak, eğitim sürecini kötüleştiren her şey, bu amaçla tasarlanmamış olsa bile düzenleyici görevi görebilir. Örneğin, daha küçük bir öğrenme hızı seçmek optimizasyon sürecini aksatarak eğitimi düzenleyebilir ancak genellikle öğrenme hızını bu şekilde seçmek istemeyiz. Bilimsel hiperparametrelerin her ayarı için "en iyi" denemenin, bilimsel veya rahatsız edici hiperparametrelerin bazılarının "kötü" değerlerini tercih edecek şekilde seçilebileceğini unutmayın.

• Eğitim veya doğrulama hatasında adım adım yüksek varyans var mı? Bu durumda, aşağıdaki iki durum da olumsuz etkilenebilir:

  • Bilimsel hiperparametrelerin farklı değerlerini karşılaştırabilme Bunun nedeni, her denemenin rastgele bir şekilde "şanslı" veya "şanssız" adımda sona ermesidir.
  • Üretimde en iyi denemenin sonucunu yeniden üretme beceriniz. Bunun nedeni, üretim modelinin çalışmadakiyle aynı "şanslı" adımda sona ermeyebilmesidir.

  Adımdan adıma varyansın en olası nedenleri şunlardır:

  • Her grup için eğitim kümesinden rastgele örnekler alınması nedeniyle grup varyansı.
  • Küçük doğrulama kümeleri
  • Eğitimin son aşamalarında çok yüksek bir öğrenme hızı kullanma.

  Olası çözümler şunlardır:

  • Toplu işlem boyutunu artırma
  • Daha fazla doğrulama verisi elde etme
  • Öğrenme hızı azalmasını kullanma
  • Polyak ortalaması kullanma.

• Denemeler, eğitimin sonunda hâlâ iyileşiyor mu? Bu durumda, "işlem sınırlı" rejimindesiniz ve eğitim adımlarının sayısını artırmaktan veya öğrenme oranı planını değiştirmekten yararlanabilirsiniz.

• Eğitim ve doğrulama kümelerindeki performans, son eğitim adımından çok önce doygunluğa ulaştı mı? Bu durumda, "not compute-bound" (hesaplama sınırlı değil) rejiminde olduğunuz ve eğitim adımlarının sayısını azaltabileceğiniz anlaşılır.

Bu listenin dışında, kayıp eğrileri incelenerek birçok ek davranış da anlaşılabilir. Örneğin, eğitim sırasında eğitim kaybının artması genellikle eğitim ardışık düzeninde bir hata olduğunu gösterir.

İzolasyon grafikleriyle bir değişikliğin faydalı olup olmadığını algılama

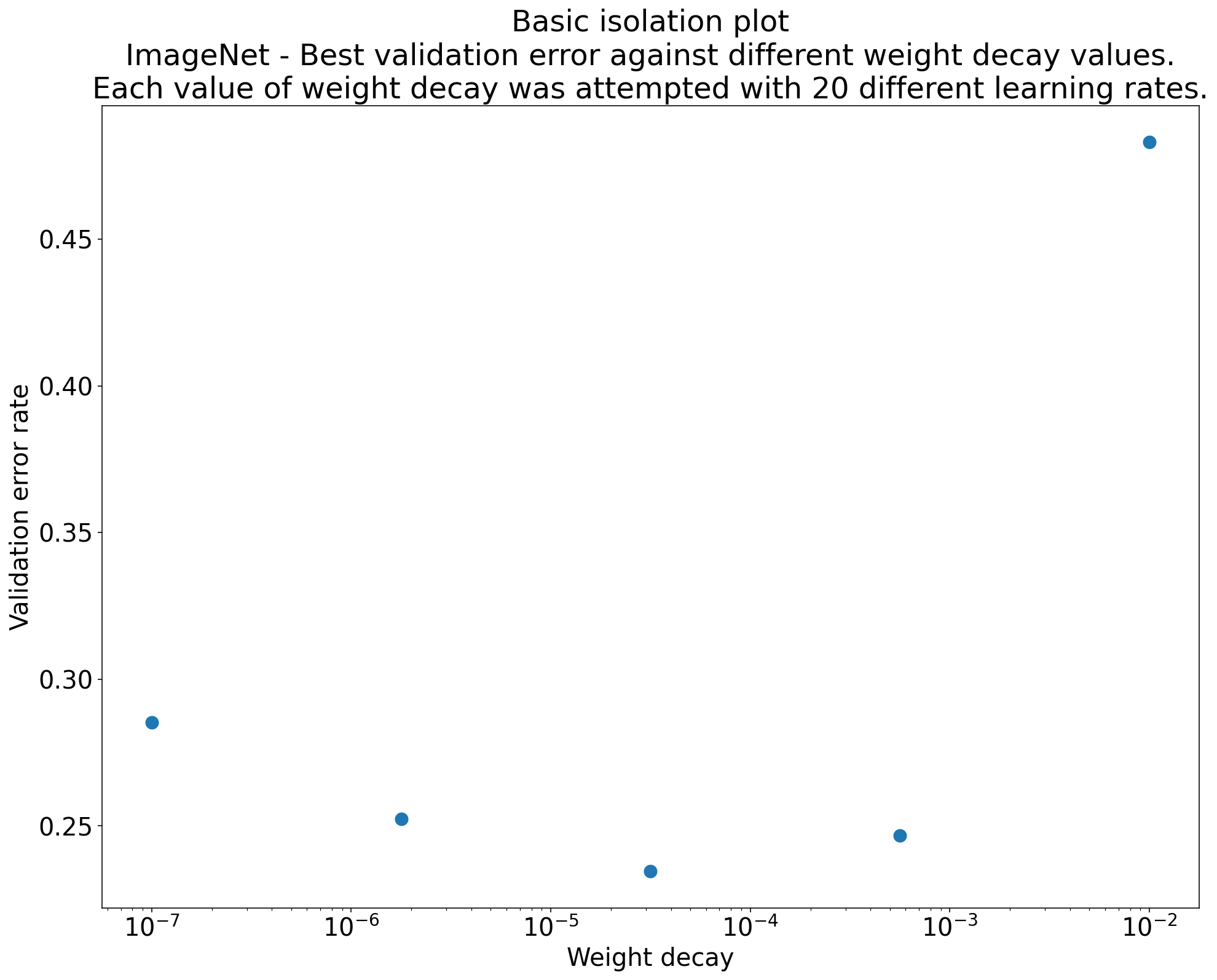
Şekil 2: ImageNet üzerinde eğitilmiş ResNet-50 için ağırlık azalmasıyla ilgili en iyi değeri araştıran izolasyon grafiği.

 

Çoğu zaman, bir dizi denemenin amacı bilimsel bir hiperparametrenin farklı değerlerini karşılaştırmaktır. Örneğin, en iyi doğrulama hatasına neden olan ağırlık azalması değerini belirlemek istediğinizi varsayalım. İzolasyon grafiği, temel hiperparametre ekseni grafiğinin özel bir durumudur. Bir izolasyon grafiğindeki her nokta, bazı (veya tüm) rahatsız edici hiperparametrelerdeki en iyi denemenin performansına karşılık gelir. Diğer bir deyişle, rahatsız edici hiperparametreler "optimize edildikten" sonra model performansını çizin.

İzolasyon grafiği, bilimsel hiperparametrenin farklı değerleri arasında eşit şartlarda karşılaştırma yapmayı kolaylaştırır. Örneğin, Şekil 2'deki izolasyon grafiği, ImageNet üzerinde eğitilmiş belirli bir ResNet-50 yapılandırması için en iyi doğrulama performansını sağlayan ağırlık azalması değerini gösterir.

Amaç, ağırlık azaltmanın dahil edilip edilmeyeceğini belirlemekse bu grafikteki en iyi noktayı ağırlık azaltma içermeyen temel değerle karşılaştırın. Adil bir karşılaştırma için temel modelin öğrenme hızı da eşit derecede iyi ayarlanmalıdır.

(Yarı)rastgele arama tarafından oluşturulan verileriniz olduğunda ve izolasyon grafiği için sürekli bir hiperparametre kullanmayı düşündüğünüzde, temel hiperparametre ekseni grafiğinin x ekseni değerlerini gruplandırarak ve gruplar tarafından tanımlanan her dikey dilimde en iyi denemeyi alarak izolasyon grafiğini yaklaşık olarak hesaplayabilirsiniz.

Genel olarak faydalı olan grafikleri otomatikleştirme

Grafik oluşturmak ne kadar zor olursa onlara o kadar az bakarsınız. Bu nedenle, altyapınızı mümkün olduğunca fazla grafik oluşturacak şekilde otomatik olarak ayarlamanızı öneririz. En azından, bir denemede değiştirdiğiniz tüm hiperparametreler için temel hiperparametre ekseni grafikleri oluşturmanızı öneririz.

Ayrıca, tüm denemeler için otomatik olarak kayıp eğrileri oluşturmanızı öneririz. Ayrıca, her çalışmanın en iyi birkaç denemesini bulmayı ve bunların kayıp eğrilerini incelemeyi mümkün olduğunca kolaylaştırmanızı öneririz.

Başka birçok faydalı olası grafik ve görselleştirme ekleyebilirsiniz. Geoffrey Hinton'ı farklı kelimelerle ifade etmek gerekirse:

Her yeni grafikte yeni bir şey öğrenirsiniz.

Aday değişikliğini kabul edip etmeyeceğinize karar verme

Özet: Modelimizde veya eğitim prosedürümüzde değişiklik yapıp yapmayacağımıza ya da yeni bir hiperparametre yapılandırması kullanıp kullanmayacağımıza karar verirken sonuçlarınızdaki farklı varyasyon kaynaklarını göz önünde bulundurun.

Bir modeli iyileştirmeye çalışırken belirli bir aday değişiklik, başlangıçta mevcut yapılandırmaya kıyasla daha iyi bir doğrulama hatası elde edebilir. Ancak denemenin tekrarlanması, tutarlı bir avantaj olmadığını gösterebilir. En önemli tutarsız sonuç kaynakları, aşağıdaki geniş kategorilerde gruplandırılabilir:

• Eğitim prosedürü varyansı, yeniden eğitme varyansı veya deneme varyansı: Aynı hiperparametreleri ancak farklı rastgele başlangıç değerlerini kullanan eğitim çalıştırmaları arasındaki varyasyon. Örneğin, farklı rastgele başlatmalar, eğitim verilerinin karıştırılması, bırakma maskeleri, veri artırma işlemlerinin kalıpları ve paralel aritmetik işlemlerin sıralamaları, deneme varyansının olası kaynaklarıdır.
• Hiperparametre arama varyansı veya çalışma varyansı: Hiperparametreleri seçme prosedürümüzün neden olduğu sonuçlardaki varyasyon. Örneğin, belirli bir arama alanı ile aynı denemeyi yapabilir ancak yarı rastgele arama için iki farklı başlangıç değeri kullanabilir ve farklı hiperparametre değerleri seçebilirsiniz.
• Veri toplama ve örnekleme varyansı: Eğitim, doğrulama ve test verileri için rastgele bölme işleminden kaynaklanan varyans veya daha genel olarak eğitim verisi oluşturma sürecinden kaynaklanan varyans.

Evet, titiz istatistiksel testler kullanarak sonlu bir doğrulama kümesinde tahmin edilen doğrulama hata oranlarını karşılaştırabilirsiniz. Ancak genellikle deneme varyansı tek başına, aynı hiperparametre ayarlarını kullanan iki farklı eğitilmiş model arasında istatistiksel olarak anlamlı farklar oluşturabilir.

Hiperparametreler alanındaki tek bir noktanın ötesine geçen sonuçlar çıkarmaya çalışırken en çok çalışma varyansı konusunda endişeleniriz. Çalışma varyansı, deneme sayısına ve arama alanına bağlıdır. Çalışma varyansının deneme varyansından daha büyük olduğu ve çok daha küçük olduğu durumlarla karşılaştık. Bu nedenle, aday değişikliği yapmadan önce denemeler arası varyansı karakterize etmek için en iyi denemeyi N kez çalıştırmayı düşünebilirsiniz. Genellikle, işlem hattında büyük değişiklikler yapıldıktan sonra deneme varyansını yeniden karakterize etmeniz yeterli olur ancak bazı durumlarda daha yeni tahminlere ihtiyacınız olabilir. Diğer uygulamalarda, deneme varyansını karakterize etmek, değmeyecek kadar maliyetlidir.

Yalnızca gerçek iyileşmeler sağlayan değişiklikleri (yeni hiperparametre yapılandırmaları dahil) benimsemek isteseniz de belirli bir değişikliğin yardımcı olacağı konusunda tam kesinlik talep etmek de doğru bir yaklaşım değildir. Bu nedenle, yeni bir hiperparametre noktası (veya başka bir değişiklik) temelden daha iyi bir sonuç elde ederse (hem yeni noktanın hem de temelin yeniden eğitme varyansını olabildiğince dikkate alarak) gelecekteki karşılaştırmalar için yeni temel olarak benimsemeniz gerekir. Ancak yalnızca ekledikleri karmaşıklığı aşan iyileştirmeler sağlayan değişiklikleri uygulamanızı öneririz.

Keşif sona erdikten sonra

Özet: İyi arama alanları aramayı bitirip hangi hiperparametrelerin ayarlanmaya değer olduğuna karar verdikten sonra Bayes optimizasyonu araçları ilgi çekici bir seçenek olabilir.

Sonunda, öncelikleriniz ayarlama sorunu hakkında daha fazla bilgi edinmekten, başlatmak veya başka bir şekilde kullanmak için tek bir en iyi yapılandırma oluşturmaya kayacak. Bu noktada, en iyi gözlemlenen deneme etrafındaki yerel bölgeyi rahatça içeren ve yeterince örneklenmiş, hassas bir arama alanı olmalıdır. Keşif çalışmanız, ayarlanacak en önemli hiperparametreleri ve mümkün olduğunca büyük bir ayarlama bütçesi kullanarak nihai bir otomatik ayarlama çalışması için arama alanı oluşturmak üzere kullanabileceğiniz makul aralıklarını ortaya çıkarmış olmalıdır.

Artık ayarlama sorunuyla ilgili analizleri en üst düzeye çıkarmakla ilgilenmediğiniz için yarı rastgele aramanın birçok avantajı geçerliliğini yitirir. Bu nedenle, en iyi hiperparametre yapılandırmasını otomatik olarak bulmak için Bayes optimizasyon araçlarını kullanmanız gerekir. Open-Source Vizier, Bayes optimizasyonu algoritmaları da dahil olmak üzere makine öğrenimi modellerini ayarlamaya yönelik çeşitli gelişmiş algoritmalar uygular.

Arama alanının, farklı noktalardan oluşan önemli bir hacme sahip olduğunu varsayalım. Bu noktalar, NaN eğitim kaybına veya ortalamadan çok daha kötü bir eğitim kaybına neden olur. Bu durumda, farklılaşan denemeleri uygun şekilde işleyen kara kutu optimizasyon araçlarını kullanmanızı öneririz. (Bu sorunla başa çıkmanın mükemmel bir yolu için Bilinmeyen Kısıtlamalarla Bayesian Optimizasyonu başlıklı makaleyi inceleyin.) Açık kaynaklı Vizier, denemeleri uygunsuz olarak işaretleyerek farklı noktaları işaretlemeyi destekler.Ancak yapılandırmasına bağlı olarak Gelbart ve diğerlerinin tercih ettiği yaklaşımı kullanmayabilir.

Keşif sona erdikten sonra test kümesindeki performansı kontrol etmeyi düşünebilirsiniz. Prensip olarak, doğrulama kümesini eğitim kümesine dahil edebilir ve Bayes optimizasyonu ile bulunan en iyi yapılandırmayı yeniden eğitebilirsiniz. Ancak bu yalnızca söz konusu iş yüküyle gelecekte lansman yapılmayacaksa (ör. tek seferlik bir Kaggle yarışması) uygundur.