Научный подход к улучшению производительности модели

Для целей настоящего документа:

Конечная цель разработки машинного обучения — максимизировать полезность развернутой модели.

Обычно вы можете использовать одни и те же основные шаги и принципы, описанные в этом разделе, для решения любой проблемы машинного обучения.

В этом разделе сделаны следующие предположения:

• У вас уже есть полностью работающий конвейер обучения и конфигурация, которая дает приемлемый результат.
• У вас достаточно вычислительных ресурсов, чтобы проводить содержательные эксперименты по настройке и параллельно запускать как минимум несколько обучающих заданий.

Стратегия постепенной настройки

Рекомендация: начните с простой конфигурации. Затем постепенно вносите улучшения, углубляя понимание проблемы. Убедитесь, что любое улучшение основано на убедительных доказательствах.

Мы предполагаем, что ваша цель — найти конфигурацию, которая максимизирует производительность вашей модели. Иногда ваша цель — максимально улучшить модель к установленному сроку. В других случаях вы можете совершенствовать модель бесконечно; например, постоянное улучшение модели, используемой в производстве.

В принципе, можно максимизировать производительность, используя алгоритм автоматического поиска во всем пространстве возможных конфигураций, но это непрактичный вариант. Пространство возможных конфигураций чрезвычайно велико, и пока не существует достаточно сложных алгоритмов, позволяющих эффективно исследовать это пространство без участия человека. Большинство алгоритмов автоматического поиска полагаются на созданное вручную пространство поиска, определяющее набор конфигураций для поиска, и эти пространства поиска могут иметь немалое значение.

Самый эффективный способ максимизировать производительность — начать с простой конфигурации и постепенно добавлять функции и улучшения, одновременно углубляя понимание проблемы.

Мы рекомендуем использовать алгоритмы автоматического поиска на каждом этапе настройки и постоянно обновлять области поиска по мере роста вашего понимания. По мере исследования вы, естественно, будете находить все лучшие и лучшие конфигурации, и поэтому ваша «лучшая» модель будет постоянно улучшаться.

Термин «запуск» относится к обновлению нашей лучшей конфигурации (которая может соответствовать или не соответствовать фактическому запуску серийной модели). Для каждого «запуска» вы должны убедиться, что изменение основано на убедительных доказательствах, а не просто на случайной случайности, основанной на удачной конфигурации, — чтобы не добавлять ненужной сложности в конвейер обучения.

На высоком уровне наша стратегия постепенной настройки включает в себя повторение следующих четырех шагов:

1. Выберите цель для следующего раунда экспериментов. Убедитесь, что цель имеет соответствующую область действия.
2. Разработайте следующий раунд экспериментов. Разработайте и проведите серию экспериментов, ведущих к этой цели.
3. Учитесь на результатах экспериментов. Оцените эксперимент по контрольному списку.
4. Определите, следует ли принимать изменение кандидата.

Оставшаяся часть этого раздела подробно описывает эту стратегию.

Выберите цель для следующего раунда экспериментов.

Если вы попытаетесь добавить несколько функций или ответить на несколько вопросов одновременно, возможно, вам не удастся различить влияние отдельных факторов на результаты. Примеры целей включают в себя:

• Попробуйте потенциальное улучшение конвейера (например, новый регуляризатор, выбор предварительной обработки и т. д.).
• Понять влияние конкретного гиперпараметра модели (например, функции активации).
• Минимизируйте ошибку проверки.

Отдавайте приоритет долгосрочному прогрессу над краткосрочными улучшениями ошибок валидации.

Резюме: В большинстве случаев ваша основная цель — разобраться в проблеме настройки.

Мы рекомендуем тратить большую часть времени на понимание проблемы и сравнительно немного времени на то, чтобы максимально повысить производительность проверочного набора. Другими словами, тратьте большую часть своего времени на «исследование» и лишь небольшую часть на «эксплуатацию». Понимание проблемы имеет решающее значение для максимизации конечной производительности. Приоритизация понимания, а не краткосрочных выгод помогает:

• Избегайте запуска ненужных изменений, которые присутствовали в хорошо работающих запусках просто по исторической случайности.
• Определите, к каким гиперпараметрам ошибка проверки наиболее чувствительна, какие гиперпараметры взаимодействуют больше всего и, следовательно, их необходимо перенастраивать вместе, а также какие гиперпараметры относительно нечувствительны к другим изменениям и, следовательно, могут быть исправлены в будущих экспериментах.
• Предложите потенциальные новые функции, которые стоит попробовать, например новые регуляризаторы, если переобучение является проблемой.
• Определите функции, которые не помогают и, следовательно, могут быть удалены, что снижает сложность будущих экспериментов.
• Определите, когда улучшения от настройки гиперпараметров, вероятно, насыщаются.
• Сузьте пространство поиска вокруг оптимального значения, чтобы повысить эффективность настройки.

Со временем вы поймете проблему. Затем вы можете сосредоточиться исключительно на ошибке проверки, даже если эксперименты не максимально информативны о структуре задачи настройки.

Разработайте следующий раунд экспериментов

Резюме: Определите, какие гиперпараметры являются научными, мешающими и фиксированными для экспериментальной цели. Создайте последовательность исследований для сравнения различных значений научных гиперпараметров, оптимизируя при этом неприятные гиперпараметры. Выберите пространство поиска неприятных гиперпараметров, чтобы сбалансировать затраты на ресурсы с научной ценностью.

Определить научные, неприятные и фиксированные гиперпараметры

Для данной цели все гиперпараметры попадают в одну из следующих категорий:

• научные гиперпараметры — это те, влияние которых на производительность модели вы пытаетесь измерить.
• Неудобные гиперпараметры — это те, которые необходимо оптимизировать, чтобы справедливо сравнивать различные значения научных гиперпараметров. Гиперпараметры помех аналогичны параметрам помех в статистике.
• фиксированные гиперпараметры имеют постоянные значения в текущем раунде экспериментов. Значения фиксированных гиперпараметров не должны меняться при сравнении различных значений научных гиперпараметров. Фиксируя определенные гиперпараметры для набора экспериментов, вы должны признать, что выводы, полученные в результате экспериментов, могут быть недействительны для других настроек фиксированных гиперпараметров. Другими словами, фиксированные гиперпараметры создают оговорки для любых выводов, которые вы делаете из экспериментов.

Например, предположим, что ваша цель следующая:

Определите, имеет ли модель с большим количеством скрытых слоев меньшую ошибку проверки.

В этом случае:

• Скорость обучения — это неприятный гиперпараметр, поскольку справедливо сравнивать модели с разным количеством скрытых слоев можно только в том случае, если скорость обучения настраивается отдельно для каждого количества скрытых слоев. (Оптимальная скорость обучения обычно зависит от архитектуры модели).
• Функция активации может быть фиксированным гиперпараметром, если в предыдущих экспериментах вы определили, что лучшая функция активации не чувствительна к глубине модели. Или вы готовы ограничить свои выводы о количестве скрытых слоев для покрытия этой функции активации. Альтернативно, это может быть неприятным гиперпараметром, если вы готовы настраивать его отдельно для каждого количества скрытых слоев.

Конкретный гиперпараметр может быть научным гиперпараметром, неприятным гиперпараметром или фиксированным гиперпараметром; обозначение гиперпараметра меняется в зависимости от цели эксперимента. Например, функция активации может быть любой из следующих:

• Научный гиперпараметр: ReLU или tanh лучше подходят для решения нашей проблемы?
• Неприятный гиперпараметр: лучше ли лучшая пятислойная модель, чем лучшая шестислойная модель, если вы допускаете несколько различных возможных функций активации?
• Фиксированный гиперпараметр: для сетей ReLU помогает ли добавление пакетной нормализации в определенной позиции?

При планировании нового раунда экспериментов:

1. Определите научные гиперпараметры для экспериментальной цели. (На этом этапе вы можете считать все остальные гиперпараметры неприятными гиперпараметрами.)
2. Преобразуйте некоторые неприятные гиперпараметры в фиксированные гиперпараметры.

Имея безграничные ресурсы, вы бы оставили все ненаучные гиперпараметры как ненужные гиперпараметры, чтобы выводы, которые вы сделаете из своих экспериментов, были свободны от предостережений относительно фиксированных значений гиперпараметров. Однако чем больше неприятных гиперпараметров вы пытаетесь настроить, тем выше риск того, что вам не удастся настроить их достаточно хорошо для каждого параметра научных гиперпараметров и в конечном итоге вы придете к неверным выводам из своих экспериментов. Как описано в следующем разделе , вы можете противостоять этому риску, увеличив вычислительный бюджет. Однако ваш максимальный бюджет ресурсов зачастую меньше, чем потребуется для настройки всех ненаучных гиперпараметров.

Мы рекомендуем преобразовать нежелательный гиперпараметр в фиксированный гиперпараметр, если предостережения, вносимые при его исправлении, менее обременительны, чем затраты на его включение в качестве нежелательного гиперпараметра. Чем больше неприятный гиперпараметр взаимодействует с научными гиперпараметрами, тем сложнее зафиксировать его значение. Например, наилучшее значение силы снижения веса обычно зависит от размера модели, поэтому сравнение моделей разных размеров, предполагающее одно конкретное значение снижения веса, не будет очень информативным.

Некоторые параметры оптимизатора

Как правило, некоторые гиперпараметры оптимизатора (например, скорость обучения, импульс, параметры графика скорости обучения, бета-версии Адама и т. д.) являются неприятными гиперпараметрами, поскольку они имеют тенденцию больше всего взаимодействовать с другими изменениями. Эти гиперпараметры оптимизатора редко являются научными гиперпараметрами, поскольку такая цель, как «какова наилучшая скорость обучения для текущего конвейера?» не дает большого понимания. В конце концов, лучшие настройки в любом случае могут измениться при следующем изменении конвейера.

Вы можете время от времени исправлять некоторые гиперпараметры оптимизатора из-за ограничений ресурсов или из-за особенно убедительных доказательств того, что они не взаимодействуют с научными параметрами. Однако обычно следует предполагать, что гиперпараметры оптимизатора необходимо настраивать отдельно, чтобы обеспечить справедливое сравнение между различными настройками научных гиперпараметров, и поэтому их не следует исправлять. Более того, нет априорной причины предпочитать одно значение гиперпараметра оптимизатора другому; например, значения гиперпараметров оптимизатора обычно никак не влияют на вычислительные затраты прямых проходов или градиентов.

Выбор оптимизатора

Выбор оптимизатора обычно бывает следующим:

• научный гиперпараметр
• фиксированный гиперпараметр

Оптимизатор — это научный гиперпараметр, если ваша экспериментальная цель предполагает проведение объективных сравнений между двумя или более разными оптимизаторами. Например:

Определите, какой оптимизатор выдает наименьшую ошибку проверки за заданное количество шагов.

В качестве альтернативы вы можете сделать оптимизатор фиксированным гиперпараметром по ряду причин, в том числе:

• Предыдущие эксперименты показывают, что лучший оптимизатор для вашей задачи настройки не чувствителен к текущим научным гиперпараметрам.
• Вы предпочитаете сравнивать значения научных гиперпараметров с помощью этого оптимизатора, поскольку его кривые обучения легче анализировать.
• Вы предпочитаете использовать этот оптимизатор, поскольку он использует меньше памяти, чем альтернативы.

Гиперпараметры регуляризации

Гиперпараметры, введенные с помощью метода регуляризации, обычно являются неприятными гиперпараметрами. Однако выбор того, включать ли вообще технику регуляризации, является либо научным, либо фиксированным гиперпараметром.

Например, регуляризация отсева усложняет код. Поэтому, решая, включать ли регуляризацию отсева, вы можете сделать «отсутствие отсева» или «отсев» научным гиперпараметром, а уровень отсева — неприятным гиперпараметром. Если вы решите добавить в конвейер регуляризацию отсева на основе этого эксперимента, то частота отсева станет неприятным гиперпараметром в будущих экспериментах.

Архитектурные гиперпараметры

Архитектурные гиперпараметры часто являются научными или фиксированными гиперпараметрами, поскольку изменения архитектуры могут повлиять на затраты на обслуживание и обучение, задержку и требования к памяти. Например, количество слоев обычно является научным или фиксированным гиперпараметром, поскольку оно имеет тенденцию иметь драматические последствия для скорости обучения и использования памяти.

Зависимости от научных гиперпараметров

В некоторых случаях наборы мешающих и фиксированных гиперпараметров зависят от значений научных гиперпараметров. Например, предположим, что вы пытаетесь определить, какой оптимизатор в импульсе Нестерова и Адаме выдает наименьшую ошибку проверки. В этом случае:

• Научный гиперпараметр — оптимизатор, принимающий значения {"Nesterov_momentum", "Adam"}
• optimizer="Nesterov_momentum" вводит гиперпараметры {learning_rate, momentum} , которые могут быть либо неудобными, либо фиксированными гиперпараметрами.
• optimizer="Adam" вводит гиперпараметры {learning_rate, beta1, beta2, epsilon} , которые могут быть либо неудобными, либо фиксированными гиперпараметрами.

Гиперпараметры, которые присутствуют только для определенных значений научных гиперпараметров, называются условными гиперпараметрами . Не думайте, что два условных гиперпараметра одинаковы только потому, что у них одинаковое имя! В предыдущем примере условный гиперпараметр learning_rate является другим гиперпараметром optimizer="Nesterov_momentum" и optimizer="Adam" . Его роль схожа (хотя и не идентична) в обоих алгоритмах, но диапазон значений, которые хорошо работают в каждом из оптимизаторов, обычно различается на несколько порядков.

Создайте набор исследований

После определения научных и неприятных гиперпараметров вам следует разработать исследование или последовательность исследований, чтобы добиться прогресса в достижении экспериментальной цели. Исследование определяет набор конфигураций гиперпараметров, которые необходимо запустить для последующего анализа. Каждая конфигурация называется пробной . Создание исследования обычно включает в себя выбор следующего:

• Гиперпараметры, которые различаются в разных испытаниях.
• Значения, которые могут принимать эти гиперпараметры ( пространство поиска ).
• Количество испытаний.
• Алгоритм автоматического поиска для выборки такого количества испытаний из пространства поиска.

Альтернативно вы можете создать исследование, указав набор конфигураций гиперпараметров вручную.

Целью исследований является одновременное:

• Запустите конвейер с разными значениями научных гиперпараметров.
• «Оптимизация» (или «оптимизация») нежелательных гиперпараметров, чтобы сравнение между различными значениями научных гиперпараметров было максимально справедливым.

В простейшем случае вы должны провести отдельное исследование для каждой конфигурации научных параметров, где каждое исследование учитывает неприятные гиперпараметры. Например, если ваша цель — выбрать лучшего оптимизатора из Импульса Нестерова и Адама, вы можете провести два исследования:

• Одно исследование, в котором optimizer="Nesterov_momentum" и неприятные гиперпараметры равны {learning_rate, momentum}
• Еще одно исследование, в котором optimizer="Adam" и неприятные гиперпараметры — это {learning_rate, beta1, beta2, epsilon} .

Вы сравните два оптимизатора, выбрав наиболее эффективное испытание из каждого исследования.

Вы можете использовать любой алгоритм безградиентной оптимизации, включая такие методы, как байесовская оптимизация или эволюционные алгоритмы, для оптимизации неприятных гиперпараметров. Однако мы предпочитаем использовать квазислучайный поиск на этапе настройки из-за множества преимуществ, которые он имеет в этой настройке. После завершения исследования мы рекомендуем использовать современное программное обеспечение для байесовской оптимизации (если оно доступно).

Рассмотрим более сложный случай, когда вы хотите сравнить большое количество значений научных гиперпараметров, но проводить такое количество независимых исследований нецелесообразно. В этом случае вы можете сделать следующее:

• Включите научные параметры в то же пространство поиска, что и неприятные гиперпараметры.
• Используйте алгоритм поиска для выборки значений как научных, так и неприятных гиперпараметров в одном исследовании.

При таком подходе условные гиперпараметры могут вызвать проблемы. В конце концов, трудно указать пространство поиска, если набор мешающих гиперпараметров не одинаков для всех значений научных гиперпараметров. В этом случае наше предпочтение использованию квазислучайного поиска перед более сложными инструментами оптимизации «черного ящика» еще сильнее, поскольку это гарантирует, что различные значения научных гиперпараметров будут выбраны равномерно. Независимо от алгоритма поиска убедитесь, что он ищет научные параметры равномерно.

Найдите баланс между информативными и доступными экспериментами.

При планировании исследования или последовательности исследований выделите ограниченный бюджет для адекватного достижения следующих трех целей:

• Сравнение достаточно разных значений научных гиперпараметров.
• Настройка мешающих гиперпараметров в достаточно большом пространстве поиска.
• Достаточно плотная выборка пространства поиска неприятных гиперпараметров.

Чем лучше вы сможете достичь этих трех целей, тем больше информации вы сможете извлечь из эксперимента. Сравнение как можно большего количества значений научных гиперпараметров расширяет объем знаний, которые вы получаете в результате эксперимента.

Включение как можно большего количества неприятных гиперпараметров и разрешение каждому неприятным гиперпараметрам варьироваться в максимально широком диапазоне повышает уверенность в том, что «хорошее» значение неприятных гиперпараметров существует в пространстве поиска для каждой конфигурации научных гиперпараметров. В противном случае вы можете провести несправедливые сравнения между значениями научных гиперпараметров, не выполнив поиск возможных областей пространства неприятных гиперпараметров, где могут находиться лучшие значения для некоторых значений научных параметров.

Выбирайте пространство поиска неприятных гиперпараметров как можно плотнее. Это повысит уверенность в том, что процедура поиска найдет хорошие настройки для неприятных гиперпараметров, которые могут существовать в вашем пространстве поиска. В противном случае вы можете провести несправедливые сравнения между значениями научных параметров из-за того, что некоторым значениям окажется больше удачи при выборке неприятных гиперпараметров.

К сожалению, улучшения в любом из этих трех измерений требуют одного из следующих действий:

• Увеличение количества испытаний и, следовательно, увеличение стоимости ресурсов.
• Найдите способ сэкономить ресурсы в одном из других измерений.

У каждой проблемы есть свои особенности и вычислительные ограничения, поэтому распределение ресурсов по этим трем целям требует определенного уровня знаний предметной области. После проведения исследования всегда старайтесь понять, достаточно ли хорошо в исследовании были настроены неприятные гиперпараметры. То есть исследование охватывало достаточно большое пространство, чтобы справедливо сравнить научные гиперпараметры (как более подробно описано в следующем разделе).

Учитесь на результатах экспериментов

Рекомендация: Помимо попыток достичь исходной научной цели каждой группы экспериментов, пройдите контрольный список дополнительных вопросов. Если вы обнаружите проблемы, пересмотрите и повторите эксперименты.

В конечном итоге каждая группа экспериментов преследует конкретную цель. Вам следует оценить доказательства, которые эксперименты предоставляют для достижения этой цели. Однако, если вы зададите правильные вопросы, вы часто сможете найти проблемы, которые нужно исправить, прежде чем данный набор экспериментов сможет достичь своей первоначальной цели. Если вы не задаетесь этими вопросами, вы можете сделать неправильные выводы.

Поскольку проведение экспериментов может оказаться дорогостоящим, вам также следует извлечь из каждой группы экспериментов другие полезные сведения, даже если эти сведения не имеют непосредственного отношения к текущей цели.

Прежде чем анализировать данную серию экспериментов, чтобы добиться прогресса в достижении первоначальной цели, задайте себе следующие дополнительные вопросы:

• Достаточно ли велико пространство поиска? Если оптимальная точка исследования находится вблизи границы пространства поиска в одном или нескольких измерениях, поиск, вероятно, недостаточно широк. В этом случае запустите другое исследование с расширенным пространством поиска.
• Вы выбрали достаточно точек из пространства поиска? Если нет, наберите больше очков или будьте менее амбициозны в целях настройки.
• Какая часть испытаний в каждом исследовании невозможна? То есть какие испытания расходятся, получают очень плохие значения потерь или вообще не выполняются, потому что нарушают какое-то неявное ограничение? Если очень большая часть точек в исследовании невозможна, отрегулируйте пространство поиска, чтобы избежать выборки таких точек, что иногда требует перепараметризации пространства поиска. В некоторых случаях большое количество недопустимых точек может указывать на ошибку в обучающем коде.
• Есть ли у модели проблемы с оптимизацией?
• Чему вы можете научиться из тренировочных кривых лучших испытаний? Например, имеют ли лучшие испытания кривые обучения, соответствующие проблемам переобучения?

При необходимости на основе ответов на предыдущие вопросы уточните самое последнее исследование или группу исследований, чтобы улучшить пространство поиска и/или выбрать больше исследований, или предпримите какие-либо другие корректирующие действия.

Ответив на предыдущие вопросы, вы сможете оценить доказательства, которые эксперименты предоставляют для достижения вашей первоначальной цели; например, оценка того, полезно ли изменение .

Определите плохие границы пространства поиска

Пространство поиска считается подозрительным, если лучшая точка, выбранная из него, находится близко к его границе. Возможно, вы найдете еще лучшую точку, если расширите диапазон поиска в этом направлении.

Чтобы проверить границы пространства поиска, мы рекомендуем отображать завершенные испытания на так называемых базовых графиках оси гиперпараметров . В них мы строим график целевого значения проверки в зависимости от одного из гиперпараметров (например, скорости обучения). Каждая точка на графике соответствует одному испытанию.

Целевое значение валидации для каждого испытания обычно должно быть лучшим значением, достигнутым в ходе обучения.

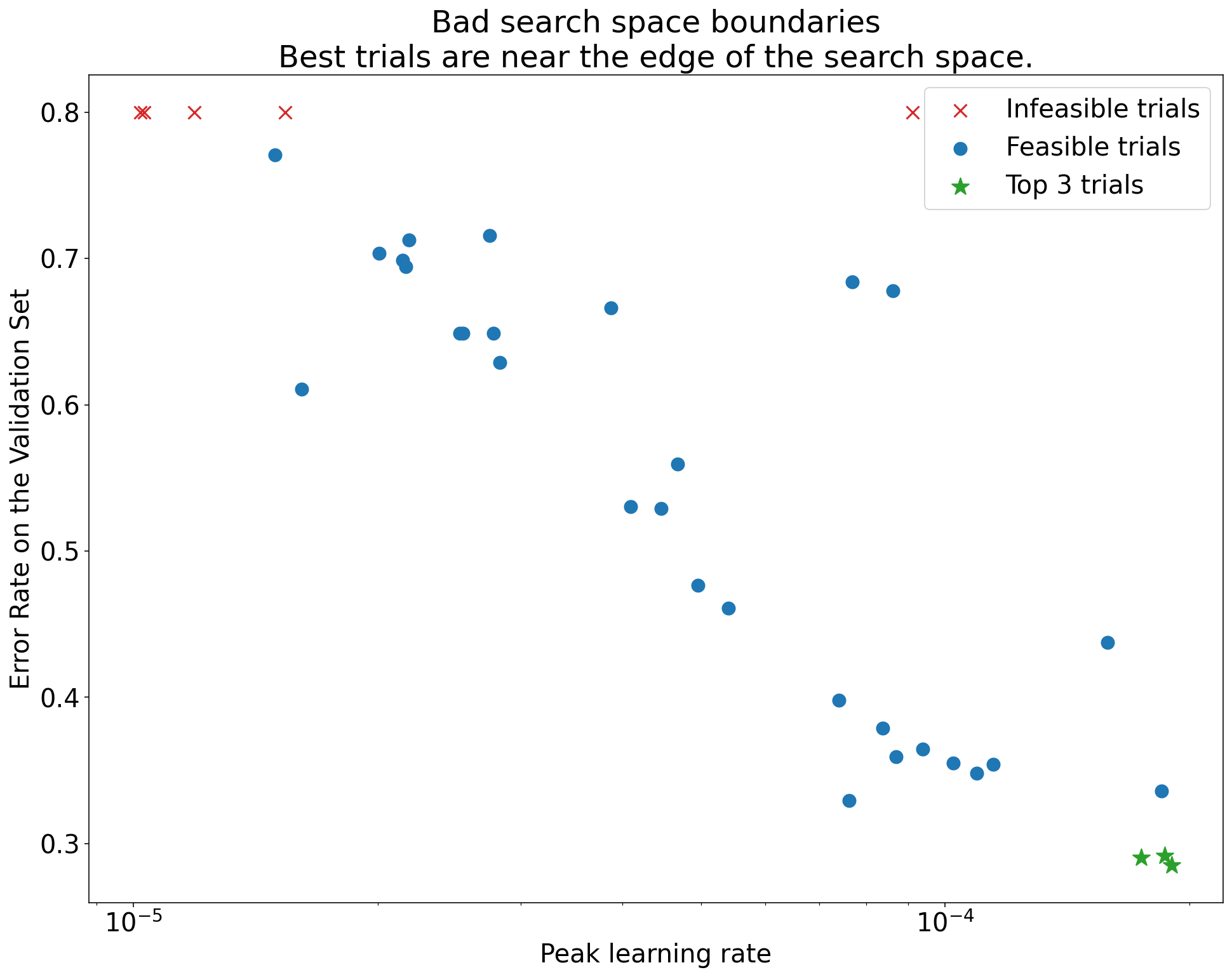
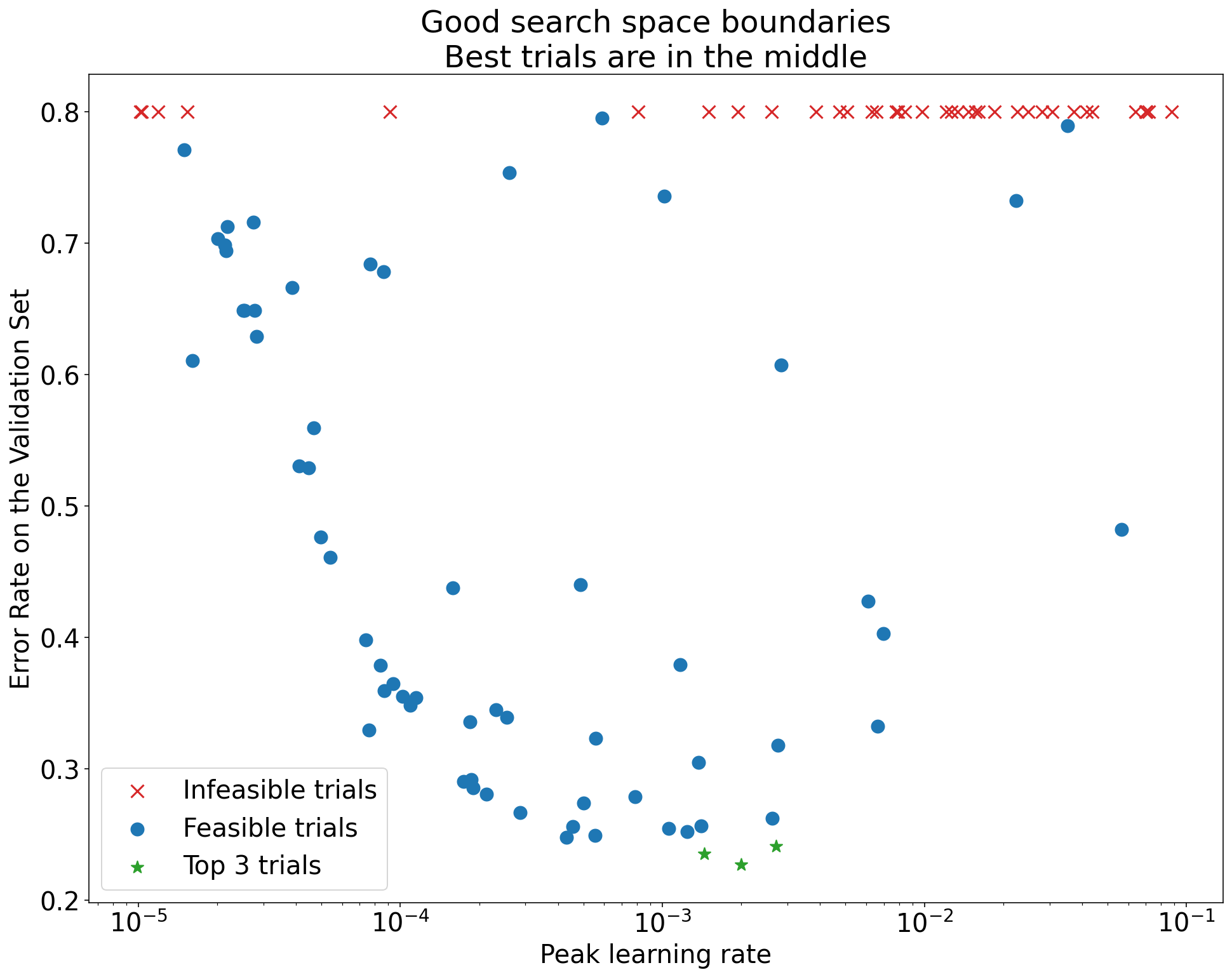
Рисунок 1: Примеры плохих и приемлемых границ пространства поиска.

Графики на рисунке 1 показывают частоту ошибок (чем меньше, тем лучше) в зависимости от начальной скорости обучения. Если лучшие точки группируются ближе к краю пространства поиска (в некотором измерении), вам может потребоваться расширить границы пространства поиска до тех пор, пока лучшая наблюдаемая точка не перестанет находиться близко к границе.

Часто исследование включает в себя «неосуществимые» испытания, которые расходятся во мнениях или дают очень плохие результаты (отмечены красным крестиком на рисунке 1). Если все испытания невозможны для скорости обучения, превышающей некоторое пороговое значение, и если наиболее эффективные испытания имеют скорость обучения на границе этого региона, модель может страдать от проблем со стабильностью, не позволяющих ей получить доступ к более высоким скоростям обучения .

Недостаточно выборки достаточного количества точек в пространстве поиска.

В общем, может быть очень сложно определить, достаточно ли плотно выбрано пространство поиска. 🤖 Проведение большего количества испытаний лучше, чем меньшее количество испытаний, но большее количество испытаний приводит к очевидным дополнительным затратам.

Поскольку очень сложно определить, достаточно ли вы отобрали проб, мы рекомендуем:

• Выборка того, что вы можете себе позволить.
• Калибровка вашей интуитивной уверенности путем многократного просмотра различных графиков осей гиперпараметров и попыток понять, сколько точек находится в «хорошей» области пространства поиска.

Изучите кривые обучения

Резюме: Изучение кривых потерь — это простой способ определить распространенные виды сбоев и помочь вам определить приоритетность возможных следующих действий.

Во многих случаях основная цель ваших экспериментов требует только рассмотрения ошибки валидации каждого испытания. Однако будьте осторожны, сводя каждое испытание к одному числу, поскольку такой фокус может скрыть важные детали того, что происходит под поверхностью. Для каждого исследования мы настоятельно рекомендуем смотреть кривые потерь хотя бы в нескольких лучших исследованиях. Даже если в этом нет необходимости для решения основной экспериментальной задачи, изучение кривых потерь (включая потери при обучении и потери при проверке) является хорошим способом определить распространенные режимы сбоя и помочь вам определить приоритетность действий, которые следует предпринять дальше.

При изучении кривых потерь сосредоточьтесь на следующих вопросах:

• Были ли в каких-либо испытаниях выявлены проблемы переобучения? Проблема переобучения возникает, когда ошибка проверки начинает увеличиваться во время обучения. В экспериментальных условиях, когда вы оптимизируете нежелательные гиперпараметры, выбирая «лучшее» испытание для каждого набора научных гиперпараметров, проверьте наличие проблемного переобучения по крайней мере в каждом из лучших испытаний, соответствующих настройкам сравниваемых научных гиперпараметров. Если какое-либо из лучших испытаний демонстрирует проблемное переоснащение, выполните одно или оба из следующих действий:

  • Повторите эксперимент с дополнительными методами регуляризации.
  • Перенастройте существующие параметры регуляризации перед сравнением значений научных гиперпараметров. Это может быть неприменимо, если научные гиперпараметры включают параметры регуляризации, поскольку в этом случае неудивительно, если низкие настройки этих параметров регуляризации приведут к проблемному переоснащению.

  Уменьшить переобучение часто легко, используя общие методы регуляризации, которые добавляют минимальную сложность кода или дополнительные вычисления (например, регуляризация с отсевом, сглаживание меток, затухание веса). Поэтому обычно нетрудно добавить один или несколько из них в следующий раунд экспериментов. Например, если научным гиперпараметром является «количество скрытых слоев», а лучшее испытание, в котором используется наибольшее количество скрытых слоев, демонстрирует проблемное переоснащение, то мы рекомендуем повторить попытку с дополнительной регуляризацией вместо немедленного выбора меньшего количества скрытых слоев.

  Даже если ни одно из «лучших» испытаний не выявило проблем с переоснащением, проблема все равно может возникнуть, если она возникнет в любом из испытаний. Выбор лучшего испытания подавляет конфигурации, демонстрирующие проблемную переобучение, и отдает предпочтение тем, которые этого не делают. Другими словами, выбор лучшего пробного варианта благоприятствует конфигурациям с большей регуляризацией. Однако все, что ухудшает тренировку, может действовать как регуляризатор, даже если это не было задумано. Например, выбор меньшей скорости обучения может упорядочить обучение, затруднив процесс оптимизации, но обычно мы не хотим выбирать скорость обучения таким образом. Обратите внимание, что «лучшее» испытание для каждого набора научных гиперпараметров может быть выбрано таким образом, чтобы отдавать предпочтение «плохим» значениям некоторых научных или неприятных гиперпараметров.

• Существует ли высокая пошаговая дисперсия в обучении или ошибка проверки на поздних этапах обучения? Если это так, это может помешать обоим из следующих действий:

  • Ваша способность сравнивать различные значения научных гиперпараметров. Это потому, что каждое испытание случайным образом заканчивается на «удачном» или «неудачном» шаге.
  • Ваша способность воспроизвести результат лучшего испытания на производстве. Это потому, что производственная модель может не закончиться на том же «счастливом» этапе, как в исследовании.

  Наиболее вероятными причинами ступенчатых отклонений являются:

  • Отклонение партии из-за случайной выборки примеров из обучающего набора для каждой партии.
  • Небольшие наборы проверки
  • Использование слишком высокой скорости обучения на поздних этапах обучения.

  Возможные средства правовой защиты включают в себя:

  • Увеличение размера пакета.
  • Получение дополнительных данных проверки.
  • Использование снижения скорости обучения.
  • Использование усреднения Поляка.

• Улучшаются ли результаты испытаний в конце тренировки? Если да, то вы находитесь в режиме «с привязкой к вычислениям» и можете получить выгоду от увеличения количества этапов обучения или изменения графика скорости обучения.

• Насыщается ли производительность обучающего и проверочного наборов задолго до финального этапа обучения? Если это так, это означает, что вы находитесь в режиме «без привязки к вычислениям» и что вы можете уменьшить количество шагов обучения.

Помимо этого списка, при изучении кривых потерь можно обнаружить множество дополнительных особенностей поведения. Например, увеличение потерь при обучении во время обучения обычно указывает на ошибку в конвейере обучения.

Определение полезности изменения с помощью графиков изоляции

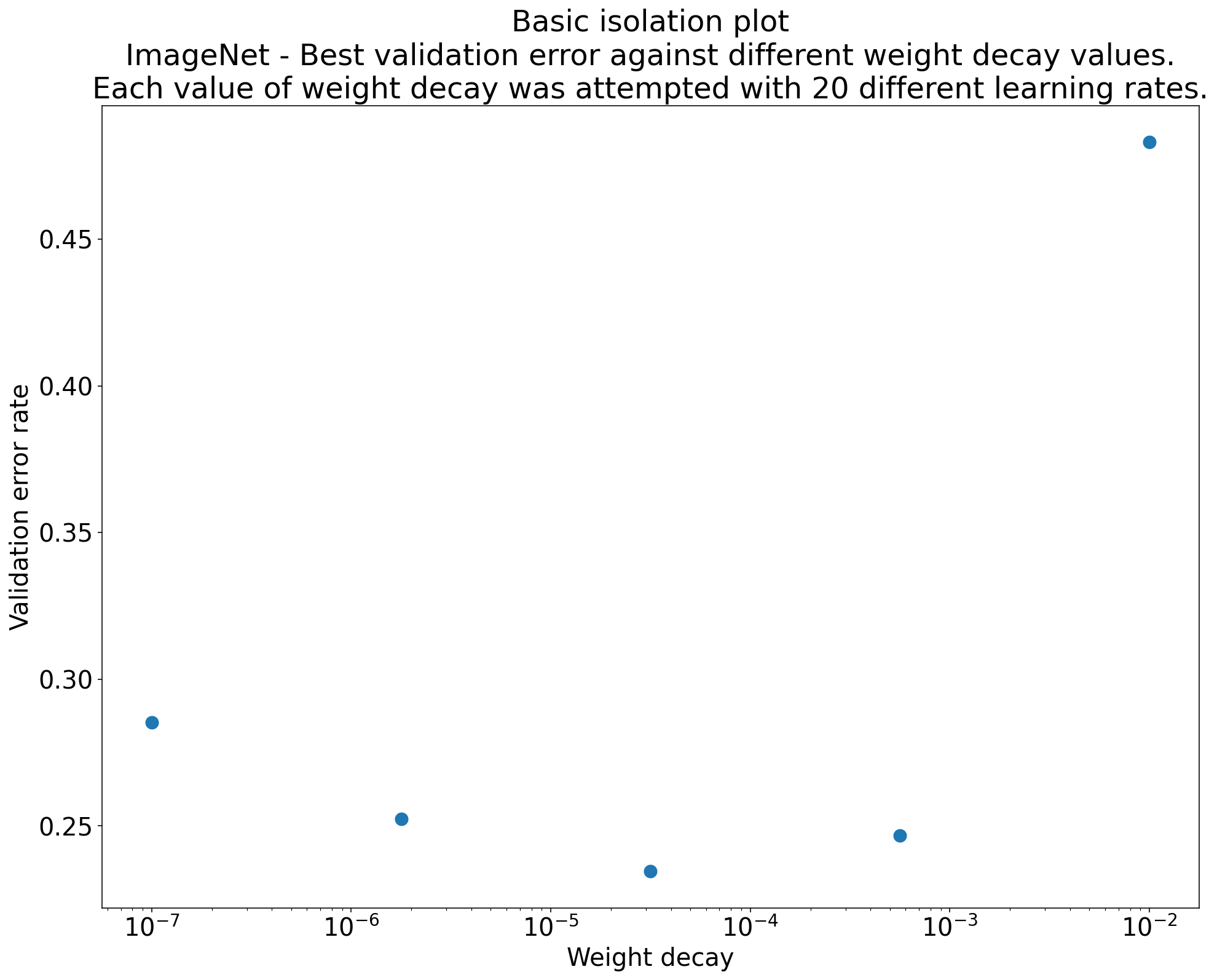
Рисунок 2: Изолирующий график, на котором исследуется наилучшее значение снижения веса для ResNet-50, обученного на ImageNet.

Часто целью серии экспериментов является сравнение различных значений научного гиперпараметра. Например, предположим, что вы хотите определить значение снижения веса, которое приводит к наилучшей ошибке проверки. График изоляции — это частный случай графика основной оси гиперпараметров. Каждая точка на графике изоляции соответствует результатам лучшего испытания по некоторым (или всем) неприятным гиперпараметрам. Другими словами, постройте график производительности модели после «оптимизации» неприятных гиперпараметров.

График изоляции упрощает выполнение сравнения яблок с яблоками между различными значениями научного гиперпараметра. Например, график изоляции на рисунке 2 показывает значение снижения веса, которое обеспечивает наилучшую производительность проверки для конкретной конфигурации ResNet-50, обученной на ImageNet.

Если цель состоит в том, чтобы определить, включать ли вообще снижение веса, то сравните лучшую точку на этом графике с базовой линией отсутствия снижения веса. Для справедливого сравнения базовый уровень также должен иметь одинаково хорошо настроенную скорость обучения.

Если у вас есть данные, сгенерированные в результате (квази)случайного поиска, и вы рассматриваете непрерывный гиперпараметр для графика изоляции, вы можете аппроксимировать график изоляции, группируя значения оси X основного графика оси гиперпараметра и выбирая лучшее испытание в каждом вертикальном срезе. определяется ведрами.

Автоматизируйте общие полезные графики

Чем больше усилий требуется для создания графиков, тем меньше вероятность, что вы будете смотреть на них столько, сколько следует. Поэтому мы рекомендуем настроить вашу инфраструктуру для автоматического создания как можно большего количества участков. Как минимум, мы рекомендуем автоматически создавать основные графики осей гиперпараметров для всех гиперпараметров, которые вы меняете в эксперименте.

Кроме того, мы рекомендуем автоматически создавать кривые потерь для всех испытаний. Кроме того, мы рекомендуем как можно проще найти несколько лучших испытаний каждого исследования и изучить их кривые потерь.

Вы можете добавить много других полезных потенциальных графиков и визуализаций. Перефразируя Джеффри Хинтона :

Каждый раз, когда вы создаете что-то новое, вы узнаёте что-то новое.

Определите, следует ли принять изменение кандидата

Резюме: Принимая решение о внесении изменений в нашу модель или процедуру обучения или о принятии новой конфигурации гиперпараметров, обратите внимание на различные источники изменений в ваших результатах.

При попытке улучшить модель конкретное изменение кандидата может изначально достичь лучшей ошибки проверки по сравнению с действующей конфигурацией. Однако повторение эксперимента не может продемонстрировать постоянное преимущество. Неофициально, наиболее важные источники противоречивых результатов могут быть сгруппированы в следующие широкие категории:

• Дисперсия процедуры обучения, дисперсия переподготовки или дисперсия испытаний : различия между тренировочными прогонами, которые используют одни и те же гиперпараметры, но разные случайные семена. Например, различные случайные инициализации, перетасовки данных обучающих данных, маски для отсева, модели операций по увеличению данных и порядок параллельных арифметических операций являются потенциальными источниками дисперсии испытаний.
• Дисперсия поиска гиперпараметра или дисперсия исследования : изменение результатов, вызванных нашей процедурой для выбора гиперпараметров. Например, вы можете провести один и тот же эксперимент с определенным пространством поиска, но с двумя разными семенами для квази-риндома и в конечном итоге выбирая различные значения гиперпараметрических.
• Сбор данных и дисперсия выборки : дисперсия от любого вида случайного разделения на обучение, валидацию и тестирование данных или дисперсию из -за процесса генерации обучающих данных в целом.

Верно, вы можете сравнить частоту ошибок проверки, оцененные в конечном валидации с использованием привередливых статистических тестов. Однако часто только дисперсия испытания может привести к статистически значимым различиям между двумя различными обученными моделями, которые используют одинаковые настройки гиперпараметра.

Мы больше всего обеспокоены дисперсией обучения при попытке сделать выводы, которые выходят за рамки индивидуальной точки в пространстве гиперпараметров. Разница в исследовании зависит от количества испытаний и пространства поиска. Мы видели случаи, когда дисперсия исследования больше, чем дисперсия испытания и случаи, когда она намного меньше. Поэтому, прежде чем внедрить изменение кандидата, рассмотрите возможность выполнения лучшего испытания и времен для характеристики дисперсии забегающего испытания. Обычно вы можете сойти с рук только с решактеризированием дисперсии испытаний после серьезных изменений в трубопроводе, но в некоторых случаях вам могут понадобиться более свежие оценки. В других приложениях характеристика дисперсии пробной дисперсии слишком дорого, чтобы стоить того.

Хотя вы хотите только внедрить изменения (включая новые конфигурации гиперпараметра), которые дают реальные улучшения, требуя полной уверенности в том, что данное изменение помогает не подходит. Следовательно, если новая точка гиперпараметра (или другое изменение) получает лучший результат, чем базовая линия (с учетом дисперсии переподготовки как новой точки, так и базовой линии как можно лучше), то вам, вероятно, следует принять его как новую Базовая линия для будущих сравнений. Тем не менее, мы рекомендуем внедрить только изменения, которые вызывают улучшения, которые перевешивают любую сложность, которую они добавляют.

После разведки завершается

Резюме: Инструменты байесовской оптимизации являются убедительным вариантом, как только вы закончите поиск хороших поисковых пространств, и решили, какие гиперпараметры стоят настройки.

В конечном итоге ваши приоритеты будут переходить от более подробного изучения проблемы настройки к созданию единственной лучшей конфигурации для запуска или иного использования. В этот момент должно быть утонченное пространство поиска, в котором комфортно содержится локальная область вокруг наиболее наблюдаемого испытания и было адекватно отобрано. Ваша исследовательская работа должна была выявить наиболее важные гиперпараметры для настройки и их разумные диапазоны, которые вы можете использовать для построения пространства поиска для окончательного автоматизированного исследования настройки с использованием как можно более крупного бюджета настройки.

Поскольку вы больше не заботитесь о максимизации понимания проблемы настройки, многие преимущества квази-риндома больше не применяются. Поэтому вам следует использовать инструменты байесовской оптимизации, чтобы автоматически найти лучшую конфигурацию гиперпараметра. Vizier с открытым исходным кодом реализует множество сложных алгоритмов для настройки моделей ML, включая алгоритмы байесовской оптимизации.

Предположим, что пространство поиска содержит нетривиальный объем дивергентных точек , что означает, что точки, которые получают потерю обучения NAN или даже потери обучения, многие стандартные отклонения хуже среднего. В этом случае мы рекомендуем использовать инструменты оптимизации черного ящика, которые правильно обрабатывают испытания, которые расходятся. (См. Байесовская оптимизация с неизвестными ограничениями для отличного способа решения этой проблемы.) Vizier с открытым исходным кодом имеет поддержку для маркировки дивергентных очков, отмечая испытания как невозмутимые, хотя она может не использовать наш предпочтительный подход от Gelbart et al. , в зависимости от того, как это настроено.

После разведка завершается, рассмотрите возможность проверки производительности на наборе тестирования. В принципе, вы можете даже сложить валидацию в обучающий набор и перепродать лучшую конфигурацию, найденную с помощью байесовской оптимизации. Тем не менее, это уместно только в том случае, если с этой конкретной рабочей нагрузкой не будет будущих запусков (например, одноразовая конкуренция Kaggle).

,

Для целей этого документа:

Конечная цель разработки машинного обучения - максимизировать полезность развернутой модели.

Обычно вы можете использовать те же основные шаги и принципы в этом разделе по любой проблеме ML.

Этот раздел делает следующие предположения:

• У вас уже есть полностью работающий тренировочный конвейер, а также конфигурация, которая получает разумный результат.
• У вас достаточно вычислительных ресурсов для проведения значимых экспериментов по настройке и для проведения хотя бы нескольких тренировочных работ параллельно.

Постепенная стратегия настройки

Рекомендация: Начните с простой конфигурации. Затем постепенно улучшайте улучшения, создавая понимание проблемы. Убедитесь, что любое улучшение основано на убедительных доказательствах.

Мы предполагаем, что ваша цель - найти конфигурацию, которая максимизирует производительность вашей модели. Иногда ваша цель - максимизировать улучшение модели за счет фиксированного срока. В других случаях вы можете продолжать улучшать модель на неопределенный срок; Например, постоянно улучшая модель, используемую в производстве.

В принципе, вы можете максимизировать производительность, используя алгоритм для автоматического поиска всего пространства возможных конфигураций, но это не практичный вариант. Пространство возможных конфигураций чрезвычайно большое, и еще нет никаких алгоритмов, достаточно сложных, чтобы эффективно искать в этом пространстве без руководства человека. Большинство автоматизированных алгоритмов поиска полагаются на пространство поиска вручную, которое определяет набор конфигураций для поиска, и эти поисковые пространства могут иметь немало значения.

Наиболее эффективный способ максимизации производительности - начать с простой конфигурации и постепенно добавлять функции и улучшить, создавая понимание проблемы.

Мы рекомендуем использовать автоматизированные алгоритмы поиска в каждом раунде настройки и постоянно обновлять поисковые пространства по мере роста вашего понимания. Как вы исследуете, вы, естественно, найдете лучшие и лучшие конфигурации, и поэтому ваша «лучшая» модель будет постоянно улучшаться.

Термин «запуск» относится к обновлению нашей лучшей конфигурации (которая может или не может соответствовать фактическому запуску производственной модели). Для каждого «запуска» вы должны убедиться, что изменение основано на убедительных доказательствах, а не просто случайной случайности, основанной на счастливой конфигурации, так что вы не добавляете ненужную сложность в тренировочный трубопровод.

На высоком уровне наша стратегия инкрементной настройки включает в себя повторение следующих четырех шагов:

1. Выберите цель для следующего раунда экспериментов. Убедитесь, что цель соответствующим образом охвачена.
2. Проектируйте следующий раунд экспериментов. Проектируйте и выполните набор экспериментов, которые продвигаются к этой цели.
3. Учитесь на экспериментальных результатах. Оценить эксперимент с контрольным списком.
4. Определить, принять ли изменение кандидата.

Остальная часть этого раздела подробно описывает эту стратегию.

Выберите цель для следующего раунда экспериментов

Если вы попытаетесь добавить несколько функций или ответить на несколько вопросов одновременно, вы не сможете распутать отдельные эффекты на результаты. Пример цели включают:

• Попробуйте потенциальное улучшение трубопровода (например, новый регулятор, выбор предварительной обработки и т. Д.).
• Понять влияние конкретного гиперпараметра модели (например, функция активации)
• Минимизировать ошибку проверки.

Распределить приоритет долгосрочного прогресса по сравнению с краткосрочными улучшениями ошибок проверки

Резюме: в большинстве случаев ваша основная цель - получить представление о проблеме настройки.

Мы рекомендуем потратить большую часть вашего времени, чтобы получить представление о проблеме, и сравнительно мало времени, жадно сосредоточенного на максимизации производительности в наборе валидации. Другими словами, проведите большую часть своего времени на «Исследование» и лишь небольшую сумму на «эксплуатация». Понимание проблемы имеет решающее значение для максимизации окончательной производительности. Приоритетное понимание по поводу краткосрочного роста помогает:

• Избегайте запуска ненужных изменений, которые оказались в хорошо эффективных пробегах только в результате исторической аварии.
• Определите, какие гиперпараметры, погрешность проверки наиболее чувствительна, к какому гиперпараметрам взаимодействует больше всего и, следовательно, необходимо перенаправить вместе, и какие гиперпараметры относительно нечувствительны к другим изменениям и, следовательно, могут быть зафиксированы в будущих экспериментах.
• Предложите потенциальные новые функции, чтобы попробовать, такие как новые регулялизации, когда переживание является проблемой.
• Определите особенности, которые не помогают и, следовательно, могут быть удалены, уменьшая сложность будущих экспериментов.
• Признайте, когда улучшения от настройки гиперпараметров, вероятно, насыщены.
• Ужмите наши поисковые пространства вокруг оптимального значения, чтобы повысить эффективность настройки.

В конце концов, вы поймете проблему. Затем вы можете сосредоточиться исключительно на ошибке проверки, даже если эксперименты не максимально информативны о структуре задачи настройки.

Разработать следующий раунд экспериментов

Резюме: Определите, какие гиперпараметры являются научными, неприятностью и фиксированными гиперпараметрами для экспериментальной цели. Создайте последовательность исследований для сравнения различных значений научных гиперпараметров, одновременно оптимизируя недостатки гиперпараметров. Выберите пространство поиска недостатков гиперпараметров, чтобы сбалансировать затраты на ресурсы с научной ценностью.

Определить научные, неприятности и фиксированные гиперпараметры

Для данной цели все гиперпараметры попадают в одну из следующих категорий:

• Научные гиперпараметры - это те, чье влияние на производительность модели - это то, что вы пытаетесь измерить.
• Несузначности гиперпараметры - это те, которые необходимо оптимизировать, чтобы справедливо сравнить различные значения научных гиперпараметров. Гиперпараметры неприятностей аналогичны параметрам неприятностей в статистике.
• Фиксированные гиперпараметры имеют постоянные значения в текущем раунде экспериментов. Значения фиксированных гиперпараметров не должны меняться, когда вы сравниваете различные значения научных гиперпараметров. Исправляя определенные гиперпараметры для набора экспериментов, вы должны признать, что выводы, полученные из экспериментов, могут быть недопустимыми для других настроек фиксированных гиперпараметров. Другими словами, фиксированные гиперпараметры создают предостережения для любых выводов, которые вы делаете из экспериментов.

Например, предположим, что ваша цель заключается в следующем:

Определите, имеет ли модель с более скрытыми уровнями более низкую ошибку проверки.

В этом случае:

• Скорость обучения - это гиперпараметт неприятностей, потому что вы можете справедливо сравнить модели с различным количеством скрытых слоев, если скорость обучения настроена отдельно для каждого количества скрытых слоев. (Оптимальная скорость обучения обычно зависит от модельной архитектуры).
• Функция активации может быть фиксированным гиперпараметром, если вы определили в предыдущих экспериментах, что лучшая функция активации не чувствительна к глубине модели. Или вы готовы ограничить свои выводы о количестве скрытых слоев, чтобы покрыть эту функцию активации. В качестве альтернативы, это может быть гиперпараметром неприятностей, если вы готовы настроить его отдельно для каждого количества скрытых слоев.

Конкретным гиперпараметром может быть научный гиперпараметт, недостаток гиперпараметра или фиксированный гиперпараметр; Обозначение гиперпараметра меняется в зависимости от целей эксперимента. Например, функция активации может быть любым из следующих:

• Scientific Hyperparameter: Relu или Tanh является лучшим выбором для нашей проблемы?
• Nuisers Hyperparameter: лучшая пятислойная модель лучше, чем лучшая шестислойная модель, когда вы разрешаете несколько различных возможных функций активации?
• Фиксированный гиперпараметт: для рецидивов помогает ли добавление нормализации пакетов в определенном положении?

При разработке нового раунда экспериментов:

1. Определите научные гиперпараметры для экспериментальной цели. (На этом этапе вы можете считать, что все другие гиперпараметры являются недостатками гиперпараметров.)
2. Преобразовать некоторые недостатки гиперпараметров в фиксированные гиперпараметры.

Благодаря безграничным ресурсам вы оставили бы все ненаучные гиперпараметры в качестве недовольных гиперпараметров, так что выводы, которые вы делаете из своих экспериментов, свободны от предостережения о фиксированных значениях гиперпараметра. Тем не менее, чем более неприятности гиперпараметры вы пытаетесь настроить, тем больше риск того, что вы не сможете настраивать их достаточно хорошо для каждой обстановки научных гиперпараметра и в конечном итоге достигают неправильных выводов из ваших экспериментов. Как описано в более позднем разделе , вы можете противостоять этому риску, увеличив вычислительный бюджет. Тем не менее, ваш максимальный бюджет ресурсов часто меньше, чем потребовался бы для настройки всех слаженных гиперпараметров.

Мы рекомендуем преобразовать недостаток гиперпараметра в фиксированный гиперпараметр, когда предостережения, представленные путем его исправления, менее обременительны, чем стоимость включения его в качестве гиперпараметра неприятностей. Чем больше вредный гиперпараметр взаимодействует с научными гиперпараметрами, тем более вредно исправить его ценность. Например, наилучшее значение прочности распада веса обычно зависит от размера модели, поэтому сравнение различных размеров модели, предполагая, что одно конкретное значение распада веса не было бы очень проницательным.

Некоторые параметры оптимизатора

Как правило, некоторые гиперпараметры оптимизатора (например, скорость обучения, импульс, параметры графика обучения, бета -версии Адама и т. Д.) - это недостатки гиперпараметров, поскольку они имеют тенденцию взаимодействовать с другими изменениями. Эти гиперпараметры оптимизатора редко являются научными гиперпараметрами, потому что такая цель, как «какой уровень обучения является наилучшим для текущего трубопровода?» не дает много понимания. В конце концов, лучшая настройка может измениться с следующим изменением трубопровода в любом случае.

Вы могли бы иногда исправить некоторые гиперпараметры оптимизатора из -за ограничений ресурсов или особенно убедительных доказательств того, что они не взаимодействуют с научными параметрами. Тем не менее, вы должны, как правило, должны предположить, что вы должны настраивать гиперпараметры оптимизатора отдельно, чтобы провести справедливое сравнение между различными настройками научных гиперпараметров, и, следовательно, не следует фиксировать. Кроме того, не существует априорной причины предпочитать одну оптимизационную ценность гиперпараметра над другим; Например, значения гиперпараметра оптимизатора обычно не влияют на вычислительные затраты на переходные проходы или градиенты.

Выбор оптимизатора

Выбор оптимизатора, как правило, либо:

• Научный гиперпараметр
• фиксированный гиперпараметр

Оптимизатор - это научный гиперпараметр, если ваша экспериментальная цель включает в себя проведение справедливых сравнений между двумя или более различными оптимизаторами. Например:

Определите, какой оптимизатор производит самую низкую ошибку проверки в заданном количестве шагов.

В качестве альтернативы, вы можете сделать оптимизатор фиксированным гиперпараметром по разным причинам, в том числе:

• Предыдущие эксперименты показывают, что лучший оптимизатор для вашей проблемы настройки не чувствителен к современным научным гиперпараметрам.
• Вы предпочитаете сравнивать значения научных гиперпараметров, используя этот оптимизатор, потому что его кривые обучения легче рассуждать.
• Вы предпочитаете использовать этот оптимизатор, потому что он использует меньше памяти, чем альтернативы.

Регуляризация гиперпараметров

Гиперпараметры, представленные методом регуляризации, обычно являются недостижимыми гиперпараметрами. Тем не менее, выбор того, следует ли включать метод регуляризации вообще, является либо научным, либо фиксированным гиперпараметром.

Например, регуляризация отсева добавляет сложность кода. Поэтому при принятии решения о том, следует ли включать регуляризацию отсева, вы можете сделать «без отсевания» против «выпадающего» научного гиперпараметра, но оценивает недостаток гиперпараметра. Если вы решите добавить регуляризацию отсева в трубопровод на основе этого эксперимента, то скорость отсева будет недостатком в будущих экспериментах.

Архитектурные гиперпараметры

Архитектурные гиперпараметры часто являются научными или фиксированными гиперпараметрами, потому что изменения архитектуры могут повлиять на затраты на обслуживание и обучение, задержку и требования к памяти. Например, количество слоев, как правило, является научным или фиксированным гиперпараметром, поскольку он имеет тенденцию иметь существенные последствия для скорости обучения и использования памяти.

Зависимости от научных гиперпараметров

В некоторых случаях наборы неприятностей и фиксированных гиперпараметров зависят от значений научных гиперпараметров. Например, предположим, что вы пытаетесь определить, какой оптимизатор в Nesterov Momentum и Adam производит в самой низкой ошибке проверки. В этом случае:

• Научный гиперпараметр - это оптимизатор, который принимает значения {"Nesterov_momentum", "Adam"}
• Значение optimizer="Nesterov_momentum" вводит гиперпараметры {learning_rate, momentum} , которые могут быть либо неприятностью, либо фиксированными гиперпараметрами.
• Значение optimizer="Adam" вводит гиперпараметры {learning_rate, beta1, beta2, epsilon} , которые могут быть либо неприятностью, либо фиксированными гиперпараметрами.

Гиперпараметры, которые присутствуют только для определенных значений научных гиперпараметров, называются условными гиперпараметрами . Не думайте, что два условных гиперпараметры одинаковы только потому, что они имеют одинаковое имя! В предыдущем примере условный гиперпараметт, называемый learning_rate является другим гиперпараметром для optimizer="Nesterov_momentum" чем для optimizer="Adam" . Его роль похожа (хотя и не идентична) в двух алгоритмах, но диапазон значений, которые хорошо работают в каждом из оптимизаторов, обычно отличается несколькими порядками величины.

Создать набор исследований

После выявления научных и неприятностей гиперпараметров, вы должны разработать исследование или последовательность исследований, чтобы добиться прогресса в достижении экспериментальной цели. В исследовании указывается набор конфигураций гиперпараметрических данных, которые будут выполнены для последующего анализа. Каждая конфигурация называется испытанием . Создание исследования обычно включает в себя выбор следующего:

• Гиперпараметры, которые различаются в разных испытаниях.
• Значения, которые могут взять эти гиперпараметры ( пространство поиска ).
• Количество испытаний.
• Автоматизированный алгоритм поиска, чтобы попробовать столько испытаний из пространства поиска.

В качестве альтернативы, вы можете создать исследование, указав набор конфигураций гиперпараметрических вручную вручную.

Целью исследований является одновременно:

• Запустите конвейер с различными значениями научных гиперпараметров.
• «Оптимизировать» (или «оптимизация над»), гиперпараметры неприятностей, так что сравнение между различными значениями научных гиперпараметров настолько справедливо.

В простейшем случае вы проведете отдельное исследование для каждой конфигурации научных параметров, где каждое исследование настраивает на недостатке гиперпараметров Nuiseance. Например, если ваша цель состоит в том, чтобы выбрать лучший оптимизатор из Nesterov Momentum и Adam, вы можете создать два исследования:

• Одно исследование, в котором optimizer="Nesterov_momentum" и недостатки гиперпараметров - {learning_rate, momentum}
• Другое исследование, в котором optimizer="Adam" и недостижимые гиперпараметры - {learning_rate, beta1, beta2, epsilon} .

Вы бы сравнили два оптимизатора, выбирая наиболее эффективное исследование из каждого исследования.

Вы можете использовать любой алгоритм оптимизации без градиентов, в том числе такие методы, как байесовская оптимизация или эволюционные алгоритмы, для оптимизации недостатков гиперпараметров Nuisers. Тем не менее, мы предпочитаем использовать квази-рэндом поиск на этапе разведки настройки из-за различных преимуществ, которые он имеет в этом настройке. После того, как разведка завершается, мы рекомендуем использовать современное программное обеспечение для оптимизации байесовской оптимизации (если оно доступно).

Рассмотрим более сложный случай, когда вы хотите сравнить большое количество значений научных гиперпараметров, но нецелесообразно провести столько независимых исследований. В этом случае вы можете сделать следующее:

• Включите научные параметры в том же пространстве поиска, что и недостатки гиперпараметров.
• Используйте алгоритм поиска для выборки значений как научных, так и недостаточных гиперпараметров в одном исследовании.

При использовании этого подхода условные гиперпараметры могут вызвать проблемы. В конце концов, трудно указать пространство поиска, если только набор недовольных гиперпараметров одинаковы для всех значений научных гиперпараметров. В этом случае наше предпочтение использования квази-риндома поиска над более любимыми инструментами оптимизации черного ящика еще сильнее, поскольку он гарантирует различные значения научных гиперпараметров, будут отображаться равномерно. Независимо от алгоритма поиска, убедитесь, что он равномерно поиск научных параметров.

Положите баланс между информативными и доступными экспериментами

При разработке исследования или последовательности исследований распределите ограниченный бюджет для адекватного достижения следующих трех целей:

• Сравнение достаточно различных значений научных гиперпараметров.
• Настройка неприятности гиперпараметры на достаточно большое пространство поиска.
• Отбор проб поиска недостаточно плотно плотно.

Чем лучше вы можете достичь этих трех целей, тем больше понимания вы можете извлечь из эксперимента. Сравнение как можно большего количества значений научных гиперпараметров расширяет объем понимания, которые вы получаете от эксперимента.

Включая как можно больше недостатков гиперпараметров и позволяет каждому гиперпараметру неприятности варьироваться в максимально широком диапазоне, увеличивает уверенность в том, что в пространстве поиска существует «хорошее» значение недостатков. В противном случае вы можете провести несправедливое сравнение между значениями научных гиперпараметров, не исходя из возможных областей пространства гиперпараметрических недостатков, где лучшие значения могут заключаться в некоторых значениях научных параметров.

Образуйте пространство поиска недостатков гиперпараметров как можно плотно. Это повышает уверенность в том, что процедура поиска найдет какие -либо хорошие настройки для недостатков гиперпараметров, которые существуют в вашем пространстве поиска. В противном случае вы можете провести несправедливое сравнение между значениями научных параметров из -за некоторых значений, которые получают более удачи с отбором выборки гиперпараметров неприятностей.

К сожалению, улучшения в любом из этих трех измерений требуют любого из следующих:

• Увеличение количества испытаний и, следовательно, увеличение стоимости ресурса.
• Поиск способа сохранить ресурсы в одном из других измерений.

Каждая проблема имеет свои собственные идиосинкразии и вычислительные ограничения, поэтому распределение ресурсов по этим трем целям требует некоторого уровня знаний о домене. После проведения исследования всегда старайтесь понять, достаточно ли настраивали исследование, достаточно хорошо. То есть в исследовании искали достаточно большое пространство, достаточно широко, чтобы справедливо сравнить научные гиперпараметры (как описано более подробно в следующем разделе).

Учиться на экспериментальных результатах

Рекомендация: В дополнение к попытке достичь первоначальной научной цели каждой группы экспериментов, пройти контрольный список дополнительных вопросов. Если вы обнаружите проблемы, пересмотрите и повторите эксперименты.

В конечном счете, каждая группа экспериментов имеет определенную цель. Вы должны оценить доказательства, которые эксперименты предоставляют для этой цели. Однако, если вы задаете правильные вопросы, вы часто можете найти проблемы, которые можно исправить, прежде чем данный набор экспериментов может достичь своей первоначальной цели. Если вы не задаете эти вопросы, вы можете сделать неправильные выводы.

Поскольку эксперименты по работе с экспериментами могут быть дорогими, вы также должны извлечь другие полезные знания из каждой группы экспериментов, даже если эти понимания не имеют отношения к нынешней цели.

Перед анализом данного набора экспериментов, чтобы добиться прогресса в достижении своей первоначальной цели, задайте себе следующие дополнительные вопросы:

• Достаточно ли большое пространство поиска? Если оптимальная точка из исследования находится вблизи границы пространства поиска в одном или нескольких измерениях, поиск, вероятно, недостаточно широкий. В этом случае запустите другое исследование с расширенным пространством поиска.
• Вы пробовали достаточно очков из пространства поиска? Если нет, запустите больше очков или будьте менее амбициозны в целях настройки.
• Какая часть испытаний в каждом исследовании невозможна? То есть, какие испытания расходятся, получают действительно плохие значения потери или вообще не могут работать, потому что они нарушают какое -то неявное ограничение? Когда очень большая часть точек в исследовании невозможна, отрегулируйте пространство поиска, чтобы избежать выборки таких точек, что иногда требует репараметрирования пространства поиска. В некоторых случаях большое количество невозможных точек может указывать на ошибку в коде обучения.
• Модель проявляют проблемы оптимизации?
• Что вы можете узнать из кривых тренировок лучших испытаний? Например, имеют ли лучшие испытания кривые обучения, соответствующие проблематичному переоснащению?

При необходимости, основываясь на ответах на предыдущие вопросы, уточните самое последнее исследование или группу исследований, чтобы улучшить пространство поиска и/или выборки дополнительных испытаний, или предпринять некоторые другие корректирующие действия.

После того, как вы ответили на предыдущие вопросы, вы можете оценить доказательства, которые эксперименты предоставляют для вашей первоначальной цели; Например, оценка того, полезно ли изменение .

Определить плохие границы пространства поиска

Пространство поиска подозрительно, если лучшая точка, отобранная из него, близко к его границе. Вы можете найти еще лучшую точку, если вы расширите диапазон поиска в этом направлении.

Чтобы проверить границы пространства поиска, мы рекомендуем построить заполненные испытания на то, что мы называем основными графиками оси гиперпараметрических . В них мы планируем объективное значение валидации по сравнению с одним из гиперпараметров (например, скорость обучения). Каждая точка на графике соответствует одному испытанию.

Целевое значение проверки для каждого испытания, как правило, должно быть наилучшим значением, которое он достигал в ходе обучения.

Рисунок 1: Примеры плохих границ пространства поиска и приемлемых границ пространства поиска.

Графики на рисунке 1 показывают частоту ошибок (более низкий уровень) по сравнению с начальной скоростью обучения. Если лучшие точки кластер к краю пространства поиска (в некотором измерении), вам может потребоваться расширить границы пространства поиска, пока самая лучшая наблюдаемая точка больше не будет близок к границе.

Часто исследование включает в себя «невозможные» испытания, которые расходятся или получают очень плохие результаты (отмечены красными XS на рисунке 1). Если все испытания невозможны для ставок обучения, превышающего некоторую пороговую стоимость, и если наиболее эффективные испытания имеют показатели обучения на грани этого региона, модель может страдать от проблем стабильности, мешающих ему получить доступ к более высоким уровням обучения .

Не отбирая достаточно точек в пространстве поиска

В целом, может быть очень трудно понять, достаточно ли выбран пространство поиска. 🤖 Запуск большего количества испытаний лучше, чем провести меньше испытаний, но больше испытаний генерирует очевидную дополнительную стоимость.

Поскольку это так сложно узнать, когда вы выбрали достаточно, мы рекомендуем:

• Выборка того, что вы можете себе позволить.
• Калибровать вашу интуитивную уверенность в неоднократном рассмотрении различных графиков оси гиперпараметров и попытки понять, сколько очков находится в «хорошей» области пространства поиска.

Изучите кривые обучения

Резюме: Изучение кривых потерь - это простой способ выявления общих режимов отказа и может помочь вам расставить приоритеты в потенциальных следующих действиях.

Во многих случаях основная цель ваших экспериментов требует только рассмотрения ошибки проверки каждого испытания. Тем не менее, будьте осторожны, приведя каждое испытание до одного числа, потому что этот фокус может скрыть важные подробности о том, что происходит под поверхностью. Для каждого исследования мы настоятельно рекомендуем взглянуть на кривые потери , по крайней мере, самые лучшие испытания. Даже если это не необходимо для решения основной экспериментальной цели, изучение кривых потерь (включая как потери обучения, так и потери проверки) - хороший способ определения общих режимов отказа и может помочь вам определить приоритетные действия, какие действия предпринять дальше.

При изучении кривых потерь сосредоточьтесь на следующих вопросах:

• Какое -либо из испытаний демонстрирует проблемную переосмысление? Проблемная переосмысление происходит, когда ошибка проверки начинает увеличиваться во время обучения. В экспериментальных условиях, где вы оптимизируете гиперпараметры неприятностей, выбирая «лучшее» исследование для каждого настройки научных гиперпараметров, проверьте проблематичную переосмысление, по крайней мере, в каждом из лучших испытаний, соответствующих настройкам научных гиперпараметров, которые вы сравниваете. Если какое -либо из лучших испытаний демонстрирует проблематичный переосмысление, сделайте любое или оба из следующих:

  • Повторный эксперимент с дополнительными методами регуляризации
  • Перед сравнением значений научных гиперпараметров переведите существующие параметры регуляризации. Это может не применяться, если научные гиперпараметры включают параметры регуляризации, так как тогда было бы не удивительно, если бы настройки низкой прочности этих параметров регуляризации привели к проблемному переоснащению.

  Снижение переосмысления часто проста с использованием общих методов регуляризации, которые добавляют минимальную сложность кода или дополнительные вычисления (например, регуляризация отсева, сглаживание метки, распад веса). Следовательно, обычно тривиально добавить один или несколько из них в следующий раунд экспериментов. Например, если научный гиперпараметр представляет собой «количество скрытых слоев», а лучшее испытание, которое использует наибольшее количество скрытых слоев, демонстрирует проблематичный переосмысление, то мы рекомендуем повторить с помощью дополнительной регуляризации вместо немедленного выбора меньшего числа скрытых слоев.

  Even if none of the "best" trials exhibit problematic overfitting, there might still be a problem if it occurs in any of the trials. Selecting the best trial suppresses configurations exhibiting problematic overfitting and favors those that don't. In other words, selecting the best trial favors configurations with more regularization. However, anything that makes training worse can act as a regularizer, even if it wasn't intended that way. For example, choosing a smaller learning rate can regularize training by hobbling the optimization process, but we typically don't want to choose the learning rate this way. Note that the "best" trial for each setting of the scientific hyperparameters might be selected in such a way that favors "bad" values of some of the scientific or nuisance hyperparameters.

• Is there high step-to-step variance in the training or validation error late in training? If so, this could interfere with both of the following:

  • Your ability to compare different values of the scientific hyperparameters. That's because each trial randomly ends on a "lucky" or "unlucky" step.
  • Your ability to reproduce the result of the best trial in production. That's because the production model might not end on the same "lucky" step as in the study.

  The most likely causes of step-to-step variance are:

  • Batch variance due to randomly sampling examples from the training set for each batch.
  • Small validation sets
  • Using a learning rate that's too high late in training.

  Possible remedies include:

  • Increasing the batch size.
  • Obtaining more validation data.
  • Using learning rate decay.
  • Using Polyak averaging.

• Are the trials still improving at the end of training? If so, you are in the "compute bound" regime and may benefit from increasing the number of training steps or changing the learning rate schedule.

• Has performance on the training and validation sets saturated long before the final training step? If so, this indicates that you are in the "not compute-bound" regime and that you may be able to decrease the number of training steps.

Beyond this list, many additional behaviors can become evident from examining the loss curves. For example, training loss increasing during training usually indicates a bug in the training pipeline.

Detecting whether a change is useful with isolation plots

Figure 2: Isolation plot that investigates the best value of weight decay for ResNet-50 trained on ImageNet.

Often, the goal of a set of experiments is to compare different values of a scientific hyperparameter. For example, suppose you want to determine the value of weight decay that results in the best validation error. An isolation plot is a special case of the basic hyperparameter axis plot. Each point on an isolation plot corresponds to the performance of the best trial across some (or all) of the nuisance hyperparameters. In other words, plot the model performance after "optimizing away" the nuisance hyperparameters.

An isolation plot simplifies performing an apples-to-apples comparison between different values of the scientific hyperparameter. For example, the isolation plot in Figure 2 reveals the value of weight decay that produces the best validation performance for a particular configuration of ResNet-50 trained on ImageNet.

If the goal is to determine whether to include weight decay at all, then compare the best point from this plot against the baseline of no weight decay. For a fair comparison, the baseline should also have its learning rate equally well tuned.

When you have data generated by (quasi)random search and are considering a continuous hyperparameter for an isolation plot, you can approximate the isolation plot by bucketing the x-axis values of the basic hyperparameter axis plot and taking the best trial in each vertical slice defined by the buckets.

Automate generically useful plots

The more effort it is to generate plots, the less likely you are to look at them as much as you should. Therefore, we recommend setting up your infrastructure to automatically produce as many plots as possible. At a minimum, we recommend automatically generating basic hyperparameter axis plots for all hyperparameters that you vary in an experiment.

Additionally, we recommend automatically producing loss curves for all trials. Furthermore, we recommend making it as easy as possible to find the best few trials of each study and to examine their loss curves.

You can add many other useful potential plots and visualizations. To paraphrase Geoffrey Hinton :

Every time you plot something new, you learn something new.

Determine whether to adopt the candidate change

Summary: When deciding whether to make a change to our model or training procedure or adopt a new hyperparameter configuration, note the different sources of variation in your results.

When trying to improve a model, a particular candidate change might initially achieve a better validation error compared to an incumbent configuration. However, repeating the experiment might demonstrate no consistent advantage. Informally, the most important sources of inconsistent results can be grouped into the following broad categories:

• Training procedure variance, retrain variance, or trial variance : the variation between training runs that use the same hyperparameters but different random seeds. For example, different random initializations, training data shuffles, dropout masks, patterns of data augmentation operations, and orderings of parallel arithmetic operations are all potential sources of trial variance.
• Hyperparameter search variance, or study variance : the variation in results caused by our procedure to select the hyperparameters. For example, you might run the same experiment with a particular search space but with two different seeds for quasi-random search and end up selecting different hyperparameter values.
• Data collection and sampling variance : the variance from any sort of random split into training, validation, and test data or variance due to the training data generation process more generally.

True, you can compare validation error rates estimated on a finite validation set using fastidious statistical tests. However, often the trial variance alone can produce statistically significant differences between two different trained models that use the same hyperparameter settings.

We are most concerned about study variance when trying to make conclusions that go beyond the level of an individual point in hyperparameters space. The study variance depends on the number of trials and the search space. We have seen cases where the study variance is larger than the trial variance and cases where it is much smaller. Therefore, before adopting a candidate change, consider running the best trial N times to characterize the run-to-run trial variance. Usually, you can get away with only recharacterizing the trial variance after major changes to the pipeline, but you might need fresher estimates in some cases. In other applications, characterizing the trial variance is too costly to be worth it.

Although you only want to adopt changes (including new hyperparameter configurations) that produce real improvements, demanding complete certainty that a given change helps isn't the right answer either. Therefore, if a new hyperparameter point (or other change) gets a better result than the baseline (taking into account the retrain variance of both the new point and the baseline as best as you can), then you probably should adopt it as the new baseline for future comparisons. However, we recommend only adopting changes that produce improvements that outweigh any complexity they add.

After exploration concludes

Summary: Bayesian optimization tools are a compelling option once you're done searching for good search spaces and have decided what hyperparameters are worth tuning.

Eventually, your priorities will shift from learning more about the tuning problem to producing a single best configuration to launch or otherwise use. At that point, there should be a refined search space that comfortably contains the local region around the best observed trial and has been adequately sampled. Your exploration work should have revealed the most essential hyperparameters to tune and their sensible ranges that you can use to construct a search space for a final automated tuning study using as large a tuning budget as possible.

Since you no longer care about maximizing insight into the tuning problem, many of the advantages of quasi-random search no longer apply. Therefore, you should use Bayesian optimization tools to automatically find the best hyperparameter configuration. Open-Source Vizier implements a variety of sophisticated algorithms for tuning ML models, including Bayesian Optimization algorithms.

Suppose the search space contains a non-trivial volume of divergent points , meaning points that get NaN training loss or even training loss many standard deviations worse than the mean. In this case, we recommend using black-box optimization tools that properly handle trials that diverge. (See Bayesian Optimization with Unknown Constraints for an excellent way to deal with this issue.) Open-Source Vizier has supports for marking divergent points by marking trials as infeasible, although it may not use our preferred approach from Gelbart et al. , depending on how it is configured.

After exploration concludes, consider checking the performance on the test set. In principle, you could even fold the validation set into the training set and retrain the best configuration found with Bayesian optimization. However, this is only appropriate if there won't be future launches with this specific workload (for example, a one-time Kaggle competition).

,

For the purposes of this document:

The ultimate goal of machine learning development is to maximize the usefulness of the deployed model.

You can typically use the same basic steps and principles in this section on any ML problem.

This section makes the following assumptions:

• You already have a fully-running training pipeline along with a configuration that obtains a reasonable result.
• You have enough computational resources to conduct meaningful tuning experiments and to run at least several training jobs in parallel.

The incremental tuning strategy

Recommendation: Start with a simple configuration. Then, incrementally make improvements while building up insight into the problem. Make sure that any improvement is based on strong evidence.

We assume that your goal is to find a configuration that maximizes the performance of your model. Sometimes, your goal is to maximize model improvement by a fixed deadline. In other cases, you can keep improving the model indefinitely; for example, continually improving a model used in production.

In principle, you could maximize performance by using an algorithm to automatically search the entire space of possible configurations, but this is not a practical option. The space of possible configurations is extremely large and there are not yet any algorithms sophisticated enough to efficiently search this space without human guidance. Most automated search algorithms rely on a hand-designed search space that defines the set of configurations to search in, and these search spaces can matter quite a bit.

The most effective way to maximize performance is to start with a simple configuration and incrementally add features and make improvements while building up insight into the problem.

We recommend using automated search algorithms in each round of tuning and continually updating search spaces as your understanding grows. As you explore, you will naturally find better and better configurations and therefore your "best" model will continually improve.

The term "launch" refers to an update to our best configuration (which may or may not correspond to an actual launch of a production model). For each "launch," you must ensure that the change is based on strong evidence—not just random chance based on a lucky configuration—so that you don't add unnecessary complexity to the training pipeline.

At a high level, our incremental tuning strategy involves repeating the following four steps:

1. Pick a goal for the next round of experiments. Make sure that the goal is appropriately scoped.
2. Design the next round of experiments. Design and execute a set of experiments that progresses towards this goal.
3. Learn from the experimental results. Evaluate the experiment against a checklist.
4. Determine whether to adopt the candidate change.

The remainder of this section details this strategy.

Pick a goal for the next round of experiments

If you try to add multiple features or answer multiple questions at once, you may not be able to disentangle the separate effects on the results. Example goals include:

• Try a potential improvement to the pipeline (for example, a new regularizer, preprocessing choice, etc.).
• Understand the impact of a particular model hyperparameter (for example, the activation function)
• Minimize validation error.

Prioritize long term progress over short term validation error improvements

Summary: Most of the time, your primary goal is to gain insight into the tuning problem.

We recommend spending the majority of your time gaining insight into the problem and comparatively little time greedily focused on maximizing performance on the validation set. In other words, spend most of your time on "exploration" and only a small amount on "exploitation". Understanding the problem is critical to maximize final performance. Prioritizing insight over short term gains helps to:

• Avoid launching unnecessary changes that happened to be present in well-performing runs merely through historical accident.
• Identify which hyperparameters the validation error is most sensitive to, which hyperparameters interact the most and therefore need to be retuned together, and which hyperparameters are relatively insensitive to other changes and can therefore be fixed in future experiments.
• Suggest potential new features to try, such as new regularizers when overfitting is an issue.
• Identify features that don't help and therefore can be removed, reducing the complexity of future experiments.
• Recognize when improvements from hyperparameter tuning have likely saturated.
• Narrow our search spaces around the optimal value to improve tuning efficiency.

Eventually, you'll understand the problem. Then, you can focus purely on the validation error even if the experiments aren't maximally informative about the structure of the tuning problem.

Design the next round of experiments

Summary: Identify which hyperparameters are scientific, nuisance, and fixed hyperparameters for the experimental goal. Create a sequence of studies to compare different values of the scientific hyperparameters while optimizing over the nuisance hyperparameters. Choose the search space of nuisance hyperparameters to balance resource costs with scientific value.

Identify scientific, nuisance, and fixed hyperparameters

For a given goal, all hyperparameters fall into one of the following categories:

• scientific hyperparameters are those whose effect on the model's performance is what you're trying to measure.
• nuisance hyperparameters are those that need to be optimized over in order to fairly compare different values of the scientific hyperparameters. Nuisance hyperparameters are similar to nuisance parameters in statistics.
• fixed hyperparameters have constant values in the current round of experiments. The values of fixed hyperparameters shouldn't change when you compare different values of scientific hyperparameters. By fixing certain hyperparameters for a set of experiments, you must accept that conclusions derived from the experiments might not be valid for other settings of the fixed hyperparameters. In other words, fixed hyperparameters create caveats for any conclusions you draw from the experiments.

For example, suppose your goal is as follows:

Determine whether a model with more hidden layers has lower validation error.

В этом случае:

• Learning rate is a nuisance hyperparameter because you can only fairly compare models with different numbers of hidden layers if the learning rate is tuned separately for each number of hidden layers. (The optimal learning rate generally depends on the model architecture).
• The activation function could be a fixed hyperparameter if you have determined in prior experiments that the best activation function is not sensitive to model depth. Or, you are willing to limit your conclusions about the number of hidden layers to cover this activation function. Alternatively, it could be a nuisance hyperparameter if you are prepared to tune it separately for each number of hidden layers.

A particular hyperparameter could be a scientific hyperparameter, nuisance hyperparameter, or fixed hyperparameter; the hyperparameter's designation changes depending on the experimental goal. For example, activation function could be any of the following:

• Scientific hyperparameter: Is ReLU or tanh a better choice for our problem?
• Nuisance hyperparameter: Is the best five-layer model better than the best six-layer model when you allow several different possible activation functions?
• Fixed hyperparameter: For ReLU nets, does adding batch normalization in a particular position help?

When designing a new round of experiments:

1. Identify the scientific hyperparameters for the experimental goal. (At this stage, you can consider all other hyperparameters to be nuisance hyperparameters.)
2. Convert some nuisance hyperparameters into fixed hyperparameters.

With limitless resources, you would leave all non-scientific hyperparameters as nuisance hyperparameters so that the conclusions you draw from your experiments are free from caveats about fixed hyperparameter values. However, the more nuisance hyperparameters you attempt to tune, the greater the risk that you fail to tune them sufficiently well for each setting of the scientific hyperparameters and end up reaching the wrong conclusions from your experiments. As described in a later section , you could counter this risk by increasing the computational budget. However, your maximum resource budget is often less than would be needed to tune all non-scientific hyperparameters.

We recommend converting a nuisance hyperparameter into a fixed hyperparameter when the caveats introduced by fixing it are less burdensome than the cost of including it as a nuisance hyperparameter. The more a nuisance hyperparameter interacts with the scientific hyperparameters, the more damaging to fix its value. For example, the best value of the weight decay strength typically depends on the model size, so comparing different model sizes assuming a single specific value of the weight decay wouldn't be very insightful.

Some optimizer parameters

As a rule of thumb, some optimizer hyperparameters (eg the learning rate, momentum, learning rate schedule parameters, Adam betas etc.) are nuisance hyperparameters because they tend to interact the most with other changes. These optimizer hyperparameters are rarely scientific hyperparameters because a goal like "what is the best learning rate for the current pipeline?" doesn't provide much insight. After all, the best setting could change with the next pipeline change anyway.

You might fix some optimizer hyperparameters occasionally due to resource constraints or particularly strong evidence that they don't interact with the scientific parameters. However, you should generally assume that you must tune optimizer hyperparameters separately to make fair comparisons between different settings of the scientific hyperparameters, and thus shouldn't be fixed. Furthermore, there is no a priori reason to prefer one optimizer hyperparameter value over another; for example, optimizer hyperparameter values don't usually affect the computational cost of forward passes or gradients in any way.

The choice of optimizer

The choice of optimizer is typically either:

• a scientific hyperparameter
• a fixed hyperparameter

An optimizer is a scientific hyperparameter if your experimental goal involves making fair comparisons between two or more different optimizers. Например:

Determine which optimizer produces the lowest validation error in a given number of steps.

Alternatively, you might make the optimizer a fixed hyperparameter for a variety of reasons, including:

• Prior experiments suggest that the best optimizer for your tuning problem is not sensitive to current scientific hyperparameters.
• You prefer to compare values of the scientific hyperparameters using this optimizer because its training curves are easier to reason about.
• You prefer to use this optimizer because it uses less memory than the alternatives.

Regularization hyperparameters

Hyperparameters introduced by a regularization technique are typically nuisance hyperparameters. However, the choice of whether or not to include the regularization technique at all is either a scientific or fixed hyperparameter.

For example, dropout regularization adds code complexity. Therefore, when deciding whether to include dropout regularization, you could make "no dropout" vs "dropout" a scientific hyperparameter but dropout rate a nuisance hyperparameter. If you decide to add dropout regularization to the pipeline based on this experiment, then the dropout rate would be a nuisance hyperparameter in future experiments.

Architectural hyperparameters

Architectural hyperparameters are often scientific or fixed hyperparameters because architecture changes can affect serving and training costs, latency, and memory requirements. For example, the number of layers is typically a scientific or fixed hyperparameter since it tends to have dramatic consequences for training speed and memory usage.

Dependencies on scientific hyperparameters

In some cases, the sets of nuisance and fixed hyperparameters depends on the values of the scientific hyperparameters. For example, suppose you are trying to determine which optimizer in Nesterov momentum and Adam produces in the lowest validation error. В этом случае:

• The scientific hyperparameter is the optimizer, which takes values {"Nesterov_momentum", "Adam"}
• The value optimizer="Nesterov_momentum" introduces the hyperparameters {learning_rate, momentum} , which might be either nuisance or fixed hyperparameters.
• The value optimizer="Adam" introduces the hyperparameters {learning_rate, beta1, beta2, epsilon} , which might be either nuisance or fixed hyperparameters.

Hyperparameters that are only present for certain values of the scientific hyperparameters are called conditional hyperparameters . Don't assume two conditional hyperparameters are the same just because they have the same name! In the preceding example, the conditional hyperparameter called learning_rate is a different hyperparameter for optimizer="Nesterov_momentum" than for optimizer="Adam" . Its role is similar (although not identical) in the two algorithms, but the range of values that work well in each of the optimizers is typically different by several orders of magnitude.

Create a set of studies

After identifying the scientific and nuisance hyperparameters, you should design a study or sequence of studies to make progress towards the experimental goal. A study specifies a set of hyperparameter configurations to be run for subsequent analysis. Each configuration is called a trial . Creating a study typically involves choosing the following:

• The hyperparameters that vary across trials.
• The values those hyperparameters can take on (the search space ).
• The number of trials.
• An automated search algorithm to sample that many trials from the search space.

Alternatively, you can create a study by specifying the set of hyperparameter configurations manually.

The purpose of the studies is to simultaneously:

• Run the pipeline with different values of the scientific hyperparameters.
• "Optimizing away" (or "optimizing over") the nuisance hyperparameters so that comparisons between different values of the scientific hyperparameters are as fair as possible.

In the simplest case, you would make a separate study for each configuration of the scientific parameters, where each study tunes over the nuisance hyperparameters. For example, if your goal is to select the best optimizer out of Nesterov momentum and Adam, you could create two studies:

• One study in which optimizer="Nesterov_momentum" and the nuisance hyperparameters are {learning_rate, momentum}
• Another study in which optimizer="Adam" and the nuisance hyperparameters are {learning_rate, beta1, beta2, epsilon} .

You would compare the two optimizers by selecting the best performing trial from each study.

You can use any gradient-free optimization algorithm, including methods such as Bayesian optimization or evolutionary algorithms, to optimize over the nuisance hyperparameters. However, we prefer to use quasi-random search in the exploration phase of tuning because of a variety of advantages it has in this setting. After exploration concludes, we recommend using state-of-the-art Bayesian optimization software (if it is available).

Consider a more complicated case where you want to compare a large number of values of the scientific hyperparameters but it is impractical to make that many independent studies. In this case, you can do the following:

• Include the scientific parameters in the same search space as the nuisance hyperparameters.
• Use a search algorithm to sample values of both the scientific and nuisance hyperparameters in a single study.

When taking this approach, conditional hyperparameters can cause problems. After all, it is hard to specify a search space unless the set of nuisance hyperparameters is the same for all values of the scientific hyperparameters. In this case, our preference for using quasi-random search over fancier black-box optimization tools is even stronger, since it guarantees different values of the scientific hyperparameters will be sampled uniformly. Regardless of the search algorithm, ensure that it searches the scientific parameters uniformly.

Strike a balance between informative and affordable experiments

When designing a study or sequence of studies, allocate a limited budget to adequately achieve the following three goals:

• Comparing enough different values of the scientific hyperparameters.
• Tuning the nuisance hyperparameters over a large enough search space.
• Sampling the search space of nuisance hyperparameters densely enough.

The better you can achieve these three goals, the more insight you can extract from the experiment. Comparing as many values of the scientific hyperparameters as possible broadens the scope of the insights you gain from the experiment.

Including as many nuisance hyperparameters as possible and allowing each nuisance hyperparameter to vary over as wide a range as possible increases confidence that a "good" value of the nuisance hyperparameters exists in the search space for each configuration of the scientific hyperparameters. Otherwise, you might make unfair comparisons between values of the scientific hyperparameters by not searching possible regions of the nuisance hyperparameter space where better values might lie for some values of the scientific parameters.

Sample the search space of nuisance hyperparameters as densely as possible. Doing so increases confidence that the search procedure will find any good settings for the nuisance hyperparameters that happen to exist in your search space. Otherwise, you might make unfair comparisons between values of the scientific parameters due to some values getting luckier with the sampling of the nuisance hyperparameters.

Unfortunately, improvements in any of these three dimensions require either of the following:

• Increasing the number of trials, and therefore increasing the resource cost.
• Finding a way to save resources in one of the other dimensions.

Every problem has its own idiosyncrasies and computational constraints, so allocating resources across these three goals requires some level of domain knowledge. After running a study, always try to get a sense of whether the study tuned the nuisance hyperparameters well enough. That is, the study searched a large enough space extensively enough to fairly compare the scientific hyperparameters (as described in greater detail in the next section).

Learn from the experimental results

Recommendation: In addition to trying to achieve the original scientific goal of each group of experiments, go through a checklist of additional questions. If you discover issues, revise and rerun the experiments.

Ultimately, each group of experiments has a specific goal. You should evaluate the evidence the experiments provide toward that goal. However, if you ask the right questions, you can often find issues to correct before a given set of experiments can progress towards their original goal. If you don't ask these questions, you may draw incorrect conclusions.

Since running experiments can be expensive, you should also extract other useful insights from each group of experiments, even if these insights are not immediately relevant to the current goal.

Before analyzing a given set of experiments to make progress toward their original goal, ask yourself the following additional questions:

• Is the search space large enough? If the optimal point from a study is near the boundary of the search space in one or more dimensions, the search is probably not wide enough. In this case, run another study with an expanded search space.
• Have you sampled enough points from the search space? If not, run more points or be less ambitious in the tuning goals.
• What fraction of the trials in each study are infeasible? That is, which trials diverge, get really bad loss values, or fail to run at all because they violate some implicit constraint? When a very large fraction of points in a study are infeasible, adjust the search space to avoid sampling such points, which sometimes requires reparameterizing the search space. In some cases, a large number of infeasible points can indicate a bug in the training code.
• Does the model exhibit optimization issues?
• What can you learn from the training curves of the best trials? For example, do the best trials have training curves consistent with problematic overfitting?

If necessary, based on the answers to the preceding questions, refine the most recent study or group of studies to improve the search space and/or sample more trials, or take some other corrective action.

Once you have answered the preceding questions, you can evaluate the evidence the experiments provide towards your original goal; for example, evaluating whether a change is useful .

Identify bad search space boundaries

A search space is suspicious if the best point sampled from it is close to its boundary. You might find an even better point if you expand the search range in that direction.

To check search space boundaries, we recommend plotting completed trials on what we call basic hyperparameter axis plots . In these, we plot the validation objective value versus one of the hyperparameters (for example, learning rate). Each point on the plot corresponds to a single trial.

The validation objective value for each trial should usually be the best value it achieved over the course of training.

Figure 1: Examples of bad search space boundaries and acceptable search space boundaries.

The plots in Figure 1 show the error rate (lower is better) against the initial learning rate. If the best points cluster towards the edge of a search space (in some dimension), then you might need to expand the search space boundaries until the best observed point is no longer close to the boundary.

Often, a study includes "infeasible" trials that diverge or get very bad results (marked with red Xs in Figure 1). If all trials are infeasible for learning rates greater than some threshold value, and if the best performing trials have learning rates at the edge of that region, the model may suffer from stability issues preventing it from accessing higher learning rates .

Not sampling enough points in the search space

In general, it can be very difficult to know if the search space has been sampled densely enough. 🤖 Running more trials is better than running fewer trials, but more trials generates an obvious extra cost.

Since it is so hard to know when you have sampled enough, we recommend:

• Sampling what you can afford.
• Calibrating your intuitive confidence from repeatedly looking at various hyperparameter axis plots and trying to get a sense of how many points are in the "good" region of the search space.

Examine the training curves

Summary: Examining the loss curves is an easy way to identify common failure modes and can help you prioritize potential next actions.

In many cases, the primary objective of your experiments only requires considering the validation error of each trial. However, be careful when reducing each trial to a single number because that focus can hide important details about what's going on below the surface. For every study, we strongly recommend looking at the loss curves of at least the best few trials. Even if this is not necessary for addressing the primary experimental objective, examining the loss curves (including both training loss and validation loss) is a good way to identify common failure modes and can help you prioritize what actions to take next.

When examining the loss curves, focus on the following questions:

• Are any of the trials exhibiting problematic overfitting? Problematic overfitting occurs when the validation error starts increasing during training. In experimental settings where you optimize away nuisance hyperparameters by selecting the "best" trial for each setting of the scientific hyperparameters, check for problematic overfitting in at least each of the best trials corresponding to the settings of the scientific hyperparameters that you're comparing. If any of the best trials exhibits problematic overfitting, do either or both of the following:

  • Rerun the experiment with additional regularization techniques
  • Retune the existing regularization parameters before comparing the values of the scientific hyperparameters. This may not apply if the scientific hyperparameters include regularization parameters, since then it wouldn't be surprising if low-strength settings of those regularization parameters resulted in problematic overfitting.

  Reducing overfitting is often straightforward using common regularization techniques that add minimal code complexity or extra computation (for example, dropout regularization, label smoothing, weight decay). Therefore, it's usually trivial to add one or more of these to the next round of experiments. For example, if the scientific hyperparameter is "number of hidden layers" and the best trial that uses the largest number of hidden layers exhibits problematic overfitting, then we recommend retrying with additional regularization instead of immediately selecting the smaller number of hidden layers.

  Even if none of the "best" trials exhibit problematic overfitting, there might still be a problem if it occurs in any of the trials. Selecting the best trial suppresses configurations exhibiting problematic overfitting and favors those that don't. In other words, selecting the best trial favors configurations with more regularization. However, anything that makes training worse can act as a regularizer, even if it wasn't intended that way. For example, choosing a smaller learning rate can regularize training by hobbling the optimization process, but we typically don't want to choose the learning rate this way. Note that the "best" trial for each setting of the scientific hyperparameters might be selected in such a way that favors "bad" values of some of the scientific or nuisance hyperparameters.

• Is there high step-to-step variance in the training or validation error late in training? If so, this could interfere with both of the following:

  • Your ability to compare different values of the scientific hyperparameters. That's because each trial randomly ends on a "lucky" or "unlucky" step.
  • Your ability to reproduce the result of the best trial in production. That's because the production model might not end on the same "lucky" step as in the study.

  The most likely causes of step-to-step variance are:

  • Batch variance due to randomly sampling examples from the training set for each batch.
  • Small validation sets
  • Using a learning rate that's too high late in training.

  Possible remedies include:

  • Increasing the batch size.
  • Obtaining more validation data.
  • Using learning rate decay.
  • Using Polyak averaging.

• Are the trials still improving at the end of training? If so, you are in the "compute bound" regime and may benefit from increasing the number of training steps or changing the learning rate schedule.

• Has performance on the training and validation sets saturated long before the final training step? If so, this indicates that you are in the "not compute-bound" regime and that you may be able to decrease the number of training steps.

Beyond this list, many additional behaviors can become evident from examining the loss curves. For example, training loss increasing during training usually indicates a bug in the training pipeline.

Detecting whether a change is useful with isolation plots

Figure 2: Isolation plot that investigates the best value of weight decay for ResNet-50 trained on ImageNet.

Often, the goal of a set of experiments is to compare different values of a scientific hyperparameter. For example, suppose you want to determine the value of weight decay that results in the best validation error. An isolation plot is a special case of the basic hyperparameter axis plot. Each point on an isolation plot corresponds to the performance of the best trial across some (or all) of the nuisance hyperparameters. In other words, plot the model performance after "optimizing away" the nuisance hyperparameters.

An isolation plot simplifies performing an apples-to-apples comparison between different values of the scientific hyperparameter. For example, the isolation plot in Figure 2 reveals the value of weight decay that produces the best validation performance for a particular configuration of ResNet-50 trained on ImageNet.

If the goal is to determine whether to include weight decay at all, then compare the best point from this plot against the baseline of no weight decay. For a fair comparison, the baseline should also have its learning rate equally well tuned.

When you have data generated by (quasi)random search and are considering a continuous hyperparameter for an isolation plot, you can approximate the isolation plot by bucketing the x-axis values of the basic hyperparameter axis plot and taking the best trial in each vertical slice defined by the buckets.

Automate generically useful plots

The more effort it is to generate plots, the less likely you are to look at them as much as you should. Therefore, we recommend setting up your infrastructure to automatically produce as many plots as possible. At a minimum, we recommend automatically generating basic hyperparameter axis plots for all hyperparameters that you vary in an experiment.

Additionally, we recommend automatically producing loss curves for all trials. Furthermore, we recommend making it as easy as possible to find the best few trials of each study and to examine their loss curves.

You can add many other useful potential plots and visualizations. To paraphrase Geoffrey Hinton :

Every time you plot something new, you learn something new.

Determine whether to adopt the candidate change

Summary: When deciding whether to make a change to our model or training procedure or adopt a new hyperparameter configuration, note the different sources of variation in your results.

When trying to improve a model, a particular candidate change might initially achieve a better validation error compared to an incumbent configuration. However, repeating the experiment might demonstrate no consistent advantage. Informally, the most important sources of inconsistent results can be grouped into the following broad categories:

• Training procedure variance, retrain variance, or trial variance : the variation between training runs that use the same hyperparameters but different random seeds. For example, different random initializations, training data shuffles, dropout masks, patterns of data augmentation operations, and orderings of parallel arithmetic operations are all potential sources of trial variance.
• Hyperparameter search variance, or study variance : the variation in results caused by our procedure to select the hyperparameters. For example, you might run the same experiment with a particular search space but with two different seeds for quasi-random search and end up selecting different hyperparameter values.
• Data collection and sampling variance : the variance from any sort of random split into training, validation, and test data or variance due to the training data generation process more generally.

True, you can compare validation error rates estimated on a finite validation set using fastidious statistical tests. However, often the trial variance alone can produce statistically significant differences between two different trained models that use the same hyperparameter settings.

We are most concerned about study variance when trying to make conclusions that go beyond the level of an individual point in hyperparameters space. The study variance depends on the number of trials and the search space. We have seen cases where the study variance is larger than the trial variance and cases where it is much smaller. Therefore, before adopting a candidate change, consider running the best trial N times to characterize the run-to-run trial variance. Usually, you can get away with only recharacterizing the trial variance after major changes to the pipeline, but you might need fresher estimates in some cases. In other applications, characterizing the trial variance is too costly to be worth it.

Although you only want to adopt changes (including new hyperparameter configurations) that produce real improvements, demanding complete certainty that a given change helps isn't the right answer either. Therefore, if a new hyperparameter point (or other change) gets a better result than the baseline (taking into account the retrain variance of both the new point and the baseline as best as you can), then you probably should adopt it as the new baseline for future comparisons. However, we recommend only adopting changes that produce improvements that outweigh any complexity they add.

After exploration concludes

Summary: Bayesian optimization tools are a compelling option once you're done searching for good search spaces and have decided what hyperparameters are worth tuning.

Eventually, your priorities will shift from learning more about the tuning problem to producing a single best configuration to launch or otherwise use. At that point, there should be a refined search space that comfortably contains the local region around the best observed trial and has been adequately sampled. Your exploration work should have revealed the most essential hyperparameters to tune and their sensible ranges that you can use to construct a search space for a final automated tuning study using as large a tuning budget as possible.

Since you no longer care about maximizing insight into the tuning problem, many of the advantages of quasi-random search no longer apply. Therefore, you should use Bayesian optimization tools to automatically find the best hyperparameter configuration. Open-Source Vizier implements a variety of sophisticated algorithms for tuning ML models, including Bayesian Optimization algorithms.

Suppose the search space contains a non-trivial volume of divergent points , meaning points that get NaN training loss or even training loss many standard deviations worse than the mean. In this case, we recommend using black-box optimization tools that properly handle trials that diverge. (See Bayesian Optimization with Unknown Constraints for an excellent way to deal with this issue.) Open-Source Vizier has supports for marking divergent points by marking trials as infeasible, although it may not use our preferred approach from Gelbart et al. , depending on how it is configured.

After exploration concludes, consider checking the performance on the test set. In principle, you could even fold the validation set into the training set and retrain the best configuration found with Bayesian optimization. However, this is only appropriate if there won't be future launches with this specific workload (for example, a one-time Kaggle competition).

,

For the purposes of this document:

The ultimate goal of machine learning development is to maximize the usefulness of the deployed model.

You can typically use the same basic steps and principles in this section on any ML problem.

This section makes the following assumptions:

• You already have a fully-running training pipeline along with a configuration that obtains a reasonable result.
• You have enough computational resources to conduct meaningful tuning experiments and to run at least several training jobs in parallel.

The incremental tuning strategy

Recommendation: Start with a simple configuration. Then, incrementally make improvements while building up insight into the problem. Make sure that any improvement is based on strong evidence.

We assume that your goal is to find a configuration that maximizes the performance of your model. Sometimes, your goal is to maximize model improvement by a fixed deadline. In other cases, you can keep improving the model indefinitely; for example, continually improving a model used in production.

In principle, you could maximize performance by using an algorithm to automatically search the entire space of possible configurations, but this is not a practical option. The space of possible configurations is extremely large and there are not yet any algorithms sophisticated enough to efficiently search this space without human guidance. Most automated search algorithms rely on a hand-designed search space that defines the set of configurations to search in, and these search spaces can matter quite a bit.

The most effective way to maximize performance is to start with a simple configuration and incrementally add features and make improvements while building up insight into the problem.

We recommend using automated search algorithms in each round of tuning and continually updating search spaces as your understanding grows. As you explore, you will naturally find better and better configurations and therefore your "best" model will continually improve.

The term "launch" refers to an update to our best configuration (which may or may not correspond to an actual launch of a production model). For each "launch," you must ensure that the change is based on strong evidence—not just random chance based on a lucky configuration—so that you don't add unnecessary complexity to the training pipeline.

At a high level, our incremental tuning strategy involves repeating the following four steps:

1. Pick a goal for the next round of experiments. Make sure that the goal is appropriately scoped.
2. Design the next round of experiments. Design and execute a set of experiments that progresses towards this goal.
3. Learn from the experimental results. Evaluate the experiment against a checklist.
4. Determine whether to adopt the candidate change.

The remainder of this section details this strategy.

Pick a goal for the next round of experiments

If you try to add multiple features or answer multiple questions at once, you may not be able to disentangle the separate effects on the results. Example goals include:

• Try a potential improvement to the pipeline (for example, a new regularizer, preprocessing choice, etc.).
• Understand the impact of a particular model hyperparameter (for example, the activation function)
• Minimize validation error.

Prioritize long term progress over short term validation error improvements

Summary: Most of the time, your primary goal is to gain insight into the tuning problem.

We recommend spending the majority of your time gaining insight into the problem and comparatively little time greedily focused on maximizing performance on the validation set. In other words, spend most of your time on "exploration" and only a small amount on "exploitation". Understanding the problem is critical to maximize final performance. Prioritizing insight over short term gains helps to:

• Avoid launching unnecessary changes that happened to be present in well-performing runs merely through historical accident.
• Identify which hyperparameters the validation error is most sensitive to, which hyperparameters interact the most and therefore need to be retuned together, and which hyperparameters are relatively insensitive to other changes and can therefore be fixed in future experiments.
• Suggest potential new features to try, such as new regularizers when overfitting is an issue.
• Identify features that don't help and therefore can be removed, reducing the complexity of future experiments.
• Recognize when improvements from hyperparameter tuning have likely saturated.
• Narrow our search spaces around the optimal value to improve tuning efficiency.

Eventually, you'll understand the problem. Then, you can focus purely on the validation error even if the experiments aren't maximally informative about the structure of the tuning problem.

Design the next round of experiments

Summary: Identify which hyperparameters are scientific, nuisance, and fixed hyperparameters for the experimental goal. Create a sequence of studies to compare different values of the scientific hyperparameters while optimizing over the nuisance hyperparameters. Choose the search space of nuisance hyperparameters to balance resource costs with scientific value.

Identify scientific, nuisance, and fixed hyperparameters

For a given goal, all hyperparameters fall into one of the following categories:

• scientific hyperparameters are those whose effect on the model's performance is what you're trying to measure.
• nuisance hyperparameters are those that need to be optimized over in order to fairly compare different values of the scientific hyperparameters. Nuisance hyperparameters are similar to nuisance parameters in statistics.
• fixed hyperparameters have constant values in the current round of experiments. The values of fixed hyperparameters shouldn't change when you compare different values of scientific hyperparameters. By fixing certain hyperparameters for a set of experiments, you must accept that conclusions derived from the experiments might not be valid for other settings of the fixed hyperparameters. In other words, fixed hyperparameters create caveats for any conclusions you draw from the experiments.

For example, suppose your goal is as follows:

Determine whether a model with more hidden layers has lower validation error.

В этом случае:

• Learning rate is a nuisance hyperparameter because you can only fairly compare models with different numbers of hidden layers if the learning rate is tuned separately for each number of hidden layers. (The optimal learning rate generally depends on the model architecture).
• The activation function could be a fixed hyperparameter if you have determined in prior experiments that the best activation function is not sensitive to model depth. Or, you are willing to limit your conclusions about the number of hidden layers to cover this activation function. Alternatively, it could be a nuisance hyperparameter if you are prepared to tune it separately for each number of hidden layers.

A particular hyperparameter could be a scientific hyperparameter, nuisance hyperparameter, or fixed hyperparameter; the hyperparameter's designation changes depending on the experimental goal. For example, activation function could be any of the following:

• Scientific hyperparameter: Is ReLU or tanh a better choice for our problem?
• Nuisance hyperparameter: Is the best five-layer model better than the best six-layer model when you allow several different possible activation functions?
• Fixed hyperparameter: For ReLU nets, does adding batch normalization in a particular position help?

When designing a new round of experiments:

1. Identify the scientific hyperparameters for the experimental goal. (At this stage, you can consider all other hyperparameters to be nuisance hyperparameters.)
2. Convert some nuisance hyperparameters into fixed hyperparameters.

With limitless resources, you would leave all non-scientific hyperparameters as nuisance hyperparameters so that the conclusions you draw from your experiments are free from caveats about fixed hyperparameter values. However, the more nuisance hyperparameters you attempt to tune, the greater the risk that you fail to tune them sufficiently well for each setting of the scientific hyperparameters and end up reaching the wrong conclusions from your experiments. As described in a later section , you could counter this risk by increasing the computational budget. However, your maximum resource budget is often less than would be needed to tune all non-scientific hyperparameters.

We recommend converting a nuisance hyperparameter into a fixed hyperparameter when the caveats introduced by fixing it are less burdensome than the cost of including it as a nuisance hyperparameter. The more a nuisance hyperparameter interacts with the scientific hyperparameters, the more damaging to fix its value. For example, the best value of the weight decay strength typically depends on the model size, so comparing different model sizes assuming a single specific value of the weight decay wouldn't be very insightful.

Some optimizer parameters

As a rule of thumb, some optimizer hyperparameters (eg the learning rate, momentum, learning rate schedule parameters, Adam betas etc.) are nuisance hyperparameters because they tend to interact the most with other changes. These optimizer hyperparameters are rarely scientific hyperparameters because a goal like "what is the best learning rate for the current pipeline?" doesn't provide much insight. After all, the best setting could change with the next pipeline change anyway.

You might fix some optimizer hyperparameters occasionally due to resource constraints or particularly strong evidence that they don't interact with the scientific parameters. However, you should generally assume that you must tune optimizer hyperparameters separately to make fair comparisons between different settings of the scientific hyperparameters, and thus shouldn't be fixed. Furthermore, there is no a priori reason to prefer one optimizer hyperparameter value over another; for example, optimizer hyperparameter values don't usually affect the computational cost of forward passes or gradients in any way.

The choice of optimizer

The choice of optimizer is typically either:

• a scientific hyperparameter
• a fixed hyperparameter

An optimizer is a scientific hyperparameter if your experimental goal involves making fair comparisons between two or more different optimizers. Например:

Determine which optimizer produces the lowest validation error in a given number of steps.

Alternatively, you might make the optimizer a fixed hyperparameter for a variety of reasons, including:

• Prior experiments suggest that the best optimizer for your tuning problem is not sensitive to current scientific hyperparameters.
• You prefer to compare values of the scientific hyperparameters using this optimizer because its training curves are easier to reason about.
• You prefer to use this optimizer because it uses less memory than the alternatives.

Regularization hyperparameters

Hyperparameters introduced by a regularization technique are typically nuisance hyperparameters. However, the choice of whether or not to include the regularization technique at all is either a scientific or fixed hyperparameter.

For example, dropout regularization adds code complexity. Therefore, when deciding whether to include dropout regularization, you could make "no dropout" vs "dropout" a scientific hyperparameter but dropout rate a nuisance hyperparameter. If you decide to add dropout regularization to the pipeline based on this experiment, then the dropout rate would be a nuisance hyperparameter in future experiments.

Architectural hyperparameters

Architectural hyperparameters are often scientific or fixed hyperparameters because architecture changes can affect serving and training costs, latency, and memory requirements. For example, the number of layers is typically a scientific or fixed hyperparameter since it tends to have dramatic consequences for training speed and memory usage.

Dependencies on scientific hyperparameters

In some cases, the sets of nuisance and fixed hyperparameters depends on the values of the scientific hyperparameters. For example, suppose you are trying to determine which optimizer in Nesterov momentum and Adam produces in the lowest validation error. В этом случае:

• The scientific hyperparameter is the optimizer, which takes values {"Nesterov_momentum", "Adam"}
• The value optimizer="Nesterov_momentum" introduces the hyperparameters {learning_rate, momentum} , which might be either nuisance or fixed hyperparameters.
• The value optimizer="Adam" introduces the hyperparameters {learning_rate, beta1, beta2, epsilon} , which might be either nuisance or fixed hyperparameters.

Hyperparameters that are only present for certain values of the scientific hyperparameters are called conditional hyperparameters . Don't assume two conditional hyperparameters are the same just because they have the same name! In the preceding example, the conditional hyperparameter called learning_rate is a different hyperparameter for optimizer="Nesterov_momentum" than for optimizer="Adam" . Its role is similar (although not identical) in the two algorithms, but the range of values that work well in each of the optimizers is typically different by several orders of magnitude.

Create a set of studies

After identifying the scientific and nuisance hyperparameters, you should design a study or sequence of studies to make progress towards the experimental goal. A study specifies a set of hyperparameter configurations to be run for subsequent analysis. Each configuration is called a trial . Creating a study typically involves choosing the following:

• The hyperparameters that vary across trials.
• The values those hyperparameters can take on (the search space ).
• The number of trials.
• An automated search algorithm to sample that many trials from the search space.

Alternatively, you can create a study by specifying the set of hyperparameter configurations manually.

The purpose of the studies is to simultaneously:

• Run the pipeline with different values of the scientific hyperparameters.
• "Optimizing away" (or "optimizing over") the nuisance hyperparameters so that comparisons between different values of the scientific hyperparameters are as fair as possible.

In the simplest case, you would make a separate study for each configuration of the scientific parameters, where each study tunes over the nuisance hyperparameters. For example, if your goal is to select the best optimizer out of Nesterov momentum and Adam, you could create two studies:

• One study in which optimizer="Nesterov_momentum" and the nuisance hyperparameters are {learning_rate, momentum}
• Another study in which optimizer="Adam" and the nuisance hyperparameters are {learning_rate, beta1, beta2, epsilon} .

You would compare the two optimizers by selecting the best performing trial from each study.

You can use any gradient-free optimization algorithm, including methods such as Bayesian optimization or evolutionary algorithms, to optimize over the nuisance hyperparameters. However, we prefer to use quasi-random search in the exploration phase of tuning because of a variety of advantages it has in this setting. After exploration concludes, we recommend using state-of-the-art Bayesian optimization software (if it is available).

Consider a more complicated case where you want to compare a large number of values of the scientific hyperparameters but it is impractical to make that many independent studies. In this case, you can do the following:

• Include the scientific parameters in the same search space as the nuisance hyperparameters.
• Use a search algorithm to sample values of both the scientific and nuisance hyperparameters in a single study.

When taking this approach, conditional hyperparameters can cause problems. After all, it is hard to specify a search space unless the set of nuisance hyperparameters is the same for all values of the scientific hyperparameters. In this case, our preference for using quasi-random search over fancier black-box optimization tools is even stronger, since it guarantees different values of the scientific hyperparameters will be sampled uniformly. Regardless of the search algorithm, ensure that it searches the scientific parameters uniformly.

Strike a balance between informative and affordable experiments

When designing a study or sequence of studies, allocate a limited budget to adequately achieve the following three goals:

• Comparing enough different values of the scientific hyperparameters.
• Tuning the nuisance hyperparameters over a large enough search space.
• Sampling the search space of nuisance hyperparameters densely enough.

The better you can achieve these three goals, the more insight you can extract from the experiment. Comparing as many values of the scientific hyperparameters as possible broadens the scope of the insights you gain from the experiment.

Including as many nuisance hyperparameters as possible and allowing each nuisance hyperparameter to vary over as wide a range as possible increases confidence that a "good" value of the nuisance hyperparameters exists in the search space for each configuration of the scientific hyperparameters. Otherwise, you might make unfair comparisons between values of the scientific hyperparameters by not searching possible regions of the nuisance hyperparameter space where better values might lie for some values of the scientific parameters.

Sample the search space of nuisance hyperparameters as densely as possible. Doing so increases confidence that the search procedure will find any good settings for the nuisance hyperparameters that happen to exist in your search space. Otherwise, you might make unfair comparisons between values of the scientific parameters due to some values getting luckier with the sampling of the nuisance hyperparameters.

Unfortunately, improvements in any of these three dimensions require either of the following:

• Increasing the number of trials, and therefore increasing the resource cost.
• Finding a way to save resources in one of the other dimensions.

Every problem has its own idiosyncrasies and computational constraints, so allocating resources across these three goals requires some level of domain knowledge. After running a study, always try to get a sense of whether the study tuned the nuisance hyperparameters well enough. That is, the study searched a large enough space extensively enough to fairly compare the scientific hyperparameters (as described in greater detail in the next section).

Learn from the experimental results

Recommendation: In addition to trying to achieve the original scientific goal of each group of experiments, go through a checklist of additional questions. If you discover issues, revise and rerun the experiments.

Ultimately, each group of experiments has a specific goal. You should evaluate the evidence the experiments provide toward that goal. However, if you ask the right questions, you can often find issues to correct before a given set of experiments can progress towards their original goal. If you don't ask these questions, you may draw incorrect conclusions.

Since running experiments can be expensive, you should also extract other useful insights from each group of experiments, even if these insights are not immediately relevant to the current goal.

Before analyzing a given set of experiments to make progress toward their original goal, ask yourself the following additional questions:

• Is the search space large enough? If the optimal point from a study is near the boundary of the search space in one or more dimensions, the search is probably not wide enough. In this case, run another study with an expanded search space.
• Have you sampled enough points from the search space? If not, run more points or be less ambitious in the tuning goals.
• What fraction of the trials in each study are infeasible? That is, which trials diverge, get really bad loss values, or fail to run at all because they violate some implicit constraint? When a very large fraction of points in a study are infeasible, adjust the search space to avoid sampling such points, which sometimes requires reparameterizing the search space. In some cases, a large number of infeasible points can indicate a bug in the training code.
• Does the model exhibit optimization issues?
• What can you learn from the training curves of the best trials? For example, do the best trials have training curves consistent with problematic overfitting?

If necessary, based on the answers to the preceding questions, refine the most recent study or group of studies to improve the search space and/or sample more trials, or take some other corrective action.

Once you have answered the preceding questions, you can evaluate the evidence the experiments provide towards your original goal; for example, evaluating whether a change is useful .

Identify bad search space boundaries

A search space is suspicious if the best point sampled from it is close to its boundary. You might find an even better point if you expand the search range in that direction.

To check search space boundaries, we recommend plotting completed trials on what we call basic hyperparameter axis plots . In these, we plot the validation objective value versus one of the hyperparameters (for example, learning rate). Each point on the plot corresponds to a single trial.

The validation objective value for each trial should usually be the best value it achieved over the course of training.

Figure 1: Examples of bad search space boundaries and acceptable search space boundaries.

The plots in Figure 1 show the error rate (lower is better) against the initial learning rate. If the best points cluster towards the edge of a search space (in some dimension), then you might need to expand the search space boundaries until the best observed point is no longer close to the boundary.

Often, a study includes "infeasible" trials that diverge or get very bad results (marked with red Xs in Figure 1). If all trials are infeasible for learning rates greater than some threshold value, and if the best performing trials have learning rates at the edge of that region, the model may suffer from stability issues preventing it from accessing higher learning rates .

Not sampling enough points in the search space

In general, it can be very difficult to know if the search space has been sampled densely enough. 🤖 Running more trials is better than running fewer trials, but more trials generates an obvious extra cost.

Since it is so hard to know when you have sampled enough, we recommend:

• Sampling what you can afford.
• Calibrating your intuitive confidence from repeatedly looking at various hyperparameter axis plots and trying to get a sense of how many points are in the "good" region of the search space.

Examine the training curves

Summary: Examining the loss curves is an easy way to identify common failure modes and can help you prioritize potential next actions.

In many cases, the primary objective of your experiments only requires considering the validation error of each trial. However, be careful when reducing each trial to a single number because that focus can hide important details about what's going on below the surface. For every study, we strongly recommend looking at the loss curves of at least the best few trials. Even if this is not necessary for addressing the primary experimental objective, examining the loss curves (including both training loss and validation loss) is a good way to identify common failure modes and can help you prioritize what actions to take next.

When examining the loss curves, focus on the following questions:

• Are any of the trials exhibiting problematic overfitting? Problematic overfitting occurs when the validation error starts increasing during training. In experimental settings where you optimize away nuisance hyperparameters by selecting the "best" trial for each setting of the scientific hyperparameters, check for problematic overfitting in at least each of the best trials corresponding to the settings of the scientific hyperparameters that you're comparing. If any of the best trials exhibits problematic overfitting, do either or both of the following:

  • Rerun the experiment with additional regularization techniques
  • Retune the existing regularization parameters before comparing the values of the scientific hyperparameters. This may not apply if the scientific hyperparameters include regularization parameters, since then it wouldn't be surprising if low-strength settings of those regularization parameters resulted in problematic overfitting.

  Reducing overfitting is often straightforward using common regularization techniques that add minimal code complexity or extra computation (for example, dropout regularization, label smoothing, weight decay). Therefore, it's usually trivial to add one or more of these to the next round of experiments. For example, if the scientific hyperparameter is "number of hidden layers" and the best trial that uses the largest number of hidden layers exhibits problematic overfitting, then we recommend retrying with additional regularization instead of immediately selecting the smaller number of hidden layers.

  Even if none of the "best" trials exhibit problematic overfitting, there might still be a problem if it occurs in any of the trials. Selecting the best trial suppresses configurations exhibiting problematic overfitting and favors those that don't. In other words, selecting the best trial favors configurations with more regularization. However, anything that makes training worse can act as a regularizer, even if it wasn't intended that way. For example, choosing a smaller learning rate can regularize training by hobbling the optimization process, but we typically don't want to choose the learning rate this way. Note that the "best" trial for each setting of the scientific hyperparameters might be selected in such a way that favors "bad" values of some of the scientific or nuisance hyperparameters.

• Is there high step-to-step variance in the training or validation error late in training? If so, this could interfere with both of the following:

  • Your ability to compare different values of the scientific hyperparameters. That's because each trial randomly ends on a "lucky" or "unlucky" step.
  • Your ability to reproduce the result of the best trial in production. That's because the production model might not end on the same "lucky" step as in the study.

  The most likely causes of step-to-step variance are:

  • Batch variance due to randomly sampling examples from the training set for each batch.
  • Small validation sets
  • Using a learning rate that's too high late in training.

  Possible remedies include:

  • Increasing the batch size.
  • Obtaining more validation data.
  • Using learning rate decay.
  • Using Polyak averaging.

• Are the trials still improving at the end of training? If so, you are in the "compute bound" regime and may benefit from increasing the number of training steps or changing the learning rate schedule.

• Has performance on the training and validation sets saturated long before the final training step? If so, this indicates that you are in the "not compute-bound" regime and that you may be able to decrease the number of training steps.

Beyond this list, many additional behaviors can become evident from examining the loss curves. For example, training loss increasing during training usually indicates a bug in the training pipeline.

Detecting whether a change is useful with isolation plots

Figure 2: Isolation plot that investigates the best value of weight decay for ResNet-50 trained on ImageNet.

Often, the goal of a set of experiments is to compare different values of a scientific hyperparameter. For example, suppose you want to determine the value of weight decay that results in the best validation error. An isolation plot is a special case of the basic hyperparameter axis plot. Each point on an isolation plot corresponds to the performance of the best trial across some (or all) of the nuisance hyperparameters. In other words, plot the model performance after "optimizing away" the nuisance hyperparameters.

An isolation plot simplifies performing an apples-to-apples comparison between different values of the scientific hyperparameter. For example, the isolation plot in Figure 2 reveals the value of weight decay that produces the best validation performance for a particular configuration of ResNet-50 trained on ImageNet.

If the goal is to determine whether to include weight decay at all, then compare the best point from this plot against the baseline of no weight decay. For a fair comparison, the baseline should also have its learning rate equally well tuned.

When you have data generated by (quasi)random search and are considering a continuous hyperparameter for an isolation plot, you can approximate the isolation plot by bucketing the x-axis values of the basic hyperparameter axis plot and taking the best trial in each vertical slice defined by the buckets.

Automate generically useful plots

The more effort it is to generate plots, the less likely you are to look at them as much as you should. Therefore, we recommend setting up your infrastructure to automatically produce as many plots as possible. At a minimum, we recommend automatically generating basic hyperparameter axis plots for all hyperparameters that you vary in an experiment.

Additionally, we recommend automatically producing loss curves for all trials. Furthermore, we recommend making it as easy as possible to find the best few trials of each study and to examine their loss curves.

You can add many other useful potential plots and visualizations. To paraphrase Geoffrey Hinton :

Every time you plot something new, you learn something new.

Determine whether to adopt the candidate change

Summary: When deciding whether to make a change to our model or training procedure or adopt a new hyperparameter configuration, note the different sources of variation in your results.

When trying to improve a model, a particular candidate change might initially achieve a better validation error compared to an incumbent configuration. However, repeating the experiment might demonstrate no consistent advantage. Informally, the most important sources of inconsistent results can be grouped into the following broad categories:

• Training procedure variance, retrain variance, or trial variance : the variation between training runs that use the same hyperparameters but different random seeds. For example, different random initializations, training data shuffles, dropout masks, patterns of data augmentation operations, and orderings of parallel arithmetic operations are all potential sources of trial variance.
• Hyperparameter search variance, or study variance : the variation in results caused by our procedure to select the hyperparameters. For example, you might run the same experiment with a particular search space but with two different seeds for quasi-random search and end up selecting different hyperparameter values.
• Data collection and sampling variance : the variance from any sort of random split into training, validation, and test data or variance due to the training data generation process more generally.

True, you can compare validation error rates estimated on a finite validation set using fastidious statistical tests. However, often the trial variance alone can produce statistically significant differences between two different trained models that use the same hyperparameter settings.

We are most concerned about study variance when trying to make conclusions that go beyond the level of an individual point in hyperparameters space. The study variance depends on the number of trials and the search space. We have seen cases where the study variance is larger than the trial variance and cases where it is much smaller. Therefore, before adopting a candidate change, consider running the best trial N times to characterize the run-to-run trial variance. Usually, you can get away with only recharacterizing the trial variance after major changes to the pipeline, but you might need fresher estimates in some cases. In other applications, characterizing the trial variance is too costly to be worth it.

Although you only want to adopt changes (including new hyperparameter configurations) that produce real improvements, demanding complete certainty that a given change helps isn't the right answer either. Therefore, if a new hyperparameter point (or other change) gets a better result than the baseline (taking into account the retrain variance of both the new point and the baseline as best as you can), then you probably should adopt it as the new baseline for future comparisons. However, we recommend only adopting changes that produce improvements that outweigh any complexity they add.

After exploration concludes

Summary: Bayesian optimization tools are a compelling option once you're done searching for good search spaces and have decided what hyperparameters are worth tuning.

Eventually, your priorities will shift from learning more about the tuning problem to producing a single best configuration to launch or otherwise use. At that point, there should be a refined search space that comfortably contains the local region around the best observed trial and has been adequately sampled. Your exploration work should have revealed the most essential hyperparameters to tune and their sensible ranges that you can use to construct a search space for a final automated tuning study using as large a tuning budget as possible.

Since you no longer care about maximizing insight into the tuning problem, many of the advantages of quasi-random search no longer apply. Therefore, you should use Bayesian optimization tools to automatically find the best hyperparameter configuration. Open-Source Vizier implements a variety of sophisticated algorithms for tuning ML models, including Bayesian Optimization algorithms.

Suppose the search space contains a non-trivial volume of divergent points , meaning points that get NaN training loss or even training loss many standard deviations worse than the mean. In this case, we recommend using black-box optimization tools that properly handle trials that diverge. (See Bayesian Optimization with Unknown Constraints for an excellent way to deal with this issue.) Open-Source Vizier has supports for marking divergent points by marking trials as infeasible, although it may not use our preferred approach from Gelbart et al. , depending on how it is configured.

After exploration concludes, consider checking the performance on the test set. In principle, you could even fold the validation set into the training set and retrain the best configuration found with Bayesian optimization. However, this is only appropriate if there won't be future launches with this specific workload (for example, a one-time Kaggle competition).