Une approche scientifique pour améliorer les performances des modèles

Pour les besoins du présent document:

L'objectif final du développement du machine learning est de maximiser l'utilité du modèle déployé.

Vous pouvez généralement utiliser les mêmes étapes et principes de base dans cette section pour tout problème de ML.

Cette section repose sur les hypothèses suivantes:

• Vous disposez déjà d'un pipeline d'entraînement complet, ainsi que d'une configuration qui obtient un résultat raisonnable.
• Vous disposez de suffisamment de ressources de calcul pour réaliser des tests de réglage pertinents et pour exécuter au moins plusieurs tâches d'entraînement en parallèle.

Stratégie de réglage incrémentiel

Recommandation: commencez avec une configuration simple. Apportez ensuite des améliorations de manière incrémentielle tout en apportant des insights sur le problème. Assurez-vous que toute amélioration repose sur des preuves solides.

Nous partons du principe que votre objectif est de trouver une configuration qui maximise les performances de votre modèle. Parfois, votre objectif est de maximiser l'amélioration du modèle dans un délai fixe. Dans les autres cas, vous pouvez continuer à améliorer le modèle indéfiniment, par exemple en améliorant continuellement un modèle utilisé en production.

En principe, vous pouvez maximiser les performances en utilisant un algorithme pour effectuer une recherche automatique dans tout l'espace des configurations possibles, mais cette option n'est pas pratique. L'espace des configurations possibles est extrêmement vaste et il n'existe pas encore d'algorithmes suffisamment sophistiqués pour effectuer des recherches efficaces dans cet espace sans intervention humaine. La plupart des algorithmes de recherche automatisés reposent sur un espace de recherche conçu manuellement qui définit l'ensemble des configurations à rechercher. Ces espaces de recherche peuvent avoir un peu d'importance.

Le moyen le plus efficace de maximiser les performances consiste à commencer par une configuration simple, puis à ajouter progressivement des fonctionnalités, puis à apporter des améliorations tout en apportant des informations sur le problème.

Nous vous recommandons d'utiliser des algorithmes de recherche automatisés lors de chaque réglage et de mettre à jour les espaces de recherche en continu à mesure que vous comprenez le fonctionnement. Au fil de votre exploration, vous trouverez naturellement de meilleures configurations et, par conséquent, votre "meilleur" modèle s'améliorera en permanence.

Le terme "lancer" fait référence à une mise à jour de notre meilleure configuration (qui peut correspondre ou non à un lancement réel d'un modèle de production). Pour chaque "lancement", vous devez vous assurer que la modification est basée sur une preuve forte, et pas simplement sur une probabilité aléatoire basée sur une configuration porte-bonheur, afin d'éviter de complexifier inutilement le pipeline d'entraînement.

De manière générale, notre stratégie de réglage incrémentiel implique de répéter les quatre étapes suivantes:

1. Choisissez un objectif pour la prochaine série de tests. Assurez-vous que la portée de l'objectif est appropriée.
2. Concevez la prochaine série de tests. Concevez et exécutez un ensemble de tests qui progressent dans le but.
3. Inspirez-vous des résultats du test. Comparer le test à une checklist.
4. Déterminez s'il convient d'adopter la modification candidate.

Le reste de cette section détaille cette stratégie.

Choisissez un objectif pour la prochaine série de tests

Si vous essayez d'ajouter plusieurs caractéristiques ou de répondre à plusieurs questions à la fois, vous ne pourrez peut-être pas dissocier les effets distincts sur les résultats. Voici quelques exemples d'objectifs:

• Essayez d'améliorer le pipeline (par exemple, un nouveau régulateur, un choix de prétraitement, etc.).
• Comprendre l'impact d'un hyperparamètre particulier du modèle (par exemple, la fonction d'activation)
• Réduisez les erreurs de validation.

Privilégier la progression à long terme plutôt que les améliorations à apporter aux erreurs de validation à court terme

Résumé: la plupart du temps, votre objectif principal est de mieux comprendre le problème de réglage.

Nous vous recommandons de passer la majeure partie de votre temps à vous familiariser avec le problème et relativement peu de temps consacré à l'optimisation des performances sur l'ensemble de validation. En d'autres termes, consacrez la plupart de votre temps à l'exploration et un petit nombre à l'exploitation. Il est essentiel de comprendre le problème pour maximiser les performances finales. Prioriser les insights plutôt que les gains à court terme permet de:

• Évitez de lancer des modifications inutiles qui se produisent dans des exécutions performantes à l'aide d'un accident historique.
• Identifiez les hyperparamètres auxquels l'erreur de validation est le plus sensible, quels hyperparamètres interagissent le plus et doivent donc être réglés ensemble, et quels hyperparamètres sont relativement insensibles aux autres modifications et peuvent donc être corrigés dans les tests suivants.
• Suggérez de nouvelles fonctionnalités potentielles à essayer, telles que de nouveaux régulateurs en cas de surapprentissage.
• Identifiez les fonctionnalités qui ne sont pas utiles et qui peuvent donc être supprimées, ce qui réduit la complexité des tests futurs.
• Détectez à quel moment les améliorations apportées au réglage des hyperparamètres ont probablement été saturées.
• Réduisez nos espaces de recherche autour de la valeur optimale pour améliorer l'efficacité des réglages.

Vous comprendrez enfin le problème. Vous pouvez ensuite vous concentrer uniquement sur l'erreur de validation, même si les tests ne sont pas extrêmement instructifs sur la structure du problème de réglage.

Concevoir la prochaine série de tests

Résumé: identifiez les hyperparamètres scientifiques, nuisibles et fixes pour l'objectif expérimental. Créez une séquence d'études pour comparer différentes valeurs d'hyperparamètres scientifiques tout en optimisant les nuisances nuisibles. Choisissez l'espace de recherche des hyperparamètres nuisibles pour équilibrer les coûts des ressources avec la valeur scientifique.

Identifier les hyperparamètres scientifiques, nuisibles et fixes

Pour un objectif donné, tous les hyperparamètres appartiennent à l'une des catégories suivantes:

• Les hyperparamètres scientifiques dont l'effet sur les performances du modèle est ce que vous essayez de mesurer
• Les hyperparamètres de nuisance sont ceux qui doivent être optimisés afin de comparer équitablement les différentes valeurs des hyperparamètres scientifiques. Les hyperparamètres de nuisance sont semblables aux paramètres de nuisance dans les statistiques.
• Les hyperparamètres fixes ont des valeurs constantes dans la série de tests en cours. Les valeurs d'hyperparamètres fixes ne doivent pas changer lorsque vous comparez différentes valeurs d'hyperparamètres scientifiques. En corrigeant certains hyperparamètres pour un ensemble de tests, vous devez accepter que les conclusions tirées des tests ne soient pas valides pour les autres paramètres des hyperparamètres fixes. En d'autres termes, les hyperparamètres fixes créent des mises en garde concernant les conclusions que vous tirez des tests.

Par exemple, supposons que votre objectif soit le suivant:

Déterminez si un modèle comportant plus de couches cachées présente une erreur de validation plus faible.

Dans ce cas :

• Le taux d'apprentissage est un hyperparamètre gênant, car vous ne pouvez comparer objectivement des modèles avec un nombre différent de couches cachées que si le taux d'apprentissage est réglé séparément pour chaque nombre de couches masquées. (Le taux d'apprentissage optimal dépend généralement de l'architecture du modèle.)
• La fonction d'activation peut être un hyperparamètre fixe si vous avez déterminé dans les précédents tests que la meilleure fonction d'activation n'est pas sensible à la profondeur du modèle. Vous pouvez également limiter votre concordance concernant le nombre de couches masquées pour couvrir cette fonction d'activation. Il peut également s'agir d'un hyperparamètre nuisible si vous êtes prêt à le régler séparément pour chaque nombre de couches masquées.

Un hyperparamètre scientifique peut être un hyperparamètre scientifique, un hyperparamètre inutile ou un hyperparamètre fixe. La désignation de l'hyperparamètre change en fonction de l'objectif expérimental. Par exemple, la fonction d'activation peut être l'une des suivantes:

• Hyperphysique scientifique: la fonction ReLU ou est-elle plus adaptée à notre problème ?
• Hypernuisance: le meilleur modèle à cinq couches est-il préférable au meilleur modèle à six couches lorsque vous autorisez plusieurs fonctions d'activation différentes ?
• Hyperparamètre fixe: pour les réseaux ReLU, l'ajout d'une normalisation par lot à une position spécifique peut-il aider ?

Lorsque vous concevez une nouvelle série de tests:

1. Identifier les hyperparamètres scientifiques pour l'objectif expérimental À ce stade, vous pouvez considérer tous les autres hyperparamètres comme des hyperparamètres de nuisance.
2. Convertissez certains hyperparamètres nuisibles en hyperparamètres fixes.

Avec des ressources illimitées, vous laisseriez tous les hyperparamètres non scientifiques comme hyperparamètres nuisibles, afin que les conclusions que vous tirez de vos tests ne soient pas mises en garde concernant les valeurs d'hyperparamètres fixes. Toutefois, plus vous essayez de régler des hyperparamètres nuisibles, plus vous risquez de les régler mal pour chaque paramètre des hyperparamètres scientifiques et d'obtenir des conclusions erronées lors de vos tests. Comme décrit dans une section ultérieure, vous pouvez contourner ce risque en augmentant le budget de calcul. Cependant, votre budget de ressources maximal est souvent inférieur à celui nécessaire pour régler tous les hyperparamètres non scientifiques.

Nous vous recommandons de convertir un hyperparamètre nuisible en un hyperparamètre fixe lorsque les mises en garde introduites par la correction sont moins coûteuses que l'ajout d'un hyperparamètre inutile. Plus un hyperparamètre nuisible interagit avec les hyperparamètres scientifiques, plus sa valeur peut être endommagée. Par exemple, la meilleure valeur de l'intensité de la décomposition de pondération dépend généralement de la taille du modèle. Par conséquent, il ne serait pas très pertinent de comparer différentes tailles de modèle en supposant qu'une seule valeur spécifique de la dépréciation des pondérations soit appliquée.

Certains paramètres de l'optimiseur

En règle générale, certains hyperparamètres de l'optimiseur (par exemple, le taux d'apprentissage, le seuil, les paramètres de planification du taux d'apprentissage, les versions bêta d'Adam, etc.) sont très gênants, car ils ont tendance à interagir le plus avec d'autres modifications. Ces hyperparamètres d'optimiseur sont rarement scientifiques, car un objectif tel que "quel est le meilleur taux d'apprentissage pour le pipeline actuel" ne fournit pas beaucoup d'insights. En effet, le meilleur paramètre peut quand même être modifié avec le changement de pipeline suivant.

Vous pouvez parfois corriger certains hyperparamètres de l'optimiseur en raison de contraintes au niveau des ressources ou de preuves particulièrement importantes qu'ils n'interagissent pas avec les paramètres scientifiques. Cependant, vous devez généralement partir du principe que vous devez régler les hyperparamètres de l'optimiseur séparément pour effectuer des comparaisons équitables entre les différents paramètres d'hyperparamètres scientifiques et que vous ne devez donc pas résoudre ce problème. De plus, il n'y a pas de raison prioritaire de privilégier une valeur d'hyperparamètre d'optimiseur. Par exemple, les valeurs d'hyperparamètres de l'optimiseur n'ont généralement aucune incidence sur le coût de calcul des passes vers l'avant ou des gradients.

Le choix de l'optimiseur

L'optimiseur est généralement le suivant:

• un hyperparamètre scientifique
• un hyperparamètre fixe

Un optimiseur est un hyperparamètre scientifique si votre objectif expérimental consiste à effectuer des comparaisons équitables entre plusieurs optimiseurs différents. Exemple :

Déterminez quel optimiseur génère l'erreur de validation la plus faible au cours d'un nombre d'étapes donné.

Vous pouvez également transformer l'optimiseur en hyperparamètre fixe pour diverses raisons, y compris les suivantes:

• Des tests précédents suggèrent que le meilleur optimiseur pour votre problème de réglage n'est pas sensible aux hyperparamètres scientifiques actuels.
• Vous préférez comparer les valeurs des hyperparamètres scientifiques avec cet optimiseur, car ses courbes d'entraînement sont plus faciles à comprendre.
• Vous préférez utiliser cet optimiseur, car il utilise moins de mémoire que les autres.

Hyperparamètres de régularisation

Les hyperparamètres introduits par une technique de régularisation sont généralement des hyperparamètres de nuisance. Toutefois, le choix d'inclure ou non la technique de régularisation est un hyperparamètre scientifique ou fixe.

Par exemple, la régularisation par abandon accroît la complexité du code. Par conséquent, au moment de décider d'inclure la régularisation par abandon, vous pouvez définir "aucun abandon" comme "abandon" comme un hyperparamètre scientifique, mais un taux d'abandon élevé. Si vous décidez d'ajouter une régularisation par abandon au pipeline en fonction de ce test, le taux d'abandon sera un hyperparamètre nuisible dans les tests suivants.

Hyperparamètres architecturaux

Les hyperparamètres d'architecture sont souvent des hyperparamètres scientifiques ou fixes, car les modifications d'architecture peuvent affecter les coûts de diffusion et d'entraînement, la latence et les besoins en mémoire. Par exemple, le nombre de couches est généralement un hyperparamètre scientifique ou fixe, car il a tendance à avoir des conséquences dramatiques sur la vitesse d'entraînement et l'utilisation de la mémoire.

Dépendances vis-à-vis des hyperparamètres scientifiques

Dans certains cas, les ensembles de nuisances et d'hyperparamètres fixes dépendent des valeurs des hyperparamètres scientifiques. Supposons que vous essayiez de déterminer quel optimiseur dans la dynamique Nesterov et Adam produit l'erreur de validation la plus faible. Dans ce cas :

• L'hyperparamètre scientifique est l'optimiseur, qui accepte des valeurs {"Nesterov_momentum", "Adam"}.
• La valeur optimizer="Nesterov_momentum" introduit les hyperparamètres {learning_rate, momentum}, qui peuvent être problématiques ou des hyperparamètres fixes.
• La valeur optimizer="Adam" introduit les hyperparamètres {learning_rate, beta1, beta2, epsilon}, qui peuvent être problématiques ou des hyperparamètres fixes.

Les hyperparamètres qui ne sont présents que pour certaines valeurs d'hyperparamètres scientifiques sont appelés hyperparamètres conditionnels. Supposons que deux hyperparamètres conditionnels soient identiques, car ils portent le même nom. Dans l'exemple précédent, l'hyperparamètre conditionnel appelé learning_rate est un hyperparamètre différent pour optimizer="Nesterov_momentum" et optimizer="Adam". Son rôle est semblable (bien que pas identique) dans les deux algorithmes, mais la plage de valeurs qui fonctionne bien dans chacun des optimiseurs est généralement différente de plusieurs ordres de grandeur.

Créer un ensemble d'études

Après avoir identifié les hyperparamètres scientifiques et problématiques, vous devez concevoir une étude ou une séquence d'études pour atteindre l'objectif expérimental. Une étude spécifie un ensemble de configurations d'hyperparamètres à exécuter pour une analyse ultérieure. Chaque configuration est appelée essai. Pour créer une étude, vous devez généralement choisir ce qui suit:

• Les hyperparamètres qui varient selon les essais.
• Les valeurs de ces hyperparamètres (l'espace de recherche)
• Nombre d'essais.
• Algorithme de recherche automatisé pour échantillonner autant d'essais à partir de l'espace de recherche.

Vous pouvez également créer une étude en spécifiant manuellement l'ensemble des configurations d'hyperparamètres.

Ces études visent à:

• Exécutez le pipeline avec différentes valeurs d'hyperparamètres scientifiques.
• "Optimiser à distance" (ou "optimiser") les hyperparamètres problématiques, afin que les comparaisons entre différentes valeurs des hyperparamètres scientifiques soient aussi équitables que possible

Dans le cas le plus simple, vous devez effectuer une étude distincte pour chaque configuration des paramètres scientifiques, où chaque étude réglera les hyperparamètres des nuisances. Par exemple, si votre objectif est de sélectionner le meilleur optimiseur entre Nesterov et Adam, vous pouvez créer deux études:

• Une étude dans laquelle optimizer="Nesterov_momentum" et les hyperparamètres nuisibles sont {learning_rate, momentum}
• Une autre étude dans laquelle optimizer="Adam" et les hyperparamètres nuisibles sont {learning_rate, beta1, beta2, epsilon}.

Pour comparer les deux optimiseurs, sélectionnez l'essai le plus performant de chaque étude.

Vous pouvez utiliser n'importe quel algorithme d'optimisation sans gradient, y compris des méthodes telles que l'optimisation bayésienne ou les algorithmes évolutifs, pour optimiser les hyperparamètres nuisibles. Nous préférons toutefois utiliser la recherche quasi aléatoire lors de l'exploration du réglage en raison de divers avantages de ce paramètre. Une fois l'exploration terminée, nous vous recommandons d'utiliser un logiciel d'optimisation bayésien de pointe (le cas échéant).

Prenons un cas plus compliqué où vous souhaitez comparer un grand nombre de valeurs d'hyperparamètres scientifiques, mais qu'il n'est pas pratique d'effectuer autant d'études indépendantes. Dans ce cas, vous pouvez effectuer les opérations suivantes:

• Incluez les paramètres scientifiques dans le même espace de recherche que les hyperparamètres indésirables.
• Utilisez un algorithme de recherche pour échantillonner les valeurs des hyperparamètres scientifiques et nuisibles dans une seule étude.

Si vous adoptez cette approche, les hyperparamètres conditionnels peuvent poser problème. Après tout, il est difficile de spécifier un espace de recherche, sauf si l'ensemble des hyperparamètres de nuisance est le même pour toutes les valeurs des hyperparamètres scientifiques. Dans ce cas, notre préférence pour l'utilisation d'une recherche quasi aléatoire plutôt que d'outils d'optimisation plus sophistiqués par cette boîte noire est encore plus forte, car elle garantit différentes valeurs d'hyperparamètres scientifiques à échantillonner de manière uniforme. Quel que soit l'algorithme de recherche, assurez-vous qu'il recherche les paramètres scientifiques de manière uniforme.

Trouvez le bon équilibre entre des tests d'information et des tests abordables.

Lorsque vous concevez une étude ou une séquence d'études, allouez un budget limité pour atteindre les trois objectifs suivants:

• Comparer suffisamment de valeurs différentes d'hyperparamètres scientifiques.
• Régler les hyperparamètres nuisibles sur un espace de recherche suffisamment important.
• Échantillonner les hyperparamètres des nuisances de façon suffisamment importante.

Plus ces trois objectifs seront pertinents, plus vous pourrez en tirer des enseignements. La comparaison d'un maximum de valeurs d'hyperparamètres scientifiques permet d'étendre la portée des insights obtenus.

Le fait d'inclure autant d'hyperparamètres de nuisance que possible et de permettre à chacun d'entre eux de cibler une plage aussi large que possible augmente la confiance qu'une "bonne" valeur des hyperparamètres de nuisance existe dans l'espace de recherche pour chaque configuration des hyperparamètres scientifiques. Sinon, vous pourriez effectuer des comparaisons injustes entre les valeurs d'hyperparamètres scientifiques si vous ne recherchez pas les régions possibles de l'espace d'hyperparamètres nuisibles, où de meilleures valeurs pourraient s'afficher pour certaines valeurs des paramètres scientifiques.

échantillonner l'espace de recherche des hyperparamètres nuisibles le plus fortement possible. De cette façon, vous serez plus sûr que la procédure de recherche trouve les bons paramètres d'hyperparamètres problématiques dans votre espace de recherche. Sinon, vous pourriez effectuer des comparaisons injustes entre les valeurs des paramètres scientifiques, car certaines valeurs auront plus de chance avec l'échantillonnage des hyperparamètres nuisibles.

Malheureusement, les améliorations apportées à l'une de ces trois dimensions nécessitent l'une des configurations suivantes:

• Augmenter le nombre d'essais et donc augmenter le coût des ressources.
• Trouver un moyen d'économiser les ressources dans l'une des autres dimensions

Chaque problème a ses propres idiosyncrasies et contraintes de calcul. Par conséquent, l'allocation de ressources entre ces trois objectifs nécessite un certain niveau de connaissance du domaine. Après avoir exécuté une étude, essayez toujours de savoir si elle a correctement réglé les hyperparamètres nuisibles. Autrement dit, l'étude a effectué une recherche sur un espace suffisamment important pour comparer équitablement les hyperparamètres scientifiques (comme décrit plus en détail dans la section suivante).

Tirer parti des résultats des tests

Recommandation: En plus d'essayer d'atteindre l'objectif scientifique d'origine de chaque groupe d'expérimentations, passez en revue une checklist de questions supplémentaires. Si vous découvrez des problèmes, modifiez-les et relancez-les.

En fin de compte, chaque groupe de tests a un objectif spécifique. Vous devez évaluer les preuves que les tests fournissent pour atteindre cet objectif. Cependant, si vous vous posez les bonnes questions, vous pouvez souvent trouver des problèmes à corriger avant qu'un ensemble de tests donné puisse progresser vers leur objectif d'origine. Si vous ne posez pas ces questions, vous risquez de dessiner des conclusions incorrectes.

L'exécution de tests peut être coûteuse. Vous devez donc également extraire d'autres insights utiles de chaque groupe de tests, même s'ils ne sont pas immédiatement pertinents par rapport à l'objectif actuel.

Avant d'analyser un ensemble donné de tests pour progresser vers leur objectif d'origine, posez-vous les questions supplémentaires suivantes:

• L'espace de recherche est-il suffisamment grand ? Si le point optimal d'une étude est proche de la limite de l'espace de recherche dans une ou plusieurs dimensions, la recherche n'est probablement pas assez large. Dans ce cas, exécutez une autre étude avec un espace de recherche étendu.
• Avez-vous échantillonné suffisamment de points dans l'espace de recherche ? Si ce n'est pas le cas, accordez plus de points ou soyez moins ambitieux dans vos objectifs de réglage.
• Quelle fraction des essais de chaque étude est impossible ? Autrement dit, quels essais essaient de diverger, obtiennent des valeurs de perte très mauvaises ou ne s'exécutent pas du tout, car ils ne respectent pas une contrainte implicite ? Lorsqu'une très grande partie des points d'une étude est impossible, ajustez l'espace de recherche pour éviter l'échantillonnage de ces points, qui nécessite parfois de redéfinir l'espace de recherche. Dans certains cas, un grand nombre de points infaisables peuvent indiquer un bug dans le code d'entraînement.
• Le modèle présente-t-il des problèmes d'optimisation ?
• Quels enseignements pouvez-vous tirer des courbes d'entraînement des meilleurs essais ? Par exemple, les meilleurs essais ont-ils une courbe d'entraînement cohérente avec le surapprentissage problématique ?

Si nécessaire, affinez les études ou groupes d'études les plus récents afin d'améliorer l'espace de recherche et/ou d'échantillonner d'autres essais, ou prenez d'autres mesures correctives en fonction des réponses aux questions précédentes.

Une fois que vous avez répondu aux questions précédentes, vous pouvez évaluer les preuves fournies par les tests pour atteindre votre objectif d'origine (par exemple, évaluer l'utilité d'un changement).

Identifier les limites de l'espace de recherche incorrect

Un espace de recherche est suspect si le meilleur point échantillonné à partir de celui-ci se trouve à proximité de sa limite. Il se peut que vous trouviez un point encore plus intéressant si vous élargissez la plage de recherche dans cette direction.

Pour vérifier les limites de l'espace de recherche, nous vous recommandons de tracer les essais terminés sur ce que nous appelons des graphiques d'axe des hyperparamètres de base. Ils représentent la valeur d'objectif de validation par rapport à l'un des hyperparamètres (par exemple, le taux d'apprentissage). Chaque point du graphique correspond à un seul essai.

La valeur de l'objectif de validation pour chaque essai doit généralement être la meilleure valeur qu'elle ait obtenue au cours de l'entraînement.

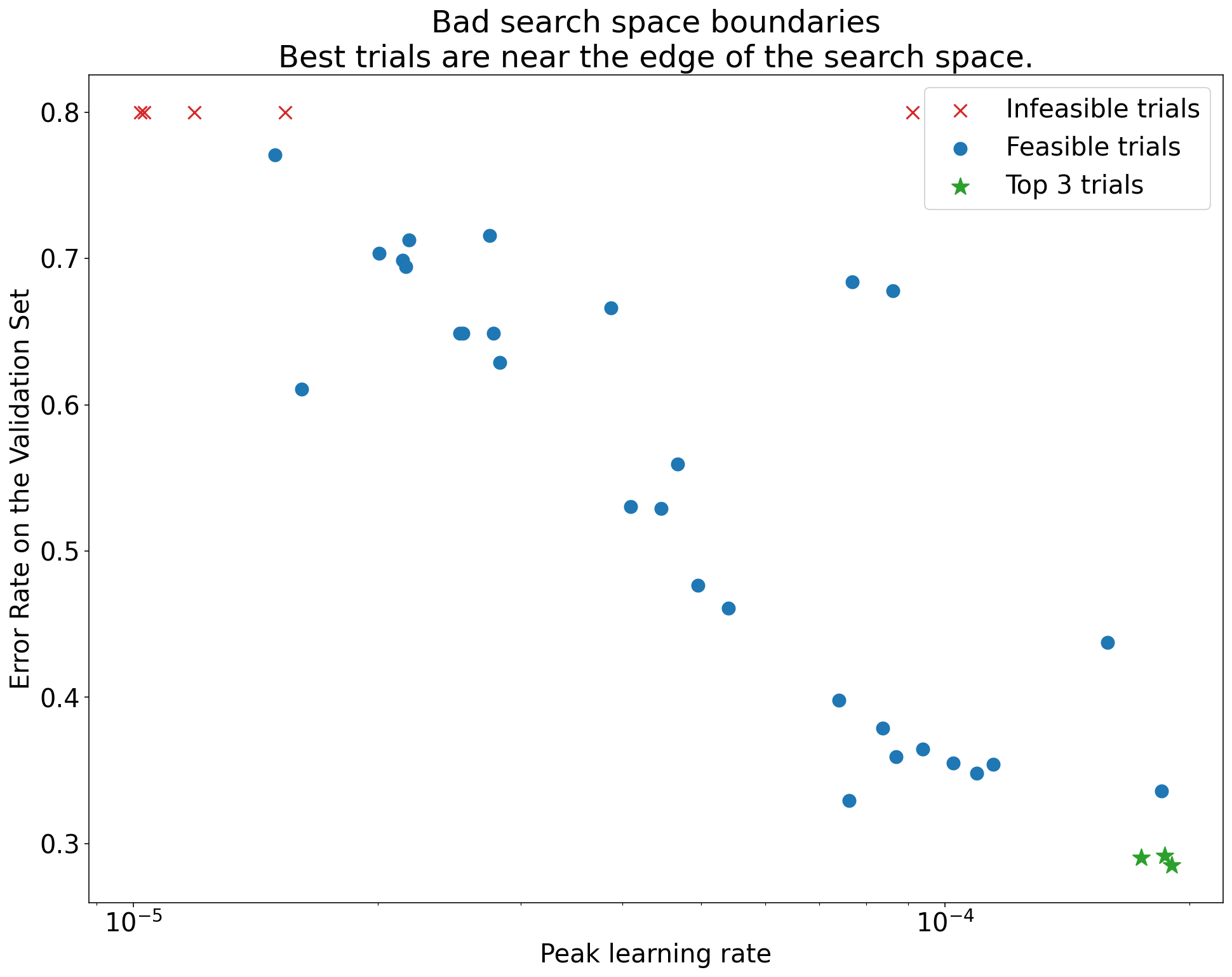
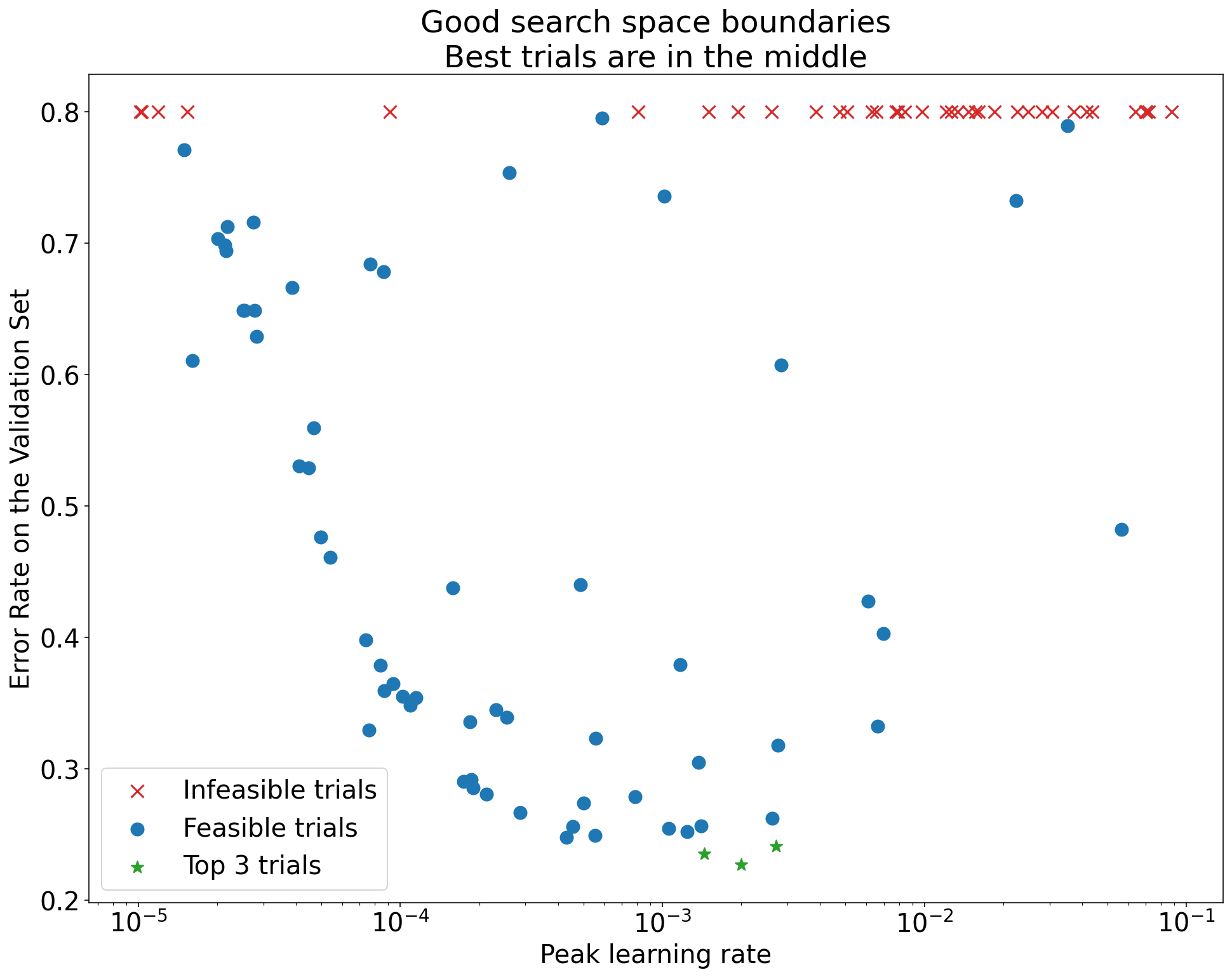
Figure 1:Exemples de limites d'espace de recherche incorrectes et de limites d'espace de recherche acceptables.

Les graphiques de la figure 1 indiquent le taux d'erreur (un pourcentage faible est préférable) par rapport au taux d'apprentissage initial. Si les meilleurs points sont regroupés vers le bord d'un espace de recherche (dans une dimension donnée), vous devrez peut-être étendre les limites de l'espace de recherche jusqu'à ce que le meilleur point observé ne soit plus proche de la limite.

Souvent, une étude inclut des essais "irréalisables" qui divergent ou obtiennent de très mauvais résultats (avec des "X" rouges dans la figure 1). Si tous les essais sont impossibles pour les taux d'apprentissage supérieurs à une certaine valeur de seuil, et si les essais les plus performants présentent des taux d'apprentissage à la périphérie de cette région, le modèle peut présenter des problèmes de stabilité qui l'empêchent d'accéder à des taux d'apprentissage plus élevés.

Échantillons de points insuffisants dans l'espace de recherche

En général, il peut être très difficile de savoir si l'espace de recherche a été suffisamment échantillonné. 💥 Il est préférable d'exécuter plus d'essais que de commencer, mais un plus grand nombre d'essais entraîne un coût supplémentaire évident.

Comme il est très difficile de savoir quand vous avez assez d'échantillons, nous vous recommandons:

• Échantillonnez ce que vous pouvez vous permettre.
• Pour calibrer votre confiance intuitive en examinant de manière répétée les tracés des différents hyperparamètres et en essayant d'avoir une idée du nombre de points dans la "bonne" région de l'espace de recherche.

Examiner les courbes d'entraînement

Résumé: l'examen des courbes de perte est un moyen simple d'identifier les modes de défaillance courants et peut vous aider à prioriser les actions potentielles.

Dans de nombreux cas, l'objectif principal de vos tests ne nécessite que l'erreur de validation de chaque essai. Toutefois, soyez prudent lorsque vous limitez chaque essai à un seul chiffre, car il peut masquer des détails importants sur ce qui se passe en dessous de la surface. Pour chaque étude, nous vous recommandons vivement de vérifier les courbes de perte du moins des meilleurs essais. Même si cela n'est pas nécessaire pour répondre à l'objectif expérimental principal, examiner les courbes de fonction de perte (y compris la perte d'entraînement et la perte de validation) est un bon moyen d'identifier les modes de défaillance courants et peut vous aider à hiérarchiser les mesures à prendre.

Lorsque vous examinez les courbes de fonction de perte, concentrez-vous sur les questions suivantes:

• L'un des essais présente-t-il un surapprentissage problématique ? Le surapprentissage pose problème lorsque l'erreur de validation commence à augmenter lors de l'entraînement. Dans les paramètres expérimentaux, où vous optimisez les hyperparamètres de nuisance en sélectionnant le "meilleur" essai pour chaque paramètre des hyperparamètres scientifiques, recherchez d'éventuels problèmes de surapprentissage dans au moins chacun des meilleurs essais correspondant aux paramètres des hyperparamètres scientifiques que vous comparez. Si l'un des meilleurs essais présente un surapprentissage problématique, effectuez l'une des opérations suivantes ou les deux:

  • Réexécuter le test avec des techniques de régularisation supplémentaires
  • Ajustez les paramètres de régularisation existants avant de comparer les valeurs des hyperparamètres scientifiques. Cela peut ne pas s'appliquer si les hyperparamètres scientifiques incluent des paramètres de régularisation, car il ne serait pas étonnant que les paramètres de force faible de ces paramètres de régularisation entraînent un surapprentissage problématique.

  Il est souvent facile de réduire le surapprentissage à l'aide de techniques de régularisation courantes qui ajoutent une complexité minimale au code ou des calculs supplémentaires (par exemple, la régularisation par abandon, le lissage d'étiquettes et la dépréciation du poids). Par conséquent, il est généralement simple d'en ajouter un ou plusieurs au prochain test. Par exemple, si l'hyperviseur scientifique est "nombre de couches masquées" et que le meilleur essai qui utilise le plus grand nombre de couches cachées présente un surapprentissage problématique, nous vous recommandons de réessayer avec une régularisation supplémentaire au lieu de sélectionner immédiatement le plus petit nombre de couches masquées.

  Même si aucun des "meilleurs" essais ne présente un problème de surapprentissage, un problème peut survenir s'il se produit dans l'un des essais. Sélectionner le meilleur essai supprime les configurations présentant un surapprentissage problématique et privilégie celles qui ne le sont pas. En d'autres termes, sélectionner le meilleur essai favorise les configurations avec plus de régularisation. Cependant, tout ce qui empire l'entraînement peut agir en tant que régulateur, même s'il n'était pas prévu ainsi. Par exemple, choisir un taux d'apprentissage plus faible permet de régulariser l'entraînement en encadrant le processus d'optimisation. Cependant, nous ne voulons généralement pas choisir ce taux. Notez que le "meilleur" essai pour chaque paramètre des hyperparamètres scientifiques peut être sélectionné de manière à favoriser les valeurs "mauvaises" pour certains hyperparamètres scientifiques.

• Y a-t-il une variance pas à pas en nombre d'erreurs d'entraînement ou de validation en fin d'entraînement ? Si oui, cela peut interférer avec les deux éléments suivants:

  • Capacité à comparer différentes valeurs des hyperparamètres scientifiques. Cela s'explique par le fait que chaque essai se termine de manière aléatoire par une étape "chance" ou "chance".
  • Capacité à reproduire le résultat du meilleur essai en production. En effet, le modèle de production peut ne pas se terminer par la même étape "chance " que dans l'étude.

  Voici les causes les plus probables de variance étape par étape:

  • La variance par lot due aux exemples d'échantillonnage aléatoire de l'ensemble d'entraînement pour chaque lot.
  • Petits ensembles de validation
  • Utiliser un taux d'apprentissage trop élevé en fin d'entraînement

  Voici les recours possibles:

  • Augmenter la taille de lot.
  • Obtenir plus de données de validation
  • Utiliser la dépréciation du taux d'apprentissage
  • Utiliser la moyenne de Polyak.

• Les essais s'améliorent-ils toujours à la fin de la formation ? Si tel est le cas, vous êtes dans le régime du "calcul lié" et vous pouvez augmenter le nombre d'étapes d'entraînement ou modifier la planification du taux d'apprentissage.

• Les performances des ensembles d'entraînement et de validation sont-elles bien saturées bien avant la dernière étape de l'entraînement ? Si tel est le cas, cela signifie que vous utilisez le régime "non lié au calcul" et que vous pouvez peut-être réduire le nombre d'étapes d'entraînement.

Au-delà de cette liste, de nombreux comportements supplémentaires peuvent devenir évidents en examinant les courbes de fonction de perte. Par exemple, une augmentation de la perte d'entraînement pendant l'entraînement indique généralement un bug dans le pipeline d'entraînement.

Déterminer si un changement est utile avec les graphiques d'isolation

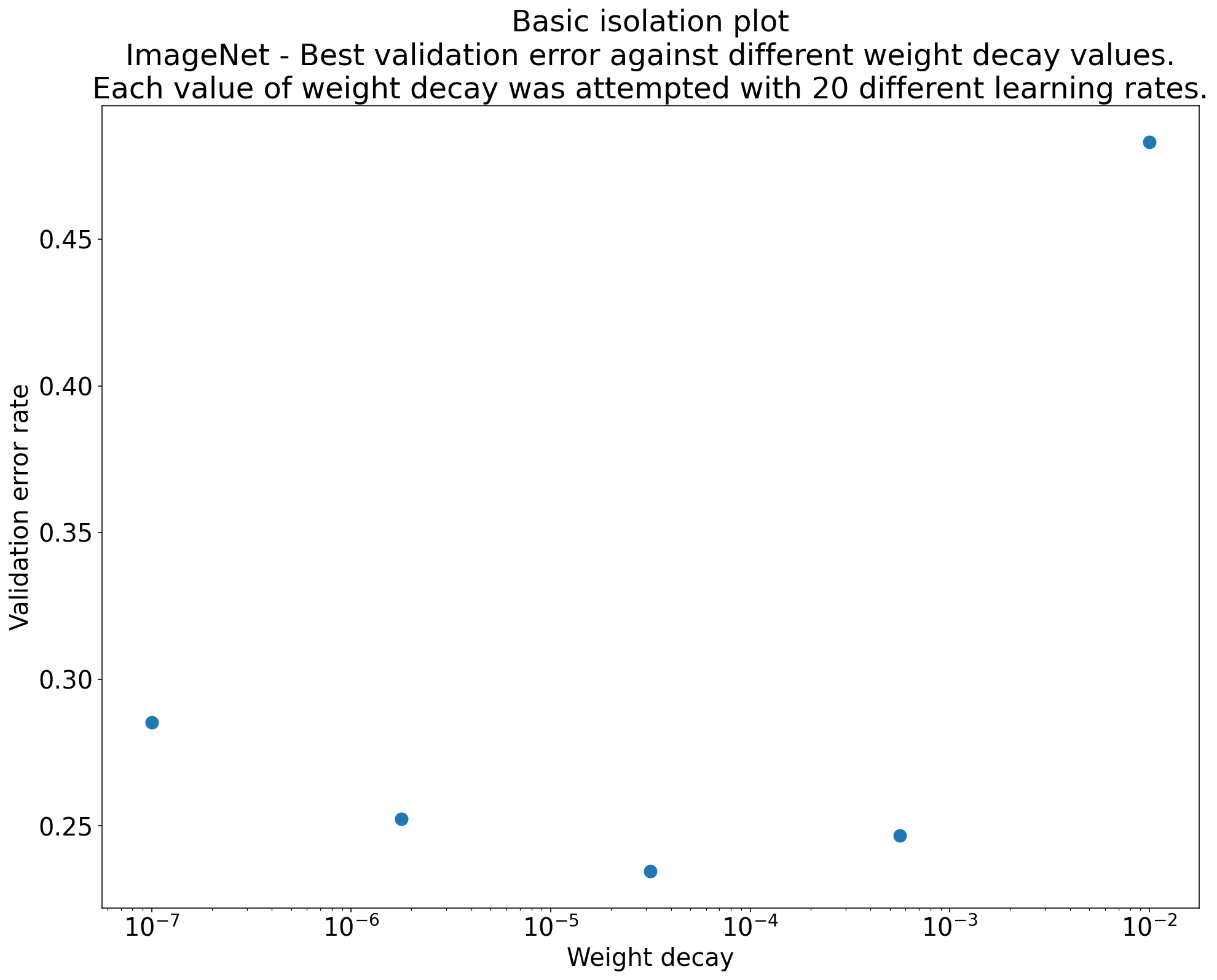
Figure 2:Graphique d'isolation qui examine la meilleure valeur de dépréciation du poids pour ResNet-50 entraîné sur ImageNet.

 

L'objectif d'un ensemble de tests est souvent de comparer différentes valeurs d'un hyperparamètre scientifique. Par exemple, supposons que vous souhaitiez déterminer la valeur de la dépréciation du poids qui génère la meilleure erreur de validation. Un graphique d'isolation est un cas particulier du graphique d'axe des hyperparamètres de base. Chaque point d'un graphique d'isolation correspond aux performances du meilleur essai sur certains (ou tous) des hyperparamètres nuisibles. En d'autres termes, tracez les performances du modèle après avoir optimisé les hyperparamètres indésirables.

Un graphique d'isolation simplifie l'exécution d'une comparaison équitable entre différentes valeurs de l'hyperparamètre scientifique. Par exemple, le graphique d'isolation de la figure 2 révèle la valeur de la dépréciation du poids qui produit les meilleures performances de validation pour une configuration particulière du ResNet-50 entraîné sur ImageNet.

Si l'objectif est de déterminer si la dégradation de la pondération doit être incluse, comparez le meilleur point de ce graphique à la référence de la dépréciation sans pondération. Pour une comparaison objective, le taux d'apprentissage de la référence doit également être parfaitement évalué.

Si vous disposez de données générées par la recherche aléatoire (quasi) et que vous envisagez d'utiliser un hyperparamètre continu pour un graphique d'isolation, vous pouvez obtenir une approximation du graphique en binnant les valeurs de l'axe des abscisses du graphique d'hyperparamètres de base et en effectuant le meilleur essai dans chaque tranche verticale définie par les buckets.

Automatiser les tracés génériques

Plus il est difficile de générer des tracés, moins vous êtes susceptible de les regarder autant que vous le souhaitez. Par conséquent, nous vous recommandons de configurer votre infrastructure pour qu'elle produise automatiquement un maximum de tracés. Au minimum, nous vous recommandons de générer automatiquement des graphiques d'axe de base pour tous les hyperparamètres que vous modifiez dans un test.

De plus, nous vous recommandons de générer automatiquement des courbes de fonction de perte pour tous les essais. De plus, nous vous recommandons de faciliter autant que possible le meilleur test de chaque étude et d'examiner leurs courbes de fonction de perte.

Vous pouvez ajouter de nombreux autres tracés et visualisations potentiels utiles. Pour compléter Geoffrey Hinton:

Chaque fois que vous tracez quelque chose de nouveau, vous apprenez quelque chose de nouveau.

Déterminer si le changement de candidat doit être adopté

Résumé: Lorsque vous décidez si vous souhaitez modifier le modèle ou la procédure d'entraînement, ou adopter une nouvelle configuration d'hyperparamètres, notez les différentes sources de variation dans vos résultats.

Lorsque vous essayez d'améliorer un modèle, une modification candidate spécifique peut initialement permettre d'obtenir une meilleure erreur de validation par rapport à une configuration déjà en place. Toutefois, répéter le test peut ne pas présenter d'avantage cohérent. De manière informelle, les sources les plus importantes de résultats incohérents peuvent être regroupées dans les grandes catégories suivantes:

• Variance de la procédure d'entraînement, variance de réentraînement ou variance d'essai : variation entre les exécutions d'entraînement qui utilisent les mêmes hyperparamètres, mais des graines aléatoires différentes. Par exemple, différentes initialisations aléatoires, brassages de données d'entraînement, masques d'abandon, modèles d'opérations d'augmentation des données et ordres d'opérations arithmétiques parallèles sont des sources potentielles de variance d'essai.
• Variance des recherches d'hyperparamètres ou variance d'étude: variation des résultats causée par notre procédure de sélection des hyperparamètres. Par exemple, vous pouvez exécuter le même test avec un espace de recherche particulier, mais avec deux valeurs initiales différentes pour la recherche quasi aléatoire et finir par sélectionner des valeurs d'hyperparamètres différentes.
• Collecte et variance d'échantillonnage de données: variance à partir de n'importe quelle sorte de répartition aléatoire entre les données d'entraînement, de validation et de test, ou la variance due au processus de génération de données d'entraînement de manière plus générale.

Vrai, vous pouvez comparer les taux d'erreur de validation estimés sur un ensemble de validation fini à l'aide de tests statistiques rapides. Cependant, seule la variance d'essai peut générer des différences statistiquement pertinentes entre deux modèles différents qui utilisent les mêmes paramètres d'hyperparamètres.

Lorsque nous essayons de tirer des conclusions qui dépassent le niveau d'un point individuel dans l'espace des hyperparamètres, nous nous soucions plus de la variance de l'étude. La variance de l'étude dépend du nombre d'essais et de l'espace de recherche. Nous avons constaté que la variance de l'étude était plus importante que la variance d'essai et que celle-ci était beaucoup plus faible. Par conséquent, avant d'adopter une modification candidate, envisagez d'exécuter les meilleurs N essais pour caractériser la variance d'un essai à exécuter. En règle générale, vous pouvez vous contenter de recaractèrer la variance d'essai après des modifications majeures du pipeline, mais vous aurez peut-être besoin d'estimations plus récentes dans certains cas. Dans d'autres applications, la définition de la variance d'essai est trop coûteuse.

Bien que vous ne souhaitiez adopter que les modifications (y compris les nouvelles configurations d'hyperparamètres) qui produisent des améliorations réelles, vous ne pouvez pas non plus vous demander la certitude qu'un changement donné est utile. Par conséquent, si un nouveau point d'hyperparamètres (ou une autre modification) obtient un meilleur résultat que la référence (en tenant compte de la variance de réentraînement du nouveau point et de la référence aussi précisément que possible), vous devriez probablement l'adopter comme nouvelle référence pour de futures comparaisons. Toutefois, nous vous recommandons de n'adopter que les modifications qui génèrent des améliorations qui compensent toute complexité supplémentaire.

Une fois l'exploration terminée

Résumé: les outils d'optimisation bayésiennes sont une option intéressante une fois que vous avez terminé de rechercher des espaces de recherche pertinents et que vous avez choisi les hyperparamètres à ajuster.

À terme, vos priorités ne seront plus liées aux problèmes de réglage, mais à la production d'une seule configuration optimale à lancer ou à utiliser. À ce stade, vous devriez disposer d'un espace de recherche raffiné contenant la région locale autour du meilleur essai observé et ayant été échantillonné de manière adéquate. Votre travail d'exploration doit avoir révélé les hyperparamètres les plus importants à régler, ainsi que leurs plages pertinentes que vous pouvez utiliser pour créer un espace de recherche dans le cadre d'une étude finale sur le réglage automatisé, avec un budget d'ajustement le plus élevé possible.

Étant donné que vous ne vous intéressez plus à l'optimisation des informations sur le problème de réglage, de nombreux avantages de la recherche quasi aléatoire ne s'appliquent plus. Par conséquent, vous devez utiliser les outils d'optimisation bayésiennes pour trouver automatiquement la meilleure configuration d'hyperparamètres. Open Source Vizier met en œuvre divers algorithmes sophistiqués pour régler les modèles de ML, y compris des algorithmes d'optimisation bayésienne.

Supposons que l'espace de recherche contienne un volume important de points divers, c'est-à-dire des points qui ont une perte d'entraînement NaN ou même une perte d'entraînement de nombreuses différences standards moins bonnes que la moyenne. Dans ce cas, nous vous recommandons d'utiliser des outils d'optimisation par boîte noire qui gèrent correctement les essais qui diffèrent. Pour plus d'informations sur la résolution de ce problème, consultez Optimisation bayésienne avec des contraintes inconnues. La solution Open Source Vizier permet de marquer des points divergents en marquant les essais comme impossibles à mettre en œuvre, bien qu'elle puisse ne pas utiliser notre approche préférée de Gelbart et al., selon sa configuration.

Une fois l'exploration terminée, vérifiez les performances sur l'ensemble de test. En principe, vous pouvez même intégrer l'ensemble de validation à l'ensemble d'entraînement et réentraîner la meilleure configuration trouvée avec l'optimisation bayésienne. Toutefois, cela ne convient que s'il n'y aura pas de lancement ultérieur avec cette charge de travail spécifique (par exemple, un concours Kaggle ponctuel).