Présentation des réseaux de neurones convolutifs
La construction de modèles pour la classification d'images a connu une avancée majeure avec la découverte qu'un réseau de neurones convolutif pouvait être utilisé pour extraire progressivement des représentations de niveau toujours plus élevé du contenu de l'image. Au lieu de prétraiter les données pour obtenir des caractéristiques dérivées telles que la texture et la forme, un réseau de neurones convolutif utilise uniquement les données de pixel brutes de l'image comme entrée, "apprend" comment extraire ces caractéristiques et, enfin, infère l'objet qu'elles constituent.
Pour commencer, le réseau de neurones convolutif reçoit une carte de caractéristiques d'entrée, c'est-à-dire une matrice tridimensionnelle dont la taille des deux premières dimensions correspond à la longueur et à la largeur en pixels des images. La taille de la troisième dimension est 3 (correspondant aux 3 canaux d'une image couleur: rouge, vert et bleu). Le réseau de neurones convolutif se compose d'une pile de modules, dont chacun effectue trois opérations.
1. Produit de convolution
Une convolution extrait les tuiles de la carte de caractéristiques d'entrée et leur applique des filtres pour calculer de nouvelles caractéristiques, produisant ainsi une carte de caractéristiques de sortie, ou caractéristique convoluée (dont la taille et la profondeur peuvent être différentes de celles de la carte de caractéristiques d'entrée). Les convolutions sont définies par deux paramètres:
- Taille des tuiles extraites (généralement 3x3 ou 5x5 pixels).
- Profondeur de la carte de caractéristiques de sortie, qui correspond au nombre de filtres appliqués
Lors d'une convolution, les filtres (matrices de la même taille que la tuile) se déplacent horizontalement et verticalement sur la grille de la carte de caractéristiques d'entrée, un pixel à la fois, extrayant chaque tuile correspondante (voir figure 3).
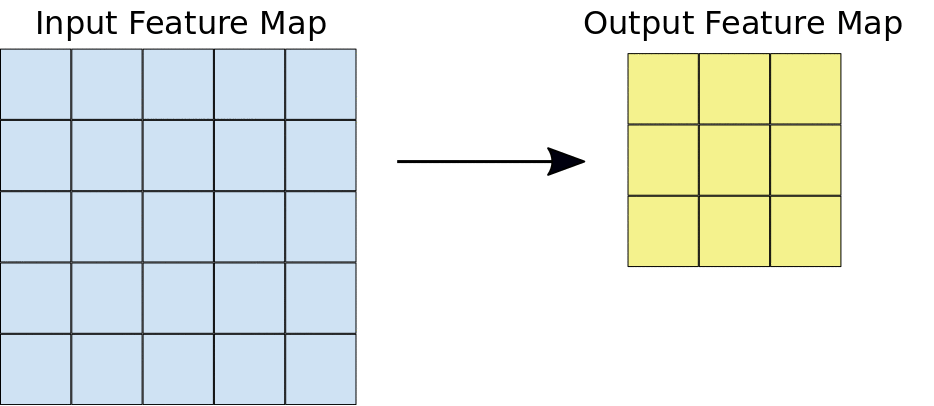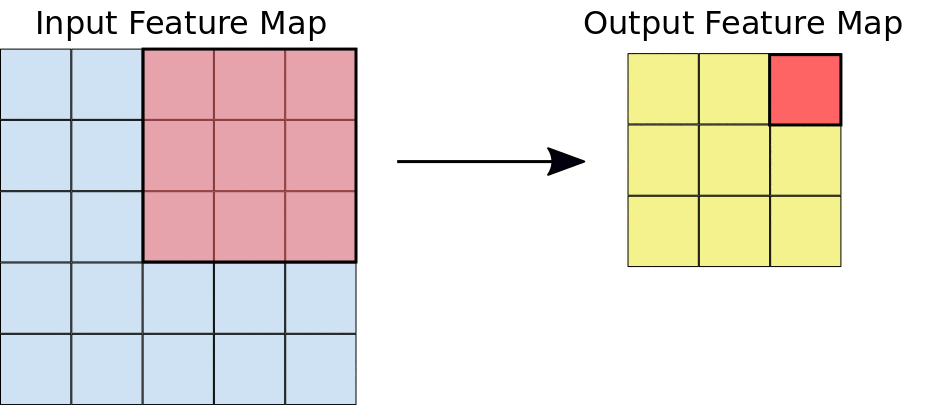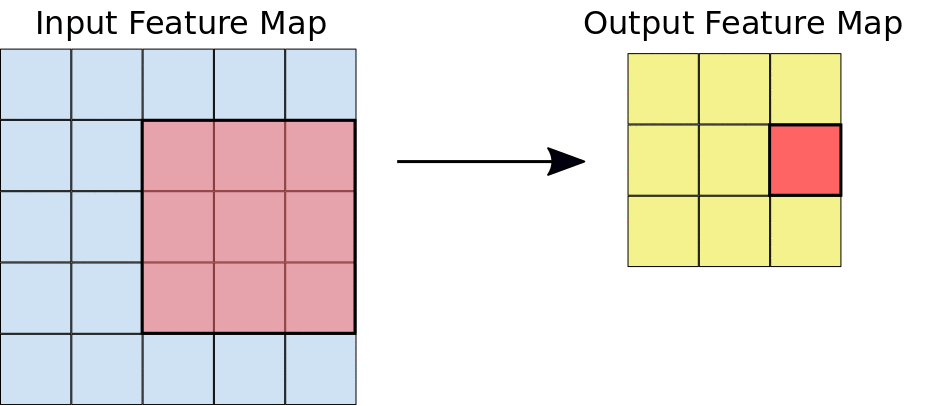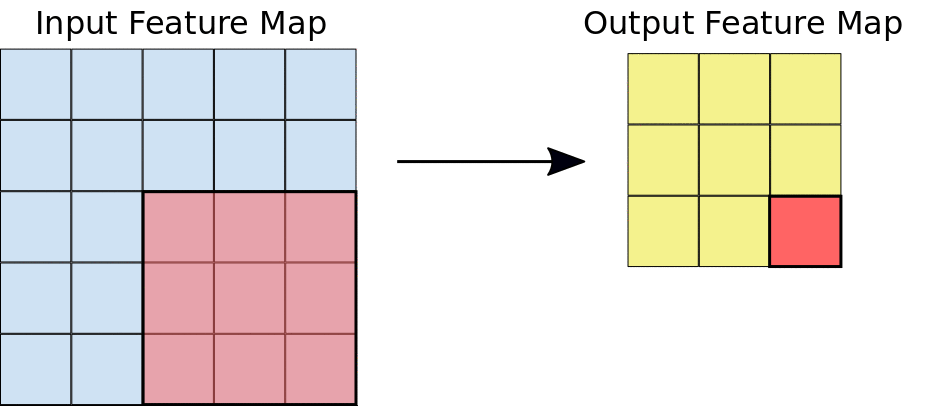Figure 3. une convolution 3x3 de profondeur 1 effectuée sur une carte de caractéristiques d'entrée 5x5, également de profondeur 1. Comme il y a neuf emplacements 3x3 possibles pour extraire les tuiles de la carte de caractéristiques 5x5, cette convolution génère une carte de caractéristiques de sortie 3x3.
Pour chaque paire filtre-tuile, le réseau de neurones convolutif multiplie la matrice de filtres par la matrice de tuiles au niveau des éléments, puis additionne tous les éléments de la matrice résultante pour obtenir une seule valeur. La valeur résultante de chaque paire filtre-tuile est ensuite insérée dans la matrice de caractéristique convoluée (voir les figures 4a et 4b).
Figure 4a. À gauche: une carte de caractéristiques d'entrée 5x5 (profondeur 1). À droite: une convolution 3x3 (profondeur 1).
Figure 4b. À gauche: la convolution 3x3 est appliquée à la carte de caractéristiques d'entrée 5x5. À droite: la caractéristique convoluée résultante. Cliquez sur une valeur de la carte de caractéristiques de sortie pour afficher la manière dont elle a été calculée.
Pendant l'apprentissage, le réseau de neurones convolutif "apprend" les valeurs optimales des matrices de filtre qui lui permettent d'extraire des caractéristiques significatives (textures, arêtes, formes) à partir de la carte de caractéristiques d'entrée. Le nombre de caractéristiques que le réseau de neurones convolutif peut extraire augmente avec le nombre de filtres (profondeur de la carte de caractéristiques de sortie) appliqués à l'entrée. Cependant, les filtres constituant la majorité des ressources déployées par le réseau de neurones convolutif, le temps d'apprentissage augmente aussi avec l'addition de filtres. De plus, chaque filtre ajouté au réseau fournit moins de valeurs incrémentielles que le précédent. C'est pourquoi les ingénieurs cherchent à construire des réseaux qui utilisent le nombre minimal de filtres requis pour extraire les caractéristiques nécessaires à une classification précise des images.
2. ReLU
Après chaque opération de convolution, le réseau de neurones convolutif applique une transformation ReLU (unité de rectification linéaire) à la fonction convoluée, afin d'introduire la non-linéarité dans le modèle. La fonction ReLU, \(F(x)=max(0,x)\), renvoie x pour toutes les valeurs de x > 0 et renvoie 0 pour toutes les valeurs de x ≤ 0.
3. Pooling
La transformation ReLU est suivie d'une étape de pooling, dans laquelle le réseau de neurones convolutif sous-échantillonne la caractéristique convoluée (pour réduire le temps de traitement), diminuant ainsi le nombre de dimensions de la carte de caractéristiques tout en préservant les informations les plus critiques de la caractéristique. Un algorithme couramment utilisé pour ce processus est le pooling maximal.
Le pooling maximal fonctionne de la même manière que la convolution. c'est-à-dire par déplacement sur la carte de caractéristiques et extraction des tuiles d'une taille spécifiée. Pour chaque tuile, la valeur maximale est transférée vers une nouvelle carte de caractéristiques et toutes les autres valeurs sont supprimées. Les opérations de pooling maximal utilisent deux paramètres:
- Taille du filtre de pooling maximal (généralement 2x2 pixels)
- Stride: distance, en pixels, séparant chaque tuile extraite. Contrairement à la convolution, dans laquelle les filtres se déplacent sur la carte de caractéristiques pixel par pixel, dans le pooling maximal, le pas détermine les emplacements où chaque tuile est extraite. Dans le cas d'un filtre 2x2, un pas de 2 signifie que l'opération de pooling maximal extrait toutes les tuiles 2x2 de la carte de caractéristiques (voir la figure 5) qui ne se chevauchent pas.
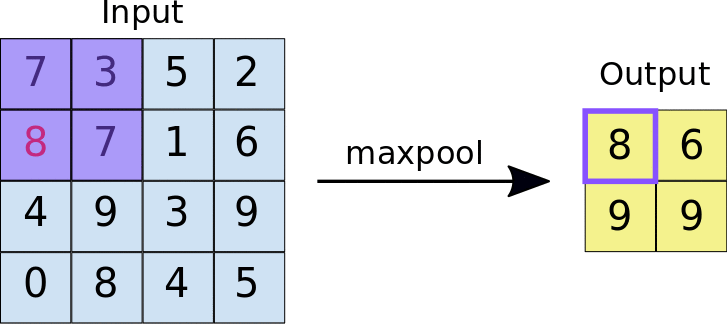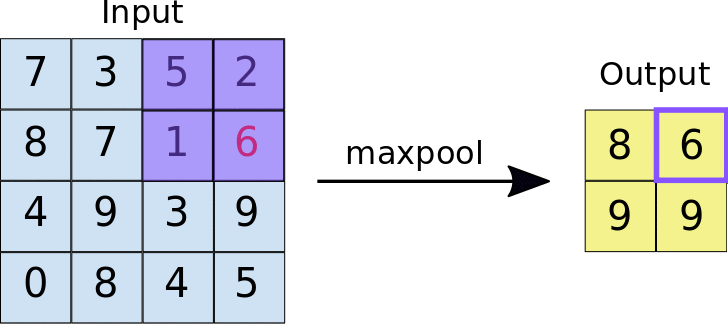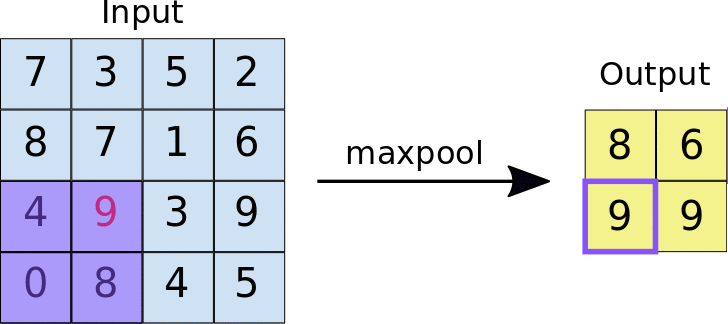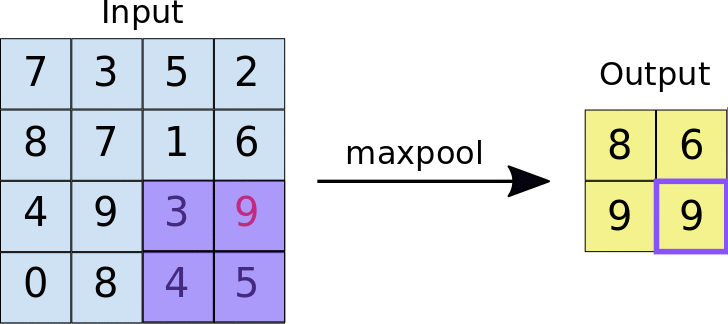
Figure 5. À gauche: pooling maximal sur une carte de caractéristiques 4x4 avec un filtre 2x2 et un pas de 2. À droite: résultat de l'opération de pooling maximal. Notez que la carte de caractéristiques résultante est maintenant de 2x2, et ne conserve que les valeurs maximales de chaque tuile.
Couches entièrement connectées
À la fin d'un réseau de neurones convolutif se trouvent une ou plusieurs couches entièrement connectées (lorsque deux couches sont "entièrement connectées", chaque nœud de la première couche est connecté à chaque nœud de la deuxième couche). Leur rôle est d'effectuer une classification basée sur les caractéristiques extraites par les convolutions. Généralement, la couche entièrement connectée finale contient une fonction d'activation softmax, qui fournit une valeur de probabilité comprise entre 0 et 1 pour chacune des étiquettes de classification que le modèle tente de prédire.
La figure 6 illustre la structure de bout en bout d'un réseau de neurones convolutif.
Figure 6. Le réseau de neurones représenté ici contient deux modules de convolution (convolution + ReLU + pooling) pour l'extraction de caractéristiques, et deux couches entièrement connectées pour la classification. D'autres réseaux de neurones convolutifs peuvent contenir plus ou moins de modules convolutifs et de couches entièrement connectées. Les ingénieurs réalisent souvent des expériences pour déterminer la configuration qui produit les meilleurs résultats pour leur modèle.